IN THIS CHAPTER

Calculating measures for center and spread

Interpreting your results properly

Compiling the results for a data discussion

Before data are organized in a chart or graph, the first step is to summarize them — that is, find a few numbers and/or words that can tell the story of the data in a nutshell. For quantitative data, the most important characteristics are the shape of the data (which you see in Chapter 4), where the center is located, and how much variability or spread is in the data. You may also want to point out any outliers in the data (numbers that appear far from the rest). And like everything else in statistics, there’s room for people to stretch the truth in how they choose to summarize their data (or in what they choose not to tell you). So it’s good to know the big ideas of how data are summarized and what to look for in terms of interpreting and evaluating data summaries. That’s what you practice in this chapter.

Finding and Interpreting Measures of Center

The most common way to summarize quantitative data is to describe where the center is. One way of thinking about what center means is to ask, “What’s a typical value in this data set?” You can measure the center of a data set in different ways, and the method you choose can greatly influence the conclusions people make about the data.

The mean of a data set is also known as the average. To find the mean, add all the numbers in the data set and divide by the number of numbers. The notation for the sample mean is , and the formula for the sample mean is . In this case the capital sigma stands for sum, and the subscript “i” starts at 1 and ends with n, so you are summing each value in the data set from to . Then divide by n.

The median of a data set is the true middle value when the data are ordered from smallest to largest. To find the median, order the data and pick the middle number(s). If you have an odd number of numbers, only one value is in the middle. If you have an even number of numbers, you pinpoint two values in the middle and determine the average of the two to get the median.

See the following for an example of calculating the mean and median.

Finding and Interpreting Measures of Spread

Variation is one of the most important concepts in statistics. It measures how much the values in a sample or a population fluctuate. Values that appear close together indicate a small amount of variation. Values that are spread out indicate a large amount of variation.

A very crude measure of spread is the range. The statistical definition of range is the biggest number in the data set minus the smallest number. The range is a single value, not a pair of values, and is entirely based on only two numbers. Both numbers can be outliers, which is why range can be a crude measure of spread.

Because range is such a crude measure, by far the most common measure of variation is the standard deviation. The standard deviation represents the “typical” distance from any point in the data set to the mean. Roughly speaking, standard deviation gives you the average distance from the mean.

To find the standard deviation of data from a sample, you first find the mean (refer to the previous section). After that, follow these steps:

1. Take each number in the data set, subtract the mean, and square the result.
2. Add up all these so-called “squared deviations” and divide by 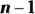(n is the size of the data set).
3. Take the square root to undo the squaring you did earlier.

The notation for sample standard deviation is s, and the formula is .

See the following for an example of calculating and interpreting standard deviation.

Using Percentiles and the Interquartile Range

When dealing with skewed data (data that aren’t symmetric but rather lopsided off to one side), it’s often better to work with the median as the measure of center, because it’s not affected by the skewness as much as the mean is. And along this line, you can measure the spread of skewed data by focusing mainly on the range of the middle 50 percent of the data — called the interquartile range, or IQR. To understand IQR, you need to review percentiles — the kth percentile is a point in the data set where k% of the data lies below it. So if your height is at the 70th percentile, for example, that means 70 percent of the people are shorter than you. Certain numbers that represent the 25th and 75th percentiles have special names because they divide the data into quarters; they are called the first quartile, or Q1, and the third quartile, or Q3, respectively.

Note that computers can calculate quartiles for you, and that’s how you’ll normally get them done.

But, for example, suppose that you have 10 numbers (ordered) 1, 3, 5, 6, 7, 8, 10, 12, 13, 13. The Q3 would be the number that is three-fourths of the way through the data. One way to think of it is to find the median first (7.5 here), which would be the middle of the data. The median now divides the data into two halves, the upper half and the lower half. The Q1 would be the median of the lower half of the data (half of a half is a quarter), which here is the median of 1, 3, 5, 6, 7, which is 5. The Q3 would be the median of the upper half of the data; the median of 8, 10, 12, 13, 13 is 12. (Other computer programs may give slightly different answers to finding quartiles, but you get the big picture here.)

When you calculate the IQR you are ignoring any skewness or outliers that may lie on either end. To find the IQR, you find the range of the middle 50% of the data; you take . So if the 75th percentile (Q3) for height was 60 inches and the 25th percentile (Q1) was 53 inches, then the IQR for height would be inches.

Answers to Problems in Summarizing Quantitative Data

1 The mean (or average) doesn’t have to be one of the numbers in the data set, but it can be. For example, in the data set 1, 2, the mean is 1.5, which isn’t in the data set; however, in the data set 1, 2, 3, the mean is 2.

2 The median will be one of the numbers in the data set if the set has an odd number of values in it, because the set has one distinct middle value in that case. If the set has an even number of values, you find the median by averaging the two middle values, and the answer may or may not be one of the values in the data set. For example, if the data set is 1, 2, 3, 4, the median is 2.5, which isn’t included in the data set; however, if the data set is 1, 3, 3, 4, the median is , which is included.

3 If you don’t order the data to find the median, you get a different answer. For example, look at the data set 1, 5, 2. The median is 2, but if you don’t order the data, it would be 5. And if you reorder the same data set to be 2, 1, 5, you get a different answer for the median: 1. So you should always order the data from smallest to largest to always get the same answer for the median. For the mean, you add up all the values in the data set and divide by the size of the data set. Using the commutative property for addition (and you thought you’d never use algebra later in life!), you know that . Even if you reorder the data, you still get the same sum. So you don’t have to order the data to always get the same answer for the mean of a given data set.

4 Outliers attract the mean toward them and away from the rest of the data. For example, the mean and the median of the data set 1, 2, 3 is 2. Suppose that you have the data set 1, 2, 297. The mean is now divided by 3, which is . However, the median of the data set 1, 2, 297 is still 2.

Outliers affect the mean, but they don’t affect the median. The mean gets pulled in the direction of the outlier and may not truly represent a “typical” value in the data set.

5 This problem gives you one way to check your answer to see if it makes sense.

1. Because it averages out all the data in the set, the mean has to be somewhere between the largest and smallest values in the data set.
2. The mean could equal the maximum value in a data set if all the values in the data set are the same; otherwise, any other value that isn’t at the maximum pulls the mean down.

6 Many answers are possible. The key is to put the same number in the middle. One possible answer: data set 1: 100, 200, 300; data set 2: 199, 200, 201. The mean and median of both data sets is 200. These two data sets have the same center with totally different ranges (or spreads). If you want to tell the story about a data set, the center isn’t enough because it can’t distinguish between two data sets with different spreads.

7 This problem really points out what happens to the measures of center when you add any constant to all the values in the data set.

1. The mean also increases by $1,000 to $51,000, because you literally pick up all the salaries, move them up $1,000 on the number line, and put them back down, which moves the mean by the same amount.
2. The median also increases by the same amount, to $51,000, for the same reason.

Adding or subtracting a constant to or from all the values in a data set changes the mean and median by that same constant. Be careful — that constant could be negative as well as positive.

8 This scenario highlights what happens when you multiply all the data by a constant. Here, the constant is 1.1, because you take the old salary, call it X, and add 10% of the X to it: . But, so, in other words, 1.10 times the original salary gets you the new salary.

1. The mean also increases by 10% to become , because you multiply each value in the data set by 1.1.
2. The median also increases by 10% to become $55,000 for the same reason.

9 The standard deviation can’t be negative because of the squaring that goes on in its calculation. However, it can be 0, although it happens only when the data set has no deviation in it — in other words, when all the data are exactly the same value. For example, 1, 1, 1 or 2, 2, 2, 2, 2 are two data sets with a standard deviation of 0.

10 If you choose 1, 1, 5, 5, you get the largest standard deviation possible, because these numbers are as far as possible from the mean (which is 3).

11 Adding a constant to the data doesn’t change the standard deviation, because you just relocate the data in a different spot on the number line; you don’t change how far apart the values are from the mean.

12 Multiplying by a constant changes the standard deviation. If you multiply an entire data set by 1.1, the spread increases. Suppose that two employees have salaries of $30,000 and $50,000 — right now, the figures are $20,000 apart. With a 10% raise, they become $33,000 and $55,000, making them $22,000 apart (the rich get richer, and the poor get less rich). If you recalculate the standard deviation, you find that it goes up here by a factor of 1.1 as well.

The new standard deviation becomes c times the old standard deviation, when you multiply the data set by a nonnegative constant c. If you multiply the data by a negative constant, , the new standard deviation becomes |c| times the old standard deviation (again, because of the squaring that goes on, the negative sign disappears). Also note that if c is a number between 0 and 1, the new standard deviation gets smaller than the old one.

13 The median is 3.5 and divides the data into the lower half (1, 2, 3) and the upper half (4, 5, 6). The median of the lower half is Q1, which is 2, and the median of the upper half is Q3, which is 5. IQR is then .

14 In this case, the median is 2, Q1 equals 2, and Q3 also equals 2, so the IQR is . This makes sense because there is no spread in this data set anywhere, least of all in the middle 50 percent of the data.

15 IQR is not affected by skewness or outliers because it measures only the range in the middle 50 percent of the data. It does not pay attention at all to the numbers on the outside edges, which is where skewness or outliers show up.