chapter two
choose an effective visual
Once you’ve taken time to understand the context and planned your communication in a low-tech fashion, as we practiced in Chapter 1, comes the question: when I have some data I need to show, how do I do that in an effective way? This is the topic we’ll tackle next.
There is no single “right” answer when it comes to how to visualize data. Any data can be graphed countless different ways. Often, it takes iterating—looking at the data one way, looking at it another way, and perhaps even another—to discover a view that will help us create that magical “ah ha” moment of understanding that graphs done well can do.
Speaking of iterating, we have some forthcoming exercises that will encourage you to do just that. Through the exercises in this chapter, we’ll create and evaluate a number of different types of graphs, helping us understand both the advantages and limitations of different individual pictures of the data. Our go-tos will mainly be the usual suspects—lines and bars—but we’ll look at some twists on graph types introduced in SWD as well.
Let’s practice choosing an effective visual!
First, we’ll review the main lessons from SWD Chapter 2.
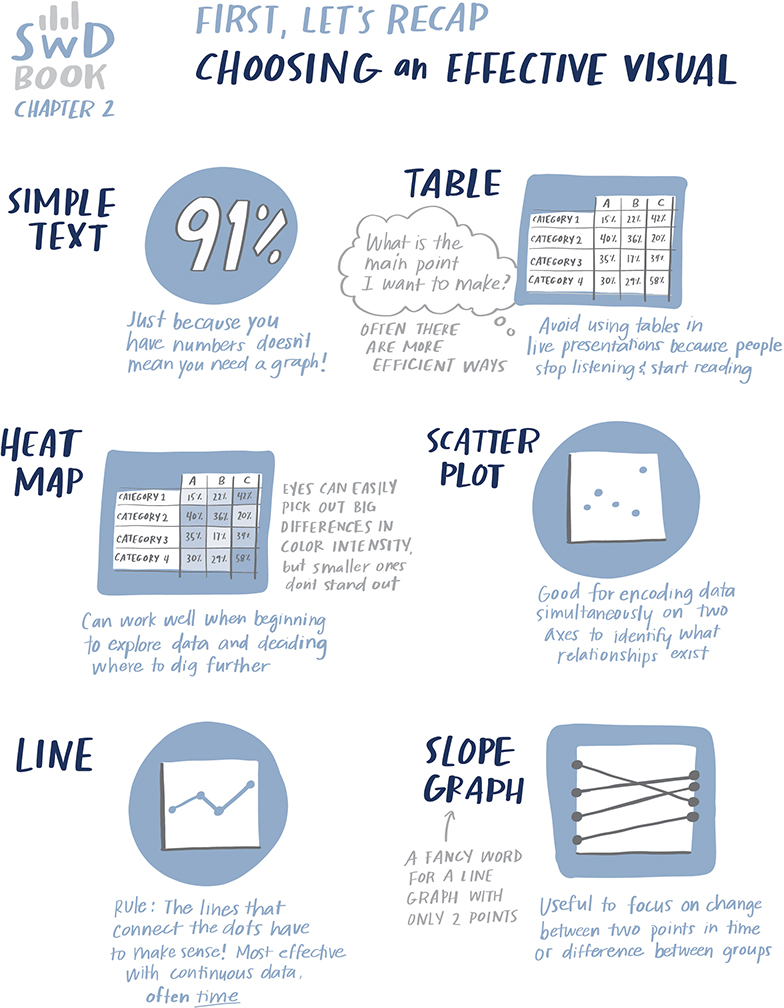



Exercise 2.1: improve this table
Frequently, when we first aggregate our data, we put it into a table. Tables allow us to scan rows and columns, reading the data and comparing the numbers. Let’s look at an example table and explore both how we can improve it and take things a step further to visualize the data it contains.
Figure 2.1a shows the breakdown of new clients by tier for the recent year. Use this table to complete the following steps.
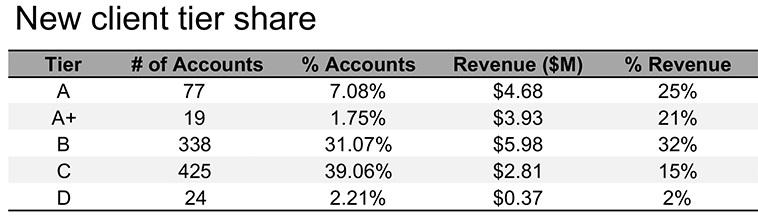
Figure 2.1a Original table
STEP 1: Review the data in Figure 2.1a. What observations can you make? Do you have to make any assumptions when interpreting this data? What questions do you have about this data?
STEP 2: Consider the layout of the table in Figure 2.1a. Let’s assume you’ve been told this information must be communicated in a table. Are there any changes you would make to the way the data is presented or the overall manner in which the table is designed? Download the data and create your improved table.
STEP 3: Let’s assume the main comparison you want to make is between how accounts are distributed across the tiers compared to how revenue is distributed—and that you have the freedom to make bigger changes (it’s not required to be a table). How would you visualize this data? Create a graph in the tool of your choice.
Solution 2.1: improve this table
STEP 1: When I encounter this table, I start reading and scanning down columns and across rows. In terms of specific observations, I might start by noticing that the majority of accounts are in Tiers B and C, while Tiers A and A+—though they don’t make up a huge number (or percentage) of accounts—do make up a meaningful amount of revenue. In terms of questions, I wonder if the tiers are in order: I would think A+ belongs above A and am confused that they don’t appear that way in the table (perhaps due to alphabetical sorting?).
I wish there was a “Total” row at the bottom, because in the absence of this I find myself wanting to add up numbers. In fact, it’s when I start to do that when I notice some bigger issues. The third column (% Accounts)—which I assume means percent of total accounts—sums to 81.16%. The final column (% Revenue)—which I assume means percent of total revenue—sums to 95%. So now I’m unsure whether these really are percent of total or something else. If they are, then there must be some “Other” or “Non-tier” category that I’d want to include in order to have the full picture.
When I focus on the numbers themselves, two digits of significance (places past the decimal point) seem like a lot for the % Accounts column given the scale of the numbers. When showing data like this, you should be thoughtful about the appropriate level of detail. There isn’t necessarily a single “right” answer, but you want to avoid too many digits of significance. This can make the numbers themselves harder to interpret and recall and may convey a false sense of accuracy. Is the difference between 7.08% and 7.09% meaningful? If not, we can drop a digit by rounding. Here, given the scale of the numbers and differences between them, I would round to whole numbers across all except the fourth column depicting revenue. There we are already summarizing in millions and it seems like we would lose important differences between the dollar volumes by rounding to a whole number, so there I’d round to one digit past the decimal point.
Figure 2.1b is an improved table that addresses the preceding points.

Figure 2.1b Slightly improved table
STEP 2: There are additional improvements I can make to this table. When tables are designed well, the actual design fades to the background so that we focus on the numbers in a way that makes sense. I recommend against shading every other row and instead am an advocate for white space (and limited light borders) to set apart columns and rows as needed. Speaking of white space, I typically avoid center-aligned text in graphs (because it creates hanging text and jagged edges that look messy) in favor of left- or right-aligning text. In the case of tables, however, I do sometimes opt for center alignment because of the separation this creates between columns (another common practice in tables is to right-align numbers or align by decimal point, which allows you to easily eyeball relative size). I can group the accounts-related columns and revenue-related columns with a single title (and under that, number and percent), which will reduce some redundancy of titles and also give me more space to be specific about what the columns represent. Doing so also allows me to make the columns narrower so the table overall takes up less space. These are some specific tips—I’ll also put forth a couple of more general ones: consider the zigzagging “z” and where your eyes are drawn.
Consider the zigzagging “z”: Without other visual cues, your audience will typically start at the top left of your visual (for example, your table) and do zigzagging “z’s” across to take in the information. When we think about applying this to how we design our tables, it means you want to put the most important data at the top and at the left—when you can do so in the context of the overall data in a way that makes sense. In other words, if there are super-categories or data that needs to be taken into account together, keep them in the order that makes sense. In this particular example, I’d sort my tiers starting with the top (that is indeed A+) and decreasing as we move down the table. Going left to right, I’m happy enough with the way it is structured. I want to keep the distribution of accounts and percent of accounts next to each other since those relate to each other. If revenue were more important than accounts, I could move the two revenue columns leftwards, but I can also use other ways to focus attention there. Let’s discuss that next.
Where are your eyes drawn? Similarly to how we focus attention thoughtfully in graphs as part of explanatory analysis (something we’ll explore in detail in Chapter 4), we can also focus our audience’s attention in tabular data to establish hierarchy of information. This can be especially useful in instances where you can’t put the most important stuff leftward or at the top (because other constraints dictate the ordering). Despite this, you can still indicate relative importance to your viewers. Look back to Figure 2.1b: where are your eyes drawn? Mine go to the very first row where the column titles are Tier, # of Accounts, and so on. This isn’t even the data! Rather than use up ink and draw attention there, I can be conscious about where I want to direct attention in the data and take intentional steps to get my audience to look there. This can be done through sparing use of color or by outlining a specific cell or column or row. Adding visual aspects to some of the data in the table is another way to draw attention there: colors and pictures grab our attention when they are used judiciously.
If we assume the primary comparison we’d like our audience to make is between the distribution of % Accounts compared to % Revenue, I could apply heatmapping (using relative intensity of color to indicate relative value) to just those two columns. See Figure 2.1c.

Figure 2.1c Table with heatmapping
As another approach, I could embed horizontal bar charts in place of the heatmapping. See Figure 2.1d. This does work quite well to direct attention to those columns and allows us to see how the shape of the distribution varies across the two. However, the specific comparison between % Accounts and % Revenue for a given tier is harder, since these bars aren’t aligned to a common baseline. Tip: If you are working in Excel, conditional formatting is available that will allow you to create heatmapping or embedded bars in a table with ease.

Figure 2.1d Table with embedded bars
STEP 3: Let’s take it a step further and focus on the data that is in the bars in Figure 2.1d and review some different ways we could graph it. When I hear a term like “percent of total,” it makes me think of parts of a whole—which might cause us to look to the pie chart. In this case, since we are interested in both % of Accounts and % of Revenue, we could depict this with a pair of pies. See Figure 2.1e.

Figure 2.1e A pair of pies
I’m not a big fan of pies—I sometimes joke that there’s one thing worse than a single pie: two pies!
Let me back up, though, and say that pies can work well if we want to make the point that one piece of the whole is very small, or another piece of the whole is very big. The challenge for me is that pies break down pretty quickly if we want to say anything more nuanced than that. This is because our eyes’ ability to accurately measure and compare areas is limited, so when the segments are similar in size, it is difficult for us to assess which is bigger or by how much. If that’s a comparison that is important, we’ll want to represent it differently.
In this instance, the primary comparison we want our audience to make is between the various segments in the pie on the left and those in the pie on the right. This is difficult for two reasons: the area challenge mentioned above and the spatial separation between pies. This is further compounded by the fact that the segments are in different places on the right as a result of how the data differs between the breakdown on the left compared to the right. Basically, if any of the data is different between the pies (which it should be if we have something interesting to say about it!) then all the pieces are in different places across the two pies—making them hard to compare. In general, you want to identify the primary comparison you want your audience to make and put those things as physically close together and align to a common baseline to make that comparison easy.
Let’s start by aligning each measure to its own baseline, with a view similar to the bars embedded in the table previously. See Figure 2.1f.

Figure 2.1f Two horizontal bar charts
In Figure 2.1f, it’s very easy for us to compare the % of Total Accounts across tiers. It’s also easy to compare the % of Total Revenue across tiers. I can attempt to compare accounts to revenue, but this is harder because they aren’t aligned to a common baseline. If I want to allow for that as well, then I could pull both of these series into a single graph. See Figure 2.1g.

Figure 2.1g Horizontal dual series bar chart
With the arrangement in Figure 2.1g, the easiest comparison for me to make is, for a given tier, the % of Total Accounts compared to the % of Total Revenue. These elements are both the closest together and they are aligned to a common baseline. Bingo!
We could also flip this graph on its side into a vertical bar chart, or column chart. See Figure 2.1h.

Figure 2.1h A vertical bar chart
When we depict data in this manner, the primary comparison our eyes are making is the endpoints of the paired bars relative to each other and to the baseline. Let’s draw some lines to further highlight this comparison. See Figure 2.1i.
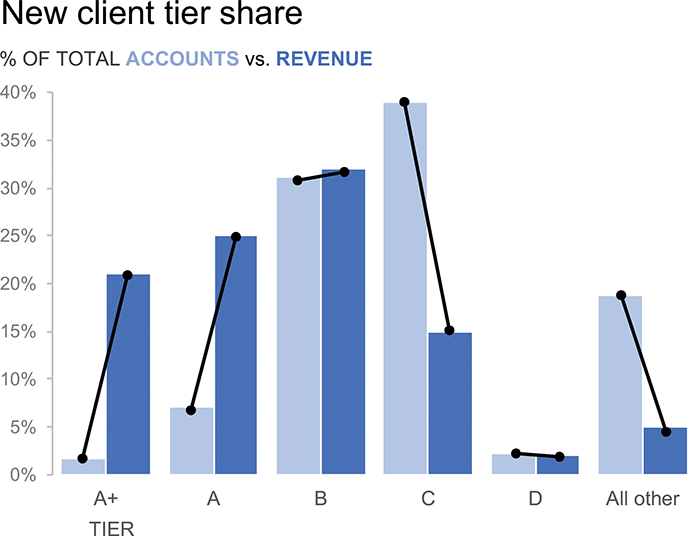
Figure 2.1i Let’s draw some lines
Now that we’ve drawn the lines, we don’t need the bars anymore. I’ve removed those in Figure 2.1j.

Figure 2.1j Take away the bars
Next, I’ll collapse all of these lines and label everything directly. This yields the slopegraph shown in Figure 2.1k.

Figure 2.1k A slopegraph
Slopegraph is really just a fancy word for a line graph that only has two points in it. By drawing lines between the % of Total Accounts and % of Total Revenue for a given tier, we can quickly see where the two measures differ. Revenue as a proportion of total is quite a lot lower for Tier C and All other (indicated by lines sloping downwards), while revenue as a proportion of total is much higher for tiers A+ and A. In other words, though A+ and A make up a very small proportion of accounts (9% combined), together they account for nearly 50% of revenue!
We’ve looked at a number of ways to visualize this data. You likely made your own observations along the way about what worked well and what did not. What I’ve illustrated isn’t exhaustive; I could have added a dot plot to the mix or calculated revenue per account and visualized that. That said, we don’t typically have to go through every possible view of the data to find one that works. Perhaps both absolute values and percent of total are important, in which case the table might be the easiest way to show these different measures after all. If we can narrow our focus to a specific comparison or two, or a specific point we want to make, that will help us choose a way to show the data that will facilitate this.
Any data can be graphed countless different ways. This exercise illustrates how moving through different representations of our data allows us to more (or less) easily see different things. Allow yourself time to iterate and complete the additional exercises that will give you more practice at this important junction in the process!
Exercise 2.2: visualize!
Let’s look at another table. The following shows the number of meals served each year as part of a corporate giving program. Spend a moment looking at the data. What is interesting about it?
Notice how much work it is to process a column of numbers like this. We read data that is presented to us in tabular form, which—though this may seem like a simple way to show the numbers—actually takes a ton of brainpower! When I scan these numbers, I see the jump from 2010 to 2011, and another between 2013 and 2014. You probably did, too. But if you’re like me, it means you started at the top of the table and got there by scanning down the second column—comparing each new number to the one(s) before it.
Let’s practice easing how hard our brains must work by making the data more visual. Download this data. Create the following visuals in the tool of your choice.
STEP 1: Apply heatmapping to the second column of values.
STEP 2: Create a bar graph.
STEP 3: Create a line graph.
STEP 4: Choose: which of the visuals you’ve created do you like best? Are there any other ways you would graph this data?
Solution 2.2: visualize!
Pretty much anything we do to visualize the data originally shown in table form in Figure 2.2a is going to make it more quickly understandable. Let’s check out a few ways we can ease the processing.

Figure 2.2a Table showing meals served over time
STEP 1: First, let’s apply some heatmapping. Most graphing applications have built-in functionality that will allow you to do this with ease. You can pick colors and choose how to apply them to the data. For example, I’ve created the following in Excel by applying conditional formatting to the second column of values. I indicated a 3-color scale, with lowest value white, 50th percentile light green and maximum value green. In some situations, you could add a legend to make it clear how to interpret the colors. In this case, I just want to give a general sense that more intense color represents bigger values and vice versa. Eyeballing it, this sense is intuitive given the numbers and relative intensity within the same hue.
In Figure 2.2b, I’m perhaps more inclined to notice how much lower the number of meals served in 2010 was—it’s totally white—less than a third of the next closest number! I can also quickly observe that 2016 had the greatest number of meals served without having to read the numbers. The relative intensity of color helps me more quickly interpret the relative quantitative values.

Figure 2.2b Table with heatmapping
Related to this, I should point out that our eyes are pretty good at picking out big differences in intensity, but we have a harder time with more minor differences. This means that if there is something interesting about all of those medium shades of green, that’s a little harder to quickly grasp and I might want to find a way to more fully visualize the values. Let’s do that next.
STEP 2: Figure 2.2c shows a bar graph I could make based on this data. I chose to keep the y-axis for reference. Almost instantly, we can get a general sense of magnitude of the various bars. I thickened the bars from the default graph so there is less of a gap between them, which makes it easier for my eyes to follow along the tops of the bars and compare them to each other. I like the idea of bars. We do have a continuous variable on the x-axis (time), but we can categorize it into years, which may make sense if we want to focus on a specific year at a time and have clear demarcation between the years.

Figure 2.2c Bar chart
STEP 3: We can also show this data as a line graph; see Figure 2.2d. In this iteration, I decided to omit the y-axis and instead labeled only the beginning and end data points. This makes it easy (and obvious) for my audience to compare the number of meals served in 2010 to 2019. The rest of the values would have to be visually estimated. If there are other values you thought your audience would be particularly interested in (for example, the high point in 2016), you could also add data markers and labels to those points specifically.

Figure 2.2d Line graph
When I remove the y-axis, I’ll often use the subtitle space for the axis title. Here, given the graph title, you could probably argue that the subtitle is redundant and perhaps unnecessary. I’d rather be explicit so there is no question for my audience about what they are viewing. That said, another reasonable person might make a different decision.
I’ve used green in the visuals in this exercise, mainly to make it clear that—while I often default to blue—blue certainly isn’t our only choice when it comes to using color in our visuals. We’ll talk more about color as part of the exercises in Chapter 4.
You inevitably made different design choices with your heatmap, bar graph, and line chart, and that’s totally fine. The examples here and throughout are meant to be illustrative, not prescriptive. We’ll look more specifically at aspects of design in Chapter 5.
STEP 4: Which do I like best? When I look back over the visuals I created, I’m surprised at my own answer to this one. Going into it, I thought for sure I’d prefer the line. It’s the cleanest and it takes up the least amount of ink. But seeing them together, and taking the limited context into account, I actually prefer the bar chart (Figure 2.2c). If there is a clear start and end to the program within each year, I’d provide this segmented picture. That said, I do think the overall trend is easier to see with the line graph. Additionally, if there were context that I wanted to annotate via text on the graph, I’d likely choose the line, which has more space to accommodate this.
As we saw in solution 2.1, this is another illustration that there is no single right approach for visualizing data. Two different people faced with the same data visualization challenge may opt for different approaches. Of utmost importance is that we are clear about what we want to enable our audience to see and choose a view that will help facilitate that.
Exercise 2.3: let’s draw
One of the best tools we all have at our disposal when visualizing data is a blank piece of paper. If I’m ever feeling stuck or am looking for a creative solution, I get out a fresh sheet and start sketching. You don’t need to be an artist to reap the important benefits of drawing. When working on paper, we remove the constraints of our tools (or what we know how to do with our tools). We are also less likely to form attachment to our work (the way we do after we’ve taken the time to create it with our computer). There’s also simply something about empty space waiting to be filled that can help spark creativity.
Let’s do a quick practice exercise using this important instrument: paper. The following graph (Figure 2.3a) shows capacity and demand measured in number of project hours over time. It is currently graphed as a horizontal bar chart. But is this the only way to show this data? Certainly not!

Figure 2.3a Let’s draw this data!
Get a blank piece of paper and set a timer for 10 minutes. How many different ways can you come up with to potentially visualize this data? Draw them! (Don’t worry about plotting every specific data point exactly—make it quick and dirty to get an overall sense of what each visual could look like.) When the timer goes off, look over your sketches. Which do you like best and why?
Solution 2.3: let’s draw!
After 10 minutes, my paper is filled with six different ways to depict the data. See Figure 2.3b.

Figure 2.3b My data drawings
Starting at the top left, my initial sketch simply turns the horizontal bars upright so that time can move from left to right along the x-axis in a way that is intuitive. My second graph (top right) turns the bars into lines. I find it easier to focus on the gap with this view. But I wanted to do some more playing with bars of various forms, so my third iteration (middle left) goes back to those. I made Demand thinner and behind Capacity, in hopes that this would make it clear how much we’re meeting out of the potential of what could be met. As a twist on that, we could stack the bars, which I’ve done in the middle right picture. The stacked series becomes the Unmet Demand (note that this stacked version only works if Demand is always greater than or equal to Capacity—it would get tricky if Demand were to fall below Capacity). My penultimate view (bottom left) re-envisions the bars as dots and connects them to bring attention to the difference (this would still work if Demand falls below Capacity so long as we’ve made the Demand circles distinct from those representing Capacity, for example, by coloring them differently). My final illustration simply plots the trend of Unmet Demand. With this last one, we lose the context of the overall magnitude of Demand and Capacity, but depending on our goals, that may be okay.
When it comes to which I like best, I prefer the stacked bars (middle right) if Demand is always higher than Capacity, as it is for the data we’re graphing. That said, I think any of these views could potentially work. There are definitely other ways to show this data as well. Compare your drawings to mine. Did you come up with any similar graphs? Where do our ideas differ? Which do you like best out of the full group (yours plus mine)?
Let’s continue working with this data and determine how we can make one of the sketches come to life in our tools! Move on to Exercise 2.4.
Exercise 2.4: practice in your tool
Consider the sketches created as part of Exercise 2.3—both the ones you drew and the ones I sketched. Pick one (or more for extra credit!), download the data, and create in the tool of your choice.
Solution 2.4: practice in your tool
I’m an overachiever, so I created all of the views I drew by hand in Excel. See Figures 2.4a - 2.4f.
Basic bars. First is the basic bar graph, or column chart. See Figure 2.4a. I’ve intentionally filled in Capacity and left Demand as an outline to try to visually differentiate what we’re able to meet compared to the unmet capacity. I don’t love this graph—and I think I like it less than I did in my drawn version. I appreciate the idea of just having the outline for Capacity, yet I find the outline plus the white space between the bars visually jarring. I also feel this is the view out of all of them that directs the least amount of attention to the gap between Capacity and Demand, which seems like an important aspect of this data.

Figure 2.4a Basic bars
In this case I chose to use the subtitle space for my legend. I’ll sometimes do this if there isn’t an obvious place to label the data directly. As an alternative, I could try directly labeling the first or last set of bars and using those as my legend.
Line graph. The line graph is a cleaner design compared to the bars, because it simply takes up less ink. I chose to label the lines (and also added data labels) at the ends of the lines, eliminating any confusion over which series is which and reducing the work of going back and forth between a legend and the data. I like that the line allows us to focus on either Capacity or Demand, and it also makes the comparison of them really easy, so we can see the gap between the lines and quickly identify where it is growing and where it is shrinking. I bolded the Capacity line so our attention would go there first, then see the context of the greater Demand. See Figure 2.4b.

Figure 2.4b Line graph
Overlapping bars. We go back to bars in Figure 2.4c, which shows an atypical approach: making the bars overlap. I’ve made the Capacity series slightly transparent so that it is clear that the Demand series starts at zero and isn’t meant to be interpreted as being stacked.

Figure 2.4c Overlapping bars
I like this iteration better than I anticipated when I sketched it on paper. That said, I could imagine an audience might find it confusing or off-putting since it doesn’t look like a typical bar chart. If I wanted to use this graph, it would be a good one to show to a couple people and get feedback to see whether others find it confusing or if it could get the job done.
Stacked bars. With stacked bars, I kept Capacity plotted at the baseline, but then changed the second series to Unmet Demand so it could be stacked on top. I switched my emphasis to Unmet Demand, making it blue and rendering Capacity in a light grey. I like this view.
Dot plot. This is another view that could catch my audience off guard. It feels intuitive to me, but I have to recognize that pretty much any way I graph this data is going to feel intuitive because I’ve spent time with the data: I know what it represents and what I want my audience to take away. It may not be as obvious to them, however. Again, soliciting feedback would be a good way to test and assess.
While I’m not sure I love this one, I am impressed at my own Excel wizardry used to create it. The circles are actually data markers on two line graphs (one for Demand, another for Capacity) where I’ve chosen not to show the actual line and made the data markers huge so I’d have room to center the data label within each point. The shaded region that connects the dots is Unmet Demand, which is a stacked bar that sits on top of a second inclusion of the Capacity series (unfilled so you don’t see the bottom series in the stack). This is what I call brute force Excel at its finest!
Graph the difference. My final view is a simple line graph that plots the Unmet Demand (Demand minus Capacity). This is my least favorite of all (or maybe I’d rate it as tied for last with the basic bars), as it feels like too much context is omitted when we go from the two data series to plotting the difference. See Figure 2.4f.
How did the visual(s) you made in your tool turn out? Which out of all of them do you like best and why?
In absence of any context, I’d choose the Stacked Bar in Figure 2.4d. I like that it’s easy to see both how Unmet Demand and Capacity are changing over time and I appreciate how this view makes it easy to focus attention on the decreasing Unmet Demand.

Figure 2.4d Stacked bars
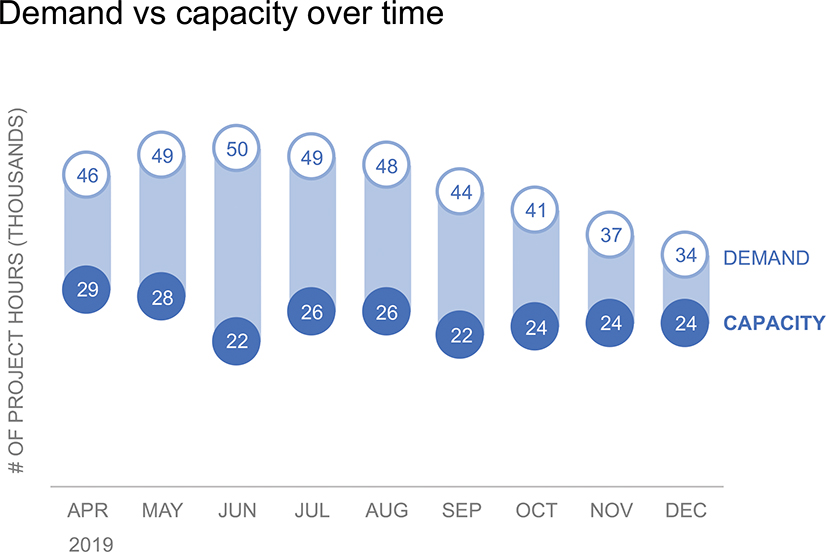

Figure 2.4f Graph the difference
We will revisit this data in context of the broader dashboard it originated from in Chapter 6.
Exercise 2.5: how would you show this data?
The following table shows attrition rate for a 1-year associate training program for a given company. Spend a moment familiarizing yourself with it, then answer the following questions.

QUESTION 1: How many different ways can you come up with to show this data? Draw or create in the tool of your choice.
QUESTION 2: How would you show the average in the various views you’ve created?
QUESTION 3: Which of the visuals you’ve created do you like best and why?
Solution 2.5: how would you show this data?
QUESTIONS 1 & 2: There are many potential ways we could show this data, depending on our audience and our goals. I came up with six different potential visuals and integrated the Average into each. Let’s review and discuss each of these.
Simple text. Just because we have numbers doesn’t mean we need a graph! In some situations we can simply communicate a number or two. For example, I could summarize all of this data by saying, “The attrition rate for this program has averaged 7.5% over the past ten years.” This doesn’t give us any sense of the range over time, or basis for comparison, which in some cases would be simplifying too much. If that’s important, perhaps I could say something like, “The attrition rate has varied from 1% to 15% over the past decade, and was 9.1% in 2019.” Or if I want to focus on more recent data, which may be more relevant, I could say, “The attrition rate for this program has increased in recent years, from 4.5% in 2017 to 9.1% in 2019.”
Each time you create a visual, come up with a sentence that answers the question, “So what?” (Exercises 6.2, 6.7, 6.11, 7.5, and 7.6 will ask you to do this explicitly.) You may find that you can communicate with that sentence, eliminating the need for the graph altogether. When you do have more data you need to communicate, consider what context is helpful and how you can visualize it. Let’s look at some ways to graph the data next.
Dot plot. I can use points to illustrate attrition rate (y-axis) by year (x-axis). I incorporated the average by adding a line to the graph, which allows us to easily see when we’ve been above and below average over time. See Figure 2.5b.

Figure 2.5b Dot plot
Line graph. Rather than plot the points, I could visualize the lines that connect them so we can more easily see the trend over time. Figure 2.5c illustrates this. I retained the thin dotted line for the Average, but moved my labeling of it (and also abbreviated) so that it would better fit given this new layout of the data. I also chose to put a data marker and label on the final data point. This makes the comparison between the most recent point of data and the average an obvious one for my audience.

Figure 2.5c Line graph
I tried a second iteration on the line graph, using shaded area for the Average, rather than a line. See Figure 2.5d. I prefer the original line view in Figure 2.5c, but I could envision scenarios with different data that might cause me to choose another approach.

Figure 2.5d Line graph with shaded area depicting average
Area graph. After trying out area for the Average, I decided to switch it up and depict the Attrition Rate with area and revert back to a line for the Average. See Figure 2.5e. I chose a lighter blue for the Average line so it would show up both against the empty white background as well as when it overlaps the area encoding attrition rate. In each visual, I’ve labeled the Average differently—this is mainly due to the space available and the shape of it. Alternate views of the data may cause you to make other design modifications like this as well.

Figure 2.5e Area graph
I don’t love this one. It takes up a lot of ink for what we’re trying to show and makes it seem like there’s something important about the area under the curve, which isn’t the case here. I don’t use a lot of area graphs in general.
Bar graph. Finally, I tried plotting this data as a bar chart. See Figure 2.5f. I preserved the Average as a line, labeling it again differently from prior views given the layout of the overall graph.
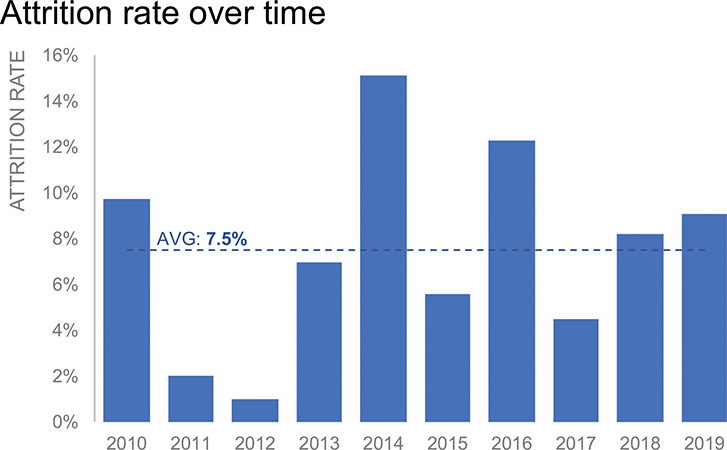
Figure 2.5f Bar graph
QUESTION 3: Which do I like best? I’m happy with the preceding bar chart, but I like the line graph in Figure 2.5c best of all. Connecting the dots via lines makes it easy to see the trend in Attrition Rate over time. I can easily compare it to the Average. It doesn’t use a lot of ink, which leaves me space to add commentary if it makes sense to do so.
Exercise 2.6: let’s visualize the weather
I’m a big fan of bar charts. They are easy to read—our eyes and brains are great at comparing lengths when aligned to a common baseline, which is what the bar chart does for us. We take in the information in bar charts by comparing the relative heights of the bars to each other and the baseline, so it’s easy to see which is biggest and by how much. Also the familiarity of bar charts can be useful when communicating: since most people already know how to read them, they can focus their brainpower on what to do with the data rather than try to figure out how to read the graph.
Let’s take a look at an example bar chart. See Figure 2.6a, which shows the weather forecast for the next six days measured by the expected daily high in degrees Fahrenheit.

Figure 2.6a The weather forecast
QUESTION 1: Imagine you are preparing for a Sunday afternoon at the park. What temperature would you estimate for the high on Sunday?
QUESTION 2: You are planning your children’s clothes for the coming week and trying to decide what type of jacket or coat they’ll need midweek. What temperature might you estimate for the high on Wednesday?
QUESTION 3: What other observations can you make from this data?
Solution 2.6: visualize the weather
While the temperature may appear to be somewhere in the 90s on Sunday and in the 40s on Wednesday, that’s not actually the case. Let’s take a closer look.
It turns out that Sunday is 74 degrees while Wednesday is 58 degrees. How is that possible? The initial graph in Figure 2.6a does not have a y-axis that starts at zero. Rather, it begins at 50. This distorts the data, making it so we can’t accurately compare the temperature day to day. See Figure 2.6b, which adds both the y-axis and data labels to the original graph.

Figure 2.6b Bar charts must have a zero baseline!
Let’s redesign the graph to start the y-axis at zero. Figure 2.6c shows the side-by-side. Notice the difference this makes in interpreting the data.

Figure 2.6c Let’s compare the two graphs
What looked like a large deviation from the average on the left of Figure 2.6c looks comparatively a lot smaller on the right. With this view, you’d likely make a different decision when it comes to how thick the kids’ coats should be on Wednesday!
There aren’t a lot of hard-and-fast rules when it comes to visualizing data. But there are a few, and we’ve just witnessed one of them broken: bar charts must have a zero baseline. Because of the way our eyes compare the endpoints of the bars to each other and the baseline, we need the context of the full bar there in order to make that an accurate visual comparison.
There are no exceptions.
That said, this is not a rule that applies to all graphs. With bars, you can’t chop or zoom because of the way we compare the ends of the bars relative to each other and the axis. But with points (scatterplots or dot plots) or lines (line graphs, slopegraphs), we focus primarily on the relative positions of the points in space, and in the case of line graphs, the relative slopes of the lines that connect the points. Mathematically, as we zoom, the relative positions and slopes remain constant. You still want to take context into account and avoid overzooming and making minor changes or differences look like a big deal. Though sometimes minor changes or differences are a big deal, so if you find yourself needing to change the axis to highlight this, reach for points or lines, not bars.
On a related note, I’ve heard the idea raised that a zero baseline for weather doesn’t make sense, since temperatures can be negative, and zero (particularly on a Fahrenheit scale) isn’t meaningful. In the case of a short-term weather forecast, like we looked at here, the bars are fine so long as we do have a zero baseline allowing us to compare the day by day expectations accurately. On the other hand, if we take the case of climate change, for example, a couple degrees change in global temperatures—which is nearly impossible to see in bars with a zero baseline—is meaningful. This isn’t a good argument for changing to a non-zero baseline bar chart, but rather for not using bars to illustrate this data. We could shift to a line graph or graph the change in temperature instead of absolutes to bring focus to the small but meaningful differences. As always, we should step back and think critically about what we want to show, then choose an appropriate visual to facilitate this.
Exercise 2.7: critique!
Speaking of points (mentioned in the solution to the previous exercise), let’s take a look at some next, in the context of critiquing a less than ideal graph.
See Figure 2.7a, which is a dot plot showing the bank index over time for a number of national banks. Assume you work at Financial Savings.

Figure 2.7a Bank index
QUESTION 1: What questions do you have about this data?
QUESTION 2: If you were designing the graph, what changes would you make? How would you visualize this data?
Solution 2.7: critique!
QUESTION 1: This graph seems to incite many more questions than it answers! My first question is: what exactly is the metric being plotted? I might assume “Bank Index” is some type of customer satisfaction score, and that the higher the number, the better. But what if this is really something like bank teller errors? I’d interpret that data very differently.
My next question is, do we need all of the data? We can see at the top that the red and yellow data points represent our company (Financial Savings) and the Industry Average, respectively (these also seem like odd color choices, though I guess they are bright in an attempt to stand out against all of the other color in this graph). I assume all of these dots roll up into the average (which is another question I have: is that the case?). This begs yet another question: do we need all of those individual data points or would showing only Financial Savings and the Industry Average work? When you consider getting rid of data, you always want to think through what context you lose when doing so. Here, by summarizing with the average, we’d lose line of sight to the spread across competitors. Depending on our goals, this may or may not be important.
In terms of other questions, I’m also curious what the red circle in 2019 is meant to highlight. I appreciate the thought process behind it: someone looked at this data and thought “I’d like you to look here” and drew a red circle. This presents a couple of challenges, however. First, there’s so much competing for our attention in the graph with all the various colored dots that we might not even notice the red circle. Second, when we do notice it, it isn’t immediately clear what it is trying to point out to us.
My final questions are: So what? What does this data show us? What’s the story?
QUESTION 2: Let’s shift from asking questions to redesigning how we show this data. It turns out the metric being graphed is branch satisfaction, where the higher the number, the better. I’ll assume that we care most about how Financial Savings compares to the Industry Average. Simply making that decision means I can declutter this graph a ton and focus on the data points for Financial Savings and the Industry Average.
Speaking of data points, this data is over time. We can plot it as points, but I’d be apt to connect the points and display this data in a line graph. Lines will help us more easily see the change over time and can also help highlight interesting things when it comes to how these lines interact with each other: if one is always above the other, the lines will help us see the gap. If that’s not the case, lines will help us see when one series crosses the other, which will be interesting as we try to answer the question, “So what?”
Figure 2.7b shows my makeover of this visual.

Figure 2.7b Revamped graph
Decluttering and changing the graph to lines helps us focus on the data. I’ve titled and labeled everything directly, so there’s no need to make assumptions or hunt around for how to interpret the data. I used the title space to answer the question, “So what?”
With an additional understanding of what’s driving the ups and downs in satisfaction for our business and the industry, I could take this even further. In a live meeting or presentation, I could build it line by line or time point by time point, which would allow me to focus my audience’s attention as I talk through relevant context. If it needs to stand on its own, I could put text directly on the graph to annotate what’s causing the changes we see. We’ll look at a number of examples that employ these strategies as we get further along. We’ll revisit this example and look at a scenario where we keep all of the original data in Chapter 4.
Next, let’s redesign another graph.
Exercise 2.8: what’s wrong with this graph?
Sometimes, we design a graph with the best of intentions, but inadvertently make things difficult for our audience. Let’s take a look at an example where this is the case and discuss how we can improve it.
Continuing in the banking industry, next let’s imagine you work as an analyst in consumer credit risk management. For those who may not be familiar—when people take out loans, some portion of those people don’t repay them. These loans move through various levels of delinquency: 30-days past due, 60-days past due, and so on. Once they become 180 days past due, they are categorized as “Non-Performing Loans.” After reaching this stage of delinquency, despite collection activities, many still don’t repay and this results in a loss. Banks have to reserve money for these potential losses.
Now that we’re past credit risk 101, let’s talk about the data. You’ve been asked to create a graph showing how Non-Performing Loan (NPL) volume compares to the Loan Loss Reserves over time. Look at Figure 2.8a. Take note of how your eyes move as you process this information. What is confusing about this graph? How would you improve it?

Figure 2.8a What is confusing in this graph?
Solution 2.8: what’s wrong with this graph?
In considering how I process this data, I start out by doing a lot of back and forth between the bars, the lines, and the legend at the bottom of the graph to try to interpret the data. I scan the y-axes to see what those are. After some reading and thinking about it, I figured out that the lines—Loan Loss Reserves % and NPL Rate—are meant to be read against the secondary y-axis on the right-hand side of the graph. This means the bars—Loan Loss Reserves and NPLs—should be read against the primary y-axis on the left. This seems more difficult than it needs to be.
Going back to the Loan Loss Reserves % and NPL Rate: I’m not sure what the denominator is. I might assume that it’s the total loan portfolio—but I’d rather this be made clear so I don’t have to assume! I’m also unsure these lines add any value—they aren’t adding any new information. There may be additional context that would cause me to make a different decision, but in the absence of that I’m going to focus on the volume—the dollars—and not confuse things by also showing the rate. As a bonus, this decision will eliminate the secondary y-axis (I recommend against the use of dual y-axes in general; for alternate approaches to the secondary y-axis, refer to Chapter 2 in SWD).
It’s only after all this that I start paying attention to the x-axis and notice the biggest issue: we have inconsistent time intervals. Upon first glance (and several thereafter—perhaps you didn’t even catch this problem), I started reading the x-axis to see it is in units of years and then assumed that continues to be the case as we move from left to right. When we read each label, however, we find that after 2018, the time interval changes to quarters, and after Q4 it seems we’ve broken out December on its own. This is not good!
I can appreciate the thought process that presumably led to this. December is probably the most recent month. Showing years for historical context is helpful, but then it’s nice to also show greater granularity (e.g. quarterly, monthly) for the more recent time periods.
Sometimes inconsistent time intervals are a reality—we might be missing data or simply have something that occurs inconsistently over time. In that situation, we need to denote that visually and make it clear to our audience. The same bar or line shouldn’t be used to represent a year and a quarter, as this can too easily lead to incorrect interpretation and false observations.
We have a couple of options for overcoming this challenge. If we have all of the quarterly data, I’d be apt to just plot that. Bars will get messy simply because there would be so many of them, but given that we’re getting rid of the two data series that were originally depicted by lines, we could swap the original bars and plot the volume with lines. Or if for some reason we don’t want to or can’t show the quarterly data, and leave it all in one graph, one option would be to space the x-axis such that each year takes up the same width that the four quarters together take up. If I did this, I would exclude year 2019 so there isn’t redundancy between that and the four quarters that are broken out separately.
As another alternative, we could split this data into two graphs: one to show the annual data for 2014 through 2019, and then a second to break out the quarterly data just for 2019. This would allow me to title each explicitly and make the difference in time components clear. I would also compress the quarterly data more than the annual data to help visually reinforce the shorter time periods. The makeover incorporating these changes is shown in Figure 2.8b.
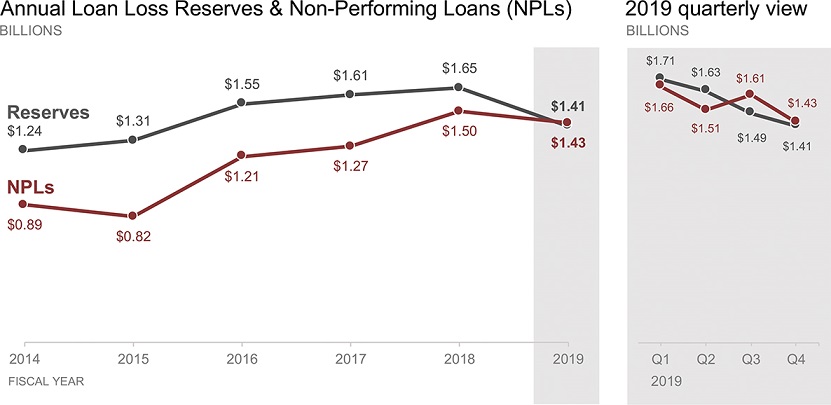
Figure 2.8b An alternative view
In this case, I chose to label the data directly so we can compare the volume of NPLs to that of Reserves without the work of having to estimate it from an axis. I maintained two decimal places of significance so there wouldn’t be instances where two points of different heights shared the same value (for example, the third and fourth points on the Reserves line would both round to $1.6M, which could cause confusion since the heights are visibly different) and so we can easily interpret the smaller but meaningful differences in the recent quarterly numbers. I used shading to tie the final data point in the first graph (2019) to the quarterly breakout for 2019 in the right graph. It is very important in showing the data like this to ensure that the y-axis minimum and maximum are set to be the same amount across the two graphs, so that the audience can compare the quarterly data points to the annual ones according to their relative height.
With this visual, I’ve taken away a lot of things that were making us do work in the original. Instead of trying to understand the graph, we can focus on the data. I can see that the gap between NPLs and our Loan Loss Reserves has narrowed markedly over time. Both were increasing through 2018, but decreased in 2019. 2019 marks the first time that NPL volume exceeds the Loan Loss Reserves. On a quarterly basis, this happened in Q3 and Q4. This seems pretty important, so we should probably take some action!
Now that you’ve practiced with me, it’s time to tackle some additional examples on your own.

Exercise 2.9: let’s draw
As illustrated in Exercise 2.3, some of our best tools for figuring out how to show our data are a blank piece of paper and pen or pencil. Let’s practice using these important instruments!
The following data shows the average time to close a deal (measured in days) for direct and indirect sales teams across four products for a given company. Spend a moment to familiarize yourself with this data.
Get a blank piece of paper and set a timer for 10 minutes. How many different ways can you come up with to potentially visualize this data? Draw them! (Don’t worry about plotting every specific data point exactly—quick and dirty to get an overall sense of what each visual could look like will suffice.) When the timer goes off, look over your sketches. Which do you like best and why?

As part of this, what assumptions are you making about this data? What additional context do you wish you had?
Exercise 2.10: practice in your tool
STEP 1: Refer back to the sketches you created as part of Exercise 2.9. Pick one (or more for extra credit!), download the data, and create in the tool of your choice.
STEP 2: After creating your graph(s), pause and reflect upon the following.
QUESTION 1: What was helpful about sketching?
QUESTION 2: Did you find anything about the drawing process annoying or frustrating?
QUESTION 3: Was creating a graph in your tool different after first sketching it?
QUESTION 4: Can you envision using this approach (draw options first, then create in your tool) in the future? In what situations?
Write a few sentences summarizing your thoughts.
Exercise 2.11: improve this visual
Imagine you work for a regional health care center and want to assess the relative success of a recent flu vaccination education and administration program across your medical centers.
You have a dashboard where related metrics are reported and your colleague pulled the following visual from it. Take a moment to study Figure 2.11 and answer the following questions.

Figure 2.11 Original visual from dashboard
QUESTION 1: How is the data sorted? How else could we sort it? In what circumstances would you make a different decision about how to order the data?
QUESTION 2: There is currently a horizontal line to show the average. How do you feel about this? How else could you show the average?
QUESTION 3: What if there were a target—how might you incorporate it? Assume the target is 10%. How would you show this? Now assume the target is 25%. Does this change what you would show or how you would show it?
QUESTION 4: The graph contains a data table. Do you find this effective? What are the pros and cons of embedding a data table within a graph? Would you keep it or eliminate it in this case?
QUESTION 5: The graph currently shows the proportion who received the vaccination. What if you wanted to focus on the opportunity—the proportion who did not receive the vaccination—how could you visualize this?
QUESTION 6: How would you graph this data? Download it and create your ideal view in the tool of your choice.
Exercise 2.12: which graph would you choose?
Any set of data can be graphed many ways and varying views allow us to see different things. Let’s look at a specific instance of numerous graphs plotting the same data.
You are visualizing data from your employee survey and want to show how employees responded this year compared to last year to the retention item “I plan to be working here in one year.” Figures 2.12a through 2.12d depict four different views of the exact same data. Spend some time examining each, then answer the following questions.

Figure 2.12a Pies
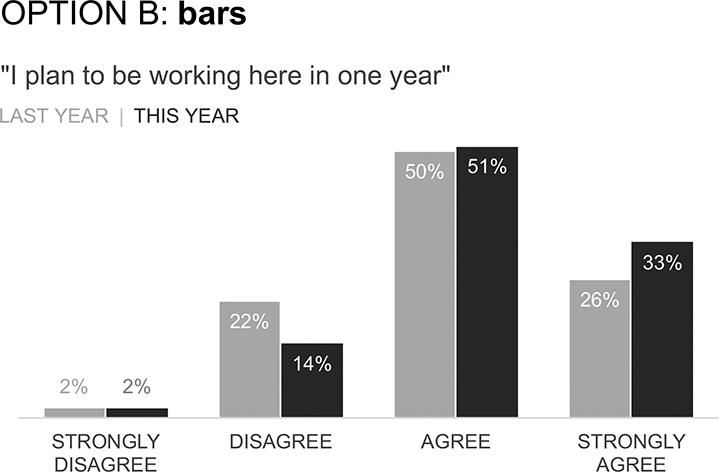


Figure 2.12d Slopegraph
QUESTION 1: What do you like about each graph? What can you easily see or compare?
QUESTION 2: What is difficult about the given view? Are there limitations or other considerations of which to be aware?
QUESTION 3: If you were tasked with communicating this data, which option would you choose and why?
QUESTION 4: Grab a friend or colleague and talk through the various options together. Do they agree with your preferred view, or is there a preference for another? Did your discussion highlight anything interesting that you hadn’t previously considered?
Exercise 2.13: what’s wrong with this graph?
Consider Figure 2.13, which shows response and completion rates for an email marketing campaign where email recipients were asked to complete a survey.

Figure 2.13 What’s wrong with this graph?
STEP 1: List three things that are not ideal about this graph. What makes it challenging?
STEP 2: For each of the three things you’ve listed, describe how you would overcome the given challenge.
STEP 3: Download the data. Create your visual that puts into practice the strategies you’ve outlined.
Exercise 2.14: visualize & iterate
As we’ve seen through a number of examples so far, visualizing data—when done well—can help us spark a magical “ah ha” moment of understanding in our audience. But often it takes iterating—looking at the data numerous ways—both to better understand the nuances of the data and what we want to highlight, as well as to figure out a way that will work for our audience. Let’s practice visualizing and iterating.
Imagine you work at a medical device company and are looking at data that shows patient-reported pain levels when a component of a certain device is turned on and when it is turned off. Figure 2.14 shows the data.

Figure 2.14 Let’s visualize & iterate
STEP 1: Make a list: how many potential methods can you come up with to visualize this data? What different graphs might work? List as many as you can.
STEP 2: From the list you’ve made, create at least four different views of this data (draw or realize in the tool of your choice).
STEP 3: Answer the following related questions:
QUESTION 1: What do you like about each visual? What is easy to compare?
QUESTION 2: What considerations or limitations should you take into account with each?
QUESTION 3: Which view would you use if you were communicating this data?
Exercise 2.15: learn from examples
A great deal can be learned from the data visualizations that others create—both the good and the not so good. When you see a nice graph, pause and reflect: what makes it effective? What can you learn from it that you can apply in your own work? When you see a not-so-good example, do the same thing: stop and examine what was not done well and how you can avoid similar issues in your own work. Let’s practice learning from examples.
Find a graph from the media that’s done well and another that is less than ideal. Answer the following questions for each of these examples.
QUESTION 1: What do you like about it? What makes it effective? Make a list!
QUESTION 2: What do you not like about the example? What limits its effectiveness? How would you approach it differently?
QUESTION 3: What learnings from this process can you generalize to guide your future work?
Exercise 2.16: participate in #SWDchallenge
One of the best ways to learn is to do. The #SWDchallenge is a monthly challenge where readers of our blog practice and apply data visualization and storytelling skills. You can take part, too! Think of it as a safe space to try something new: test out a new tool, technique, or approach. Everyone is encouraged to participate and all backgrounds, experience levels, and tools are welcome.
We announce a new topic at storytellingwithdata.com at the beginning of each month. Participants have a set amount of time to find data and create and share their visual and related commentary. Historically, the focus has been on different graph types, but we sometimes change it up with a tip to try or a specific topic. This is meant to be a fun reason to flex your skills and share your work with others.
All submissions received by the deadline are shared in a recap post later in the given month. The monthly challenges and recap posts are archived at storytellingwithdata.com/SWDchallenge.
There are a number of exercises you can undertake related to this challenge. Visit storytellingwithdata.com/SWDchallenge and tackle one (or more!) of the following:
- Participate! Take part in the live challenge by creating and sharing your work. Or choose a past one as inspiration to flex your data visualization skills. This can be done on your own, with a partner, or as a small team. Share your creations on social media, tagging #SWDchallenge.
- Emulate! Pick a recap post from the archives and review submissions. Select a visual you like and work to recreate it in the tool of your choice. Are there any aspects you would tackle differently than the original author?
- Critique! Select a recap post from the archives and examine submissions. Pick three you believe are effective and describe what is done well. Consider how you could generalize the learnings to apply to your own work. Pick three designs you believe are not ideal and reflect on the issues you see and how you could overcome them. What common challenges can you generalize from this that you can overcome in your own work?
- Run your own challenge! Get a group of colleagues or friends together, pick a past challenge (or create your own), and run your own version: everyone has a set amount of time to find data and create their visual. Share them with each other. Get together to discuss, giving everyone the opportunity to share their creation and receive feedback from others. Examine what you learn from this process that you can apply to future work. See Exercise 9.4 for more on how this fun process can help cultivate a feedback culture.

Exercise 2.17: draw it!
Consider a current project where you need to visualize data. Grab a blank piece of paper and a pen or pencil. Set a timer for 10 minutes and see how many ideas you can sketch out for how to potentially show your data.
When the timer goes off, step back and take inventory of what you’ve created. Which view(s) do you like best? Why is that?
Show your sketches to someone else. Explain to them what you want to communicate. Which visuals(s) do they like best? Why is that?
If you ever feel stuck or are looking for an innovative approach and having trouble coming up with one on your own, grab a conference room with a whiteboard and a creative colleague or two. Talk them through what you want to show. Start drawing—and redrawing. Debate as you mock up the different views: what works well? What is lacking? Which visuals(s) are worthy of creating in your tools? Can you do it on your own, or if not, what or who can help you realize your ideas?
Exercise 2.18: iterate in your tool
Allowing yourself time and flexibility to iterate through different views of your data allows you both to better understand the nuances and determine which way of showing the data might help you achieve that magical “ah ha” moment of understanding that you seek in your audience.
Take some data you’d like to visualize. Open your favorite graphing tool and start creating different visuals. How many ways can you come up with to look at the data? Set a timer for 30 minutes and iterate to create different views of the data in your graphing application.
When the timer goes off, assess for each: what are the pros and cons? What do you want to enable your audience to see? Which iteration(s) will facilitate this? If unsure, jump to Exercise 2.21, which provides some tips for soliciting feedback from others.
Exercise 2.19: consider these questions
When you create a graph, it’s not surprising that it makes sense to you. You are familiar with the data, and you know what to look at and what is important. Don’t assume this is necessarily true for your audience. After you’ve made your graph, ask the following questions to help determine whether further iteration is necessary.
- What are you trying to show? What do you want to enable your audience to do with your data? Does the visual you’ve created facilitate this? What takeaways are easiest to see? What comparisons are easiest to make? What things are harder to do given the way you are showing the data?
- How important is it? Is this a critical issue or merely something that people might find interesting? What are the stakes? Is it a scenario where quick and dirty is okay? What level of perfection is warranted? What level of accuracy is required?
- Who is your audience? Is your audience familiar with the data you are presenting or is it new? Does it fit in with their preconceived notions, or may it challenge a held belief? Does your audience expect the data to be presented in a certain way? What are the pros and cons of following the norm in this situation compared to doing something new or unexpected? What questions will your audience have and how can you anticipate and be prepared to seamlessly address them?
- Is your audience familiar with the type of graph? Anytime we use something less familiar to our audience, we are introducing a hurdle: we either have to get them to listen to us long enough to tell them how to read the graph, or get them to spend enough time with it to figure it out on their own. If you’re using something less familiar, have a good reason for it. Does this view let your audience easily see something that would otherwise be difficult, or create a new insight that isn’t possible with more familiar ways of graphing the data? Consider also: how much time do you want to spend talking about the graph—how much of your audience’s brainpower do you want them to spend trying to understand the graph versus what the data in the graph shows?
- How are you presenting the information? Will you be there live in person to talk through the data, set context, and answer questions, or are you sending something around that has to be processed on its own? Especially in the case where you aren’t there, you need to take intentional steps to make it clear to your audience what the graph represents, how to read it, and how you want them to process your data.
Exercise 2.20: say it out loud
After you’ve created your graph or your slide, practice talking through it out loud. If you’ll be presenting the data in a live setting (a meeting or presentation), put it on the big screen and practice discussing it as you would in a meeting. Even in the instance when you will send it off for your audience to process the data on their own, there can be important benefits to talking through your graphs.
First, set up how to read the graph, what it shows, and what each axis represents. Then talk through the data and what important observations can be made. What you say may reveal pointers on how to iterate. If you find yourself saying things like, “This isn’t important” or “Ignore that,” these are cues for elements you can push to the background (or in some instances, eliminate entirely). Similarly, when you hear how you direct attention when talking through the data, consider how you can achieve this visually through the way you design the graph.
In the case where you will be presenting the data live, practicing out loud will also help make the ultimate delivery smoother. First, do this on your own. Once you feel good about that, practice talking through it with someone else and get their feedback. The next exercise (Exercise 2.21) provides more pointers for getting good graph feedback.
Want to learn more benefits to saying it out loud? Listen to Episode 6 of the storytelling with data podcast (storytellingwithdata.com/podcast), which focuses on this topic.
Exercise 2.21: solicit feedback
You’ve created a graph and you think it’s pretty awesome. The challenge is that you know your work better than probably anybody else and since you’re the one who created the graph, of course it’s going to make sense to you. But will it work for your audience?
Or what about the scenario where you’ve iterated in your tool—you’ve created several different views of the data but aren’t entirely sure which one will work best?
In each of these cases, I recommend soliciting feedback from others.
Create your visual or set of graphs and find a helpful friend or colleague. It can be someone without any context. Have them talk you through their thought process for taking in the information, including:
- What do they pay attention to?
- What questions do they have?
- What observations do they make?
This conversation can help you understand whether the visual you’ve created is serving its intended purpose, or if it isn’t, give you pointers on where to concentrate your iterations. Ask questions. Discuss your design choices and talk about what is working effectively and what might not be as obvious to someone who is less close to the data. Seeking feedback from various sources can also be beneficial: think about when it would be helpful to get feedback from someone in a totally different role than your own.
Also, watch initial facial responses: there is a microsecond that passes before people censor their physical reactions. If you see any furrowing of brows or pursing of lips—any general face-scrunching—these are micro-cues that something may not be working quite right. Pay attention to these cues and work to refine your visuals. If people are having a hard time with your graph, don’t assume it’s them. Consider what you can do to make the information easier to take in: perhaps you can more clearly title or label, use sparing color to focus attention, or choose a different graph type to get your point across more easily.
You’ll find additional guidance for giving and receiving effective feedback in Exercise 9.3.
Exercise 2.22: build a data viz library
Collect and build a library of the effective data visualization examples created and used at work. You can do this on your own, or this can be an excellent undertaking for a team or organization. Be thoughtful how you organize the content for easy searchability (for example, by graph type, topic, or tool). Make files available to download so others can see the specifics of how they were made and modify for use in their own work. You can also add effective examples that you encounter externally from the media, blogs, or #SWDchallenge.
Make effective data visualization a team goal. To ensure continued focus, host a regular friendly competition, where individuals can nominate their own or their colleagues’ examples of effective data visualization. Each month or quarter, choose winners and archive their work in the shared library. This can be a great ongoing source of inspiration: if someone is feeling stuck, they have something to turn to and flip through for possible ideas. It is also an excellent resource for new hires, so they have examples of effective data visualization in your work environment, helping set the right expectations for their own work.
Exercise 2.23: explore additional resources
There are many additional resources out there when it comes to choosing an effective graph or getting inspiration from other people’s creations. Practicing, getting feedback, and iterating are keys to success. That said, here are a few chart choosers I’m aware of that you may find helpful when it comes to figuring out what graphs might work for your specific needs:
- Chart Chooser (Juice Analytics, labs.juiceanalytics.com/chartchooser). Use their filters to find the right chart type for your needs, download as Excel or PowerPoint templates and insert your own data.
- The Chartmaker Directory (Visualizing Data, chartmaker.visualisingdata.com). Explore the matrix of chart type by tool and click the circles to see solutions and examples.
- Graphic Continuum (PolicyViz, policyviz.com/?s=graphic+continuum). The poster includes more than 90 graphic types grouped into six categories. Also check out the related Match It Game and Cards.
- Interactive Chart Chooser (Depict Data Studio, depictdatastudio.com/charts). Explore the interactive chart chooser using filters.
Check out the following collections to browse other people’s work for inspiration. For each graph you encounter, pause to reflect on what works well (or not so well) and consider how you can use (or avoid!) similar aspects in your own work:
- Information Is Beautiful Awards (informationisbeautifulawards.com). These annual awards celebrate excellence and beauty in data visualizations, infographics, interactives, and informative art. The archives contain hundreds of data visualizations.
- Reddit: Data Is Beautiful (reddit.com/r/dataisbeautiful). A place for visual representations of data: graphs, charts, and maps.
- Tableau Public Gallery (public.tableau.com/s/gallery). Stunning data visualization examples from across the web created with Tableau Public. In particular, check out the Greatest Hits Gallery using the drop-down menu.
- The R Graph Gallery (r-graph-gallery.com). Looking for inspiration or help? Here you will find hundreds of distinctive graphics made with the R programming language, including code.
- Xenographics (xeno.graphics). Xeno.graphics is a repository of novel, innovative, and experimental visualizations to help inspire, fight xenographphobia and popularize new chart types.
Exercise 2.24: let’s discuss
Consider the following questions related to Chapter 2 lessons and exercises. Discuss with a partner or group.
- How is the way that we process tables different from how we process graphs? What are the pros and cons of presenting data in tabular form? In what circumstances does it make sense to use a table? In what scenarios should you avoid a table?
- One common decision when graphing data is whether to have a y-axis that is titled and labeled or omit the axis and label the data directly. What considerations should you make when determining which is better for a given situation?
- When is it okay to have a non-zero baseline when graphing data?
- Why is paper a good tool for graphing data? Were the exercises in this chapter that asked you to draw helpful? Will you use this low-tech method in your work going forward? Why or why not?
- What is the purpose of graphing a given set of data multiple ways? Why is it important to iterate and look at different views of your data? When will you take the time to do this going forward? When does it not make sense to spend time on this?
- The examples in SWD and in this book are mostly basic charts: a lot of lines and bars. When does it make sense to use a graph that is more novel or less familiar? What are the pros and cons of using a graph that your audience may not have previously encountered? What steps can you take in this situation to help ensure success?
- Are there any cases where data has historically been graphed a certain way by your team or your organization that you believe should be changed? How might you drive this change? What sort of resistance or pushback do you anticipate? How can you address this?
- What is one specific goal you will set for yourself or your team related to the strategies outlined in this chapter? How can you hold yourself (or your team) accountable to this? Who will you turn to for feedback?
