4
Quantum Computing
Manisha Bharti* and Tanvika Garg
National Institute of Technology, Delhi, India
Abstract
Quantum computers can bring about development in various fields like science and medicine that could save lives. Quantum computing can be instrumental in the advancement of machine learning so that illness can be diagnosed very quickly. With its help materials can be discovered so that efficient structures and devices can be made. It helps to bring about development in financial strategies so that one could lead a better life in retirement. There are various benefits of classical computing that one can experience in day-to-day life. But there are many challenges in today’s world which cannot be solved using classical computing. So quantum computing is developed that can be used to enhance the various algorithms in different fields.
Keywords: Entanglement, superposition, qubits, optical quantum computing
4.1 Introduction
Quantum Computing is the modernization of computing. It is based on quantum mechanics and its phenomena. Quantum computing is the combination of physics, computer science, information theory and mathematics. It provides lower energy consumption, higher computational power and better speed than the classical computers. These can be achieved by controlling how the small objects behave, i.e., microscopic particles like atoms, electrons, photons, etc.
4.2 A Brief History of Quantum Computing
The idea of a quantum mechanics-based computational device was first thought about in the 1970s and early 1980s by scientists such as Paul A. Beniof of Arogonne National Laboratory in Illinois, David Deustch of the University of Oxford, Charles H. Bennet of the IBM Thomas J. Watson Research Centre and Richard P. Feynman of Caltech. When the scientists were thinking about the limitations of computation, they came up with this idea. In 1982, Feynman made an attempt to conceptualize the computer based on the quantum physics principles. He came up with a model that showcases how the computations could be performed using quantum system. He also explained the way a machine can simulate physical problems based on quantum physics.
In other words, a physicist would be capable of performing experiments in quantum physics using a quantum mechanical computer. Feynman later made an analysis that quantum computers can solve such problems that a classical computer cannot solve. The reason behind this is that a classical computer needs exponentially growing time to solve such problems while a quantum computer takes polynomial time to perform such a calculation.
In 1985, Deutsch proposed that the theory that Feynman asserted could be used to make a general-purpose quantum computer. He showed that any physical process can be modelled by a quantum computer. Thus, a quantum computer would be far more capable than a traditional classical computer. So, in order to find other interesting applications for quantum computers, efforts were made by scientists of those times. But not much success was achieved in this regard. In 1994, Peter Shor came up with an idea of using quantum computers to crack a problem in number theory, namely factorisation. This breakthrough transformed quantum computing from just an academic curiosity to something that was of great interest to many in the world.
At present, there is a need of high security, bandwidth and computational requirement. This could not be fulfilled by the classical approach. The classical approach does not provide a solution in computing that one can rely upon. The approach led to the development of physics (quantum) along with quantum computing. Efficient algorithms are required to be developed in the field of computing in order to use the quantum mechanics’ principles in this field.
The quantum mechanics’ basic postulates that govern quantum computing, entanglement and polarization, and applications such as quantum cryptography, teleportation, etc., are described in the next section.
4.3 Postulate of Quantum Mechanics
Quantum computing is ruled by four postulates. These postulates are the outcome of the observations which we get through experiments. These postulates are given as follows [2]:
“The actual state of any closed physical system can be described by means of a so-called state vector v having complex coefficients and unit length in a Hilbert space V, i.e., complex linear vector space (state space) equipped with an inner product.” [2]
“The evolution of any closed physical system in time can be characterized by means of unitary transforms depending only on the starting and finishing time of the evolution.” [2]
“Any quantum measurement can be described by means of a set of measurement operators {Mm}, where m stands for the possible results of the measurement. The probability of measuring m if the system is in state v can be calculated as” [2]
“The state space of a composite physical system W can be determined using the tensor product of the individual systems W = V ⊗ Y. Furthermore, having defined v ∈ V and y ∈ Y then the joint state of the composite system is w = v ⊗ y" [2].
4.4 Polarization and Entanglement
Polarization is achieved by orienting the oscillations that are perpendicular to the plane in which a transverse wave is travelling. In context of the quantum computing, photons are a bunch of light particles. These particles obey all the above postulates and preserve the polarization property [3]. The vertical and horizontal polarizations of light are explained by the following figures.
The vertical and horizontal polarizations are represented by pv and ph.The angular polarization is represented by pθ [1]. In the classical approach, we can transmit any of the horizontal or vertical polarized light in order to send logic bit 1. We do not transmit anything for logic bit 0. We can also perform the encoding of the light that is vertically polarised to logic 1 and horizontally polarised to logic 0 and then transmit it. This method makes it easier to obtain the information from the bit received [1]. The light which is polarized, if transmitted in 45 degree one cannot tell of it being logic 1 or 0 because it is at equal distance from the two axes. Therefore, half of it is decoded as logic 0 and other half of it as logic 1 by quantum measurement device. This is a random detection. The quantum mechanics’ indeterminacy is emphasized by it. This can be explained by taking the example of the tossing of a coin [1].
Let say there are three engineers, Bob, Alice and Eve. Alice wishes to send information to Bob, i.e., ‘heads’ as ‘1’ and tails as ‘0’. This transmission has no difficulty till Eve comes in between. Eve changes the state of the coin randomly which it takes from Alice. This leads to the confusion for Bob and error in the reception occurs. Bob and Alice learnt about quantum mechanics. They took the decision to use its properties in this situation. The rotation of the coin is performed by Alice. And then she sends it to Bob. In between, Eve takes the coin and flips it. But Bob knows that the direction of rotation represents the information and not heads or tails. So it is easy for him to decode clockwise as logic 1 and anticlockwise as logic 0. In the quantum mechanics scenario, the coin is replaced by photon and the rotation by polarization [4].
Another spectacular physical phenomenon is Entanglement or quantum superposition, which is seen in the quantum computing world. The quantum states of these particles could not be independently described when they interact in such a way. The generation of particles could be done in such a way that they have entangled states. The particles are able to preserve their states (quantum) even though they are very far away from each other [3].
This scenario is again explained by the example of Alice, Bob, and the coin. This time Alice tosses two coins in place of one coin. She asks Bob to catch both of them. Four possible outcomes can be obtained by Bob. In order to ensure that both the coins rotate in the same manner simultaneously, Alice sticks a rod to them. Bob receives only two states which could either tails or heads. The scenario can be elaborated. Suppose Bob and Alice are three miles away from each other. The rod’s length is increased to three miles. Alice asks Bob to collect the coin from three miles away after she has tossed it. Bob receives the same information as both the coins are in the same state. This could be related to the quantum communication world. The photonic entanglement can be represented as the two coins, the transmitter is Alice, the receiver is Bob and the distance is the channel [7].
The entanglement and polarization phenomena are very interesting and useful. They can be extended into applications that are security based like quantum key distribution, quantum cryptography, etc. [4].
4.5 Applications and Advancements
4.5.1 Cryptography, Teleportation and Communication Networks
In this application, the transfer of particle’s quantum state takes place over a distance. This phenomenon is based on the quantum entanglement that has been mentioned before. The information moves from one point to another in the phenomenon of teleportation. Cryptography and computing is one of the major applications of entanglement [1]. Mathematical problems and algorithms are the basis of conventional cryptography. So if the algorithm is cracked efficiently, the security of the information is lost. Here, entanglement comes into the picture. The attempt of eavesdropping alters the situation and can also be analysed. This makes the communication reliable without using complicated procedures and algorithms [9]. This helps for the establishment of secure quantum communication [5].
4.5.2 Quantum Computing and Memories
This is the field in which entanglement and superposition is directly used to perform operations on data. This idea was first introduced by Richard Feynman and Yuri Maninwere [3]. Quantum computers will be more efficient than classical ones, with fewer problems. Along with integer factorization, many other algorithms and problems are analysed by making use of quantum computing techniques [8, 11].
A huge amount of inventions have occurred in this domain. Researchers have invented different quantum computer models. Some of them are one-way quantum computer, quantum gate array, topological quantum computer, and adiabatic quantum computer. It has been found by researchers that quantum computers based on the architecture of Von-Neumann are possible. Also, Quantum computing breakthrough with integrated circuits (superconducting) is also possible [9].
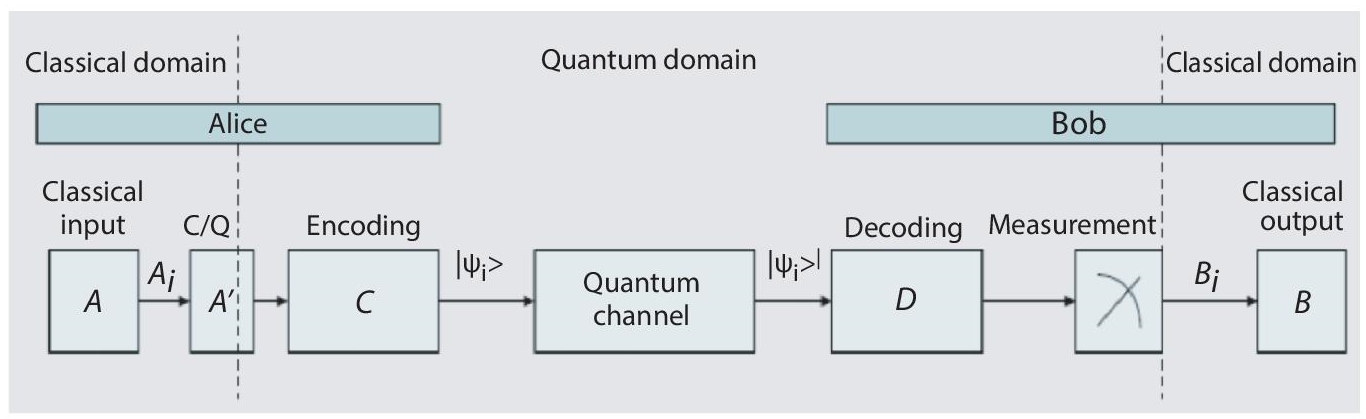
Figure 4.1 Quantum satellite transmission [Bacsardi et al., [4].
4.5.3 Satellite Communication Based on Quantum Computing
A quantum channel is a channel that carries out the transmission related to classical and quantum information. Figure 4.3 depicts classical information’s transmission done by the sender to the receiver through quantum channel (satellite). The starting of communication is done in classical domain which is later converted to quantum domain. This can be seen as an analogy to the channel coding and source coding in the domain related to classical computing. The channel is used to send data. The damaged bits are received by Bob. The quantum transformations (block D) are performed by him. Finally, the data is measured by him [10].

Figure 4.2 Configurations of satellite communication [Marshall et al., [6].
Figure 4.3 Vertical and horizontal polarization [1, 9].
4.5.4 Machine Learning & Artificial Intelligence
Artificial intelligence and machine learning are the booming areas in the 2020s. These emerging technologies have affected the lives of humans. Some widespread applications in everyday life are in voice, handwriting and image recognition. It has become challenging for traditional computers to provide that level of accuracy and speed, which has led to the development of quantum computers that provide processing of complex problems in fractions of a second. This would have taken traditional computers thousands of years.
4.6 Optical Quantum Computing
Light’s basic unit is the photon. A photon is encoded by using polarization. Optical quantum computing basically uses polarization. The electromagnetic theory defines light’s physical nature. The direction of light’s electric part is defined by the direction of polarization. If the vertical and horizontal directions are defined as 1 and 0 by using the concept of polarization encoding, then other polarizations, e.g., elliptical polarization, π/4-polarization and circular polarization are the superposition of 1 and 0.
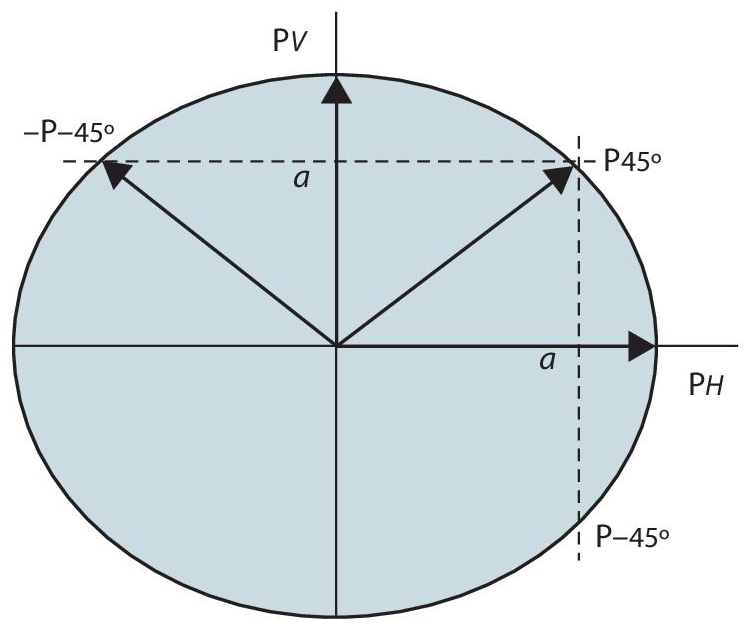
Figure 4.4 Representation of vector of different polarizations (photon) [1] Sandorlme et al., [9].
A photon passes through the component and makes a measurement on its polarization state [13, 14].
4.7 Experimental Realisation of Quantum Computer
The simple architecture helps in making the quantum computer smaller, faster and cheaper. The intricacies (conceptual) are causing difficulty in its experimental realization. Many attempts have been made in this field with fruitful outputs. However, the time is not far away when the digital computer will be fully replaced by the quantum computer. Some of the many attempts that have been made are summarized below.
4.7.1 Hetero-Polymers
The first quantum computer based on hetero-polymer was built in 1988 by Teich and was later improved by Lloyd in 1993. The array of atoms formed in linear fashion is utilised as cells (memory) in a hetero-polymer computer. The storage of information is done on a cell when the pumping of the corresponding atom is performed into an excited state. Instructions are given to the hetero-polymer by making use of laser pulses. The duration and the shape of the pulse decides the computation’s nature that is performed on chosen atoms.
4.7.2 Ion Traps
A quantum computer based on an ion trap was first proposed by Cirac and Zoller in 1995 and it was worked on first by Monroe and collaborators in 1995 and then by Schwarzchild in 1996. This computer performs the encoding of data in ions’ energy states and in modes of vibration between the ions. Conceptually, a separate laser operates each ion. It was demonstrated that the ion trap computer can be helpful in evaluating Fourier transforms which leads to Shor’s factoring algorithm (based on Fourier transforms).
4.7.3 Quantum Electrodynamics Cavity
A quantum electrodynamics (QED) cavity computer was invented by Turchette and collaborators in 1995. This computer has a cesium atoms filled in QED cavity. It also consists of an arrangement of lasers, polarizer, phase shift detectors and mirrors.
4.7.4 Quantum Dots
Quantum dot technology-based quantum computers use simple architecture. They also use less sophisticated theoretical, experimental, and mathematical skills. The fabrication of quantum gates is done using quantum dots array in which the connection of dots is carried out by using the split gate technique. This technique has an advantage; the controlling of quibits is done electrically.
4.8 Challenges of Quantum Computing
Quantum computing, if built in large scale, is a novel technology that can carry out computation powerfully. However the processes such as fabrication, verification and architecture are some of the challenges that it presents. As it has to store a complex information in one bit, the building, verification and designing of quantum computers become very difficult. They are fragile and should be operated at low temperatures. It very often gives more errors than classical computers, so error correction is one of the dominant tasks that are needed to be performed in the building of quantum computers.
4.9 Conclusion and Future Scope
Many universities, research groups, and colleges are working on this topic, hence the quantum computing field is developing rapidly. More and more research is being done and is used in various applications. The challenge in this field is to move from carrying out experiments to controlling the phenomenon of quantum computing. The conventional computer’s performance can be exceeded by the system which obeys quantum mechanical laws. It might take years to build the quantum computers commercially but it would definitely bring about a revolution.
References
- 1. Bacsardi, L., and S. Imre. “Supporting Space Communications with Quantum Communications Links.” Global Space Exploration Conference. 2012.
- 2. Imre, Sándor, and Ferenc Balazs. Quantum Computing and Communications: An Engineering Approach. John Wiley & Sons, 2005.
- 3. Imre, Sándor, and Laszlo Gyongyosi. Advanced Quantum Communications: An Engineering Approach. John Wiley & Sons, 2012.
- 4. Bacsardi, Laszlo. “Satellite communication over quantum channel.” ActaAstronautica 61.1 (2007): 151-159.
- 5. Villoresi, Paolo, et al. “Experimental verification of the feasibility of a quantum channel between space and Earth.” New Journal of Physics 10.3(2008): 033038.
- 6. W. Marshall, “NASA Earth-Satellite Links: Phone Sat,” 1st NASA Quantum Future Technologies Conf., 2012.
- 7. Morong, William, Alexander Ling, and Daniel Oi. “Quantum optics for space platforms.” Optics and Photonics News 23.10 (2012): 42-49.
- 8. A. Einstein, B. Podolsky, and N. Rosen, “Can Quantum mechanical Description of Physical Reality Be Considered Complete?” Phys. Rev., vol. 47, 1935.
- 9. SándorImre, Quantum Communications: Explained for communication Engineers, IEEE Communications Magazine, August 2013.
- 10. Bacsardi, Laszlo, On the way to quantum based satellite communications, IEEE Communications Magazine, August 2013.
- 11. Quantum communicatons leap out of the lab, Nature Physics, 24 April 2014, Vol. 508.
- 12. Crystal quantum memories for quantum communication, Science Daily, 14 July 2014.
- 13. Armando N. Pinto, Nuno A. Silva, Álvaro J. Almeida, and Nelson J. Muga, Using Quantum Technologies to Improve Fiber Optic Communication Systems, IEEE Communication Magazine, August 2013.
- 14. http://physics.about.com/od/quantumphysics/f/quantumcomp.htm
Note
- *Corresponding author: *[email protected]; [email protected]
