16
Comparative Analysis on Material Handling Device Selection Using Hybrid FMCDM Methodology
Bipradas Bairagi*
Department of Mechanical Engineering, Haldia Instritute of Technology, Haldia, India
Abstract
Nowadays, manufacturing industry worldwide is facing ferocious competition, due to which its existence is under question mark. In this circumstance, decision makers in the industry are constantly searching the way of making right decision in every aspect. Right selection of material handling device (MHD) is one of the major area of decision making. This chapter aims to make right decision by combining a number of conventional FMCDM tools, viz. FAHP, FTOPSIS, FMOORA, FVIKOR, FGT, and COPRAS-G techniques through group decision-making process to select the best material handling device. FAHP is used to evaluate criteria weights. To take the merits of diverse evaluation processes, this chapter systematically and reasonably combines all the five remaining tools to introduce a novel super-hybrid approach with the help of entropy method. Solution of an empirical problem on MHD selection is illustrated which establishes the applicability of the approach. The study finds that the present approach is useful and effective to select the best material handling device in FMCDM environment.
Keywords: FMCDM, fuzzy TOPSIS, fuzzy MOORA, fuzzy VIKOR, fuzzy grey theory, COPRAS-G
16.1 Introduction
Selection of proper Material Handling Device (MHD) is one of the most imperative managerial decisions. In general, decision makers judge a number of significant criteria while selecting MHD for industrial purpose. However, proper selection of MHD for industrial application is extremely essential. The followings are the brief literature survey in the broad areas of material handling equipment selection published in different open journals.
Goswami and Behera made an investigation for the capability and applicability of two well-known MCDM approaches ARAS and COPRAS for the evaluation and selection of conveyors, AGV and robots as material handling equipment [1]. Soufi et al. introduced an AHP based MCDM methodology for the evaluation and selection of material handling equipment to be utilized in manufacturing systems [2]. Satyam et al. applied a multi attribute decision making approach for evaluation and selection of conveyors as material handling equipment [3]. Nguyen et al. advocated a combined multi criteria decision making model for the evaluation and selection of conveyor as the material handling equipment based on fuzzy analytical hierarchy process and fuzzy ARAS with vague and imprecision information [4]. Mathewa and Sahua made a comparison among the novel multicriteria decision making approaches by solving a problem on material handling equipment selection [5].
Poon et al. used genetic algorithm to address MHE selection and operation allocation on selection of industrial conveyor [6]. Fonseca et al. proposed a knowledge-based method for selection of conveyor equipment as material handling equipment [7]. Tuzkaya et al. integrated FMCDM methodologies such as ANP and PROMETHEE utilizing fuzzy set for MHE selection [8]. Chatterjee et al. solved and compared robot selection problem using two MCDM techniques [9]. Shih developed TOPSIS-based group decision algorithm to choose robots applying incremental based benefit–cost ratio [10].
Kahraman et al. proposed a fuzzy hierarchical TOPSIS model for selection of industrial robotic systems [11]. Sujono and Lashkari proposed a method for simultaneously determining the operation allocation and material handling system [12]. Kulak developed a decision support system for MHE selection under fuzzy environment FUMAHES [13]. Lashkari et al. suggested an MH selection and operation allocation model in a cellular based manufacturing system [14].
Chan et al. developed a smart MHE selection advisor (MHESA) [15]. Chu and Lin proposed a FTOPSIS approach where the objective criteria values were transformed into index without dimension to make sure compatibility among linguistic terms and crisp value of subjective and objective criteria respectively. Through internal arithmetic of fuzzy numbers, the defuzzying of weighted rating into crisp values by the ranking method of mean of removals and determination of closeness coefficient, the robots were ranked [16].
The above literature survey reveals that some of the past researchers have applied MCDM techniques for solving material handling device (MHD) selection problem. However, this endeavor is inadequate for exhaustive and extensive decision making regarding proper selection of MHD from thousands of available alternatives under multiple conflicting criteria of diverse categories. Therefore an effort in the chapter is made to suggest appropriate techniques in making right decision by combining a number of conventional FMCDM tools, viz. FAHP, FTOPSIS, FMOORA, FVIKOR, FGT, and COPRAS-G techniques through group decision-making process to select the best material handling devices.
This research has the following objectives: (a) Comparative study of the results of the MHD evaluation problem (b) Aiding decision makers by providing the way of making more accurate decision.
The rest of the chapter is divided into several subsections. Section 16.2 describes FAHP provide Entropy methods as weight evaluation techniques. Section 16.3 briefly states the steps of six MCDM methodologies. A practical problem on material handling devices selection is specified in section 16.4. The next section 16.5 illustrates the calculation along with discussion with some salient points of the chapter. And last, Section 16.6 is dedicated to make suggestions for the direction of future research.
16.2 MCDM Techniques
16.2.1 FAHP
The concept of FAHP is briefly stated below.
Step 1: Frame a weight matrix in linguistic terms assessed by comparison between every pair of criteria.
Step 2: Transform the linguistic terms into respective fuzzy numbers.
Step 3: Build fuzzy average weight matrix.
Step 4: Calculate Geometric Mean (GM) of the fuzzy weights for each criterion.
Step 5: Calculate fuzzy weights for each criterion.
16.2.2 Entropy Method as Weights (Influence) Evaluation Technique
Entropy weighting method has been utilized to assess the objective (quantitative) weights of the FMCDM tools those are fused together to construct the proposed super hybrid approach. The step by step process of entropy method is illustrated below [17].
Step 1. Carry out the normalization of scores/ratings of the decision matrix using the following equation.
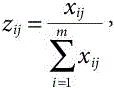
zij is normalized crisp value, xij crisp rating of ith alternative by jth method. Here i, j stand for a natural number less than or equal to m and n respectively, m is alternative number and n is criteria number.
Step 2. Calculate the entropy of each criterion with the following equation.
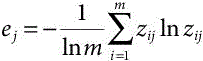
Step 3. Calculate weight (importance) of the jth criterion by the equation.
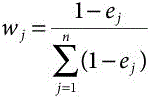
wj stands for objective (crisp) weight for jth criterion (here, methods to be integrated) 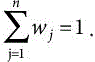
16.3 The Proposed Hybrid and Super Hybrid FMCDM Approaches
The conception of fuzzy set theory when applied in MCDM environment is termed FMCDM [18]. FMCDM approach can support in decision making by evaluating, selecting the most excellent alternative. This chapter integrates five FMCDM techniques (Fuzzy TOPSIS, Fuzzy MOORA, Fuzzy VIKOR, Fuzzy Grey Theory and COPRAS-G) independently with FAHP for the purpose.
Five integrated techniques have been combined together with entropy method to construct the super hybrid algorithm which is constructed to take the merits of diverse evaluation procedures. The abovementioned five well-known MCDM techniques are used in MHD selection due to their wide and successful applications by past researchers in finding the best alternatives. Hybrid FMCDM approaches are described in subsection 16.3.1 to 16.3.5 whereas the proposed super hybrid approach is furnished in subsection 16.3.6.
16.3.1 TOPSIS
TOPSIS was developed and advocated by Hwang and Yoon [19]. FTOPSIS is the integration of theory of fuzzy set with TOPSIS. In past several researchers extended the TOPSIS in fuzzy environment. TOPSIS is a reference point approach. TOPSIS/FTOPSIS is on the basis of the idea that chosen alternative be supposed to have the least Euclidian distance from PIS and the highest Euclidian distance from the NIS. In this technique a worse score of one criterion can be canceled out by a better score of another criterion. Since TOPSIS/FTOPSIS permit trade-offs between criteria hence it is a compensatory method. TOPSIS/FTOPSIS gives an additional sensitive form of representation which takes in or rule out alternative resolution based on rigid cut-offs. The practical steps of FTOPSIS technique are stated below.
Step1: Build the decision matrix consisting of fuzzy numbers.
Step 2: Make the weight matrix consisting of fuzzy numbers.
Step 3: Perform the normalization process the fuzzy ratings.
Step 4: Compute the weighted normalized decision matrix with fuzzy numbers.
Step 5: Find the fuzzy PIS and Fuzzy NIS.
Step 6: Determine separation measures, positive and negative, for each alternative.
Step 7: Find relative closeness for each alternative.
Step 8: Determine the modified closeness coefficients by using the normalizing equation.
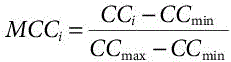
Where, MCCi is the modified closeness coefficient of alternative i, CC is the closeness coefficient of alternative i, CCmax is the maximum modifiedi closeness coefficient of the alternatives and CCmin is the minimum closeness coefficient of the alternatives. The value of MCCi ranges from 0 to 1; in other words, 0 ≤ MCCi ≤1.
Step 9: Select the best alternative with the highest MCCi and identify the worst alternative with the least MCCi .
16.3.2 FMOORA Method
Brauers and Zavadakas was first to introduce MOORA method [20]. FMOORA or fuzzy MOORA method is the concept of integration of Fuzzy set with classical MOORA. FMOORA is composed of of the following steps.
Step 1: Construction of decision matrix
Step 2: Normalization of the fuzzy performance ratings
Step 3: Determination of net score
Step 4: Best non-fuzzy performance (BNP) of each alternative is computed
Step 5: The best alternative has the maximum BNP value and the worst alternative has the minimum BNP value.
16.3.3 FVIKOR
VIKOR (Visekriterijumsko KOmpromisno Rangiranje) is an MCDM method associated with optimization and compromise. VIKOR was introduced by Zeleny [21]. VIKOR method is stated below.
Step 1: Decision matrix is constructed with fuzzy performance rating.
Step 2: PIS and NIS are determined of each criterion.
Step 3: Determine the optimal solution of alternatives’ comprehensive evaluation (Si) and the worst solution of alternatives’ comprehensive evaluation (Ri).
Step 4: Compute the value of Qi for each alternative.
Step 5: Arrange the alternatives as per the increasing sequence of defuzzyfied Si, Ri and Qi values. The alternative with the least value corresponds to the best one and alternative with the largest value is associated with the highest rank. Thus, three ranks of the alternatives are obtained.
Step 6: Check whether both of the state of acceptable advantage and stability in decision-making simultaneously satisfy.
16.3.4 Fuzzy Grey Theory (FGT)
Fuzzy grey theory is an efficient technique for analysis of mathematical systems characterized by uncertain information and insufficient data in fuzzy environment [22]. The procedural steps with various normalization techniques used for different sense of the criteria are furnished below [23].
Step 1: Reference data is set. Reference data consists of the most favorable value or target value for each criterion.
Step 2: Performance values for each alternative with respect to each criterion determined.
Step 3: Normalization of performance values is accomplished.
Step 4: The differences between data sets are computed. Global maximum and global minimum for each criterion are determined.
Step 5: Grey relation coefficient is evaluated.
Step 6: The fuzzy grey relational grade (GRG) is computed.
Step 7: The alternative having the maximum value of objective GRG is the most excellent alternative and the alternative with the minimum objective GRG is the worst alternative.
16.3.5 COPRAS –G
The concept of integration of Gray system theory with COPRAS (Complex Proportional assessment) is termed as COPRAS-G. COPRAS-G is a relatively fresh technique for the alternative appraisal in interval considering multiple criteria. COPRAS-G method has the following simple steps.
Step1: Form a decision matrix consisting of performance rating of alternatives in interval.
Step 2: Carryout the normalization of performance rating.
Step 3: Construct the weight matrix.
Step 4: Compute weighted normalized decision matrix.
Step 5: Calculate the average value of weighted normalized rating for every alternative with respect to each benefit criterion.
Step 6: Compute the average value of weighted normalized rating for every alternative with respect to each cost criterion.
Step 7: Evaluate relative weight of every alternative.
Step 8: Determine the degree of utility for every alternative.
Step 9: Determine modified utility index by using the normalizing equation.
Step 10: Select the alternative having the highest value of utility index or modified utility index.
16.3.6 Super Hybrid Algorithm
In this research, a super hybrid algorithm is introduced by integrating FTOPSIS, FMOORA, FVIKOR, fuzzy grey theory, and COPRAS-G. Each of these MCDM tools has computational and functional capability for finding the best alternative. To incorporate all these merits into the selection index of the paramount alternative, the research advocates the use of the following formula.
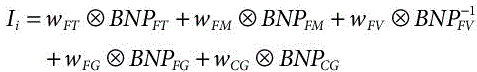
where, the notations represent the following implication.
Ii denotes the objective measure of ith MHD selection index. The higher the value of Ii, the better is the MHD. Hence higher value of Ii is desirable. The alternative associated with the highest value is the best solution. Where, wFT, wFM, wFV ,wFG and wCG denote the weight of fuzzy MOORA, fuzzy VIKOR, fuzzy grey theory, and COPRAS-G respectively. Entropy is considered as weight measuring method due to its inherent ability to calculate weights based on decision data, i.e. BNP obtained by the tools. A careful observation shows that the weights are directly proportional to dispersion of the BNP values. BNPFT, BNPFM, BNPFV, BNPFG and BNPCG are the BNP of ithMHD, obtained by respective methods. In the above equation, (![]() the reciprocal of BNPFV) is used as it is associated with benefit value.
the reciprocal of BNPFV) is used as it is associated with benefit value.
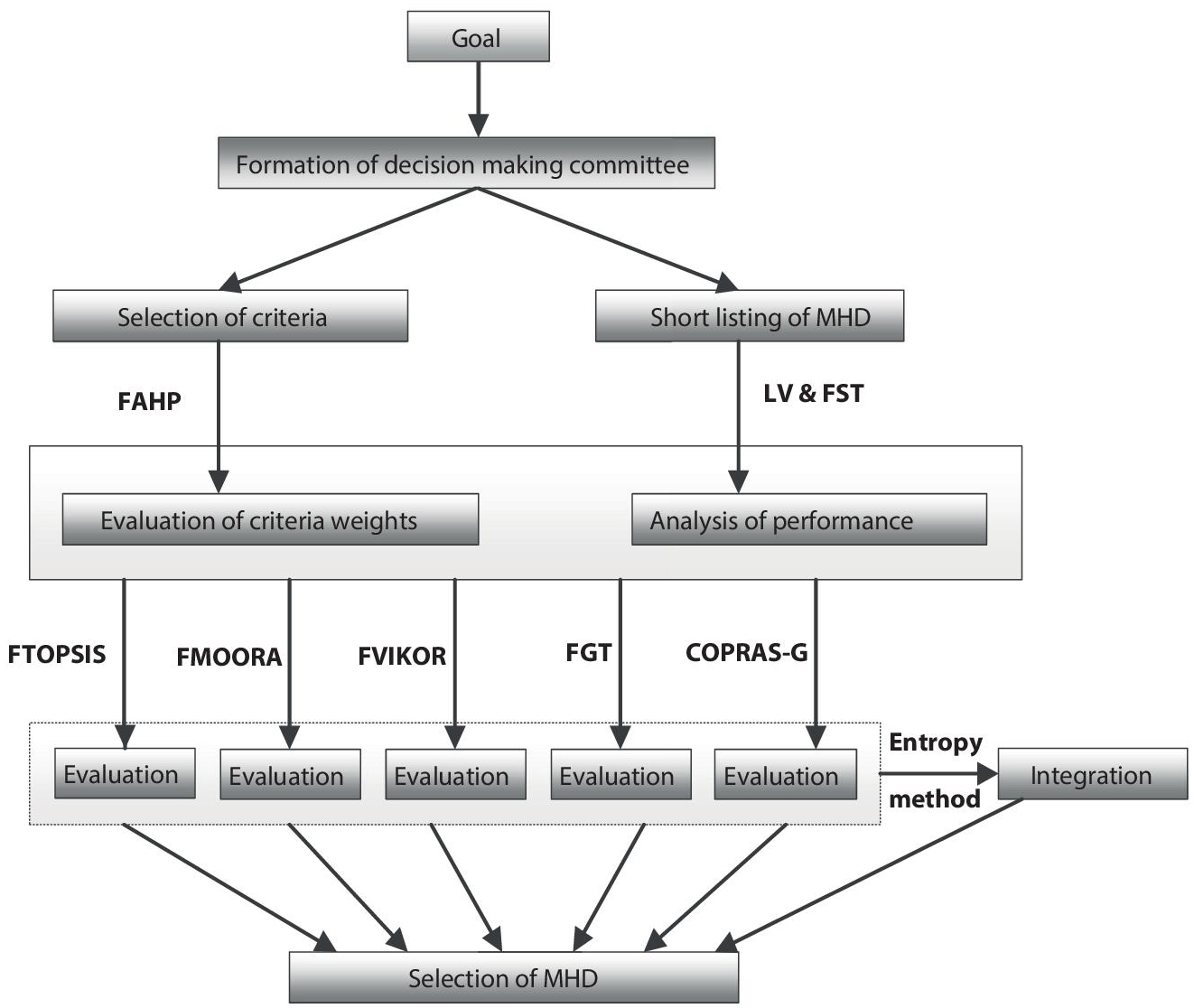
Figure 16.1 Decision making framework for MHD selection.
An evaluation framework for the selection of MHD is shown in Figure 16.1. These six proposed methodologies are illustrated with a real life problem of MHD selection under FMCDM environment. The problem on MHD selection is defined in the following section.
16.4 Illustrative Example
An Eastern Indian manufacturing organization needs to decide on the top MHD before ordering it to the vendors. The organization makes a team/committee which preliminary screens five different material handling devices. The committee unanimously considers six selection criteria. The five MHDs are denoted by MHD1, MHD2, MHD3, MHD4 and MHD5. Six selection criteria under consideration are C1: Cost, C2: Floor/Aisle space requirement, C3: Limitation/constraints, C4: Load Capacity, C5: Traveling Distance and C6: Life Period.
C1, C2, C3 are criteria of cost category. C4, C5 and C6 are criteria of benefit category. Subjective criteria are assessed by linguistic terms which are transformed into fuzzy numbers as per Table 16.1. Handbook of MH system design is the source of assess data. Fuzzy numbers, linguistic variables, TFN, (TFN)-1 for criteria weights are accommodated in Table 16.2. Cost is objective criterion, and expressed in crisp number. Remaining five criteria are subjective in nature and assessed by fuzzy data, as in Table 16.3. Decision matrix in TFNs has been shown in Table 16.4. Weighted and normalized version of decision matrix is in Table 16.5. The problem on MHD selection is solved by the proposed method for the best solution. A systematic study of the result along with short discussions is described in the subsequent section.
Table 16.1 Fuzzy numbers, linguistic variables, and scale of TFNs for ratings.
| Fuzzy numbers | Linguistic variables | Scale of TFNs |
| 1~ | Very poor | (0, 1, 3) |
| 3~ | Poor | (1, 3, 5) |
| 5~ | Medium | (3, 5, 7) |
| 7~ | Good | (5, 7, 9) |
| 9~ | Very good | (7, 9, 10) |
Table 16.2 Fuzzy numbers, linguistic variables, TFN, (TFN)-1 for criteria weights.
| Fuzzy numbers | Linguistic variables | Scales of TFN | (TFN)-1 |
| 1~ | Equally Important | (1, 1, 2) | (1/2, 1, 1) |
| 3~ | Weakly Important | (2, 3, 4) | (1/4, 1/3, 1/2) |
| 5~ | Essentially Important | (4, 5, 6) | (1/6, 1/5, 1/4) |
| 7~ | Very Important | (6, 7, 8) | (1/8, 1/7, 1/6) |
| 9~ | Absolutely Important | (8, 9, 9) | (1/9, 1/9, 1/8) |
Table 16.3 Decision matrix for MHD selection problem.
| B/C | (C) | (C) | (C) | (B) | (B) | (B) |
| Criteria → | Cost ($) | Floor space | Limitation | Load capacity | Traveling distance | Life period |
| MHD1 | 450 | Good | Good | Very Good | Poor | Medium |
| MHD2 | 79.5 | Poor | Medium | Very low | Poor | Good |
| MHD3 | 520 | Poor | Very Good | Poor | Medium | Medium |
| MHD4 | 377 | Poor | Medium | Medium | Poor | Medium |
| MHD5 | 502 | Medium | Poor | Good | Medium | Medium |
Table 16.4 Decision matrix in terms of triangular fuzzy numbers.
| MHDi | 3Cost | Floor space | Limitation | Load capacity | Travelling distance | Life period |
| MHD1 | (405,450,495) | (5,7,9) | (5,7,9) | (7,9,10) | (1,3,5) | (3,5,7) |
| MHD2 | (71.5,79.5,87.4) | (1,3,5) | (3,5,7) | (0,1,3) | (1,3,5) | (5,7,9) |
| MHD3 | (468,520,572) | (1,3,5) | (7,9,10) | (1,3,5) | (3,5,7) | (3,5,7) |
| MHD4 | (339,377,415) | (1,3,5) | (3,5,7) | (3,5,7) | (1,3,5) | (3,5,7) |
| MHD5 | (451,502,552) | (3,5,7) | (1,3,5) | (5,7,9) | (3,5,7) | (3,5,7) |
3Cost data are transformed into TFNs by 10% expansion in both sides.
Table 16.5 Weighted normalized performance ratings.
| MHD | Cost | Floor space requirement | Limitations | Load capacity | Traveling distance | Life period |
| MHD1 | (0.30, .49, 0.72) | (0.24, .48, 0.78) | (0.04, 0.18, 0.42) | (0.44, 0.75, 1) | (0.06, .24, 0.49) | (0.08, .24, .48) |
| MHD2 | (0.05,0.13).09, | (0.05, .20, 0.44) | (0.02,0.33)0.13, | (0, 0.08, 0.3) | (0.06,.49).24, | (0.13,0.61).33, |
| MHD3 | (0.34, .53, 0.84) | (0.05, .20, 0.44) | (0.06, 0.23, 0.47) | (0.06, 0.25, 0.5) | (0.17, .40, .68) | (0.08, .24, .48) |
| MHD4 | (0.29, .42, 0.61) | (0.05, .20, 0.44) | (0.02, 0.13, 0.33) | (0.19, 0.42, 0.7) | (0.06, .24, .49) | (0.08, .24, .48) |
| MHD5 | (0.33, .55, 0.81) | (0.14, 0.34, 0.61) | (0.01, 0.09, 0.24) | (0.32, 0.58, 0.9) | (0.17, .40, .68) | (0.08, .24, 0.48) |
| PIS | (0, 0, 0) | (0, 0, 0) | (0, 0, 0) | (1, 1, 1) | (1, 1, 1) | (1, 1, 1) |
| NIS | (1, 1, 1) | (1, 1, 1) | (1, 1, 1) | (0, 0, 0) | (0, 0, 0) | (0, 0, 0) |
16.5 Results and Discussions
FAHP is employed to compute criteria weights in fuzzy form. Entropy method is utilized to calculate the influence of five FMCDM tools to construct the super hybrid approach. The FMCDM techniques along with their super hybrid approach evaluate and select the most excellent alternative. A very short description of the solution by the suggested tools has been given from subsection 16.5.1 to 16.5.6.
16.5.1 FTOPSIS
In FTOPSIS methodology, normalization operation of fuzzy assessment of devices has been accomplished. Weighted normalized rating, PIS, NIS, Separation measures and closeness coefficients are determined. The ranking of the devices by FTOPSIS is MHD2>>MHD5>>MHD4>>MHD1>>MHD3. In FTOPSIS, MHD 2 attains the maximum closeness coefficient (0.5438) which ensures maximum proximity to PIS. Therefore, MHD 2 is the best material handling device as per FTOPSIS.
16.5.2 FMOORA
Decision matrix in weighted normalized version in MOORA is identical as found in TOPSIS. Sum of weighted normalized values under benefit and non benefit criteria, and net scores are evaluated. The ranking of the devices is MHD2>>MHD5>>MHD4>>MHD1>>MHD3. In MOORA, MHD 2 has the highest net score (0.80) that ensures its maximum net benefit. Hence, with MOORA method, MHD 2 is the material handling device.
16.5.3 FVIKOR
FVIKOR ranks the MHDs based on Si, Ri, and Qi values. MHDs ranking order cas per Si values is MHD2>>MHD5>>MHD3>>MHD4>>MHD1. As per Ri values the rank is MHD4>>MHD3>>MHD5=MHD1>>MHD2. As per Qi values the ranking of the MHDs is MHD2>>MHD5>> MHD3>>MHD4>>MHD1. In FVIKOR, MHD 2 has the maximum Si, Ri, and Qi values which satisfy both the conditions of acceptable advantage and acceptable stability ensuring maximum proximity to the optimum solution. Thus, as per FVIKOR method, MHD 2 is regarded the best material handling device.
16.5.4 Fuzzy Grey Theory (FGT)
In FGT analysis, fuzzy rating is normalized. The deviation between data sets is calculated. These deviations, global maximum and minimum are determined. Every data point is changed to grey relational coefficient. Grey relational grade for every MHD is calculated. It is evident that the ranking of the NIPVs is MHD2>>MHD4>>MHD5>>MHD1>>MHD3. Hence, by fuzzy grey theory analysis, MHD 2 with the highest gray relational grade is the best material handling device.
16.5.5 COPRAS-G
In COPRAS-G method, fuzzy ratings are normalized. Weighted normalized rating is also calculated. Average values under benefit and cost criteria are computed. Relative weight of every MHD is calculated. Utility degree is computed. In COPRAS-G, the ranking order of the MHDs is MHD2>>MHD4>>MHD5>>MHD3>>MHD1. So, as per solution by COPRAS-G, MHD 2 with the maximum utility degree is considered as the best one. It is evident from the solutions by five MCDM techniques (Fuzzy TOPSIS, Fuzzy MOORA, Fuzzy VIKOR, Fuzzy Grey Theory and COPRAS-G) that MHD 2 is the best non-power industrial vehicle. But other MHDs have inconsistent ranking order.
16.5.6 Super Hybrid Approach (SHA)
The proposed super hybrid approach assimilates five integrated FMCDM techniques. The decision matrix for this methodology comprises of the BNPs previously obtained by the five FMCDM approaches. This method presumes unequal influences (weights) of the five FMCDM methods. The entropy method is utilized to calculate the individual influence in terms of objective weight by employing the BNPs matrix. The weights of the FMCDM tools by entropy method are computed as, wFT = 0.0019, wFM = 0.8136, wFV = 0.0818, wFG = 0.0113, and wCG = 0.0914 respectively. The BNP values and the influences of the FMCDM methods are integrated to compute MHD selection indices (Ii) and are shown in Table 16.6. The MHD selection index (I1) for MHD1 can be calculated as shown below.
Table 16.6 MHD selection indices and ranking by proposed super hybrid approach.
| FTOPSIS | FMOORA | FVIKOR | FGT | COPRAS-G | Ii | Ranking | |
| Weights | 0.0019 | 0.8136 | 0.0818 | 0.0113 | 0.0914 | --- | --- |
| MHD1 | 0.5049 | 0.13 | 0.9024 | 1.4353 | 2.2162 | 0.3993 | 4 |
| MHD2 | 0.5438 | 0.8 | 0.4024 | 1.8641 | 4.8893 | 1.1527 | 1 |
| MHD3 | 0.486 | -0.3 | 0.6737 | 1.4313 | 2.6805 | 0.0731 | 5 |
| MHD4 | 0.5212 | 0.41 | 0.7486 | 1.5576 | 3.4131 | 0253 | 3 |
| MHD5 | 0.5363 | 0.73 | 0.5367 | 1.5335 | 2.7631 | 0.9087 | 2 |
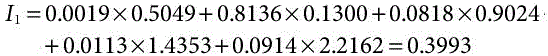
Similarly, the other MHD selection indices are I2 = 1.1527, I3 = 0.0731, I4 = 0.7253 and I5 = 0.9087.
As seen from the above calculation, the MHD2 has the highest MHD selection index (I2 = 1.1527) MHD3 has the least value of selection index (I3 = 0.0731). The ranking of the MHDs obtained by the SHA is 5-1-4-2-3. Therefore, the super hybrid approach clearly indicates that MHD2 is the best alternative.
The analysis of the results shows that MHD2 is the best material handling device in all the methods. The ranks of the MHDs by FMOORA, FTOPSIS and the proposed super hybrid approach are exactly identical. The ranking orders of the MHDs by FVIKOR, fuzzy grey theory COPRAS-G almost matches. A number of MHD has different ranks owing to dissimilar measures. The graph represents the ranks of the MHDs by conventional is shown in Figure 16.2. Ranking order by super hybrid approach is shown in Figure 16.3. The average value of Spearman rank correlation coefficients found to be 0.85, which is well within the acceptable limit (Table 16.7).
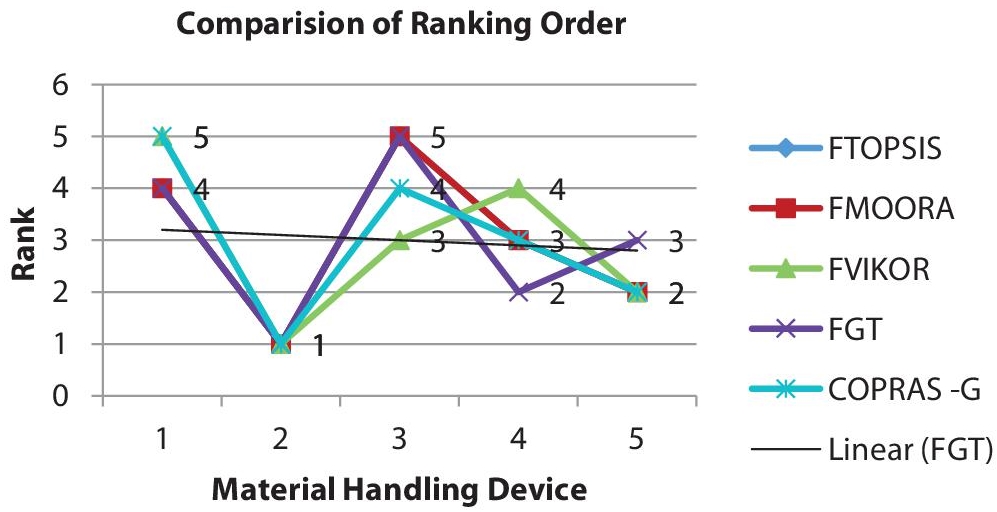
Figure 16.2 Comparison of ranking order.

Figure 16.3 Ranks of MHDs by super hybrid approach.
Table 16.7 Spearman rank correlation coefficients.
| Methodologies | FTOPSIS | FMOORA | FVIKOR | FGT | COPRAS-G | SHA | Average value |
| FTOPSIS | 1 | 1 | 0.7 | 0.9 | 0.8 | 1 | 0.85 |
| FMOORA | 1 | 1 | 0.7 | 0.9 | 0.8 | 1 | |
| FVIKOR | 0.7 | 0.7 | 1 | 0.5 | 0.7 | 0.7 | |
| FGT | 0.9 | 0.9 | 0.5 | 1 | 0.9 | 0.9 | |
| COPRAS-G | 0.8 | 0.8 | 0.7 | 0.9 | 1 | 0.8 | |
| SHA | 1 | 1 | 0.7 | 0.9 | 0.8 | 1 |
16.6 Conclusions
Selection of material handling devices (MHD) is a significant function of decision makers in the manufacturing industry. In many circumstances, the success and existence of manufacturing unit/organization rely on the proper selection of material handling equipment, especially nonpowered industrial vehicles. Hence, evaluation and selection of non-powered industrial vehicles is essential though adequate investigation regarding this subject has not been reported in the open journals. The current work attempts to mitigate the literature gaps. For the purpose, a decision problem on available MHDs is constructed in the unconstructed, uncertain, ambiguous and fuzzy environment. In such condition, theory of fuzzy set is a suitable means to cope with this sort of problems. In actual decision-making procedure, the decision maker is incapable/reluctant to state his/her assessment accurately in numerical value, and the estimation is expressed in linguistic terms.
The application of five FMCDM techniques (Fuzzy TOPSIS, Fuzzy MOORA, Fuzzy VIKOR, Fuzzy Grey Theory and COPRAS-G) along with super hybrid approach reveals the best MHD. The consequence of the evaluation process found by various optimization approaches shows the conformity in finding the best solution. The proposed six methodologies illustrated in the present paper can be utilized in the future managerial decision making procedures in the practical case. The result ensures that the FMCDM methodologies including super hybrid approach as useful and effective FMCDM tools in evaluation and selection of MHDs. Utilization of different conversion scales, different fuzzy numbers, and incorporation of fuzzy performance values in the super hybrid algorithm might be directions of further research.
References
- 1. Goswami, S.S. and Behera, D.K., Solving material handling equipment selection problems in an industry with the help of entropy integrated COPRAS and ARAS MCDM techniques, in: Process Integration Optimization and Sustainability, vol. 5, pp. 947–973, 2021.
- 2. Soufi, Z., David, P., Yahouni, Z., A methodology for the selection of material handling equipment in manufacturing systems, in: IFAC-Papers Online, vol. 54, pp. 122–127, 2021.
- 3. Satyam, F., Satywan, K., Avinash, K., Application of multi-attribute decision-making methods for the selection of conveyor. Res. Square, 1–18, 2021.
- 4. Nguyen, H.-T.N., Siti, D., Nukman, Y., Hideki, A., An integrated MCDM model for conveyor equipment evaluation and selection in an FMC based on a fuzzy AHP and fuzzy ARAS in the presence of vagueness. PloS One, 11, 2016.
- 5. Mathewa, M. and Sahua, S., Comparison of new multi-criteria decision making methods for material handling equipment selection. Manage. Sci. Lett., 8, 139–150, 2018.
- 6. Poon, T.C., Choy, K.L., Cheng, C.K., Lao, S.I., Lam, H.Y., Effective selection and allocation of material handling equipment for stocha production material demand problems using genetic algorithm. Exp. Syst. Appl., 38, 12497– 12505, 2011.
- 7. Fonseca, D.J., Uppal, G., Greene, T.J., A knowledge-based system for conveyor equipment selection. Exp. Syst. Appl., 26, 615–623, 2004.
- 8. Tuzkaya, G., Gülsün, B., Kahraman, C., Özgen, D., An integrated fuzzy multi-criteria decision making methodology for material handling equipment selection problem and an application. Exp. Syst. Appl., 37, 2853–2863, 2010.
- 9. Chatterjee, P., Athawale, V.M., Chakraborty, S., Selection of industrial robots using compromise ranking and outranking methods. Robot. Comput. Integr. Manuf., 26, 5, 483–489, 2010.
- 10. Shih, H.S., Incremental analysis for MCDM with an application to group TOPSIS. Eur. J. Oper. Res., 186, 720–734, 2008.
- 11. Kahraman, C., Cevik, S., Ates, N.Y., Gulbay, M., Fuzzy Multi-criteria evaluation of industrial robotic systems. Comput. Ind. Eng., 52, 414–433, 2007.
- 12. Sujono, S. and Lashkari, R.S., A multi-objective model of operation allocation and material handling system selection in FMS design. Int. J. Prod. Econ., 105, 116–133, 2007.
- 13. Kulak, O., A decision support system for fuzzy multi-attribute selection of material handling equipments. Exp. Syst. Appl., 29, 310–319, 2005.
- 14. Lashkari, R.S., Boparai, R., Paulo, J., Towards an integrated model of operation allocation and material handling selection in cellular manufacturing systems. Int. J. Prod. Econ., 87, 115–139, 2004.
- 15. Chan, F.T.S., Ip, R.W.L., Lau, H., Integration of expert system with AHP for the design of material handling equipment system selection. J. Mater. Process. Technol., 116, 137 –145, 2001.
- 16. Chu, T.C. and Lin, Y.C., A fuzzy TOPSIS method for robot selection. Int. J. Adv. Manufac. Technol., 21, 284–290, 2003.
- 17. Ding, J.F. and Liang, G.S., Using fuzzy MCDM to select partners of strategic alliances for liner shipping. Inf. Sci., 173, 197–225, 2005.
- 18. Bellman, R.E. and Zadeh, L.A., Decision-making in a fuzzy environment. Manage. Sci., 17, B141–B164, 1970.
- 19. Hwang, C.L. and Yoon, K., Multiple attribute decision making methods and applications, Springer-Verlag, New York, 1981.
- 20. Brauers, W.K.M. and Zavadakas, E.K., The MOORA method and its application to privatization in a transition economy. Control Cybern., 35, 445–469, 2006.
- 21. Zeleny, M., Multiple criteria decision making, McGraw-Hill, New York, 1982.
- 22. Ozcan, T., Celebi, N., Esnaf, S., Comparative analysis of multi-criteria decision-making methodologies and implementation of a warehouse location selection problem. Exp. Syst. Appl., 38, 9773–9779, 2011.
- 23. Yuan, X., Grey relational evaluation of final situation of listed company. J. Modern Account. Audit., 3, 41–44, 2007.
- 24. Apple, J.M., Material handling systems design, John Willy and Sons, New York, 1972.
Note
- * Email: [email protected]
