Chapter 11
The t-Distribution
IN THIS CHAPTER
Discovering characteristics of the t-distribution
Seeing the relationship between the Z- and t-distributions
Understanding and using the t-table
The t-distribution is one of the mainstays of data analysis. You may have heard of the “t-test,” for example, which is often used to compare two groups in medical studies and scientific experiments.
This short chapter covers the basic characteristics and uses of the t-distribution. You find out how it compares to the normal distribution (more on that in Chapter 10) and how to use the t-table to find probabilities and percentiles.
Basics of the t-Distribution
In this section, you get an overview of the t-distribution, its main characteristics, when it’s used, and how it’s related to the Z-distribution (see Chapter 10).
Comparing the t- and Z-distributions
The normal distribution is that well-known bell-shaped distribution whose mean is μ and whose standard deviation is σ (see Chapter 10 for more on the normal distribution). The most commonly used normal distribution is the standard normal (also called the Z-distribution), whose mean is 0 and standard deviation is 1.
The t-distribution can be thought of as a cousin of the standard normal distribution — it looks similar in that it’s centered at zero and has a basic bell shape, but it’s shorter and flatter than the Z-distribution. Its standard deviation is proportionally larger compared to the Z, which is why you see the fatter tails on each side.
Figure 11-1 compares the t- and standard normal (Z-) distributions in their most general forms.
FIGURE 11-1: Comparing the standard normal (Z-) distribution to a generic t-distribution.
The t-distribution is typically used to study the mean of a population rather than to study the individuals within a population. In particular, it is used in many cases when you use data to estimate the population mean — for example, to estimate the average price of all the new homes in California. Or, when you use data to test someone’s claim about the population mean — for example, is it true that the mean price of all the new homes in California is $500,000?
These procedures are called confidence intervals and hypothesis tests and are discussed in Chapters 14 and 15, respectively.
The connection between the normal distribution and the t-distribution is that the t-distribution is often used for analyzing the mean of a population if the population itself has a normal distribution (or fairly close to it). Its role is especially important if your data set is small or if you don’t know the standard deviation of the population (which is often the case).
When statisticians use the term t-distribution, they aren’t talking about just one individual distribution. There is an entire family of specific t-distributions, depending on what sample size is being used to study the population mean. Each t-distribution is distinguished by what statisticians call its degrees of freedom (df). In situations where you have one population and your sample size is n, the degrees of freedom for the corresponding t-distribution is n – 1. For example, a sample of size 10 uses a t-distribution with 10 – 1, or 9, degrees of freedom, denoted t9 (pronounced tee sub-nine). Situations involving two populations use different degrees of freedom and are discussed in Chapter 16.
Discovering the effect of variability on t-distributions
When t-distributions are based on smaller sample sizes, they have larger standard deviations than those based on larger sample sizes. Their shapes are flatter; their values are more spread out. That’s because results based on smaller data sets are more variable than results based on large data sets.
The larger the sample size is, the larger the degrees of freedom will be, and the more the t-distributions will look like the standard normal distribution (Z-distribution). A rough cutoff point where the t- and Z-distributions become similar enough that either could be used (at least similar enough for jazz or government work) is around 
.
Figure 11-2 shows what different t-distributions look like for different sample sizes and how they all compare to the standard normal (Z-) distribution.
FIGURE 11-2: A comparison of t-distributions for different sample sizes to the Z-distribution.
Using the t-Table
Each normal distribution has its own mean and standard deviation that classify it, so finding probabilities for each normal distribution on its own is not the way to go. Thankfully, you can standardize the values of any normal distribution to become values on a standard normal (Z-) distribution (whose mean is 0 and standard deviation is 1) and use a Z-table (found in the Appendix) to find probabilities. (Chapter 10 has info on normal distributions.)
In contrast, a t-distribution is not classified by its mean and standard deviation, but by the sample size of the data set being used (n). Unfortunately, there is no single “standard t-distribution” that you can use to transform the numbers and find probabilities on a table. Because it wouldn’t be humanly possible to create a table of probabilities and corresponding t-values for every possible t-distribution, statisticians created one table showing certain values of t-distributions for a selection of degrees of freedom and a selection of probabilities. This table is called the t-table (it appears in the Appendix). In this section, you find out how to determine probabilities, percentiles, and critical values (for confidence intervals) using the t-table.
Finding probabilities with the t-table
Each row of the t-table (Table A-2 in the Appendix) represents a different t-distribution, classified by its degrees of freedom. The columns represent various common greater-than probabilities, such as 0.40, 0.25, 0.10, and 0.05. The numbers across a row indicate the values on the t-distribution (the t-values) corresponding to the greater-than probabilities shown at the top of the columns. Rows are arranged by degrees of freedom.
Another term for greater-than probability is right-tail probability, which indicates that such probabilities represent areas on the right-most end (tail) of the t-distribution.
The steps for finding a probability related to a sample mean X when you need to use the t-distribution are very similar to those when using the normal distribution. The only difference comes at the end because of the different way that the t-table is arranged:
- Draw a picture of the distribution.
- Translate the problem into one of the following:
, 
, or 
. Shade in the area on your picture. Standardize a (and/or b) to a t-score using the formula:
, where s is the sample standard deviation.- Calculate the degrees of freedom
, and find that corresponding row in the t-table (Table A-2 in the Appendix). If 
, use the row labeled “z” at the bottom. Scan across the row until you find your t-score or a value very close to it. Now look up at the header in the same column. Make note of that value of p.
Note: If your t-score isn’t really close to any of the values in the df row, say within 0.1, then find which two values it falls between. Now look up at the headers and make note of which two values of p the probability must fall between. Though you won’t be able to find a precise single answer, you’ll at least be able to give a range that you know the probability lies within.
6a. If you need a “tail” probability — that is, 
or 
— you’re done. The value of p you found is the probability.
6b. If you need a probability that’s everything except a tail (one that cuts through the middle) — that is, 
or 
— take 1 minus the result from Step 5.
Note: If you had to make note of two values of p, subtract each from 1. The probability is in that range.
- If you need a “between-two-values” probability — that is,
— do Steps 1–6 for b (the larger of the two values) and again for a (the smaller of the two values), and subtract the results.
The probability that X is equal to any single value is 0 for any continuous random variable (just like the normal and t). So, 
, and also 
. This isn’t true of discrete random variables.
For example, the second row of the t-table is for the 
distribution. With 2 degrees of freedom, you see that the second number, 0.816, is the value on the t2 distribution whose area to its right (its right-tail probability) is 0.25 (see the heading for the second column). In other words, the probability that t2 is greater than 0.816 equals 0.25. In probability notation, that means 
.
The next number in row two of the t-table is 1.886, which lies in the 0.10 column. This means the probability of being greater than 1.886 on the t2 distribution is 0.10. Because 1.886 falls to the right of 0.816, there is less area under the curve to the right of 1.886, so its right-tail probability is lower.
Q. The weights of single-dip ice cream cones at Bob’s ice cream parlor have a normal distribution with a mean of 8 ounces. If you order six single-dip ice cream cones for you and your friends, what’s the chance that they weigh an average of at least 9 ounces with a standard deviation of 1 ounce?
A. You want 
, the probability that the average weight of the cones is 9 ounces or more. Converting the 9 to a standard score, you get 
. Calculate 
and look at that row in the t-table (Table A-2). Scanning across that row, you find that none of the t-values are that close, but 
does fall between 2.015 and 2.571 in that row. By the note in Step 6, move up to the column header and see that this corresponds to probability values of 0.05 and 0.025, respectively. You were looking for a tail probability, 
, and that is exactly what the t-table provides, so you are done! Because your t-value falls between the two in the row, your probability has to fall between the ones given at the top. The probability that the average ice cream cone weight is greater than 9 ounces is between 0.025 and 0.05, or between 2.5 and 5 percent. (Not really great odds of getting more ice cream than you paid for.)
1
Suppose the average length of a stay in Europe for American tourists is 17 days. You choose a random sample of 16 American tourists. The sample of 16 tourists stays an average of 18.5 days or more with a standard deviation of 4.5 days. What’s the chance of that happening?
2 Suppose a class’s test scores have a mean of 80. You randomly choose 25 students from the class. What’s the chance that the group’s average test score is less than 82 with a standard deviation of 5?
Figuring percentiles for the t-distribution
You can also use the t-table (in the Appendix) to find percentiles for a t-distribution. A percentile is a number on a distribution whose less-than probability is the given percentage; for example, the 95th percentile of the t-distribution with 
degrees of freedom is that value of 
whose left-tail (less-than) probability is 0.95 (and whose right-tail probability is 0.05). (See Chapter 5 for particulars on percentiles.)
The normal table shows “less than” probabilities, so when you want to find a percentile, the normal table is ready to go. However, the t-table shows “greater than” probabilities. If you want to calculate a percentile using the t-table, you need to subtract the value of p you find (based on the right tail) from 1 to get the desired percentile’s probability (the left tail).
Suppose you have a sample of size 10 and you want to find the 95th percentile of its corresponding t-distribution. You have 
degrees of freedom, so you look at the row for 
. The 95th percentile is the number where 95 percent of the values lie below it and 5 percent lie above it, so you want the right-tail area to be 0.05. Move across the column headers until you find the column for 0.05. Matching the column for 0.05 with the row where 
gives you the cell with 
. This is the 95th percentile of the t-distribution with 9 degrees of freedom.
Now, if you increase the sample size to 
, the value of the 95th percentile decreases; look at the row for 
degrees of freedom, and in the column for 0.05 (a right-tail probability of 0.05), you find 
. Notice that the 95th percentile for the t19 distribution is less than the 95th percentile for the t9 distribution (1.833). This is because larger degrees of freedom indicate a smaller standard deviation and the t-values are more concentrated about the mean, so you reach the 95th percentile with a smaller value of t. (See the section, “Discovering the effect of variability on t-distributions,” earlier in this chapter.)
You might look at the very bottom of the t-table and see percentages like 90 percent, 95 percent, and 99 percent already listed for you. But these are not to be used for calculating any of the percentile problems you’re working on here. Move your eyes to the left and you’ll see that the row is titled “CI,” short for “confidence interval.” This last row is only to be used if constructing confidence intervals as described in the section, “Picking out t*-values for confidence intervals,” in this chapter and Chapter 14.
Q. Suppose you find the mean of ten quiz scores, convert it to a standard score, and check the table to find out it’s equal to the 99th percentile.
- What’s the standard score?
- Compare the result to the standard score you have to get to be at the 99th percentile on the Z-distribution.
A. The t-distributions push you farther out to get to the same percentile that the Z-distribution would.
- Your sample size is
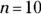, so you need the t-distribution with 
degrees of freedom, also known as the t9 distribution. If you want a 99th percentile, that means 99 percent is in the lower (left-end) tail, and 1 percent is in the upper (right-end) tail. Using the t-table (Table A-2 in the Appendix), you find the column header with the right-tail probability of 0.01. Matching the row for 
and the column for 0.01, you find the t-value to be 
. - Using the Z-distribution (Table A-1) and looking for the left-tail probability closest to 0.99, you find that 0.9901 corresponds to a z-value of 2.33. You could also get a more precise value using the z row in the t-table. That gives the exact z-value for a 99th percentile, which has 0.01 in the right tail, to be 2.326. The standard score associated with the 99th percentile is around 2.33, which is much smaller than the 2.821 from Part A of this question. The number from Part B is smaller because the t-distribution is flatter than the Z-distribution, with more area or probability out in the tails. So to get all the way out to the 99th percentile, you have to go farther out on the t-distribution than on the normal curve.
3 Suppose you collect data on ten products and check their weights. The average should be 10 ounces, but your sample mean is 9 ounces with a standard deviation of 2 ounces.
- Find the standard score.
- What percentile is the standard score found in Part A closest to?
- Suppose the mean really is 10 ounces. Do you find these results unusual? Use probabilities to explain.
Picking out t*-values for confidence intervals
Confidence intervals estimate population parameters, such as the population mean, by using a statistic (for example, the sample mean) plus or minus a margin of error. (See Chapter 14 for all the information you need on confidence intervals and more.) To compute the margin of error for a confidence interval, you need a critical value (the number of standard errors you add and subtract to get the margin of error you want; see Chapter 14). When the sample size is large (at least 30), you use critical values on the Z-distribution (shown in Chapter 14) to build the margin of error. When the sample size is small (less than 30) and/or the population standard deviation is unknown, you use the t-distribution to find critical values.
To help you find critical values for the t-distribution, you can use the last row of the t-table, which lists common confidence levels, such as 80 percent, 90 percent, and 95 percent. To find a critical value, look up your confidence level in the bottom row of the table; this tells you which column of the t-table you need. Intersect this column with the row for your df (see Chapter 14 for degrees of freedom formulas). The number you see is the critical value (or the t*-value) for your confidence interval. For example, if you want a t*-value for a 90 percent confidence interval when you have 9 degrees of freedom, go to the bottom of the table, find the column for 90 percent, and intersect it with the row for 
. This gives you a t*-value of 1.833 (rounded).
Across the top row of the t-table, you see right-tail probabilities for the t-distribution. But confidence intervals involve both left- and right-tail probabilities (because you add and subtract the margin of error). So half of the probability left from the confidence interval goes into each tail. You need to take that into account. For example, a t*-value for a 90 percent confidence interval has 5 percent for its greater-than probability and 5 percent for its less-than probability (taking 100 percent minus 90 percent and dividing by 2). Using the top row of the t-table, you would have to look for 0.05 (rather than 10 percent, as you might be inclined to do). But using the bottom row of the table, you just look for 90 percent. (The result you get using either method ends up being in the same column.)
When looking for t*-values for confidence intervals, use the bottom row of the t-table as your guide rather than the headings at the top of the table.
Studying Behavior Using the t-Table
You can use computer software to calculate any probabilities, percentiles, or critical values you need for any t-distribution (or any other distribution) if it’s available to you. (On exams it may not be available.) However, one of the nice things about using a table (rather than computer software) to find probabilities is that the table can tell you information about the behavior of the distribution itself — that is, it can give you the big picture. Here are some nuggets of big-picture information about the t-distribution you can glean by scanning the t-table (in the Appendix).
As the degrees of freedom increase, the values on each t-distribution become more concentrated around the mean, eventually resembling the Z-distribution (see Chapter 10). The t-table confirms this pattern as well. Because of the way the t-table is set up, if you choose any column and move down through the numbers in the column, you’re increasing the degrees of freedom (and sample size) and keeping the right-tail probability the same. As you do this, you see the t-values getting smaller and smaller, indicating the t-values are becoming closer to (hence, more concentrated around) the mean.
I labeled the second-to-last row of the t-table with a z in the df column. This indicates the “limit” of the t-values as the sample size (n) goes to infinity. The t-values in this row are approximately the same as the z-values on the Z-table (in the Appendix) that correspond to the same greater-than probabilities. This confirms what you already know: As the sample size increases, the t- and the Z-distributions look more and more alike. For example, the t-value in row 30 of the t-table corresponding to a right-tail probability of 0.05 (column 0.05) is 1.697. This lies close to 
, the value corresponding to a right-tail area of 0.05 on the Z-distribution. (See row Z of the t-table.)
It doesn’t take a super-large sample size for the values on the t-distribution to get close to the values on a Z-distribution. For example, when 
and 
, the values in the t-table are already quite close to the corresponding values on the Z-table.
Practice Questions Answers and Explanations
1 You want 
, the probability that the average is 18.5 days or more. Converting the 18.5 to a standard score, you get 
. Calculate 
and look at that row in the t-table (Table A-2). Scanning across that row, you find the value 1.345 in the third column. This is close enough to your 
to use. Moving up to the column header, you see that this corresponds to a probability value of 0.10. Because you were looking for a tail probability, 
, and that is exactly what the t-table provides, you are done! The probability that the average is 18.5 days or more is 0.10, or 10 percent.
2 You want 
, the probability that the average is less than 82. Converting the 82 to a standard score, you get 
. Calculate 
and look at that row in the t-table (Table A-2). Scanning across that row, you find the value 2.06 in the third column. This is close enough to your 
to use. Moving up to the column header, you see that this corresponds to a probability value of 0.025. Because you were looking for a probability that cuts through the middle 
, using Step 6b you get 
. The probability that the student average is less than 82 is 0.975, or 97.5 percent.
If the area under the curve that you want cuts through the middle and contains everything but a little tail, then the final probability has to be at least 50 percent. If you would have finished this last problem and said that the answer was 0.025, that should have set off alarms because the picture of 
covers over half of the curve.
3 Here you compare what you expect to see with what you actually get (which comes up in hypothesis testing; see Chapter 15). The basic information here is that you have 
, 
, 
, and 
. Anytime you have the sample standard deviation (s) and not the population standard deviation 
, you should use a t-distribution.
- The standard score is
. - The standard score is negative, meaning you’re 1.58 standard deviations below the mean on the
distribution 
. Because the t-distribution is symmetric, the area below the negative standard score is equal to the area above the positive version of the standard score. In the row with 
, the value 1.58 lies between 1.38 and 1.83, which correspond to 0.10 and 0.05 in the “greater-than” tails, respectively. So the value –1.58 lies between –1.38 and –1.83, which correspond to 0.10 and 0.05 in the “less-than” tails, respectively. Thus, –1.58 lies between the 10th percentile and the 5th percentile on the 
distribution. - The results aren’t entirely unusual because, according to Part B, they happen between 5 percent and 10 percent of the time.
If you’re ready to test your skills a bit more, take the following chapter quiz that incorporates all the chapter topics.
Whaddya Know? Chapter 11 Quiz
Quiz time! Complete each problem to test your knowledge on the various topics covered in this chapter. You can then find the solutions and explanations in the next section.
1 The t-distribution looks exactly like the Z-distribution. True or false?
2 What is the mean of the t-distribution?
3 Each t-distribution in the family of all t-distributions is characterized by its ____________________.
4 As you increase the sample size, the degrees of freedom increase, and the t-distribution looks more and more like ____________________.
5 The standard deviation of the t-distribution is ____________________ than the standard deviation of the Z-distribution.
6 Suppose your sample size is 10. What are the degrees of freedom for the corresponding t-distribution?
7 Suppose 
. What’s the probability that t is greater than 2.09?
8 Suppose 
. What’s the probability of being less than 6.87?
9 What is the 90th percentile of the 
distribution?
10 What does the next-to-last row of the t-table represent and why is it on the t-table?
Answers to Chapter 11 Quiz
1 False. The t-distribution is fatter and flatter than the Z-distribution. Although it has a mound in the middle like the Z-distribution, its tails are thicker. It’s kind of like you sat on top of the Z-distribution and it spread itself out — seriously!
2 Zero
3 degrees of freedom
4 theZ-distribution
5 larger
6 
7 0.025, according to the t-table with 19 degrees of freedom. Follow to the top of the column where 2.09 is found (the row is 19), and you find 0.025.
8 
. According to the t-table intersecting row 5 (5 degrees of freedom) and the column where 6.87 resides, you find 
. You want 
, so take one minus this amount.
If your particular value of t is not on the t-table, you can locate it between two other t-values in the appropriate row, and list its probability as being between their two corresponding probabilities at the top of their columns. Or you may use technology to find the exact value.
9 1.32. Look in row 22 because the degrees of freedom in this case are 22; then go across the top and find the column that has 0.10 probability in the upper part of the distribution (column 0.10). Intersect this row and column to find 1.32. This number has 10% of the values above it, but it also has 90% of the values below it, making it the 90th percentile of the 
distribution.
10 The next-to-last row of the t-table represents certain values on the Z-distribution whose right-tail areas (greater-than probabilities) are listed at the top of their respective columns. It’s on the t-table because as the df of the t-distribution increase as you move down a particular column, you can see the values in the column (values on those t-distributions) get closer and closer to the values on the Z-distribution. If n is large, you can see that using the z-value is about the same as using the t-value with what would have been a large df.