Chapter 11. Machine Learning with MLlib
MLlib is Spark’s library of machine learning functions. Designed to run in parallel on clusters, MLlib contains a variety of learning algorithms and is accessible from all of Spark’s programming languages. This chapter will show you how to call it in your own programs, and offer common usage tips.
Machine learning itself is a topic large enough to fill many books,17 so unfortunately, in this chapter, we will not have the space to explain machine learning in detail. If you are familiar with machine learning, however, this chapter will explain how to use it in Spark; and even if you are new to it, you should be able to combine the material here with other introductory material. This chapter is most relevant to data scientists with a machine learning background looking to use Spark, as well as engineers working with a machine learning expert.
Overview
MLlib’s design and philosophy are simple: it lets you invoke various algorithms on distributed datasets, representing all data as RDDs. MLlib introduces a few data types (e.g., labeled points and vectors), but at the end of the day, it is simply a set of functions to call on RDDs. For example, to use MLlib for a text classification task (e.g., identifying spammy emails), you might do the following:
-
Start with an RDD of strings representing your messages.
-
Run one of MLlib’s feature extraction algorithms to convert text into numerical features (suitable for learning algorithms); this will give back an RDD of vectors.
-
Call a classification algorithm (e.g., logistic regression) on the RDD of vectors; this will give back a model object that can be used to classify new points.
-
Evaluate the model on a test dataset using one of MLlib’s evaluation functions.
One important thing to note about MLlib is that it contains only parallel algorithms that run well on clusters. Some classic ML algorithms are not included because they were not designed for parallel platforms, but in contrast MLlib contains several recent research algorithms for clusters, such as distributed random forests, K-means||, and alternating least squares. This choice means that MLlib is best suited for running each algorithm on a large dataset. If you instead have many small datasets on which you want to train different learning models, it would be better to use a single-node learning library (e.g., Weka or SciKit-Learn) on each node, perhaps calling it in parallel across nodes using a Spark map(). Likewise, it is common for machine learning pipelines to require training the same algorithm on a small dataset with many configurations of parameters, in order to choose the best one. You can achieve this in Spark by using parallelize() over your list of parameters to train different ones on different nodes, again using a single-node learning library on each node. But MLlib itself shines when you have a large, distributed dataset that you need to train a model on.
Finally, in Spark 1.0 and 1.1, MLlib’s interface is relatively low-level, giving you the functions to call for different tasks but not the higher-level workflow typically required for a learning pipeline (e.g., splitting the input into training and test data, or trying many combinations of parameters). In Spark 1.2, MLlib gains an additional (and at the time of writing still experimental) pipeline API for building such pipelines. This API resembles higher-level libraries like SciKit-Learn, and will hopefully make it easy to write complete, self-tuning pipelines. We include a preview of this API at the end of this chapter, but focus primarily on the lower-level APIs.
System Requirements
MLlib requires some linear algebra libraries to be installed on your machines. First, you will need the gfortran runtime library for your operating system. If MLlib warns that gfortran is missing, follow the setup instructions on the MLlib website. Second, to use MLlib in Python, you will need NumPy. If your Python installation does not have it (i.e., you cannot import numpy), the easiest way to get it is by installing the python-numpy or numpy package through your package manager on Linux, or by using a third-party scientific Python installation like Anaconda.
MLlib’s supported algorithms have also evolved over time. The ones we discuss here are all available as of Spark 1.2, but some of the algorithms may not be present in earlier versions.
Machine Learning Basics
To put the functions in MLlib in context, we’ll start with a brief review of machine learning concepts.
Machine learning algorithms attempt to make predictions or decisions based on training data, often maximizing a mathematical objective about how the algorithm should behave. There are multiple types of learning problems, including classification, regression, or clustering, which have different objectives. As a simple example, we’ll consider classification, which involves identifying which of several categories an item belongs to (e.g., whether an email is spam or non-spam), based on labeled examples of other items (e.g., emails known to be spam or not).
All learning algorithms require defining a set of features for each item, which will be fed into the learning function. For example, for an email, some features might include the server it comes from, or the number of mentions of the word free, or the color of the text. In many cases, defining the right features is the most challenging part of using machine learning. For example, in a product recommendation task, simply adding another feature (e.g., realizing that which book you should recommend to a user might also depend on which movies she’s watched) could give a large improvement in results.
Most algorithms are defined only for numerical features (specifically, a vector of numbers representing the value for each feature), so often an important step is feature extraction and transformation to produce these feature vectors. For example, for text classification (e.g., our spam versus non-spam case), there are several methods to featurize text, such as counting the frequency of each word.
Once data is represented as feature vectors, most machine learning algorithms optimize a well-defined mathematical function based on these vectors. For example, one classification algorithm might be to define the plane (in the space of feature vectors) that “best” separates the spam versus non-spam examples, according to some definition of “best” (e.g., the most points classified correctly by the plane). At the end, the algorithm will return a model representing the learning decision (e.g., the plane chosen). This model can now be used to make predictions on new points (e.g., see which side of the plane the feature vector for a new email falls on, in order to decide whether it’s spam). Figure 11-1 shows an example learning pipeline.
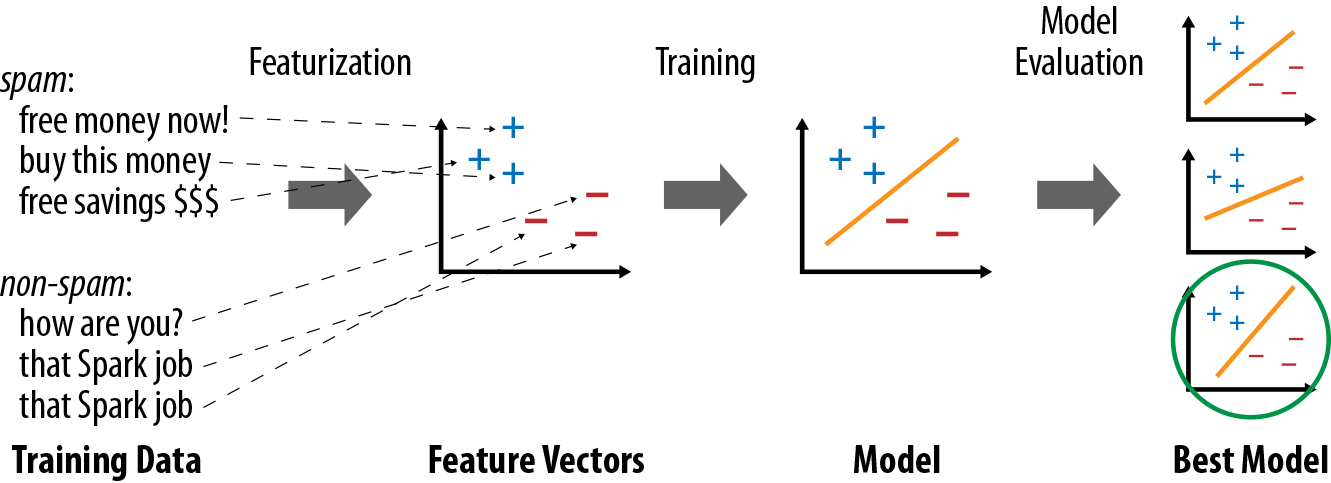
Figure 11-1. Typical steps in a machine learning pipeline
Finally, most learning algorithms have multiple parameters that can affect results, so real-world pipelines will train multiple versions of a model and evaluate each one. To do this, it is common to separate the input data into “training” and “test” sets, and train only on the former, so that the test set can be used to see whether the model overfit the training data. MLlib provides several algorithms for model evaluation.
Example: Spam Classification
As a quick example of MLlib, we show a very simple program for building a spam classifier (Examples 11-1 through 11-3). This program uses two MLlib algorithms: HashingTF, which builds term frequency feature vectors from text data, and Logistic RegressionWithSGD, which implements the logistic regression procedure using stochastic gradient descent (SGD). We assume that we start with two files, spam.txt and normal.txt, each of which contains examples of spam and non-spam emails, one per line. We then turn the text in each file into a feature vector with TF, and train a logistic regression model to separate the two types of messages. The code and data files are available in the book’s Git repository.
Example 11-1. Spam classifier in Python
frompyspark.mllib.regressionimportLabeledPointfrompyspark.mllib.featureimportHashingTFfrompyspark.mllib.classificationimportLogisticRegressionWithSGDspam=sc.textFile("spam.txt")normal=sc.textFile("normal.txt")# Create a HashingTF instance to map email text to vectors of 10,000 features.tf=HashingTF(numFeatures=10000)# Each email is split into words, and each word is mapped to one feature.spamFeatures=spam.map(lambda:tf.transform(.split(" ")))normalFeatures=normal.map(lambda:tf.transform(.split(" ")))# Create LabeledPoint datasets for positive (spam) and negative (normal) examples.positiveExamples=spamFeatures.map(lambdafeatures:LabeledPoint(1,features))negativeExamples=normalFeatures.map(lambdafeatures:LabeledPoint(0,features))trainingData=positiveExamples.union(negativeExamples)trainingData.cache()# Cache since Logistic Regression is an iterative algorithm.# Run Logistic Regression using the SGD algorithm.model=LogisticRegressionWithSGD.train(trainingData)# Test on a positive example (spam) and a negative one (normal). We first apply# the same HashingTF feature transformation to get vectors, then apply the model.posTest=tf.transform("O M G GET cheap stuff by sending money to ...".split(" "))negTest=tf.transform("Hi Dad, I started studying Spark the other ...".split(" "))"Prediction for positive test example:%g"%model.predict(posTest)"Prediction for negative test example:%g"%model.predict(negTest)
Example 11-2. Spam classifier in Scala
importorg.apache.spark.mllib.regression.LabeledPointimportorg.apache.spark.mllib.feature.HashingTFimportorg.apache.spark.mllib.classification.LogisticRegressionWithSGDvalspam=sc.textFile("spam.txt")valnormal=sc.textFile("normal.txt")// Create a HashingTF instance to map email text to vectors of 10,000 features.valtf=newHashingTF(numFeatures=10000)// Each email is split into words, and each word is mapped to one feature.valspamFeatures=spam.map(=>tf.transform(.split(" ")))valnormalFeatures=normal.map(=>tf.transform(.split(" ")))// Create LabeledPoint datasets for positive (spam) and negative (normal) examples.valpositiveExamples=spamFeatures.map(features=>LabeledPoint(1,features))valnegativeExamples=normalFeatures.map(features=>LabeledPoint(0,features))valtrainingData=positiveExamples.union(negativeExamples)trainingData.cache()// Cache since Logistic Regression is an iterative algorithm.// Run Logistic Regression using the SGD algorithm.valmodel=newLogisticRegressionWithSGD().run(trainingData)// Test on a positive example (spam) and a negative one (normal).valposTest=tf.transform("O M G GET cheap stuff by sending money to ...".split(" "))valnegTest=tf.transform("Hi Dad, I started studying Spark the other ...".split(" "))println("Prediction for positive test example: "+model.predict(posTest))println("Prediction for negative test example: "+model.predict(negTest))
Example 11-3. Spam classifier in Java
importorg.apache.spark.mllib.classification.LogisticRegressionModel;importorg.apache.spark.mllib.classification.LogisticRegressionWithSGD;importorg.apache.spark.mllib.feature.HashingTF;importorg.apache.spark.mllib.linalg.Vector;importorg.apache.spark.mllib.regression.LabeledPoint;JavaRDD<String>spam=sc.textFile("spam.txt");JavaRDD<String>normal=sc.textFile("normal.txt");// Create a HashingTF instance to map email text to vectors of 10,000 features.finalHashingTFtf=newHashingTF(10000);// Create LabeledPoint datasets for positive (spam) and negative (normal) examples.JavaRDD<LabeledPoint>posExamples=spam.map(newFunction<String,LabeledPoint>(){publicLabeledPointcall(String){returnnewLabeledPoint(1,tf.transform(Arrays.asList(.split(" "))));}});JavaRDD<LabeledPoint>negExamples=normal.map(newFunction<String,LabeledPoint>(){publicLabeledPointcall(String){returnnewLabeledPoint(0,tf.transform(Arrays.asList(.split(" "))));}});JavaRDD<LabeledPoint>trainData=positiveExamples.union(negativeExamples);trainData.cache();// Cache since Logistic Regression is an iterative algorithm.// Run Logistic Regression using the SGD algorithm.LogisticRegressionModelmodel=newLogisticRegressionWithSGD().run(trainData.rdd());// Test on a positive example (spam) and a negative one (normal).VectorposTest=tf.transform(Arrays.asList("O M G GET cheap stuff by sending money to ...".split(" ")));VectornegTest=tf.transform(Arrays.asList("Hi Dad, I started studying Spark the other ...".split(" ")));System.out.println("Prediction for positive example: "+model.predict(posTest));System.out.println("Prediction for negative example: "+model.predict(negTest));
As you can see, the code is fairly similar in all the languages. It operates directly on RDDs—in this case, of strings (the original text) and LabeledPoints (an MLlib data type for a vector of features together with a label).
Data Types
MLlib contains a few specific data types, located in the org.apache.spark.mllib package (Java/Scala) or pyspark.mllib (Python). The main ones are:
Vector-
A mathematical vector. MLlib supports both dense vectors, where every entry is stored, and sparse vectors, where only the nonzero entries are stored to save space. We will discuss the different types of vectors shortly. Vectors can be constructed with the
mllib.linalg.Vectorsclass. LabeledPoint-
A labeled data point for supervised learning algorithms such as classification and regression. Includes a feature vector and a label (which is a floating-point value). Located in the
mllib.regressionpackage. Rating-
A rating of a product by a user, used in the
mllib.recommendationpackage for product recommendation. - Various
Modelclasses -
Each
Modelis the result of a training algorithm, and typically has apredict()method for applying the model to a new data point or to an RDD of new data points.
Most algorithms work directly on RDDs of Vectors, LabeledPoints, or Ratings. You can construct these objects however you want, but typically you will build an RDD through transformations on external data—for example, by loading a text file or running a Spark SQL command—and then apply a map() to turn your data objects into MLlib types.
Working with Vectors
There are a few points to note for the Vector class in MLlib, which will be the most commonly used one.
First, vectors come in two flavors: dense and sparse. Dense vectors store all their entries in an array of floating-point numbers. For example, a vector of size 100 will contain 100 double values. In contrast, sparse vectors store only the nonzero values and their indices. Sparse vectors are usually preferable (both in terms of memory use and speed) if at most 10% of elements are nonzero. Many featurization techniques yield very sparse vectors, so using this representation is often a key optimization.
Second, the ways to construct vectors vary a bit by language. In Python, you can simply pass a NumPy array anywhere in MLlib to represent a dense vector, or use the mllib.linalg.Vectors class to build vectors of other types (see Example 11-4).18 In Java and Scala, use the mllib.linalg.Vectors class (see Examples 11-5 and 11-6).
Example 11-4. Creating vectors in Python
fromnumpyimportarrayfrompyspark.mllib.linalgimportVectors# Create the dense vector <1.0, 2.0, 3.0>denseVec1=array([1.0,2.0,3.0])# NumPy arrays can be passed directly to MLlibdenseVec2=Vectors.dense([1.0,2.0,3.0])# .. or you can use the Vectors class# Create the sparse vector <1.0, 0.0, 2.0, 0.0>; the methods for this take only# the size of the vector (4) and the positions and values of nonzero entries.# These can be passed as a dictionary or as two lists of indices and values.sparseVec1=Vectors.sparse(4,{0:1.0,2:2.0})sparseVec2=Vectors.sparse(4,[0,2],[1.0,2.0])
Example 11-5. Creating vectors in Scala
importorg.apache.spark.mllib.linalg.Vectors// Create the dense vector <1.0, 2.0, 3.0>; Vectors.dense takes values or an arrayvaldenseVec1=Vectors.dense(1.0,2.0,3.0)valdenseVec2=Vectors.dense(Array(1.0,2.0,3.0))// Create the sparse vector <1.0, 0.0, 2.0, 0.0>; Vectors.sparse takes the size of// the vector (here 4) and the positions and values of nonzero entriesvalsparseVec1=Vectors.sparse(4,Array(0,2),Array(1.0,2.0))
Example 11-6. Creating vectors in Java
importorg.apache.spark.mllib.linalg.Vector;importorg.apache.spark.mllib.linalg.Vectors;// Create the dense vector <1.0, 2.0, 3.0>; Vectors.dense takes values or an arrayVectordenseVec1=Vectors.dense(1.0,2.0,3.0);VectordenseVec2=Vectors.dense(newdouble[]{1.0,2.0,3.0});// Create the sparse vector <1.0, 0.0, 2.0, 0.0>; Vectors.sparse takes the size of// the vector (here 4) and the positions and values of nonzero entriesVectorsparseVec1=Vectors.sparse(4,newint[]{0,2},newdouble[]{1.0,2.0});
Finally, in Java and Scala, MLlib’s Vector classes are primarily meant for data representation, but do not provide arithmetic operations such as addition and subtraction in the user API. (In Python, you can of course use NumPy to perform math on dense vectors and pass those to MLlib.) This was done mainly to keep MLlib small, because writing a complete linear algebra library is beyond the scope of the project. But if you want to do vector math in your programs, you can use a third-party library like Breeze in Scala or MTJ in Java, and convert the data from it to MLlib vectors.
Algorithms
In this section, we’ll cover the key algorithms available in MLlib, as well as their input and output types. We do not have space to explain each algorithm mathematically, but focus instead on how to call and configure these algorithms.
Feature Extraction
The mllib.feature package contains several classes for common feature transformations. These include algorithms to construct feature vectors from text (or from other tokens), and ways to normalize and scale features.
TF-IDF
Term Frequency–Inverse Document Frequency, or TF-IDF, is a simple way to generate feature vectors from text documents (e.g., web pages). It computes two statistics for each term in each document: the term frequency (TF), which is the number of times the term occurs in that document, and the inverse document frequency (IDF), which measures how (in)frequently a term occurs across the whole document corpus. The product of these values, TF ![]() IDF, shows how relevant a term is to a specific document (i.e., if it is common in that document but rare in the whole corpus).
IDF, shows how relevant a term is to a specific document (i.e., if it is common in that document but rare in the whole corpus).
MLlib has two algorithms that compute TF-IDF: HashingTF and IDF, both in the mllib.feature package. HashingTF computes a term frequency vector of a given size from a document. In order to map terms to vector indices, it uses a technique known as the hashing trick. Within a language like English, there are hundreds of thousands of words, so tracking a distinct mapping from each word to an index in the vector would be expensive. Instead, HashingTF takes the hash code of each word modulo a desired vector size, S, and thus maps each word to a number between 0 and S–1. This always yields an S-dimensional vector, and in practice is quite robust even if multiple words map to the same hash code. The MLlib developers recommend setting S between ![]() and
and ![]() .
.
HashingTF can run either on one document at a time or on a whole RDD. It requires each “document” to be represented as an iterable sequence of objects—for instance, a list in Python or a Collection in Java. Example 11-7 uses HashingTF in Python.
Example 11-7. Using HashingTF in Python
>>>frompyspark.mllib.featureimportHashingTF>>>sentence="hello hello world">>>words=sentence.split()# Split sentence into a list of terms>>>tf=HashingTF(10000)# Create vectors of size S = 10,000>>>tf.transform(words)SparseVector(10000,{3065:1.0,6861:2.0})>>>rdd=sc.wholeTextFiles("data").map(lambda(name,text):text.split())>>>tfVectors=tf.transform(rdd)# Transforms an entire RDD
Tip
In a real pipeline, you will likely need to preprocess and stem words in a document before passing them to TF. For example, you might convert all words to lowercase, drop punctuation characters, and drop suffixes like ing. For best results you can call a single-node natural language library like NLTK in a map().
Once you have built term frequency vectors, you can use IDF to compute the inverse document frequencies, and multiply them with the term frequencies to compute the TF-IDF. You first call fit() on an IDF object to obtain an IDFModel representing the inverse document frequencies in the corpus, then call transform() on the model to transform TF vectors into IDF vectors. Example 11-8 shows how you would compute IDF starting with Example 11-7.
Example 11-8. Using TF-IDF in Python
frompyspark.mllib.featureimportHashingTF,IDF# Read a set of text files as TF vectorsrdd=sc.wholeTextFiles("data").map(lambda(name,text):text.split())tf=HashingTF()tfVectors=tf.transform(rdd).cache()# Compute the IDF, then the TF-IDF vectorsidf=IDF()idfModel=idf.fit(tfVectors)tfIdfVectors=idfModel.transform(tfVectors)
Note that we called cache() on the tfVectors RDD because it is used twice (once to train the IDF model, and once to multiply the TF vectors by the IDF).
Scaling
Most machine learning algorithms consider the magnitude of each element in the feature vector, and thus work best when the features are scaled so they weigh equally (e.g., all features have a mean of 0 and standard deviation of 1). Once you have built feature vectors, you can use the StandardScaler class in MLlib to do this scaling, both for the mean and the standard deviation. You create a StandardScaler, call fit() on a dataset to obtain a StandardScalerModel (i.e., compute the mean and variance of each column), and then call transform() on the model to scale a dataset. Example 11-9 demonstrates.
Example 11-9. Scaling vectors in Python
frompyspark.mllib.featureimportStandardScalervectors=[Vectors.dense([-2.0,5.0,1.0]),Vectors.dense([2.0,0.0,1.0])]dataset=sc.parallelize(vectors)scaler=StandardScaler(withMean=True,withStd=True)model=scaler.fit(dataset)result=model.transform(dataset)# Result: {[-0.7071, 0.7071, 0.0], [0.7071, -0.7071, 0.0]}
Normalization
In some situations, normalizing vectors to length 1 is also useful to prepare input data. The Normalizer class allows this. Simply use Normalizer().transform(rdd). By default Normalizer uses the ![]() norm (i.e, Euclidean length), but you can also pass a power p to
norm (i.e, Euclidean length), but you can also pass a power p to Normalizer to use the ![]() norm.
norm.
Word2Vec
Word2Vec19 is a featurization algorithm for text based on neural networks that can be used to feed data into many downstream algorithms. Spark includes an implementation of it in the mllib.feature.Word2Vec class.
To train Word2Vec, you need to pass it a corpus of documents, represented as Iterables of Strings (one per word). Much like in “TF-IDF”, it is recommended to normalize your words (e.g., mapping them to lowercase and removing punctuation and numbers). Once you have trained the model (with Word2Vec.fit(rdd)), you will receive a Word2VecModel that can be used to transform() each word into a vector.
Note that the size of the models in Word2Vec will be equal to the number of words in your vocabulary times the size of a vector (by default, 100). You may wish to filter out words that are not in a standard dictionary to limit the size. In general, a good size for the vocabulary is 100,000 words.
Statistics
Basic statistics are an important part of data analysis, both in ad hoc exploration and understanding data for machine learning. MLlib offers several widely used statistic functions that work directly on RDDs, through methods in the mllib.stat.Statistics class. Some commonly used ones include:
Statistics.colStats(rdd)-
Computes a statistical summary of an RDD of vectors, which stores the min, max, mean, and variance for each column in the set of vectors. This can be used to obtain a wide variety of statistics in one pass.
Statistics.corr(rdd, method)-
Computes the correlation matrix between columns in an RDD of vectors, using either the Pearson or Spearman correlation (
methodmust be one ofpearsonandspearman). Statistics.corr(rdd1, rdd2, method)-
Computes the correlation between two RDDs of floating-point values, using either the Pearson or Spearman correlation (
methodmust be one ofpearsonandspearman). Statistics.chiSqTest(rdd)-
Computes Pearson’s independence test for every feature with the label on an RDD of
LabeledPointobjects. Returns an array ofChiSqTestResultobjects that capture the p-value, test statistic, and degrees of freedom for each feature. Label and feature values must be categorical (i.e., discrete values).
Apart from these methods, RDDs containing numeric data offer several basic statistics such as mean(), stdev(), and sum(), as described in “Numeric RDD Operations”. In addition, RDDs support sample() and sampleByKey() to build simple and stratified samples of data.
Classification and Regression
Classification and regression are two common forms of supervised learning, where algorithms attempt to predict a variable from features of objects using labeled training data (i.e., examples where we know the answer). The difference between them is the type of variable predicted: in classification, the variable is discrete (i.e., it takes on a finite set of values called classes); for example, classes might be spam or nonspam for emails, or the language in which the text is written. In regression, the variable predicted is continuous (e.g., the height of a person given her age and weight).
Both classification and regression use the LabeledPoint class in MLlib, described in “Data Types”, which resides in the mllib.regression package. A LabeledPoint consists simply of a label (which is always a Double value, but can be set to discrete integers for classification) and a features vector.
Tip
For binary classification, MLlib expects the labels 0 and 1. In some texts, –1 and 1 are used instead, but this will lead to incorrect results. For multiclass classification, MLlib expects labels from 0 to C–1, where C is the number of classes.
MLlib includes a variety of methods for classification and regression, including simple linear methods and decision trees and forests.
Linear regression
Linear regression is one of the most common methods for regression, predicting the output variable as a linear combination of the features. MLlib also supports L1 and L2 regularized regression, commonly known as Lasso and ridge regression.
The linear regression algorithms are available through the mllib.regression.LinearRegressionWithSGD, LassoWithSGD, and RidgeRegressionWithSGD classes. These follow a common naming pattern throughout MLlib, where problems involving multiple algorithms have a “With” part in the class name to specify the algorithm used. Here, SGD is Stochastic Gradient Descent.
These classes all have several parameters to tune the algorithm:
numIterations-
Number of iterations to run (default:
100). stepSize-
Step size for gradient descent (default:
1.0). intercept-
Whether to add an intercept or bias feature to the data—that is, another feature whose value is always 1 (default:
false). regParam-
Regularization parameter for Lasso and ridge (default:
1.0).
The way to call the algorithms differs slightly by language. In Java and Scala, you create a LinearRegressionWithSGD object, call setter methods on it to set the parameters, and then call run() to train a model. In Python, you instead use the class method LinearRegressionWithSGD.train(), to which you pass key/value parameters. In both cases, you pass in an RDD of LabeledPoints, as shown in Examples 11-10 through 11-12.
Example 11-10. Linear regression in Python
frompyspark.mllib.regressionimportLabeledPointfrompyspark.mllib.regressionimportLinearRegressionWithSGDpoints=# (create RDD of LabeledPoint)model=LinearRegressionWithSGD.train(points,iterations=200,intercept=True)"weights:%s, intercept:%s"%(model.weights,model.intercept)
Example 11-11. Linear regression in Scala
importorg.apache.spark.mllib.regression.LabeledPointimportorg.apache.spark.mllib.regression.LinearRegressionWithSGDvalpoints:RDD[LabeledPoint]=// ...vallr=newLinearRegressionWithSGD().setNumIterations(200).setIntercept(true)valmodel=lr.run(points)println("weights: %s, intercept: %s".format(model.weights,model.intercept))
Example 11-12. Linear regression in Java
importorg.apache.spark.mllib.regression.LabeledPoint;importorg.apache.spark.mllib.regression.LinearRegressionWithSGD;importorg.apache.spark.mllib.regression.LinearRegressionModel;JavaRDD<LabeledPoint>points=// ...LinearRegressionWithSGDlr=newLinearRegressionWithSGD().setNumIterations(200).setIntercept(true);LinearRegressionModelmodel=lr.run(points.rdd());System.out.printf("weights: %s, intercept: %s ",model.weights(),model.intercept());
Note that in Java, we need to convert our JavaRDD to the Scala RDD class by calling .rdd() on it. This is a common pattern throughout MLlib because the MLlib methods are designed to be callable from both Java and Scala.
Once trained, the LinearRegressionModel returned in all languages includes a predict() function that can be used to predict a value on a single vector. The RidgeRegressionWithSGD and LassoWithSGD classes behave similarly and return a similar model class. Indeed, this pattern of an algorithm with parameters adjusted through setters, which returns a Model object with a predict() method, is common in all of MLlib.
Logistic regression
Logistic regression is a binary classification method that identifies a linear separating plane between positive and negative examples. In MLlib, it takes LabeledPoints with label 0 or 1 and returns a LogisticRegressionModel that can predict new points.
The logistic regression algorithm has a very similar API to linear regression, covered in the previous section. One difference is that there are two algorithms available for solving it: SGD and LBFGS.20 LBFGS is generally the best choice, but is not available in some earlier versions of MLlib (before Spark 1.2). These algorithms are available in the mllib.classification.LogisticRegressionWithLBFGS and WithSGD classes, which have interfaces similar to LinearRegressionWithSGD. They take all the same parameters as linear regression (see the previous section).
The LogisticRegressionModel from these algorithms computes a score between 0 and 1 for each point, as returned by the logistic function. It then returns either 0 or 1 based on a threshold that can be set by the user: by default, if the score is at least 0.5, it will return 1. You can change this threshold via setThreshold(). You can also disable it altogether via clearThreshold(), in which case predict() will return the raw scores. For balanced datasets with about the same number of positive and negative examples, we recommend leaving the threshold at 0.5. For imbalanced datasets, you can increase the threshold to drive down the number of false positives (i.e., increase precision but decrease recall), or you can decrease the threshold to drive down the number of false negatives.
Tip
When using logistic regression, it is usually important to scale the features in advance to be in the same range. You can use MLlib’s StandardScaler to do this, as seen in “Scaling”.
Support Vector Machines
Support Vector Machines, or SVMs, are another binary classification method with linear separating planes, again expecting labels of 0 or 1. They are available through the SVMWithSGD class, with similar parameters to linear and logisitic regression. The returned SVMModel uses a threshold for prediction like LogisticRegressionModel.
Naive Bayes
Naive Bayes is a multiclass classification algorithm that scores how well each point belongs in each class based on a linear function of the features. It is commonly used in text classification with TF-IDF features, among other applications. MLlib implements Multinomial Naive Bayes, which expects nonnegative frequencies (e.g., word frequencies) as input features.
In MLlib, you can use Naive Bayes through the mllib.classification.NaiveBayes class. It supports one parameter, lambda (or lambda_ in Python), used for smoothing. You can call it on an RDD of LabeledPoints, where the labels are between 0 and C–1 for C classes.
The returned NaiveBayesModel lets you predict() the class in which a point best belongs, as well as access the two parameters of the trained model: theta, the matrix of class probabilities for each feature (of size ![]() for C classes and D features), and
for C classes and D features), and pi, the C-dimensional vector of class priors.
Decision trees and random forests
Decision trees are a flexible model that can be used for both classification and regression. They represent a tree of nodes, each of which makes a binary decision based on a feature of the data (e.g., is a person’s age greater than 20?), and where the leaf nodes in the tree contain a prediction (e.g., is the person likely to buy a product?). Decision trees are attractive because the models are easy to inspect and because they support both categorical and continuous features. Figure 11-2 shows an example tree.
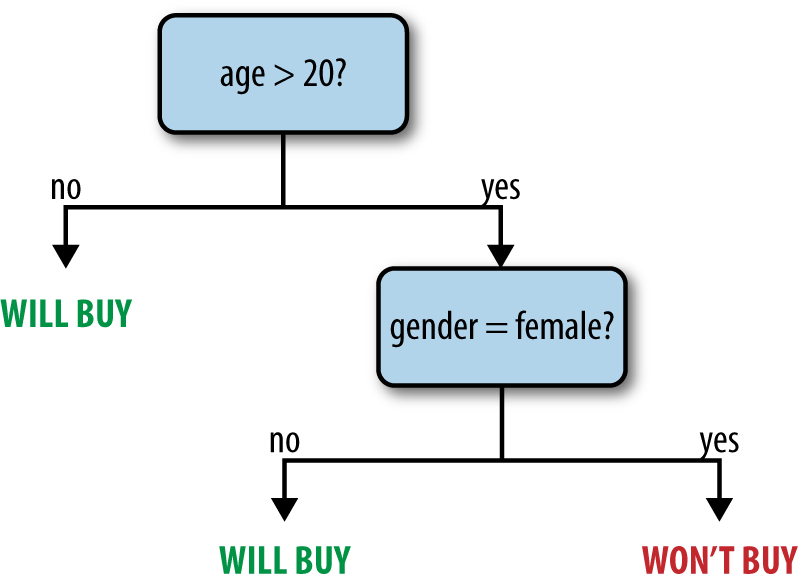
Figure 11-2. An example decision tree predicting whether a user might buy a product
In MLlib, you can train trees using the mllib.tree.DecisionTree class, through the static methods trainClassifier() and trainRegressor(). Unlike in some of the other algorithms, the Java and Scala APIs also use static methods instead of a DecisionTree object with setters. The training methods take the following parameters:
data-
RDD of
LabeledPoint. numClasses(classification only)-
Number of classes to use.
impurity-
Node impurity measure; can be
giniorentropyfor classification, and must bevariancefor regression. maxDepth-
Maximum depth of tree (default:
5). maxBins-
Number of bins to split data into when building each node (suggested value:
32). categoricalFeaturesInfo-
A map specifying which features are categorical, and how many categories they each have. For example, if feature 1 is a binary feature with labels 0 and 1, and feature 2 is a three-valued feature with values 0, 1, and 2, you would pass
{1: 2, 2: 3}. Use an empty map if no features are categorical.
The online MLlib documentation contains a detailed explanation of the algorithm used. The cost of the algorithm scales linearly with the number of training examples, number of features, and maxBins. For large datasets, you may wish to lower maxBins to train a model faster, though this will also decrease quality.
The train() methods return a DecisionTreeModel. You can use it to predict values for a new feature vector or an RDD of vectors via predict(), or print the tree using toDebugString(). This object is serializable, so you can save it using Java Serialization and load it in another program.
Finally, in Spark 1.2, MLlib adds an experimental RandomForest class in Java and Scala to build ensembles of trees, also known as random forests. It is available through RandomForest.trainClassifier and trainRegressor. Apart from the per-tree parameters just listed, RandomForest takes the following parameters:
numTrees-
How many trees to build. Increasing
numTreesdecreases the likelihood of overfitting on training data. featureSubsetStrategy-
Number of features to consider for splits at each node; can be
auto(let the library select it),all,sqrt,log2, oronethird; larger values are more expensive. seed-
Random-number seed to use.
Random forests return a WeightedEnsembleModel that contains several trees (in the weakHypotheses field, weighted by weakHypothesisWeights) and can predict() an RDD or Vector. It also includes a toDebugString to print all the trees.
Clustering
Clustering is the unsupervised learning task that involves grouping objects into clusters of high similarity. Unlike the supervised tasks seen before, where data is labeled, clustering can be used to make sense of unlabeled data. It is commonly used in data exploration (to find what a new dataset looks like) and in anomaly detection (to identify points that are far from any cluster).
K-means
MLlib includes the popular K-means algorithm for clustering, as well as a variant called K-means|| that provides better initialization in parallel environments.21 K-means|| is similar to the K-means++ initialization procedure often used in single-node settings.
The most important parameter in K-means is a target number of clusters to generate, K. In practice, you rarely know the “true” number of clusters in advance, so the best practice is to try several values of K, until the average intracluster distance stops decreasing dramatically. However, the algorithm takes only one K at a time. Apart from K, K-means in MLlib takes the following parameters:
initializationMode-
The method to initialize cluster centers, which can be either “k-means||” or “random”;
k-means||(the default) generally leads to better results but is slightly more expensive. maxIterations-
Maximum number of iterations to run (default:
100). runs-
Number of concurrent runs of the algorithm to execute. MLlib’s K-means supports running from multiple starting positions concurrently and picking the best result, which is a good way to get a better overall model (as K-means runs can stop in local minima).
Like other algorithms, you invoke K-means by creating a mllib.clustering.KMeans object (in Java/Scala) or calling KMeans.train (in Python). It takes an RDD of Vectors. K-means returns a KMeansModel that lets you access the clusterCenters (as an array of vectors) or call predict() on a new vector to return its cluster. Note that predict() always returns the closest center to a point, even if the point is far from all clusters.
Collaborative Filtering and Recommendation
Collaborative filtering is a technique for recommender systems wherein users’ ratings and interactions with various products are used to recommend new ones. Collaborative filtering is attractive because it only needs to take in a list of user/product interactions: either “explicit” interactions (i.e., ratings on a shopping site) or “implicit” ones (e.g., a user browsed a product page but did not rate the product). Based solely on these interactions, collaborative filtering algorithms learn which products are similar to each other (because the same users interact with them) and which users are similar to each other, and can make new recommendations.
While the MLlib API talks about “users” and “products,” you can also use collaborative filtering for other applications, such as recommending users to follow on a social network, tags to add to an article, or songs to add to a radio station.
Alternating Least Squares
MLlib includes an implementation of Alternating Least Squares (ALS), a popular algorithm for collaborative filtering that scales well on clusters.22 It is located in the mllib.recommendation.ALS class.
ALS works by determining a feature vector for each user and product, such that the dot product of a user’s vector and a product’s is close to their score. It takes the following parameters:
rank-
Size of feature vectors to use; larger ranks can lead to better models but are more expensive to compute (default:
10). iterations-
Number of iterations to run (default:
10). lambda-
Regularization parameter (default:
0.01). alpha-
A constant used for computing confidence in implicit ALS (default:
1.0). numUserBlocks,numProductBlocks-
Number of blocks to divide user and product data in, to control parallelism; you can pass –1 to let MLlib automatically determine this (the default behavior).
To use ALS, you need to give it an RDD of mllib.recommendation.Rating objects, each of which contains a user ID, a product ID, and a rating (either an explicit rating or implicit feedback; see upcoming discussion). One challenge with the implementation is that each ID needs to be a 32-bit integer. If your IDs are strings or larger numbers, it is recommended to just use the hash code of each ID in ALS; even if two users or products map to the same ID, overall results can still be good. Alternatively, you can broadcast() a table of product-ID-to-integer mappings to give them unique IDs.
ALS returns a MatrixFactorizationModel representing its results, which can be used to predict() ratings for an RDD of (userID, productID) pairs.23 Alternatively, you can use model.recommendProducts(userId, numProducts) to find the top numProducts() products recommended for a given user. Note that unlike other models in MLlib, the MatrixFactorizationModel is large, holding one vector for each user and product. This means that it cannot be saved to disk and then loaded back in another run of your program. Instead, you can save the RDDs of feature vectors produced in it, model.userFeatures and model.productFeatures, to a distributed filesystem.
Finally, there are two variants of ALS: for explicit ratings (the default) and for implicit ratings (which you enable by calling ALS.trainImplicit() instead of ALS.train()). With explicit ratings, each user’s rating for a product needs to be a score (e.g., 1 to 5 stars), and the predicted ratings will be scores. With implicit feedback, each rating represents a confidence that users will interact with a given item (e.g., the rating might go up the more times a user visits a web page), and the predicted items will be confidence values. Further details about ALS with implicit ratings are described in Hu et al., “Collaborative Filtering for Implicit Feedback Datasets,” ICDM 2008.
Dimensionality Reduction
Principal component analysis
Given a dataset of points in a high-dimensional space, we are often interested in reducing the dimensionality of the points so that they can be analyzed with simpler tools. For example, we might want to plot the points in two dimensions, or just reduce the number of features to train models more effectively.
The main technique for dimensionality reduction used by the machine learning community is principal component analysis (PCA). In this technique, the mapping to the lower-dimensional space is done such that the variance of the data in the low-dimensional representation is maximized, thus ignoring noninformative dimensions. To compute the mapping, the normalized correlation matrix of the data is constructed and the singular vectors and values of this matrix are used. The singular vectors that correspond to the largest singular values are used to reconstruct a large fraction of the variance of the original data.
PCA is currently available only in Java and Scala (as of MLlib 1.2). To invoke it, you must first represent your matrix using the mllib.linalg.distributed.RowMatrix class, which stores an RDD of Vectors, one per row.24 You can then call PCA as shown in Example 11-13.
Example 11-13. PCA in Scala
importorg.apache.spark.mllib.linalg.Matriximportorg.apache.spark.mllib.linalg.distributed.RowMatrixvalpoints:RDD[Vector]=// ...valmat:RowMatrix=newRowMatrix(points)valpc:Matrix=mat.computePrincipalComponents(2)// Project points to low-dimensional spacevalprojected=mat.multiply(pc).rows// Train a k-means model on the projected 2-dimensional datavalmodel=KMeans.train(projected,10)
In this example, the projected RDD contains a two-dimensional version of the original points RDD, and can be used for plotting or performing other MLlib algorithms, such as clustering via K-means.
Note that computePrincipalComponents() returns a mllib.linalg.Matrix object, which is a utility class representing dense matrices, similar to Vector. You can get at the underlying data with toArray.
Singular value decomposition
MLlib also provides the lower-level singular value decomposition (SVD) primitive. The SVD factorizes an ![]() matrix
matrix ![]() into three matrices
into three matrices ![]() , where:
, where:
-
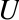 is an orthonormal matrix, whose columns are called left singular vectors.
is an orthonormal matrix, whose columns are called left singular vectors. -
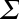 is a diagonal matrix with nonnegative diagonals in descending order, whose diagonals are called singular values.
is a diagonal matrix with nonnegative diagonals in descending order, whose diagonals are called singular values. -
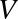 is an orthonormal matrix, whose columns are called right singular vectors.
is an orthonormal matrix, whose columns are called right singular vectors.
For large matrices, usually we don’t need the complete factorization but only the top singular values and its associated singular vectors. This can save storage, denoise, and recover the low-rank structure of the matrix. If we keep the top ![]() singular values, then the dimensions of the resulting matrices will be
singular values, then the dimensions of the resulting matrices will be ![]() ,
, ![]() , and
, and ![]() .
.
To achieve the decomposition, we call computeSVD on the RowMatrix class, as shown in Example 11-14.
Example 11-14. SVD in Scala
// Compute the top 20 singular values of a RowMatrix mat and their singular vectors.valsvd:SingularValueDecomposition[RowMatrix,Matrix]=mat.computeSVD(20,computeU=true)valU:RowMatrix=svd.U// U is a distributed RowMatrix.vals:Vector=svd.s// Singular values are a local dense vector.valV:Matrix=svd.V// V is a local dense matrix.
Model Evaluation
No matter what algorithm is used for a machine learning task, model evaluation is an important part of end-to-end machine learning pipelines. Many learning tasks can be tackled with different models, and even for the same algorithm, parameter settings can lead to different results. Moreover, there is always a risk of overfitting a model to the training data, which you can best evaluate by testing the model on a different dataset than the training data.
At the time of writing (for Spark 1.2), MLlib contains an experimental set of model evaluation functions, though only in Java and Scala. These are available in the mllib.evaluation package, in classes such as BinaryClassificationMetrics and MulticlassMetrics, depending on the problem. For these classes, you can create a Metrics object from an RDD of (prediction, ground truth) pairs, and then compute metrics such as precision, recall, and area under the receiver operating characteristic (ROC) curve. These methods should be run on a test dataset not used for training (e.g., by leaving out 20% of the data before training). You can apply your model to the test dataset in a map() function to build the RDD of (prediction, ground truth) pairs.
In future versions of Spark, the pipeline API at the end of this chapter is expected to include evaluation functions in all languages. With the pipeline API, you can define a pipeline of ML algorithms and an evaluation metric, and automatically have the system search for parameters and pick the best model using cross-validation.
Tips and Performance Considerations
Preparing Features
While machine learning presentations often put significant emphasis on the algorithms used, it is important to remember that in practice, each algorithm is only as good as the features you put into it! Many large-scale learning practitioners agree that feature preparation is the most important step to large-scale learning. Both adding more informative features (e.g., joining with other datasets to bring in more information) and converting the available features to suitable vector representations (e.g., scaling the vectors) can yield major improvements in results.
A full discussion of feature preparation is beyond the scope of this book, but we encourage you to refer to other texts on machine learning for more information. However, with MLlib in particular, some common tips to follow are:
-
Scale your input features. Run features through
StandardScaleras described in “Scaling” to weigh features equally. -
Featurize text correctly. Use an external library like NLTK to stem words, and use IDF across a representative corpus for TF-IDF.
-
Label classes correctly. MLlib requires class labels to be 0 to C–1, where C is the total number of classes.
Configuring Algorithms
Most algorithms in MLlib perform better (in terms of prediction accuracy) with regularization when that option is available. Also, most of the SGD-based algorithms require around 100 iterations to get good results. MLlib attempts to provide useful default values, but you should try increasing the number of iterations past the default to see whether it improves accuracy. For example, with ALS, the default rank of 10 is fairly low, so you should try increasing this value. Make sure to evaluate these parameter changes on test data held out during training.
Caching RDDs to Reuse
Most algorithms in MLlib are iterative, going over the data multiple times. Thus, it is important to cache() your input datasets before passing them to MLlib. Even if your data does not fit in memory, try persist(StorageLevel.DISK_ONLY).
In Python, MLlib automatically caches RDDs on the Java side when you pass them from Python, so there is no need to cache your Python RDDs unless you reuse them within your program. In Scala and Java, however, it is up to you to cache them.
Recognizing Sparsity
When your feature vectors contain mostly zeros, storing them in sparse format can result in huge time and space savings for big datasets. In terms of space, MLlib’s sparse representation is smaller than its dense one if at most two-thirds of the entries are nonzero. In terms of processing cost, sparse vectors are generally cheaper to compute on if at most 10% of the entries are nonzero. (This is because their representation requires more instructions per vector element than dense vectors.) But if going to a sparse representation is the difference between being able to cache your vectors in memory and not, you should consider a sparse representation even for denser data.
Level of Parallelism
For most algorithms, you should have at least as many partitions in your input RDD as the number of cores on your cluster to achieve full parallelism. Recall that Spark creates a partition for each “block” of a file by default, where a block is typically 64 MB. You can pass a minimum number of partitions to methods like SparkContext.textFile() to change this—for example, sc.textFile("data.txt", 10). Alternatively, you can call repartition(numPartitions) on your RDD to partition it equally into numPartitions pieces. You can always see the number of partitions in each RDD on Spark’s web UI. At the same time, be careful with adding too many partitions, because this will increase the communication cost.
Pipeline API
Starting in Spark 1.2, MLlib is adding a new, higher-level API for machine learning, based on the concept of pipelines. This API is similar to the pipeline API in SciKit-Learn. In short, a pipeline is a series of algorithms (either feature transformation or model fitting) that transform a dataset. Each stage of the pipeline may have parameters (e.g., the number of iterations in LogisticRegression). The pipeline API can automatically search for the best set of parameters using a grid search, evaluating each set using an evaluation metric of choice.
The pipeline API uses a uniform representation of datasets throughout, which is SchemaRDDs from Spark SQL in Chapter 9. SchemaRDDs have multiple named columns, making it easy to refer to different fields in the data. Various pipeline stages may add columns (e.g., a featurized version of the data). The overall concept is also similar to data frames in R.
To give you a preview of this API, we include a version of the spam classification examples from earlier in the chapter. We also show how to augment the example to do a grid search over several values of the HashingTF and LogisticRegression parameters. (See Example 11-15.)
Example 11-15. Pipeline API version of spam classification in Scala
importorg.apache.spark.sql.SQLContextimportorg.apache.spark.ml.Pipelineimportorg.apache.spark.ml.classification.LogisticRegressionimportorg.apache.spark.ml.feature.{HashingTF,Tokenizer}importorg.apache.spark.ml.tuning.{CrossValidator,ParamGridBuilder}importorg.apache.spark.ml.evaluation.BinaryClassificationEvaluator// A class to represent documents -- will be turned into a SchemaRDDcaseclassLabeledDocument(id:Long,text:String,label:Double)valdocuments=// (load RDD of LabeledDocument)valsqlContext=newSQLContext(sc)importsqlContext._// Configure an ML pipeline with three stages: tokenizer, tf, and lr; each stage// outputs a column in a SchemaRDD and feeds it to the next stage's input columnvaltokenizer=newTokenizer()// Splits each email into words.setInputCol("text").setOutputCol("words")valtf=newHashingTF()// Maps email words to vectors of 10000 features.setNumFeatures(10000).setInputCol(tokenizer.getOutputCol).setOutputCol("features")vallr=newLogisticRegression()// Uses "features" as inputCol by defaultvalpipeline=newPipeline().setStages(Array(tokenizer,tf,lr))// Fit the pipeline to the training documentsvalmodel=pipeline.fit(documents)// Alternatively, instead of fitting once with the parameters above, we can do a// grid search over some parameters and pick the best model via cross-validationvalparamMaps=newParamGridBuilder().addGrid(tf.numFeatures,Array(10000,20000)).addGrid(lr.maxIter,Array(100,200)).build()// Builds all combinations of parametersvaleval=newBinaryClassificationEvaluator()valcv=newCrossValidator().setEstimator(lr).setEstimatorParamMaps(paramMaps).setEvaluator(eval)valbestModel=cv.fit(documents)
The pipeline API is still experimental at the time of writing, but you can always find the most recent documentation for it in the MLlib documentation.
Conclusion
This chapter has given an overview of Spark’s machine learning library. As you can see, the library ties directly to Spark’s other APIs, letting you work on RDDs and get back results you can use in other Spark functions. MLlib is one of the most actively developed parts of Spark, so it is still evolving. We recommend checking the official documentation for your Spark version to see the latest functions available in it.
17 Some examples from O’Reilly include Machine Learning with R and Machine Learning for Hackers.
18 If you use SciPy, Spark also recognizes scipy.sparse matrices of size N×1 as length-N vectors.
19 Introduced in Mikolov et al., “Efficient Estimation of Word Representations in Vector Space,” 2013.
20 LBFGS is an approximation to Newton’s method that converges in fewer iterations than stochastic gradient descent. It is described at http://en.wikipedia.org/wiki/Limited-memory_BFGS.
21 K-means|| was introduced in Bahmani et al., “Scalable K-Means++,” VLDB 2008.
22 Two research papers on ALS for web-scale data are Zhou et al.’s “Large-Scale Parallel Collaborative Filtering for the Netflix Prize” and Hu et al.’s “Collaborative Filtering for Implicit Feedback Datasets,” both from 2008.
23 In Java, start with a JavaRDD of Tuple2<Integer, Integer> and call .rdd() on it.
24 In Java, start with a JavaRDD of Vectors, and then call .rdd() on it to convert it to a Scala RDD.
