Chapter 2
Bits, Bytes, and Words
Computers store and process digital data. Numbers, text, images, sound, and video must be stored in memory before computers can process them.
We shall explain the organization of computer memory and how numbers, characters, and other data are represented with bit patterns. Binary numbers, modular arithmetic, US-ASCII, and Unicode character encoding will be covered.
2.1 Digital Computers
Modern computers are digital because they store and process discrete rather than continuous information.
- Discrete data–Data are discrete when only certain distinct separate values are allowed. The number of chickens, letter grades, basketball scores, age, income, integers, fractions, and so on are examples. Discrete values have gaps in them.
- Continuous data–Data are continuous when all values in a continuous range, finite or infinite, are allowed. Length, weight, volume, temperature, pressure, speed, brightness, and so on are examples. Continuous values have no gaps separating them. Thus, even in a small range, there are an infinite number of continuous values.
In the past, analog computers processed continuous electronic waves. Such analog signals are hard to store, transmit, or reproduce precisely. In contrast, digital computers use integers to represent information and therefore avoid these critical problems. A continuous value, that of a sound wave, for example, can be digitized by sampling values at a number of discrete points (Figure 2.1). With enough sampling points, the continuous sound wave can be recreated. For example, a continuous sine wave f (x) = sin(x) has an infinite number of continuous values between x = 0 and x = π. To digitize the sine function, we can pick points δ = π/1000 apart and use values at 1001 discrete points: sin(δ), sin(δ), sin(2 * δ), sin(3 * δ), and so on all the way to sin(π).
Information, represented in digital form, must be stored in computer memory to be processed. The most basic memory unit is a bit, which can represent either a 1 or a 0. A byte is a group of 8 bits. A word consists of several (usually 4 or 8) bytes (Figure 2.2). Note in computing, as shown in Figure 2.2, we count starting from zero.
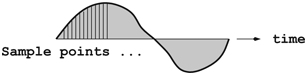
FIGURE 2.1 Sampling a Continuous Wave
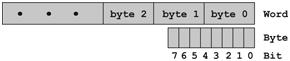
FIGURE 2.2 Bit, Byte, and Word
In a computer, the Central Processing Unit (CPU) is where logic computation on data takes place. The CPU loads data from memory in order to process them, then stores the results back to memory. A word is normally the smallest integral data entity a CPU is designed to manipulate. The size of the word, measured in bits, is determined by the size of CPU registers. A CPU register is able to load from and store to cache/RAM (Random Access Memory) all its bits as a unit at once. The word size is one of the most important hardware architecture features of a computer. For most modern computers, the word size is either 32 (4 bytes) or 64 (8 bytes).
For modern general purpose computers, the entire memory is an array of bytes (Figure 2.3), each of which can be addressed directly (called byte addressing), hence the term random access memory. A word of length n can hold memory addresses ranging from 0 to at most 2n – 1. Assuming each address has a byte, then the memory can have at most 2 n bytes. The actual allowable size of your RAM is often well below this theoretic upper bound due to other hardware limitations.
Digital information must be encoded by zeros and ones and stored in memory in order to be processed. Information stored in RAM is volatile and will disappear when the system is turned off. Nonvolatile or persistent data storage is provided by one or more storage drives, including hard-disk drives (HHD) or solid-state drives (SSD).
In computer product specifications, available memory in cache, RAM, or data storage is given in byte units:

FIGURE 2.3 Memory Array of Bytes
- kilobyte (KB) = 1024 bytes
- megabyte (MB) = 1024 KB
- gigabyte (GB) = 1024 MB
- terabyte (TB) = 1024 GB
- petabyte (PB) = 1024 TB
Typical computer RAM sizes range from 1GB to 16GB.
Ordinarily, K (kilo) is a prefix for 1000 (in the metric system), but digitally (in the binary system), K is 1024. Similarly, as far as memory or data sizes go, M (Mega) is KK, Giga is KM, Tera is KG, and Peta is KT, keeping in mind always that K is 1024 1
Bit Patterns
The basic way to represent data in computer memory is to use bit patterns. A bit pattern is a particular sequence of zeros and ones presented in a fixed number of bits. Table 2.1 shows all possible patterns made up of three bits. Each bit has two variations, 0 and 1. For each value of bit 1, there are two values for bit 0, resulting in 2 x 2 = 22 two-bit patterns. Similarly, for each value of bit 2, there are 4 patterns for bits 0 and 1, giving 2 x 22 = 23 three-bit patterns.
In general, the total number of different patterns with n bits is 2 n . Therefore, a byte can give you 28 = 256 bit patterns, a 32-bit word 232 = 4294967296 bit patterns, and a 64-bit word 264 = 18446744073709551616 bit patterns.
In a digital computer, bit patterns are the only way to represent data. And, the same bit patterns can be used to represent different types of data, such as a number, a character, or a network address. We will see how numbers are represented next.
TABLE 2.1 The Eight 3-Bit Patterns

2.2 Binary Numbers
To compute with numbers, we need to represent them in memory. For integers, the binary number system uses only zeros and ones and is therefore particularly suited to be stored as bit patterns.
Numerals
Numerals are symbols we use to write down numbers. The numerals we use today (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) are Arabic numerals derived from the Hindu- Arabic numeral system. Different civilizations have invented and used their own symbols for numbers. Figure 2.4 shows the Roman and Egyptian numerals.

FIGURE 2.4 Roman and Egyptian Numerals
And Figure 2.5 shows ancient Chinese numerals. Simplified modern versions of these are still in use today.

FIGURE 2.5 Ancient Chinese Numerals

FIGURE 2.6 Larger Chinese Numerals
With the digits, the Arabic numerals, we can write down numbers from zero to nine. We still need a way to represent larger numbers. We can invent new symbols, of course. Figure 2.6 shows some modern Chinese symbols for larger numbers.
How will we create new symbols to keep up with ever larger numbers? A systematic way must be found. An ingenuous solution is the place value system. For example, with three digits side by side, we can write down numbers up to, but not including, a thousand. Thus, the notation 379 means three hundreds, seven tens, and nine ones, or
379 = 3 × 102 + 7 × 10 + 9 × 1
With the place value system, larger numbers simply require more places. Thus, we have a system for creating new symbols for numbers by combining the numerals. Such numbers, where each place represents a power of 10, are known as base-10 numbers or decimal numbers.
Base-2 Numbers
Binary numbers also use a place value system, just like decimal numbers, except the base is 2, not 10. We use only two numerals, 0 and 1, for binary numbers. Using one place, only two numbers can be represented, namely 0 and 1. To represent two in binary, we need to go to the next place. Thus, the binary number 10 means two
1 × 2 + 0 × 1
and the binary number 11 means three
1 × 2+1 × 1
Similarly, 101 means five
1 × 22 + 0 × 2+1 × 1
With four bits, we can represent numbers from zero to fifteen (Table 2.2). Keep in mind that, just as in decimal numbers, the least significant digit (bit) has the rightmost position and the most significant bit has the leftmost position. And the bit and byte positions are always counted from the right.
TABLE 2.2 Four-Bit Binary Numbers

To get familiar with binary notation, take any binary number in Table 2.2 and add 1 to it, carrying to the next higher position as you would in doing addition, you will get the bit pattern for the next binary number. Also visit these interactive demos on the CT website: Demo: UpCounter and Demo: DownCounter.
It is not surprising if you find binary numbers confusing at first. After all, as far as numbers, the decimal system is our mother tongue and is firmly ingrained in our thinking. Look at Figure 2.7 and see how you feel yourself. Binary numbers would become easier if we memorize the powers of 2 as well as we do powers of 10. Here goes: 2 (bit 2), 4 (bit 3), 8 (bit 4), 16 (bit 5), 32 (bit 6), 64 (bit 7), 128 (bit 8), 256 (bit 9), 512 (bit 10), 1024 (bit 11), 2048 (bit 12), and so on.

FIGURE 2.7 Popular T-shirt Design
Inside a digital computer, numbers are naturally in binary, and hardware support is provided for their operations, as long as they fit in a single word. A 32- or 64-bit word can represent numbers from 0 to 232 – 1 or 264 – 1. That’s a lot of numbers. Still, it is far from covering all numbers. To handle larger numbers, we can use multiple words and write software for manipulating them.
CT: MEANING OF SYMBOLS
Anyone can invent a symbol and assign it a meaning. The same symbol may have another meaning in a different context. Do not guess a symbol’s meaning by its appearance. Always refer to its definition within the intended context.
Numerals and numbers from different cultures, as well as the place value system, are examples.
Ancient Chinese Binary Symbols
I-Ching (![]() ), a Chinese text that traces back to the 3rd to the 2nd millennium BCE, introduced two symbols, yin (- -) and yang (–). Combinations of three or six yin-yang symbols form the 8 trigrams (
), a Chinese text that traces back to the 3rd to the 2nd millennium BCE, introduced two symbols, yin (- -) and yang (–). Combinations of three or six yin-yang symbols form the 8 trigrams (![]() Figure 2.8) or the 64 hexagrams (
Figure 2.8) or the 64 hexagrams (![]() ). Thus, the concept of repeating two symbols to form increasingly more symbols is an ancient one.
). Thus, the concept of repeating two symbols to form increasingly more symbols is an ancient one.
- Numbers in Other Bases

FIGURE 2.8 I-Ching Trigrams ( )
)
2.2.1 Numbers in Other Bases
While we are at it, why don’t we look at numbers in other bases? Octal numbers are base 8 and use digits 0–7. Hexadecimal (hex) numbers are base 16 and use digits 0–9 followed by A (ten), B (eleven), C (twelve), D (thirteen), E (fourteen), and F (fifteen). The symbol 10 stands for eight in octal and sixteen in hexadecimal. The symbol 25 means
2 × 8 + 5 (21 in octal)
2 × 16 + 5 (37 in hex)
For interactive demos, visit the CT website (Demo: OctalCounter and Demo: HexCounter).
TABLE 2.3 Numbers in Different Bases

Three bits are needed for each octal digit and four bits for each hexadecimal digit. A byte of all 1s can represent the hex number FF (two hundred fifty- five). In general, we can use numbers in any base we desire, and we are not, limited by having two hands with ten digits.
CT: EVALUATE DIFFERENT OPTIONS
No feature in a system should be treated as rigid or sacred. Ask “what if it is changed?” and you will begin to think flexibly, acquire a deeper understanding, and, perhaps, even make a breakthrough.
Go to the CT website to experiment with counters where you can set the base
(Demo: ArbCounter).
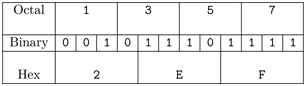
Octal and hex numbers are often used as a shorthand for the bit patterns representing them. Each octal digit specifies a 3-bit pattern, and each hex digit specifies a 4-bit pattern. Also, distinct prefixes, 0x for hex and 0 for octal, are used to denote such numbers. This is especially true in programming languages. Table 2.4 shows the bits for each digit of 01357 or 0x2EF.
TABLE 2.4 Octal and Hex Bit Patterns
Mixed-Base Numbers
Decimal numbers use powers of ten as place values; binary numbers powers of two; octal numbers powers of eight; and hex numbers powers of sixteen. Talking about flexible thinking, what about asking the question why the place values must always be a power of some fixed number?
Well, there is no reason for that at all. In fact, we can use any desired value for each place. Such numbers are called mixed-radix or mixed-base numbers. For instance, how about numbers with place values 1, 60, 60, 24, 7? Would that be crazy?
Actually, we use such numbers every day, literally. We have 60 seconds in a minute, 60 minutes in an hour, 24 hours in a day, and 7 days in a week, don’t we? And we have 12 inches in a foot, 3 feet in a yard, and 1760 yards in a mile. Granted, such length measurements should have long ago been replaced by the metric system.
Applying abstraction (CT: ABSTRACT AWAY, Section 1.2), we realize that the place-value numbering system’s essence, its intrinsic nature, is “a preassigned value for each place,” and nothing more.
2.3 Positive and Negative Integers
Using binary notation, a word with n bits can represent numbers 0 to 2n – 1. These are known as unsigned numbers. But, we most definitely also need to work with signed numbers. If an integer is positive, we don’t have a problem representing it. But what about negative integers?
An obvious idea is to use the highest bit in a word as a sign bit and use the rest of the word for the magnitude of the integer. If the highest bit is 1, then it is a negative number. If it is 0, a positive number. To make it easier to visualize, let’s pretend that the word size is 3:
| 000 (is 0) | 001 (is 1) | 010 (is 2) | 011 (is 3) |
| 100 (is 0) | 101 (is -1) | 110 (is -2) | 111 (is -3) |
With sign and magnitude, using n bits, we can represent 2 n−1 – 1 positive numbers, 2n−1 – 1 negative numbers, and zero twice.
The sign and magnitude method does not work as well as the two’s complement method, which is widely used by computers. From the binary representation of an integer m, we use the following algorithm to find the binary representation of –m.
Algorithm 2sComplement:
Input: An integer m
Output: Returns –m
- Obtain the bit pattern for m
- Obtain a new binary number by flipping each bit in m (switch 0 to 1, and 1 to 0)
- Add 1 to the resulting number and return it as value Again, for n = 3, we have the following 8 numbers
| 000 (is 0) | 001 (is 1) | 010 (is 2) | 011 (is 3) | 100 (is 4 or -4) |
| 000 (is 0) | 111 (is -1) | 110 (is -2) | 101 (is -3) | 100 (is 4 or -4) |
Figure 2.9 shows an application of the two’s complement algorithm with an 8-bit word.

FIGURE 2.9 Obtaining Negative 98
Note the following.
- The same algorithm turns a positive number into a negative number and vice versa.
- There is only one representation for zero.
- Negative numbers have a leading (left-most) one bit, and positive numbers have a leading zero bit, except 2n−1, whose positive and negative representations turn out to be the same. Theoretically, this number is the most negative and most positive number possible for an n-bit word. But, most programming languages treat this number as negative. And define the largest positive number to be 2n−1–1.
- Adding the representation of m and –m results in zero, discarding any carry to the next, nonexistent, higher bit position (Section 2.4).
Try adding 98 and –98 in Figure 2.9 yourself.
Using the two’s complement system for negative numbers has a very important advantage. Namely, the fundamental arithmetic operations of addition, subtraction, and multiplication (Section 2.4) do not need to check the sign of the number and can proceed as if all numbers are non-negative (Demo: SignedCounter). For division, the simplest way is to convert to positive, perform the division, and adjust the signs of the quotient and remainder later. Further, these procedures don’t need changing when working with an increased word length.
2.4 Modular Arithmetic
As mentioned before, a word of size n can represent 2n numbers, zero to 2n – 1 for unsigned integers and –2n−1 to 2n−1 for signed integers. CPU-supported arithmetic on such word-size numbers (addition, subtraction, multiplication, and integer division 2 ) must produce results stored within a single word. To work within the limit imposed by the word length, modular arithmetic is used. We will describe modular arithmetic, a mathematical concept, presently.
In modular arithmetic, we limit the size of possible integers by a positive integer called the modulus. If m is the modulus, then the possible integers range from 0 to m – 1. With modular arithmetic, when a result is out of range, we add or subtract a multiple of m to bring the result in range. Let’s see how this is done.
Definition: For modulus m and two arbitrary integers a and b, a is congruent to b modulo m if m divides (a – b) evenly.
In other words, a is congruent to b modulo m if the remainder of a – b divided by the modulus is zero. We use
a ≡ b mod m
to denote that a is congruent to b modulo m. Let’s look at an example where m = 2.
Thus, the set of all integers is divided into two disjoint subsets: the even and the odd numbers. All members within each subset are congruent mod 2. Each subset is called a congruence class mod 2. Under the modulus 2, we can use 0 to represent any even number and 1 to represent any odd number.
Now for modulus 16, we have
and so on for a total of 16 congruent classes.
Use of modular arithmetic can be found on the familiar watch face (Figure 2.10), where we have a limit of twelve hour marks. We count from 0 to the 11th hour, then start to reuse the marks again. This is why we need to use AM and PM to distinguish which hour it is out of the 24 hours in a day.
Modular congruence is an equivalence relation, because it satisfies all of the following three conditions.
For any integers a, b, c and modulus m > 0
- Reflexivity: a ≡ a mod m (Proof: a – a = 0, which is divisible by m.)
- Symmetry: a ≡b mod m implies b ≡ a mod m (Proof: If m divides (a – b), then it divides (b – a).)
- Transitivity: a ≡ b mod m and b ≡ c mod m implies a ≡ c mod m (Proof: m divides (a – b) – (b – c) because it divides both terms.)

FIGURE 2.10 Watch Face
Computationally, “mod m” simply means “divide by m and take remainder.” For an expression exp involving addition, subtraction, and multiplication, exp mod m can be computed by performing mod m whenever necessary to reduce the size of the operands and intermediate results. The final result will always be the same. This way, we keep the numbers under computation always within 0 through m – 1. There is no overflow problem for division. To compute a/b, the fact that both a and b are already correctly represented means their quotient and remainder must also be in the correct range.
Computer hardware supports modular arithmetic with a modulus m = 2n, where n is the word size (32 or 64, for example). This is done simply by ignoring any overflow to the left of the nth bit. Using modular arithmetic meets the need to work within the limit imposed by the word length.
Note that if a sequence of arithmetic operations on integers results in a final answer within the modular range, then using modular arithmetic for all those operations will result in the same answer. This happens even if some intermediate result may cause overflow.
For simplicity, consider numbers in 4-bit words. The allowable bit patterns range from 0 to 15. The arithmetic computation 3 x 7 – 4 x 5, when carried out this way,
3 × 7 mod 16 producing 5
4 × 5 mod 16 producing 4
5 − 4 mod 16 producing 1
gives you the correct final answer, namely 1.
CT: MIND RESOURCE LIMITATIONS
Be mindful of resource limitations. Find ways to operate within such limitations. Use resources wisely. Guard against running out of resources.
Keeping this in mind may help you avoid running out of gas on a trip or motivate you to conserve, reuse, and recycle materials.
In many programming languages, C/C++ and Java included, arithmetic operations (+, –, *, and /) are implicitly modular. And the operator % is used for an explicit mod operation:
x % m (divide x by m and take remainder).
Modular arithmetic is not only important for understanding arithmetic on binary numbers in a computer. It is also used widely in mathematics and extensively in modern cryptography.
CT: SYMBOLS CAN BE DECEIVING
Pay special attention to the same symbol when used in a different context. It may mean similar but different things. Such confusion may not cause problems immediately. That is dangerous.
Beware that the familiar mathematical symbols +, –, *, and / mean modular arithmetic in programming languages. Failure to guard against overflow in programs is a source of bugs hard to find. Such a program may work most of the time until some input situation causes an overflow.
When working with signed numbers, overflow occurs:
- When adding two positive numbers and getting a negative result.
- When adding two negative numbers and getting a positive result.
- When multiplying two numbers and getting the wrong sign in the result.
Such conditions are commonly disregarded in hardware, and programmers must detect these overflow conditions in their programs.
An actual example in advertising may help illustrate this CT concept.
An ad for drop down cloth hanger claims to save space in your closet by showing a picture of a closet full of clothing, side by side with a picture of the closet half empty using the product. The caption read, “The same closet using wonder hangers.” When Consumer Reports pointed out that the pictures actually showed different numbers of clothing pieces, the company responded: “We only said the closet was the same.” Ha ha ha, buyers beware.
2.5 Base Conversion
Now let’s challenge ourselves to the task of finding the binary representation for any particular integer a > 0. Given any non-negative integer a and base b, our goal is to find the base b digits for a.
To illustrate our method, let’s look at an example and think about it backwards.
a = 13 =1 × 23 + 1 × 22 + 0 × 2 + 1
The binary notation for a =13 is 1101, where d 0 = 1 (digit 0), d 1 =0 (digit 1), d2 = 1, and d3 = 1. a = 13 = d3 × 23 + d2 × 22 + d 1 × 2 + do
If we divide both sides of the preceding equation by 2 and take remainder, we have
d 0 = remainder(a, 2) .
Now we set a to (a – d 0)/2, and get
a = d 3 × 22 + d 2 × 2 + di .
This leads to the value of d 1
d 1 = remainder(a, 2) .
Then we set a to (a – d 1)/2 and repeat the same steps until a becomes zero. The general algorithm for base conversion can now be specified.
Algorithm baseConversion:
Input: Non-negative number to be converted a, the desired base b Output: Displays sequence of digits for a in base b
- Set i = 0
- Set di = remainder(a, b), set a = quotient(a, b)
- If a = 0, then display base b digits di through d 0 and terminate
- Set i = i +1
- Go to step 2
Call the algorithm with b = 2 for converting to binary, b = 8 to octal, and so on. Go to the CT website for an interactive version (Demo: BaseConversion).
CT: START FROM THE END
It is natural to start from the beginning. But starting from the end can often be an effective problem-solving strategy.
When deriving algorithm baseConversion, we assumed we had the desired digits, the end result (namely the d¿s), already. Then, we see how each digit can be easily obtained by integer quotient and remainder operations.
In planning an event, such as a birthday party, a wedding, or an academic conference, it is best to plan for the “EVENT” day first, then what must be complete on EVENT –1 day or EVENT –1 week, and so on. Working backwards like this, we can sequence the order of tasks and allocate enough time for each task–and finally, when to start and what to do first!
In a sense, the starting and ending points are conceptually the same. For example, when taking a trip from home to destination A, we would produce a copy of the Google Maps directions. But, we may forget that we also need directions to come back home. If we computize, we would have directions from destination A back home printed at the same time. Actually, it would be more convenient for users if Google Maps automatically produces round-trip directions by default, or at least as an option 3 .
Now, let’s turn our attention to data representation for characters.
2.6 Characters
Number processing is fundamental, but computers need to handle other types of data, among which perhaps the most important is text or character data. Again, bit patterns are used to represent individual characters. And there are a few widely used standards for character code including US-ASCII and UNICODE.
2.6.1 US-ASCII
Basically, each character can be assigned a different binary number whose bit pattern represents that character. For example, the American Standard Code for Information Interchange (US-ASCII) uses 7 bits (binary 0 to 127) to represent 128 characters: 0–9, A–Z, a–z, SPACE, CR, NEWLINE, punctuation marks, symbols, and control characters.
Table 2.5 shows the US-ASCII code (in decimal) for some common characters. Such tables are also widely available in octal and hex.
TABLE 2.5 US-ASCII for Common Characters
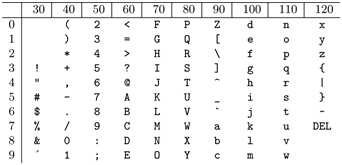
Thus, we have, for example, these character representations

Note that the code for characters ‘0’–’9’ are not the same as the binary number representations for 0–9 as numbers. The ASCII code for characters also results in an induced ordering of characters, known as a collating sequence. The ordering is based on the numerical value of each character’s ASCII code. For example
‘0’<‘1’< ... <‘9’<‘A’<‘B’< ... <‘Z’<‘a’<‘b’< ... <‘z’.
The collating sequence makes it easy to arrange texts, such as a list of names, into a standard order. A collating sequences may facilitate arranging text into an alphabetical order, but that may not be the same as the traditional ordering used in dictionaries.
US-ASCII is a subset of ISO-8859-1, a standard consisting of 191 eight-bit encoded characters commonly used in Western languages.
2.6.2 Unicode
Unicode is an international standard for encoding, representation, and handling of text data from most of the world’s writing systems. It now contains more than 110,000 characters from 100 languages/scripts. The Unicode Consortium, an international collaboration, publishes and updates the Unicode standard.
Unicode allows the use of characters from all of the covered languages, which is practically all languages known to men, in a single written document. This is very advantageous, especially in a world increasingly interconnected by the Internet and the Web. The success of Unicode and its widespread use brought about standards on software internationalization and localization.
Unicode uses hexadecimal (hex) 0 through 10FFFF, a total of 1,114,112 code points, to represent character symbols. Each code point is denoted U+, followed by 4 to 6 hex digits (Table 2.4, Section 2.2.1). As an example, here is the author’s Chinese name with Unicode in hex.
| U+738B | U+58eb | U+5f18 | % |
Among different Unicode encoding formats, UTF-8 is the most widely used. The Demo: UnicodeLookup tool at the CT website shows the UNICODE of any character you input.
UTF-8
UTF-8 is a particularly efficient and widely used encoding format for Unicode. UTF-8 encodes each Unicode code point using 1 to 4 octets (an octet is 8 bits or a byte in the Unicode standard). Earlier positions in the Unicode character set, which are used more often, require fewer bytes. UTF-8 is US- ASCII compatible because the first 128 Unicode characters are exactly those from US-ASCII and are encoded with the same 8-bit pattern as US-ASCII. Therefore, any valid US-ASCII encoded character is also the same UTF-8 Unicode character.
The UTF-8 encoding format can be explained simply as follows.
- The first 128 code points (U+0000-U+007F) use one byte, 0 followed by 7-bit US-ASCII code for the target character (0□□□□□□□).
- The next 1920 code points (U+0080-U+07FF) use two bytes: first byte=110 followed by 5 bits (110□□□□□), second byte=10 followed by 6 bits (10□□□□□□). The 11 useful bits are more than enough for the 1920 code points.
- The next 63487 code points (U+0800-U+FFFF) use three bytes: first byte=1110 followed by 4 bits (1110□□□□), next two bytes each in the form 10 followed by 6 bits (10□□□□□□).
- The remaining code points (U+10000-U+1FFFFF) use four bytes: first byte=11110 followed by 3 bits (11110□□□), the next three bytes each in the form 10 followed by 6 bits (10□□□□□□).
Note with UTF-8, the first byte of a multibyte representation specifies the number of bytes by the count of leading 1 bits. Nonleading bytes all start with 10 to distinguish them from leading bytes.
With UTF-8, US-ASCII coded documents are automatically Unicode texts. UTF-8 is now recommended for all webpages, email messages, programming languages, operating systems, and applications.
Reuse of Bit Patterns
You must have figured out by now that a given bit pattern may represent a binary number or a character. For example, the bit pattern
01000001
represents 65 or the character ‘A’. The question is, how do we know which one? Again, the answer is “context.”
CT: DATA CONTEXT
The same bit pattern can be interpreted differently depending on the context where it is used.
We must provide a context to treat any given bit pattern to indicate if it is a number, a character, or something else. The context can be deduced from where the pattern is used or by explicitly provided indications. For example, in evaluating the expression x > 0, we know the value of x needs to be interpreted as a number. A programming language usually supplies a way to declare the data type of a variable. The type informs a program how to interpret the data representation associated with any given variable.
2.7 Editing Text
One of the most basic tasks on a computer is text editing. You would use a text editor to input text, make changes (add, delete, revise text), search for character strings, save the result, and perform other functions. A text file contains plain text, meaning that from start to finish,it contains just a string of characters. Data and program source code files on a computer are usually in plain text. Text editors help you produce such plain text files.
Default text editors are usually made available by your operating system, for example Notepad/Wordpad for Microsoft Windows, TextEdit for Mac System X, and vi and gedit for Linux. Text editors that are free to download include vim/gvim (Linux, Windows and Mac), emacs (Linux, Windows and Mac), TextWrangler (Mac) and notepad++ (Windows).
Find a good text editor, learn it well, and you are well on your way to writing and editing computer codes efficiently. The CT website has materials to help you learn Vi/Vim and Emacs.
Word processing programs such as MS Word™, LibreOffice, LTEX, and Adobe Acrobat™, are different from text editors. These help you create reports, presentations, and other well formatted and styled documents mostly for human consumption. Document files produced by word processors contain formatting and display code so they can be presented nicely for viewing or printing.
Input Methods
A keyboard allows us to type data into a computer. When a key is pressed or released, an event is generated that is detected by the operating system. An operating system has an internal keycode table that assigns a different numerical keycode to each key on the keyboard.
Here are some example keycodes from Linux.
| key ESC | 1 | key TAB | 15 |
| key A | 30 | key S | 31 |
| key D | 32 | key L Shift | 42 |
| key F1 | 59 | key UP | 103 |
A keycode can then lead to a character encoding. Some keycodes, such as those for function keys or arrow keys, correspond to no character code.
The default character encoding is determined by the computer’s locale setting. The locale determines the region, language, time, currency, and other such features used by a computer. For example, the locale can be set to “en_US.UTF-8” for a computer in the USA.
Using a Western keyboard, we can easily enter US-ASCII characters. For other characters, we need to add language support as well as input methods for the desired languages. Having set up multiple input methods, you can then switch from one input method to another at will to enter data from the keyboard.
Figure 2.11 shows three available input methods: English (standard keyboard), Chinese Pinyin, and English (Dvorak keyboard). Usually, CNTL+SPACE (pressing SPACE while holding down the CONTROL key) will switch to the next available input method.
As an example, Figure 2.12 shows the a keyboard layout for entering Traditional Chinese characters using phonetics.
On a touch screen, you can use a specialized on-screen keyboard to enter characters in different languages. Better yet, with voice recognition you can just say the words to create text input. Figure 2.13 shows the Chinese Pinyin keyboard on an Android phone.

FIGURE 2.11 Input Methods

FIGURE 2.12 Keyboard Layout for Chinese Phonetic Symbols
Modern applications, including Web browsers, email clients, text editors, and document processors support Unicode text, provided that the necessary language support and display fonts have been installed on your system.

FIGURE 2.13 Chinese Phonetic Input on Android Phone
2.8 Data Output
Data encoded in binary allow fast processing and storage on the computer. Yet, we still need to output data for human consumption. This means displaying numbers, characters, and images, playing audio and video, and so on.
In the early days, operators used card punches to punch holes on stiff paper cards (Figure 2.14) as input to batch-processing computers housed in climate-controlled machine rooms. And the computed results were output to line printers. Early line printers were washing-machine sized objects that impact print text, one line at a time, usually on continuous-feed form sheets. Turn-around time was measured in hours and even days.

FIGURE 2.14 A Punch Card
Later in history, CRT (cathode ray tube) monitors, connected to any given computer, provided concurrent access (input and output) by multiple users to time-sharing systems. Users enjoyed immediate interactions with computers and productivity increased tremendously. CRT monitors are monochrome (one color) and display characters (US-ASCII) with hardware-defined shapes.
Computers today have full-color, high-resolution LCD/LED graphics displays supported by dedicated GPU (Graphics Processor Unit) hardware. The pixel rendering of characters is controlled by font files. A font is a particular style or design of the appearance of the characters. For example, Serif fonts add little lines at the end of strokes. Sans Serif fonts are without such added decorations. Well-known font families include Times New Roman, Helvetica, and Courier. As an example, Figure 2.15 shows a particular Courier font design.
Within a font family, you can also call for a variant style, such as italic and boldface. Normally, fonts are proprietary, requiring permission/fee for their use. But, free fonts in the public domain do exist. Many fonts have been designed before the age of computers or even typewriters. Typefaces for computers are stored in font files that allow easy size scaling. Your computer comes with a collection of fonts. Additional fonts can be downloaded and installed. Applications usually allow you to pick from available fonts to customize the display of characters. Figure 2.16 shows a set of fonts for Chinese characters. Different typefaces or fonts can be made available to support displaying characters in any given language.

FIGURE 2.15 A Courier Font

FIGURE 2.16 Chinese Fonts
The ability to output characters makes displaying numbers a breeze. Numbers represented in binary are converted to decimal (base 10) and the digits (0-9) are displayed as characters for humans to read.
CT: DELIVER THE MESSAGE
Information must be conveyed in a form that can be understood and processed by the receiver.
This is so true for human-to-human, human-animal, and human-computer communication, as professor Temple Grandin, famous for her contributions to communications with autistic children and animals alike, would surely tell you.
Exercises
- 2.1 What is the difference between digital and analog signals? Please explain.
- 2.2 What is a word? How many bytes in a word? Explain clearly.
- 2.3 What is a bit pattern? Let n be the number of bits. What is the number of different bit patterns for n = 3, n = 4, n = 8, or n = 32?
- 2.4 What is the decimal value of the binary number 101? 10101101?
- 2.5 Write down the octal and hex representations for the decimal number 911. Show your calculations, as well as the final answers.
- 2.6 Find the two’s complement binary number –103. Show your calculations, and verify that when it is added to 103, you get zero. Extra credit: Prove that the two’s complement algorithm always produces the negative of any m.
- 2.7 What is an equivalence relation?
- 2.8 Compute 139 mod 16. Hint: The result is between 0 and 15.
- 2.9 What the difference between text editing and word processing?
- 2.10 What is UNICODE? UTF-8? What’s the difference?
- 2.11 What is a keycode? Who defines keycodes?
- 2.12 Computize: What does the word “actual” mean in Spanish? In English? What CT principle does it demonstrate?
- 2.13 Computize: The byte 01000010 represents what number? Or what ASCII character? What CT principle does it demonstrate?
- 2.14 Computize: What bit pattern representation is used for 303 as a telephone area code or as the number three hundred and three? How do we tell them apart?
- 2.15 Group discussion topic: Mary had a little lamb. Context and semantics.
- 2.16 In-class group activity: Invite two teams of four students, team A and B, to the front of the class. Each team member has large letters 0,1,...,9,A,B,C,D,E,F, each letter on a separate sheet of paper. The CT website has ready-to-print letters. Team A is the binary team and B the octal team, say. The class will shout out a number, in a given range, for both teams to form the correct display. The faster team wins and gets to sit down. The winning team members can pick others in class to replace them. The instructor will keep it fun, encouraging, and interesting.
Footnote
1 In actual usage, there is often confusion between the metric and binary interpretations.
2 Integer division can produce an integer quotient or an integer remainder.
3 No such Google Maps provision as of Fall 2015.
