CHAPTER 8

The Time Value of Money

Discounting and Net Present Values¹

This chapter deals with compounding and discounting. For students of accounting, it is a critical component in understanding long-term liabilities. After the basics are presented, the chapter will discuss how to value annuities (equal periodic payments), bonds (debt obligations), and perpetuities (payments that continue forever).

The Time Value of Money

The time value of money is one of the most powerful concepts in finance. It is a concept that small children express when they say, “I want it now, not later, now!” Quite simply, the idea is that a dollar today (or anything, for that matter) is worth more than a dollar tomorrow.

An easy way to start the explanation of the time value of money is to consider a bank account. If you invest $100 in a bank account at the start of the year and earn 5 percent annual interest on your funds during the course of the year, how much will you have at the end of the year? You will have $105, which is your original deposit of $100 plus the interest of $5 that you earned during the year ($100 × 5%). This means that with a 5 percent interest rate, $100 today is equivalent to $105 in a year. Conversely, $105 in a year is worth $100 today at that interest rate.

Taking an amount today and computing what it will be worth in the future is called compounding. Taking an amount in the future and figuring out what it would be worth today is called discounting. Compounding and discounting are inverses of each other.

What if you leave the $105 in the bank for a second year, again earning 5 percent? How much would you have at the end of the second year? You would have $110.25. You start the second year with $105 and earn an additional $5.25 of interest during the second year ($105 × 5%). You earned more in interest during the second year ($5.25) than in the first year ($5.00) because you began the second year with more money. In the second year, you earned $5 interest on the original $100 plus an additional $0.25, which is 5 percent interest on the $5 that you earned the first year. In the second year, you are earning interest on your interest. This example also means that $110.25 in 2 years is worth $100 today.

We can represent the above visually with the following time line:

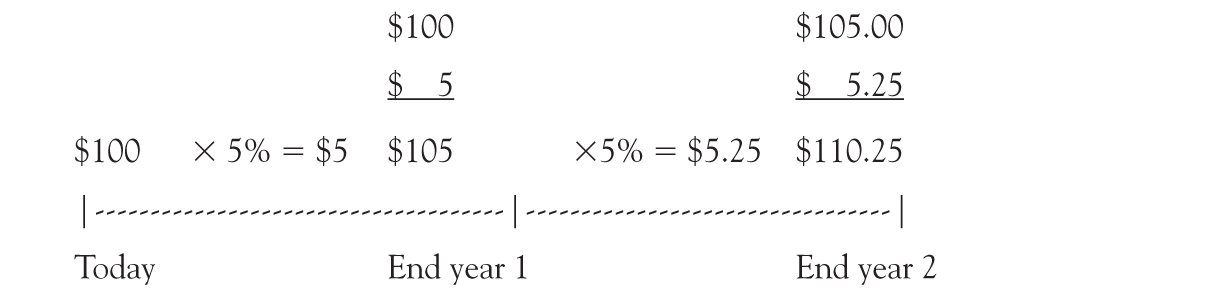
We will consider today to be the present, so the $100 is our present value (or PV for short). The $105 value is a future value (FV), as is the $110.25. To differentiate between the two, we call the $105 the FV at time 1 (FV₁) and the $110.25 the FV at time 2 (FV₂). We can relabel our time line as follows:

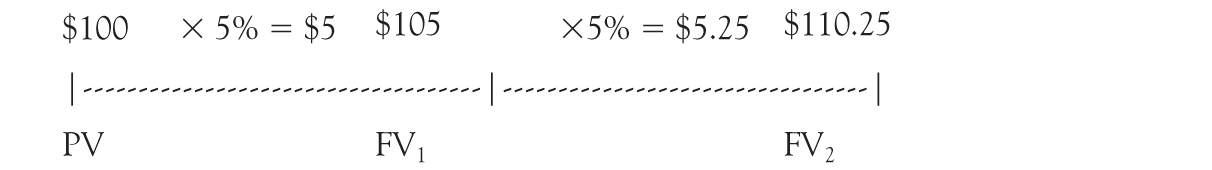
The 5 percent is our interest rate, denoted as r (also sometimes denoted as i). This allows us to put our time line into a formula:

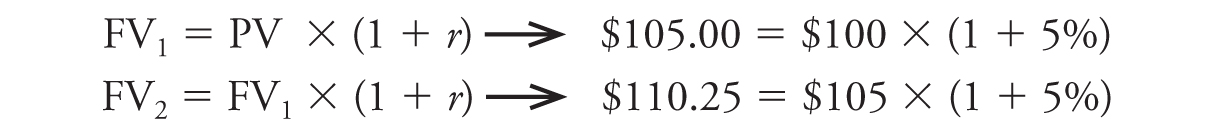
We use algebraic substitution to get:

FV₂ = FV₁ × (1 + r) = PV × (1 + r) × (1 + r) = PV × (1 + r)²

In the above example, $110.25 = $100 × (1.05)²

We can generally write that for any future period n:

FV_n = PV × (1 + r)ⁿ

where, at an interest rate of r per period, the FV n periods from now is equal to the current value times (1 + r)ⁿ.

This compounding of a PV into a FV is a concept familiar to most, including those not involved in finance. We encounter this regularly when we put money in the bank and collect interest.

Discounting a FV to a PV is usually new to those unfamiliar with finance. It is, however, as noted above, the inverse of compounding. Mathematically, it works as follows:

We divide both sides of the equation FV_n = PV × (1 + r)ⁿ by (1 + r)ⁿ to get the PV:

PV = FV_n / (1 + r)ⁿ

Using the numbers from our example above, discounting FV₂ of $110.25 backward for 2 years at an interest rate of 5 percent gives us $100 today.

PV = $110.25 / (1.05)² = $100

That is it. This is the essence of compounding (going forward), discounting (bringing backward), and the time value of money. We will now apply this concept to different situations.

More on Compounding and Discounting

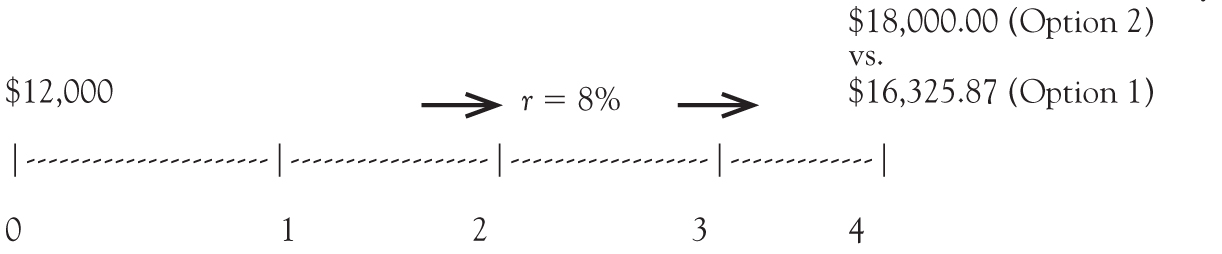
Let us use another example to illustrate compounding and discounting. Imagine you are offered a lump sum payment of $12,000 today (Option 1) or $18,000 at the end of 4 years (Option 2) and that your yearly interest rate is 8 percent.² Which is worth more: the $12,000 today or the $18,000 in 4 years?

To answer this, we have to choose one date and then compare the value of the two options on that date (it can be any date: today, at the end of 4 years, or any date in between). Let us start by finding the value of the two options at the end of 4 years. By definition, Option 2 is $18,000 in 4 years. What is the value of Option 1 in 4 years? That is, how much is $12,000 today worth in 4 years? From our equations above, with PV = $12,000, r = 8%, and n = 4.

FV_n = PV × (1 + r)ⁿ = $12,000 × (1.08)⁴ = $16,325.87

It is therefore better to choose the lump sum of $18,000 in 4 years than to take the $12,000 today and invest it at 8 percent for 4 years.

To repeat, taking the $12,000 today and computing its FV is called compounding.

Visually:

We can also answer the question of which option is worth more by comparing the two options today. By definition, the value of Option 1 is $12,000 today. What is the value of Option 2 today? That is, how much is $18,000 in 4 years, worth today? Using our equation above with FV = $18,000, r = 8%, and n = 4.

This has a PV = $18,000 / (1.08)⁴ = $13,230.54

Taking the $18,000 in the future and computing its value today is called discounting.

Visually:

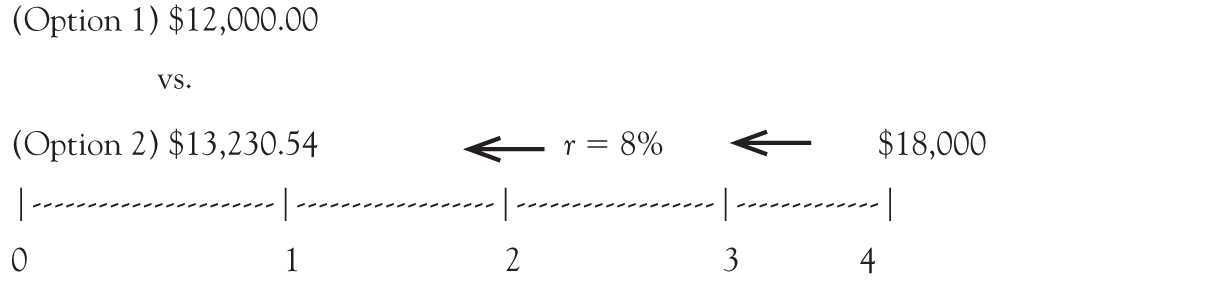
It is important to note that compounding Option 1 to calculate its FV and discounting Option 2 to calculate its PV both reveal that the $18,000 in 4 years is worth more than $12,000 today. The results are the same regardless of which direction we go (calculating the FV or the PV).

Thus by using compounding and/or discounting, we can take two different options and compare them at the same point in time, and we will get the same answer as to which has more value. The results are consistent: The PV of Option 2 is greater than the PV of Option 1 and the FV of Option 2 is greater than the FV of Option 1.

The Periodic Interest Rate

When talking about interest rates and compounding, it is important to be clear about the period being used. In the examples above we assumed the interest rates were for 1 year, which means that they were applied once a year at the end of each year. However, it is quite common to have an interest rate compounded more than once a year. A common example in the United States is that most bonds pay interest (or coupons) twice a year. This means that the compound rate is the stated (or annual) rate on the bond divided by two.

Let us consider a U.S. bond with an 8 percent stated interest rate that is compounded twice a year. This means the bond actually pays 4 percent every 6 months. The 4 percent paid every 6 months is more than 8 percent paid once a year. Why? If the bond’s original cost is $100, then at the end of the first 6 months it earns $4 in interest (4% × $100). The interest for the second 6 months is again 4 percent, but this time it would be 4 percent of $104, which equals $4.16. If the bond matures at the end of the year, an investor would get back the original $100 cost (called the “principal”) plus combined interest of $4 and $4.16 for a total of $108.16. If the bond paid interest only once a year, to receive the same year-end amount would require a rate of 8.16 percent.

Thus, the actual (or effective) interest rate over a period depends on how often the interest is compounded.

In the example above, $12,000 with an 8 percent stated interest rate compounded annually, gave us a total of $16,325.87 in 4 years. If the example is changed and the $12,000 now has a stated interest rate of 8 percent compounded quarterly, the computation is 2 percent every 3 months (i.e., the stated 8 percent rate is divided into four quarters or 2 percent each quarter). If we want to find how much the $12,000 is worth in 4 years when compounding quarterly, then r is the 2 percent rate and n is 16 (remember, n is the number of periods, our periods in this example are quarters, and there are 16 quarters in 4 years).³

Our computation is now:

FV_n = PV × (1 + r)ⁿ
FV₁₆ = $12,000 × (1.02)¹⁶ = $16,473.43

Note that FV₁₆ at 8 percent compounded quarterly over 4 years ($12,000 × (1.02)¹⁶) gives us more than the $16,325.87 (or $12,000 × (1.08)⁴) calculated above where compounding was done annually.

We can use this concept to generate a once-a-year equivalent interest rate, called the annual percentage rate (APR), which is useful in comparing interest rates that compound over different intervals.⁴

The formula to convert compounding more than once a year to an APR is:

APR = (1 + r / j)^{n j} − 1,

where j is the number of times a year interest is compounded.

Annuities

An annuity is a contract with equal periodic payments. Importantly, despite the name of “annuity,” the periods do not have to be annual. Home mortgage payments are a type of annuity (a large sum is borrowed, and then equal monthly payments are made for the next 10, 20, or 30 years). Also, most debt contracts are the combination of an annuity (the periodic interest payment) as well as a final lump sum repayment.

Note, there are tables that provide the PV or FV of annuities. Today, these have been replaced with computer spreadsheets where the value of an annuity can be found by simply putting each payment into a cell of the spreadsheet and discounting or compounding it.

Let us look at ordinary annuities first and then at annuities due. An ordinary annuity is when the payments are made at the END of each period and an annuity due is when the payments are made at the START of each period.

As an example: Assume an equal payment of $300,000 is made at the end of June and December for 2 years, with the first payment in June 2014. Also assume an interest rate of 12 percent compounded semiannually (i.e., 6 percent every 6 months or an APR of 12.36 percent⁵). What is the value on January 1, 2014? The answer would look as follows:

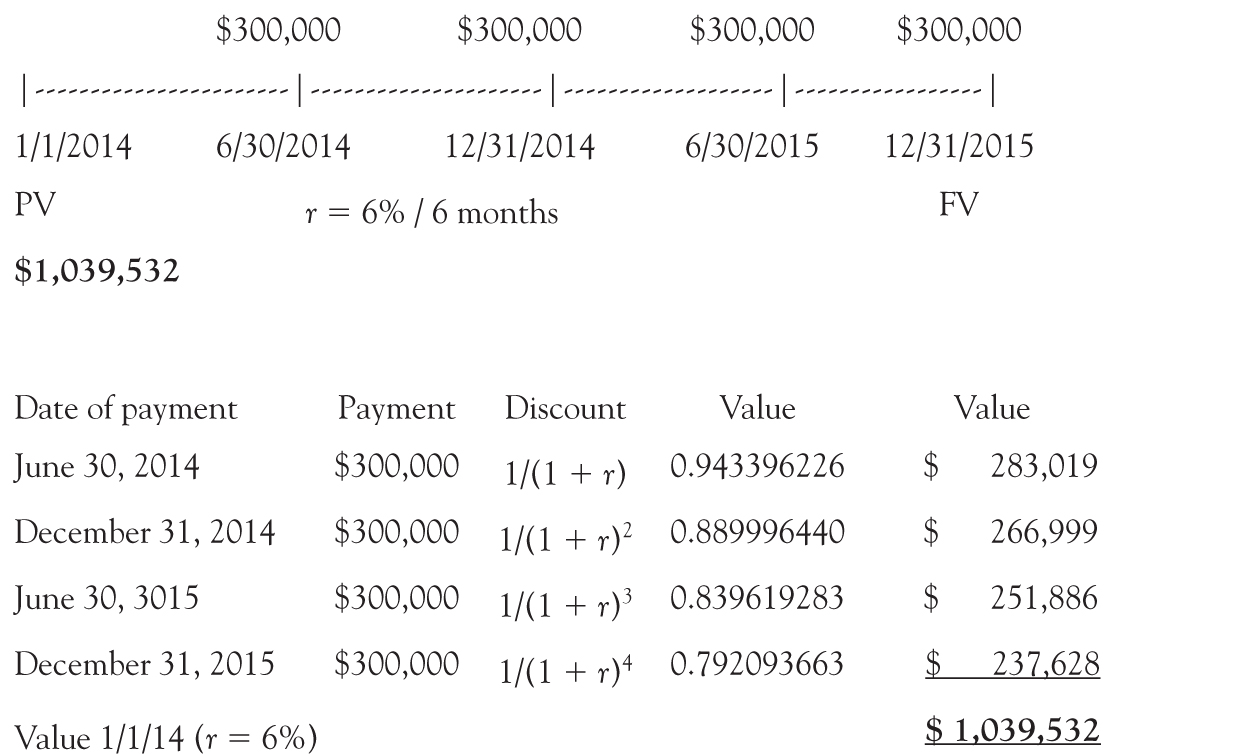
The above can also be computed by taking out the equal periodic payment and multiplying by the sum of the values as follows:

How much would the firm have to pay on January 1, 2014, to eliminate the debt (e.g., a lump sum, one-time payment instead of the four $300,0000 payments) if the discount rate is 12 percent compounded semiannually (or 6 percent every 6 months)? The answer is $1,039,532.

Alternatively, how much would the firm have to pay on December 31, 2015, to eliminate the debt (e.g., a lump sum, one-time, payment instead of the four $300,0000 payments) if the discount rate is 12 percent compounded semiannually (or 6 percent every 6 months)? The answer is $1,312,385.

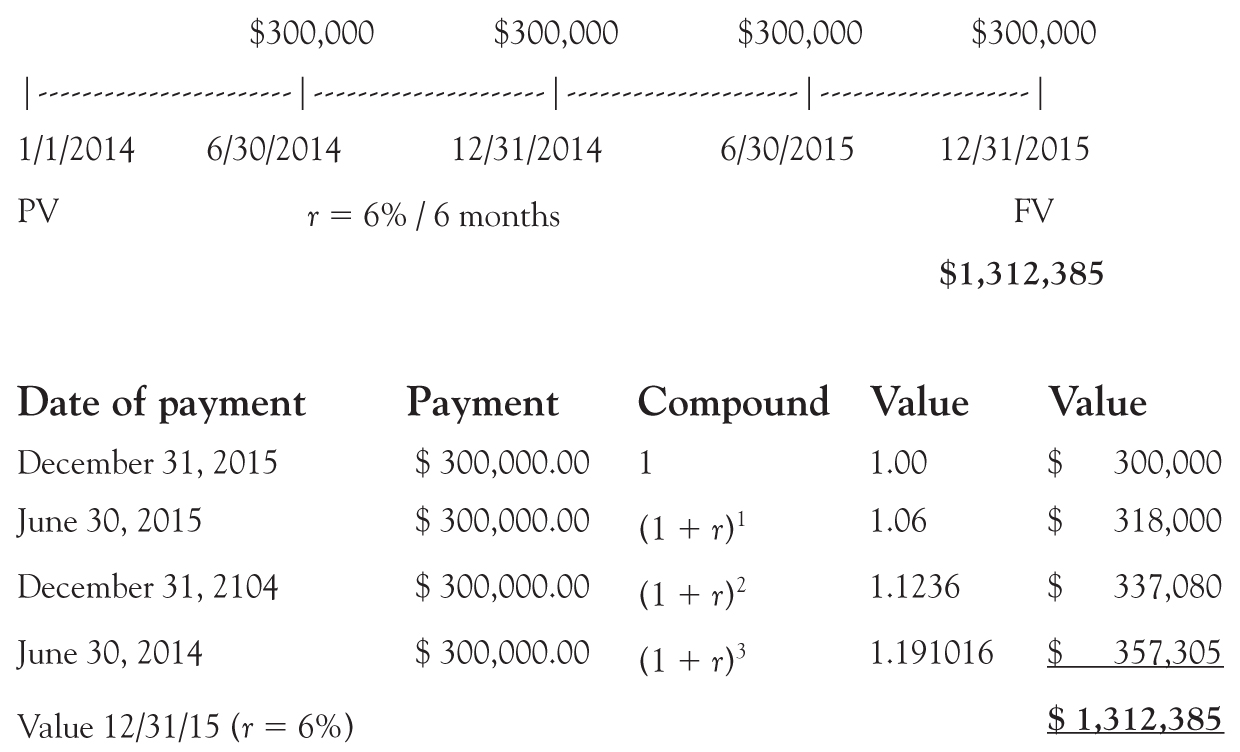
Alternately, the total FV at the end of the annuity in December 2015 can be computed as follows:

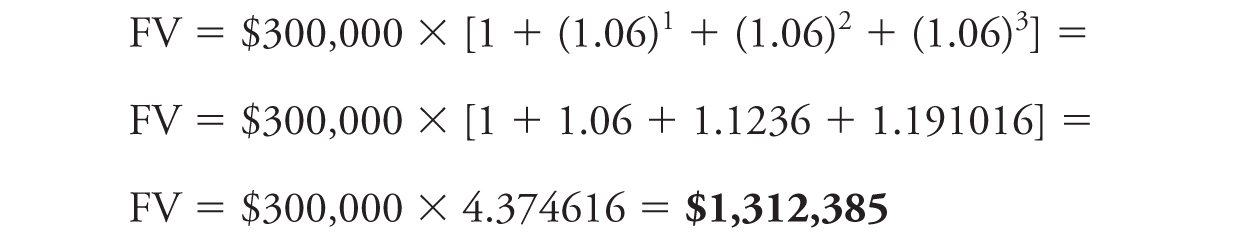
Note that once you know the FV, you can discount it to get the PV, and once you know the PV, you can compound it to get the FV:

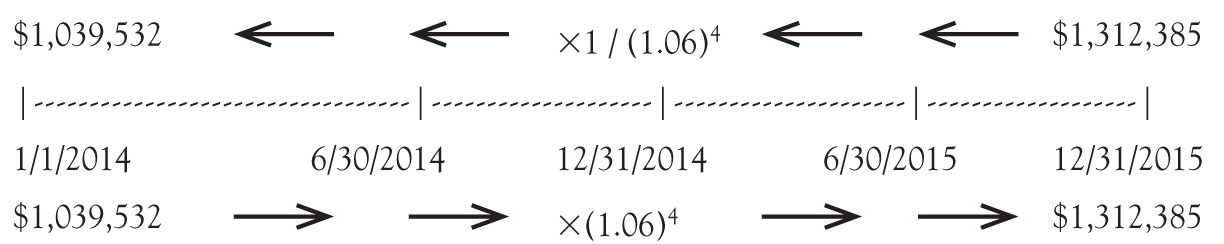
An important caveat when using the discounting computation:

CORRECT: 1 / (1 + r)¹ + 1 / (1 + r)² + 1 / (1 + r)³ + . . . + 1 / (1 + r)ⁿ

This is NOT the same as:

INCORRECT: 1 / ((1 + r)¹ + (1 + r)² + (1 + r)³ + . . . + (1 + r)ⁿ)

 

An Ordinary Annuity vs. an Annuity Due

The presentation above is for an ordinary annuity. As stated, an “ordinary” annuity is one with periodic payments made at the END of each period and the final payment is on the FV date.

In contrast, an annuity “due” is one with payments made at the START of each period and the first payment is made on the PV date and the last payment is one period prior to the FV date (above it would be January 1, 2014, June 30, 2014, January 1, 2015, and June 30, 2015).

Let us compare an ordinary annuity and an annuity due where each have four payments of $300,000 as in the example above. Our timelines would look as follows:⁶

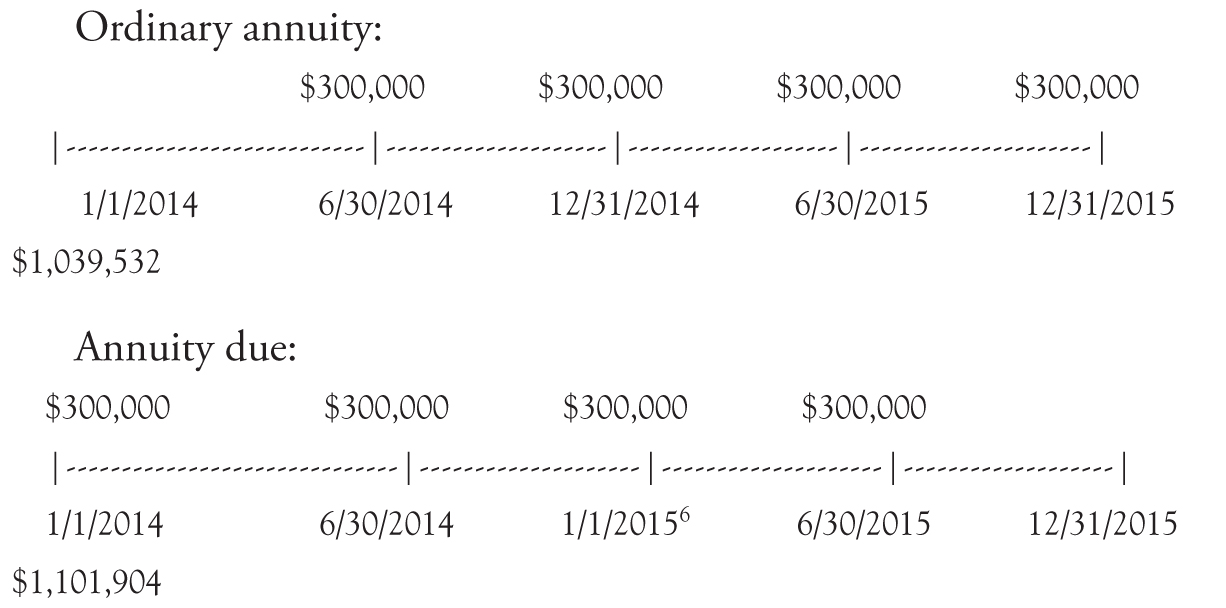
Does an ordinary annuity or an annuity due have a higher PV? As shown, by discounting all the payments, the annuity due is worth more ($1,101,904) than the ordinary annuity ($1,039,532). Notice that both have three payments at the same time (June 30, 2014; December 31, 2014; and June 30, 2015). The difference between the two annuities is that the annuity due’s four payments start with a payment on the PV date of January 1, 2014, whereas the ordinary annuity’s first payment is 6 months later on June 30, 2014. Thus, the difference is the value of one payment today (in this case on January 1, 2014) vs. one payment at the end (in this case on December 31, 2015).

How much is a payment of $300,000 made on January 1, 2104, worth on January 1, 2014? It is worth exactly $300,000.

How much is a payment of $300,000 made on December 31, 2015, worth on January 1, 2014? It is worth $237,628 (using our formula, that would be PV = FV₄ / (1 + r)⁴ = $300,000 / (1.06)⁴ = $237,628).

The difference in the value of an annuity due and an ordinary annuity in the above example is: $300,000 − $237,628 = $62,372. This is the same result as comparing the total of the annuity due and the total of the ordinary annuity ($1,101,904 − $1,039,532 = $62,372) because all other payments are identical.

This means that, at any positive interest rate, an annuity due is worth more than an ordinary annuity (e.g., receiving a payment on January 1, 2014, is preferred over receiving a payment on December 31, 2015).

Does an ordinary annuity or an annuity due have a higher FV? Think about this for a moment. It is the same answer as above: The annuity due (which has its first payment on January 1, 2014) compounds more interest than the ordinary annuity (which has its first payment on June 30, 2014).

Remember that the math has to equate. Discounting (going back to the present) or compounding (going forward to the future) has the same answer of which annuity is better. Let us find the exact difference in values to prove it. In the previous example, the ordinary annuity has a payment of $300,000 on the future date of December 31, 2015. At the FV date of December 31, 2015, that payment is worth $300,000. On the other hand, the annuity due has a $300,000 payment on January 1, 2014. On December 31, 2015, the annuity due’s first payment will be worth $378,743 (because $300,000 × (1.06)⁴ = $378,743). Thus, comparing the FVs of these two payments, ordinary annuity ($300,000) and of the annuity due ($378,743), shows us that the annuity due is worth $78,743 more on December 31, 2015, over the ordinary annuity.

Just to close the math loop, note that the annuity due was worth $62,372 more on January 1, 2014, and $78,743 more on December 31, 2105. These two numbers equate: the PV of $78,743 is $62,372, and the FV of $62,372 is $78,743.

Most car leases are set up as annuity dues with 3 or 4 years of equal monthly payments and the first one due at signing (and often some additional up-front charges). Why are car leases set up as annuity dues? Because the annuity due is worth more? Not necessary, it all depends on the payments. Although the deal can be set in multiple ways, let us focus on three: a lump sum payment at the start (the cash price of the car), an annuity due, or an ordinary annuity. The lump sum payment at the start means the buyer is paying the full cost of the car at the beginning and no future payments are owed. Let us set the cost of the car at a specific amount and examine the difference in paying with an annuity due vs. an ordinary annuity.

What are the periodic payments in our example if the one-time cash payment today (i.e., the purchase price) is $22,038? If the payments are made at the start of the year using an annual percentage yield (APY) of 12.36 percent (which means 12 percent compounded semiannually), then the annuity due would have four equal payments of $6,000 (on January 1, 2014; June 30, 2014; January 1, 2015; and June 30, 2015) and the ordinary annuity would have four equal payments of $6,360 (on June 30, 2014; December 31, 2014; June 30, 2015; and December 31, 2015).

How do we calculate the periodic payments of $6,000 for the annuity due option and $6,360 for the ordinary annuity option? We use the formula above but this time solve for an unknown payment to equal the PV (purchase price) of $22,038.

Note that THERE IS NO DIFFERENCE IN THE VALUE! All three options are worth the same when compared in PV terms (or FV terms): a single lump sum payment of $22,038 (i.e., the PV), four payments of $6,000 with the first paid today (i.e., annuity due), or four payments of $6,360 with the first paid in 6 months (i.e., ordinary due). However, the vendor may believe it is easier to sell the product if the four lease payments are advertised as $6,000 instead of $6,360.⁷

Bond Valuation⁸

There are numerous types of bonds, but the most common is an ordinary bond where the issuer agrees to make periodic payments plus a single large payment at the end of the bond’s life. This single payment at the end of the bond’s life is called the par or face value of the bond. The issuer also makes equal periodic payments (twice per year is the standard in the United States and once is the standard in Europe) over the life of the bond. These equal periodic payments are called the coupons and are usually set as a fixed percentage (called the coupon rate) of the par or face value of the bond.

Let us illustrate with an example. A firm agrees to pay $1 million at the end of 4 years (the face value) plus an additional $50,000 at the end of each year for 4 years (the coupon).

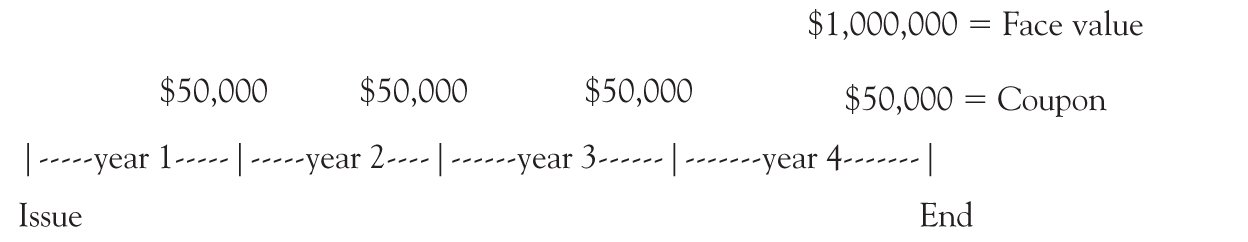
The $1 million is the face value or par value of the bond. The $50,000 is the annual coupon, and it could be stated as a rate (called the coupon rate or stated rate). In this case, the coupon rate would be 5 percent of the par value (5% × $1,000,000 = $50,000). Knowing the coupon rate and the face value gives you the coupon. Knowing the coupon and the face value gives you the coupon rate.

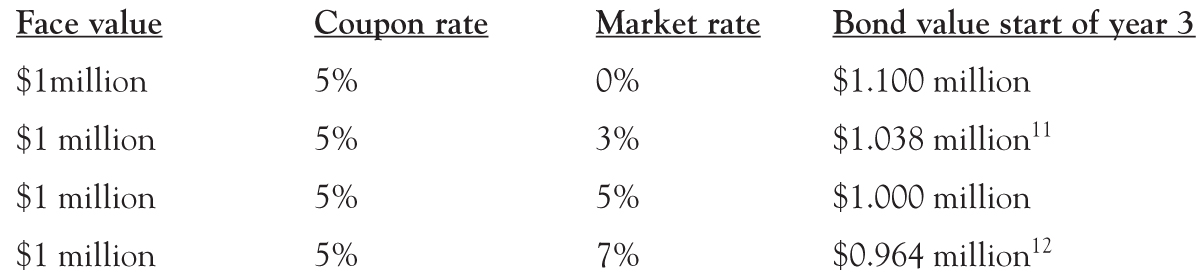
What is the bond worth today, at the start of the bond’s life? This depends on the market rate or yield of the bond. This is the interest rate the market will pay given the terms of the bond, the economic conditions, and the market’s assessment of the likelihood the firm will be able to make all payments. It is the discount rate which equates the price of the bond in the market and the bond’s payments. The market rate fluctuates over time (in contrast to the coupon rate which is set in the terms of the bond). Let us start by setting the market rate equal to the coupon rate of 5 percent.

The bond’s price is computed with a PV calculation:

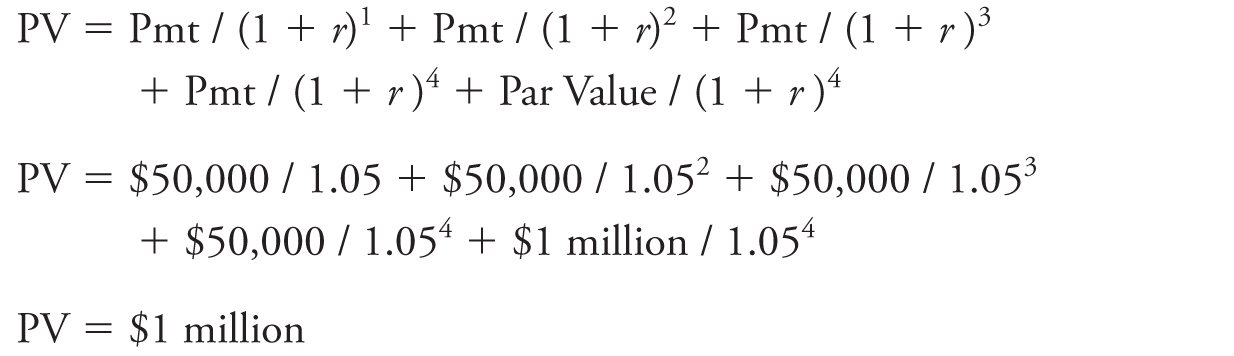
In this case, the bond is issued at par, which means the bond’s issue price (e.g., the price at the time the bond is first issued) equals its par value. Whenever the bond is at par, the market rate and the coupon rate are the same. Conversely, whenever a bond’s coupon rate equals the market rate, the price of the bond is the par value. Note that the coupon rate determines the amount of the coupon (in this case, 5% a year × $1 million par value = $50,000 a year). Once set, the coupon does not change (it is a contractual amount).⁹

Now, what happens if the market rate falls?¹⁰ The price (what someone else would pay you for the bond) of the bond will increase. This occurs because the denominator in the discounting formula above is the market rate. If you hold a numerator constant and lower a denominator, the result increases. Take the extreme case: Imagine that the market interest rate falls to a rate of zero 2 years after the bond is issued. What is the value of the bond?

PV = Pmt / (1 + r)¹ + Pmt / (1 + r)² + Par value / (1 + r)²

At the start of the third year, the bond has three payments remaining: two interest payments of $50,000 each as well as the final par value payment of $1 million. In other words, by the end of the bond’s life, it will pay $1.1 million. At a 5 percent market rate, the bond would have a price of $1.0 million.

50,000 / 1.05 + $50,000 / 1.05² + $1 million / 1.05² = $1.0 million

At a 0 percent market rate, the bond has a price of $1.1 million

50,000 / 1.00 + $50,000 / 1.00² + $1 million / 1.00² = $1.1 million

The calculation at a 0 percent market rate is always very easy, you simply add up all the future cash payments, no discounting is required as the denominator is always 1. Think about this:

Look at the above and then answer the following:

If the market rate is 7 percent (which means above the 5 percent coupon rate), will the price of the bond be more or less than $1 million? If the market rate is 3 percent (above 0 percent but below 5 percent), will the price of the bond be more or less than $1 million? More or less than $1.1 million? Write down your answer.

We have a simple way to understand what happens to bond prices as market rates rise and fall. The approach also helps us check any calculations to ensure they are not seriously wrong. The maximum price of the bond, which occurs at a 0 percent rate (extreme even for safe government bonds), is $1.1 million. As shown above, at a 0 percent rate, the price of the bond is the sum of all future payments (in this case, the two coupons of $50,000 each and the par value of $1 million). The price of the bond at par, when the market rate equals the coupon rate, is $1 million.

If the market rate rises above the coupon rate, the price of the bond falls below the par value. If the market rate falls below the coupon rate, the price of the bond will increase above par but will remain below the maximum price from using a zero coupon rate.

Why does the price of a bond decrease when market rates increase, and increase when market rates decrease? Because the numerator is the bond’s coupons and par value that are set by the bond contract and do not change, whereas the market rate that can change is in the denominator.

PV = Pmt / (1 + r)¹ + Pmt / (1 + r)² + . . . + Pmt / (1 + r)ⁿ + Par Value / (1 + r)ⁿ

This can be seen using the par value and coupon rate of our example:

The above can also be understood with the following example. Imagine our firm issues a second $1 million face value bond at the start of year 3. This bond will have a 2-year life, so it matures on the exact same date as the first bond, which has a 4-year life and is halfway done. The second bond pays interest once a year on December 31, so it has two more coupon payments. If this second bond has its coupon rate set at the market rate, and the market rate is 7 percent at the time, this bond will be issued at par of $1 million (70,000 / 1.07 + $70,000 / 1.07² + $1 million / 1.07² = $1.0 million).

Although the issue price of the second bond is the same as the issue price of the first bond in year 1 (i.e., $1 million), the second bond now pays an annual payment of $70,000 (7 percent of par) compared to the first bond, which pays only $50,000 (5 percent of par).

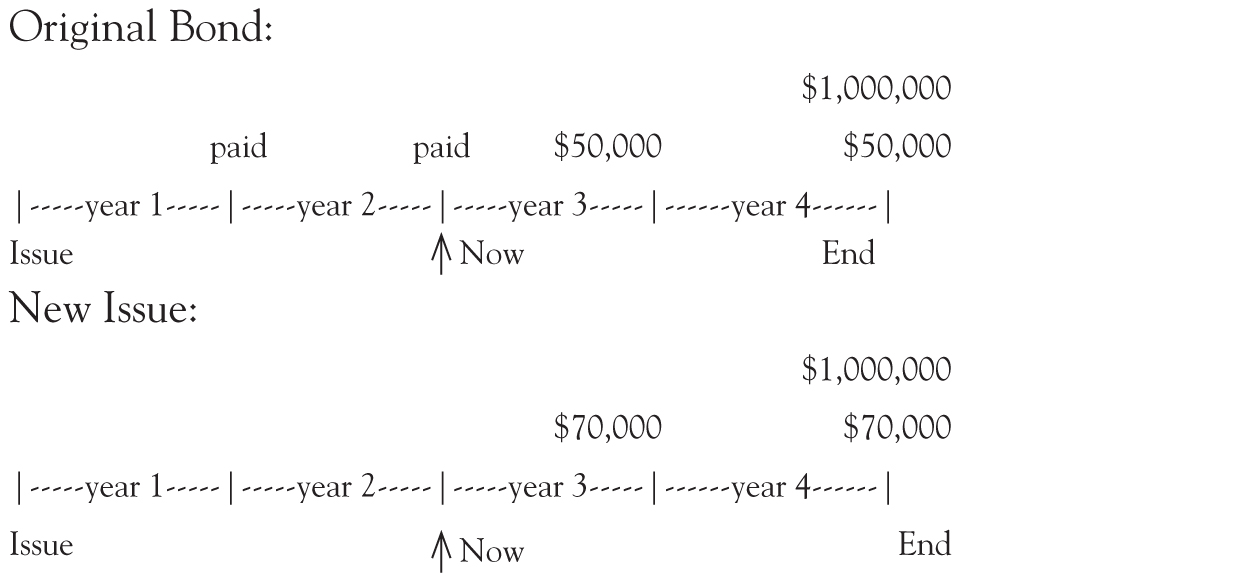
Which bond has a higher net present value (NPV) (which bond would you rather own): The one paying $50,000 a year for the next 2 years plus $1 million at the end, or the one paying $70,000 a year for the next 2 years plus $1 million at the end? The latter is worth $1 million ($70,000 / 1.07 + $1,070,000 / 1.07²). The first bond is worth less: As computed above, it is worth $964,000 ($50,000 / 1.07 + $1,050,000 / 1.07²).

Note, the $36,000 difference in the PVs ($1,000,000 − $964,000) can also be calculated by discounting the $20,000 difference ($70,000 − $50,000) in the PV of the two coupon payments at 7 percent.

$36,000 = $20,000 / 1.07 + $20,000 / 1.07²

As market interest rates increase (decrease), the value of outstanding bonds will fall (rise) because their future cash flows are worth less (more).

The Bottom Line

The time value of money is one of the most important concepts in finance. Your author strongly recommends always drawing a time line to ensure the dates and amounts are correct.

The next chapter discusses the accounting for long-term liabilities which use time values.

_________________

¹Part of this chapter is copied from Asquith and Weiss: Lessons in Finance © 2016. Reprinted with permission.

²In a business context, this is equivalent to investing $12,000 today and receiving $18,000 in 4 years (the original $12,000 plus interest). The “appropriate” interest rate reflects the risk of the investment, which includes inflation.

³There is no reason that the rate could not be stated for a time period of less than a year (e.g., 2 percent every 3 months). It is simply convention to state the rate for a year, which then has to be divided by the number of times it is compounded during the year.

⁴It is also called the annual percentage yield (APY) that readers may recognize from their credit cards or mortgages.

⁵Apply the formula APR = (1 + r / j)^{n × j} − 1. In this case, (1 + 12% / 2)^{1 × 2} − 1 = 12.36%.

⁶A one-day difference, December 31, 2014, and January 1, 2015, is ignored (i.e., the one-day interest on $1 million at 5 percent is about $137).

⁷A total of $22,038 also equates to a monthly annuity due payment of $1,024 vs. a monthly ordinary annuity due payment of $1,034 with 24 monthly payments or $722 and $729 with 36 monthly payments or $572 and $577 with 48 monthly payments, respectively, at an interest rate of 12.36 percent APY (or 11.7107 compounded monthly).

⁸A bond is a long-term debt obligation. Bonds are discussed in more depth in Chapter 9.

⁹There are some bonds where the coupon rate is based on a market rate (e.g., prime plus 2 percent), but these are more complex bonds and their pricing would be much more difficult.

¹⁰This could happen either because the government rate falls or because the firm’s cash flows to repay the debt become less risky.

¹¹50,000 / 1.03 + $50,000 / 1.03² + $1 million / 1.03² = $1.038 million.

¹²50,000 / 1.07 + $50,000 / 1.07² + $1 million / 1.07² = $0.964 million.