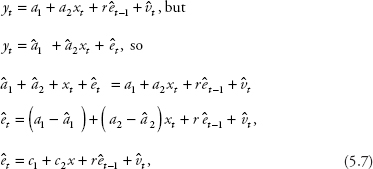CHAPTER 5

Simple Dynamic Models in Time-Series Data

Having learned about heteroscedasticity, Touro was wondering what particular problems could occur with time-series data. Prof. Metric commends him for a good question and says that we will discuss these problems in this chapter and will be able to:

Prof. Metric says that dynamic models examine the continuous impact of any change over more than one period. We will examine the effect in three ways: lag values of the error, lag values of the dependent variables, and lag values of the explanatory variables.

Autocorrelation

Prof. Metric says that a static model for time-series data contains only variables of the contemporaneous period for all explanatory and dependent variables. In this case, if all classic assumptions are also satisfied, then regression of time-series data is similar to that of cross-sectional data; that is, OLS produces BLUE results. Thus, this static model does not need any correction before running a regression, and the simple-regression model is written as:

where Cov(e_t, e_z) = 0 for t ≠ z.

Or, for multiple regressions:

where Cov(e_t,e_z) = 0 for t ≠ z.

Prof. Metric reminds us that we already had hands-on experience in Chapter 3 performing a regression of EXPS_t on RGDP_t and EXCHA_t.

However, if the classic assumption (iv) for time series Cov(e_t,e_z) = 0 for t ≠ z is violated even when all explanatory and dependent variables are in the current period—that is, Cov(e_t,e_z) ≠ 0 for t ≠ z—then we have a dynamic model with lag values of the error, and the problem is called autocorrelation or serial correlation. Given equation (5.1), the autocorrelation equations with one lag error and k lag errors are written respectively as:

Combining equation (5.3a) or equation (5.3b) with equation (5.1) yields the following model for one lag error or k lag errors, respectively:

In equations (5.4a) and (5.4b), v_t has a constant variance

and cov(v_t, v_z) = 0; t ≠ z.

We also assume that all series are stationary, |r_k| < 1 for k = 1, 2,…, k.

In addition, it can be shown that

Hence, e_t is also homoscedastic.

However, the covariance of e_t and e_t−k is not homoscedastic. Specifically, it can be shown that

From these results, the population correlation function is:

Since (5.4a) has only one lag value of the errors, k = 1, and corr(e_t,e_t-1) = r.

Equations (5.4a) and (5.4b) and (5.5) tell us that there are certain relations between the error terms of two or more periods, so the model has an autocorrelation problem.

Prof. Metric says that the two consequences of the autocorrelation are similar to those of heteroscedasticity:

Also, similar to heteroscedasticity, the correction for each problem will be discussed separately in the next section.

Detecting Autocorrelation

We learn that we can examine an autocorrelation function or carry out an LM test to detect autocorrelation.

Autocorrelation Function

The series r_k, where k = 1, 2,…, k, is called the autocorrelation function or the correlogram of the errors. This function reveals the correlation between the errors that are two periods apart through k periods apart. The estimated correlation function, which is a sample version of equation (5.5) is:

Thus, we can perform a regression of equation (5.2), obtain the residual ȇ_t, and generate thee lag values of ȇ_t so that we can calculate each . We then compare this with the ratio ±1.96 / T^1/2, similar to equation (1.15). The value ±1.96 is the 95 percent bounds of a standard normal distribution, and T is the sample size. We will reject the null hypothesis of no autocorrelation if

In this case, one or more lag error terms are correlated to the current error term, implying that the autocorrelation problem exists.

Booka asks, “Why do we have to use t = k+1 in equation (5.6)?” Taila offers an explanation,

Prof. Metric is very pleased with Taila’s explanation and says that we will have a chance to practice this method in the Exercises section. Most econometric software programs provide a graph of the correlogram with the bounds ± 1.96 / T^1/2, called the 95 percent Bartlett Band, superimposed on the graph so that we do not have to calculate it by hand. The terminology “Barlett Band” comes from a seminal work on this subject by Bartlett (1946). For Excel, we will have to buy an Add-in tool called NumXL, so Prof. Metric does not require us to draw this graph.

LM Test

We focus on the case with one lag error first. The empirical version of equation (5.4a) contains ê_t−1 and :

where c₁ = a₁ − and c₂ = a₂ − ,

Hence, the procedure for performing the LM test for (5.4a) is as follows.

Estimate equation (5.7) and obtain R² for the four-step LM test:

Next, Prof. Metric gives us an example, “Suppose estimating the model in equation (5.7) yields R² = 0.205, and the sample size T = 24, then what is the test results?”

We work on the test as follows:

Prof. Metric says that the test can be extended to equation (5.4b) in the same manner except that J will be equal to the number of lag errors that need to be tested.

Correcting Autocorrelation

Retrogress backward one period:

so

Hence, we can estimate the following model:

where = y_t − ry_t−1, = 1 − r, = x_t − rx_t−1.

Prof. Metric reminds us to use the “Constant is Zero” or “No Constant” command in any econometric package, because is no longer a constant. Estimating model (5.8) will yield BLUE results because the serially correlated error, e_t, is substituted out. In practice, r is nonexistent, and we need the estimated autocorrelation coefficient of the errors in equation (5.6).

He also reminds us that the predicted values are for = y_t − ry_t−1, so we need to calculate the predicted value of y:

where y_t−1 is the actual value of y at period (t − 1), and can be calculated using the formula in equation (5.6).

Autoregressive Models

We now move to the autoregressive (AR) model, which contains the lag dependent variables instead of the lag values of the error term. Prof. Metric says that this model requires special time-series analyses, because it involves only the dependent variable and its own lags instead of the addition of any external explanatory variable.

The Model

A dependent variable in an AR model can contain many lag values. Hence, the model can be denoted as AR(n) where n is the number of lag dependent variables, and the model is called the AR of order n. A model is called an autoregressive model of order one if the dependent variable is correlated to its first lag only. This model is denoted as AR(1) and can be written as:

If the coefficient estimate |a| < 1, then the series gradually approaches zero when the time, t, approaches infinity, and is said to be stationary. When |a| ≥ 1, the series is said to be nonstationary. If |a| >1, then the series explodes as t approaches infinity. If |a| = 1, then the series keeps winding aimlessly upward and downward with no real pattern and so is said to follow a random walk. In this case, equation (5.9) becomes:

The model in equation (5.10) is called a “random walk,” because the movement of the series is so random that the best you can guess about what happens in the next period is to look at the result in the current period and then add some random error to it. This behavior is in fact illustrated in equation (5.10).

Prof. Metric says that e_t is still assumed to be an independent random variable with a mean of zero and a constant variance. He also says that if all lag variables are stationary as in equation (5.9) and there is no autocorrelation, then the OLS estimation produces BLUE results. For example, a model with one constant and two lag values can be estimated using the OLS technique and is written as:

Point Prediction

Booka offers an example from her company: estimating a stationary AR(1) model of the demand for econometrics books gives the following results:

DEMAND_t = 69 + 0.9 DEMAND_t−1.

Demand value for last year is DEMAND_t−1 = 480 volumes. Thus, we calculate the demand for this year as:

DEMAND_t = 69 + 0.9*480 = 501 (volumes).

This process can be extended into the future and is called “recursion by the law of iterated projections” (the recursive principle for short). The proof is provided in Hamilton (1994).

Interval Prediction

The formula for the standard error of the prediction se(p) with T as the sample size is shown in Hill, Griffiths, and Lim (2011) as:

Prof. Metric gives us an example of SSE = 120 and T = 32. He tells us to use these hypothetical values in calculating the interval prediction for this year.

We start with the point prediction of 501. The standard error of the prediction is:

Next, we decide to choose a 95 percent confidence interval. Typing =TINV(0.05, 30) into an Excel cell gives us t_C = t_{(0.975, 30)} = 2.042. Finally, we calculate the interval prediction as:

DEMAND_t = 501 ± 2*2.042 = (497; 505).

Thus, this year Booka will need to order between 497 and 505 volumes of econometrics books. We think it might be best to play it safe and follow the upper bound of 505 volumes.

First-Difference Model

Prof. Metric tells us that if a series follows a random walk, we might end up with a spurious regression, which produces significant regression results, but from completely unrelated data. There are two cases that need to be addressed separately. The first case is addressed in this section because it involves only lag dependent variables. The second case will be discussed in section 3 because it involves external lag variables.

If one of the lag dependent variables is unit coefficient (a_k = 1), then taking the first difference of the equation can turn it into a stationary series of a first-difference model. For example, taking the first difference of equation (5.10) yields the following model:

Δy_t is a stationary series because e_t is an independent random variable with a mean of zero and a constant variance; there is no aimless factor in it. Any series that can be made stationary by taking the first difference (e.g., y_t in equation (5.10)) is said to be integrated of order one, which is denoted as an I(1) with the letter I standing for “integrated.” The stationary model obtained by taking the first difference (e.g., Δy_t in equation (5.12)) is said to be integrated of order zero and is denoted as an I(0).

This characteristic can be extended to estimating an AR(n) model, in which (n − 1) series are stationary—for example, an AR(2) model that has the first lag series nonstationary:

We can take the first difference of y_t to obtain the following model:

Since the series becomes stationary, this equation can be estimated using the OLS technique.

We then have hands-on experience with an I(0) model. Touro offers an equation for the values of his tour-package sales:

ΔSALE_t = SALE_t − SALE_t−1 = 0.11 * SALE_t−2.

Data on sale values for the previous years are: SALE_t−1 = $4,400 and SALE_t−2 = $4,600.

ΔSALE_t = 0.11 * 4,600 = $506.

We work on the problem and are able to calculate the predicted sale value for this year as:

SALE_t = ΔSALE_t + SALE_t−1 = $506 + $4,400 = $4,906.

Prof. Metric tells us that an I(1) series is also called a first-difference stationary series.

Other Simple Dynamic Models

We learn that this section only discusses other dynamic models under the assumption that all series are stationary. More in-depth discussions of nonstationarity will be offered in the later chapters.

Distributed Lag Models

Distributed lag (DL) models contain lag values of explanatory variables in addition to the lag dependent variables. If all classic assumptions are satisfied, then OLS can be performed.

A general DL model is written as:

For example, if spending on nondurable goods (SPEND) depends on wage (WAGE) of current period and the past period, then the model is:

SPEND_t = 30 + 0.3 * WAGE_t + 0.2 * WAGE_t−1.

Suppose monthly data for WAGE_t = $2,800 and WAGE_t−1 = $3,000, then the predicted value can be calculated as:

SPEND_t = 30 + 0.3 * 2,800 + 0.2 * 3,000 = 30 + 840 + 600 = 1,470

Interval prediction can be calculated using the formula for the standard error of the prediction in equation (5.11).

Autoregressive Distributed Lag Models

Another model, which includes lagged dependent variables in addition to other explanatory variables, is called the autoregressive distributed lag (ARDL) model. Again, if all classic assumptions are observed, then OLS can be performed. For example:

Suppose WAGE_t−1 = $3,000 and SPEND_t−1 = $2,000 for previous month, then a prediction can be obtained:

SPEND_t = 60 + 0.4 * 3000 + 0.4 * 2000 = 60 + 1,200 + 800 = 2,060

We learn that a general ARDL should have lagged values of the dependent variables in addition to current and lagged values of the other explanatory variables. The model is written as follows:

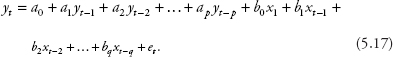
That is, if we use the notation ARDL(p, q) for the model, then p represents the number of lagged y’s, and q represents the number of lagged x’s. For example, an ARDL(1, 2) is called an ARDL of order (1,2) and is written as:

In this case, we will lose two data points when we generate the data for our regressions (in fact, we only lose one observation for y but two observations for x, so we still have to eliminate the first two rows in the dataset). Note that we also lose five degrees of freedom performing any hypothetical test on the model in equation (5.18).

To decide how many lag values we should include in an ARDL model, we should make sure that there is no omitted variable by checking on the statistical significance of coefficient estimates. Other than that, we should use fewest numbers of lags that eliminates serial correlation. Including too many lag values will increase the number of irrelevant variables and inflate the variances of coefficient estimates.

Data Analyses

Prof. Empirie tells us that we will apply Excel estimation to most of the models learned in the theoretical sections: models with lag values of the error (autocorrelation), models with lag dependent variables (AR models), those with lag values of the explanatory variables (DL models), and unit root test for all three models. However, Excel is not the ideal software to perform a Box-Jenkins procedure, so we will skip this procedure.

Autocorrelation

Testing Autocorrelation

The file Ch05.xls., Fig 5.1 contains data on salary (SAL) and spending (SPEND). We notice that Prof. Empirie has also copied and pasted SAL in column A into column E for our convenience in a later regression. First, we regress SPEND on SAL:

Next, we regress the Residuals e_t on e_t−1 and SAL.

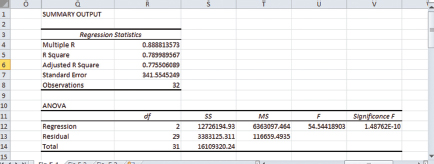
Figure 5.1 shows sections of this second regression with the number of observations and R².

From this figure, T = 32 and R² = 0.79, so LM_STAT = 32*0.79 = 25.28. Typing =CHIINV(0.05,1) into any cell gives you = 3.84. Since LM_STAT > , we reject the null hypothesis, meaning r is different from zero and implying that autocorrelation exists.

Figure 5.1 T and R² for autocorrelation test

Prof. Empirie points out to us that we always use R² instead of adjusted R² even when the model has more than one explanatory variable. This is also true for the heteroscedasticity tests in Chapter 4 because we wish to play safe and avoid missing the borderline cases.

Regressing with Autocorrelation

Prof. Empirie tells us that the first four columns of the file Ch05.xls. Fig.5.2 are the same as those in the file Ch05.xls.Fig.5.1. The commands for this section will continue from that step.

Next, we need to regress SPEND* on X1* and SAL*.

Figure 5.2 reports the regression results.

From this figure, the estimated equation is:

Because SPEND* = SPEND_t − rSPEND_t−1, to obtain predicted values of SPEND_t:

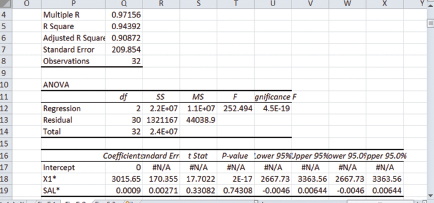
Figure 5.2 Regressing with autocorrelation: The results

We learn that we can calculate interval prediction as usual.

DL Models

Invo has collected data on the Singapore-Australia real exchange rate (EXCHA) and exports from Australia to Singapore (EXPS) in millions of dollars. The data are available in the file Ch05.xls.Fig. 5.3. We proceed to regress EXPS_t on EXCHA_t−1:

The results of the estimated coefficients are displayed in Figure 5.3.

In the data file, the predicted value of EXPS₂₀₁₃ is in cell F56. The value can be verified by this equation:

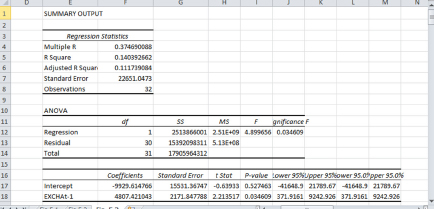
Figure 5.3 DL model: Regression results

Prof. Empirie says that the estimation procedure for an ARDL model is a combination of an AR model estimation and a DL estimation; thus, there is no need to discuss in detail in the class.

Exercises

Table 5.1 Residuals from an OLS estimation with sample size T = 4

t	1	2	3	4
êt	−0.18	0.4	−0.34	0.045