Classic PCA is a linear projection method that works well if the data is linearly separable. However, in the case of linearly non-separable data, a non-linear approach is required. The basic idea of working with linearly inseparable data is to project it into a space with a larger number of dimensions, where it becomes linearly separable. We can choose a non-linear mapping function, 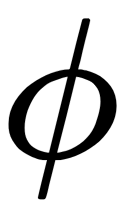, so that the sample mapping, x, can be written as 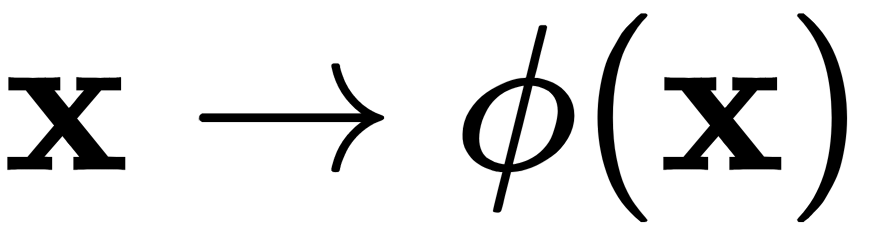. This is called the kernel function. The term kernel describes a function that calculates the scalar product of mapping (in a higher-order space) samples x with 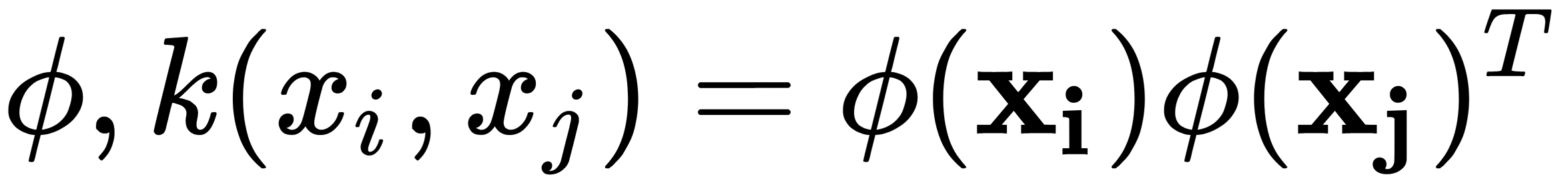. This scalar product can be interpreted as the distance measured in the new space. In other words, the  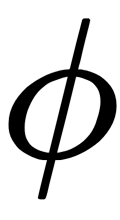function maps the original d-dimensional elements into the k-dimensional feature space of a higher dimension by creating non-linear combinations of the original objects. For example, a function that displays 2D samples, 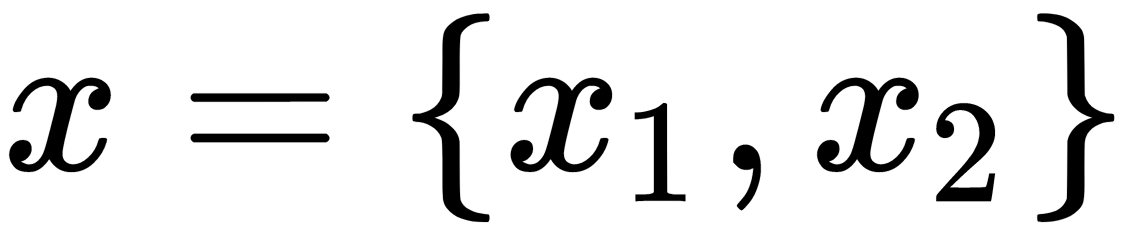, in 3D space can look like .

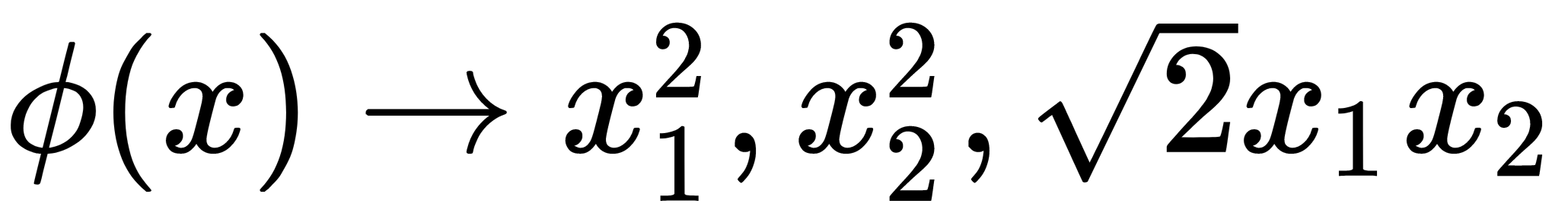In a linear PCA approach, we are interested in the principal components that maximize the variance in the dataset. We can maximize variance by calculating the eigenvectors (principal components) that correspond to the largest eigenvalues based on the covariance matrix of our data and project our data onto these eigenvectors. This approach can be generalized to data that is mapped into a higher dimension space using the kernel function. But in practice, the covariance matrix in a multidimensional space is not explicitly calculated since we can use a method called the kernel trick. The kernel trick allows us to project data onto the principal components without explicitly calculating the projections, which is much more efficient. The general approach is as follows:

1. Compute the kernel matrix equal to .
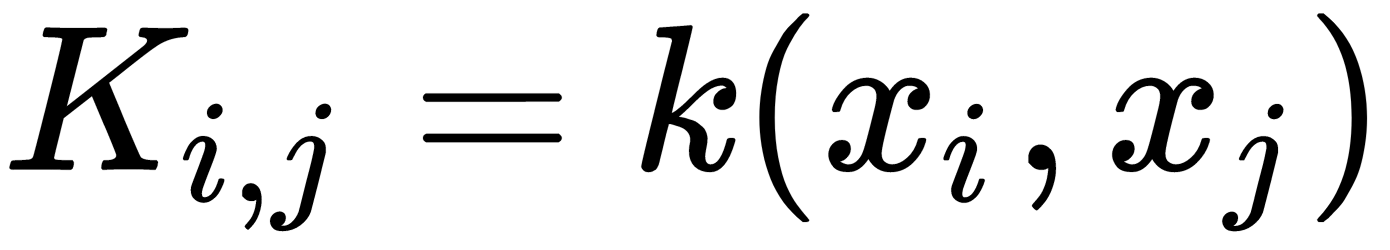2. Make it so that it has a zero mean value, , where is a matrix of N x N size with 1/N elements.
3. Calculate the eigenvalues and eigenvectors of .
4. Sort the eigenvectors in descending order, according to their eigenvalues.
5. Take 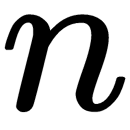 eigenvectors that correspond to the largest eigenvalues, where  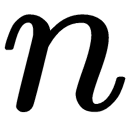is the number of dimensions of a new feature space.

These eigenvectors are projections of our data onto the corresponding main components. The main difficulty of this process is selecting the correct kernel and configuring its hyperparameters. Two frequently used kernels are the polynomial kernel 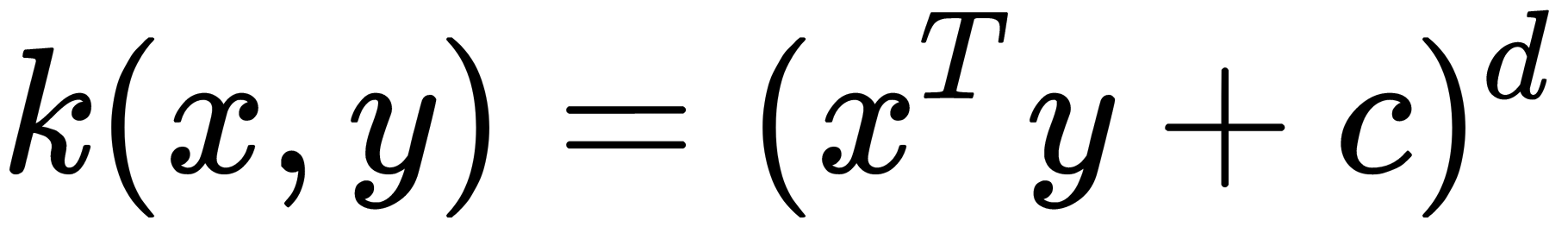and the Gaussian (RBF)  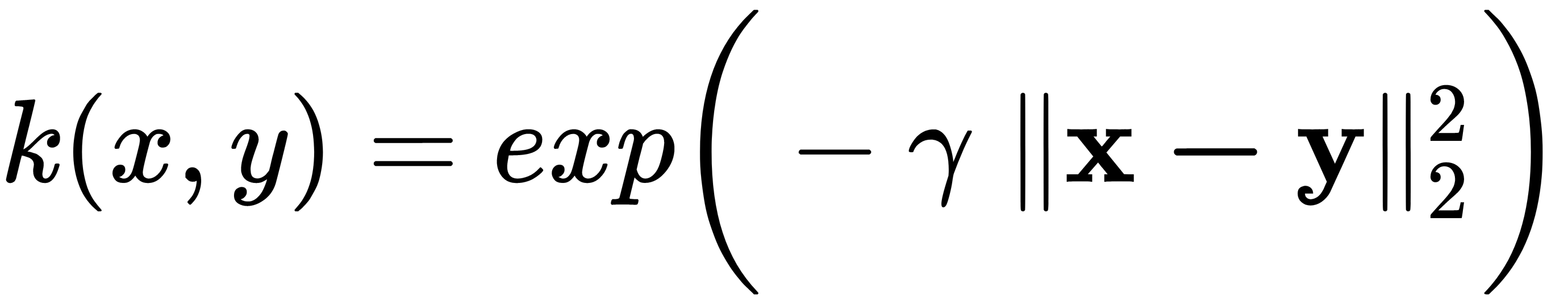ones.