12

Value at Risk

Uses and Abuses

Christopher L. Culp, Merton H. Miller and Andrea M. P. Neves

Value at risk (“VAR”) is now viewed by many as indispensable ammunition in any serious corporate risk manager's arsenal. VAR is a method of measuring the financial risk of an asset, portfolio, or exposure over some specified period of time. Its attraction stems from its ease of interpretation as a summary measure of risk and consistent treatment of risk across different financial instruments and business activities. VAR is often used as an approximation of the “maximum reasonable loss” a company can expect to realize from all its financial exposures.

VAR has received widespread accolades from industry and regulators alike.¹ Numerous organizations have found that the practical uses and benefits of VAR make it a valuable decision support tool in a comprehensive risk management process. Despite its many uses, however, VAR – like any statistical aggregate – is subject to the risk of misinterpretation and misapplication. Indeed, most problems with VAR seem to arise from what a firm does with a VAR measure rather than from the actual computation of the number.

Why a company manages risk affects how a company should manage – and, hence, should measure – its risk.² In that connection, we examine the four “great derivatives disasters” of 1993–1995 – Procter & Gamble, Barings, Orange County, and Metallgesellschaft – and evaluate how ex ante VAR measurements likely would have affected those situations. We conclude that VAR would have been of only limited value in averting those disasters and, indeed, actually might have been misleading in some of them.

WHAT IS VAR?

Value at risk is a summary statistic that quantifies the exposure of an asset or portfolio to market risk, or the risk that a position declines in value with adverse market price changes.³ Measuring risk using VAR allows managers to make statements like the following: “We do not expect losses to exceed $1 million on more than 1 out of the next 20 days.”⁴

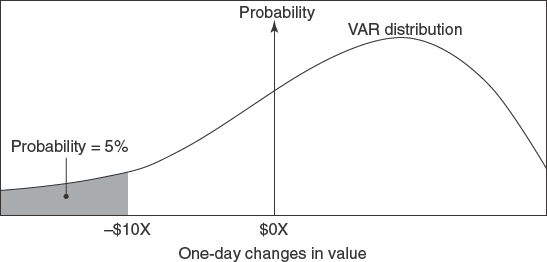
To arrive at a VAR measure for a given portfolio, a firm must generate a probability distribution of possible changes in the value of some portfolio over a specific time or “risk horizon” – e.g., one day.⁵ The value at risk of the portfolio is the dollar loss corresponding to some pre-defined probability level – usually 5% or less – as defined by the left-hand tail of the distribution. Alternatively, VAR is the dollar loss that is expected to occur no more than 5% of the time over the defined risk horizon. Figure 12.1, for example, depicts a one-day VAR of $10X at the 5% probability level.

The Development of VAR

VAR emerged first in the trading community.⁶ The original goal of VAR was to systematize the measurement of an active trading firm's risk exposures across its dealing portfolios. Before VAR, most commercial trading houses measured and controlled risk on a desk-by-desk basis with little attention to firm-wide exposures. VAR made it possible for dealers to use risk measures that could be compared and aggregated across trading areas as a means of monitoring and limiting their consolidated financial risks.

VAR received its first public endorsement in July 1993, when a group representing the swap dealer community recommended the adoption of VAR by all active dealers.⁷ In that report, the Global Derivatives Study Group of The Group of Thirty urged dealers to “use a consistent measure to calculate daily the market risk of their derivatives positions and compare it to market risk limits. Market risk is best measured as ‘value at risk’ using probability analysis based upon a common confidence interval (e.g., two standard deviations) and time horizon (e.g., a one-day exposure). [emphasis added]”⁸

The italicized phrases in The Group of Thirty recommendation draw attention to several specific features of VAR that account for its wide-spread popularity among trading firms. One feature of VAR is its consistent measurement of financial risk. By expressing risk using a “possible dollar loss” metric, VAR makes possible direct comparisons of risk across different business lines and distinct financial products such as interest rate and currency swaps.

Figure 12.1

In addition to consistency, VAR also is probability-based. With whatever degree of confidence a firm wants to specify, VAR enables the firm to associate a specific loss with that level of confidence. Consequently, VAR measures can be interpreted as forward-looking approximations of potential market risk.

A third feature of VAR is its reliance on a common time horizon called the risk horizon. A one-day risk horizon at, say, the 5% probability level tells the firm, strictly speaking, that it can expect to lose no more than, say, $10X on the next day with 95% confidence. Firms often go on to assume that the 5% confidence level means they stand to lose more than $10X on no more than five days out of 100, an inference that is true only if strong assumptions are made about the stability of the underlying probability distribution.⁹

The choice of this risk horizon is based on various motivating factors. These may include the timing of employee performance evaluations, key decision-making events (e.g., asset purchases), major reporting events (e.g., board meetings and required disclosures), regulatory examinations, tax assessments, external quality assessments, and the like.

Implementing VAR

To estimate the value at risk of a portfolio, possible future values of that portfolio must be generated, yielding a distribution – called the “VAR distribution” – like that we saw in Figure 12.1. Once the VAR distribution is created for the chosen risk horizon, the VAR itself is just a number on the curve – viz., the change in the value of the portfolio leaving the specified amount of probability in the left-hand tail.

Creating a VAR distribution for a particular portfolio and a given risk horizon can be viewed as a two-step process.¹⁰ In the first step, the price or return distributions for each individual security or asset in the portfolio are generated. These distributions represent possible value changes in all the component assets over the risk horizon.¹¹ Next, the individual distributions somehow must be aggregated into a portfolio distribution using appropriate measures of correlation.¹² The resulting portfolio distribution then serves as the basis for the VAR summary measure.

An important assumption in almost all VAR calculations is that the portfolio whose risk is being evaluated does not change over the risk horizon. This assumption of no turnover was not a major issue when VAR first arrived on the scene at derivatives dealers. They were focused on one- or two-day – sometimes intra-day – risk horizons and thus found VAR both easy to implement and relatively realistic. But when it comes to generalizing VAR to a longer time horizon, the assumption of no portfolio changes becomes problematic. What does it mean, after all, to evaluate the one-year VAR of a portfolio using only the portfolio's contents today if the turnover in the portfolio is 20–30% per day?

Methods for generating both the individual asset risk distributions and the portfolio risk distribution range from the simplistic to the indecipherably complex. Because our goal in this paper is not to evaluate all these mechanical methods of VAR measurement, readers are referred elsewhere for explanations of the nuts and bolts of VAR computation.¹³ Several common methods of VAR calculation are summarized in the Appendix.

Uses of VAR

The purpose of any risk measurement system and summary risk statistic is to facilitate risk reporting and control decisions. Accordingly, dealers quickly began to rely on VAR measures in their broader risk management activities. The simplicity of VAR measurement greatly facilitated dealers' reporting of risks to senior managers and directors. The popularity of VAR owes much to Dennis Weatherstone, former chairman of JP Morgan & Co., Inc., who demanded to know the total market risk exposure of JP Morgan at 4:15pm every day. Weatherstone's request was met with a daily VAR report.

VAR also proved useful in dealers' risk control efforts.¹⁴ Commercial banks, for example, used VAR measures to quantify current trading exposures and compare them to established counterparty risk limits. In addition, VAR provided traders with information useful in formulating hedging policies and evaluating the effects of particular transactions on net portfolio risk. For managers, VAR became popular as a means of analyzing the performance of traders for compensation purposes and for allocating reserves or capital across business lines on a risk-adjusted basis.

Uses of VAR by Non-Dealers. Since its original development as a risk management tool for active trading firms, VAR has spread outside the dealer community. VAR now is used regularly by non-financial corporations, pension plans and mutual funds, clearing organizations, brokers and futures commission merchants, and insurers. These organizations find VAR just as useful as trading firms, albeit for different reasons.

Some benefits of VAR for non-dealers relate more to the exposure monitoring facilitated by VAR measurement than to the risk measurement task itself. For example, a pension plan with funds managed by external investment advisors may use VAR for policing its external managers. Similarly, brokers and account merchants can use VAR to assess collateral requirements for customers.

VAR AND CORPORATE RISK MANAGEMENT OBJECTIVES

Firms managing risks may be either value risk managers or cash flow risk managers.¹⁵ A value risk manager is concerned with the firm's total value at a particular point in time. This concern may arise from a desire to avoid bankruptcy, mitigate problems associated with informational asymmetries, or reduce expected tax liabilities.¹⁶ A cash flow risk manager, by contrast, uses risk management to reduce cash flow volatility and thereby increase debt capacity.¹⁷ Value risk managers thus typically manage the risks of a stock of assets, whereas cash flow risk managers manage the risks of a flow of funds. A risk measure that is appropriate for one type of firm may not be appropriate for others.

Value Risk Managers and VAR-Based Risk Controls

As the term value at risk implies, organizations for which VAR is best suited are those for which value risk management is the goal. VAR, after all, is intended to summarize the risk of a stock of assets over a particular risk horizon. Those likely to realize the most benefits from VAR thus include clearing houses, securities settlement agents,¹⁸ and swap dealers. These organizations have in common a concern with the value of their exposures over a well-defined period of time and a wish to limit and control those exposures. In addition, the relatively short risk horizons of these enterprises imply that VAR measurement can be accomplished reliably and with minimal concern about changing portfolio composition over the risk horizon.

Many value risk managers have risks arising mainly from agency transactions. Organizations like financial clearinghouses, for example, are exposed to risk arising from intermediation services rather than the risks of proprietary position taking. VAR can assist such firms in monitoring their customer credit exposures, in setting position and exposure limits, and in determining and enforcing margin and collateral requirements.

Total vs. Selective Risk Management

Most financial distress-driven explanations of corporate risk management, whether value or cash flow risk, center on a firm's total risk.¹⁹ If so, such firms should be indifferent to the composition of their total risks. Any risk thus is a candidate for risk reduction.

Selective risk managers, by contrast, deliberately choose to manage some risks and not others. Specifically, they seek to manage their exposures to risks in which they have no comparative informational advantage – for the usual financial ruin reasons – while actively exposing themselves, at least to a point, to risks in which they do have perceived superior information.²⁰

For firms managing total risk, the principal benefit of VAR is facilitating explicit risk control decisions, such as setting and enforcing exposure limits. For firms that selectively manage risk, by contrast, VAR is useful largely for diagnostic monitoring or for controlling risk in areas where the firm perceives no comparative informational advantage. An airline, for example, might find VAR helpful in assessing its exposure to jet fuel prices; but for the airline to use VAR to analyze the risk that seats on its aircraft are not all sold makes little sense.

Consider also a hedge fund manager who invests in foreign equity because the risk/return profile of that asset class is desirable. To avoid exposure to the exchange rate risk, the fund could engage an “over-lay manager” to hedge the currency risk of the position. Using VAR on the whole position lumps together two separate and distinct sources of risk – the currency risk and the foreign equity price risk. And reporting that total VAR without a corresponding expected return could have disastrous consequences. Using VAR to ensure that the currency hedge is accomplishing its intended aims, by contrast, might be perfectly legitimate.

VAR AND THE GREAT DERIVATIVES DISASTERS

Despite its many benefits to certain firms, VAR is not a panacea. Even when VAR is calculated appropriately, VAR in isolation will do little to keep a firm's risk exposures in line with the firm's chosen risk tolerances. Without a well-developed risk management infrastructure – policies and procedures, systems, and well-defined senior management responsibilities – VAR will deliver little, if any, benefits. In addition, VAR may not always help a firm accomplish its particular risk management objectives, as we shall see.

To illustrate some of the pitfalls of using VAR, we examine the four “great derivatives disasters” of 1993–1995: Procter & Gamble, Orange County, Barings, and Metallgesellschaft.²¹ Proponents of VAR often claim that many of these disasters would have been averted had VAR measurement systems been in place. We think otherwise.²²

Procter & Gamble

During 1993, Procter & Gamble (“P&G”) undertook derivatives transactions with Bankers Trust that resulted in over $150 million in losses.²³ Those losses traced essentially to P&G's writing of a put option on interest rates to Bankers Trust. Writers of put options suffer losses, of course, whenever the underlying security declines in price, which in this instance meant whenever interest rates rose. And rise they did in the summer and autumn of 1993.

The put option actually was only one component of the whole deal. The deal, with a notional principal of $200 million, was a fixed-for-floating rate swap in which Bankers Trust offered P&G 10 years of floating-rate financing at 75 basis points below the commercial paper rate in exchange for the put and fixed interest payments of 5.3% annually. That huge financing advantage of 75 basis points apparently was too much for P&G's treasurer to resist, particularly because the put was well out-of-the-money when the deal was struck in May 1993. But the low financing rate, of course, was just premium collected for writing the put. When the put went in-the-money for Bankers Trust, what once seemed like a good deal to P&G ended up costing millions of dollars.

VAR would have helped P&G, if P&G also had in place an adequate risk management infrastructure – which apparently it did not. Most obviously, senior managers at P&G would have been unlikely to have approved the original swap deal if its exposure had been subject to a VAR calculation. But that presupposes a lot.

Although VAR would have helped P&G's senior management measure its exposure to the speculative punt by its treasurer, much more would have been needed to stop the treasurer from taking the interest rate bet. The first requirement would have been a system for measuring the risk of the swaps on a transactional basis. But VAR was never intended for use on single transactions.²⁴ On the contrary, the whole appeal of the concept initially was its capacity to aggregate risk across transactions and exposures. To examine the risk of an individual transaction, the change in portfolio VAR that would occur with the addition of that new transaction should be analyzed. But that still requires first calculating the total VAR.²⁵ So, for P&G to have looked at the risk of its swaps in a VAR context, its entire treasury area would have needed a VAR measurement capability.

Implementing VAR for P&G's entire treasury function might seem to have been a good idea anyway. Why not, after all, perform a comprehensive VAR analysis on the whole treasury area and get transactional VAR assessment capabilities as an added bonus? For some firms, that is a good idea. But for other firms, it is not. Many non-financial corporations like P&G, after all, typically undertake risk management in their corporate treasury functions for cash flow management reasons.²⁶ VAR is a value risk measure, not a cash flow risk measure. For P&G to examine value at risk for its whole treasury operation, therefore, presumes that P&G was a value risk manager, and that may not have been the case. Even had VAR been in place at P&G, moreover, the assumption that P&G's senior managers would have been monitoring and controlling the VARs of individual swap transactions is not a foregone conclusion.

Barings

Barings PLC failed in February 1995 when rogue trader Nick Leeson's bets on the Japanese stock market went sour and turned into over $1 billion in trading losses.^27,28 To be sure, VAR would have led Barings senior management to shut down Leeson's trading operation in time to save the firm – if they knew about it. If P&G's sin was a lack of internal management and control over its treasurer, then Barings was guilty of an even more cardinal sin. The top officers of Barings lost control over the trading operation not because no VAR measurement system was in place, but because they let the same individual making the trades also serve as the recorder of those trades – violating one of the most elementary principles of good management.

The more interesting question emerging from Barings is why top management seems to have taken so long to recognize that a rogue trader was at work. For that purpose, a fully functioning VAR system would certainly have helped. Increasingly, companies in the financial risk-taking business use VAR as a monitoring tool for detecting unauthorized increases in positions.²⁹ Usually, this is intended for customer credit risk management by firms like futures commission merchants. In the case of Barings, however, such account monitoring would have enabled management to spot Leeson's run-up in positions in his so-called “arbitrage” and “error” accounts.

VAR measurements at Barings, on the other hand, would have been impossible to implement, given the deficiencies in the overall information technology (“IT”) systems in place at the firm. At any point in time, Barings' top managers knew only what Leeson was telling them. If Barings' systems were incapable of reconciling the position build-up in Leeson's accounts with the huge wire transfers being made by London to support Leeson's trading in Singapore, no VAR measure would have included a complete picture of Leeson's positions. And without that, no warning flag would have been raised.

Orange County

The Orange County Investment Pool (“OCIP”) filed bankruptcy in December 1994 after reporting a drop in its market value of $1.5 billion. For many years, Orange County maintained the OCIP as the equivalent of a money market fund for the benefit of school boards, road building authorities, and other local government bodies in its territory. These local agencies deposited their tax and other collections when they came in and paid for their own wage and other bills when the need arose. The Pool paid them interest on their deposits – handsomely, in fact. Between 1989 and 1994, the OCIP paid its depositors 400 basis points more than they would have earned on the corporate Pool maintained by the State of California – roughly $750 million over the period.³⁰

Most of the OCIP's investments involved leveraged purchases of intermediate-term securities and structured notes financed with “reverse repos” and other short-term borrowings. Contrary to conventional wisdom, the Pool was making its profits not from “speculation on falling interest rates” but rather from an investment play on the slope of the yield curve.³¹ When the Federal Reserve started to raise interest rates in 1994, the intermediate-term securities declined in value and OCIP's short-term borrowing costs rose.

Despite the widespread belief that the leverage policy led to the fund's insolvency and bankruptcy filing, Miller and Ross, after examining the OCIP's investment strategy, cash position, and net asset value at the time of the filing, have shown that the OCIP was not insolvent. Miller and Ross estimate that the $20 billion in total assets on deposit in the fund had a positive net worth of about $6 billion. Nor was the fund in an illiquid cash situation. OCIP had over $600 million of cash on hand and was generating further cash at a rate of more than $30 million a month.³² Even the reported $1.5 billion “loss” would have been completely recovered within a year – a loss that was realized only because Orange County's bankruptcy lawyers forced the liquidation of the securities.³³

Jorion has taken issue with Miller and Ross's analysis of OCIP, arguing that VAR would have called the OCIP investment program into question long before the $1.5 billion loss was incurred.³⁴ Using several different VAR calculation methods, Jorion concludes that OCIP's one-year VAR at the end of 1994 was about $1 billion at the 5% confidence level. Under the usual VAR interpretation, this would have told OCIP to expect a loss in excess of $1 billion in one out of the next 20 years.

Even assuming Jorion's VAR number is accurate, however, his interpretation of the VAR measure was unlikely to have been the OCIP's interpretation – at least not ex ante when it could have mattered. The VAR measure in isolation, after all, takes no account of the upside returns OCIP was receiving as compensation for that downside risk. Remember that OCIP was pursuing a very deliberate yield curve, net cost-of-carry strategy, designed to generate high expected cash returns. That strategy had risks, to be sure, but those risks seem to have been clear to OCIP treasurer Robert Citron – and, for that matter, to the people of Orange County who re-elected Citron treasurer in preference to an opposing candidate who was criticizing the investment strategy.³⁵

Had Orange County been using VAR, however, it almost certainly would have terminated its investment program upon seeing the $1 billion risk estimate. The reason probably would not have been the actual informativeness of the VAR number, but rather the fear of a public outcry at the number. Imagine the public reaction if the OCIP announced one day that it expected to lose more than $1 billion over the next year in one time out of 20. But that reaction would have far less to do with the actual risk information conveyed by the VAR number than with the lack of any corresponding expected profits reported with the risk number. Just consider, after all, what the public reaction would have been if the OCIP publicly announced that it would gain more than $1 billion over the next year in one time out of 20!³⁶

This example highlights a major abuse of VAR – an abuse that has nothing to do with the meaning of the value at risk number but instead traces to the presentation of the information that number conveys. Especially for institutional investors, a major pitfall of VAR is to highlight large potential losses over long time horizons without conveying any information about the corresponding expected return. The lesson from Orange County to would-be VAR users thus is an important one – for organizations whose mission is to take some risks, VAR measures of risks are meaningful only when interpreted alongside estimates of corresponding potential gains.

Metallgesellschaft

MG Refining & Marketing, Inc. (“MGRM”), a U.S. subsidiary of Metallgesellschaft AG, reported $1.3 billion in losses by year-end 1993 from its oil trading activities. MGRM's oil derivatives were part of a marketing program under which it offered long-term customers firm price guarantees for up to 10 years on gasoline, heating oil, and diesel fuel purchased from MGRM.³⁷ The firm hedged its resulting exposure to spot price increases with short-term futures contracts to a considerable extent. After several consecutive months of falling prices in the autumn of 1993, however, MGRM's German parent reacted to the substantial margin calls on the losing futures positions by liquidating the hedge, thereby turning a paper loss into a very real one.³⁸

Most of the arguments over MGRM – in press accounts, in the many law suits the case engendered, and in the academic literature – have focused on whether MGRM was “speculating” or “hedging.” The answer, of course, is that like all other merchant firms, they were doing both. They were definitely speculating on the oil “basis” – inter-regional, intertemporal, and inter-product differences in prices of crude, heating oil, and gasoline. That was the business they were in.³⁹ The firm had expertise and informational advantages far beyond those of its customers or of casual observers playing the oil futures market. What MGRM did not have, of course, was any special expertise about the level and direction of oil prices generally. Here, rather than take a corporate “view” on the direction of oil prices, like the misguided one the treasurer of P&G took on interest rates, MGRM chose to hedge its exposure to oil price levels.

Subsequent academic controversy surrounding the case has mainly been not whether MGRM was hedging, but whether they were over-hedging – whether the firm could have achieved the same degree of insulation from price level changes with a lower commitment from MGRM's ultimate owner-creditor Deutsche Bank.⁴⁰ The answer is that the day-to-day cash-flow volatility of the program could have been reduced by any number of cash flow variance-reducing hedge ratios.⁴¹ But the cost of chopping off some cash drains when prices fell was that of losing the corresponding cash inflows when prices spiked up.⁴²

Conceptually, of course, MGRM could have used VAR analysis to measure its possible financial risk. But why would they have wanted to do so? The combined marketing/hedging program, after all, was hedged against changes in the level of oil prices. The only significant risks to which MGRM's program was subject thus were basis and rollover risks – again, the risk that MGRM was in the business of taking.⁴³

A much bigger problem at MGRM than the change in the value of its program was the large negative cash flows on the futures hedge that would have been offset by eventual gains in the future on the fixed-price customer contracts. Although MGRM's former management claims it had access to adequate funding from Deutsche Bank (the firm's leading creditor and stock holder), perhaps some benefit might have been achieved by more rigorous cash flow simulations. But even granting that, VAR would have told MGRM very little about its cash flows at risk. As we have already emphasized, VAR is a value-based risk measure.

For firms like MGRM engaged in authorized risk-taking – like Orange County and unlike Leeson/Barings – the primary benefit of VAR really is just as an internal “diagnostic monitoring” tool. To that end, estimating the VAR of MGRM's basis trading activities would have told senior managers and directors at its parent what the basis risks were that MGRM actually was taking. But remember, MGRM's parent appears to have been fully aware of the risks MGRM's traders were taking even without a VAR number. In that sense, even the monitoring benefits of VAR for a proprietary trading operation would not have changed MGRM's fate.⁴⁴

ALTERNATIVES TO VAR

VAR certainly is not the only way a firm can systematically measure its financial risk. As noted, its appeal is mainly its conceptual simplicity and its consistency across financial products and activities. In cases where VAR may not be appropriate as a measure of risk, however, other alternatives are available.

Cash Flow Risk

Firms concerned not with the value of a stock of assets and liabilities over a specific time horizon but with the volatility of a flow of funds often are better off eschewing VAR altogether in favor of a measure of cash flow volatility. Possible cash requirements over a sequence of future dates, for example, can be simulated. The resulting distributions of cash flows then enable the firm to control its exposure to cash flow risk more directly.⁴⁵ Firms worried about cash flow risk for preserving or increasing their debt capacities thus might engage in hedging, whereas firms concerned purely about liquidity shortfalls might use such cash flow stress tests to arrange appropriate standby funding.

Abnormal Returns and Risk-Based Capital Allocation

Stulz suggests managing risk-taking activities using abnormal returns – i.e., returns in excess of the risk free rate – as a measure of the expected profitability of certain activities. Selective risk management then can be accomplished by allocating capital on a risk-adjusted basis and limiting capital at risk accordingly. To measure the risk-adjusted capital allocation, he suggests using the cost of new equity issued to finance the particular activity.⁴⁶

On the positive side, Stulz's suggestion does not penalize selective risk managers for exploiting perceived informational advantages, whereas VAR does. The problem with Stulz's idea, however, lies in any company's capacity actually to implement such a risk management process. More properly, the difficulty lies in the actual estimation of the firm's equity cost of capital. And in any event, under M&M proposition three, all sources of capital are equivalent on a risk-adjusted basis. The source of capital for financing a particular project thus should not affect the decision to undertake that project. Stulz's reliance on equity only is thus inappropriate.

Shortfall Risk

VAR need not be calculated by assuming variance is a complete measure of “risk,” but in practice this often is how VAR is calculated. (See the Appendix.) This assumption can be problematic when measuring exposures in markets characterized by non-normal (i.e., non-Gaussian) distributions – e.g., return distributions that are skewed or have fat tails. If so, as explained in the Appendix, a solution is to generate the VAR distribution in a manner that does not presuppose variance is an adequate measure of risk. Alternatively, other summary risk measures can be calculated.

For some organizations, asymmetric distributions pose a problem that VAR on its own cannot address, no matter how it is calculated. Consider again the OCIP example, in which the one-year VAR implied a $1 billion loss in one year out of 20. With a symmetric portfolio distribution, that would also imply a $1 billion gain in one year out of 20. But suppose OCIP's investment program had a positively skewed return distribution. Then, the $1 billion loss in one year out of 20 might be comparable to, say, a $5 billion gain in one year of 20.

One of the problems with interpreting VAR thus is interpreting the confidence level – viz., 5% or one year in 20. Some organizations may consider it more useful not to examine the loss associated with a chosen probability level but rather to examine the risk associated with a given loss – the socalled “doomsday” return below which a portfolio must never fall. Pension plans, endowments, and some hedge funds, for example, are concerned primarily with the possibility of a “shortfall” of assets below liabilities that would necessitate a contribution from the plan sponsor.

Shortfall risk measures are alternatives to VAR that allow a risk manager to define a specific target value below which the organization's assets must never fall and they measure risk accordingly. Two popular measures of shortfall risk are below-target probability (“BTP”) and below-target risk (“BTR”).⁴⁷

The advantage of BTR, in particular, over VAR is that it penalizes large shortfalls more than small ones.⁴⁸ BTR is still subject to the same misinterpretation as VAR when it is reported without a corresponding indication of possible gains. VAR, however, relies on a somewhat arbitrary choice of a “probability level” that can be changed to exaggerate or to de-emphasize risk measures. BTR, by contrast, is based on a real target – e.g., a pension actuarial contribution threshold – and thus reveals information about risk that can be much more usefully weighed against expected returns than a VAR measure.⁴⁹

CONCLUSION

By facilitating the consistent measurement of risk across distinct assets and activities, VAR allows firms to monitor, report, and control their risks in a manner that efficiently relates risk control to desired and actual economic exposures. At the same time, reliance on VAR can result in serious problems when improperly used. Would-be users of VAR are thus advised to consider the following three pieces of advice:

First, VAR is useful only to certain firms and only in particular circumstances. Specifically, VAR is a tool for firms engaged in total value risk management, where the consolidated values of exposures across a variety of activities are at issue. Dangerous misinterpretations of the risk facing a firm can result when VAR is wrongly applied in situations where total value risk management is not the objective, such as at firms concerned with cash flow risk rather than value risk.

Second, VAR should be applied very carefully to firms selectively managing their risks. When an organization deliberately takes certain risks as a part of its primary business, VAR can serve at best as a diagnostic monitoring tool for those risks. When VAR is analyzed and reported in such situations with no estimates of corresponding expected profits, the information conveyed by the VAR estimate can be extremely misleading.

Finally, as all the great derivatives disasters illustrate, no form of risk measurement – including VAR – is a substitute for good management. Risk management as a process encompasses much more than just risk measurement. Although judicious risk measurement can prove very useful to certain firms, it is quite pointless without a well-developed organizational infrastructure and IT system capable of supporting the complex and dynamic process of risk taking and risk control.

NOTES

The authors thank Kamaryn Tanner for her previous work with us on this subject.

1. See, for example, Global Derivatives Study Group, Derivatives: Practices and Principles (Washington, D.C.: July 1993), and Board of Governors of the Federal Reserve System, SR Letter 93–69 (1993). Most recently, the Securities and Exchange Commission began to require risk disclosures by all public companies. One approved format for these mandatory financial risk disclosures is VAR. For a critical assessment of the SEC's risk disclosure rule, see Merton H. Miller and Christopher L. Culp, “The SEC's Costly Disclosure Rules,” Wall Street Journal (June 22, 1996).

2. This presupposes, of course, that “risk management” is consistent with valuemaximizing behavior by the firm. For the purpose of this paper, we do not consider whether firms should be managing their risks. For a discussion of that issue, see Christopher L. Culp and Merton H. Miller, “Hedging in the Theory of Corporate Finance: A Reply to Our Critics,” Journal of Applied Corporate Finance, Vol. 8, No. 1 (Spring 1995): 121–127, and René M. Stulz, “Rethinking Risk Management,” Journal of Applied Corporate Finance, Vol. 9, No. 3 (Fall 1996): 8–24.

3. More recently, VAR has been suggested as a framework for measuring credit risk, as well. To keep our discussion focused, we examine only the applications of VAR to market risk measurement.

4. For a general description of VAR, see Philippe Jorion, Value at Risk (Chicago: Irwin Professional Publishing, 1997).

5. The risk horizon is chosen exogenously by the firm engaging in the VAR calculation.

6. An early precursor of VAR was SPAN™ – Standard Portfolio Analysis of Risk – developed by the Chicago Mercantile Exchange for setting futures margins. Now widely used by virtually all futures exchanges, SPAN is a nonparametric, simulation-based “worst case” measure of risk. As will be seen, VAR, by contrast, rests on well-defined probability distributions.

7. This was followed quickly by a similar endorsement from the International Swaps and Derivatives Association. See Jorion, cited previously.

8. Global Derivatives Study Group, cited previously.

9. This interpretation assumes that asset price changes are what the technicians call “iid,” independently and identically distributed – i.e., that price changes are drawn from essentially the same distribution every day.

10. In practice, VAR is not often implemented in a clean two-step manner, but discussing it in this way simplifies our discussion – without any loss of generality.

11. Especially with instruments whose payoffs are non-linear, a better approach is to generate distributions for the underlying “risk factors” that affect an asset rather than focus on the changes in the values of the assets themselves. To generate the value change distribution of an option on a stock, for example, one might first generate changes in the stock price and its volatility and then compute associated option price changes rather than generating option price changes “directly.” For a discussion, see Michael S. Gamze and Ronald S. Rolighed, “VAR: What's Wrong With This Picture?” unpublished manuscript, Federal Reserve Bank of Chicago (1997).

12. If a risk manager is interested in the risk of a particular financial instrument, the appropriate risk measure to analyze is not the VAR of that instrument. Portfolio effects still must be considered. The relevant measure of risk is the marginal risk of that instrument in the portfolio being evaluated. See Mark Garman, “Improving on VAR,” Risk Vol. 9, No. 5 (1996): 61–63.

13. See, for example, Jorion, cited previously, Rod A. Beckström and Alyce R. Campbell, “Value-at-Risk (VAR): Theoretical Foundations,” in An Introduction to VAR, Rod Beckström and Alyce Campbell, eds (Palo Alto, Ca.: CAATS Software, Inc., 1995), and James V. Jordan and Robert J. Mackay, “Assessing Value at Risk for Equity Portfolios: Implementing Alternative Techniques,” in Derivatives Handbook, Robert J. Schwartz and Clifford W. Smith, Jr., eds (New York: John Wiley & Sons, Inc., 1997).

14. See Rod A. Beckström and Alyce R. Campbell, “The Future of Firm-Wide Risk Management,” in An Introduction to VAR, Rod Beckström and Alyce Campbell, eds (Palo Alto, Ca.: CAATS Software, Inc., 1995).

15. For a general discussion of the traditional corporate motivations for risk management, see David Fite and Paul Pfleider, “Should Firms Use Derivatives to Manage Risk?” in Risk Management: Problems & Solutions, William H. Beaver and George Parker, eds (New York: McGraw-Hill, Inc., 1995).

16. See, for example, Clifford Smith and René Stulz, “The Determinants of Firms' Hedging Policies,” Journal of Financial and Quantitative Analysis, Vol. 20 (1985): 391– 405.

17. See, for example, Kenneth Froot, David Scharfstein, and Jeremy Stein, “Risk Management: Coordinating Corporate Investment and Financing Policies,” Journal of Finance Vol. 48 (1993): 1629–1658.

18. See Christopher L. Culp and Andrea M.P. Neves, “Risk Management by Securities Settlement Agents,” Journal of Applied Corporate Finance Vol. 10, No. 3 (Fall 1997): 96–103.

19. See, for example, Smith and Stulz, cited previously, and Froot, Scharfstein, and Stein, cited previously.

20. See Culp and Miller (Spring 1995), cited previously, and Stulz, cited previously.

21. In truth, Procter & Gamble was the only one of these disasters actually caused by derivatives. See Merton H. Miller, “The Great Derivatives Disasters: What Really Went Wrong and How to Keep it from Happening to You,” speech presented to JP Morgan & Co. (Frankfurt, June 24, 1997) and chapter two in Merton H. Miller, Merton Miller on Derivatives (New York: John Wiley & Sons, Inc., 1997).

22. The details of all these cases are complex. We thus refer readers elsewhere for discussions of the actual events that took place and limit our discussion here only to basic background. See, for example, Stephen Figlewski, “How to Lose Money in Derivatives,” Journal of Derivatives Vol. 2, No. 2 (Winter 1994): 75–82.

23. See, for example, Figlewski, cited previously, and Michael S. Gamze and Karen McCann, “A Simplified Approach to Valuing an Option on a Leveraged Spread: The Bankers Trust, Procter & Gamble Example,” Derivatives Quarterly Vol. 1, No. 4 (Summer 1995): 44–53.

24. Recently, some have advocated that derivatives dealers should evaluate the VAR of specific transactions from the perspective of their counterparties in order to determine counterparty suitability. Without knowing the rest of the counterparty's risk exposures, however, the VAR estimate would be meaningless. Even with full knowledge of the counterparty's total portfolio, the VAR number still might be of no use in determining suitability for reasons to become clear later.

25. See Garman, cited previously.

26. See, for example, Judy C. Lewent and A. John Kearney, “Identifying, Measuring, and Hedging Currency Risk at Merck,” Journal of Applied Corporate Finance Vol. 2, No. 4 (Winter 1990): 19–28, and Deana R. Nance, Clifford W. Smith, and Charles W. Smithson, “On the Determinants of Corporate Hedging,” Journal of Finance Vol. 48, No. 1 (1993): 267–284.

27. See, for example, Hans R. Stoll, “Lost Barings: A Tale in Three Parts Concluding with a Lesson,” Journal of Derivatives Vol. 3, No. 1 (Fall 1995): 109–115, and Anatoli Kuprianov, “Derivatives Debacles: Case Studies of Large Losses in Derivatives Markets,” in Derivatives Handbook: Risk Management and Control, Robert J. Schwartz and Clifford W. Smith, Jr., eds. (New York: John Wiley & Sons, Inc., 1997).

28. Our reference to rogue traders is not intended to suggest, of course, that rogue traders are only found in connection with derivatives. Rogue traders have caused the banks of this world far more damage from failed real estate (and copper) deals than from derivatives.

29. See Christopher Culp, Kamaryn Tanner, and Ron Mensink, “Risks, Returns and Retirement,” Risk Vol. 10, No. 10 (October 1997): 63–69.

30. Miller, cited previously.

31. When the term structure is upward sloping, borrowing in short-term markets to leverage longer-term government securities generates positive cash carry. A surge in inflation or interest rates, of course, could reverse the term structure and turn the carry negative. That is the real risk the treasurer was taking. But it was not much of a risk. Since the days of Jimmy Carter in the late 1970s, the U.S. term structure has never been downward sloping and nobody in December 1994 thought it was likely to be so in the foreseeable future.

32. Merton H. Miller and David J. Ross, “The Orange County Bankruptcy and its Aftermath: Some New Evidence,” Journal of Derivatives, Vol. 4, No. 4 (Summer 1997): 51–60.

33. Readers may wonder why, then, Orange County did declare bankruptcy. That story is complicated, but a hint might be found in the payment of $50 million in special legal fees to the attorneys that sued Merrill Lynch for $1.5 billion for selling OCIP the securities that lost money. In short, lots of people gained from OCIP's bankruptcy, even though OCIP was not actually bankrupt. See Miller, cited previously, and Miller and Ross, cited previously.

34. Philippe Jorion, “Lessons From the Orange County Bankruptcy,” Journal of Derivatives Vol. 4, No. 4 (Summer 1997): 61–66.

35. Miller and Ross, cited previously.

36. Only for the purpose of this example, we obviously have assumed symmetry in the VAR distribution.

37. A detailed analysis of the program can be found in Christopher L. Culp and Merton H. Miller, “Metallgesellschaft and the Economics of Synthetic Storage,” Journal of Applied Corporate Finance Vol. 7, No. 4 (Winter 1995): 62–76.

38. For an analysis of the losses incurred by MGRM – as well as why they were incurred – see Christopher L. Culp and Merton H. Miller, “Auditing the Auditors,’ Risk Vol. 8, No. 4 (1995): 36–39.

39. Culp and Miller (Winter 1995, Spring 1995), cited previously, explain this in detail.

40. See Franklin R. Edwards and Michael S. Canter, “The Collapse of Metallgesellschaft: Unhedgeable Risks, Poor Hedging Strategy, or Just Bad Luck?,” Journal of Applied Corporate Finance Vol. 8, No. 1 (Spring 1995): 86–105.

41. See, for example, Froot, Scharfstein, and Stein, cited previously.

42. A number of other reasons also explain MGRM's reluctance to adopt anything smaller than a “one-for-one stack-and-roll” hedge. See Culp and Miller (Winter 1995, Spring 1995).

43. The claim that MGRM was in the business of trading the basis has been disputed by managers of MGRM's parent and creditors. Nevertheless, the marketing materials of MGRM – on which the parent firm signed off – suggests otherwise. See Culp and Miller (Spring 1995), cited previously.

44. Like P&G and Barings, what happened at MGRM was, in the end, a management failure rather than a risk management failure. For details on how management failed in the MGRM case, see Culp and Miller (Winter 1995, Spring 1995). For a redacted version of the story, see Christopher L. Culp and Merton H. Miller, “Blame Mismanagement, Not Speculation, for Metall's Woes,” Wall Street Journal Europe (April 25, 1995).

45. See Stulz, cited previously.

46. See Stulz, cited previously.

47. See Culp, Tanner, and Mensink, cited previously. For a complete mathematic discussion of these concepts, see Kamaryn T. Tanner, “An Asymmetric distribution Model for Portfolio Optimization,” manuscript, Graduate School of Business, The University of Chicago (1997).

48. BTP accomplishes a similar objective but does not weight large deviations below the target more heavily than small ones.

49. See Culp, Tanner, and Mensink, cited previously, for a more involved treatment of shortfall risk as compared to VAR.

APPENDIX: CALCULATING VAR

To calculate a VAR statistic is easy once you have generated the probability distribution for future values of the portfolio. Creating that VAR distribution, on the other hand, can be quite hard, and the methods available range from the banal to the utterly arcane. This appendix reviews a few of those methods.

Variance-Based Approaches

By far the easiest way to create the VAR distribution used in calculating the actual VAR statistic is just to assume that distribution is normal (i.e., Gaussian). Mean and variance are “sufficient statistics” to fully characterize a normal distribution. Consequently, knowing the variance of an asset whose return is normally distributed is all that is needed to summarize the risk of that asset.

Using return variances and covariances as inputs, VAR thus can be calculated in a fairly straightforward way.¹ First consider a single asset. If returns on that asset are normally distributed, the 5th percentile VAR is always 1.65 standard deviations below the mean return. So, the variance is a sufficient measure of risk to compute the VAR on that asset – just subtract 1.65 times the standard deviation from the mean. The risk horizon for such a VAR estimate corresponds to the frequency used to compute the input variance.

Now consider two assets. In that case, the VAR of the portfolio of two assets can be computed in a similar manner using the variances of the two assets' returns. These variance-based risk measures then are combined using the correlation of the two assets' returns. The result is a VAR estimate for the portfolio.

The simplicity of the variance-based approach to VAR calculations lies in the assumption of normality. By assuming that returns on all financial instruments are normally distributed, the risk manager eliminates the need to come up with a VAR distribution using complicated modeling techniques. All that really must be done is to come up with the appropriate variances and correlations.

At the same time, however, by assuming normality, the risk manager has greatly limited the VAR estimate. Normal distributions, after all, are symmetric. Any potential for skewness or fat tails in asset returns thus is totally ignored in the variance-only approach.

In addition to sacrificing the possibility that asset returns may not be normally distributed, the variance-only approach to calculating VAR also relies on the critical assumption that asset returns are totally independent across increments of time. A multi-period VAR can be calculated only by calculating a single-period VAR from the available data and then extrapolating the multi-day risk estimate. For example, suppose variances and correlations are available for historical returns measured at the daily frequency. To get from a one-day VAR to a T-day VAR – where T is the risk horizon of interest – the variance-only approach requires that the one-day VAR is multiplied by the square root of T.

For return variances and correlations measured at the monthly frequency or lower, this assumption may not be terribly implausible. For daily variances and correlations, however, serial independence is a very strong and usually an unrealistic assumption in most markets. The problem is less severe for short risk horizons, of course. So, using a one-day VAR as the basis for a five-day VAR might be acceptable, whereas a one-day VAR would be highly problematic in most markets.

Computing Volatility Inputs

Despite its unrealistic assumptions, simple variance-based VAR calculations are probably the dominant application of the VAR measure today. The approach is especially popular for corporate end users of derivatives, principally because the necessary software is cheap and easy to use.

All variance-based VAR measures, however, are not alike. The sources of inputs used to calculate VAR in this manner can differ widely. The next several subsections summarize several popular methods for determining these variances.² Note that these methods are only methods of computing variances on single assets. Correlations still must be determined to convert the VARs of individual assets into portfolio VARs.

Moving Average Volatility. One of the simplest approaches to calculating variance for use in a variance-based VAR calculating involves estimating a historical moving average of volatility. To get a moving average estimate of variance, the average is taken over a rolling window of historical volatility data. For example, given a 20-day rolling window,³ the daily variance used for one-day VAR calculations would be the average daily variance over the most recent 20 days. To calculate this, many assume a zero mean daily return and then just average the squared returns for the last 20 trading days. On the next day, a new return becomes available for the volatility calculation. To maintain a 20-day measurement window, the first observation is dropped off and the average is recomputed as the basis of the next day's VAR estimate.

More formally, denote the daily return from time t – 1 to time t as r_t. Assuming a zero mean daily return, the moving average volatility over a window or the last D days is calculated as follows:

where v_t is the daily volatility estimate used as the VAR input on day t.

Because moving-average volatility is calculated using equal weights for all observations in the historical time series, the calculations are very simple. The result, however, is a smoothing effect that causes sharp changes in volatility to appear as plateaus over longer periods of time, failing to capture dramatic changes in volatility.

Risk Metrics. To facilitate one-day VAR calculations and extrapolated risk measures for longer risk horizons, JP Morgan – in association with Reuters – began making available their RiskMetrics™ data sets. This data includes historical variances and covariances on a variety of simple assets – sometimes called “primitive securities.”⁴ Most other assets have cash flows that can be “mapped” into these simpler RiskMetricsTM assets for VAR calculation purposes.⁵

In the RiskMetrics data set, daily variances and correlations are computed using an “exponentially weighted moving average.” Unlike the simple moving-average volatility estimate, an exponentially weighted moving average allows the most recent observations to be more influential in the calculation than observations further in the past. This has the advantage of capturing shocks in the market better than the simple moving average and thus is often regarded as producing a better volatility for variance-based VAR than the equal-weighted moving average alternative.

Conditional Variance Models. Another approach for estimating the variance input to VAR calculations involves the use of “conditional variance” time series methods. The first conditional variance model was developed by Engle in 1982 and is known as the autoregressive conditional heteroskedasticity (“ARCH”) model.⁶ ARCH combines an autoregressive process with a moving average estimation method so that variance still is calculated in the rolling window manner used for moving averages.

Since its introduction, ARCH has evolved into a variety of other conditional variance models, such as Generalized ARCH (“GARCH”), Integrated GARCH (“IGARCH”), and exponential GARCH (“EGARCH”). Numerous applications of these models have led practitioners to believe that these estimation techniques provide better estimates of (time-series) volatility than simpler methods.

For a GARCH(1,1) model, the variance of an asset's return at time t is presumed to have the following structure:

The conditional variance model thus incorporates a recursive moving average term. In the special case where a₀ = 0 and a₁ + a₂ = 1, the GARCH(1,1) model reduces exactly to the exponentially weighted moving average formulation for volatility.⁷

Using volatilities from a GARCH model as inputs in a variance-based VAR calculation does not circumvent the statistical inference problem of presumed normality. By incorporating additional information into the volatility measure, however, more of the actual time series properties of the underlying asset return can be incorporated into the VAR estimate than if a simple average volatility is used.

Implied Volatility. All of the above methods of computing volatilities for variance-based VAR calculations are based on historical data. For more of a forward-looking measure of volatility, option-implied volatilities sometimes can be used to calculate VAR.

The implied volatility of an option is defined as the expected future volatility of the underlying asset over the remaining life of the option. Many studies have concluded that measures of option-implied volatility are, indeed, the best predictor of future volatility.⁸ Unlike time series measures of volatility that are entirely backward-looking, option implied volatility is “backed-out” of actual option prices – which, in turn, are based on actual transactions and expectations of market participants – and thus is inherently forward-looking.

Any option-implied volatility estimate is dependent on the particular option pricing model used to derive the implied volatility. Given an observed market price for an option and a presumed pricing model, the implied volatility can be determined numerically. This variance may then be used in a VAR calculation for the asset underlying the option.

Non-Variance VAR Calculation Methods

Despite the simplicity of most variance-based VAR measurement methods, many practitioners prefer to avoid the restrictive assumptions underlying that approach – viz., symmetric return distributions that are independent and stable over time. To avoid these assumptions, a risk manager must actually generate a full distribution of possible future portfolio values – a distribution that is neither necessarily normal nor symmetric.⁹

Historical simulation is perhaps the easiest alternative to variance-based VAR. This approach generates VAR distributions merely by “re-arranging” historical data – viz., re-sampling time series data on the relevant asset prices or returns. This can be about as easy computationally as variance-based VAR, and it does not presuppose that everything in the world is normally distributed. Nevertheless, the approach is highly dependent on the availability of potentially massive amounts of historical data. In addition, the VAR resulting from a historical simulation is totally sample dependent.

More advanced approaches to VAR calculation usually involve some type of forward-looking simulation model, such as Monte Carlo. Implementing simulation methods typically is computationally intensive, expensive, and heavily dependent on personnel resources. For that reason, simulation has remained largely limited to active trading firms and institutional investors. Nevertheless, simulation does enable users to depart from the RiskMetrics normality assumptions about underlying asset returns without forcing them to rely on a single historical data sample. Simulation also eliminates the need to assume independence in returns over time – viz., VAR calculations are no longer restricted to one-day estimates that must be extrapolated over the total risk horizon.

NOTES

1. A useful example of this methodology is presented in Anthony Saunders, “Market Risk,” The Financier Vol. 2, No. 5 (December 1995).

2. For more methods, see Jorion (1997), cited previously.

3. The length of the window is chosen by the risk manager doing the VAR calculation.

4. Jorion (1997), cited previously.

5. For a detailed explanation of this approach, see JP Morgan/Reuters, Risk Metrics – Technical Document, 4th ed. (1996).

6. Robert Engle, “Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of United Kingdom Inflation,” Econometrica Vol. 50 (1982): 391– 407.

7. See Jorion (1997), cited previously.

8. See, for example, Phillipe Jorion, “Predicting Volatility in the Foreign Exchange Market,” Journal of Finance, Vol. 50 (1995): 507–528.

9. Variance-based approaches avoid the problem of generating a new distribution by assuming that distribution.