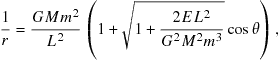Analytic Geometry
The great French mathematician and philosopher René Descartes (1596–1650) is usually credited with developing the network of relationships that exist between algebraic quantities—such as numbers and functions—and their geometrical analogs—points and curves. Descartes was also responsible for the notion that the world is made up of two fundamentally different substances, mind and matter. From our enlightened modern viewpoint, Cartesian mind/body dualism is almost certainly misguided, but that does not compromise Descartes’ contributions when he stuck to mathematics. (Descartes is also responsible for the intellectual’s raison d’être, “cogito ergo sum”—I think therefore I am.)
5.1 Functions and Graphs
A function in mathematics is a relation that associates corresponding members of two different sets. For example, the expression
![]() (5.1)
(5.1)
says that if you give me a quantity x, called the independent variable, I have a rule which will produce a quantity y, the dependent variable. Often such a functional relation is written more compactly as ![]() . A function is called single-valued if x uniquely determines y, such as
. A function is called single-valued if x uniquely determines y, such as ![]() or
or ![]() , but multivalued if x can give more than one possible value of y. For example,
, but multivalued if x can give more than one possible value of y. For example, ![]() is double-valued since it can equal
is double-valued since it can equal ![]() and
and ![]() has an infinite number of values,
has an infinite number of values, ![]() . The set of values x for which a function is defined is known as its domain. The domain might be limited in specific cases, say, to real x or to
. The set of values x for which a function is defined is known as its domain. The domain might be limited in specific cases, say, to real x or to ![]() . The possible values of y consistent with the choice of domain are known as its range. For example,
. The possible values of y consistent with the choice of domain are known as its range. For example, ![]() and
and ![]() have the range [−1, +1] when the domain of x is the real numbers.
have the range [−1, +1] when the domain of x is the real numbers.
If dependent and independent variables are not explicitly distinguished, their relationship can be expressed as an implicit function
![]() (5.2)
(5.2)
For example, ![]() , the equation for the unit circle, can be solved for either
, the equation for the unit circle, can be solved for either ![]() or
or ![]() .
.
In this chapter, we will be considering only relations involving two variables. Later we will generalize to more variables. A functional relation ![]() can be represented by a curve on the two-dimensional
can be represented by a curve on the two-dimensional ![]() -plane, a Cartesian coordinate system. The distance between two points
-plane, a Cartesian coordinate system. The distance between two points ![]() and
and ![]() can be found using Pythagoras’ theorem:
can be found using Pythagoras’ theorem:
![]() (5.3)
(5.3)
We will also be using polar coordinates, in which a point on the plane is represented by its distance from the origin r, and its direction with respect to the x-axis, designated by the polar angle ![]() . The Cartesian and polar coordinate systems are related by
. The Cartesian and polar coordinate systems are related by
![]() (5.4)
(5.4)
which we have already encountered in the phasor representation of complex numbers. Figure 5.1 shows schematically how a functional relation, ![]() , or its polar equivalent
, or its polar equivalent ![]() , can be represented in these alternative coordinate systems.
, can be represented in these alternative coordinate systems.
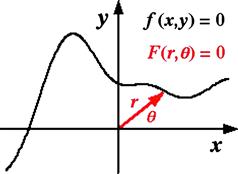
Figure 5.1 Plot of functional relation ![]() in Cartesian coordinates or the corresponding relation
in Cartesian coordinates or the corresponding relation ![]() in polar coordinates.
in polar coordinates.
As certain functions become familiar to you, association with the shape of their curves will become almost reflexive. As Frank Lloyd Wright might have put it, “form follows function.”
5.2 Linear Functions
The simplest functional relation between two variables has the general form
![]() (5.5)
(5.5)
which can represented by a straight line. The standard form in Cartesian coordinates is
![]() (5.6)
(5.6)
which is sketched in Figure 5.2. It is to your future advantage to be able to understand linear equations from several different points of view. A linear relation means that increasing or decreasing the independent variable x by a given amount will cause a proportionate increase or decrease in the dependent variable y. The y-intercept is the point where the line crosses the y-axis, where ![]() . Equation (5.6) shows that occurs at
. Equation (5.6) shows that occurs at ![]() . The x-intercept, where
. The x-intercept, where ![]() , occurs at the point
, occurs at the point ![]() . An alternative form for the equation in terms of its intercepts is
. An alternative form for the equation in terms of its intercepts is
![]() (5.7)
(5.7)
The parameter m in Eq. (5.6) is called the slope. It measures how steeply y rises or falls with x. Differential calculus, which we begin in the next chapter, is at its most rudimentary level, the computation of slopes of functions at different points. The slope tells how many units of y you go up or down when you travel along one unit of x. Symbolically,
![]() (5.8)
(5.8)
where ![]() in universal mathematical usage represents the change in the quantity to which it is affixed. For example,
in universal mathematical usage represents the change in the quantity to which it is affixed. For example,
![]() (5.9)
(5.9)
Slope might be used to describe the degree of inclination of a road. If a mountain road rises 5 m for every 100 m of horizontal distance on the map (which would be called a “5% grade”), the slope equals 5/100 = 0.05. In the following chapter on differential calculus, we will identify the slope with the first derivative, using the notation:
![]() (5.10)
(5.10)
Only for a straight line does ![]() . For other functions, we will need to consider the limits as
. For other functions, we will need to consider the limits as ![]() and
and ![]() .
.

Figure 5.2 Standard form for equation of straight line. ![]() , and
, and ![]() are the
are the ![]() -intercept,
-intercept, ![]() -intercept and slope, respectively. The alternative intercept form of the equation can be written
-intercept and slope, respectively. The alternative intercept form of the equation can be written ![]() .
.
Note that ![]() has the form of a tangent of a right triangle with sides
has the form of a tangent of a right triangle with sides ![]() and
and ![]() (opposite/adjacent). If
(opposite/adjacent). If ![]() is the angle that the line makes with the horizontal (x) axis, we can identify
is the angle that the line makes with the horizontal (x) axis, we can identify
![]() (5.11)
(5.11)
A horizontal line, representing an equation ![]() , has slope
, has slope ![]() . A vertical line, representing an equation
. A vertical line, representing an equation ![]() , has slope
, has slope ![]() . Another line drawn perpendicular to the given straight line with slope m must make an angle
. Another line drawn perpendicular to the given straight line with slope m must make an angle ![]() with the horizontal. The slope of the perpendicular, say
with the horizontal. The slope of the perpendicular, say ![]() , is then given by
, is then given by
![]() (5.12)
(5.12)
having exploited several trigonometric relations. We arrive thereby at a general result for the slopes of two mutually perpendicular curves at their point of intersection:
![]() (5.13)
(5.13)
One of Euclid’s axioms was that through any two points, one and only one straight line can be drawn. Translated into analytic geometry this implies that two points ![]() and
and ![]() suffice to determine the equation for a straight line. In principle, the equation can be determined by writing Eq. (5.6) successively using
suffice to determine the equation for a straight line. In principle, the equation can be determined by writing Eq. (5.6) successively using ![]() and
and ![]() and solving the simultaneous equations for m and b; or, alternatively, solving Eq. (5.7) for a and b. A more illuminating approach is to focus on the slope of the line. Since the slope of a straight line is constant, we can write (5.8) using
and solving the simultaneous equations for m and b; or, alternatively, solving Eq. (5.7) for a and b. A more illuminating approach is to focus on the slope of the line. Since the slope of a straight line is constant, we can write (5.8) using ![]() and
and ![]() computed between any two points. For example between the points
computed between any two points. For example between the points ![]() and
and ![]() ,
,
![]() (5.14)
(5.14)
which determines the slope m. If ![]() stands for some arbitrary point on the line then, likewise,
stands for some arbitrary point on the line then, likewise,
![]() (5.15)
(5.15)
This equation can be solved for y to give an equation for the line
![]() (5.16)
(5.16)
With the identification ![]() , this takes the standard form of Eq. (5.6).
, this takes the standard form of Eq. (5.6).
5.3 Conic Sections
Mathematically, a right-circular cone is a surface swept out by a straight line, with one point—the vertex—kept fixed while the line sweeps around a circular path. You would have to place two ice-cream cones point-to-point to simulate a mathematical cone, as shown in Figure 5.3. Greek mathematicians (Apollonius is usually credited) discovered that planes intersecting the cone at different angles produce several interesting curves, which are called conic sections. Degenerate cases, in which the plane passes through the vertex, give either a single point, a straight line, or two intersecting lines. The nondegenerate conic sections, illustrated in Figure 5.4, are circles, ellipses, parabolas, and hyperbolas.

Figure 5.3 Mathematical definition of a cone and one possible physical realization. Each of the two sheets on opposite sides of the vertex is called a nappe.

Figure 5.4 Intersections of the cone and plane showing how the different conic sections are generated.
A right-circular cone can be represented by the three-dimensional equation:
![]() (5.17)
(5.17)
For each value ![]() , this corresponds to a circle of radius z. Also, by analogy with Eq. (5.7) for a straight line, we surmise that the equation for a plane in three dimensions has the form
, this corresponds to a circle of radius z. Also, by analogy with Eq. (5.7) for a straight line, we surmise that the equation for a plane in three dimensions has the form
![]() (5.18)
(5.18)
The intersection of the cone with an arbitrary plane is satisfied by points ![]() which are simultaneous solutions of Eqs. (5.17) and (5.18). The equation for the surface of intersection, in the form
which are simultaneous solutions of Eqs. (5.17) and (5.18). The equation for the surface of intersection, in the form ![]() , can be obtained by eliminating z between the two equations. This implies that a conic section has the general form
, can be obtained by eliminating z between the two equations. This implies that a conic section has the general form
![]() (5.19)
(5.19)
Assuming it is nondegenerate, the form of the conic section is determined by its discriminant, ![]() . If the discriminant is positive, it is a hyperbola, if it is negative, an ellipse or a circle. A discriminant of zero implies a parabola. The coefficients
. If the discriminant is positive, it is a hyperbola, if it is negative, an ellipse or a circle. A discriminant of zero implies a parabola. The coefficients ![]() , and F help determine the location and scale of the figure.
, and F help determine the location and scale of the figure.
The simplest nondegenerate conic section is the circle. A circle centered at ![]() with a radius of a satisfies the equation
with a radius of a satisfies the equation
![]() (5.20)
(5.20)
The unit circle is the special case when ![]() . A circle viewed from an angle has the apparent shape of an ellipse. An ellipse centered at
. A circle viewed from an angle has the apparent shape of an ellipse. An ellipse centered at ![]() with semimajor axis a and semiminor axis b, as shown in Figure 5.5, is described by the equation
with semimajor axis a and semiminor axis b, as shown in Figure 5.5, is described by the equation
![]() (5.21)
(5.21)
It is assumed that ![]() , so that the long axis of the ellipse is oriented in the x-direction. When
, so that the long axis of the ellipse is oriented in the x-direction. When ![]() , the ellipse degenerates into a circle.
, the ellipse degenerates into a circle.
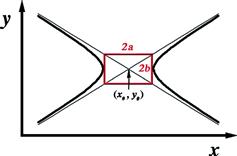
Figure 5.6 represents a hyperbola with the equation:
![]() (5.22)
(5.22)
The hyperbola can likewise be characterized by a semimajor axis a and a semiminor axis b, which, in this case, define a rectangle centered about ![]() . The two branches of the hyperbola are tangent to the rectangle, as shown. A distinctive feature are the asymptotes, the two diagonals of the rectangle extended to infinity. Their equations are
. The two branches of the hyperbola are tangent to the rectangle, as shown. A distinctive feature are the asymptotes, the two diagonals of the rectangle extended to infinity. Their equations are
![]() (5.23)
(5.23)
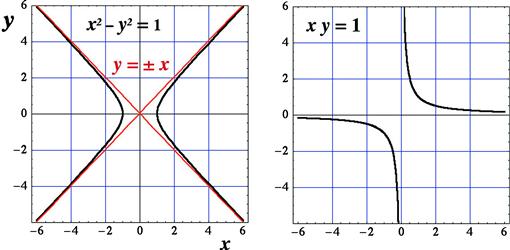
When ![]() , the asymptotes become perpendicular, and we obtain what is called an equiangular or rectangular hyperbola. A simple example is the unit hyperbola
, the asymptotes become perpendicular, and we obtain what is called an equiangular or rectangular hyperbola. A simple example is the unit hyperbola
![]() (5.24)
(5.24)
Recalling that ![]() , we can make a transformation of coordinates in which
, we can make a transformation of coordinates in which ![]() and
and ![]() . This simplifies the equation to
. This simplifies the equation to
![]() (5.25)
(5.25)
The hyperbola has been rotated by 45° and the asymptotes have become the coordinate axes themselves. These rectangular hyperbolas are shown in Figure 5.7. More generally, hyperbolas of the form ![]() represent relations in which y is inversely proportional to x. An important example is Boyle’s law relating the pressure and volume of an ideal gas at constant temperature, which can be expressed as
represent relations in which y is inversely proportional to x. An important example is Boyle’s law relating the pressure and volume of an ideal gas at constant temperature, which can be expressed as ![]() .
.
We have already considered parabolas of the form ![]() , in connection with the quadratic formula. Analogous “sideways” parabolas can be obtained when the roles of x and y are reversed. Parabolas, as well as ellipses and hyperbolas, can be oriented obliquely to the axes by appropriate choices of B, the coefficient of xy, in the conic-section equation (5.19), the simplest example being the
, in connection with the quadratic formula. Analogous “sideways” parabolas can be obtained when the roles of x and y are reversed. Parabolas, as well as ellipses and hyperbolas, can be oriented obliquely to the axes by appropriate choices of B, the coefficient of xy, in the conic-section equation (5.19), the simplest example being the ![]() hyperbola
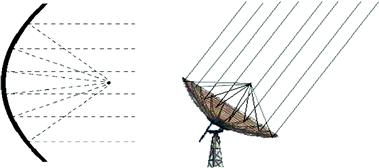
hyperbola ![]() considered above. Parabolas have the unique property that parallel rays incident upon them are reflected to a single point, called the focus, as shown in Figure 5.8. A parabola with the equation
considered above. Parabolas have the unique property that parallel rays incident upon them are reflected to a single point, called the focus, as shown in Figure 5.8. A parabola with the equation
![]() (5.26)
(5.26)
has its focus at the point ![]() . A parabola rotated about its symmetry axis generates a paraboloid. This geometry is exploited in applications where radiation needs to be concentrated at one point, such as radio telescopes, television dishes, and solar radiation collectors; also, when light emitted from a single point is to be projected as a parallel beam, as in automobile headlight reflectors.
. A parabola rotated about its symmetry axis generates a paraboloid. This geometry is exploited in applications where radiation needs to be concentrated at one point, such as radio telescopes, television dishes, and solar radiation collectors; also, when light emitted from a single point is to be projected as a parallel beam, as in automobile headlight reflectors.

5.4 Conic Sections in Polar Coordinates
The equations for conic sections can be expressed rather elegantly in polar coordinates. As shown in Figure 5.9, the origin is defined as the focus and a line corresponding to ![]() serves as the directrix. Recall the relations between the Cartesian and polar coordinates:
serves as the directrix. Recall the relations between the Cartesian and polar coordinates: ![]() . The point P will trace out the conic section, moving in such a way that the ratio of its distance to the focus r to its distance to the directrix
. The point P will trace out the conic section, moving in such a way that the ratio of its distance to the focus r to its distance to the directrix ![]() is a constant. This ratio is called the eccentricity, e (not to be confused with Euler’s
is a constant. This ratio is called the eccentricity, e (not to be confused with Euler’s ![]() ):
):
![]() (5.27)
(5.27)
The polar equation for a conic section is then found by solving for r:
![]() (5.28)
(5.28)
where the product ed is most conveniently replaced by a single constant p. The equation for a circle around the origin is simply ![]() . Thus a circle has
. Thus a circle has ![]() (think of
(think of ![]() ). Eccentricity can, in fact, be thought of as a measure of how much a conic section deviates from being circular. For
). Eccentricity can, in fact, be thought of as a measure of how much a conic section deviates from being circular. For ![]() , Eq. (5.28) represents an ellipse, for
, Eq. (5.28) represents an ellipse, for ![]() , a parabola and for
, a parabola and for ![]() , a hyperbola. Conic sections corresponding to several values of e are shown in Figure 5.10. As
, a hyperbola. Conic sections corresponding to several values of e are shown in Figure 5.10. As ![]() , the curve degenerates into a straight line. Newton showed that, under the inverse-square attraction of gravitational forces, the motion of a celestial object follows the trajectory of a conic section. The stable orbits of the planets around the Sun are ellipses, as found by Kepler’s many years of observation of planetary motions. A parabolic or hyperbolic trajectory would represent a single pass through the Solar System, possibly that of a comet. The better-known comets have large elliptical orbits with eccentricities close to 1 and thus have long intervals between appearances. Halley’s comet, for example, has
, the curve degenerates into a straight line. Newton showed that, under the inverse-square attraction of gravitational forces, the motion of a celestial object follows the trajectory of a conic section. The stable orbits of the planets around the Sun are ellipses, as found by Kepler’s many years of observation of planetary motions. A parabolic or hyperbolic trajectory would represent a single pass through the Solar System, possibly that of a comet. The better-known comets have large elliptical orbits with eccentricities close to 1 and thus have long intervals between appearances. Halley’s comet, for example, has ![]() and a period of 76 years.
and a period of 76 years.
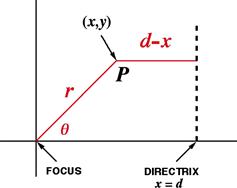
Figure 5.9 Coordinates used to represent conic sections. The point ![]() traces out a conic section as
traces out a conic section as ![]() is varied, keeping a constant value of the eccentricity.
is varied, keeping a constant value of the eccentricity.
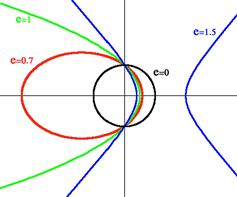
Figure 5.10 Polar plots of the conic sections, ![]() , showing circle (e = 0), ellipse (e = 0.7), parabola (e = 1), and hyperbola (e = 1.5).
, showing circle (e = 0), ellipse (e = 0.7), parabola (e = 1), and hyperbola (e = 1.5).
Ellipses and hyperbolas clearly have two distinct foci. The same ellipse or hyperbola can be constructed using its other focus and a corresponding directrix. In terms of their semimajor and semiminor axes, the eccentricities of ellipses and hyperbolas are given by
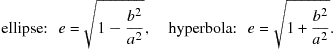 (5.29)
(5.29)
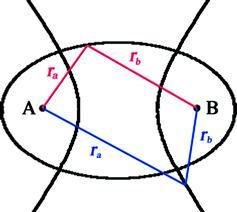
Another way of constructing ellipses and hyperbolas makes use of their two foci, labeled A and B. An ellipse is the locus of points the sum of whose distances to the two foci, ![]() , has a constant value. Different values of the sum generate a family of ellipses. Analogously, a hyperbola is the locus of points such that the difference
, has a constant value. Different values of the sum generate a family of ellipses. Analogously, a hyperbola is the locus of points such that the difference![]() is constant. The two families of confocal ellipses and hyperbolas are mutually orthogonal—that is, every intersection between an ellipse and a hyperbola meets at a
is constant. The two families of confocal ellipses and hyperbolas are mutually orthogonal—that is, every intersection between an ellipse and a hyperbola meets at a ![]() angle. This is shown in Figure 5.11.
angle. This is shown in Figure 5.11.