Trigonometry
4.1 What Use is Trigonometry?
Trigonometry, as its Greek and Latin roots suggest, is primarily the study of triangles. As we will see, circles also play a very prominent role. Trigonometric functions are, in fact, sometimes designated as circular functions. Figure 4.1 suggests how a clever caveman might determine the height y of a cliff by measuring the distance x to its base and the angle ![]() that he has to look upward. This could be done by making a scale drawing but, more elegantly, using trigonometry, the height y is equal to
that he has to look upward. This could be done by making a scale drawing but, more elegantly, using trigonometry, the height y is equal to ![]() .
.
4.2 Geometry of Triangles
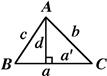
In this section we review some useful elementary results for triangles, most of them dating back to Euclid’s Elements. Figure 4.2 shows the essential elements of a triangle: the three sides, a, b, and c, the angles opposite them, A, B, and C, and the altitude h, perpendicular to the base b. There are also analogous altitudes perpendicular to a and c, not shown.
A signature feature of Euclidean space is that the angles of a triangle add up to exactly ![]() :
:
![]() (4.1)
(4.1)
(By contrast, in spherical geometry, the sum of the angles is greater than ![]() , while in hyperbolic geometry, it is less than
, while in hyperbolic geometry, it is less than ![]() .)
.)
The sides of a triangle always fulfill the triangle inequalities:
![]() (4.2)
(4.2)
Triangles can be classified according to the number of equal sides and angles, as shown on the top row of Figure 4.3. An equilateral triangle has three equal sides and three equal angles: a = b = c and A = B = C. An isosceles triangle has two equal sides and two equal angles, for example: ![]() and
and ![]() . Finally, a scalene triangle has three unequal sides and angles:
. Finally, a scalene triangle has three unequal sides and angles: ![]() and
and ![]() . A right triangle has one angle equal to
. A right triangle has one angle equal to ![]() . An acute triangle has all three of its angles less than
. An acute triangle has all three of its angles less than ![]() , while an obtuse triangle has one angle greater than
, while an obtuse triangle has one angle greater than ![]() . The last three categories are illustrated in the bottom row of Figure 4.3.
. The last three categories are illustrated in the bottom row of Figure 4.3.
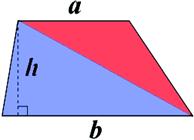
The area of a triangle is equal to ![]() . In terms of the variables shown in Figure 4.4,
. In terms of the variables shown in Figure 4.4,
![]() (4.3)
(4.3)
Another expression, known as Heron’s (or Hero’s) formula, computes the area in terms of its sides a, b, and c:
![]() (4.4)
(4.4)
where s = (a + b + c)/2, the semiperimeter of the triangle.
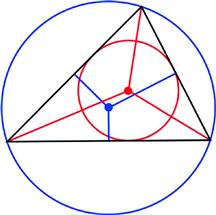
The bisectors of the three angle of a triangle intersect at a point known as the incenter, shown as a red1 point in Figure 4.4. It is the center of the circle inscribed within the triangle, known as its incircle, also colored in red. Similarly, the perpendicular bisectors of the three sides meet at another point, called the circumcenter, which is the center of the circumcircle, which circumscribes the triangle. These latter features are shown in blue. Only for an equilateral triangle do the incenter and circumcenter coincide. The three altitudes of a triangle also meet at a point, which corresponds to the centroid (or center of gravity).
4.3 The Pythagorean Theorem
For a right triangle with sides a and b and hypotenuse c
![]() (4.5)
(4.5)
A pictorial proof of the theorem was given in Section 1.3. Albert Einstein, as a schoolboy, supposedly worked out his own proof of Pythagoras’ theorem. His line of reasoning follows, although we may have changed the names of the variables he used. Figure 4.5 shows a right triangle cut by a perpendicular dropped to the hypotenuse from the opposite vertex. This produces three similar triangles since they all have the same angles ![]() , and 90°. Each length a, b, and c represents the hypotenuse of one of the triangles. Since the area of each similar triangle is proportional to the square of its corresponding hypotenuse, we can write
, and 90°. Each length a, b, and c represents the hypotenuse of one of the triangles. Since the area of each similar triangle is proportional to the square of its corresponding hypotenuse, we can write
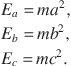 (4.6)
(4.6)
The variables E might stand for area or extent (Erstreckung in German), while m is a proportionality constant (maybe mengenproportional). Since ![]() , the ms cancel out and the result is Pythagoras’ theorem (4.5).
, the ms cancel out and the result is Pythagoras’ theorem (4.5).
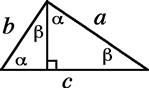
Figure 4.5 Einstein’s proof of Pythagoras’ theorem. The proof does assume, perhaps prematurely, that the angles of a triangle add up to 180°.
The preceding story is perhaps an alternative interpretation of the famous Einstein cartoon reproduced in Figure 4.6.
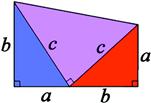
Surprisingly, an alternative proof of the Pythagorean theorem was published by James A. Garfield, the 20th president of the United States. He is speculated to have been the most mathematically knowledgable US president. As shown in Figure 4.7, three right triangles are arranged to form a trapezoid (turned sideways from its usual orientation). The area of the trapezoid is equal to (a + b)(a + b)/2. The areas of the blue,1 red, and purple triangles are, respectively, ab/2, ba/2, and ![]() . Equating the two expressions gives
. Equating the two expressions gives
![]()
which reduces to ![]() , giving Pythagoras’ theorem for both the red and blue triangles.
, giving Pythagoras’ theorem for both the red and blue triangles.
The converse of Pythagoras’ theorem is also valid. If three lengths a, b, and c satisfy Eq. (4.5), then they must form a right triangle with c as the hypotenuse. This provides a handy way for carpenters to construct a right angle: just mark off the lengths 3, 4, and 5 in., then the angle between the first two is equal to ![]() . There are, in fact, an infinite number of integer triples which satisfy
. There are, in fact, an infinite number of integer triples which satisfy ![]() , beginning with {3, 4, 5}, {5, 12, 13}, {8, 15, 17}.
, beginning with {3, 4, 5}, {5, 12, 13}, {8, 15, 17}.
Analogous relations do not exist for powers of integers greater than 2. What has long been called “Fermat’s last theorem” states that
![]() (4.7)
(4.7)
has no nonzero integer solutions x, y, and z when ![]() . This is the best known instance of a Diophantine equation, which involves only integers. Fermat wrote in his notes around 1630, “I have discovered a truly remarkable proof which this margin is too small to contain.” This turned out to have been a mischievous tease that took over three centuries to unravel. Some of the world’s most famous mathematicians have since struggled with the problem. These efforts were not entirely wasted since they stimulated significant advances in several mathematical fields including analytic number theory and algebraic geometry. Fermat’s conjecture, as it should have been called, was finally proven in 1993–1995 by the British mathematician Andrew Wiles, working at Princeton University. What we should now call the Fermat-Wiles theorem, took some 200 journal pages to present. (This whole book, let alone the margin, is too small to contain the proof!)
. This is the best known instance of a Diophantine equation, which involves only integers. Fermat wrote in his notes around 1630, “I have discovered a truly remarkable proof which this margin is too small to contain.” This turned out to have been a mischievous tease that took over three centuries to unravel. Some of the world’s most famous mathematicians have since struggled with the problem. These efforts were not entirely wasted since they stimulated significant advances in several mathematical fields including analytic number theory and algebraic geometry. Fermat’s conjecture, as it should have been called, was finally proven in 1993–1995 by the British mathematician Andrew Wiles, working at Princeton University. What we should now call the Fermat-Wiles theorem, took some 200 journal pages to present. (This whole book, let alone the margin, is too small to contain the proof!)
4.4  in the Sky
in the Sky
The Babylonians (ca. 2400 BC) observed that the annual track of the Sun across the sky took approximately 360 days. Consequently, they divided its near-circular path into ![]() , as a measure of each day’s progression. That is why we still count one spin around a circle as
, as a measure of each day’s progression. That is why we still count one spin around a circle as ![]() and a right angle as
and a right angle as ![]() . This way of measuring angles is not very fundamental from a mathematical point of view, however. Mathematicians prefer to measure distance around the circumference of a circle in units of the radius, defined as 1 radian (rad). The Greeks designated the ratio of the circumference to the diameter, which is twice the radius, as
. This way of measuring angles is not very fundamental from a mathematical point of view, however. Mathematicians prefer to measure distance around the circumference of a circle in units of the radius, defined as 1 radian (rad). The Greeks designated the ratio of the circumference to the diameter, which is twice the radius, as ![]() . Thus
. Thus ![]() corresponds to
corresponds to ![]() radians. A semicircle,
radians. A semicircle, ![]() , is
, is ![]() radians, while a right angle,
radians, while a right angle, ![]() , is
, is ![]() radians. One radian equals approximately
radians. One radian equals approximately ![]() . You should be very careful to set your scientific calculators to “radians” when doing most trigonometric manipulations.
. You should be very careful to set your scientific calculators to “radians” when doing most trigonometric manipulations.
It has been known since antiquity that ![]() is approximately equal to 3. The Old Testament (II Chronicles 4:2) contains a passage describing the building of Solomon’s temple: “Also he made a molten sea of ten cubits from brim to brim, round in compass … and a line of thirty cubits did compass it round about.” This appears to imply that the ancient Hebrews used a value of
is approximately equal to 3. The Old Testament (II Chronicles 4:2) contains a passage describing the building of Solomon’s temple: “Also he made a molten sea of ten cubits from brim to brim, round in compass … and a line of thirty cubits did compass it round about.” This appears to imply that the ancient Hebrews used a value of ![]() . Two regular hexagons inscribed in and circumscribed around a circle (Figure 4.8) establish that the value of
. Two regular hexagons inscribed in and circumscribed around a circle (Figure 4.8) establish that the value of ![]() lies in the range
lies in the range ![]() .
.
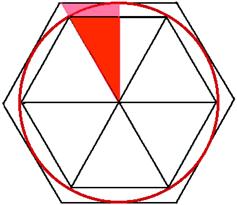
Figure 4.8 The perimeter of the inscribed hexagon equals three times the diameter of the circle. Noting that the two pink triangles are similar, you can show that the perimeter of the circumscribed hexagon equals ![]() times the diameter. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
times the diameter. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
As a practical matter, the value of ![]() could be determined with a tape measure wound around a circular object. In carpentry and sewing, an adequate approximation is
could be determined with a tape measure wound around a circular object. In carpentry and sewing, an adequate approximation is ![]() . (In 1897, the Indiana House of Representatives decreed by a vote of 67–0 that
. (In 1897, the Indiana House of Representatives decreed by a vote of 67–0 that ![]() should be simplified to exactly 3.2. The measure however never reached the floor of the Indiana Senate.) Accurate computed values of
should be simplified to exactly 3.2. The measure however never reached the floor of the Indiana Senate.) Accurate computed values of ![]() are usually obtained from power series for inverse trigonometric functions. Since we haven’t introduced these yet, let us demonstrate a method for computing
are usually obtained from power series for inverse trigonometric functions. Since we haven’t introduced these yet, let us demonstrate a method for computing ![]() which uses only the Pythagorean theorem. It was originally the idea of Archimedes to construct n-sided regular polygons inscribed in a unit circle (radius = 1). Then, as n becomes larger and larger, the perimeter of the polygon approaches the circumference of the circle. Denote the side of one such polygon by
which uses only the Pythagorean theorem. It was originally the idea of Archimedes to construct n-sided regular polygons inscribed in a unit circle (radius = 1). Then, as n becomes larger and larger, the perimeter of the polygon approaches the circumference of the circle. Denote the side of one such polygon by ![]() . Then the perimeter equals
. Then the perimeter equals ![]() and an estimate for
and an estimate for ![]() , which we can call
, which we can call ![]() , is equal to
, is equal to ![]() . For example, the hexagon in Figure 4.8 gives
. For example, the hexagon in Figure 4.8 gives ![]() .
.
Figure 4.9 shows how to calculate the length of a side ![]() of a regular polygon with 2n sides from
of a regular polygon with 2n sides from ![]() , that of a polygon with n sides. Both polygons are inscribed in the unit circle with OA = OB = OC = 1.
, that of a polygon with n sides. Both polygons are inscribed in the unit circle with OA = OB = OC = 1. ![]() is a side of the n-gon, while
is a side of the n-gon, while ![]() are sides of the 2n-gon. The segment
are sides of the 2n-gon. The segment ![]() since the radius OC drawn to the new vertex C is a perpendicular bisector of side AB. Using the Pythagorean theorem, we can find two alternative expressions for the segment CD:
since the radius OC drawn to the new vertex C is a perpendicular bisector of side AB. Using the Pythagorean theorem, we can find two alternative expressions for the segment CD:
![]()
and
![]()
 (4.8)
(4.8)
which relates the values of ![]() and
and ![]() :
:
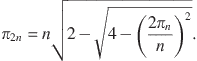 (4.9)
(4.9)
Such an iterative evaluation was first carried out by Viète in 1593, starting with an inscribed square with ![]() . This produced, for the first time, an actual formula for
. This produced, for the first time, an actual formula for ![]() , expressed as an infinite sequence of nested square roots:
, expressed as an infinite sequence of nested square roots:
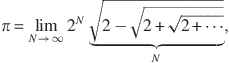 (4.10)
(4.10)
where the underbrace N indicates the total number of square-root signs. (For compactness, n − 1 has been replaced by N.) For a ![]() -sided polygon (corresponding to N = 9) this procedure gives a value accurate to six significant figures:
-sided polygon (corresponding to N = 9) this procedure gives a value accurate to six significant figures:
![]() (4.11)
(4.11)
A rational approximation giving the same accuracy is ![]() .
.
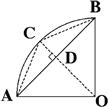
Figure 4.9 Detail of construction of an inscribed regular polygon with double the number of sides. OA = OB = OC = 1, the radius of a unit circle. AB represents a side ![]() , while AC and CB are sides
, while AC and CB are sides ![]() .
.
It has long been a popular macho sport to calculate ![]() to more and more decimal places, using methods which converge much faster than the formulas we consider. The current (2012) record is held by a Japanese supercomputer, which gives
to more and more decimal places, using methods which converge much faster than the formulas we consider. The current (2012) record is held by a Japanese supercomputer, which gives ![]() to over 10 trillion digits. While such exercises might have little or no practical value, they serve as tests for increasingly powerful supercomputers. Sequences of digits from
to over 10 trillion digits. While such exercises might have little or no practical value, they serve as tests for increasingly powerful supercomputers. Sequences of digits from ![]() can be used to generate random numbers (technically pseudorandom) for use in Monte Carlo computations and other simulations requiring random input.
can be used to generate random numbers (technically pseudorandom) for use in Monte Carlo computations and other simulations requiring random input.
Those of you taking certain physics or chemistry courses might appreciate a cute mnemonic giving ![]() to 15 digits (3.141 592 653 589 79). Adapted from James Jeans, it runs “Now I need a drink, alcoholic of course, after the heavy sessions involving quantum mechanics.”
to 15 digits (3.141 592 653 589 79). Adapted from James Jeans, it runs “Now I need a drink, alcoholic of course, after the heavy sessions involving quantum mechanics.”
4.5 Sine and Cosine
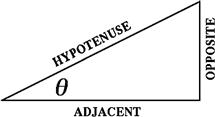
Let us focus on one angle of a right triangle, designated by ![]() in Figure 4.10. We designate the two perpendicular sides as being opposite and adjacent to the angle
in Figure 4.10. We designate the two perpendicular sides as being opposite and adjacent to the angle ![]() . The sine and cosine are then defined as the ratios
. The sine and cosine are then defined as the ratios
![]() (4.12)
(4.12)
Later we will also deal with the tangent:
![]() (4.13)
(4.13)
A popular mnemonic for remembering which ratios go with which trigonometric functions is “SOHCAHTOA,” which might be the name of your make-believe Native American guide through the trigonometric forest.
It is extremely instructive to represent the sine and cosine on the unit circle, shown in Figure 4.11, in which the hypotenuse corresponds to a radius equal to 1 unit. The circle is conveniently divided into four quadrants, I–IV, each with ![]() varying over an interval of
varying over an interval of ![]() radians from the range 0 to
radians from the range 0 to ![]() . The lengths representing
. The lengths representing ![]() are vertical lines on the unit circle while those representing
are vertical lines on the unit circle while those representing ![]() are horizontal. The cosine is closer to the angle—you might remember this by associating cosine with cozy up and sine with stand off. The functions shown in green have positive values, while those shown in red have negative values. Thus
are horizontal. The cosine is closer to the angle—you might remember this by associating cosine with cozy up and sine with stand off. The functions shown in green have positive values, while those shown in red have negative values. Thus ![]() is positive in quadrants I and II, negative in quadrants III and IV, while
is positive in quadrants I and II, negative in quadrants III and IV, while ![]() is positive in quadrants I and IV, negative in quadrants II and III. It should also be clear from the diagram that, for real values of
is positive in quadrants I and IV, negative in quadrants II and III. It should also be clear from the diagram that, for real values of ![]() ,
, ![]() and
and ![]() can have values only in the range [−1, 1].
can have values only in the range [−1, 1].

Figure 4.11 Unit circle showing ![]() and
and ![]() in each quadrant. Positive values of the functions are shown in green, negative, in red. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
in each quadrant. Positive values of the functions are shown in green, negative, in red. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Note that any angle ![]() less than 0 or greater than
less than 0 or greater than ![]() is indistinguishable on the unit circle from one in the range 0 to
is indistinguishable on the unit circle from one in the range 0 to ![]() . The trigonometric functions are periodic in
. The trigonometric functions are periodic in ![]() and have the same values for any
and have the same values for any ![]() with integer n. The functions
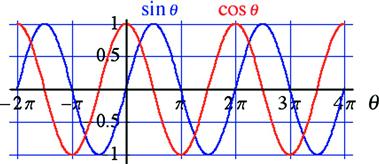
with integer n. The functions ![]() and
and ![]() are plotted in Figure 4.12. These are commonly designated as sinusoidal functions or “sine waves.” Note that sine and cosine have the same shape, being just displaced from one another by
are plotted in Figure 4.12. These are commonly designated as sinusoidal functions or “sine waves.” Note that sine and cosine have the same shape, being just displaced from one another by ![]() . It can be seen that
. It can be seen that
![]() (4.14)
(4.14)
The angle ![]() is known as the complement of
is known as the complement of ![]() . Equation (4.14) is equivalent to a catchy-sounding rule: The function of an angle is equal to the corresponding cofunction of its complement. Note that cosine and sine are even and odd functions, respectively:
. Equation (4.14) is equivalent to a catchy-sounding rule: The function of an angle is equal to the corresponding cofunction of its complement. Note that cosine and sine are even and odd functions, respectively:
![]() (4.15)
(4.15)
Whenever one of these functions goes through zero, the other has a local maximum at ![]() or minimum at
or minimum at ![]() . This follows easily from differential calculus, as we will show later. Pythagoras’ theorem translates to the fundamental trigonometric identity:
. This follows easily from differential calculus, as we will show later. Pythagoras’ theorem translates to the fundamental trigonometric identity:
![]() (4.16)
(4.16)
Note that ![]() and
and ![]() are conventionally written
are conventionally written ![]() and
and ![]() . They are not to be confused, of course, with
. They are not to be confused, of course, with ![]() and
and ![]() .
.
To compound the notational confusion, ![]() and
and ![]() are used to designate inverse trigonometric functions, also written
are used to designate inverse trigonometric functions, also written ![]() and
and ![]() , respectively. These inverse functions are related by the following correspondences:
, respectively. These inverse functions are related by the following correspondences:
![]() (4.17)
(4.17)
![]() (4.18)
(4.18)
Since ![]() and
and ![]() are periodic functions, their inverse functions must be multivalued. For example, if
are periodic functions, their inverse functions must be multivalued. For example, if ![]() , it must likewise equal
, it must likewise equal ![]() , for
, for ![]() The principal value of
The principal value of ![]() , sometimes designated
, sometimes designated ![]() , is limited to the range
, is limited to the range ![]() , corresponding to
, corresponding to ![]() . Analogously, the principal value of
. Analogously, the principal value of ![]() , likewise designated
, likewise designated ![]() , lies in the range
, lies in the range ![]() . Graphs of
. Graphs of ![]() and
and ![]() can be obtained by turning Figure 4.12 counterclockwise by
can be obtained by turning Figure 4.12 counterclockwise by ![]() and then reflecting in the
and then reflecting in the ![]() -axis.
-axis.
Several values of sine and cosine occur so frequently that they are worth remembering. Almost too obvious to mention,
![]() (4.19)
(4.19)
When ![]() or
or ![]() , so that (4.16) implies
, so that (4.16) implies
![]() (4.20)
(4.20)
which is a factor well known in electrical engineering, in connection with the rms voltage and current of an AC circuit. An equilateral triangle with side 1, cut in half, gives a “30–60–90 triangle.” Since ![]() and
and ![]() , you can show using Pythagoras’ theorem that
, you can show using Pythagoras’ theorem that
![]() (4.21)
(4.21)
As ![]() , in the first quadrant of Figure 4.11, the length of the line representing
, in the first quadrant of Figure 4.11, the length of the line representing ![]() approaches the magnitude of the arc of angle
approaches the magnitude of the arc of angle ![]() —remember this is measured in radians. This implies a very useful approximation
—remember this is measured in radians. This implies a very useful approximation
![]() (4.22)
(4.22)
For a triangle of arbitrary shape, not limited to a right triangle, two important relations connecting the lengths a,b,c of the three sides with the magnitudes of their opposite angles ![]() can be derived. In Figure 4.13, a perpendicular is drawn from any side to its opposite angle, say from angle A to side a. Call this length d. It can be seen that
can be derived. In Figure 4.13, a perpendicular is drawn from any side to its opposite angle, say from angle A to side a. Call this length d. It can be seen that ![]() and also that
and also that ![]() . Analogous relations can be found involving a and A. The result is the law of sines:
. Analogous relations can be found involving a and A. The result is the law of sines:
![]() (4.23)
(4.23)
The little triangle to the right of line d has a base given by ![]() . Therefore the base of the little triangle to the left of d equals
. Therefore the base of the little triangle to the left of d equals ![]() . Using
. Using ![]() again, and applying Pythagoras’ theorem to the left-hand right triangle, we find
again, and applying Pythagoras’ theorem to the left-hand right triangle, we find
![]() (4.24)
(4.24)
The identity (4.16) simplifies the equation, leading to the law of cosines:
![]() (4.25)
(4.25)
By et cyc we mean that the result holds for all cyclic permutations ![]() . The law of cosines is clearly a generalization of Pythagoras’ theorem, valid for all triangles. It reduces to Pythagoras’ theorem when
. The law of cosines is clearly a generalization of Pythagoras’ theorem, valid for all triangles. It reduces to Pythagoras’ theorem when ![]() , so that
, so that ![]() .
.
4.6 Tangent and Secant
Additional subsidiary trigonometric functions can be defined in terms of sine and cosine. Consider just the first quadrant of the unit circle, redrawn in Figure 4.14. Let the horizontal line containing ![]() , as well as the hypotenuse, be extended until they intersect the circle. A vertical tangent line of length
, as well as the hypotenuse, be extended until they intersect the circle. A vertical tangent line of length ![]() can then be used to construct a larger right triangle. The new hypotenuse is called a secant and labeled
can then be used to construct a larger right triangle. The new hypotenuse is called a secant and labeled ![]() . Clearly the new triangle is similar to the original one, with its horizontal side being equal to 1, the unit-circle radius. Therefore
. Clearly the new triangle is similar to the original one, with its horizontal side being equal to 1, the unit-circle radius. Therefore
![]() (4.26)
(4.26)
Also by Pythagoras’ theorem,
![]() (4.27)
(4.27)
so that
 (4.28)
(4.28)
making use of Eq. (4.16). The tangent and secant are plotted in Figure 4.14. Since ![]() , we find
, we find ![]() , since the secant is the reciprocal of the cosine. Note that
, since the secant is the reciprocal of the cosine. Note that ![]() is periodic in
is periodic in ![]() , rather than
, rather than ![]() , and can take any value from
, and can take any value from ![]() to
to ![]() .
.

Figure 4.14 Graphs of tangent (red) and secant (blue). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
It is also possible to define cofunctions in analogy with (4.14), namely the cotangent and cosecant:
![]() (4.29)
(4.29)
This completes the list of standard trigonometric functions. In terms of sine and cosine:
![]() (4.30)
(4.30)
4.7 Trigonometry in the Complex Plane
In Figure 3.4, a complex quantity z was represented by its Cartesian coordinates x and y. Alternatively, a point in the x-, y-plane can be represented in polar coordinates, usually designated r and ![]() . Conventionally, r is the distance from the origin, while
. Conventionally, r is the distance from the origin, while ![]() is the angle that the vector
is the angle that the vector ![]() makes with the positive x-axis. The coordinates in the two systems are related by
makes with the positive x-axis. The coordinates in the two systems are related by
![]() (4.31)
(4.31)
A complex quantity ![]() expressed in polar coordinates is called a phasor. In place of r we have the modulus
expressed in polar coordinates is called a phasor. In place of r we have the modulus ![]() . The angle
. The angle ![]() , now called the phase or the argument, plays the same role as in Figure 4.11, with the unit circle generalized to a circle of radius
, now called the phase or the argument, plays the same role as in Figure 4.11, with the unit circle generalized to a circle of radius ![]() . Thus the phasor representation of a complex number takes the form
. Thus the phasor representation of a complex number takes the form
![]() (4.32)
(4.32)
A convenient abbreviation which we will employ for a short while is
![]() (4.33)
(4.33)
In Figure 3.5 it was shown how multiplication of a complex numbers by i could be represented by a 90° rotation in the complex plane. Note that i can be represented by the phasor
![]() (4.34)
(4.34)
while
![]() (4.35)
(4.35)
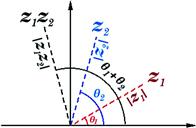
We can generalize that the product of two arbitrary phasors, say ![]() and
and ![]() , is given by
, is given by
![]() (4.36)
(4.36)
obtained by multiplying the two moduli while adding the two phases, as shown in Figure 4.15.
Consider the multiplication of the two phasors ![]() and
and ![]() to give
to give ![]() . Written out in full, this gives
. Written out in full, this gives
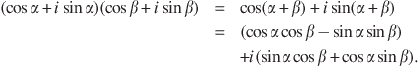 (4.37)
(4.37)
Equating the separate real and imaginary parts of each side of the equation, we obtain the two fundamental angle-sum trigonometric identities:
![]() (4.38)
(4.38)
and
![]() (4.39)
(4.39)
From (4.38) and (4.39) we can derive the corresponding relation for ![]() :
:
![]() (4.40)
(4.40)
Dividing both numerator and denominator by ![]() and introducing
and introducing ![]() and
and ![]() , we obtain
, we obtain
![]() (4.41)
(4.41)
4.8 de Moivre’s Theorem
Equation (4.36) can be applied to the square of a phasor ![]() , of modulus 1, giving
, of modulus 1, giving ![]() . This can, in fact, be extended to the nth power of z giving
. This can, in fact, be extended to the nth power of z giving ![]() . This is a famous result known as de Moivre’s theorem, which we write out in full:
. This is a famous result known as de Moivre’s theorem, which we write out in full:
![]() (4.46)
(4.46)
Beginning with de Moivre’s theorem, useful identities involving sines and cosines can be derived. For example, setting ![]() ,
,
![]() (4.47)
(4.47)
Equating the real and imaginary parts on each side of the equation, we obtain the two identities
![]() (4.48)
(4.48)
and
![]() (4.49)
(4.49)
Analogously, with ![]() in (4.46) we can derive:
in (4.46) we can derive:
![]() (4.50)
(4.50)
de Moivre’s theorem can be used to determine the nth roots of unity, namely the n complex roots of the equation
![]() (4.51)
(4.51)
Setting ![]() with
with ![]() in Eq. (4.46), we find
in Eq. (4.46), we find
![]() (4.52)
(4.52)
But, for integer k, ![]() while
while ![]() . Thus the nth roots of unity are given by
. Thus the nth roots of unity are given by
![]() (4.53)
(4.53)
When the nth roots of unity are plotted on the complex plane, they form a regular polygon with n sides, with one vertex at 1. For example, for ![]() , for
, for ![]() , for
, for ![]() . The sum of the roots for each n adds to zero.
. The sum of the roots for each n adds to zero.
4.9 Euler’s Theorem
de Moivre’s theorem, Eq. (4.46), remains valid even for noninteger values of n. Replacing n by 1/m we can write
![]() (4.54)
(4.54)
or
![]() (4.55)
(4.55)
In the limit as ![]() . At the same time
. At the same time ![]() , as noted in Eq. (4.22). We can therefore write
, as noted in Eq. (4.22). We can therefore write
![]() (4.56)
(4.56)
The limit defines the exponential function, as shown in Eq. (3.103). We arrive thereby at a truly amazing relationship:
![]() (4.57)
(4.57)
known as Euler’s theorem. (This is actually one of at least 13 theorems, formulas, and equations which goes by this name. Euler was very prolific!)
A very notable special case of Eq. (4.57), for ![]() , is
, is
![]() (4.58)
(4.58)
an unexpectedly simple connection between the three mathematical entities, e, i, and ![]() , each of which took us an entire section to introduce. This result can also be rearranged to
, each of which took us an entire section to introduce. This result can also be rearranged to
![]() (4.59)
(4.59)
sometimes called Euler’s identity. Several authors regard this as the most beautiful equation in all of mathematics. It contains what are perhaps the five most fundamental mathematical quantities: in addition to e, i, and ![]() , the additive identity 0 and the multiplicative identity 1. It also makes use of the concepts of addition, multiplication, exponentiation, and equality. Because it represents so much in one small package, the formula has been imprinted on the side of some far-ranging NASA spacecraft to demonstrate the existence of intelligent life on Earth. It is to be hoped, of course, that extraterrestrials would be able to figure out that those symbols represent a mathematical equation and not a threat of interstellar war.
, the additive identity 0 and the multiplicative identity 1. It also makes use of the concepts of addition, multiplication, exponentiation, and equality. Because it represents so much in one small package, the formula has been imprinted on the side of some far-ranging NASA spacecraft to demonstrate the existence of intelligent life on Earth. It is to be hoped, of course, that extraterrestrials would be able to figure out that those symbols represent a mathematical equation and not a threat of interstellar war.
Solving (4.57) and its complex-conjugate equation ![]() for
for ![]() and
and ![]() , we can represent these trigonometric functions in terms of complex exponentials:
, we can represent these trigonometric functions in terms of complex exponentials:
![]() (4.60)
(4.60)
and
![]() (4.61)
(4.61)
The power-series expansion for the exponential function given in Eq. (3.104) is, as we have noted, valid even for imaginary values of the exponent. Replacing x by ![]() we obtain
we obtain
![]() (4.62)
(4.62)
Successive powers of i are given sequentially by
![]() (4.63)
(4.63)
Collecting the real and imaginary parts of (4.62) and comparing with the corresponding terms in Euler’s theorem (4.57) result in power-series expansions for the sine and cosine:
![]() (4.64)
(4.64)
and
![]() (4.65)
(4.65)
4.10 Hyperbolic Functions
Hyperbolic functions are “copy-cats” of the corresponding trigonometric functions, in which the complex exponentials in Eqs. (4.60) and (4.61) are replaced by real exponential functions. The hyperbolic sine and hyperbolic cosine are defined, respectively, by
![]() (4.66)
(4.66)
Actually, hyperbolic functions result when sine and cosine are given imaginary arguments. Thus
![]() (4.67)
(4.67)
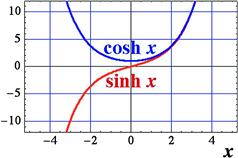
The hyperbolic sine and cosine functions are plotted in Figure 4.16. Unlike their trigonometric analogs, they are not periodic functions and both have the domains ![]() . Note that as
. Note that as ![]() both
both ![]() and
and ![]() approach
approach ![]() . The hyperbolic cosine represents the shape of a flexible wire or chain hanging from two fixed points, called a catenary (from the Latin catena = chain).
. The hyperbolic cosine represents the shape of a flexible wire or chain hanging from two fixed points, called a catenary (from the Latin catena = chain).
By solving Eq. (4.66) for ![]() and
and ![]() , we obtain the analog of Euler’s theorem for hyperbolic functions:
, we obtain the analog of Euler’s theorem for hyperbolic functions:
![]() (4.68)
(4.68)
The identity ![]() then leads to the hyperbolic analog of (4.16):
then leads to the hyperbolic analog of (4.16):
![]() (4.69)
(4.69)
The trigonometric sine and cosine are called circular functions because of their geometrical representation using the unit circle ![]() . The hyperbolic functions can analogously be based on the geometry of the unit hyperbola
. The hyperbolic functions can analogously be based on the geometry of the unit hyperbola![]() . We will develop the properties of hyperbolas, and other conic sections, in more detail in the following chapter. It will suffice for now to show the analogy with circular functions. Figure 4.17 shows the first quadrant of the unit circle and the unit hyperbola, each with specific areas
. We will develop the properties of hyperbolas, and other conic sections, in more detail in the following chapter. It will suffice for now to show the analogy with circular functions. Figure 4.17 shows the first quadrant of the unit circle and the unit hyperbola, each with specific areas ![]() and
and ![]() , respectively, shown shaded. For the circle, the area is equal to the fraction
, respectively, shown shaded. For the circle, the area is equal to the fraction ![]() of
of ![]() , the area of the unit circle. Thus
, the area of the unit circle. Thus
![]() (4.70)
(4.70)
For the unit hyperbola, we will be able to compute the area ![]() later using calculus. It will suffice for now to define a variable
later using calculus. It will suffice for now to define a variable
![]() (4.71)
(4.71)
Analogous constructions in Figure 4.17 can then be used to represent the trigonometric functions ![]() and the hyperbolic functions
and the hyperbolic functions ![]() .
.

Figure 4.17 Geometric representation of circular and hyperbolic functions. The argument of each function equals twice the corresponding shaded area.
The series expansions for the hyperbolic functions are similar to (4.64) and (4.65), except that all terms have plus signs:
![]() (4.72)
(4.72)
and
![]() (4.73)
(4.73)