In the real world, jargon doesn’t look like a mouse-dog, or even a dog-mouse; it looks just like an ordinary word! Computer scientists (and really, all scientists) love inventing new words. We call these specialized words jargon or argot. Jargon can be good, because it saves time when you’re discussing things with your colleagues. It can also be bad, because it excludes nonexperts from the conversation.

When you’re just starting out with programming, all the jargon, argot, and weird new words can be intimidating, but don’t let that stop you from learning. Jargon can be silly, or powerful, or dangerous, depending on how you use it. But no matter what words you use, if you always obfuscate instead of explicate, no one will understand you!

The Traveling Salesman problem is a classic computer science question. Given a group of cities, your goal is to find the shortest Hamiltonian path, a route that lets you visit each city only once. If you have a large number of cities, it would take a very long time to calculate that path, even for a computer. So the Wandering Salesman might be on the road for quite a while!

Instead of calculating the exact answer, the salesman looks for a path through all the towns that’s close enough to being the shortest. A very interesting aspect of the Traveling Salesman problem is that humans are pretty good at solving small examples by hand. There is much discussion about what algorithm people use in their heads while solving it. See also Hugh Rustic (Chapter 8; Chapter 8: More Than One Way to Do It).

In Userland, the Upper Bounds are a mountain range, as tall as anything can be. The Lower Bounds are valleys as low and deep as anything can be. Nothing can be higher and nothing can be lower than these two bounds.

In the real world, finding an upper and lower limit on a problem can simplify things a lot. Say you have to guess a person’s age. It’s unlikely that anyone is over 150 years old, and no one can be younger than 0 years old. So, 150 is the upper limit and 0 is the lower limit. You can narrow down the bounds even more with simple questions. Is the person still in school? If so, then he is probably younger than 30. Can the person drive a car? If so, then he is probably older than 15.

You sometimes see signs that mark a point on a highway, like “Mile 14.” Now, if there is a Mile 14, then there must be a Mile 13, and a Mile 12, and so on. Everything has to start somewhere, and Zero is where it starts. Possibly the most famous Mile Zero is in Key West, Florida. It’s at the beginning of US Route 1, which goes all the way to Canada. If you look carefully and are very lucky, you might find a Mile Zero near where you live.

When you say “A or B,” you mean that you want one of those two things, or maybe both! If you say “A xor B,” then you mean you want one and only one of those two things, not both. That’s why Xor keeps turning rainbow colors: Xor and the thing he’s currently resting on can’t be blue at the same time. If he’s sitting on a blue sign, then he must turn any color that isn’t blue! Not a great form of camouflage, is it?

Steganography is the art of hiding information inside other information, and it’s used in both the digital and the physical world. For example, you might hide a secret message by writing it with invisible ink on a piece of paper. With a computer program, you could even hide words inside sounds and pictures. A Steganosaurus is, therefore, a dinosaur that can hide itself anywhere.

Eponymous Bach is a composer, but she works with ideas instead of music. Composing is the act of combining small ideas into bigger ones to solve a problem in steps. Almost every idea is composed of smaller ideas. For example, multiplying whole numbers isn’t anything special. You can think of it as adding a number to itself and repeating:

See also Decomposing (Chapter 17; Chapter 17: Chasing Elegants) and Relating (Chapter 17; Relating). Composing, decomposing, and relating are problem-solving methods that lie at the root of all math, logic, and computer science.

Don’t let any new idea escape without putting a name on it. A name is like a handle that makes the idea easier to use.

It’s better to put a name on Ideas than on Things, because Ideas last longer.

As an idea becomes more useful and famous, its name becomes shorter and lowercase. This law eventually affected Eponymous’s friend, Andy Ampère, and his discovery about electricity.

André-Marie Ampère discovered that when electricity flows through parallel wires, the wires will either attract or repel each other, causing the wires to bend. By measuring how much they bend, you can measure how much electricity is flowing. Ampère used this idea to lay the foundation for nearly everything we know about electricity, and we measure electrical current in amperes (or amps) in his honor. (See Bach’s Third Law of Eponymy for Eponymous’s theory on why we don’t call the unit an Ampère nearly as often.)

Programmers and mathematicians sometimes use a pair of ideas, called the solution space and the problem space, to describe finding an answer to a problem.

Say you need to move a heavy box so you can unpack it; anything related to moving the box is in your problem space. Try to imagine every single thing you could possibly do to try to move that box. You could walk forward, walk backward, stick out your tongue, sing a song, write an equation, use a lever, call for help, look for a forklift, or do literally anything else you can think of. Write down as many of these possibilities as you can fit on a piece of paper.

Out of that huge space of possibilities, imagine only the ones that have a good chance of moving the box. Circle those with a red pen. The circled ones are in the solution space. They make sense because they would accomplish your goal, and the rest don’t make sense. Now, look again at all of the circled possibilities and think about which one is best (fastest, cheapest, easiest, most reliable, and so on). Underline that one in green. That’s the most sensible answer out of all the ones that make sense.

The point of this exercise is to avoid a very human, very common error: we tend to grasp at the first solution we think of and forget to consider other possibilities. This is what Eponymous means when she tells Laurie that the Wandering Salesman’s solution isn’t sensible. See also Hugh Rustic (Chapter 8; Chapter 8: More Than One Way to Do It) and Five Whys (Chapter 14; Chapter 14: In the Abstract).

The Robins aren’t really evil—they’re just hungry. They cooperate in everything they do, taking turns and making sure the work is balanced among them. Sharing work is a great way to get things done faster, and computers can share work, too!

You can find the Round Robin method almost anywhere. Imagine a bus route that takes an hour to complete. If you put two buses on that route, a bus will arrive at each stop every 30 minutes. With three buses, you’d see a bus every 20 minutes, and four means you’d see one every 15 minutes. With five buses, you’d see one every 12 minutes, and so on. Just divide 60 (the number of minutes in an hour) by the number of buses to see how often a bus should come.

But you have to be careful to make sure the buses arrive at each stop at evenly spaced times. Five buses reaching one stop all at once wouldn’t be balanced. Also, if one bus breaks down and gets delayed, this could cause all the other buses to back up!

Recursion is a way to repeat the same process over and over until you find the answer you’re looking for. When you use recursion, you run though the process, and if the answer is the one you want, you stop. If it’s not, you take the answer you found, plug it into the same process, and run it again.

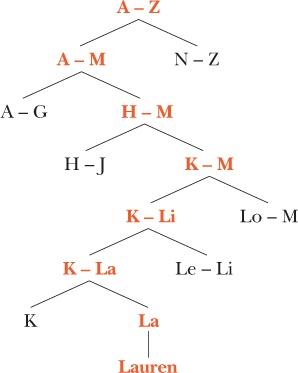
Let’s look at an example of recursion in action right here in Userland. Recall from Chapter 10 that Jane Hecate has a single, gigantic book of names. The name Lauren starts with L, so Jane should find it in the L section of her book, but that could take a while with so many pages. If Jane wants a faster way to look for Lauren, she can divide the book into two equal halves and see if L is in the first half or the second half.

Since L is in the first half, Jane can then divide the first half of the book in half, giving her two quarters of the book to search.

Lauren should be in the second quarter, so Jane can divide that quarter in half, giving her two eighths of the alphabet:

Jane can continue dividing the letter groups containing L in half until eventually she ends up with just the L section. (How many more times would Jane have to divide a set of letters in half to find L?) This way of searching for a particular piece of information is called a binary search.

See also The Garden of Forking Paths (Chapter 19; Chapter 19: Branching Out) and Chasing Your Tail (Achilles and the Tortoise).

These two characters were used by a philosopher named Zeno of Elea almost 2,500 years ago to talk about infinity. From Aristotle to Lewis Carroll to Marvin Minsky to Douglas Hofstadter, mathematics is full of stories about their adventures. It’s Tortoises all the way down.

Chasing your own tail is not always a waste of time! In computer science, there’s a type of recursion that sounds a bit like running around in circles, and it’s quite useful. In tail recursion, you perform a process, then perform the process again on the result, and repeat until you reach the final answer. For example, Jane Hecate’s binary search for the L section of her book might look something like this:

See also Recursion (Chapter 4: What the Tortoise Said to Laurie).

When people say there’s an infinite amount of something, they mean there’s no limit to how much of that thing exists. When Tortoise demonstrates how an infinite string can be less than two inches long, he shows that you can split that string into an infinite number of smaller pieces.

Infinity is big, bigger than you can imagine. But you can hold infinity in your mind simply by saying a few words. There are infinite odd numbers: 1, 3, 5, 7, and so on, up to forever. There are infinite even numbers, too: 0, 2, 4, 6, 8, and so on. No matter how hard you look, you will never find an odd number in the list of even numbers or an even number among the odd ones. That means there are at least two kinds of infinity: the even numbers and the odd numbers.

There are also infinite kinds of infinity. Think about all the numbers divisible by 3 and all the numbers not divisible by 3 (or 4, or 5). Now imagine all the numbers that no one else has thought of before. That’s another kind of infinity!

If you think about how you think, you might then start thinking about how you think about how you think, and then about how you think about how you think about how you think, and so on. This is a form of argument called infinite regress, and it can have no end. The first time you fall into this mental trap, it can be confusing or even scary. The trick is not to take it too seriously.

If you think this sounds related to recursion, you’re correct! It would be quite troubling to get stuck in a recursive process forever. In real computers, infinite recursion never actually happens because no computer can hold an infinite amount of information. When the computer runs out of room while working on something recursive, you never know what might happen. Laurie and Xor experienced this firsthand at Recursion Junction. See also Chasing Your Tail (Achilles and the Tortoise).

╞ is a logical symbol that points the way to a truth. It’s kind of like the equal sign (=), except that it shows how ideas are related instead of numbers. If all the ideas to the left of the semantic turnstile are true, then the idea on the right is also true.

Say you have two ideas: (A) “You have the password” and (B) “You may enter.” You can compose these ideas together to make a rule:

That is the rule that Ponens explained to Laurie at the gates of Symbol. (Placing two ideas on either side of that little arrow is another way to say, “IF A is true, THEN B is true.”)

But how do you know the rule is true? Maybe that’s not how you enter Symbol. So you have to show that both the rule (A → B), and the first idea, A, are true. In this case, we need to be sure that both the rule (“IF you have the password, THEN you may enter”) and the idea (“You have the password”) are true before we let anyone through the gate.

That’s what the semantic turnstile is for. We put the rule and the first idea on the left of the turnstile, and put the second idea (B, which is “You may enter” in this case) on the right:

(A → B), (A) ╞ (B)

This means “IF our rule is true and IF you actually have the password, THEN you may enter.”

Here’s the weirder part: you might have noticed that the turnstile looks a lot like an IF...THEN. IF everything to the left is true, THEN the idea on the right is true. So how do we know this rule as a whole is true? Do we need a turnstile for the turnstile?

(A → B), (A) ╞ (B) ╞ (C)

. . . and then a turnstile for that one, and for the next one?

(A → B), (A) ╞ (B) ╞ (C) ╞ (D) ╞ (E) ╞ (F) ╞ (G) . . .

In theory, you have to pass an infinite number of turnstiles before you know anything is true! It’s a wonder we are able to put our shoes on in the morning! So how do we know that anything is true? How do you know your milk will come out of the carton at breakfast tomorrow, or that your classroom won’t be on the roof when you get to school?

In practice, we simply trust that the rules we live by are true, since we’ve seen them work in the past. However, it can be fun and useful to poke into the rules, as Laurie did. Even if they turn out to make sense, you learn a lot about how they work. Poking at rules is a big part of what science is all about! See Infinite Regress (Chapter 4; Infinity) and It’s Only Logical (It’s Only Logical).

His full name is Modus Ponendo Ponens, and he represents a type of logical argument. This type of argument can come to a logical conclusion, but that conclusion might not always be true. For example, here’s how Ponens decided that the gate to Symbol is secure:

This conclusion may seem logical, but it’s not necessarily true. Logic is only as good as the assumptions it depends on. Someone, like Laurie, can say she is Eponymous Bach without actually being Eponymous Bach, and as long as she has the right password, she can waltz right into Symbol. In that case, all of the logic in the world won’t make that gate secure! See also Tollens (next) and Semantic Turnstile (Chapter 5: Welcome to Symbol).

His full name is Modus Tollendo Tollens, and, like Ponens, he represents a type of logical argument. In fact, Tollens works a lot like Ponens, but backward. For example, here’s how Tollens might decide that his door is secure:

This is how Tollens would decide Steganosauruses don’t exist:

Like Ponens, Modus Tollendo Tollens is perfectly valid logic, but it’s only as good as the assumptions it’s based on. Just because you don’t have proof that something is true, that doesn’t mean it’s automatically false, and just because you’ve never seen a Steganosaurus, that doesn’t mean they don’t exist. Maybe they live on an island you’ve never been to, or maybe they are so good at hiding that no one can see them. See It’s Only Logical (next).

Even if an idea is logical, it might not be true. It’s easy for an idea to be simple, logical, and false—if you forget to consider all of the facts. For example, people who go swimming have wet hair when they’re finished. If you see someone with wet hair, does that mean she just got out of the pool? No! Perhaps it was raining outside, or maybe she just took a shower.

It’s also easy for logic to get stuck in endless loops. See Ponens (Ponens) and Infinite Regress (Chapter 4; Infinity).

It’s quite fitting that Laurie comes from Hamilton, as her “path back to Hamilton” will be a Hamiltonian path. This type of path, named for mathematician William Hamilton, is a route by which a traveler visits every town on a map exactly once. In this book, I use the word path, but there is actually a slight difference between a Hamiltonian path and a Hamiltonian cycle, which is a path that returns to where it started.

On a map with N towns, there are (N – 1)! ÷ 2 cycles. As Tinker said, x! is shorthand for (x × (x – 1) × . . . × 2 × 1), so for a map with six towns, you’d have

(6 – 1)! ÷ 2 = 5! ÷ 2 = (5 × 4 × 3 × 2 × 1) ÷ 2 = 60 cycles!

Finding a cycle is fairly easy because there are so many possibilities; finding a short one is the hard part! See also Wandering Salesman (Chapter 0; Wandering salesman).

A Fair Coin is a coin that has an equal chance of landing with heads or tails facing up when you flip it. Real coins (like Laurie’s quarters), however, aren’t always perfectly balanced in weight, so in our world, there is no such thing as a perfectly fair coin. But for most coins, the odds of landing with either side up are close enough to fifty-fifty that we have no problem using a coin flip to choose between two options.

Even so, for important things like physics simulations, or choosing who gets to ride in the front seat, flip twice to guarantee absolute fairness. See also A Fair Flip (Chapter 11; Chapter 11: A Fair Exchange).

When Laurie used the turtle robot to make a circle, she discovered that filling in one for how-big? made a much bigger circle than she expected. What number should you plug into MOTH-CIRCLE in order to draw a circle two inches in diameter?

No matter which subject you study, there will always be problems that just don’t have a solution. We say that those problems are impossible to solve. Some problems, on the other hand, can be solved, but only under highly unlikely conditions. Those are improbable.

Thank goodness Xor was able to decode Colonel Trapp’s secret message! People have been encoding information into ciphers for others to decode since ancient times, and today, that science is called cryptography. Computers are great at creating and cracking secret codes, but you can do it, too!

One quick way to encode a message is by using a substitution cipher, which is when you replace each letter in your message with something else. For example, you could map each letter to a number:

Following these rules, “Hello!” would become “7 4 11 11 14!” But you can replace those letters with anything you want: different numbers, other letters, or even symbols you create yourself. Make your own secret message and see if your friends can crack it. Or, share your cipher with your friends so you can send each other secret messages that no one else can read!

If there are millions of possible ways to solve a difficult problem, searching for the best solution just isn’t practical. When that happens, scientists use heuristics to find an answer that is, as Hugh Rustic might say, “good enough.”

Heuristic algorithms are based on experience—on things that we know will work—but they aren’t guaranteed to be the best possible solutions. For example, Hugh Rustic’s ants find many different paths on the map at random, and by following the scent trails of other ants. Scent trails eventually dry up if no new ants follow them. The shorter a path is, the more ants follow it, which makes the scent stronger. Over time, shorter paths become more popular and longer ones fade away. Based on what Laurie saw the ants do, she knows the path is short, even if it may not be the shortest, so she can use that as a heuristic to get home more quickly.

Something to think about: Is Hugh Rustic’s ant map through Userland the shortest possible path, or is it only a short-enough path? Can you do better? Try it!

Much as Xor said, an axiom is a rule or principle that you can’t prove, but that everyone accepts as true because it just makes sense. Mathematicians, scientists, and anyone who wants to prove anything might start their argument with an axiom.

For example, the idea that part of a thing is always smaller than the entire thing is an axiom. If you cut a slice out of a pie, there’s no way that slice can be bigger than the whole pie. The same rule applies to numbers: if you take 2 away from 5, you’re left holding a 2 and a 3, and neither is more than 5.

Jane Hecate checks each letter of Laurie’s password guesses one by one until there is a mismatch with the correct password. The more letters Laurie gets correct in a row, the longer it takes for Jane to find a mismatch, which tells Laurie how close her guess is to being right.

Computer scientists call this a timing attack because the guesser watches the amount of time it takes to check each incorrect try and makes new guesses based on that. Many people who should know better make Jane’s mistake and leak information about the secret they are keeping.

As Trent Escrow explains to Laurie, you can guarantee a fifty-fifty chance of flipping heads or tails on an unbalanced coin—if you flip it twice. If you get Heads-Tails, then Heads is your answer. If you get Tails-Heads, then Tails is your answer. At least half of the time, you’ll probably flip Heads-Heads or Tails-Tails; in those cases, just start over. On average, you’ll need at least three coin flips to get a Fair flip. Try it! See also Fair Coin (Chapter 6; Hamiltonian Cycle).

. . . is not actually a crime in any jurisdiction, and that’s a good thing! Otherwise, no one would be allowed to write any stories, and myths are just stories that have been passed down to us through many generations. Some myths try to explain how the world works, and some are just for fun. Use your imagination, and maybe someday, you’ll write a story that becomes part of a future mythology.

The Doppelganger’s tale is based on a classic question in philosophy: If you replace all of the parts of a boat, do you still have the same boat? Winsome doesn’t think so. She claims she stole the Doppelganger from its owner piece by piece and left him with a copy! But what do you think? If you reassemble the old parts, which boat is the original? What if you replaced only half of the parts?

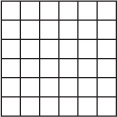
Conway’s Game of Life is a simulation of how a population of creatures might change over time. Computer scientists (and plenty of other scientists) use the Game of Life to study patterns based on simple rules. You can try it out yourself with a pencil and paper! First, grab some graph paper or draw a grid like this:

Now fill in some squares in the grid. Here’s one example:

After you’ve filled in some squares, you just have to follow a few simple rules to play the game and change your pattern:

Follow these rules to color in a new grid. Our sample grid would turn out like this after one round:

These patterns come in many types. Gliders move around. Blinkers turn on and off, like traffic lights. Some patterns even create other patterns as they go. This particular grid pattern repeats:

When scientists want to get to the root cause of a confusing problem, they’ll ask Why questions until they find out exactly Where their experiment went Wrong. But you don’t have to leave that kind of thinking to the scientists.

Play Five Whys the next time you need to figure out the solution to a problem of your own. There are a lot of mental games you can try to help you avoid or learn from mistakes. Another good rule is “Never worry alone.” Grab a friend if you’re puzzled—when you work together, you can solve any problem!

The word Byzantine can describe any extremely long and complicated process. Fortunately, Laurie was able to get all of the signatures she needed by helping the three generals, and she actually solved each of their very different problems similarly.

Laurie’s algorithm for moving the wolf, the goat, and the mandelbroccoli uses a counting argument. The idea behind a counting argument is that you can solve some problems by ignoring unimportant differences between things and counting only how many there are. For example:

Sometimes it’s the opposite: you have to count the same thing different ways to see if they add up. General Case stopped counting posts after he hit 100 feet of fence; he wasn’t thinking about holding up the last length! Count the gaps between the posts and you get 10. Count the posts, and you get 11.

When Tinker tells Laurie to count paths that are mirror images of other paths (like BCD and DCB) as one, he is also using a counting argument. This rule cuts the number of paths through Userland in half. But even cutting the number in half doesn’t help much with the Traveling Salesman problem: a Very Big Number divided by a small number is still a Very Big Number!

Mandelbroccoli does exist in our world, and it’s the weirdest-looking vegetable I know. At the market, it’s called Romanesco, and it looks a lot like a fractal. Fractals are patterns that start with one shape and repeat it infinitely, smaller and smaller, according to a set of rules.

For example, draw an equilateral triangle (a triangle with three sides that are all the same length) inside another equilateral triangle. Make sure each point from the second triangle touches the middle of a side from the first! This should create four smaller, but identical, triangles inside the original.

Now, draw an equilateral triangle inside each of those, following the same rules, and repeat until you can’t fit any more triangles. You should have something like the fractal pattern shown here. See also Infinity (Chapter 4; Infinity).

“Sierpinski triangle evolution.” Licensed under public domain via Wikimedia Commons.

This lighthouse keeper thinks the answer to every problem is more power and brute force. Even if he builds a lighthouse twice as tall, twice as wide, and twice as thick as the one that failed, the new one will still fall over eventually because he’s following the same plan.

Yet in his own way, Bruto is right when he decides to build a pyramid instead. Pyramids are much sturdier, and if you pile on enough bricks, you could eventually make a pyramid tall enough to be a lighthouse. But Bruto’s plan has enormous costs: he needs a lot more bricks, a lot more land to build on, and a lot more time to build.

Some programmers approach problems this way, too, but putting all your resources into a brute-force attempt isn’t always a sensible answer. When your algorithm collapses, don’t just pile on more bricks! Change your point of view, as Laurie did with the generals on the Island of Byzantium, and you’ll find a more effective solution. See also Five Whys (Chapter 14; Chapter 14: In the Abstract).

They don’t really exist, but don’t you wish they did?

The Fresnel whom Laurie meets on Elegant Island is named after a real scientist named Augustin-Jean Fresnel, who invented a way of focusing big lighthouse lights with only a little bit of glass. He knew that lenses didn’t have to be large and thick to focus a beam of light, so instead of one huge piece of glass, the Fresnel lens is an arrangement of small pieces of glass at different angles. Lighthouses still use this type of lens today.

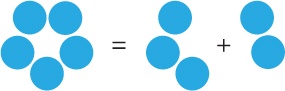
Decomposing starts with a big idea and breaks it into smaller, easier-to-understand pieces. When you know how to solve each smaller piece, you can combine those ideas to solve a bigger problem. One good way to take an idea apart is to describe it without using its name, just as Laurie did when she said you could also call a turtle a “Green Round animal with a Shell.”

Even simple ideas, like the numbers 3 and 4, can be decomposed into simpler ideas. Start with 0 and then add 1. Then add 1 again, and so on:

If you really wanted to, you could just use 0 and 1 and ditch all of the other numbers. I don’t recommend it—you’ll use up a lot of paper!—but it’s a perfectly valid way to do math. For example, let’s break an addition problem down into nothing but 0s and 1s:

2 + 2 = 4

would become

(0 + 1 + 1) + (0 + 1 + 1) = (0 + 1 + 1 + 1 + 1)

When you relate two ideas, you put them side by side and compare them, like Fresnel’s balloon and a lighthouse. With numbers, you use the less-than sign (<) to show that the number on the left is smaller than the one on the right. You use the equal sign (=) to show that the value on the left is equal to the value on the right.

You can relate things besides numbers, though that means some relations are less precise. Fresnel’s balloon isn’t exactly a lighthouse, but it’s like a lighthouse. We expect a lighthouse to have a way for people to climb up high, somewhere to stand when they get there, and a big light that faraway ships can see. Fresnel’s balloon technically has all of those things:

Winsome created the Lighthouse Network to let people in Userland send messages faster. In computer science, a network is a group of computers that are connected to one another so that they can share information. Those computers could be connected through wires or even the air!

In 1870, Émile Baudot invented a code that represented letters with different groups of 1s and 0s. This code was meant to let people share messages using electricity: if you have a switch, the power can either be on (1) or off (0). Naturally, Baudot named this code after himself. See Bach’s Laws of Eponymy (Chapter 2; Bach’s First Law of Eponymy).

We don’t use the Baudot code very often in the real world, but Ping, Fresnel, and the other members of Winsome’s Lighthouse Network use it to send messages with their lights, which can also be on (FLASH) or off (FLOOSH).

Here’s the Baudot code and the letter each number stands for, so you can make your own Lighthouse Network. Grab some friends and some flashlights, and send each other messages!

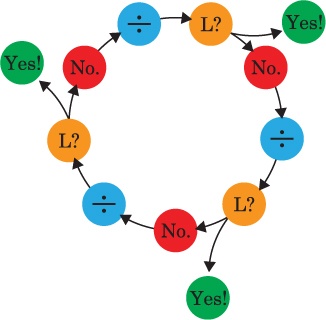
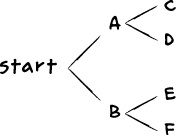
The Garden has 16,777,216 paths, but in the end, Laurie and Xor each found exactly one path that made sense for them. The number of possible paths became so small so fast because at each fork, Laurie answered an either/or question, and that cut the number of possible paths in half.

Laurie’s journey through the Garden of Forking Paths is a lot like what computer scientists call a binary search, which programmers use to look for a single piece of information in a huge list quickly. When something is binary, it has only two parts—just like the questions the Garden asked Laurie.

This little chart has four possible outcomes. If you answer the question “A or B?” with A, you cut that number in half, leaving only two possibilities. Then, at A, you have to answer “C or D?” Whichever option you pick, you’re cutting the number in half again, to one choice.

In a binary search, you would ask similar questions about your giant list of information; eventually, you’d cut the possibilities down to just one. Try it the next time you play Twenty Questions! If you choose your questions (or answers) carefully, you can arrive at virtually anything in only 20 or 30 steps. See also Recursion (Chapter 4; Chapter 4: What the Tortoise Said to Laurie).

Captain Kevin Kelvin is laying wire along the ocean to create a telegraph network. Telegraph systems let people send messages to one another over long distances without actually sending a physical object. Winsome’s Lighthouse Network is also a type of telegraph!

In Kevin’s case, letters are represented by collections of sounds, not lights. Different combinations of beeps and bloops represent different letters, and those beeps and bloops are made when Kevin’s assistant presses a button attached to the other end of the wire. The telegraph is just one of many systems people have used throughout history to talk to one another.

Lord Kelvin was a real engineer who worked on telegraphs, but he’s best known for creating the Kelvin scale to measure temperature. Unlike other temperature scales, the Kelvin scale doesn’t use numbers less than zero, so the coldest temperature that anything can be is called absolute zero. Water freezes into ice at a whopping 273.16 Kelvin!