General Rules for Recovery

The safe speed for opening a main parachute depends on a lot of things. You have to consider the mass of the rocket, since the energy at the moment the parachute opens goes up linearly with the mass of the rocket. You also need to take the strength of the recovery system into account. A parachute that opens slowly can open at a faster speed, since it slows the rocket a bit before the parachute snaps open. While we can get a handle on the speed using some basic math, and will do that later, in the end the only reliable way to know how quickly the rocket can be traveling to safely open the main parachute is to try it and see. A lot of people have done that over the years. In my own experience, I know, for example, that a 36” nylon parachute opening at 100 ft/s on a rocket the size of Callisto will tear, while a 48” parachute opening at about 50 ft/s works just fine on Deimos. Other experience seems to match my own. In the magazine Peak of Flight, issue 361, Tim Van Milligan recommends a maximum descent rate of 50 mph, which is about 73 ft/s. OpenRocket generates a warning if a parachute deploys at a speed faster than 20 m/s, which is about 66 ft/s. Based on these indices, and similar experience from a lot of other fliers, it seems reasonable to say that slowing your rocket down to about 50–75 ft/s is about right. Be sure your parachute and all other aspects of your recovery system are strong if you go for the high end of that range.

There are a lot of factors to consider for the maximum landing speed, too. We’ll get into that in detail in “Parachute Rocket Science”. Most sources recommend a landing speed of 15–20 ft/s. In fact, NAR recommends 20 ft/s as the maximum descent rate for a Level 3 rocket in its guidelines for Level 3 certification. In general, land the rocket as slowly as you can for a dual-deploy rocket. After all, the parachute doesn’t open until the rocket is pretty close to the ground, so you don’t pay much of a penalty for using a large parachute.

Table 9-1 shows the maximum allowed weight in ounces for several common parachute sizes. The desired descent speeds are shown in the column headers. The first two columns give a range of weights for landing a rocket with each parachute size, while the last two columns help you determine a good size for a drogue parachute.

As an example, let’s say I am flying Deimos on an AeroTech J350 motor using a cable cutter. According to my simulation, the rocket weighs about 69 ounces. That’s at liftoff, though. Checking the details in OpenRocket, I find that the propellant weight is around 13 ounces, so the parachute really only has to land around 56 ounces. Scanning down Table 9-1, I see that a 48” parachute will land a 45 oz rocket at 15 ft/s, and a 79 oz rocket at 20 ft/s. Deimos is in the middle of that range, so the 48” parachute should do nicely. Looking down one more row, I see that a 54” parachute will land the rocket at 15 ft/s. It’s perfectly reasonable for me to use either of those parachutes.

The table makes a lot of assumptions, some of which may not be valid for your rocket. The assumptions are:

• The rocket is being flown at sea level. Don’t use the table if your launch altitude is over 2,000 feet above sea level.

• The coefficient of drag is 0.75. This is a good value for a typical flat nylon parachute, but is low for a more expensive hemispherical parachute.

• You are using a single parachute.

If any of these assumptions are wrong, read the chapter all the way through to find out how to deal with the issue you are facing.

Packing Size

There are two ways to look at packing parachutes and shock cords into your rocket. The first is at design time, when you want to know how much room to leave so you can eventually fit the parachute and shock cord into the rocket. The second is learning the techniques to safely pack a parachute and shock cord into the minimum amount of space. Let’s start with planning space for the shock cord and parachute when designing the rocket.

Most of the rockets in this book use 9/16” tubular nylon for shock cords. This stuff is strong, generally rated for 2,000 lb loads. It’s also cheap and stands up to recovery gases pretty well, although shock cord protectors are always a good idea to keep the worst effects of the ejection charge gases away from the shock cord.

In actual testing, a 20-foot-long shock cord that was simply wadded up and stuffed into a 3”-diameter tube took about 7” of linear space. A bit of math shows that this works out to 2.5 cubic inches per foot of shock cord. That’s a pretty good value to use for planning purposes. You can use a little less with some of the techniques we’ll discuss in a moment, and you may need a bit more if you go to a larger shock cord for some reason, but this is a good way to figure out the minimum space to allow for the shock cord.

Of course, you also need to know how long the shock cord will be. Basically, the longer, the better. Longer shock cords give the rocket parts time to slow down from air drag after the ejection charge pops the pieces apart, reducing strain on the rocket. East Coast fliers also like long shock cords because they make it more likely that part of the rocket will reach the ground, even if the parachute gets snagged in a tree! The general rule of thumb is to use a shock cord that is three to 5 times the length of the rocket. Deimos and Phobos are about five feet tall, give or take, so a 20-foot shock cord is in the right range.

The space needed for a parachute depends on a lot of factors, but in general, allow 1/6 to 1/4 the diameter of the parachute. For a 48” parachute, then, you should plan 8–12” into the length of the rocket for the parachute.

In real life, the space available may not work out in such an ideal way. Body tubes come in certain sizes. You may need to increase the size of the parachute because you’re flying a heavy motor or payload, or perhaps because you are flying at altitude. That’s when some packing tricks can come in handy.

Let’s start with the shock cord. While you can stuff a 20-foot-long shock cord into a 7” section of a 3” rocket like Deimos or Phobos, that’s really not the best way to pack a shock cord. The risk of tangling is minimal, but it goes up a bit when you just stuff the cord in. A wadded mess also takes up more room than a neatly folded shock cord.

Probably the most popular way to pack a shock cord is called Z-folding (see Figure 9-1). You fold the shock cord back and forth within a given space. Once folded, use weak rubber bands at the ends of the folds or a piece of painter’s tape around the middle to hold the bundle in place. Don’t remove the rubber bands or tape. The force of ejection is more than enough to pull the rubber bands or tape off, and they actually help the process. It takes a little force to dislodge the rubber bands or tape, which absorbs some of the energy from the ejection charge.

Z-folding reduces the volume needed from about 2.5 cubic inches per foot of shock cord to about 2.1 cubic inches per foot of shock cord. That reduces the length of the tube needed in Deimos or Phobos to pack a 20-foot shock cord from 7 linear inches to 6 linear inches.

Figure 9-1. Z-folding is a common and effective way to pack a shock cord.

You’ve seen my personal favorite method for packing shock cords in the launch preparation sections of previous chapters. I like to roll the shock cord into flat pancakes, using tape to hold them together (see Figure 9-2). Just like with Z-folding, the tape helps reduce the energy from the ejection charge. Rolling also takes less space. I can pack a 20-foot shock cord into Deimos or Phobos using 5 linear inches of space. Overall, it takes about 1.8 cubic inches per foot of 9/16” tubular nylon. I also think rolling is the neatest of the three methods, and the least likely to snarl the shock cord, since each rolled bundle is independently stacked on top of the one that unfurls after it.

Figure 9-2. Rolling is a compact way to pack tubular nylon shock cord.

As you know from packing your Level 1 rocket, and perhaps from packing the Level 2 rocket, there comes a point when you fold the parachute lengthwise before wrapping it in a flame blanket. The number of times you fold the parachute is the controlling factor in how much space the parachute needs in the rocket body tube. You might think that the number of times you can fold the parachute would depend on its size, since you have to be able to stuff it into a fixed-size tube, and in an absolute sense that’s true. Large parachutes tend to be used in large rockets, though, and smaller parachutes are used in smaller rockets. Since the parachute size goes up and down with the size of the rocket, the number of times you fold it generally stays the same until you get to really big rockets. I’ve never seen a high-power rocket where the parachute could not be folded in half. That reduces the length of the parachute to 1/4 of its diameter, since the length before folding is the radius. In most cases, though, this is a fairly loose fit. You want the parachute to loosely fill the available volume so the parachute’s flame blanket provides some protection to the shock cord that is behind the parachute. Most of the time I end up folding the parachute in thirds, giving a length about 1/6 of the diameter of the parachute. It’s often possible to fold the parachute in fourths, but if you do that, be very sure the parachute can still slide in and out of the body tube easily. You do not want to have the parachute bind inside the body tube, failing to deploy because it is too tight in the tube.

The actual length needed to store the parachute in the tube is usually a bit shorter than 1/4 or 1/6 of the diameter of the parachute, because the spill hole doesn’t take up any room. The 54” parachute shown in Figure 9-3 uses about 12” of linear length when folded in half, and 8” when folded in thirds. I like the fit of the parachute better when it is folded in thirds.

Figure 9-3. Once the parachute is folded into a long narrow tube, we fold it two, three, or four times to reduce the length needed for the parachute and to make a loose plug that will protect the shock cord from the ejection charge.

These are values you can figure out on your own by playing around with your shock cord and parachute. If you are planning a rocket before you have a closet full of parachutes and shock cord, though, you may need some advice on how much space to leave before you actually have the materials in hand. Take a look at the manufacturer’s website. Many will show the recommended packing sizes for their products. The values for some common PML parachutes, many of which you have seen folded in rockets in the book, are shown in Table 9-2, with shock cord packing sizes in Table 9-3.

As you can see, for a 3” rocket like Deimos or Phobos, we should plan for around 17” of linear space for the shock cord and parachute, although we may need as little as 11”. These rockets have about that much space—a little more in some parachute bays, and a little less in others. Phobos, in particular, is a little short of space in the booster. There really isn’t enough space for a large parachute and a really large motor, like a CTI K1440W. On the other hand, you can pack the shock cord in the motor tube for shorter motors, and in the dual-deploy configuration, you can pack the larger parachute in the upper bay and the smaller drogue parachute in the booster section. I thought using the shorter, lighter, less expensive booster tube was a good design trade-off. You may disagree. If so, you can certainly lengthen the tube a bit when you build your version of the rocket.

Parachute Rocket Science

This section on parachute physics digs into two topics. The first is the energy of a falling body. It’s important to understand the ideas in this section if you want to step outside the narrow confines of using a table to select a parachute. You can’t make a reasonable choice about the acceptable descent rate of a rocket without understanding this topic. The second topic is the physics and math behind the tables from the first part of this chapter. You might want to read this section just for fun, but it also gives you the tools to really understand how to select the best possible parachute for a particular purpose.

If you’re content to use the tables for selecting a parachute, though, you can safely skip the rest of the chapter.

The Energy of a Falling Body

I’m going to make a clean break with the information you find on parachute selection in most books or articles by claiming that the recovery speed is not that important. The important factor when recovering a high-power rocket is the recovery energy. The whole point of using a recovery system is to avoid damage to people or property when the rocket lands, and that damage is caused by energy, not speed. If that seems preposterous, stop and think about this for a moment: air molecules traveling at about 505 meters per second are constantly bombarding you. Not only do they not hurt you, but if they slow down too much you get cold! A bowling ball dropped from a height of one meter is traveling over a hundred times slower, but I guarantee it will hurt more if it hits your foot. So again, it’s not the speed—at least not alone—that does the damage. It’s the energy.

Energy comes in many forms. The kind of energy associated with motion is called kinetic energy. The equation for kinetic energy is pretty simple. It is:

The reason this equation is important is because stopping a moving body requires energy, too, and the energy it takes to stop something is exactly the kinetic energy of the moving body. For a rocket falling from the sky, the energy to stop the rocket might be supplied by a small dent in the ground, a bump on a fin that bends it slightly, or any other sort of movement. In the end, most of this energy ends up as heat, but it’s not enough that you can measure the heat with instruments you are likely to have available.

The problem, though, is that the energy can also do damage to the rocket. It might chip some paint, break a fin, or crumple a body tube. It could damage things on the ground, too. This might be innocuous, like poking a hole in some dirt. If the rocket comes down with a lot of energy, though, it could do a lot of damage.

Let’s take a look at the equation for kinetic energy with this in mind. We can see that the energy goes up with the mass of the rocket. If one rocket weighs twice as much as another, and they are going the same speed, the rocket that weighs twice as much will have twice the kinetic energy. Since it is the energy we are worried about, this means we need a slower descent rate for heavier rockets.

The other factor in the equation is the velocity. This goes up as a square, though. If two rockets weigh the same, but one is moving twice as fast as the other, the faster object has four times the energy. This has impacts—sometimes literally—far outside rocketry. Think about automobile speed limits for a moment. Fifty-five miles per hour may seem insufferably slow on the highway. Let’s see what happens if we increase the speed to 78 miles per hour, though. The equation tells us that for the 55-mile-per-hour car, the kinetic energy is 3,025 multiplied by the mass of the car. At 78 miles per hour, the energy is 6,084 multiplied by the mass of the car. The energy has doubled, even though the speed only went from 55 to 78. That means the damage from a crash, both to the car and to the people in it, will be twice as bad at 78 miles per hour as it would be at 55.

Exactly the same thing happens with our rockets. As the speed goes up, the energy of the collision of the rocket with whatever it hits goes up even faster. Rockets are a lot smaller than cars, but they can go a lot faster, too. Several rockets in this book are capable of supersonic flight with larger motors. Ganymede, the Level 3 rocket shown in Chapter 13, travels at nearly 1,000 mph on a small M motor.

There are different units for kinetic energy, just like there are different units for speed and mass. While we can work in feet per second and ounces, most of the time people switch to the metric system when dealing with energy. Energy is measured in joules (J) in the metric system. In terms of kinetic energy, one joule is the energy of one half kilogram (about 1.1 pounds) moving at one meter per second (about 2.2 miles per hour). Table 9-4 shows the energy of Deimos in various configurations alongside some other moving objects.

Looking at Table 9-4 might seem a little scary, but keep in mind that two different objects with the same kinetic energy can do a very different amount of damage when they hit something. One reason is the shape of the object itself. A hard, pointed object like a dart is more likely to puncture something it hits than, say, a round object like a baseball. A rigid object like a baseball is more likely to do damage than an object that crumples. That’s definitely something to think about when picking materials for your rockets. Paper and plastic tubes will crumple in a high-speed impact, such as a ballistic return, where the parachute never pops out and the rocket careens in at terminal velocity. While Deimos will do significant damage if the parachute never opens, the fact that the body tube will shatter and crumple spreads the time of impact out significantly, which helps a lot in terms of reducing damage. Phobos is heavier, but even more telling, its fiberglass frame can survive impact with many objects. It can act like a giant dart, punching right through some materials. Not to put too fine a point on it, Deimos is a safer rocket to fly than Phobos.

Table 9-4. Kinetic energy of Deimos and miscellaneous moving objects

Object	Speed	Mass	Kinetic energy
Nitrogen molecule in air	505 m/s	4.6x10-26 kg	6x10-19 J
Deimos landing, 48” chute	5.06 m/s	1.59 kg	20.35 J
Bowling ball dropped from 1 meter	4.4 m/s	3.6 kg	35 J
90 mph baseball	40.2 m/s	0.145 kg	117 J
9 mm bullet	380 m/s	0.008 kg	578 J
100 lb boy riding a bike at 15 mph	6.7 m/s	45.4 kg	1,019 J
Pro football defensive back	8.0 m/s	90.3 kg	2,890 J
Deimos, ballistic return	102 m/s	1.59 kg	8,271 J
Deimos at max speed, J350	262 m/s	1.59 kg	54,572 J
XTerra SUV, 55 mph	24.6 m/s	2,000 kg	605,160 J

Parachute Aerodynamics

In general, we think of aerodynamics as a tool to let us decrease drag, allowing our rockets or airplanes to slip more easily through the air. The idea is just the opposite with a parachute—we want as much drag as we can get so we can slow the descent of our rocket.

The fundamental equation that governs drag is pretty simple. The force from drag is:

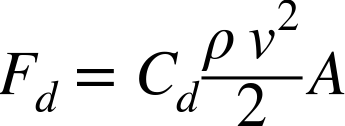
where:

ρ

The density of air.

V

The velocity of the rocket.

A

The area of the parachute.

C_d

The coefficient of drag.

F_d

The force due to drag.

We actually want to find the velocity of the rocket, not the force of drag, so let’s rearrange the equation to:

Once the parachute opens, the rocket will quickly reach terminal velocity—the point when the force of drag pushing up on the rocket exactly balances the force of gravity pulling down on the rocket (see Figure 9-4). That means we know the force of drag; it’s the same as the mass of the rocket in kilograms times the acceleration of gravity. It’s Newton’s second law of motion:

You might know the mass of the rocket in grams or the weight of the rocket in ounces rather than the mass in kilograms, but it’s easy enough to convert. Divide by 1,000 to convert from grams to kilograms. Multiply by 0.02835 to convert from ounces to kilograms. Technically, converting from ounces to kilograms also converts from force to mass, which are two entirely different things, but it works with the assumption that the rocket was weighed on the surface of the Earth. The acceleration of gravity is 9.8 meters per second squared.

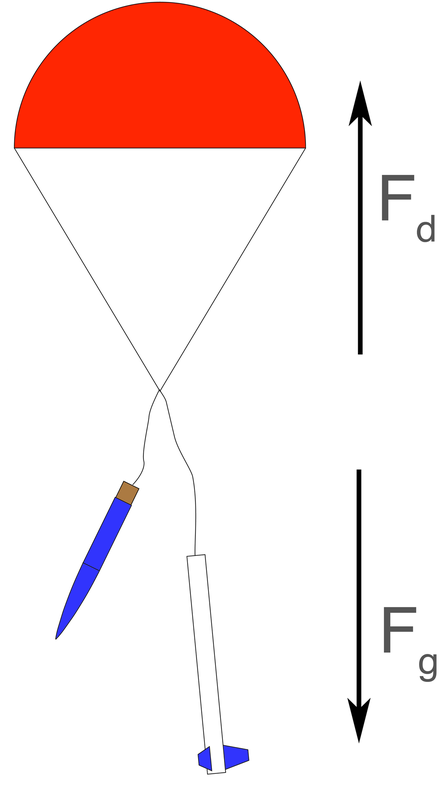
Figure 9-4. At terminal velocity, the force from gravity pulling the rocket down is exactly balanced by the force of drag.

Once all of the fuel is expended, Deimos coming down from a flight on an AeroTech J350 motor has a mass of about 1.59 kg. The force on the rocket, then, is 15.58 newtons, and at terminal velocity, that’s also the force of drag.

The density of air is about 1.22 kilograms per cubic meter. This is at sea level, and altitude does play an important part in reducing the density of the air (see Figure 9-6). Here in Albuquerque, our altitude is such that the air density is about 1.06 kilograms per cubic meter, so I generally go up one parachute size from the size shown in Table 9-1.

The area is the area of the parachute. Parachutes come in a variety of shapes. For a standard flat hexagonal six-string parachute, the area of the parachute is:

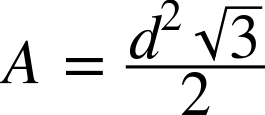
where d is the distance across the parachute, as shown in Figure 9-5. Octagonal parachutes are also common on high-power model rockets. For an octagonal parachute, the area is:

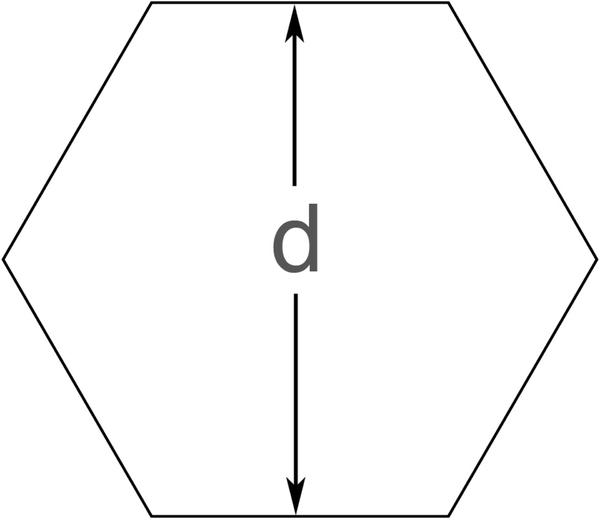
Figure 9-5. The distance across the parachute is measured from one side to the other, not from one corner to the other.

Large commercial parachutes almost always have a hole in the center, which decreases the oscillation of the parachute during descent. Subtract the area of the hole from the overall area of the parachute.

Remember to convert the size of the parachute from inches to meters, since all of the other values used in this section are in the metric system. Table 9-5 shows common parachute sizes in inches and meters, and the area in square meters.

Table 9-5. Common hexagonal and octagonal parachute sizes in inches and meters, with the area in square meters

Inches	Meters	Area (6 sides)	Area (8 sides)
12	0.305	0.080	0.077
24	0.610	0.322	0.308
36	0.914	0.724	0.693
48	1.219	1.287	1.231
54	1.372	1.629	1.559
60	1.524	2.011	1.924

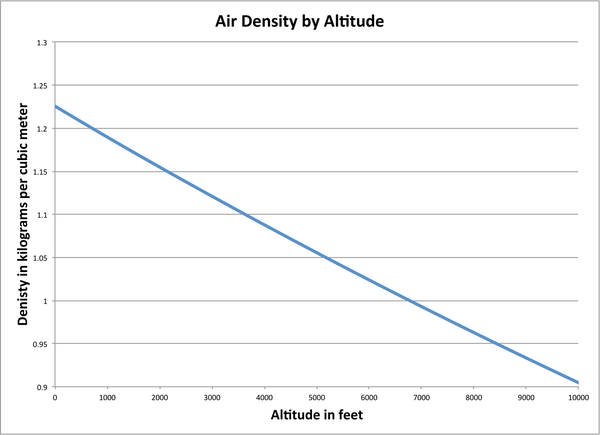
Figure 9-6. Air density varies with altitude, temperature, and humidity. This plot shows the effect of altitude.

The last term is the coefficient of drag. The generally accepted value for the coefficient of drag for a flat parachute is 0.75. This is something that can vary a lot, though. While inexpensive flat parachutes like the ones shown in this book have a coefficient of drag around 0.75, larger parachutes are often made with better shapes. An elliptical parachute, for example, has a coefficient of drag around 1.5. They are more expensive, but since the drag coefficient is twice that of a flat parachute, you can use a parachute half the size of a flat parachute, too. Fruity Chutes sells another parachute called the Iris Ultra (shown in Figure 9-7), which has a coefficient of drag around 2.2. Again, you pay more, but the advantages of using a smaller parachute that packs into a smaller space may be worth the price.

Figure 9-7. Shape does matter. While an inexpensive flat parachute has a coefficient of drag of about 0.75, this Iris Ultra from Fruity Chutes has a drag coefficient of 2.2, making it three times as efficient for the same size parachute. Photo by Fruity Chutes, used with permission.

Example: Find the speed of descent for a rocket

Let’s see how we can put all of this information to use.

Let’s say we’re getting ready for a trip to BALLS in Black Rock, Nevada, to fly the dual-deploy version of Phobos on a CTI K1440W motor. The OpenRocket simulation says this beast will propel Phobos at a speed of 1,528 ft/s, or about Mach 1.4. Is our normal 54” parachute big enough for this flight?

The equation for speed is:

We need the mass of the rocket to find the force at terminal velocity. From an OpenRocket simulation, we find that the liftoff weight of the rocket is 175 oz, and the propellant weight for the CTI K1440W is 41 oz. This gives a recovery weight of 134 oz, or 3.8 kg.

The density of air is less at Black Rock than at sea level. Checking the internet, we find that Black Rock is about 4,000 feet above sea level. Checking Figure 9-6, we find that the air density at this altitude is about 1.08 kg/m³.

An eight-sided 54” nylon parachute has an area of 1.559 m², but mine also has an 8” spill hole. Remembering to convert inches to meters and use the radius of the spill hole rather than the diameter, the area of the spill hole is:

This gives an area for the parachute of 1.527 m².

We’ll use the standard coefficient of drag for a flat parachute of 0.75.

Putting all of this together, the descent rate for Phobos will be:

This is faster than our typical upper-end descent rate of 20 ft/s. Since the impact from energy goes up as the square of velocity, going from 20 ft/s to 25 ft/s increases the energy of impact by 56%, which is quite a lot. On the other hand, Phobos is a fiberglass rocket that can take that kind of impact, and we’re flying at Black Rock, a dry lake bed with nothing but fine sand for miles in any direction. The only other people who will be at BALLS are people flying high-power rockets. It’s a judgment call. Some people might choose to use the 54” parachute, especially since they will have a drogue parachute to help slow the descent a bit. I can see that argument, but personally, I would pack my 60” hemispherical parachute. With the larger area and a drag coefficient around 1.5, this parachute will bring the rocket down with a much slower speed:

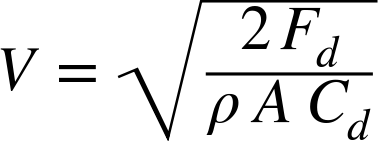
That’s a much nicer descent rate, and I’m really not worried about the rocket drifting too far with a dual-deploy recovery system and miles of flat sand for the recovery area.

Example: how much does the drogue parachute help?

Rockets like Deimos and Phobos are often flown using dual deployment with two parachutes. How much does the other parachute help with reducing the descent rate?

To find out, let’s take a typical example of Deimos flying on an AeroTech J350W motor. We’ll plan for a 48” main parachute and an 18” drogue. Let’s start by making sure the drogue parachute will slow the rocket down to a safe speed for the main parachute to open.

Working with the OpenRocket simulation, we find that the recovery weight for the dual-deploy configuration of Deimos is 83.9 oz, or a mass of 2.38 kg. We’ll use a density of 1.22 kg/m³ for a sea-level launch. A typical 18” parachute has six strings, so the area is 0.18 m². The coefficient of drag is 0.75. Putting all of this together, the descent speed with the drogue parachute is:

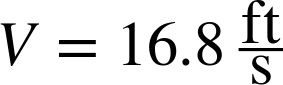
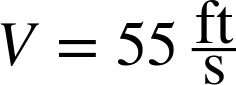
That’s in the right range. Actually, a 12” drogue works, too, since the rocket flopping around adds a fair amount of drag, but we’ll ignore that for now.

Adding the effect of the 48” main parachute is easy enough. We just need to increase the area of the parachute. With a 6” spill hole and eight shroud lines, the 48” parachute has an area of 1.22 m², for a total area of 1.4 m². The descent rate with just the 48” parachute is:

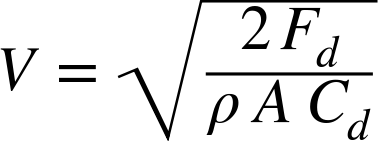
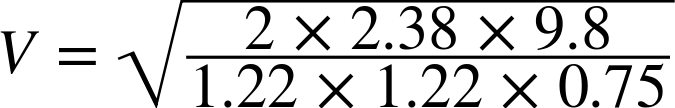
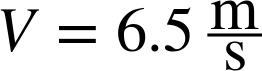
That’s close enough to 20 ft/s to feel like the 48” parachute is a good choice. Adding in the drogue, we expect a descent rate of:

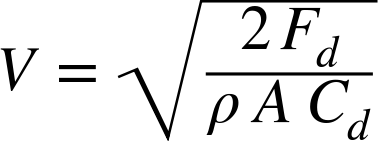
The drogue doesn’t make a significant impact, but it does help somewhat.