3
Interrelationship of the Physical Layer with Other Layers of the OSI Model
3.1 MAC Layer and Physical Layer Relationships
Having stated unequivocally in Chapter 2 that we would leave the mysteries of the LTE physical layer in the capable hands of Harri Holma and Antti Toskala it is necessary for us to take a look at the differences between guided and unguided media at the physical layer and how these differences impact on the MAC (medium access control) layer with LTE1 as a particular and specific example.
The MAC layer, OSI Layer 2 as the name implies describes the functional protocols that manage ingress and egress of traffic across each of the physical layer (Layer 1) delivery options. In terms of LTE this requires us to look at the specific challenges of delivering mobile broadband access over a particularly wide range of operational and channel conditions. The offered traffic mix may also be highly variable.
The big difference between guided media, coaxial cable, copper twisted-pair and fibre and unguided media (free-space optics and RF) is that unguided media channel conditions change faster and are harder to predict, though they can be measured and managed. Signals will typically travel along multiple reflected paths that will produce differential time delays at the receiver. Phase reversals may also have occurred at each reflection point.
This can also be observed in point-to-point microwave links where ground proximity within what is known as the Fresnel zone causes phase cancellation at the receiver. Early long-distance microwave links over the sea for example exhibited phase cancellation when the tide reached a particular height.
Slow and fast fading and time dispersion are a dominant characteristic of mobile broadband connectivity. Time dispersion becomes a particular challenge at higher data rates.
One of the narratives of this book is that our ability to process signals in both the frequency and time domain has translated/transformed this challenge into an opportunity by increasing the user experience value realisable from mobile broadband access faster than other access media. This is different from what has happened in the past. In the past, any increase in data rate in wireless systems has been matched by an equivalent increase in the data rates achievable over fibre, cable or copper. This is no longer the case. The business of mobile broadband is being transformed by transforms.
The extent of the transformation, however, is as yet unclear – this is work in progress. For example, we can show that present LTE devices can deliver high peak data rates on a single-user basis but power efficiency has not improved on a pro rata basis. Sending data faster may result in a system efficiency improvement but this is not the same as a power-efficiency improvement. Power efficiency for the single-user experience has to improve in order to realise added value. This could be achieved by increasing network density but this increases capital and operational cost, so the user will need to be charged more for access.
Similarly, the high per user data rates have an associated cost that is inflicted on other users. If the other users either do not notice or do not mind then that is fine. If they do notice and/or mind then this is effectively a loss of added value and an increase in opportunity cost. It is pointless increasing single-user value if multiple-user value decreases by an equivalent or greater amount
So there are two questions that we need to try and answer in this chapter.
Can OFDM combined with enhanced functionality at the MAC layer and higher layers of the protocol stack deliver a significant improvement in system efficiency and power efficiency and can this in turn be translated into additional single-user value? To do this we need to take a view of how transformative the transforms that we use are really going to be in terms of realisable single-user added value and how effectively contention and scheduling algorithms arbitrate between the single- and multiuser experience.
Can OFDM combined with enhanced functionality at the MAC layer and higher layers of the protocol stack be translated into multiple-user value? One argument made here is that OFDM systems are more resilient to user to user interference but this has yet to be proven in practice within fully loaded real-life networks. The real answer to this question as above is more likely to be found in contention and scheduling algorithms, both of which we explore.
3.2 OFDM and the Transformative Power of Transforms
In Chapter 2 we reviewed the Fourier transform and its role in processing OFDM signal waveforms. Essentially, the difference at the physical layer between 3G mobile broadband systems and LTE ‘4G’ systems is that Fourier transforms have replaced Hadamard–Rademacher–Walsh transforms.
So the first thing we need to try and do is quantify the difference between Hadamard–Rademacher–Walsh transforms and Fourier transforms.2
Fast Fourier transforms are already used in 3G systems and indeed in 2G systems at the application layer (layer 7) to source code voice, audio, image and video. Almost all compression algorithms use an FFT at some stage to achieve bandwidth efficiency, exploiting the ability of the Fourier transform to represent complex signals viewed in the frequency domain as a composite of simple sinusoidal signals.
In 4G radio systems we user Fourier transforms at the physical layer (layer1) to translate a symbol stream on to discrete frequency subcarriers. The effect is to provide additional frequency diversity and time diversity in that the symbols are further apart in time than the original bit stream. We do this so that we can support higher single-user data rates.
However, present cellular systems make wide use of the Hadamard transform both in the channel encoding/decoding process (convolution and block coding) and code division multiple access (CDMA). Channel coding provides time diversity. CDMA provides frequency diversity (by spreading the original data signal across a wider bandwidth). Does Fourier really deliver significant additional performance gain?
To answer this we need to consider the history of matrix maths.
3.2.1 The Origins of Matrix Maths and the Hadamard Transform
Matrix maths is the science of putting numbers in boxes or rather, arranging numbers in rows and columns (a horizontal and vertical matrix). The numbers can be binary or nonbinary.
The Sumerian abacus came into use around 2700 to 2300 BC providing a mechanism for tabling successive columns of successive orders of magnitude. The Babylonians in the third or fourth century BC used matrices on clay tablets, a forerunner of the counting tables used by the Romans. Counting tables were simply tables with a ridged edge. The tables contained sand and the sand would be divided up into squares to help in counting and calculation.
Matrix concepts were developed by the Chinese in the Han Dynasty between 200 and 100 BC to solve linear equations. This implied an understanding that matrices exhibit certain properties, later described as ‘determinants’ that are revealed when the numbers in the matrix are added or multiplied either vertically by row, horizontally or diagonally.
This understanding was documented in ‘Nine Chapters on the Mathematic Art’ put together around 100 AD and was the product of a period now often described as ‘The First Golden Age of Chinese Mathematics’ (the second golden age was in the thirteenth and fourteenth century).
Historically, it is important to realise that the development of matrix theory in China was contemporaneous with the work of Archimedes on curves and circles and Pi between 287 and 212 BC.
Thus, the origins of the Fourier transform and the Hadamard transform can both be traced back to the pre-Christian era. As with the science of geometry, it took over 1000 years before much else meaningful happened in matrix theory.
In 1683, the Japanese mathematician Takakazu Seki wrote the ‘Method of solving dissimulated problems’ that precisely described how the earlier Chinese matrix methods had been constructed.
At the same time, in Europe, Gottfried Leibniz was producing work on determinants that he called ‘resultants’. This became the basis for a body of work to which mathematicians like Cramer, Maclaurin, Bezout and Laplace all contributed throughout the eighteenth century.
The term ‘determinant’ was used by Gauss in 1801 in his ‘Disquisitiones arithmeticae’ side by side with his work on the coefficients of quadratic forms in rectangular arrays and matrix multiplication. This became the basis for a body of work to which other mathematicians such as Cauchy (who proved that every real symmetric matrix is diagonisable), Sturm, Cayley and Eisenstein contributed in the first half of the nineteenth century.
However, it was JJ Sylvester who is first credited with using the term ‘matrix’ in 1850. Sylvester defined a matrix to be ‘an oblong arrangement of terms which could be used to discover various ‘determinants’ from the square arrays contained within it.’ This work was developed in his snappily titled 1867 paper ‘Thoughts on Inverse Orthogonal Matrices, Simultaneous Sign-successions and Tesselated Pavements in two or more colours, with applications to Newton’s Rule, Ornamental Tile Work and the Theory of Numbers’. This paper established a new level of understanding about pattern behaviour in matrices (using ornamental tiles as an example). In between times, Sylvester gave maths tuition to Florence Nightingale who in turn revolutionised health care through her understanding and application of the statistical analysis of illness and associated treatment options, yet another example of applied maths.
At which point we can introduce Jacques Hadamard. Jacques Hadamard and his family survived the Prussian siege of Paris in 1870 by eating elephant meat. Hadamard obtained his doctorate in 1892 with a thesis on analytic theory and related work on determinant equality, the property that allows matrices to be used as a reversible transform. Hadamard also produced pioneering work on boundary-value problems and functional analysis and is generally seen as ‘the founding father’ of modern coding theory.
Hadamard’s work was developed by Hans Rademacher, particularly in the area of orthogonal functions now known as Rademacher functions that appeared in a paper published in 1922 and was the forerunner of pioneering work in analytic number theory. Hans Rademacher’s work was contemporaneous with the work of Joseph Leonard Walsh known as ‘Joe’ to his friends. This included a publication in 1923 on orthogonal expansions, later called ‘Walsh functions’. Joe Walsh became a full professor at Harvard in 1935 and produced pioneering work on the relationship of maths and discrete harmonic analysis.
3.2.2 The Hadamard Matrix and the Hadamard Transform
A transform changes something into something else. The process is most useful when it is reversible/bidirectional and the purpose is generally to make a particular process easier to achieve.
In our context of interest, we want to take a string of numbers and rearrange or redistribute the number string in rows and columns so that they are more easily processed. In other words, a Hadamard transform is a transform that exploits the properties of a Hadamard matrix in the same way that a Fourier transform exploits the properties of the Fourier number series (the ability to describe waveforms as a summation of sines and cosines).
3.2.3 The Properties of a Hadamard Matrix
Hadamard matrices possess a number of useful properties. Hadamard matrices are symmetric, which means that specific rows can be matched to specific columns. Hadamard matrices are orthogonal, which means that the binary product between any two rows equals zero. The binary product is simply the result of multiplying all the components of two vectors, in this case rows, together and adding the results. We will see why this is useful later.
This means that if you compare any two rows, they match in exactly N/2 places and differ in exactly N/2 places so the ‘distance’ between them is exactly N/2. We explain why ‘distance’ is useful later.
Exactly half of the places that match are +1s and the other half are −1s. Exactly half of the places that differ are (−1+1) pairs and exactly half are (+1–1) pairs (the symmetric properties of the matrix). You can turn a Hadamard matrix upside down (reverse the +1s and −1s) and it will still work.
The matrix has the property of sequency. The sequence number of each row is the product of the number of transitions from +1 to −1 in that row. A row’s sequence number is called its sequency because it measures the number of zero crossings in a given interval. Each row has its own unique sequency value that is separate from its natural order (the row number).
The Hadamard transform can therefore be correctly described as a sequency transform that is directly analogous to describing the Fourier transform as a frequency transform. In other words, given that the rows in a Hadamard matrix are orthogonal, the Hadamard transform can be used to decompose any signal into its constituent Hadamard components. In this sense it works just like a Fourier transform but with the components based on sequency rather than frequency.
As with the Fourier transform, a number of these components can be discarded without destroying the original data so the Hadamard transform can be used for compression.
The Hadamard transform can also be used for error correction. A much-quoted example is the use of Hadamard transforms to code the pictures coming back from the visits to the moon in the 1960s and the Mariner and Voyager missions to Mars. The pictures were produced by taking three black and white pictures in turn through red, green and blue filters. Each picture was considered as a thousand by thousand matrix of black and white pixels and graded on a scale of 1–16 according to its greyness (white is 1, black is 16). These grades were then used to choose a codeword in an eight error correction code based on a Hadamard matrix of order 32. The codeword was transmitted to earth and then error corrected.
It was this practical experience with applied Hadamard transforms that led on to the use of Hadamard transforms in present-generation cellular systems including GSM and CDMA.
These use convolutional and block coding to increase the distance between a 0 and a 1 or rather a −1 and a +1. The process is described in more detail below. Note that channel coding is a distinct and separate though related process to code division multiple access. Both processes exploit the properties of the Hadamard matrix.
Channel coding produces ‘coding gain’ and code division multiple access produces ‘spreading gain’. Coding gain can be of the order of 10 dB or so and spreading gain in the order of 20 dB for lower user data rates. Together they show the extent to which the Hadamard transform contributes to the link budget of legacy cellular radio systems. OFDMA systems have to improve on this benchmark on all performance metrics not purely on single per user peak data rates.
3.2.4 Differences Between the FFT and the FHT
The FFT is best at modelling curves and sinusoidal waveforms. The hardest curve to model with a Fourier transform is a step function, also known as a square wave, where the edges of the waveform exhibit a theoretically infinite number of sinusoids. In practice, these can be approximated but it is the ‘Achilles heel’ of the Fourier transform (often described as ‘the Gibbs effect’).
The FHT is best at capturing square waves. The hardest curve to model with a Hadamard transform is a basic sine/cosine curve. This is intuitively consistent with matrix theory – describing square waveforms by putting numbers into squares.
Hadamard transforms when implemented as fast Walsh Hadamard transforms use only additions and subtractions and are therefore computationally efficient.
Fourier transforms require many multiplications and are slow and expensive to execute. Fast Fourier transforms employ imperfect ‘twiddle factors’ so trade accuracy against complexity and ‘convergence delay’.
The magnitude of an FFT is invariant to phase shifts in the signal. This is not true in the case of the FHT because a circular shift in one row of the Hadamard matrix does not leave it orthogonal in other rows. This is the Achilles heel of the FHT and is a weakness that underpins the ultimate limitations of CDMA in terms of error performance and susceptibility to AM/PM distortion.
However, with this proviso, the Hadamard transform has been and remains a fundamental part of the signal processing chain in present mobile phones both in terms of its application in discrete processes such as channel coding and code division multiplexing but also in a support role to other processes.
The fact that it is simpler to execute and has different but complementary properties makes it a useful companion to the FFT and the two processes working together provide the basis for future performance gain. Having mastered the theory, let’s examine how the Hadamard transform is applied in present radio systems.
3.2.5 Some Naming Issues
For brevity and in due deference to Hans Rademacher and Mr Walsh, we shall describe these codes as Hadamard codes used as a Hadamard transform.
As with the Fourier transform, the Hadamard transform computation can be decimated to speed up the computation process in which case it is known as a fast Hadamard transform (FHT).
In some ways, the FHT is easier to implement computationally as it does not require the ‘twiddle factors’ implicit in the FFT. This is because the discrete FFT is approximating and then describing a composite sinusoidal waveform (hence the twiddle factors). The FHT is describing square waves and therefore does not need additional approximation correction factors. The fast Hadamard transform (FHT) is used on the receive path. The inverse fast Hadamard transform (IFHT) is used on the transmit path.
As we have said, the FHT has properties that are distinct and different from the FFT (the fast Fourier transform) but are also complementary.
The combination of the two techniques, the FHT and FFT together, deliver a number of specific performance advantages. These benefits should include cost reduction, improved coverage, improved capacity and more consistent and flexible radio access connectivity.
3.2.6 How the FHT and FFT Deliver Cost Reduction
In the 1970s there was a consensus that it was going to be easier (cheaper) to filter in the time domain rather than the frequency domain and by implication, to process and filter in the digital domain rather than the analogue domain.
This started the process whereby channel spacing in cellular systems has relaxed from the 25 or 30 kHz used in first-generation systems to the 200 kHz used in GSM to the 1.25 MHz or 5 MHz systems used in present 3G networks. The process is taken further, for example in WiFi systems (20 MHz) and 3G systems (1.25 or 5 MHz) or advanced 3G systems (10,15,20 or 100 MHz). The objective is to reduce the cost of RF (radio frequency) filtering both in the handset and the base station.
3.2.7 The Need to Deliver Cost Reduction and Better Performance
However, user expectations of performance increase over time. User data rates in first-generation analogue systems were typically 1200 or 2400 bits per second, GSM data rates are tens of kilobits, 3G data rates are (supposed to be) hundreds of kilobits and have to compete in the longer term with local area WiFi systems delivering tens of megabits and personal area systems delivering hundreds of megabits (potentially WiFi at 60 GHz).
The performance of a radio system can be measured in terms of the radio system’s sensitivity, selectivity and stability.
Sensitivity is the ability of the radio system to extract a wanted signal from the noise floor. Improved sensitivity translates into improved range and/or an ability to support higher data rates. In terms of the user experience, sensitivity equals coverage and capacity.
Selectivity is the ability of the radio system to extract a wanted signal in the presence of unwanted signals from other users. As with sensitivity, improved selectivity translates into improved range and capacity. However, by relaxing the RF channel spacing over time, we have thrown away some of the selectivity inherent in narrowband radio systems so have the need to replicate this in some other way. In parallel, users expect to receive voice and nonvoice services in parallel so we have the need to support multiple data streams per user, which implies a need to provide additional per user channel to channel selectivity.
Stability is the ability of the radio system to perform consistently over temperature over time, which in turn is dependent on the short- and long-term accuracy of the frequency and time reference used in the transceiver. The move to higher frequencies in the microwave band has increased the need for a more accurate frequency reference, but this has been offset by the relaxation in RF channel spacing. The combination of higher data rates and the need to deliver improved sensitivity and selectivity in the baseband processing sections of the transceiver has increased the need for a more accurate (and potentially expensive) time reference. As we shall see later, this in a sense is the Achilles heel of present CDMA systems (their inability to scale to much higher data rates without an inconveniently accurate time reference). In Chapter 2 we showed how OFDM shifts some of the hard work involved here back into the frequency domain. In terms of the user experience, stability therefore translates directly into user data rates and the consistency of the user experience.
3.3 The Role of Binary Arithmetic in Achieving Sensitivity, Selectivity and Stability
In 1937, Claude Shannon’s MIT thesis ‘A symbolic analysis of relay and switching circuits’ helped to establish the modern science of using binary arithmetic in wireless (and wireline) communications. The science was consolidated by Richard Hamming in his work on error detection and correction codes (1950), digital filtering (1977), coding and information theory (1980), numerical analysis (1989) and probability (1991). Hamming formalised the concept of distance between binary numbers and binary number strings that is in practice the foundation of modern radio system design.
Table 3.1 Coding distance – sensitivity
| Coding distance – sensitivity |
| 0–1 |
In digital radio systems, we take real-world analogue signals (voice, audio, video, image) and turn the analogue signals into a digital bit stream that is then mathematically manipulated to achieve the three ‘wanted properties’ – sensitivity, selectivity, stability.
Note that analogue comes from the Greek word meaning proportionate. Analogue implies that the output of a system should be directly proportionate (i.e. linear) to the input of the system and is continuously varying. To represent these waveforms digitally requires a sampling process that has to be sufficiently robust to ensure that analogue waveforms can be reconstructed accurately in the receiver. (Harry Nyquist ‘Certain Factors affecting telegraph speed’ 1924).
Taking this small but significant proviso into account binary numbers can be used to deliver sensitivity.
For example, considering Table 3.1, moving the 1 further away from a 0 implies an increase in distance which implies an increase in sensitivity.
The greater the distance between two strings of numbers (code streams in CDMA), the better the selectivity between users. The two codes shown in Table 3.2 differ in 10 places, which describes their ‘hamming distance’3 from each other.
If two code streams are identical (no distance between them) they can be used to lock on to each other, for example to provide a time reference from a base station to a handset or a handset to a base station. Longer strings of 0s and 1s will produce distinct spectral components in the frequency domain that can be used to provide a frequency reference. An example is given in Table 3.3.
We can also use binary numbers as a counting system. Interestingly, as we shall see later, if we start arranging 0s and 1s in a symmetric matrix of rows and columns, the binary product (sometimes known as the dot product) of the numbers in a column or row can be used to uniquely identify the position of that column or row. This is the property (described earlier) known as sequency and is the basis of many of the error coding and correction schemes used in present radio systems.
Table 3.2 Coding distance – selectivity
| Coding distance – selectivity |
| 01101011010010100 |
| 10011011101100010 |
Table 3.3 Coding distance – stability
| Coding distance – stability (code correlation) |
| 01101011010010100 |
| 01101011010010100 |
Table 3.4 Counting in binary

Table 3.5 Barker sequence
| 11-bit Barker sequence |
| +1 −1 +1 +1 −1 +1 +1 +1 −1 −1 −1 −1 |
3.3.1 Coding Distance and Bandwidth Gain
A first step to increasing the distance between a 0 and a 1 is to change a 0 into a −1 and a 1 into a +1. If we take either a −1 or a +1 and multiply by a series of −1s and +1s running at a faster rate then the bandwidth of the composite signal is expanded. The converse process applied in the receiver will take the composite ‘wideband’ signal and collapse the signal back to its original (data) bandwidth. This is the principle of spreading gain used in CDMA systems and is in many ways analogous to the bandwidth gain achieved in a wideband FM radio system.
3.3.2 An Example – The Barker Code Used in Legacy 802.11 b WiFi Systems
Basic 802.11 b WiFi systems provide an example. The original 802.11 b standard supports data rates of 1Mbit/ and 2 Mbits/s using either BPSK modulation (1 Mbit/s) or QPSK (2 Mbit/s). The data bits are multiplied with an 11-bit Barker sequence at a 1-MHz data rate that expands the data bandwidth of 2 MHz to an occupied channel bandwidth of 22 MHz, giving just over 10 dB of coding gain.
Barker sequences are named after RH Barker. The concept was introduced, in his 1953 paper on ‘Group Synchronisation of Binary Digital Systems’ read at the IEE in London. They were/are widely used in radar systems to help in distance estimation and were first used in low-cost commercial two-way radio systems in the first generation of digital cordless phones developed for the 902–908 MHz US ISM band. Note that when demodulated the codes can be sum error checked by converting to binary numbers as shown in Table 3.4.
The 11-bit Barker code used in 802.11 b is as follows shown in Table 3.5.
If we take this spreading sequence and multiply it with an input data bit –1 and apply the rule that if the signs are different, the result is a −1, if the signs are the same the result is a +1 then we get the outputs shown in Table 3.6.
As you can see, the despreading code is the same as the spreading code.
Effectively we have answered the question ‘is at a −1 or +1?’ eleven times over and it is this that gives us the spreading gain.
3.3.3 Complementary Code Keying used in 802.11 b
However, if the WiFi data rate is increased to 11 Mbits per second, the spreading gain disappears.
In this case, the Barker code is replaced with 64 different 8-bit codes. The data bits are grouped into 6-bit symbols and each 6-bit symbol is mapped to one of the 64 codes. When the receiver demodulates the symbol bit stream, the 8 bits received should be one of the 64 8-bit code sequences which correspond to one of the 6-bit input data symbols. This is described as complementary code keying and is a good example of the use of sequency in the encode–decode process.
Table 3.6 Spreading/despreading codes
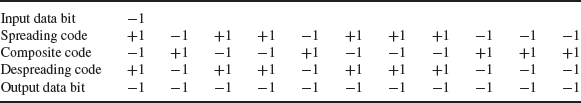
There is technically no spreading gain with this arrangement, though there is some (modest) coding gain due to the equality of distance between each of the 64 codes. The occupied bandwidth remains at 22 MHz.
The difficulty then arises as to how to manage higher user data rates. The answer with 802.11 b is to use an OFDM multiplex.
3.3.4 Walsh Codes used in IS95 CDMA/1EX EV
Present-generation wide-area cellular CDMA systems have to date not needed to support the higher data rates expected in local area systems, and for that reason have not to date needed to use an OFDM multiplex.
Code multiplexing and channel coding were therefore chosen to provide an acceptable compromise between implementation complexity and performance.
IS95 CDMA, the precursor of the CDMA2000 and 1XEV/DO system in use today, uses a 64 by 64 Hadamard matrix. This consists of 64 codes of length 64 of which code 0 is made up of all 1s and is used as a pilot and code 32 is made up of alternating 1s and 0s and is used for synchronisation. The other codes have their 0s and 1s, or rather –1s and +1s, arranged so that each of the codes is orthogonal to each other. Orthogonal in this context means that the codes are equally distinct from one another, or in other words do not interfere with each other as a product of the (FHT) transformation process. These codes are often referred to as Walsh codes (named after Joseph Walsh) but are in practice based on the Hadamard matrix. Each code has 32 places where it is different from other codes. In other words each code has a Hamming distance of 32 from other codes in the matrix.
In the uplink, every six information bits are mapped to one of the 64 bit rows of the Hadamard matrix. The 64 bits in the row are substituted for the original 6 bits and the 64 bits are modulated on to the radio carrier using QPSK modulation. This is an inverse fast Hadamard transform.
The base station applies a fast Hadamard transform on every 64 received bits. Ideally only one of the resultant FHT coefficients will be nonzero. The nonzero value determines the row number that in turn determines the 6 bits originally sent. In other words, the process exploits the property of ‘sequency’ implicit in the Hadamard matrix.
Elegantly, the IFHT/FHT delivers some useful spreading gain (64/6 = 10.75 dB). It is also error tolerant. Given that the Hamming distance between each Hadamard code is 32, up to 15 bits can be errored per block of 64 without corrupting the 64 bits actually sent.
The only slight snag is that all users are cosharing the 64 codes and have to be separated from each other by unique scrambling codes (−1s and + 1s running at the same rate as the data). The spreading codes deliver sensitivity, the scrambling codes deliver selectivity, the pilot and synchronisation codes deliver stability.
In the downlink, each row in the Hadamard matrix can be used to carry a unique channel to a unique user. Theoretically, this means 62 channels per 1.25 MHz of channel bandwidth (taking out the pilot and synchronisation channel). Every single information bit is replaced with the entire 64 bits of the users code (a 64/1 expansion). A data rate of 19.2 kbps therefore is spread to an outbound data rate of 1.2888 Mbps occupying a 1.25-MHz channel. As with the uplink, a scrambling code that is unique to the base station is also applied to provide base station to base station selectivity (actually a single code ‘pseudonoise’ sequence off set in time for each base station).
Later evolutions of IS95 have increased the matrix to 128 rather than 64 but the same principles apply. Either way, the CDMA multiplexing or channel coding have proved to be an effective format for exploiting the properties of the Hadamard matrix to deliver beneficial performance gains over simpler radio systems.
3.3.5 OVSF Codes in W-CDMA
The orthogonal variable spreading factor codes used in W-CDMA were originally conceived as a reordering of the Walsh codes used in IS95 CDMA with the added twist that user data rates could be changed every 10 milliseconds with users being moved between different lengths of spreading code (hence the ‘variable’ description used).
Table 3.7 OVSF Codes in W-CDMA
| SF4 | SF8 | SF16 |
| +1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1 | ||
| +1+1+1+1+1+1+1+1 | ||
| +1+1+1+1+1+1+1+1−1−1−1−1−1−1−1−1 | ||
| +1+1+1+1 | ||
| +1+1+1+1−1−1−1−1+1+1+1+1−1−1−1−1 | ||
| +1+1+1+1−1−1−1−1 | ||
| +1+1+1+1−1−1−1−1−1−1−1−1+1+1+1+1 | ||
| +1+1−1−1+1+1−1−1+1+1−1−1+1+1−1−1 | ||
| +1+1−1−1+1+1−1−1 | ||
| +1+1−1−1+1+1−1−1−1−1+1+1−1−1+1+1 | ||
| +1+1−1−1 | ||
| +1+1−1−1−1−1+1+1+1+1−1−1−1−1+1+1 | ||
| +1+1−1−1−1−1+1+1 | ||
| +1+1−1−1−1−1+1+1−1−1+1+1+1+1−1−1 | ||
| +1−1+1−1+1−1+1−1+1−1+1−1+1−1+1−1 | ||
| +1−1+1−1+1−1+1−1 | +1−1+1−1+1−1+1−1−1+1−1+1−1+1−1+1 | |
| +1−1+1−1 | +1−1+1−1−1+1−1+1+1−1+1−1−1+1−1+1 | |
| +1−−1+1−−1−−1+1−1+1 | +1−1+1−1−1+1−1+1−1+1−1+1+1−1+1−1 | |
| +1−1−1+1+1−1−1+1+1−1−1+1+1−1−1+1 | ||
| +1−1−1+1 | +1−1−1+1+1−1−1+1 | +1−1−1+1+1−1−1+1−1+1+1−1−1+1+1−1 |
| +1−1−1+1−1+1+1−1+1−1−1+1−1+1+1−1 | ||
| +1−1−1+1−1+1+1−1 | +1−1−1+1−1+1+1−1−1+1+1−1+1−1−1+1 |
This is shown in Table 3.7. The section in bold indicates that this is a tree-structured code. The codes to the right are longer copies of the codes to the left. The bold segment denotes a branch of the tree stretching from left to right. At SF4 (which means spreading factor 4) four users can be supported on each of 4 codes at, say a theoretical data rate of 960 kbits. The code tree then extends rightwards to SF256 (not shown for reasons of space and sanity) which would theoretically support 256 users each with a data rate of 15 kbits/s.
As the data rate changes, potentially every frame (every 10 milliseconds), users can be moved to the left or right of the code tree. However, if a user is at SF4, no users can be on codes to the right on the same branch. Similarly, if you have two users at SF8 or 4 users at SF16 on the same branch no users to the right on the same branch can be supported and so on rightwards across the branch.
A user at SF4 will have minimal spreading gain. A user at SF256 will have maximum spreading gain with a difference of just over 20 dB between the two extremes. As you would expect, this means that as a user’s data rate increases, the spreading gain decreases. The occupied bandwidth (5 MHz in this case) remains the same.
The spreading codes are used with scrambling codes (long codes) with the scrambling codes providing user to user/channel to channel selectivity on the uplink and base station to base station selectivity on the downlink. Additional short codes are used for uplink and downlink synchronisation.
This is the original Release 99 WCDMA radio layer code scheme. It provides a significant amount of flexibility both in terms of being able to support a wide range of variable (and potentially fast changing) data rates per user and a significant amount of flexibility in being able to support multiple data streams per user.
It does, however, require careful implementation both in terms of code planning and power planning. Although the variable spreading factor codes are orthogonal (hence their name orthogonal spreading factor codes), this orthogonality can be lost if code power is not carefully balanced or the nonlinearities inherent both in the radio system and the channel are not managed aggressively.
If orthogonality is compromised, unwanted error energy is projected across code channels that will then suffer from an unacceptably high error vector magnitude that in turn compromises sensitivity and selectivity that in turn compromises coverage (range) and capacity.
The mechanism for power management is an outer and inner control loop. The inner control loop also known as fast power control runs at 1500 Hz and if correctly implemented can be effective but in its own right absorbs a significant percentage of the available signal energy (about 20%).
HSPA aims to simplify this process and reduce some of the power control signalling and energy overhead by only using the SF16 part of the code tree and dispensing with fast power control. However, as you might have noticed, this takes away one of the desired properties of the OVSF code tree, which is the ability to support lots of users each with multiple simultaneous channels each at a variable data rate. In other words, much of the multiplexing capability of the OVSF code tree disappears if only SF16 is used.
The answer used in HSPA is to have a high-speed data-shared channel (HS-DSCH) that can be shared by multiple users with a MAC-driven access control based on 2 millisecond (and later 0.5 millisecond frames) that is not dissimilar to the contention based MAC used in present WiFi systems.
The challenge here is that the shared channel requires a new high-speed shared physical control channel (HSDPCCH). This control channel has to carry the channel quality indication (CQI) messages and acknowledgement/negative acknowledgement (ACK/NACK) messages that the MAC needs to decide on admission control and other factors, such as coding overhead, choice of modulation and transmission time interval.
This signalling is discontinuous, but when present increases the peak to average ratio of the transmitted (composite) signal and can also encounter relative timing issues with the other (dedicated) control channels.
If the high-speed control channel is not correctly detected, no communication takes place, which is potentially a little hazardous. The peak to average ratio can be accommodated by backing off the PA, but this has an impact on coverage (range).
In a sense, HSPA has exchanged the code-planning and power-planning challenges inherent in Release 99 WCDMA with code-sharing and power-sharing issues. This means that the RF performance of the handset and base station remains as a critical component of overall system performance.
Although some of the functional complexity at the PHY (physical) radio level has been moved to the MAC (medium access control) level, the effectiveness and efficiency of the MAC is dependent on the careful measurement and interpretation of the CQI and ACK/NACK responses.
The 7-dB step change in power that occurs when the CQI and/or ACK/NACK signalling is transmitted can trigger AM/PM distortion. This may cause phase errors that in turn will compromise CQI measurements or disrupt the ACK/NACK signalling.
This will probably be the determining factor limiting coverage and will probably require some conservative cell-geometry factors (signal versus noise rise across the cell) in order to maintain the signalling path (without which nothing else happens).
The requirement for a more complex and flexible multiplex can be met either by having a rather overcomplex code structure and/or an overcomplex MAC. Either or both can be problematic both from a radio planning and/or a handset/base station design perspective.
3.3.6 CDMA/OFDM Hybrids as a Solution
This seems to imply that something else needs to be done to allow these wide-area radio systems to deliver data rates that meet user’s likely future data-rate expectations.
The options are either to increase cell density and/or to increase the sensitivity, selectivity and stability of the handsets and base stations – preferably both.
In 1XEV, (including the most recent 1XEV-DO Revision A) handset enhancements are based on implementing receive diversity and advanced equalisation. Base-station enhancements include implementing 4-branch receive diversity (two pairs of crosspolarised spatially separated antennas) and pilot interference cancellation – a mechanism for getting unwanted signal energy out of the receive path.
A similar evolution path exists for HSPA. Advanced receiver techniques were first specified in Release 6 together with an enhanced uplink (HSUPA). Release 7 included standardised multiple antenna/MIMO proposals.
The downlink evolution road map for 1XEV and HSPA does, however, mean that we will have a combination of CDMA and OFDM in at least two mainstream wide-area cellular standards, sometimes generically described as ‘Super 3G’.
It is therefore useful to have an understanding of how a combination of CDMA and OFDM will work in terms of signal processing task partitioning.
Table 3.8 FHT/ FFT task partitioning in future radio systems

Table 3.8 shows the transforms, or rather inverse transforms used in the transmit path of a hybrid CDMA/OFDM transceiver.
The job of the inverse FFT in source coding is to take the composite time-domain waveform from the quantised voice, audio, image and video samples and to transform them to the frequency domain. The transform makes it easier to separate out the entropy (information) and redundancy in the source signal. The bandwidth of the signal is compressed. We cover this process in more detail in Chapter 9.
The bit streams representing the voice, audio, image or video samples are then channel coded using convolution and block encoding. This expands the occupied bandwidth but increases the distance between the information bits (−1s and +1s). This is an inverse Hadamard transform. The bit stream is then ‘covered’ with a spreading code and scrambling code. This is another inverse Hadamard transform. This further expands the occupied bandwidth.
The bit stream is then transformed again using an IFFT to distribute the data stream across discrete frequency subcarriers. Note that the IFFT is imposing a set of time-domain waveforms on a series of frequency subcarriers (lots of sine/cosine calculations).The number of points used in the I FFT/FFT and the characterisation of the IFFT/FFT determines the number of subcarriers and their spacing and is the basis of the ‘scaleable bandwidth’ delivered in an LTE system
In the receiver, the OFDM demultiplex (an FFT), recovers the wanted symbol energy from the discrete frequency subcarriers. The benefit here is that the symbol rate per subcarrier will be divided down by the number of subcarriers. The more subcarriers, the slower the symbol rate. This reduces intersymbol interference and makes the next stage of the process easier.
If this is a combined OFDM/CDMA system, this next stage involves the combining of the symbol stream (assuming this is a diversity or MIMO system) and the despreading and descrambling of the signal using an FHT. The result should be some useful diversity gain (courtesy of the multiple receive paths), some spreading gain (courtesy of the spreading/despreading codes) and additional selectivity (courtesy of the scrambling codes). This should make the next stage of the process easier,
This next stage is channel decoding, usually or often implemented as a turbo coder (two convolution encode/decode paths running in parallel). The FHT produces some additional ‘distance’ that translates into coding gain.
And finally, the bit stream now finally recovered from the symbol stream is delivered to the source decoder where an FFT is applied (frequency-domain to time-domain transform) to recover or rather reconstruct or synthesise the original analogue waveform.
3.4 Summary
We have studied the properties of the Hadamard transform and its practical application in present CDMA cellular systems and early generation WiFi systems. We have showed how the IFHT/FHT is used in the code division multiplex/demultiplex and in channel encoding/decoding to deliver ‘distance’ which can be translated into coverage and capacity gain. We have reviewed how the IFFT/FFT is used to add in an OFDM multiplex to slow down the channel symbol rate as a (potentially) power-efficient mechanism for accommodating higher user data rates.
Note that all these processes are absorbing processor clock cycles with the express purpose of achieving a net gain in system performance that can be translated into supporting higher data rates at lower power (the end-user benefit).
The challenge is to deliver these benefits consistently given that user expectations increase over time and that physics tends to dictate the limits of any process that we are using to realise performance gain.
In the context of HSPA, it is a real challenge to implement the PHY and MAC sufficiently robustly to provide a realistic chance of achieving the theoretical gains. The same implementation issues apply to future iterations of 1XEV/DO. In practice, it always tends to be a combination of techniques that together deliver performance improvements that are translatable into a better more consistent single-user experience. But now we need to establish how or whether this translates into an experience gain for multiple users.
3.5 Contention Algorithms
The well-established principle used in wire line and wireless systems is that a bidirectional communications channel is established between two communicating entities, people or machines for example.
In a digital system, whether wireless or wire line, the channel can be a specific time slot within a frame and the time-domain space can be shared with other users. Multiple time slot channels can also carry multiple information streams between two discrete end points or multiple end points. These information streams as stated earlier may be variable rate or in other words asynchronous. They may also have varying degrees of asymmetry as a session progresses.
In many telecommunications networks, asynchronous and asymmetric traffic is mapped on to an ATM (asynchronous transfer mode) multiplex for at least part of the end-to-end journey. Time slots in an ATM network are allocated in units of ten milliseconds.
ATM and related traffic-shaping protocols are covered in substantial detail in Chapter 8 of ‘3G Handset and Network Design’ so will not be repeated here. More usefully, we will review contention protocols used in WiFi and LTE.
As a reminder the LTE physical layer OFDM multiplex creates 15-kHz wide subcarriers that are grouped together as bundles of 12 subcarriers to make a 180-kHz resource block in the frequency domain that can then be resolved in the time domain in one-millisecond increments.
This allows the bit stream to be mapped to specific subcarriers that are experiencing favourable propagation conditions and/or to avoid subcarriers that are suffering from fast or slow fading. This increases throughput for a single user and theoretically at least should deliver a power efficiency gain as well. However, other users will potentially end up on a less favourable combination of subcarriers. The performance gain therefore comes with an opportunity cost attached for other users.
At the MAC layer contention algorithms have to arbitrate access between multiple users and manage at least four different traffic types, all with varying degrees of latency sensitivity. Voice, for example, is latency sensitive, best-effort data is not. Interactive and conversational traffic latency requirements fall between the two. Note that latency can and should be described as a first-order and second-order effect. The first-order effect is the amount of end-to-end delay. The second-order effect is how much that delay varies through a session. The theory is that the inherent variability of the channel itself is not noticeable to the user or at least not to an irritating degree.
In LTE, rather poetically, a stream of happy bits and sad bits are seeded into a best-effort data exchange. These bits describe the fullness of the buffer in the sending device. If the buffer is nearly full, sad bits will be sent to indicate that more bandwidth is needed in order to prevent buffer overflow with an implied potential loss of data. Happy bits suggest that some of the bandwidth presently allocated to that user could be reallocated to another user.
3.5.1 802.11 QOS and Prioritisation
LTE contention is therefore rather more proactive than present wire line or wireless systems in terms of real-time bandwidth reallocation, although work is still needed on realising power-efficient voice over IP.
Wire line ADSL provides a baseline model. With ADSL a number of users coshare line bandwidth with other users, the number being described as the contention ratio. Higher contention ratios will reduce single-user data rates but very high contention ratios will also reduce multiple-user throughput rates as there will be a substantial number of failed access and retry attempts that will translate into a loss of throughput. This can be both bandwidth inefficient and power inefficient.
ADSL is increasingly used for voice and real time video exchanges so the need to arbitrate between traffic with different latency requirements has increased over time.
WiFi contention protocols are similar to ADSL. The channel will be inherently less variable than wide-area LTE, though will still exhibit fast and slow fading and as with ADSL there is an end-user expectation that simultaneous voice and video calls can coexist with best-effort data both between two users and/or a multiple users including conversational conferencing.
802.11 has always traditionally been a connectionless contention-based access protocol. The traditional bandwidth allocation mechanisms, primarily the distributed coordination function and point coordination (PC) functions are not well adapted to and were never intended for time-bounded services such as real-time voice and/or video.
Table 3.9 shows the evolution of traffic shaping protocols developed by the work group under the task name 802.11 e.
Table 3.9 802.11 e QOS and prioritisation

The traditional bandwidth-allocation mechanisms used in 802.11 b (distributed coordination function and point coordination function using a point coordinator) are supplemented with two new protocols specified by the 802.11 e work groups based on traffic prioritisation (802.11 d). The new functions are EDCA – extended data channel access also known as the wireless media extension. This establishes four prioritisation levels, background, best effort (equivalent to existing DCF capabilities), video and voice. Video and voice data streams are given dedicated transmission opportunities known as TXOP. HCCA – hybrid controlled channel access, replaces or rather supplements the existing point coordination functions with the point coordinator replaced by a hybrid coordinator. The hybrid coordinator establishes eight queues in the access point ingress and egress ports, which can then treat individual data/traffic streams in accordance with their traffic specification (TSPEC).
3.5.2 802.11 f Handover
802.11 has always worked on the principle of ‘break before make’ rather than ‘make before break’. Simply put, if acknowledgement packets stop coming back, the device will channel scan and look for another beacon. The time taken to do this is typically about 70 milliseconds.
If you were walking from access point to access point within an office using WiFi for voice this would be annoying. A fast-roaming study group is looking at reducing these roaming delays to less than 50 milliseconds. The question then arises as to the degree of mobility being supported and whether the base station/access point or the user’s device should take the handover decision. Seamless ‘make before break’ handover protocols (used in cellular voice networks) imply substantial amounts of measurement reporting and a rework of the beacon structure (see 802.11 k below).
3.5.3 802.11 h Power Control
If measurement reporting is used then it makes sense to introduce power control. Power control improves the battery life/duty cycle of the user device and should generally help to reduce the noise floor, which in turn should deliver some capacity and coverage benefits. Power control, however, implies a rework of the beacon structure (see 802.11k below).
3.5.4 802.11 i Authentication and Encryption
802.11 i (ratified in June 2004) addresses the replacement of the existing (semisecure) authentication and encryption procedures known as wireline equivalent privacy (WEP) with WiFi protected access (WPA). This adds in the user authentication missing in WEP and makes it easier to implement SIM-based access – effectively bringing WiFi together with existing cellular authentication procedures. 802.i also describes a temporal key integrity protocol, a combination of WPA and AES, the American encryption standard for streamed media. The challenge here is to keep the configuration simple and to minimise any impact on header overheads and end-to-end latency budgets.
3.5.5 802.11 j Interworking
Originally established to address issues of 802.11a and Hiperlan interworking, additional work items include handover between 802.11 b, g and a and in the longer term, handover between WiFi and cellular (or alternative 802.16 /802.20 wide-area systems.)
3.5.6 802.11 k Measurement Reporting
802.11k measurement reporting introduces many of the techniques presently used in cellular (including GSM MAHO mobile-assisted handoff). Measurements collected and sent to the MIB Management Information Base) would include data rate, BER, SNR and a neighbour graph. One proposal is to use beacon compression to take out redundant information in persistent sessions and therefore release beacon bandwidth for measurement reporting. This would be known as a radio resource management beacon (RRM beacon).
3.5.7 802.11 n Stream Multiplexing
802.11n is intended as a protocol for managing multiple HDTV channel streams with additional space for simultaneous voice and data. The standard is going to mandate either the use of MIMO (multiple input/multiple output) techniques to get throughputs of up to 100 Mbit/s and/or the use of channel bonding. The headline data rate for two adjacent ‘bonded’ 40 MHz channels is 250 Mbit/s. The MAC overheads bring this down to about 175 Mbit/s.
3.5.8 802.11 s Mesh Networking
Finally (for the moment), 802.11s addresses mesh networking and ad hoc network protocols. This potentially brings WiFi into much more direct competition with Bluetooth-based personal area networks (PANS) and device access/device area networks (DANS). Mesh networking protocols may also facilitate a whole new generation of wearable WiFi products both for consumers and professional users.
3.6 The WiFi PHY and MAC Relationship
As a reminder, an 802.11 b and g access point will typically be configured in the 2.4-GHz ISM band to support 3 nonoverlapping 20 MHz radio channels with centre frequencies spaced either 30 MHz apart (Europe, Channels 1, 7 and 13) or 25 MHz apart (channels 1, 6 and 11 in the US).
Access points using the 5-GHz ISM band (802.11 a) will typically be configured to support up to 8 channels spaced 20 MHz apart (Europe Band 1 and US Band 1 and 2), with additional channels available in Band 2 in Europe and Band 3 in the US. Raw data rates of 54 Mbits/second are achievable in strong C/I conditions using high-level modulation and an OFDM multiplex to improve channel resilience.
Multiple channels capable of supporting multiple users cosharing a common 54 Mbps looks like a lot of bandwidth, but in practice there are significant MAC overheads and link budget constraints that result in substantially lower net throughput rates.
These MAC overheads increase when periodic two-way time-bounded services for example real-time voice and/or real-time voice and video need to be supported alongside best-effort services.
3.6.1 Voice and Video Frame Lengths and Arrival Rates
As shown in Table 3.10, voice frames are typically 92 bytes long and arrive every 20 milliseconds (the frame rate is determined by the syllabic rate). Video frames are 1464 bytes long and arrive every 40 milliseconds (assuming a 25 frame per second video rate). A 92-byte voice packet arriving every 20 milliseconds implies a voice data rate of 36.8 kbits/second (92 × 8 × 50). A 1464-byte video packet arriving every 40 milliseconds implies a video data rate of 292.5 kbits/second.
Table 3.10 Voice frame lengths, video frame lengths and arrival rates
| Voice frames | 92 bytes | Every 20 milliseconds |
| Video frames | 1464 bytes | Every 40 milliseconds (25 fps) |
| Data frames | 1500 bytes | |
| Fast data frames | 3000 bytes |
A combined voice and video call would have a combined data rate of 329 kbits per second. This is, however, the rate to support unidirectional voice and video. Although people do not (generally) speak at the same time, the MAC layer has to provision bidirectional periodic bandwidth (known as voice and video transmission opportunities) so the bandwidth occupancy is effectively doubled to 73.6 kbits/second to support a bidirectional voice call, 585 kbits per second to support two way video and 658 kbits per second to support two-way voice and video. This suggests a capacity of 13 voice channels per Mbit, 1.7 video channels per Mbit or 1.5 voice and video channels per Mbit (2-way video calls).
3.6.2 Data Throughput – Distance and MAC Overheads
Data throughput is dependent on the modulation used and channel coding. In 802.11 a and g, between 48 and 54 Mbps of gross data rate is available if 64 QAM is used in a lightly coded (3/4) channel, but this is dependent on having a strong C/I (carrier to interference ratio). As the C/I worsens, the gross data rate reduces to 23/36 Mbps (16 QAM), then 12–18 Mbps (QPSK), then 6–9 Mbps (BPSK) and the channel coding overhead increases from 3/4 to 1/2 (one error protection bit for each data bit). This is shown in Table 3.11.
Table 3.11 Data rates, modulation and coding in 802.11 a and g

Although there are more channels available in 802.11 a, the propagation loss is higher and the net throughput therefore falls faster as a function of distance (though this also means that access points can be positioned closer together so channel reuse can be a bit more aggressive). In 802.11g, a request to send (RTS) and clear to send (CTS) message is needed if bandwidth is coshared with an 802.11 b transmitter (known as working in mixed mode). This produces a significant decrease in real throughput. The effect of distance in 802.11a and the impact of RTS/CTS overhead in 802.11g when used with 802.11 b is shown in Table 3.12. Real throughput rates in 802.11g and 802.11a quickly fall to levels that are not much higher and sometimes lower than standard 802.11b.
RTS/CTS is a poll and response algorithm and therefore implies a scheduling delay in addition to introducing a significant protocol and time/bandwidth overhead.
Note that ‘mixed mode’ actually implies two sets of MAC overheads.
First, the way the contention MAC is managed in 802.11b is different from 802.11a and g. Both use time slot back off but 802.11 b uses a 20-microsecond slot width and a and g use 9 microseconds. If 11b devices are interoperating with 11g devices then the 20-microsecond slot length must be used. This means that contention overheads will be higher.
Similarly with 11b devices, there is a choice of a long 192-microsecond and/or short 96-microsecond preamble. The OFDM preamble is 20 microseconds. In mixed mode, either the long or short 11b preamble will need to be used to support 11b devices. This means that preamble overheads will be higher.
Table 3.12 Effect of distance on 802.11 a, b and g throughput, effect of mixed mode b and g signalling overhead on 802.11g throughput

Secondly, mixed mode now also implies that the MAC will be simultaneously loaded with time-bounded (periodic) and best-effort traffic. This will have a significant impact on throughput and capacity.
Taking these MAC overheads into account, Table 3.13 shows typical throughputs for TCP/IP best-effort data and/or UDP throughput. The table is from an Atheros White Paper and includes their proprietary bonded (40 MHz) channel solution giving a max throughput of 108 Mbps. Note that time-bounded services would normally use UDP (unacknowledged datagram protocol) rather than TCP (with transmission retries).
Table 3.13 MAC overheads when supporting TCP or UDP

SIP (session-initiation protocol) places an additional bandwidth overhead on the UDP throughput of approximately 8 kilobytes every time a voice, video or voice and video session starts or is modified.
3.6.3 Mobility, Handover and Power Control Overheads
The above also excludes any measurement and signalling overheads introduced by the need to support mobility. As long as a user stays in one place then these overheads can be avoided. This may be/probably is the case for Skype laptop users but may not/probably will not be the case for people expecting to use WiFi voice from their mobile broadband device either at a public access hot spot or on a corporate, SOHO or home wireless LAN.
Mobility overheads include the need to do measurement reporting (802.11k), the use of measurement reporting to manage handover algorithms (802.11f) and/or the use of measurement reporting to manage per packet power control (802.11h).
Most transceivers can now collect RSSI (received signal strength indication) at a per packet level. Given that the channel is reciprocal (same RF channel on the uplink and downlink) it is easier to do measurement reporting with WiFi than it is with cellular (which uses a different radio channel on the uplink and downlink each with different propagation properties).
However, it is all very well collecting this information but then you have to decide what to do with it. There has not been much point up to now in doing power control with best-effort data. If the RX level is good then you just send the data faster using higher-order modulation and/or with reduced channel coding.
Voice, video and/or voice and video combined are, however, different in that they occupy periodic bandwidth with typically a longer (more persistent) session length. If the user is close to the base station then it is worth reducing power to a level at which packet error rates can be kept above the coding threshold of the channel encoder and the error threshold of the source decoder. Reducing the TX power helps reduce battery drain on the uplink but also tends to improve receive sensitivity so the downlink usually benefits as well but care needs to be taken to make sure the power control doesn’t take up more bandwidth and/or power than it saves.
Table 3.14 Power control dynamic range in 802.11. Reproduced by permission of California EDU
| Power in dBm | Power in milliwatts/microwatts |
| 20 | 100 milliwatts |
| 17 | 50 milliwatts |
| 15 | 30 milliwatts |
| 13 | 20 milliwatts |
| 7 | 5 milliwatts |
| 0 | 1 milliwatt |
| −10 | 100 microwatts |
The range of RSSI measurement in a 802.11 transceiver is typically 60 dB. The range of power control is typically either 20 or 30 dBm as shown in Table 3.14. This is less than you find in a wide-area radio interface (35 dB for EDGE, 80 dB for 1XEV or Rel 99 UMTS) but still potentially useful. The usefulness depends (as with handover algorithms) on how mobile the user is likely to be.
Table 3.15 is taken from a University research project on mobility thresholds.4 It assumes two users a certain distance apart with one of the users walking away from the other user at 1.5 m (metres) per second. The closer the distance between the two transceivers the faster the rate of change in terms of required output power. For example, at a distance of 9 m, walking 2 m away (just over a second of elapsed time) results in a 2-dB power change. At a distance of 70 m, a distance of 20 m has to be covered before a 2-dB step change occurs (13 seconds of elapsed time). It is therefore plausible that a per packet power control algorithm could be deployed that could be reasonably stable when used in this type of ‘gentle mobility’ application and that could yield some worthwhile power savings and related link budget benefits. From a PA design perspective, however, it does mean the operating point of the amplifier will be constantly changing and this in itself has an impact on error vector magnitude and harmonics.
Table 3.15 Mobility thresholds
| Transmit power in intervals of 2 dBm | Distance (m) | Difference (m) |
| 0–2 | 7 | |
| 2–4 | 9 | 2 |
| 4–6 | 10 | 1 |
| 6–8 | 21 | 11 |
| 8–10 | 26 | 5 |
| 10–12 | 36 | 10 |
| 12–14 | 46 | 10 |
| 14–16 | 70 | 24 |
| 16–18 | 90 | 20 |
The ability to power control handsets and access points also provides an opportunity to optimise the radio system in terms of channel reuse and coverage. This will become increasingly important if voice users become a significant percentage of the offered traffic mix.
Table 3.16 Typical 802.11 a and g and b receive sensitivity

3.6.4 Impact of Receive Sensitivity on the Link Budget
The link budget is a composite of the TX power, TX accuracy (typical error vector magnitude for an 802.11g transmitter should be <1.5% and <2% for 802.11a, but is often much worse), path loss and sensitivity. Sensitivity is a function of data rate. With 802.11 a and g higher data rates are achieved by using higher-order modulation, every time the modulation state is doubled (for example from BPSK to QPSK), another 3 dB is needed on the link budget, moving from 16 QAM to 64 QAM implies a 6-dB increase. In practice, the fact that on the TX side, EVM tends to get worse with higher-order modulation means that the real implementation losses are higher. Table 3.16 shows some typical receive sensitivity figures (and some claimed sensitivity figures) at different data rates.
3.6.5 Linearity Requirements
Table 3.17 compares three generations of cellular transceiver with a WiFi (802.11 a and g) transceiver in terms of peak to average ratio (PAR), peak to mean ratio, whether the radio channels are full or half-duplex and the power-control dynamic range.
The use of OFDM in 802.11 a and g delivers some significant benefits in terms of channel resilience and ISI performance (a constant and relatively low symbol rate) but the cost is a substantial envelope variation on the composite modulated waveform (although the example
Table 3.17 Linearity comparisons between cellular and WiFi (OFDM)
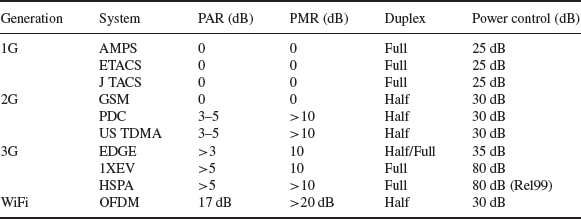
of 20 dB peak to mean is a worst-case condition with all 52 subcarriers lining up over a symbol period). This requires additional linearity from the PA, which is difficult to realise in a power-efficient manner.
In contrast, Bluetooth 2.0 EDR (which uses GFSK, four-phase DQPSK or optionally eight-phase DPSK) is arguably more power efficient.
GSM, PDC, TDMA and EDGE are described as half-duplex in that they don’t transmit and receive at the same time (except theoretically for EDGE Class 13 through 18) but they still have an RF duplex separation between transmit and receive that translates directly into an improved sensitivity figure.
WiFi is half-duplex in that it uses the same RF channel that is time division duplexed to separate the uplink and downlink. This means the sensitivity will always be less than a full duplexed cellular system using separate RF channels for the uplink and downlink.
This matters because sensitivity is part of the link budget and the link budget determines coverage (range) and capacity. On this basis it could be argued that WiFi is not particularly spectrally efficient. The additional linearity needed also means it is not particularly power efficient when compared to legacy cellular or Bluetooth systems.
3.6.6 WiFi’s Spectral-Efficiency and Power-Efficiency Limitations
So the WiFi PHY is arguably less spectrally efficient and less power efficient than cellular and probably less spectrally efficient and certainly less power efficient than Bluetooth.
The WiFi contention optimised MAC when used for connection orientated time-bounded traffic is arguably less efficient than existing connection optimised MACS used in cellular and Bluetooth voice applications.
3.6.7 Why WiFi for IP Voice and Video?
IP voice, IP video and IP voice and video are all potentially supportable on WiFi radio systems but require careful implementation in terms of PHY management (channel reuse) and MAC management (the cosharing of common bandwidth between time-bounded voice and best-effort data).
Whether WiFi is efficient or not when compared to other options is to an extent irrelevant if costs are sufficiently low to drive adoption though an inefficient PHY and MAC will always have a cost in terms of additional battery drain.
The addition of OFDM increases processing overhead in the receive chain (the cost of the receiver FFT) and processing overhead in the TX chain (the inverse FFT). The additional linearity implied by the envelope of the composite waveform also reduces TX power efficiency when compared to other radio systems.
However, OFDM is really the only way to realise data rates in the region of tens of Mbps (direct sequence spread spectrum starts to run into jitter problems at these higher speeds and you need the OFDM multiplex to slow the symbol rate down in order to control ISI and increase multipath resilience).
In the longer term, WiFi with MIMO (multiple input multiple output) is one way of getting speeds of the order of 100 Mbps or more (the other way is to deploy in the 60-GHz band or to use channel bonding at 5 GHz.
This is one of those circular arguments. The WiFi PHY and MAC were never designed to support a significant mix of time-bounded services. It is reasonable to assume that IP voice, and in the longer term IP video and IP voice and video will become a progressively more important part of the offered traffic mix (and by implication a more important part of offered traffic value). This implies that handsets and access points will need to support higher data rates.
Higher data rates are achieved by implementing mixed mode 802.11 b and g, which implies additional contention overhead. The connection based nature of voice and voice and video calls also adds contention overhead and signalling bandwidth load.
The fact that users might expect to walk around when using WiFi IP voice implies the need to manage mobility, which implies the need to introduce network-assisted handover, which implies the need to implement RSSI or packet error measurements. If you are doing RSSI or packet error measurement you may as well implement per packet power control, which will help to improve capacity and coverage (by lowering the overall noise floor and by improving sensitivity in the receiver). This in turn will help reduce some of the power budget issues. The higher data rates are needed partly because time bounded services absorb bandwidth but also because time-bounded services are more expensive to deliver in terms of PHY and MAC utilisation.
Table 3.18 Power-consumption comparisons
| Lap Top | 70% |
| WLAN Card | 9% |
| WLAN Host | 21% |
| Total | 100% |
This all has to make sense to the network operator. Probably the most significant shift here will be the inclusion of network operator-specific browsers in the next generation of SuperSIM smart cards. Rather like existing application layer WiFi browser products, these will identify preferred networks, which of course means preferred networks from a network operator perspective. At this point, WiFi becomes a profit opportunity not a threat. But also the proposition must make sense to the end user and this implies a need for power efficiency.
Table 3.18 shows how power consumption is distributed in a lap top between the computer functions and WiFi connectivity functions, in this case, 802.11g.
Note this includes the RF power budget and directly related IP uplink and downlink packet processing overheads.
Table 3.19 shows the RF power budget.
Table 3.19 RF power budget
| TX | 2 watts |
| RX | 0.9 watts |
| Listen | 0.8 watts |
| Sleep | 40 milliwatts |
The RF power consumed including TX and RX efficiency loss is a function of the duty cycle
An example is given in Table 3.20 with a duty cycle that yields an average power consumption of 1.54 watts.
It might be considered that 1.54 watts is inconsequential, but in practice there is a further 2.85 watts of associated CPU power totalling 4.389 watts. 4 watts represents a 20 to 30% reduction in battery duty cycle, four hours is reduced to three hours.
Note that the typical peak power requirement is 20 watts for a lap top, 10 to 15 watts for a larger than smart-phone device, 5 to 10 watts for a smart phone and sub-5 watts for a basic phone. The RF power budget (including related processor overheads) of a smart phone is likely to be higher than 30% due to the additional signalling load incurred by mobile applications.
Table 3.21 shows typical WiFi throughput against received signal level. The table also shows an Atheros5 implementation where higher throughputs have been achieved at these levels, the difference being the improved sensitivity in the Atheros front end. Table 3.22 shows the relationship between the link budget and the path loss which will determine the coverage radius from the base station.
There are several points to make here. Theoretically, in a noise-limited channel a 3-dB increase in power or the equivalent increase in sensitivity translates into the error rate dropping a thousand fold. However, as can be seen in the industry standard example, between −88 and −89 dBm the packet error rate triggers a change of modulation scheme which reduces the throughput from 5.5 to 2 Mbps. As with LTE, an increase in sensitivity in the user device will delay the point at which additional error coding and/or a lower-order modulation is needed.
Table 3.20 Assumed uplink duty cycles
| TCP Uplink power consumption | |
| Duty cycle | 0.6× TX + 2× listen + 0.2× receive × 0.2× sleep |
| Watts | 0.6 ×2 + 0.2× 0.8 + 0.2× 0.9 × 0.2 ×0.04 |
| Total | 1.54 watts |
Table 3.21 Sensitivity gains

But one of the areas of particular interest for cellular operators is how LTE compares with WiFi both in terms of peak data rate and the throughput power budget for local connectivity (a few metres from the base station). On a like for like basis assuming similar TX power levels in a similar channel (20 MHz at 2.4 GHz or 20 MHz at 2.6 GHz) and a similar distance from the base station then the peak data rate and average data throughputs should be similar.
LTE replaces the OFDM used on the WiFi link with an OFDM-related modulation and multiplexing scheme described as single carrier frequency division multiple access (SC-FDMA). This reduces the envelope variation on the modulated waveform that at least in theory should allow the TX path to be marginally more efficient. However, it can be said that this ‘improvement’ is only from an onerous 12 dB or 16× to an only slightly less onerous 10 dB or 10×.
The relative performance will also depend on whether LTE is used in TDD or FDD mode and what band is used for local connectivity, but the assumption would be 2.6 GHz versus 2.4 GHz or 5 GHz for the WiFi connection. An alternative is to use LTE TDD devices that have been developed for the China market. However, if operators are aspiring to use LTE as an alternative to WiFi for example in femtocells then any noticeable performance advantage will probably need to be realised by improving sensitivity and selectivity in the user device.
From a user-experience perspective the throughput at 2.4 or 2.6 GHz will be very closely determined by distance. It can be seen that in these small-cell environments user-equipment sensitivity very directly determines the user experience in terms of distance from in this case the WiFi access point.
Table 3.22 Path loss and distance
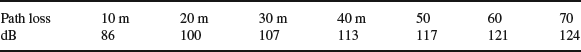
Note that in many technical papers written both about WiFi and wide-area mobile broadband, an assumption is made that high peak data rates equate to improved energy efficiency. This may be the case sometimes but not always and is dependent on how well the power down/power up algorithms are implemented in the user equipment (a function of software latency), hardware memory effects, for example in RF power amplifiers, the efficiency of the fast memory needed to cache short data bursts and the bandwidth and characteristics of the channel over which the data is transferred. The bandwidth characteristics of the channel will also determine the amount of gain realisable from MIMO operation.
Wider channel spacing, for example the 20 MHz used in WiFi and small-cell LTE deployments deliver high peak rates but the noise floor proportionately increases with bandwidth. In a large noise-limited cell it is quite possible that the average data throughput with narrower channel spacing, for example 3 or 5 MHz could be significantly higher than a 20-MHz channel used in the same propagation conditions and the megabyte per watt hour metric may be lower. For certain, the gain achievable from MIMO in larger cells will be marginal at best and may be negative in many channel conditions due to long multipath delay and/or low signal-to-noise ratio.
It is laudable and understandable that operators should expect and want LTE to be more effective and efficient than all other forms of connectivity in all operational conditions but whether this is an achievable or fiscally sensible short-term ambition must be open to question.
To get LTE to work as well or preferably better than WiFi for local connectivity implies a relatively aggressive adoption of MIMO techniques in LTE user equipment. The question then to answer is how often users will be close enough to an LTE base station to realise a real benefit from the composite MIMO LTE channel and how many of those users would actually be better served from a WiFi channel. The answer is probably not a lot or at least not enough to warrant the additional cost and complexity and weight and size and power drain added to some or most LTE devices.
For certain, it would seem that MIMO will deliver very marginal gains in larger-diameter cells, for example anything larger than a picocell or femtocell and may have a negative impact on throughput in many wide-area access channel conditions. In terms of band allocations this would suggest MIMO might be useful at 2.6 GHz and above but less useful in lower bands and more or less pointless at or below 1 GHz. This is just as well given the problems of getting enough volume and distance to achieve effective spatial antenna separation in low band device designs.
Additionally, there are proposals in LTE Advanced to bond channels together. This could either be adjacent channel bonding or bonding two channels from different bands, which would imply a need for yet another RX/TX processing path.
The rather pointless marketing pursuit of headline data rates is therefore resulting in the industry investing R and D dollars that from an end-user-experience perspective would be better being spent at least initially on optimising SISO performance within the existing band plans. In other words, present R and D priorities are probably disproportionate to the proportionate user experience gain that can be achieved. Inefficiently focused R and D spending has an associated opportunity cost (indirect cost). The direct and indirect costs of MIMO investment (and or work on channel bonding) have to be recovered from all LTE devices.
In the longer term, WiFi semiconductor vendors including Atheros are working on triband solutions that combine 2.4-GHz, 5-GHz and 60-GHz connectivity, suggesting that this may be the best option for delivering high and ultrahigh data rates in local area network environments.
Note that some parts of the industry still regard WiFi as being competitive rather than complementary to cellular connectivity. The development of recent applications where mobile broadband is used to provide connectivity to multiple WiFi devices and hybrid WiFi and mobile broadband integration in high-end automotive applications suggests this misconception will lessen over time.
In-car automotive applications are a form of machine to machine communication, albeit highly mobile. On a historic basis, automotive two-way area connectivity has been relatively narrowband and often predominantly downlink biased, GPS-based navigation being one example. Adding WiFi to the in-car environment could change this. If mobile broadband devices are integrated at the manufacturing stage then they can be reasonably easily performance optimised with efficient external antennas. They are also connected to a generously dimensioned 12-volt supply.
Devices introduced at a later stage may be much less efficient. A present example would be people using hand-held smart phones to do in car navigation. These devices can also be connected to a 12-volt supply typically via the cigarette lighter (who uses these any more for the purpose for which they were intended?). This solves the duty-cycle problem but the loading on the network can be substantial, a composite of signalling load to handle high mobility and the penetration loss into the car, particularly severe with tinted windows (of the order of 6 to 10 dB). Applications where maps are progressively downloaded into the device will be particularly bandwidth hungry.
This is an example where a particular LTE device used in a particular LTE application, which may not be the originally intended application, has the potential to inflict serious collateral damage on the network. The damage (opportunity cost to other users) will be disproportionate to the realisable subscriber and application value. If the device additionally has poor sensitivity and selectivity the collateral damage will be greater.
3.7 LTE Scheduling Gain
Scheduling gain is just one of many adaptive techniques used in any and all contemporary mobile broadband networks. These adaptive techniques can of course be used to compensate for poor channel conditions, which can be viewed as a proxy for insufficient network investment and/or poor user equipment sensitivity and selectivity, a proxy for a failure to invest in user equipment performance optimisation. This is the glass half-empty view of the world.
Alternatively, adaptive techniques can be seen as a mechanism for achieving performance extension based on network density that has been dimensioned to deliver specific user experience quality metrics across a wide range of loading conditions and user equipment where a compromise between cost and performance optimisation has been successfully achieved. This is the glass half-full view of the world. In practice, user device receive sensitivity and selectivity improves scheduler efficiency, which in turn increases the user data duty cycle.
Improving scheduler efficiency also improves e node B throughput that translates directly into lower energy cost per subscriber session supported and faster more responsive applications (improved application and task latency). This increases user value. In parallel, scheduler efficiency gain reduces network cost including energy cost. However, both the increase in user value and the decrease in network cost per subscriber served needs to be described and dimensioned.
There are three enhanced receiver options in the LTE standard:
- enhanced type 1 UEs (user equipment) with receive diversity;
- enhanced type 2 with chip-level equalisation;
- enhanced type 3 with adaptive receive diversity and chip level equalisation.
The spectral efficiency evolution for user equipment with two antennas is illustrated in Figure 3.1 showing the relative difference between HSPA Release 6, HSPA+ and LTE.
Figure 3.1 Evolution of spectral efficiency. Reproduced with permission of Nokia Siemens Networks.
These examples show the gains that can be achieved from increasing the granularity of the scheduling.
The scheduling algorithms in an e node B will be different to the scheduling algorithms used in a microcell or macrocell. In larger cells round-trip signalling delay means that the shorter scheduling options (for example half millisecond) cannot be used. Also, in the lower bands it is unlikely that the 20-MHz channel bandwidths used to get high peak data rates in WiFi or higher-band LTE networks could be deployed. This is not a problem but a function of fundamental channel properties at different frequencies.
Note that channel-sensitive scheduling does not deliver gain in larger cells or for users moving at faster than walking pace. Fast-moving users become part of the multichannel averaging process as they move through the continuously changing multipath channel.
The point about LTE is that it has been designed to be flexible enough at the physical layer to scale across a wide range of channel bandwidths and respond to a wide range of channel conditions. The ability to support 1.4 MHz, 3 MHz and 5 MHz, 10, 15 and 20 MHz channel spacing is one example.
This should deliver substantial throughput gains. However, we have said that LTE must also deliver more efficient throughput in terms of joules per bit and/or megabytes per watt hour both at the e node B and the user device (to extend the user data duty cycle) and in small cells and large cells and for stationary users and highly mobile users (potentially up to 500 kph and certainly 350 kph).
We have stated that scheduling at the physical layer in small cells can be in one-millisecond increments and/or across different OFDMA subcarriers in the frequency domain and/or across spatial channels. Scheduler signalling load is localised to the e node B.
Physical layer scheduling can be either max CQI,6 proportional fair or round robin. Max CQI scheduling allocates LTE resource blocks on the basis of measured channel quality. This is the most efficient scheduler from an operator/network perspective in terms of throughout against available bandwidth and power. However, edge of cell users would suffer very poor service. This would result in inconsistent user experience metrics that could trigger high product return and churn.
Round-robin services all users and devices in turn. It delivers the best user experience and hence lowest product return and churn,7 however, it is theoretically the least efficient option from an operator/network perspective (throughput against bandwidth and power). Proportional fair scheduling is a compromise point between these two extremes and can be set to meet specific user experience expectations.
Irrespective of where the scheduling compromise point is set, there is a directly beneficial relationship between user equipment performance and scheduler efficiency gain. Baseband interference cancellation and advanced receiver techniques will be particularly effective in interference-limited conditions; improved RF selectivity will also help. Improved RF sensitivity will be particularly helpful in noise-limited conditions.
Scheduling is also performed at packet level in order to differentiate best-effort traffic from streamed or interactive or conversational traffic and to respond to resource availability that in turn is a function of physical layer scheduling efficiency. Traditional handover to other channels and/or other bands is also supported providing opportunities to deliver macroscheduling gain.
This difference between micro- and macroscheduling gain is often underappreciated – both mechanisms work together to deliver efficiency gains, although as we are arguing these gains may be realised as spectral efficiency gain or network efficiency gain rather than per user power-efficiency gain.
LTE microscheduling and macroscheduling both rely on channel-feedback mechanisms (channel-quality indication and channel state indication) but are implemented at different time resolution, as small as a millisecond for microscheduling and typically a few seconds or several minutes for handover, depending on how fast the user is moving and the cell geometry and cell density. Packet scheduling (microscheduling) is realised in both the frequency and time domain. The CQI is computed from frequency-domain and time-domain reference symbols that are seeded into the channel data stream. The CQI measurements then determine whether QPSK, 16 QAM or 64 QAM modulation is used, the level of error coding, whether MIMO will be used and whether and how frequency selective scheduling is used. All of these will be influenced by how fast the user is moving. Frequency selective scheduling would typically be choosing say 25% of the subcarriers with the highest CQI.
In terms of e node B energy consumption, increased sensitivity in a user device operating in a noise-limited environment will result in a higher reported downlink CQI that will translate into a higher allocation of downlink time and frequency subcarrier resource blocks. A better link budget also translates into being able to support higher-order modulation and lighter error protection/correction overheads, which means that the ratio of information bits to error protection bits improves. Thus, any improvement in sensitivity will result in greater information throughput for a given amount of input energy. Note that channel coding and other adaptive physical layer mechanisms mitigate the impact of poor user equipment sensitivity or selectivity, but the bandwidth and power cost is effectively transferred to other users. The relationship of user equipment performance to overall network QOS and QOE is therefore direct and inescapable.
Given that the base station is sharing a finite amount of transmit power, for example 20 watts in a macro- or large microsite, then this means that more power is available to serve other user downlinks or put another way, the same amount of power is being used more efficiently across all users being serviced from the site.
A similar argument applies for devices with increased receive selectivity operating in an interference-limited environment.
On the uplink, user device TX efficiency will influence the user data duty cycle but TX linearity is equally important. The base station has to demodulate a signal modulated with noise- and phase-sensitive higher-order modulation. Much effort is expended in mitigating the impact of channel distortions on this complex signal but if the signal is distorted before it leaves the antenna of the user device there is not much that the base station can do with the received signal energy. This is the reason for the nearly 5× more strict EVM LTE specifications compared to WCDMA.
As with RX sensitivity, error vector magnitude is a specified performance metric described precisely in the conformance standard and user devices would generally be designed and cost engineered to exceed this standard by an acceptable but not unnecessarily large margin. A lower EVM with additional margin over and above the conformance requirement would, however, translate into higher uplink data rates and more uplink capacity at the base station.
Improving the RF performance in the front end of the user’s device reduces baseband coding overheads, which reduces baseband DC power drain. Applications will also run faster, which further reduces power drain and adds to user experience value. The benefit will accrue irrespective of where a user is in the cell though the maximum opportunity cost is likely to be incurred in edge of cell conditions. This can be said to generally apply in all macro-, micro-, pico- and femtocell topologies and also applies irrespective of whether the user is stationary or highly mobile.
3.7.1 LTE QOE and Compression
Some significant improvements are being made in compression techniques, particularly in digital TV where the DVB T2 standard is now complete and close to implementation.
However, digital TV is not power constrained and is essentially a one-way delivery medium. It also has a relatively generous first-order and second-order latency budget (first order is the amount of latency, second order is the variation between worst and best latency).
In a mobile broadband network, indeed in any two-way radio network, an increase in compression ratio means that more information can be loaded onto each bit sent. This means that the energy per bit relative to the noise floor improves. However, each bit is now carrying more information so if the bit is received in error proportionately more information is lost.
Even with all of the adaptive process in an LTE radio network, the radio channel is still an error-prone channel when compared to broadcast networks and the errors have a habit of occurring in bursts that can translate at higher layers of the protocol stack into packet errors and retries that are disruptive to compression techniques that rely on memory – the result is error extension.
Additionally, higher-order compression is computationally complex, power hungry and time hungry – the extra clock cycles needed to compress a signal in digital TV can be easily accommodated in the power and time budget both at the transmitter and the receiver (which is normally connected to the mains).
This is not the case in a mobile broadband network.
Doing higher-order compression on the user equipment TX path for instance will introduce compression delay, absorb energy and require performance parameters such as error vector magnitude to be more closely controlled (which in turn will have an impact on the user’s energy budget).
Compression techniques have generally been developed either to maximise broadcast transmission efficiency (DVB T as an example) or memory bandwidth efficiency (MP3 and MP4). These efficiency gains do not translate comfortably into a mobile broadband channel. Improvements in compression techniques may have some beneficial impact on future spectral efficiency but these benefits are likely to be marginal rather than fundamental and less useful than RF performance and baseband performance gain.
3.7.2 MOS and QOS
Measuring the quality of voice codecs is done on a well-established mean opinion score (MOS) basis and similar processes are being agreed for video perceived quality benchmarking. Note that if actual video quality stays the same but audio quality improves the perceived video quality will improve.
Similarly, user experience opinion scores will generally be higher when the delivered quality is relatively constant and will be higher than a service that is sometimes good and sometimes bad. This has an impact on scheduling implementation but it can be generally stated that any improvements in user equipment RF and baseband performance will translate directly into a better and more consistent user experience MOS.
The three companies referenced8 have web sites with information on voice and video MOS comparisons. Some additional standards work on application performance benchmarking may be useful in the longer term.
3.7.3 The Cost of Store and Forward (SMS QOS) and Buffering
Present and future mobile broadband networks have a mix of store and forward processes whose purpose is to reduce the cost of delivery both in terms of bandwidth and energy used. An example is SMS where in extreme circumstances several hours might elapse between a message being sent and received.
At the physical layer best-effort data will be buffered in the e node B or user’s device to smooth out traffic loading (which reduces the offered traffic noise) and/or to take advantage of CQI-based scheduling gain. There is an alternative argument that says short term (buffering) or longer term (store and forward) has an associated memory cost that needs to be factored in to the efficiency equation – fast memory in particular incurs a capital and operational (energy) cost.
There is also a plausible and probably understated relationship between receive sensitivity and data throughput in which it could be shown that an extra 3 dB of sensitivity translates into a doubling of the downlink data rate in a noise-limited environment. This could also be equated to a doubling of the user data duty cycle or a halving of the user power budget for the same amount of data. Similarly, it can be argued that a 3-dB improvement in selectivity would translate into a doubling of the downlink data rate in an interference-limited environment.
Some RX RF performance improvements can deliver a double benefit. Achieving better/lower phase noise in a front-end PLL and LNA improves sensitivity, but also improves the accuracy with which antenna adaptive matching can be realised.
The impact of a link budget gain in a mobile broadband network is similar to but different from the impact of a link budget gain in a legacy voice and text network. Improving the link budget in a voice and text network improves capacity and coverage, depending on whether any particular link at any particular time is noise or interference limited. The user experiences better voice quality (though the operator can trade this against capacity gain by using a lower rate codec), improved geographic coverage and in building penetration better, fewer blocked calls, fewer dropped calls and a longer duty cycle (minutes of use between battery recharge).
Improving the link budget in a mobile broadband network increases coverage and capacity and average per user data throughout rates and improves end-to-end latency. This translates into reduced application latency for the user, lower blocked session rates, lower dropped session rates and a longer data duty cycle (megabytes of use between battery recharge).
Assuming a mobile broadband network will also be supporting voice and assuming voice traffic is on an IP virtual circuit then the link budget will need to be sufficient to ensure users have the same voice quality, coverage and talk time that they have on present devices.
The link budget can be improved by increasing network density, improving base-station efficiency up to an interference threshold, or by improving user-equipment efficiency or a mix of all three.
Increasing network density has a capital and operational cost implication in terms of site acquisition, site rental, site energy costs and backhaul. The increased burstiness of offered traffic in a mobile broadband network means that backhaul needs to be overprovisioned to cope with higher peaks versus the traffic average. Backhaul costs are therefore becoming more important over time.
Improving the link budget by improving user equipment performance does not have these associated capital or operational costs. Additionally, improving TX and RX efficiency in user equipment can be shown to deliver nonlinear gains in scheduler efficiency (microscheduling gain).
If RF and baseband performance improvement in user equipment can be combined with extended band flexibility then additional gain can be achieved by implementing more comprehensive interband interoperator handover. However, every additional band increases cost and decreases sensitivity and selectivity. Additionally, interband measurements are slow and absorb network signalling bandwidth and power.
Ideally, user equipment would be capable of accessing all available bandwidth in all countries with a parallel capability to scan the available bandwidth for the best-available connectivity. To be efficient this would need a separate receive function in the user’s device (effectively a dual receiver). Such a device does not presently exist.
3.8 Chapter Summary
Using a combination of averaging, adaptation and opportunistic scheduling including in certain channel conditions spatial multiplexing and multiuser diversity, LTE delivers spectral efficiency benefits over and above HSPA Release 6 by roughly an order of three.
Power-efficiency gains are, however, presently proving to be more elusive both in WiFi and LTE devices and unless this is resolved user experience will be constrained.
OFDM in mobile broadband is allowing for high per user data rates.
Traffic-scheduling and queuing algorithms translate this into gains that can be enjoyed by multiple users cosharing the access resource, in this example a specific LTE channel resolved in both the time and frequency domain.
This is effectively algorithmic innovation at Layer 1 and Layer 2 and provides the basis for a plausible anticipation that mobile broadband will capture more access traffic from other guided and unguided access options than might have been originally expected with the only real caveat being power efficiency.
To an extent scheduling increases user device power efficiency but adequate gains are going to require a combination of algorithmic and materials innovation, a topic to which we return in later chapters.
1 LTE stands for long-term evolution and is the generic term used by the industry to describe the next generation of OFDM-based cellular radio networks.
2 We should also be covering Hilbert transforms and their role in IQ modulation but for reasons of space and brevity we recommend that you download this excellent tutorial http://www.complextoreal.com/tcomplex.htm. A less comprehensive but broader treatment can be found in the August 2011 RTT Technology Topic Transforms that can be downloaded here http://www.rttonline.com/techtopics.html.
3 Named after Richard Hamming who published a seminal paper on error coding in 1920.
4 http://www.cs.colorado.edu/department/publications/reports/docs/CU-CS-934-02.pdf.
5 Atheros is now owned by Qualcomm.
6 Channel quality indicators.
7 Churn is an industry term used to describe the migration of users from one service provider or network operator to another usually for reasons of poor service. If handset subsidies are available this can be a particularly expensive problem. Churn rates in some markets at some periods have been as high as 25% per year.
8 http://www.opticom.de/.
http://psytechnics.net/.
http://www.radvision.com/.
