6
Traitor Tracing
Teddy FURON
IRISA, University of Rennes, Inria, CNRS, France
This chapter presents the problem of traitor tracing and the most efficient solution known, Tardos codes. Tracing codes form an application overlay to the transmission layer by watermarking: a codeword is generated for each user, then inserted, by watermarking, into a confidential document to be shared. First and foremost, the chapter emphasizes the modeling of collusion when several traitors combine their copies. Thanks to this model, mathematics (statistics, information theory) give us the basic limits of this tool.
6.1. Introduction
A valuable document is distributed to a group ![]() of n users, each labeled by an integer:
of n users, each labeled by an integer: ![]() = [n], where [n] := {1, . . . , n}. These users are not to be trusted. Some of them may “leak” this document. Nothing can stop them, apart from a deterrent weapon: traitor tracing. Each user receives a unique personalized copy of the content. We assume that it is possible to do this personalization by inserting a unique codeword into the content using a watermarking technique. If a leak occurs, decoding the watermark of the illegal copy will reveal the identity of the traitor, exposing them to severe prosecution. Traitor tracing explores the case where several traitors secretly cooperate to cover their tracks and prevent identification. This group of dishonest users is called a collusion.
= [n], where [n] := {1, . . . , n}. These users are not to be trusted. Some of them may “leak” this document. Nothing can stop them, apart from a deterrent weapon: traitor tracing. Each user receives a unique personalized copy of the content. We assume that it is possible to do this personalization by inserting a unique codeword into the content using a watermarking technique. If a leak occurs, decoding the watermark of the illegal copy will reveal the identity of the traitor, exposing them to severe prosecution. Traitor tracing explores the case where several traitors secretly cooperate to cover their tracks and prevent identification. This group of dishonest users is called a collusion.
This chapter is organized as follows. Section 6.1 introduces the main components: code construction, collusion strategy, accusation with a simple decoder, based on a score function and thresholding. Section 6.2 provides a simplified proof of Tardos’ original scheme. Section 6.3 presents the many extensions found in the literature, two of which are detailed in sections 6.4 (the search for better score functions) and 6.5 (the search for better thresholding).
6.1.1. The contribution of the cryptography community
Cryptologists were the first to study this problem. They came up with a model that explains what content and collusion attack are. Content is a series of discrete symbols (e.g. bits), some of which can be modified without damaging the use of the content. Only the defender (the official source of the document) knows the location of these modifiable symbols, which they can use to insert a user’s codeword into the content. On receiving the document, the traitors can reveal certain so-called detectable positions by comparing their versions. This model, known by the name Marking Assumption, was invented by Boneh and Shaw (1998).
The model restricts what traitors can do to detectable positions. The group of c traitors is denoted by ![]() = {j1,. . . , jc} ⊂
= {j1,. . . , jc} ⊂ ![]() . The narrow-sense version (or restricted digit model) requires traitors to assemble the pirated copy of the document symbol by symbol. If they have the same symbol in a certain location, the position is not detectable and this symbol is found in the pirated copy. Otherwise, at a detectable position, they choose one of their symbols at this location, according to a certain collusion strategy. This model is summarized by:
. The narrow-sense version (or restricted digit model) requires traitors to assemble the pirated copy of the document symbol by symbol. If they have the same symbol in a certain location, the position is not detectable and this symbol is found in the pirated copy. Otherwise, at a detectable position, they choose one of their symbols at this location, according to a certain collusion strategy. This model is summarized by:
where y is the hidden sequence in pirated content, yi is its symbol at the ith position and xj,i is the hidden symbol in the copy of the jth user at position i.
Note that there are as many codewords ![]() as there are users, and their length is m.
as there are users, and their length is m.
There are other less restrictive models for collusion: the wide-sense version or arbitrary digit model (Boneh and Shaw 1998), the unreadable digit model (Boneh and Shaw 1998), the general digit model or the weak marking assumption (Safavi-Naini and Wang 2001; Fodor et al. 2018).
The second contribution of cryptologists was the definition of desirable properties of a code (group of identifiers) (Stinson and Wei 1998) and the proposal of solutions that were mainly based on error correction codes. These will not be covered since we now know that Tardos codes are better.
6.1.2. Multimedia content
In multimedia applications, content is modeled as a series of blocks (a few seconds of audio, a scene from a movie, a block of pixels from an image). A watermarking technique (see Chapter 3) hides a symbol of an identifier in each block. The idea of detectable position is useless here: everyone knows that each block hides a symbol. However, watermarking is a secret codeword primitive. Without this codeword, we assume that we cannot read or modify the hidden symbols. Therefore, an attack involves constructing the pirated copy by copying and pasting blocks from the personalized versions. Thus, the Marking Assumption model described in equation [6.1] becomes valid.
Figure 6.1 shows a standard solution in the film industry (called “DNA watermarking”). The watermarking of the video blocks is done in advance. For a binary code, there are two versions of each block: watermarked with a “1” or a “0”. The personalization during the distribution is fast because it is enough to sequentially take the blocks that hide the codeword of the user (Shahid et al. 2013). When the traitors have a certain block in only one version (watermarked with “1” for example), this symbol ends up in the pirated copy.

Figure 6.1. Sequential watermarking of a movie. A thumbnail image represents a video block, watermarked to hide the symbol “1” or “0”. The traitors sequentially form a pirated movie by selecting one of their blocks
6.1.3. Error probabilities
The most important criterion in the specifications is to avoid accusing an innocent user. The probability of accusing at least one innocent user is noted by ![]() . This probability must be low and we must make sure that it is smaller than a level ηR stated. This is what we call proof of robustness.
. This probability must be low and we must make sure that it is smaller than a level ηR stated. This is what we call proof of robustness.
The second criterion is the identification of traitors. We must set a goal:
- – “catch one”: the aim is to identify at least one traitor;
- – “catch all”: the aim is to identify all of the traitors. You must assume that all traitors participate in the collusion fairly. It is impossible to identify a traitor if they have little involvement in the counterfeiting of the pirated copy;
- – “catch a colluder”: the aim is to identify one traitor in particular.
The completeness of a scheme comes down to proving that the probability ![]() of not achieving the set goal is smaller than a certain stated level ηC. The first two aims require investigating the events of accusation of the c traitors. This is difficult because these events are not independent. The last aim is simpler because it only considers one traitor.
of not achieving the set goal is smaller than a certain stated level ηC. The first two aims require investigating the events of accusation of the c traitors. This is difficult because these events are not independent. The last aim is simpler because it only considers one traitor.
In practice, ηC should be low enough so that traitor tracing is deterrent enough. ![]() is sometimes used as a metric to compare accusation schemes that meet all of the first criterion on ηR. Other comparisons are based on the number of identified traitors (“catch many”) still under the constraint
is sometimes used as a metric to compare accusation schemes that meet all of the first criterion on ηR. Other comparisons are based on the number of identified traitors (“catch many”) still under the constraint ![]() ≤ ηR.
≤ ηR.
6.1.4. Collusion strategy
The collusion strategy, or attack, describes the process that traitors use to create pirated content, and more precisely its impact on the series of symbols that will be extracted by decoding the watermark of the pirated content. This series of symbols is called the pirated series and is denoted by y.
The descent set is the set of all pirated series that a collusion can construct from the codewords of the traitors. According to the Marking Assumption [6.1], the descent set can contain 2md series for a binary code, where md < m is the number of detectable positions. A working hypothesis is that traitors share the risk evenly (unless there are traitors among traitors; seec Zhao and Liu (2006)), which reduces the descent set. How the accusation behaves for each pirated series of this set should then be judged, and this should be done for any possible collusion of a certain size. This is impossible. It results in more assumptions about the collusion strategy.
Four hypotheses are commonly used (Furon et al. 2008):
- – memoryless (Moulin 2008, definition 2.4): as we will see later, in Tardos codes, the symbols of the identifiers are statistically independent. We make the same assumption about the symbols of the pirated series. So the value of yi depends on the traitors’ symbols at this position only {xj1,i, · · · , xjc,i};
- – permutation invariant (Moulin 2008, definition 2.5): there is no concept of order among traitors. So the way of deciding the value of yi is invariant to any permutation of {xj1,i, · · · , xjc,i}. This means that this strategy only considers the empirical distribution (the histogram) of these symbols. In the binary case, this distribution is completely defined by the number σi of symbols “1” to position i:
 (so the number “0” is c − σi);
(so the number “0” is c − σi); - – stationary: we assume that collusion has a unique strategy that it employs across all positions. So we can leave out the index i ∈ [m] later;
- – random: this strategy is not necessarily deterministic.
The following model of a collusion attack of size c comes from these four hypotheses:
The attack is then described by the probability that the traitors choose a symbol “1” in the pirated series, when they have σ “1” of c symbols in their codeword to a certain position. In other words, traitors have c + 1 biased coins. At a certain position i, they have σi symbols “1”, they then flip the coin σi to choose the value of the symbol yi. The Marking Assumption (see equation [6.1]) requires that θc,0 = 0 and θc,c = 1. Amiri and Tardos (2009) mention an eligible channel. This model defines the set Θc of size c collusion strategies of size:
Here is a list of classic strategies at each position i ∈ [m]:
- – interleaving attack (or uniform attack): traitors randomly pick which of them will place their content block into pirated content. If σ of them have block “1”, then the probability of this block ending up in the pirated copy is:
- – majority vote: traitors choose the majority symbol:
- – minority vote: traitors choose the minority symbol when possible:
- – coin flip: the traitors toss an unbiased coin to choose when given a choice:
- – all 1 attack: the traitors always choose the symbol “1” when they can, that is, if σ > 0:
- – all 0 attack: the traitors always choose the symbol “0” when they can, that is, if σ < c:
These are only a few examples; the set of available strategies Θc is actually infinite.
6.2. The original Tardos code
In this chapter, Tardos codes denote a family of codes that share the same original structure (Tardos 2003, 2008). In other words, any modification to the parameters of the code, or to the way of identifying, compared to the original version by Tardos is not a reason to change the name: these are all Tardos codes. This section offers the original version.
6.2.1. Constructing the code
The construction is done in three stages:
- – a r.v. (random variable) P ∈ (0, 1) is defined. This can be a discrete r.v. with a set of possible values
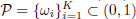 and associated probabilities {fi := Pr(P =
and associated probabilities {fi := Pr(P = 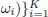 or an absolutely continuous r.v. with a probability density f : (0, 1) →
or an absolutely continuous r.v. with a probability density f : (0, 1) → 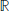 +;
+; - – the encoder takes m realizations of this r.v. independently according to its law. These realizations are stored in the vector p := (p1, . . . , pm), called secret series;
- – the encoder generates the codewords of the users by independently drawing n × m Bernoulli r.v. such that Xj,i ~
 (pi). The code X is a binary matrix of size n × m, and the codeword of the user j is xj = (xj,1, . . . , xj,m). This means that, for all users, Pr(Xj,i = 1) = pi depends on the position in the series.
(pi). The code X is a binary matrix of size n × m, and the codeword of the user j is xj = (xj,1, . . . , xj,m). This means that, for all users, Pr(Xj,i = 1) = pi depends on the position in the series.
The law of the r.v. P is public while the vector p is a secret shared with the accusation algorithm. The code is made up of n private codewords, in that a user only knows, at most, their own identifier, unless they are a traitor. By forming a collusion, traitors can share their knowledge of their c codewords.
6.2.2. The collusion strategy and its impact on the pirated series
The hypotheses on the collusion strategy in section 6.1.4 are very useful in deriving a statistical model of r.v. ![]() decoded symbols of the pirated series. We define Π(pi) := Pr(Yi = 1|pi) (the dependency in θc is omitted, unless there is ambiguity). At the index i, the symbols of the codewords of the traitors are distributed as Bernoulli r.v.
decoded symbols of the pirated series. We define Π(pi) := Pr(Yi = 1|pi) (the dependency in θc is omitted, unless there is ambiguity). At the index i, the symbols of the codewords of the traitors are distributed as Bernoulli r.v. ![]() (pi), given the construction of the code. So Σi, the number of “1” for c traitors in position i, following a binomial distribution
(pi), given the construction of the code. So Σi, the number of “1” for c traitors in position i, following a binomial distribution ![]() (c, pi):
(c, pi):
For a given position i, Yi is a Bernoulli r.v.: Yi ~ ![]() (Π(pi)) of parameter:
(Π(pi)) of parameter:
We see that Yi follows a different law from Xji and that this law depends on the collusion strategy. Note the following properties of this function illustrated in Figure 6.2:
- 1) Π(p) is a polynomial of degree at most c, where Π(0) = θc,0 = 0 and Π(1) = θc,c = 1;
- 2) two collusion strategies of the same size c produce two different distributions:
- 3) a collusion strategy produces an attack “between ‘All-0’ and ‘All-1”’, in that:
- 4) the so-called interleaving attack has the remarkable property that Π(p) is independent from c: ∀p ∈ [0, 1], Π(p) = p.

Figure 6.2. Π(p) := 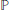 (Y = 1|p) for c = 3 a) and c = 5 b). All 1 attack: Π(p) = 1 − (1 − p)c, all 0 attack: Π(p) = pc, interleaving: Π(p) = p, coin flip: Π(p) = (1 − (1 − p)c + pc)/2, minority and majority do not have a simple formula. This function remains in the blue zone, marked by the “All-1” and “All-0” strategies
(Y = 1|p) for c = 3 a) and c = 5 b). All 1 attack: Π(p) = 1 − (1 − p)c, all 0 attack: Π(p) = pc, interleaving: Π(p) = p, coin flip: Π(p) = (1 − (1 − p)c + pc)/2, minority and majority do not have a simple formula. This function remains in the blue zone, marked by the “All-1” and “All-0” strategies
The second property proves the identifiability of the model when the size of the collusion is known. This means that we can learn the θc strategy if we see a large number of (Yi, Pi) occurrences. However, the fourth property shows that the identifiability of the model no longer remains when we do not know the size of the collusion: it is sometimes impossible to distinguish attacks of different sizes (since they generate the same distribution of symbols Yi).
In the same way, we can also calculate the distribution of Yi, knowing that one of the traitors has a “1” symbol in the i position (say xj1i = 1). Together, the collusion has σ > 0 symbols “1”, if the remaining traitors (c − 1) have σ − 1 “1”:
If xj1i = 0, the collusion has σ < c symbols “1”, if the remaining traitors (c − 1) have σ “1”:
Generally, we note Πx(pi) := ![]() (Yi = 1|pi, xj1i = x) for x ∈ {0, 1}:
(Yi = 1|pi, xj1i = x) for x ∈ {0, 1}:
The following properties are given:
- 1) Π(p) is the barycenter of Π1(p) and Π0(p) with the weights p and 1 − p:
- 2) at the extreme values of p, we have:
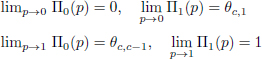
- 3) by a simple calculation: ∀p ∈ (0, 1):
where Π′(·) is the derivative of Π(·) (see equation [6.11]), with relation to p. This last equation does not have a simple interpretation, but it is essential for proving the completeness of the Tardos code (see section 6.2.3.2).
6.2.3. Accusation with a simple decoder
Once a pirated copy is found, decoding the watermark of content block by block results in the pirated series y, which is no longer random. To decide if user j is a traitor, a simple decoder calculates a score sj from the codeword xj, the pirated series y and the secret p:
where U (·): {0, 1} × {0, 1} × (0, 1) → ![]() is called the score function.
is called the score function.
The user is accused if sj > τ, where τ is a threshold. In other words, the accusation tests two hypotheses for each user: ![]() 0, the user j is innocent versus
0, the user j is innocent versus ![]() 1, the user j is guilty. Let
1, the user j is guilty. Let ![]() fp and
fp and ![]() fn be false positive (wrongly accusing someone of being innocent) and false negative probabilities (exonerating someone that is guilty) of this test for each user. The r.v. modeling the score of an innocent user (a traitor) is denoted Sinn (respectively Stra). So
fn be false positive (wrongly accusing someone of being innocent) and false negative probabilities (exonerating someone that is guilty) of this test for each user. The r.v. modeling the score of an innocent user (a traitor) is denoted Sinn (respectively Stra). So ![]() fp =
fp = ![]() (Sinn > τ) and
(Sinn > τ) and ![]() fn =
fn = ![]() (Stra < τ).
(Stra < τ).
6.2.3.1. Robustness
The robustness requires the probability ![]() of accusing one innocent user in n tests to be smaller than ηR. As the codewords of the innocent users are independent (knowing p and y), the scores are also independent:
of accusing one innocent user in n tests to be smaller than ηR. As the codewords of the innocent users are independent (knowing p and y), the scores are also independent:
where n − c is the number of innocent users.
It is easy to see that if ![]() fp < ηR/n, the constraint of equation [6.21] is respected. Robustness is not so easy since we are faced with a rare event: a classic requirement is ηR ≈ 10−3 and n ≈ 106, so much so that ηR/n is of the order 10–9.
fp < ηR/n, the constraint of equation [6.21] is respected. Robustness is not so easy since we are faced with a rare event: a classic requirement is ηR ≈ 10−3 and n ≈ 106, so much so that ηR/n is of the order 10–9.
6.2.3.2. Completeness
Completeness considers the scores of c traitors. The aim is to relate the fact that ![]() (Sj < τ) =
(Sj < τ) = ![]() fn, ∀j ∈
fn, ∀j ∈ ![]() to the total probability,
to the total probability, ![]() , for different objectives (section 6.1.3):
, for different objectives (section 6.1.3):
- – “catch one”: failing to identify at least one traitor means that none have been accused:
This aim is therefore achieved if
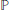 fn < ηC;
fn < ηC; - – “catch all”: failing to accuse all traitors means that at least one has not been accused. According to the union bound, we have:
which shows that the objective is achieved if
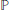 fn < ηC/c;
fn < ηC/c; - – “catch a colluder”: the probability of failing to catch a particular traitor is
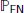 =
= 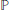 fn.
fn.
For a given level ηC, the most difficult objectives to achieve, in that ![]() fn is more constrained, are in the following order: “catch all”, “catch a colluder” and “catch one”.
fn is more constrained, are in the following order: “catch all”, “catch a colluder” and “catch one”.
6.2.4. Study of the Tardos code-Škorić original
This section explains the choices made in Tardos (2003, 2008) and the improvements offered in Škorić et al. (2008a). The proofs of robustness and completeness are simplified. We assume that ηC = ½ for a “catch one” or “catch a colluder” objective. Therefore, it is enough to show that ![]() fn < ½.
fn < ½.
The main idea is to choose a score function, such that the statistics of Sinn do not depend on the collusion strategy. So the scores of the users are compared to a universal threshold τ. Here, universal means that the threshold is set, regardless of the collusion strategy and (y, p). The constraint ![]() fp = P(Sinn > τ) must be guaranteed, whatever the size and collusion strategy. In statistical terms, the size c and the collusion strategy are nuisance parameters since they are unknown to the accusation algorithm. Ideally, the score of someone innocent must be a pivotal quantity, that is, whose distribution does not depend on nuisance parameters. In practice, only moments of orders 1 and 2 will be invariant.
fp = P(Sinn > τ) must be guaranteed, whatever the size and collusion strategy. In statistical terms, the size c and the collusion strategy are nuisance parameters since they are unknown to the accusation algorithm. Ideally, the score of someone innocent must be a pivotal quantity, that is, whose distribution does not depend on nuisance parameters. In practice, only moments of orders 1 and 2 will be invariant.
For an innocent user, insisting that ∀p ∈ (0, 1), ∀y ∈ {0, 1}, ![]() (U (Xinn, y, p)) = 0 and
(U (Xinn, y, p)) = 0 and ![]() (U (Xinn, y, p)) = 1 is equivalent to choosing the following score function (Furon et al. 2008) called Tardos-Škorić:
(U (Xinn, y, p)) = 1 is equivalent to choosing the following score function (Furon et al. 2008) called Tardos-Škorić:
We see that the score function takes positive values when the user has the same symbol as the one found in the pirated series. This quantity is especially large as this symbol is rare at this position in the code. This gives us a clue that this user is potentially a traitor. In the same way, the score function takes negative values if the symbols are different. This gives us a clue that the user is potentially innocent. Their final score reflects this evidence by adding up these quantities over all of the positions of the code. Let us define the random variables:
We see that this score function has good sense, making ![]() (Sinn) = 0 and
(Sinn) = 0 and ![]() (Sinn)= m, whatever the secret series, p, and the decoded pirated series y may be.
(Sinn)= m, whatever the secret series, p, and the decoded pirated series y may be.
Bernstein’s inequality gives an upper bound to the probability ![]() fp, which decreases exponentially with τ (Furon and Desoubeaux 2014). Other inequalities are possible (e.g. Hoeffding, Kearns and Saul). This makes it possible to find the necessary code length given in Tardos (2003, 2008). The r.v. U (Xinn,i, yi, pi) are independent (according to the construction of the code and the collusion strategy model) of zero-expectation and unit variance. Furthermore, ∀i ∈ [m], |U (Xinn, i, yi, pi)| < M, where
fp, which decreases exponentially with τ (Furon and Desoubeaux 2014). Other inequalities are possible (e.g. Hoeffding, Kearns and Saul). This makes it possible to find the necessary code length given in Tardos (2003, 2008). The r.v. U (Xinn,i, yi, pi) are independent (according to the construction of the code and the collusion strategy model) of zero-expectation and unit variance. Furthermore, ∀i ∈ [m], |U (Xinn, i, yi, pi)| < M, where ![]() . So, ∀τ > 0:
. So, ∀τ > 0:
This Bernstein bound is true for a given secret series since M depends on p. It is very useful in practice to find the value of the threshold τ, but this bound is not universal. One solution is to introduce a limit parameter 0 < t < ½, which is used to bound the score function1. The score function becomes:
One consequence is that we can now set M to ![]() . Equation [6.27] is now valid, whatever the couple (p, y).
. Equation [6.27] is now valid, whatever the couple (p, y).
As for the score of a traitor, using the properties of section 6.2.2, we can show that:

where Π′(·) is derivative of Π(·) (see equation [6.11]) in relation to p.
The choice made in the original article (Tardos 2003) by an absolutely continuous r.v. P of density:
gives:
For any strategy following the model explained in section 6.1.4, ![]() (Stra) → 2m/πc when t → 0 (in fact, we can show that 2(1 − t)c − 1 ≤ Π(1 − t) − Π(t) ≤ 1). The more traitors there are, the lower
(Stra) → 2m/πc when t → 0 (in fact, we can show that 2(1 − t)c − 1 ≤ Π(1 − t) − Π(t) ≤ 1). The more traitors there are, the lower ![]() (Stra) is, and, at the first order, the distribution of Stra converges with that of Sinn. To combat this effect, we need to increase the length of the m code.
(Stra) is, and, at the first order, the distribution of Stra converges with that of Sinn. To combat this effect, we need to increase the length of the m code.
The score Stra is a sum of m finite variance independent r.v. The law of Stra tends toward a Gaussian distribution when m → ∞, according to the central limit theorem (assuming Lindeberg’s condition to be true). So, mean and median converge asymptotically: ![]() (Stra <
(Stra < ![]() (Stra)) ≈ ½ (a more precise proof of completeness uses a probability bound that Stra deviates from its expectation, like a Chebychev bound, for example). This makes
(Stra)) ≈ ½ (a more precise proof of completeness uses a probability bound that Stra deviates from its expectation, like a Chebychev bound, for example). This makes ![]() fn smaller than ½ if τ is smaller than
fn smaller than ½ if τ is smaller than ![]() (Stra).
(Stra).
All of these elements placed end-to-end give a constraint on the length of the code m. With a probability greater than ½ (assuming this is sufficiently deterrent), a particular traitor will be identified (whatever the collusion strategy) if 2m/πc(2(1 − t)c − 1) = τ. At the same time, the probability of accusing at least one innocent user will be smaller than ηR, if ![]() by equation [6.27]. These two parts limit the length of the code:
by equation [6.27]. These two parts limit the length of the code:
where:
By making t dependent on c, we can limit G(t, c). For example, let tc := 1 − ((h+1)/2)1/c (s.t. 2(1 − tc)c − 1 = h where 0 < h < 1) to get G(tc, c) ≤ 2 for h = 0, 9. In the end, robustness and completeness are proved if ![]() (n, c, ηR, 1/2) where:
(n, c, ηR, 1/2) where:
This is an asymptotic result (using the central limit theorem for completeness). In other words, m = Ω(c2 log n/ηR).
6.2.5. Advantages
This demonstration has the following advantages.
6.2.5.1. Pedagogy
Equation [6.29] is very important for understanding the construction of the code. Suppose the set secret code, that is, f(p) = δ(p − p0). In other words, P is no longer a r.v. but a constant p0 ∈ (t, 1 − t). In this case, ![]() (Stra) = m
(Stra) = m![]() (
(![]() (Xtra, Y, p0)). The code will be even shorter, as the expectation
(Xtra, Y, p0)). The code will be even shorter, as the expectation ![]() (Stra) will be larger than
(Stra) will be larger than ![]() (Sinn) = 0.
(Sinn) = 0.
Figure 6.3 plots the function ![]() (
(![]() (Xtra, Y, p)) according to p for classical attacks. We can see that p0 = 1/2 is a great choice to fight against the collusion strategy “interleaving”, since function y is maximal. On the other hand, this choice is catastrophic for the collusion strategy “minority vote”, since the function takes a zero value in 1/2 for c = 3. It then becomes impossible to distinguish the score of someone that is innocent from the score of a traitor since they have the same expectation. For c > 3, the minority strategy even gives negative expectations. To fight against the “minority vote”, it is better to choose a value of p0 close to 0 or 1, but this is a very bad choice against interleaving, for example. Figure 6.3 shows that it is impossible to choose a satisfactory value of p0 for all of the strategies.
(Xtra, Y, p)) according to p for classical attacks. We can see that p0 = 1/2 is a great choice to fight against the collusion strategy “interleaving”, since function y is maximal. On the other hand, this choice is catastrophic for the collusion strategy “minority vote”, since the function takes a zero value in 1/2 for c = 3. It then becomes impossible to distinguish the score of someone that is innocent from the score of a traitor since they have the same expectation. For c > 3, the minority strategy even gives negative expectations. To fight against the “minority vote”, it is better to choose a value of p0 close to 0 or 1, but this is a very bad choice against interleaving, for example. Figure 6.3 shows that it is impossible to choose a satisfactory value of p0 for all of the strategies.
Since the value of p0 must be decided at the code creation before the traitors choose their attack, the game is unfair for the defender. Introducing a random variable P reverses the situation: not only can traitors no longer adapt their strategy to the pi values (since p is a secret sequence), but they must also choose a unique strategy to “fight” against all cases, i.e. all of the values stored in p. Not knowing this strategy in advance, the defender is advised to choose values across the (0, 1) support, so that on average it gives ![]() (Stra). This is shown in equation [6.31].
(Stra). This is shown in equation [6.31].

Figure 6.3. The function p → E( (Xtra, Y, p)) for c = 3 (a) and c = 5 (b)
(Xtra, Y, p)) for c = 3 (a) and c = 5 (b)
6.2.5.2. Latest developments
Robustness and completeness were proved by Tardos (2003) for code length m = 100c2 log n/ηR. This constant 100 is unusual, but understandable: a code length proportional to c2 log n/ηR was the Holy Grail at the time. Our very simplified proof finds a much smaller multiplicative constant π2, which is only twice as large as the best result π2/2 (valid asymptotically when c → ∞ (Škorić et al. 2008a)).
6.2.5.3. Worst case attack
The strength of a collusion strategy is measured by its ability to decrease ![]() (Stra), which for equation [6.29] is proportional to the quantity Π(1 − tc) − Π(tc). For a given collusion size, it is the “minority vote” attack that is the most dangerous for this score function and density f (see equation [6.30]). The article by Škorić et al. (2008a) provides the same conclusion.
(Stra), which for equation [6.29] is proportional to the quantity Π(1 − tc) − Π(tc). For a given collusion size, it is the “minority vote” attack that is the most dangerous for this score function and density f (see equation [6.30]). The article by Škorić et al. (2008a) provides the same conclusion.
6.2.6. The problems
This demonstration has three problems.
6.2.6.1. Too restrictive
This educational study is simple, but only works for ηC = ½ and asymptotically for n → ∞. A more useful proof uses an upper bound of ![]() fn, which generally depends on
fn, which generally depends on ![]() (Stra). This variance is bounded by m since
(Stra). This variance is bounded by m since ![]() (
(![]() (Xtra, Y, p)2) = 1, ∀p ∈ [t, 1 − t]. A very loose bound, such as the Chebyshev inequality, gives a good result. Suppose that
(Xtra, Y, p)2) = 1, ∀p ∈ [t, 1 − t]. A very loose bound, such as the Chebyshev inequality, gives a good result. Suppose that ![]() fn must be less than ϵ, then for all values of n:
fn must be less than ϵ, then for all values of n:
In fact, the most critical part is the proof of the robustness, where the finest possible bound is required, while the proof of completeness is less challenging.
6.2.6.2. Ill-posed problem
This problem is common in any theoretical study, starting from the specifications set out in section 6.1. The size c of the collusion is an integral part of the problem, so much so that the code depends on c. This is true for the parameters (m, t, τ). However, the true size of the collusion is not known, neither to the codeword generator nor the accusation algorithm. One way to work around the problem is to assume that c ≤ cmax. This blinds the code to the true value of c. The robustness is always guaranteed, but the completeness is proven under the assumption that the true collusion size is less than, or equal to, cmax.
6.2.6.3. Function score that is too constrained
Here is a problem with the score function U (·) (see equation [6.24]). Its choice is too constrained. It must provide separability (the score of a traitor is statistically larger than the score of someone innocent) and, at the same time, the independence regarding the collusion strategy (the distributions of Sinn and Stra are almost set, at least for the first and second statistical moments – and using an approximation for Stra). This second property is crucial in order to find a universal threshold, τ, because of equation [6.27]. Disconnecting the separability and independence from the nuisance parameters provides more freedom to find more discriminating score functions. However, finding a threshold becomes more difficult.
6.3. Tardos and his successors
Many papers have been published on Tardos codes. This section provides a review by summarizing the known results on the length of code needed, as part of section 6.2.4, other criteria and extensions.
6.3.1. Length of the code
The most known improvement on code length was provided by Škorić et al. (2008a), which mirrored the initial score function by dividing the length by two. This score function (see equation [6.24]) is now the norm.
The following works have kept the same definition of P and U (·), as in Blayer and Tassa (2008), Škorić et al. (2008a), and Laarhoven and de Weger (2014), but have developed a finer analysis to reveal smaller constants. The latest developments on the constant κ := m/(c2 log n/ηR) are as follows:
- – asymptotically when c → ∞, κ → π2/2 ≈ 4, 93 (Škorić et al. 2008a);
- – for a large collusion, κ = π2/2 + O(c−1/3) (Laarhoven and de Weger 2014);
- – for all c > 2, κ = 10.89.
6.3.2. Other criteria
6.3.2.1. Code length
This is the ultimate criterion. The authors of an article on Tardos codes propose other choices of P and U (·), and/or other bounds for error probabilities to deduce a necessary code length, depending on (c, n, ηR, ηC), smaller than latest developments. This is what has been performed in the previous articles (Tardos 2003, 2008; Blayer and Tassa 2008; Laarhoven and de Weger 2014).
6.3.2.2. Signal-to-noise ratio
Replacing the threshold τ by ![]() (Stra), we note the following condition:
(Stra), we note the following condition: ![]() (Sinn >
(Sinn > ![]() (Stra)) = ηR/n, which means that someone innocent should not have a score as high as the typical score of a traitor. A rough approximation is to say that Sinn follows a Gaussian law, since it is the sum of a large number of independent r.v. (but not of the same law, hence Lindeberg’s condition). So m ≈ ρ−1 (Φ−1(1 − ηR/n))2, where ρ is similar to a signal-to-noise ratio for a symbol coming out of the score function:
(Stra)) = ηR/n, which means that someone innocent should not have a score as high as the typical score of a traitor. A rough approximation is to say that Sinn follows a Gaussian law, since it is the sum of a large number of independent r.v. (but not of the same law, hence Lindeberg’s condition). So m ≈ ρ−1 (Φ−1(1 − ηR/n))2, where ρ is similar to a signal-to-noise ratio for a symbol coming out of the score function:
This criterion is used in the articles (Furon et al. 2008; Škorić et al. 2008a, 2008b). Special attention is given to the attack that minimizes ρ to define the code length needed to fight against a worst-case collusion. Note that the central limit theorem explains that ρ is a citerion (the larger it is, the better), but this theorem cannot be used for the proof of robustness.
6.3.2.3. Theoretical rates
A third criterion is the attainable rate of a simple decoder R(S)(P; θc), which is defined as mutual information I(Y; Xtra|P, θc) between the symbols of the pirated series and symbols of the traitor’s codeword. Section 6.4.2 provides more detail on this quantity from information theory, and defined by the equation [6.41]. As the decoder performs a hypothesis test for each user (is the user j innocent or guilty?), this quantity is the maximum among all of the simple decoders of the error exponent Efp of the probability of wrongly accusing an innocent person (for a given false negative probability ηC):
If it is not zero, ![]() fp can converge to 0, as m approaches infinity as fast as e−mR(S) (P;θc). In fact, a Chernoff type upper bound decreases toward 0 for the best simple decoder. Therefore, we guarantee
fp can converge to 0, as m approaches infinity as fast as e−mR(S) (P;θc). In fact, a Chernoff type upper bound decreases toward 0 for the best simple decoder. Therefore, we guarantee ![]() fp ≤ ηR/n if:
fp ≤ ηR/n if:
This makes the quantity R(S)(P; θc) a criteria (the larger it is, the better it is). Note that this is a theoretical result: the best score function achieving this error exponent is given by the Neyman–Pearson lemma (see section 6.4.1). However, this score function is the log-likelihood (see equation [6.40]), which requires the expression of ![]() (Y = y, Xtra = x|p, θc) and
(Y = y, Xtra = x|p, θc) and ![]() (Y = y|p, θc). This is a problem since these probabilities depend on the collusion strategy θc, which is unknown by the decoder initially. On the other hand, any simple decoder has a lower error exponent than R(S)(P; θc). Therefore, the collusion strategy minimizing this quantity will be a powerful attack for any simple decoder.
(Y = y|p, θc). This is a problem since these probabilities depend on the collusion strategy θc, which is unknown by the decoder initially. On the other hand, any simple decoder has a lower error exponent than R(S)(P; θc). Therefore, the collusion strategy minimizing this quantity will be a powerful attack for any simple decoder.
This criterion has been generalized to joint decoders. These decoders calculate a score per user group of size ℓ. These decoders are theoretically more powerful, but their complexity proportional to the number of groups of size ℓ among n is much bigger. In fact, for ℓ = c, this leads to the concept of capacity (Moulin 2008; Huang and Moulin 2012, 2014).
6.3.3. Extensions
Literature on Tardos codes proposes three families of the following extensions.
6.3.3.1. Binary codes
The idea is to keep Tardos codes binary, but the pirated series y is not necessarily binary. This is an assumption that makes sense in multimedia applications, where the codeword symbols are hidden in the content using a watermark technique. This watermark layer is not perfect when traitors degrade the quality of pirated content (by lossy compression in video, for example). Deletions (noted by × symbols) or decoding errors (decoding a “1” while “0” was hidden in the content block) produce Marking Assumption violations.
The collusion strategy itself can be more complex than just copying and pasting blocks. Traitors can also merge “1” and “0” blocks (Schaathun 2014). The simplest is to merge an average pixel-to-pixel of images to video blocks. This will disrupt the decoding of the watermark, which can result in a “1” or “0” symbol, in × deletion (as in the unreadable digit model (Boneh and Shaw 1998; Huang and Moulin 2014) or the general digit model (Safavi-Naini and Wang 2001)), or a double detection (denoted by d): the watermarking decoder detects the merging of a block containing a “1” and a block containing “0”. In other words, the pirated series is no longer binary: y ∈ {0, 1, ×, d}m.
Another extension is to work with a watermark decoder that gives soft outputs (Kuribayashi 2010, pp. 103–117; Meerwald and Furon 2012, section V.B), like the likelihoods (l1,i, l0,i) that the ith block contains the symbols “1” and “0”.
From a theoretical point of view, the difficulty is extending the Marking Assumption: we must limit the power of traitors by constraining the set of possible collusion strategies. For example, if θc,σ(×) = 1, ∀σ ∈ {0, . . . , c}, then the pirated series is just a series of deletions that cancels any chance of identifying the traitor. From a practical point of view, the difficulty is creating score functions for these new symbols, × and d, (Pérez-Freire and Furon 2009, section 4) or these soft outputs (Meerwald and Furon 2012, section V.B).
6.3.3.2. q-ary codes
Another family of extensions offers the construction of code on a q-ary alphabet: xj ∈ {0, 1, . . . , q − 1}m. The Marking Assumption stays the same: when the traitors all have the same symbol, it is found in the pirated series. The difficulty is modeling the collusion strategy for detectable positions. The models wide-sense version (or arbitrary digit model) (Barg et al. 2003) and narrow-sense version are two examples.
The generalization of the probabilistic model θc in the case of q-ary was never considered since its size is too large: θc stores all of the probabilities ![]() (y|t) for y ∈ {0, 1, . . . , q − 1} and the type t (or empirical distribution, histogram of frequencies) of the traitors’ symbols. It turns out that the number of types on c symbols of an alphabet of size q can grow as
(y|t) for y ∈ {0, 1, . . . , q − 1} and the type t (or empirical distribution, histogram of frequencies) of the traitors’ symbols. It turns out that the number of types on c symbols of an alphabet of size q can grow as ![]() , i.e. O(cq−1). Simpler models are used instead (Boesten and Škorić 2011, 2013; Huang and Moulin 2014; Škorić and Oosterwijk 2015).
, i.e. O(cq−1). Simpler models are used instead (Boesten and Škorić 2011, 2013; Huang and Moulin 2014; Škorić and Oosterwijk 2015).
6.3.3.3. Joint decoders
The final extension is the concept of joint decoders. As mentioned before, these decoders calculate a score for a group of ℓ users. Information theory shows that score functions can be more powerful: the ℓ-uplets made up of only traitors will statistically have a higher score than ℓ-uplets of innocent people. However, the number of scores to calculate is of the order O(nℓ), which quickly becomes prohibitive in calculation time.
Proceeding iteratively gives a tractable complexity. At the first iteration, simple scores are calculated, that is, one score per user. The users who have the greatest scores are suspected, and the others are innocent. The second iteration calculates the scores for all pairs among the suspected users, and so forth. The idea is to reduce the number of suspects so that each iteration calculates a more or less constant number of scores, although ℓ gradually increases.
Another idea is that an identified traitor is a snitch. Knowing the identity of certain traitors and their codewords, makes it possible to design more discriminating score functions. So, an iterative decoder can accuse someone if their score is high enough, and integrate their codeword into the score function, which will allow more separate, new scores to be calculated to find a second traitor more easily, and so on.
6.4. Research of better score functions
Among all of the further developments of the Tardos code, this section presents new, more powerful score functions for binary codes with the model described previously.
These score functions are more powerful since they are less constrained than the function of equation [6.24]. In fact, they give more separate expected scores of innocent people and traitors, but these do not have independent distributions of the collusion strategy. So, it is not possible to find a universal threshold like before. We return to this problem in section 6.5.
6.4.1. The optimal score function
The simple decoder corresponds to a series of n hypotheses tests to decide if the user j ∈ [n] is innocent or a traitor. Decision theory gives us the optimal test, that is to say the one that minimizes ![]() fn for a set
fn for a set ![]() fp. This is the Neyman–Pearson test. For this, we need to have a statistical model of the hypotheses to be tested.
fp. This is the Neyman–Pearson test. For this, we need to have a statistical model of the hypotheses to be tested.
- – If the user is innocent, then the symbols of their codeword are independent of the decoded symbols in the pirated content: Pr(Y = y, X = x|p, θc) = Pr(Y = y|p, θc)px(1 − p)(1−x).
- – If the user is a traitor, then the symbols correlate with those of the pirated copy: Pr(Y = y, X = x|p, θc) = Pr(Y = y|x, p, θc)px(1 − p)(1−x).
The optimal score function is simply the log-likelihood of the ratio of these two probabilities (we also call this accusation a maximum likelihood decoder):
The expressions of Π(·) and Πx(·) are given by equations [6.11] and [6.15]. Here, we have added the notation θc to make it clear that these functions are calculated for a given collusion strategy. In fact, this score function is only optimal if the collusion strategy is definitely θc. However, when accusing, this is never known. So this optimal score function is elusive in practice. Its interest is theoretical to measure the difference between a heuristic score function and optimality if we know the collusion strategy. Applying this test blindly proves to be dangerous: it will be optimal if the traitors really have used this strategy, it will possibly be disastrous for another strategy.
6.4.2. The theory of the compound communication channel
Let us pick out one specific traitor. Collusion can be seen as the transmission of its codeword through a binary communication channel. This channel is characterized by the transition probabilities Πx(p; θc) that depend on a state of the channel θc.
This is exactly the scenario of the compound communication channel, where a codeword is transmitted through a channel which is not totally unknown. The decoder knows that this channel belongs to a certain family, but it does not know which member of this family transmitted the codeword. Under certain conditions, it has recently been shown that a good strategy is to expect the worst (Abbe and Zheng 2010). Some channels produce more transmission errors than others. We can measure their quality by mutual information I(Y; X). The worst channel of the family is the one with the lowest measurement. If this is strictly positive, then a Neyman–Pearson decoder designed for this channel is theoretically justified. If the channel that was used is actually the worst, then the decoder is optimal. If the channel that was used is not the worst, then the decoder will at least be as powerful as the worst case.
In Tardos codes, the conditions of this compound communication channel theorem are met (Meerwald and Furon 2012). To apply this result, we need to find the worst collusion strategy, that is, the one that minimizes mutual information, as mentioned in section 6.3.2, R(S)(P; θc) = I(Y; Xtra|P, θc).
Knowing that the more traitors there are, potentially the more powerful they are (also many of us are often stupid), the decoder will assume that c ≤ cmax. Prosaically, the formula for the length of the necessary code (see equation [6.36]) says that it is pointless to want to accuse if there are more traitors. So the worst collusion strategy ![]() is one that minimizes R(S)(P; θc) for c = cmax. We will find this collusion strategy numerically, then we will put it into equation [6.40] to get a score function. We must therefore minimize the function:
is one that minimizes R(S)(P; θc) for c = cmax. We will find this collusion strategy numerically, then we will put it into equation [6.40] to get a score function. We must therefore minimize the function:
with:

Minimizing this function is not so easy when c is large. A useful simplification observes that the “interleaving” strategy quickly becomes (as c increases) one of the worst strategies in the Θc set. So the idea is to inject this model into equation [6.40] to get a new function score. This is what Laarhoven suggests (2014, equation (2)). The optimal score function for the strategy θcmax = (0, 1/cmax, . . . , (cmax–1)/cmax, 1) simplifies to:
Oosterwijk et al.’s score function (Oosterwijk et al. 2013, equation (43)) is in fact a first-order approximation when cmax is large:
Just like for the Tardos–kori decoder, the parameter t > 0 is needed to limit its amplitude. This score function is optimal, in that it produces a saddle point equilibrium for the signal-to-noise ratio criterion (see equation [6.37]) (Oosterwijk et al. 2013, th. 2).
6.4.3. Adaptive score functions
Adaptive score functions proceed in two steps. They analyze the pirated series y, knowing the secret p, to deduce an inference as to the collusion strategy. Then, they calculate a score using a score function adapted to what it has learned. This approach is sometimes called “learn and match”.
6.4.3.1. Estimation of the collusion strategy knowing c
If the decoder knows the size c but not the strategy, it can estimate θc from the observations (y, p). This is possible, according to property 2 of the function Π(·) (see equation [6.13]). The maximum likelihood estimator is given by the following formulation, which is solved numerically:
Another possibility is the expectation–maximization algorithm, since the distribution of Yi knowing pi is a mix of Bernoulli distributions. Let Σi = ∑j∈C Xj,i, that is, the number of “1” symbols that the traitors have at the index i. This variable will be a latent variable. The expectation–maximization algorithm starts by choosing a random collusion strategy, ![]() , and then iterates through the following steps.
, and then iterates through the following steps.
6.4.3.1.1. Step E
At the iteration t, this step evaluates the distribution of Σi ∈ {0, . . . , c} for an estimated strategy ![]() , because of the Bayes’ rule:
, because of the Bayes’ rule:
where Pr(Σi = σ|pi) is given by equation [6.10].
6.4.3.1.2. Step M
At the t iteration, this step gives a new estimate ![]() of the collusion strategy knowing the probabilities
of the collusion strategy knowing the probabilities ![]() of the latent variables. This is done by maximizing the expectation of the log-likelihood:
of the latent variables. This is done by maximizing the expectation of the log-likelihood: ![]() = arg max Q(θc) with:
= arg max Q(θc) with:
The (c − 1) parameters ![]() are estimated by maximizing this quantity, while
are estimated by maximizing this quantity, while ![]() , according to the Marking Assumption (see equation [6.3]). With the second derivative always being negative, maximizing means canceling the gradient given by:
, according to the Marking Assumption (see equation [6.3]). With the second derivative always being negative, maximizing means canceling the gradient given by:
So:
The algorithm iterates these two steps until the maximum of the function Q(·) no longer increases. This expectation–maximization algorithm can be generalized to take deletions or double detections into account (see section 6.3.3.1; (Furon et al. 2012, section V)).
6.4.3.2. Size of the unknown collusion
If the collusion strategy was correctly estimated, the score function used would be the likelihood ratio calculated for θc, that is, the optimal score function. However, the collusion size is unknown when accusing, which prevents c and θc (see section 6.2.2) being identified. Compared with the theory of the compound communication channel of section 6.4.2, it reverses the situation.
In fact, assume that the collusion chooses the strategy θc, and consider the set of strategies which give the same distribution of the symbols in the pirate series. Note this set, ℰ(θc) = {θ|Π(p; θ) = Π(p; θc), ∀p ∈ (0, 1)}. This set is not restricted to the singleton {θc} (hence the error of identifiability). In fact, we can show that for any integer c′ > c, there is a strategy ![]() of size c′, which “mimics” θc: ℰ(θc) ∩ Θc′ =
of size c′, which “mimics” θc: ℰ(θc) ∩ Θc′ = ![]() .
.
Suppose that c < cmax, which means ![]() is not empty. It turns out that the compound communication channel theory can be applied to this family of strategies (Meerwald and Furon 2012, annex), and that the worst strategy in this family is
is not empty. It turns out that the compound communication channel theory can be applied to this family of strategies (Meerwald and Furon 2012, annex), and that the worst strategy in this family is ![]() . This theoretically justifies the score function, set by the following cmax: (1) estimate
. This theoretically justifies the score function, set by the following cmax: (1) estimate ![]() by maximum likelihood (see equation [6.44]) or by expectation–maximization algorithm (see equation [6.48]). By saying that the collusion size is cmax, we denote this estimate; (2) use the score function equation [6.40] where
by maximum likelihood (see equation [6.44]) or by expectation–maximization algorithm (see equation [6.48]). By saying that the collusion size is cmax, we denote this estimate; (2) use the score function equation [6.40] where ![]() .
.
6.4.4. Comparison
We have seen several alternative score functions to the Tardos-Škorić one (see equation [6.24]). Some are fixed, and others adapt to the pirated series received. Here is an experimental protocol to compare them in the spirit of the proof in section 6.2.4, where ![]() fn = 1/2. We choose a certain size and a certain collusion strategy. We generate a secret sequence, p, and many codewords knowing p, we choose c of them, form a pirated series, and calculate the traitors’ and innocent people’s scores. We choose a threshold τ as the median of the traitors’ scores to have
fn = 1/2. We choose a certain size and a certain collusion strategy. We generate a secret sequence, p, and many codewords knowing p, we choose c of them, form a pirated series, and calculate the traitors’ and innocent people’s scores. We choose a threshold τ as the median of the traitors’ scores to have ![]() fn ≈ 1/2 (half of the traitors are accused). Finally, we estimate
fn ≈ 1/2 (half of the traitors are accused). Finally, we estimate ![]() fp =
fp = ![]() (Sinn > τ).
(Sinn > τ).
Figure 6.4 gives a comparison of these score functions for the classical collusion strategies from section 6.1.4. Here, the quantity indicated is ![]() , the bigger it is, the more the scores of the innocent and traitors are statistically separated, and the better the score function. The Tardos-Škorić function has almost the same performance from one strategy to another. This is the sense of his invention: the distributions of the scores Sinn and Stra are independent of θc. Its worst attack is minority voting (see section 6.2.4). The performances of the “Optimal” score function reveal the difficulty of the attack. So, “interleaving” and “coin flip” are the most dangerous collusion strategies for c = 5 (among those tested). The “Compound” and “Laarhoven” score functions are equal, with the major weakness of the majority vote for the Compound, and the minority vote for the Laarhoven score function. Finally, the adaptive score function has the performance closest to the optimal. However, it is more complex due to the estimation of
, the bigger it is, the more the scores of the innocent and traitors are statistically separated, and the better the score function. The Tardos-Škorić function has almost the same performance from one strategy to another. This is the sense of his invention: the distributions of the scores Sinn and Stra are independent of θc. Its worst attack is minority voting (see section 6.2.4). The performances of the “Optimal” score function reveal the difficulty of the attack. So, “interleaving” and “coin flip” are the most dangerous collusion strategies for c = 5 (among those tested). The “Compound” and “Laarhoven” score functions are equal, with the major weakness of the majority vote for the Compound, and the minority vote for the Laarhoven score function. Finally, the adaptive score function has the performance closest to the optimal. However, it is more complex due to the estimation of ![]() .
.
6.5. How to find a better threshold
Finding a threshold for any score function is not easy because the distribution of an innocent person’s score, Sinn, depends on the collusion strategy (except for the Tardos-Škorić strategy; equation [6.24]), which once again is unknown on accusation. This is illustrated by Figure 6.5.
One approach involves refusing to find a universal threshold which would guarantee a false positive probability, whatever the size and strategy of the collusion, and whatever the secret p. In practice, on the other hand, it is enough to find a threshold for a given realization p, and for a decoded pirated series y. Even in these conditions, the score Sinn stays a random variable, since the codewords of the innocent people were created randomly by nature: in equation [6.25], the symbol xj,i has been replaced by the r.v. Xinn,i ~ ![]() (pi).
(pi).

Figure 6.4. The quantity |log10(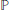 fp)| for
fp)| for 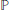 fn ≈ 1/2 for the six collusion strategies in section 6.1.4 and the five following score functions: “Compound” [6.41], “Estimate” (section 6.4.3.2), “Laarhoven” [6.42], “Optimal” [6.40], and “Tardos” [6.24]. With m = 768, c = 5, cmax = 10
fn ≈ 1/2 for the six collusion strategies in section 6.1.4 and the five following score functions: “Compound” [6.41], “Estimate” (section 6.4.3.2), “Laarhoven” [6.42], “Optimal” [6.40], and “Tardos” [6.24]. With m = 768, c = 5, cmax = 10
So we seek a specific threshold τ (p, y), such as ![]() fp = Pr(Sinn > τ (p, y)). Upper bounds give a threshold value, guaranteeing
fp = Pr(Sinn > τ (p, y)). Upper bounds give a threshold value, guaranteeing ![]() fp <
fp < ![]() /n, for example Kearns–Saul and Cramer–Chernoff inequalities (Furon and Desoubeaux 2014). However, it is difficult to know if these bounds are tight. If this is not the case, the threshold value will be very high and we risk not identifying any traitor.
/n, for example Kearns–Saul and Cramer–Chernoff inequalities (Furon and Desoubeaux 2014). However, it is difficult to know if these bounds are tight. If this is not the case, the threshold value will be very high and we risk not identifying any traitor.
Another possibility is estimating this threshold by a random Monte Carlo simulation. We generate a large number, n′, of new codewords. As these are generated after receiving y, their associated scores (for this pair (y, p)) are likely to be scores of innocent people. An estimate of τ (y, p) is the highest score ⌊n′ × ![]() /n⌋. So, a fraction
/n⌋. So, a fraction ![]() /n of n′ scores are above this threshold. The difficulty is that n′ must be greater than n/
/n of n′ scores are above this threshold. The difficulty is that n′ must be greater than n/![]() (by several orders of magnitude for good precision). If n ≈ 106 and
(by several orders of magnitude for good precision). If n ≈ 106 and ![]() ≈ 10−3, we must generate a hundred billion codewords. There are stochastic simulations suitable for estimating such small probabilities. This area of numerical probabilities is called the study of rare events. So, we can estimate the threshold τ (y, p) by importance sampling or by importance splitting, which has been implemented in Cérou et al. (2008) and Furon and Desoubeaux (2014).
≈ 10−3, we must generate a hundred billion codewords. There are stochastic simulations suitable for estimating such small probabilities. This area of numerical probabilities is called the study of rare events. So, we can estimate the threshold τ (y, p) by importance sampling or by importance splitting, which has been implemented in Cérou et al. (2008) and Furon and Desoubeaux (2014).
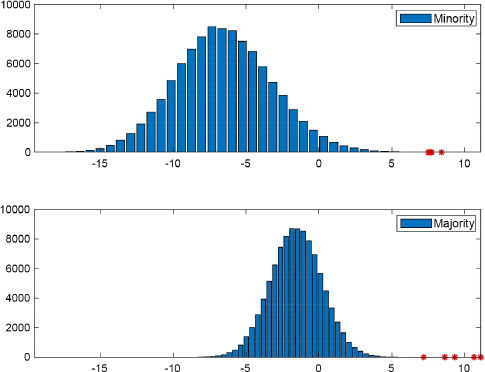
Figure 6.5. Histograms of innocent people’s scores for the “Laarhoven score function” [6.42] and two collusion strategies, “minority vote” and “majority vote”, m = 768, c = 5, cmax = 10, n = 105. Traitor scores are displayed with red asterisks
6.6. Conclusion
This chapter shows that binary Tardos codes are now well understood. It is a fully developed technology, which is now beginning to be transferred to industry. Latest developments are not so clear, regarding q-ary codes (see section 6.3.3.2). The required code length stays in O(c2 log n), but the multiplicative constant is theoretically smaller. On the other hand, creating score functions that can achieve these theoretical performances remains to be done.
Finally, let us not underestimate the great weakness of Tardos codes: accusation is an exhaustive decoding that calculates the score of all of the users. This can be a problem when n is too big and there is a time limit for accusation.
6.7. References
Abbe, E. and Zheng, L. (2010). Linear universal decoding for compound channels. IEEE Transactions on Information Theory, 56(12), 5999–6013.
Amiri, E. and Tardos, G. (2009). High rate fingerprinting codes and the fingerprinting capacity. In 20th Annual ACM-SIAM Symposium on Discrete Algorithms. ACM, New York.
Barg, A., Blakley, G.R., Kabatiansky, G.A. (2003). Digital fingerprinting codes: Problem statements, constructions, identification of traitors. IEEE Transactions on Information Theory, 49(4), 852–865.
Blayer, O. and Tassa, T. (2008). Improved versions of Tardos’ fingerprinting scheme. Designs Codes Cryptography, 48(1), 79–103.
Boesten, D. and Škorić, B. (2011). Asymptotic fingerprinting capacity for non-binary alphabets. In Information Hiding, Tomáš, F., Tomáš, P., Scott, C., Andrew, K. (eds). Springer, Berlin/Heidelberg.
Boesten, D. and Škorić, B. (2013). Asymptotic fingerprinting capacity in the combined digit model. In Proceedings of the 14th International Conference on Information Hiding, Springer-Verlag, Berkeley, 255–268.
Boneh, D. and Shaw, J. (1998). Collusion-secure fingerprinting for digital data. IEEE Transactions on Information Theory, 44, 1897–1905.
Cérou, F., Furon, T., Guyader, A. (2008). Experimental assessment of the reliability for watermarking and fingerprinting schemes. EURASIP Journal on Information Security, 414962.
Fodor, G., Schelkens, P., Dooms, A. (2018). Fingerprinting codes under the weak marking assumption. IEEE Transactions on Information Forensics and Security, 13(6), 1495–1508.
Furon, T. and Desoubeaux, M. (2014). Tardos codes for real. In Workshop on Information Forensics and Security. IEEE, Atlanta, 7.
Furon, T., Guyader, A., Cérou, F. (2008). On the design and optimization of Tardos probabilistic fingerprinting codes. In 10th Information Hiding Workshop. LNCS, Santa Barbara.
Furon, T., Guyader, A., Cérou, F. (2012). Decoding fingerprinting using the Markov chain Monte Carlo method. In Workshop on Information Forensics and Security. IEEE, Tenerife.
Huang, Y.-W. and Moulin, P. (2012). On the saddle-point solution and the large-coalition asymptotics of fingerprinting games. IEEE Transactions on Information Forensics and Security, 7(1), 160–175.
Huang, Y.W. and Moulin, P. (2014). On the fingerprinting capacity games for arbitrary alphabets and their asymptotics. IEEE Transactions on Information Forensics and Security, 9(9), 1477–1490.
Kuribayashi, M. (2010). Tardos’s Fingerprinting Code Over AWGN Channel. Springer, Berlin/Heidelberg.
Laarhoven, T. (2014). Capacities and capacity-achieving decoders for various fingerprinting games. In Workshop on Information Hiding and Multimedia Security. ACM, Salzburg.
Laarhoven, T. and de Weger, B. (2014). Optimal symmetric Tardos traitor tracing schemes. Designs, Codes and Cryptography, 71(1), 83–103.
Meerwald, P. and Furon, T. (2012). Towards practical joint decoding of binary Tardos fingerprinting codes. IEEE Transactions on Information Forensics and Security, 99, 1.
Moulin, P. (2008). Universal fingerprinting: Capacity and random-coding exponents [Online]. Available at: http://arxiv.org/abs/0801.3837.
Oosterwijk, J.-J., Škorić, B., Doumen, J. (2013). A capacity-achieving simple decoder for bias-based traitor tracing schemes. Report 2013/389, Cryptology ePrint Archive.
Pérez-Freire, L. and Furon, T. (2009). Blind decoder for binary probabilistic traitor tracing codes. In International Workshop on Information Forensics and Security. IEEE, London, 56–60.
Safavi-Naini, R. and Wang, Y. (2001). Collusion-secure q-ary fingerprinting for perceptual content. In Security and Privacy in Digital Rights Management, Sander, T. (ed.). Springer, Berlin/Heidelberg.
Schaathun, H.G. (2014). Attacks on Kuribayashi’s fingerprinting scheme. IEEE Transactions on Information Forensics and Security, 9(4), 607–609.
Shahid, Z., Chaumont, M., Puech, W. (2013). H.264/AVC video watermarking for active fingerprinting based on Tardos code. Signal, Image and Video Processing, 7(4), 679–694.
Škorić, B. and Oosterwijk, J.-J. (2015). Binary and Q-Ary Tardos codes, revisited. Design Codes Cryptography, 74(1), 75–111.
Škorić, B., Katzenbeisser, S., Celik, M. (2008a). Symmetric Tardos fingerprinting codes for arbitrary alphabet sizes. Designs, Codes and Cryptography, 46(2), 137–166.
Škorić, B., Vladimirova, T., Celik, M., Talstra, J. (2008b). Tardos fingerprinting is better than we thought. IEEE Transactions on Information Theory, 54(8), 3663–3676.
Stinson, D.R. and Wei, R. (1998). Combinatorial properties and construction of traceability schemes and frameproof code. SIAM Journal on Discrete Mathematics, 11, 41–53.
Tardos, G. (2003). Optimal probabilistic fingerprint codes. In 35th Annual ACM Symposium on Theory of Computing. ACM, San Diego, 116–125.
Tardos, G. (2008). Optimal probabilistic fingerprint codes. Journal of the ACM, 55(2).
Zhao, H.V. and Liu, K.J.R. (2006). Traitor-within-traitor behavior forensics: Strategy and risk minimization. IEEE Trans. Information Forensics and Security, 1(4), 440–456.
- For a color version of all figures in this chapter, see www.iste.co.uk/puech/multimedia1.zip.
- 1 Tardos and his successors use t to limit the probability density medium f of the r.v. P in encoding. The modification proposed here simplifies the calculations.