Solution

Optimization is a mathematical technique used to find the maximum or minimum of a given function over a set of constraints. The methods currently used in optimization have started as a set of simple results from calculus, where a single function is subject to minimization or maximization. Nowadays, these techniques include complex models involving multiple linear and nonlinear components.

In financial engineering and economics, optimization is a tool used for purposes such as designing an optimal asset portfolio allocation or more widely to determine the best investment decision from a large set of asset classes. Due to its origins in the analysis of scarce resources and their optimum use, linear programming has been a favorite tool for economists and financial analysts—which shows why optimization is such a common technique in financial programming. Effectively, every time we need to make a decision on asset allocation given a large number of scenarios, optimization becomes a useful tool to help select the best decision.

In the code example in the section “Using LP Solver Libraries,” we consider how to interface with existing libraries that can be used to solve a large class of optimization problems. To keep the discussion well contained, I employ an open source library called GLPK (Gnu Linear Programming Kit) , which will be also used as a basis for future examples. GLPK is simple to use, but it is a C-based library only. This means that it provides no direct support for C++ high-level concepts such as classes, templates, and containers. Therefore, as part of the discussion, I will show you how to create a class that provides a basic C++ interface to GLPK and other solvers.

First, however, I give you some preliminary information about the kinds of problems that can be solved with an optimization engine, starting with linear programming. Then, I present some code that can be used to translate simple linear models into calls to the solver application programming interface (API).

Linear Programming Concepts

The first case of optimization that you will learn about is characterized by an objective represented as a linear function. This objective is then optimized over a set of linear functions, also called constraints . Such optimization problems are called linear programming (LP) problems, and they constitute an important class of mathematical models that have been widely used in disciplines such as financial analysis and economics.

Using a more formal (mathematical) definition, LP is the area of optimization that deals with the determination of the minimum or maximum value of a linear function over a set of linear constraints. Each constraint is of the form

Similarly, the function that you want to optimize over (also known as objective function ) is a linear function. This results in a problem that can be denoted in the following way:

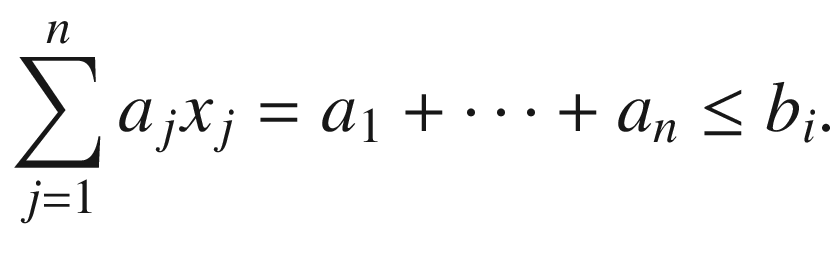
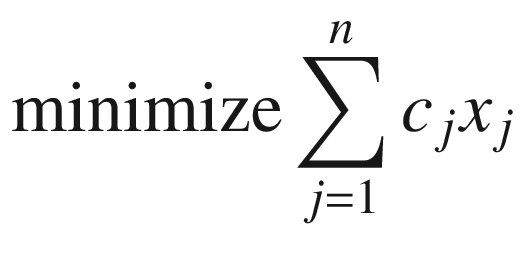
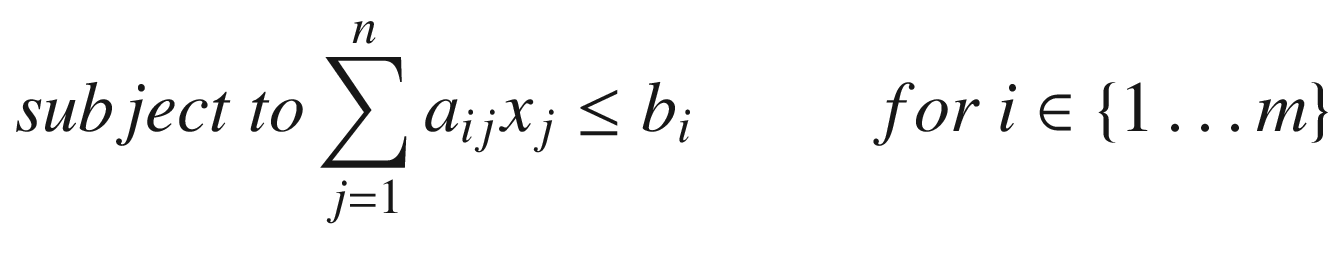
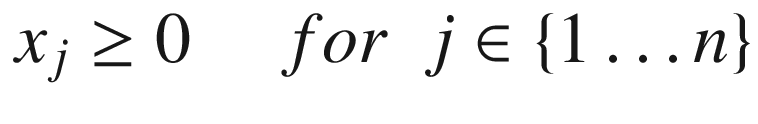
In these equations, x_j is a variable, and a_i j , b_i, and c_j are constant values. These parameters are frequently provided as matrix A and two vectors, b and c. Due to its generic characteristics, this type of problem can assume several forms, depending on the exact value for the given coefficients, as well as if they are zero or nonzero. Also, variations of the problem involve the change of the ≤ relation to ≥ or = in one or more equations. Finally, the problem can require the maximization, rather than the minimization, of the objective function. All these variants can be easily shown to be equivalent to each other, in the sense that it is possible to convert them to a particular form and use the same algorithm in their solution.

Solving an LP problem can be done with the help of a method called simplex algorithm . The basic approach of the simplex algorithm is to consider the geometric region defined by the constraints in a multidimensional space and start to visit the corners of this object in a well-defined way—until an optimal solution is found.

In essence, the mechanics of solving an LP problem are not very different from solving a sequence of linear systems, and a few strategies have been devised using this general strategy. The simplex algorithm, which is still the most common technique to solve LP problems, proceeds by defining a sequence of modified linear systems that are shown to be equivalent to the original while at the same time improving the value of the objective function. One of the advantages of the simplex algorithm is that its properties are well known—mathematical analyses of the simplex algorithm throughout the years have considered several important questions such as its convergence and performance.

While the operation of the simplex algorithm is not difficult to describe, the implementation of such an algorithm contains a lot of intricate edge cases. To avoid such issues, most frequently, you will be using an LP solver library, which has been especially designed to hide the complexities of the implementation. Essentially, a solver provides just a simple API so that users can call the algorithms, provide necessary data, and retrieve the results.

Using LP Solver Libraries

There are several commercial and free libraries that implement the simplex algorithm (and even a few more efficient algorithms for this problem). In this section, to give a flavor of how the process of modeling and LP works, we use a simple but well-maintained open source library called GLPK. With GLPK, it is possible to solve from medium- to relatively large-size LP problems (as well as a few other model variants such as mixed-integer programs).

To start using GLPK from C++, the first step is to download and compile the source code. You will find a version of this software in the Gnu website (at the time I checked, the URL was www.gnu.org/software/glpk). Unlike many math open source libraries, GLPK is very easy to compile and install. You need to decompress the file and build the library using the configure and make commands (these instructions work on UNIX systems, but you can download software such as Cygwin that will allow you to perform the same commands in Windows).

First, an object of LPSolver type can be created if you pass a matrix A, a vector b, and a vector c to the constructor. These parameters are interpreted as the coefficients of the objective function as well as the constraints of the LP.

The API function is called glp_set_prob_name. The first parameter, as for most other functions in GLPK, is a pointer to the LP data structure. The second parameter, a string, is unique for this API call.

The isValid member function checks if the object has been properly initialized. The setMaximization and setMinimization member functions can be used to define the direction of the optimization.

Finally, an example LP is used to test the LPSolver class. In this example, I provided objective function coefficients equal to 10, 6, and 4. The right-hand side of the constraints is also provided as a vector. Finally, the constraints of the problem are given in the form of Matrix object A.

Complete Code

Running the Code

Here, you see the first output of GLPK. By default, GLPK displays the best solutions and the number of iterations it has taken to achieve the results. You can see that after two iterations of the simplex algorithm, GLPK found a solution with an objective value equal to 756.

Solution

One of the main uses of optimization techniques is in the support of investment decisions. In this respect, there are several concepts that can be optimized based on the known properties of investment classes. For a few types of investments, such as bonds, it is easier to determine the returns of the investment, as well as some basic information about the risk for that class of investments. This knowledge translates into more accurate models, particularly the ones that can be employed to optimize profits for the investor.

This section presents a very simple version of a decision support system modeled using linear programming. This problem shows the basic geometric process that is used to solve LPs (even the most complicated ones).

Consider the process of introducing two new financial products to the market in a large bank. The process is usually defined by a number of practical constraints on resources necessary for these investments. Suppose that the bank wants to add two classes of new products to the market: new bond-based products and new mortgage-backed derivatives products. The question is how many hours should be spent on the development of these new products. Let’s call these two variables x and y. Since the bank unit receives payment from its clients based on the number of hours spent on these tasks, the goal is to maximize the amount paid per hours. For bonds, the cost is $5.3K per hour spent on that activity, while the price is $7.1K for derivatives.

In terms of constraints, the bank unit has to consider research expenditures costs. The cost of working with bonds is negative because its costs can be offset by other activities in that area. For derivatives, the full cost of research is considered. The maximum cost spent on marketing for these financial products is prorated by working hours too. Thus, it depends on the values of x and y. It is known that there is a constant of $3K for working hours on bond-related products, while the multiplier for derivatives work is $1K.

Finally, there is a limit on the amount of human resources available for these two tasks. While there are only six units of human resources allocated to these tasks, each hour of bond-related work is eight times more demanding than for derivatives. Notice also that the two variables in this example are clearly non-negative.

The model described previously has only two unknowns, x and y, and therefore can be readily plotted as seen in Figure 12-1. Being an inequality, each constraint results in a half-space that is defined by the equality line. For example, 3x + y ≤ 4 is the half-space defined by all points under the line 3x + y = 4.

To find a solution for a two-dimensional LP model like the one described previously, you can concentrate on the intersections of all half-spaces defined by the constraints. The intersection is, by definition of the problem, contained in the first quadrant of the plot because it is known that x ≥ 0 and y ≥ 0. It is possible then to recognize the area contained in the intersection of all other half-spaces. The result is a polygonal area, whose border is defined by a set of lines derived from the given constraints.

To find a solution for such an LP, you just need to calculate the value of the objective function at each of the corners of the area defined by the constraints. The corner that gives the best value of the objective function is, by definition of the linear objective function, the best that can be found for the problem.

While the process described previously is easy to perform for two-dimensional problems, it becomes quite difficult to accomplish for higher dimensions. As the number of dimensions and constraints increases, the number of corners grows exponentially. It takes a more sophisticated algorithm (such as the simplex algorithm) to find the best corner of the multidimensional space that defines the optimum solution for the given LP.

To demonstrate how the problem is solved in practice, I show you the C++ implementation of the proposed two-dimensional LP. The class, called TwoDimensionalLPSolver , is a blueprint of how such a problem can be implemented using the LPSolver described in the previous section.

First, you need to create the model, which is described using a matrix A, a vector b (the right-hand side of the constraints), and a vector c (the cost vector). The necessary data is provided in the main function. Once the data is available, it can be used to create an object of class LPSolver. The solve() function in the LPSolver class will then perform any necessary data conversion and call the GLPK library to find the optimum solution.

Complete Code

Running the Code

From the output listed in the example, you can see that the optimal solution was achieved at the vertex (0.173, 3.763), which corresponds to the intersection of equations –2.1x + y = 3.4 and 3.1x + y ≤ 4. At that point, the objective function has a value of 27.63, which can be interpreted as the profit achieved by the department in spending the given number of hours in the two financial products that were discussed earlier.

Solution

After continuous LP problems, MIP problems are probably the most common type of optimization problem that practitioners need to deal with. In terms of modeling, the biggest difference between LP and MIP is that such problems have one or more decision variables that are required to be integer numbers—unlike LP problems, where all decision variables are continuous (normally real numbers).

Integer variables are ideal for cases where you need to make decisions that are exclusive within a small- to medium-size set. Moreover, these decision variables may be applicable to resources that are not divisible. For example, you can use such variables to decide on the number of local branches for a commercial bank or on the number of different stocks included in a portfolio. These are common examples of resources that can only be used in integer quantities.

A special type of integer variable is a binary decision variable, also called a 0–1 decision variable. These are variables that can assume only a 0 or 1 (all-or-nothing) value. They are the purest form of integer variable, because they allow one to decide between only two alternative choices. As you can expect, many MIP problems make use of binary variables as their primary way to reach an optimal decision.

In terms of techniques for problem solving, MIP problems are a lot more complicated than LP problems. While there are very efficient algorithms available to solve LP formulations, not all MIP problems are readily solvable by current computer algorithms. As a short explanation, this occurs because when a decision variable is an integer, it creates “jumps” in the objective function that make it much harder to search for the optimum solution. So, unlike LP problems where the optimal vertex of the set of feasible solutions can be quickly determined, MIP solvers need to spend much more time generating possible solutions and testing if they are optimal. This exponential explosion of options is the main reason why MIP problems are much more difficult to solve than LP problems.

Most LP libraries have been extended to deal with at least some forms of MIP. GLPK implements a generic algorithm for MIP solving, called branch-and-cut. With this algorithm, it is possible to solve small- to moderate-size MIPs to optimality. More complicated MIP problems, however, may not be solvable using this technique, depending on the structure of the required problem.

In this coding example, you will see how to extend the LPSolver class to deal with MIP problems, in addition to classical LP problems. In the next section, you will see an example of how to use the LPSolver class to model and solve a MIP problem.

The main reason I decided to inherit from LPSolver, instead of creating a new unrelated class, is that in terms of modeling, MIP problems are very close to LP problems. The only additional thing you need to do in the latter case is to tell which variables are integer or binary and call the right version of the function that solves and retrieves values found by GLPK.

The other part of the puzzle is to implement a new version of the solve member function. The new version supersedes the original version in LPSolver and calls specific functions for MIP, such as glp_mip_obj_val. One of the differences is that, for MIP problems, you are required to solve the corresponding LP problem first, as a way to create an initial feasible solution for the continuous problem. After that, you can call the MIP solver, which will create the solution-search algorithm based on a tree of possible integer values.

Complete Code

Running the Code

Notice that the main function has a very simple MIP model as part of the test code. The previous output just shows how the data is printed by default by GLPK. At each step of the process, it shows the current solution found and its objective cost.