Remember that you have been commissioned to build a Time Machine Store. Apart from a beautiful design and an intuitive user experience, a good web store should adapt itself to the customers’ likes and needs by keeping track of clients and analyzing their behavior. With that information, better campaigns, such as discounts or targeted ads, can be developed, increasing sales. For these tasks, many data-mining algorithms have been developed. In this chapter you will focus on clustering algorithms, which try to find groups of related clients. You will use a specific implementation of clustering, called K-means, using Haskell.
The K-means algorithm is better understood in terms of a set of vectors. Each vector is an aggregation of numeric variables describing a client, product, or purchase, and each vector changes in every iteration. In an imperative language, these vectors would be modeled as a set of variables that are updated in a loop. The solution presented in this chapter will start with a basic implementation where you will keep track of all the information. I’ll then introduce lenses, which are used to manipulate and query data structures in a concise way; you’ll refine the code and split it into a set of basic combinators that glue together the different parts.
Looking at those combinators and their relation to other data types will lead to the notion of monad, one of the central idioms (and type classes) in Haskell code. You will explore its definition and laws and compare it to the other pervasive type class, the functor. Many instances of the Monad class are available in the Haskell Platform; in this chapter, I will focus on those related in some way to keeping track of state.
The idea of monad is not complex, but it has enormous ramifications in Haskell. For that reason, both this chapter and the next one are devoted to understanding monads in depth.
Data Mining
Discovering the different types of clients that use the time machine store, based on their user information and their purchase history. Clustering tries to discern groups (or clusters in data mining jargon) of elements that share common properties. The hope is that, using this information, the marketing team can better target their campaigns.
Detecting the purchase habits of each type of client. This will allow you to tailor the discounts (there will be more discussions about discounts in the last part of the book). For that matter, the idea is to learn association rules and later use them to derive conclusions.
Note Since the store is selling time machines, you could use the machines to travel in time and look at trends in the future. However, this is sort of dishonest, so you should try to use current data and technology to perform better in the market.
Implementing K-means
K-means is one of the simplest algorithms for performing clustering on a set of data. The information in this case is represented as a set of points in n-dimensional space, with each of them representing a different observed fact. The similarity between two facts corresponds to the proximity of the points. The concrete task of the algorithm will be dividing the whole set of points into k partitions, such that the aggregated distance of the points in each partition is minimized.
Note
The number of partitions to create is usually represented as k and must be explicitly given as input to the algorithm. This need to specify the number of partitions up front is one of the shortcomings of K-means. Different methods are proposed in the literature to determine the best value to provide. The Wikipedia article at http://en.wikipedia.org/wiki/Determining_the_number_of_clusters_in_a_data_set summarizes the different approaches.
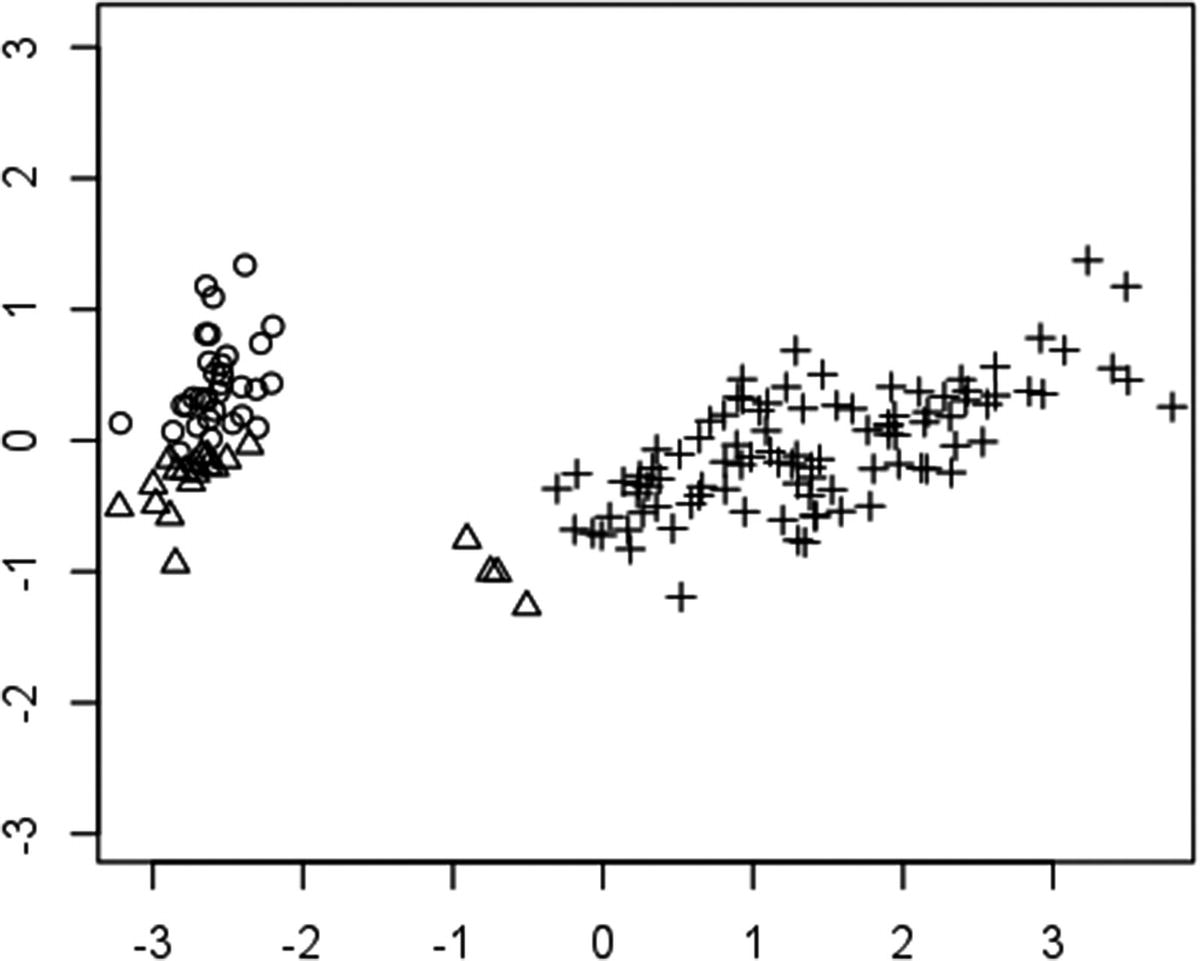
Clusters obtained for an example data set
Note
The Haskell Report allows instance declarations only for types whose shape is a name followed by a list of distinct type variables. The previous definition doesn’t follow that lead, so the compiler complains. However, GHC supports those declarations if you enable the FlexibleInstances extension.
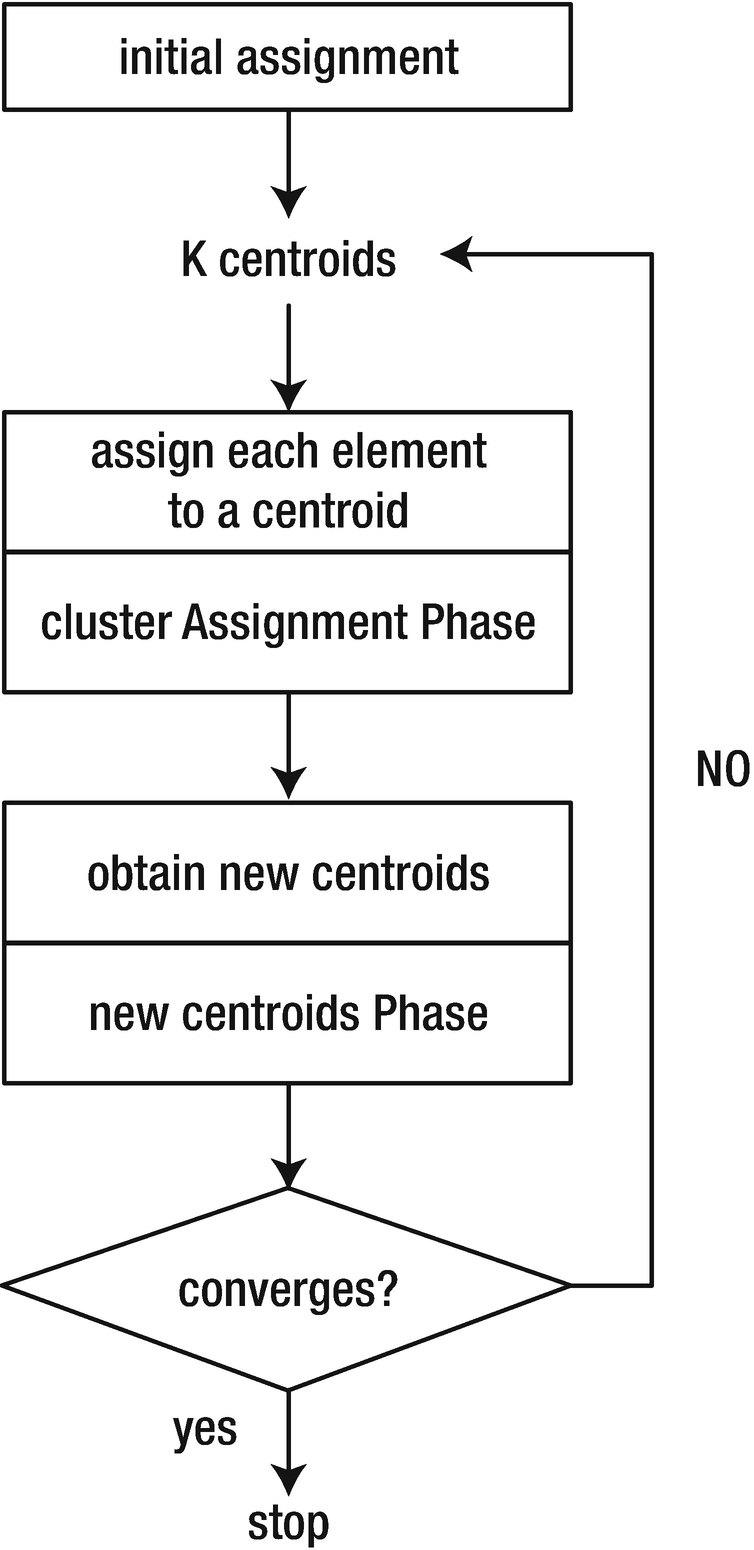
K-means algorithm
The cluster assignment phase should receive the current centroids and the elements of the set and decide which centroid each element corresponds with. This is done based on the proximity. Since you have a key (cluster) to values (points) mapping, it makes sense to use a Map to hold the assignments. This implies that you need to include an extra Ord v constraint in the Vector type class because Map keys must fulfill that requirement.
To check whether you’ve understood how all the pieces of this initial implementation of K-means fit together, complete Exercise 6-1, where the code is instrumented to produce some statistics of a run of the algorithm.
Exercise 6-1. Counting The Number Of Steps
While profiling the performance of iterative algorithms, it’s common to look at the number of recursive steps that have been done until reaching the threshold. Enhance the previous implementation of K-means to provide this value as an extra output of the kMeans function.
Lenses
The K-means algorithm is usually expressed in a more imperative way, in which the centroids and the error are variables that are updated in each iteration until the threshold is greater than the error. One of big differences between more usual languages and Haskell is the query and access to data structures, which should be made using either pattern matching or records, with the record update syntax or via the helper functions that are created automatically by the compiler.
Lenses allow you to query and update data structures using syntax much closer to the typical dot notation found in other languages. However, that notation is defined completely in a library, not as part of the language. This should give you a taste of the great power of the Haskell language, which allows you to express the scaffolding of data access and update the language.
A lens wraps together a getter and a setter for a specific field in a data structure. In that way, it’s similar to a JavaBean or a C# property. Apart from that, a particular lens library includes a number of combinators to mix together several lenses (e.g., for chaining accesses to deeper parts of a structure) and to provide more recognizable syntax (e.g., using += to update a numeric field by adding some amount).
You may have noticed that in the previous paragraph I used the phrasing a lens library instead of the lens library. The Haskell community doesn’t have a preferred or definite library for this task. Some of the lens packages are lens, fclabels, data-accessor, and data-lens. The most commonly used one is the lens library by Edward A. Kmett. There’s one problem, though: that library is huge. For that reason, we shall start with the microlens library , which provides the most common features from lens in a more digestible fashion. In any case, the main ideas remain the same among all the packages. They differ in the theoretical basis (how lenses are represented internally and composed) and in the implementation itself, but not much in the external interface.
Although I speak of “the microlens library,” there is in fact a constellation of libraries. The microlens library proper provides just the core abstractions. Instead, I assume that you have added microlens-platform as a dependency to your project, or installed the library before starting a GHCi session. That library exposes the most important functionality from the microlens library under a single Lens.Micro.Platform module, the one you need to import.
Previously, the definitions used record syntax, but I have included here the raw ones because once you create lenses for them, the usefulness of using record assessors disappears.
Et voilà! The code you wanted has been written for you in the background.
Template Haskell
Template Haskell is the name of a metaprogramming facility included in GHC. Metaprogramming is the name given to those techniques that allow you to modify the code that will be generated by a compiler, usually generating new code automatically. In the language Lisp, metaprogramming is a form of compile-time macros.
You saw an example of metaprogramming: the deriving mechanism for built-in type classes. Template Haskell provides an extensible interface to the GHC compiler and allows library authors to provide their own code modification facilities, like the microlens library does. There are many other libraries in Hackage making use of Template Haskell; for example, derive includes the automatic derivation of many other type classes, such as NFData.
Template Haskell is not part of the Haskell 2010 Report so, as usual, your code won’t be easily portable to other Haskell compilers as it stands. However, GHC provides a command-line argument, -ddump-splices, which outputs the code that Template Haskell generated, and you can copy it back if you need full compatibility.
As mentioned, many other lenses are included in the library distribution for lists, maps, and sets. If you decide to use microlens, don’t forget to check these instances.
Exercise 6-2 applies the information about the microlens library to time machines. I encourage you to go through that exercise to get a good idea of lenses.
Exercise 6-2. Time Machine Lenses
Generate lenses for the TimeMachine data type you created in previous chapters, including all the information mentioned before and also a price. Using the operators introduced here, create a function that, given a list of time machines, increases the price by a given percentage.
Note
The derivation of lenses via Template Haskell must appear before any use of them in other code. Thus, you must be careful about writing the previous code before the definition of the new kMeans code.
As you can see, the error will be saved in a field, and also you are saving the number of steps, something that you were asked to include in a previous exercise. The new algorithm kMeans' will be seen as a series of changes in that state. It first creates the assignments and then updates the centroids, the error, and the number of steps. These three last steps are implemented using lenses. Finally, the algorithm must check the stopping condition by comparing the error to the threshold, which is also a field in the state data type. The kMeans function also changes to return only the centroids from the full state.
Notice that the way in which you compute the error has also been changed. Instead of return pairs of (old centroid, new centroid) when updating the centroids, it takes the centroids in the current and previous stats and performs the aggregation of their distance using sum and zipWith. Exercise 6-3 asks you to finish this implementation with lenses by writing the code of the cluster assignment phase.
Exercise 6-3. K-Means Lenses
The implementation of the algorithm using lenses is not yet complete. The function clusterAssignments is missing. Starting from the version shown in the previous section, write these functions (which now operate on full states) using lenses.
Discovering Monads
One of the pillars of Haskell philosophy is reusability. For that reason, while learning the language and its libraries, it’s useful from time to time to step back and look at the code you’ve already written, looking for common patterns that could be abstracted. In this section you will think about abstractions related to Maybe values and to state handling. The same kind of structure will appear in both cases, leading you to the notion of a monad that will be the core of this section.
Watching Out for Incomplete Data
In the previous section there’s an explicit assumption that you already have all the information that will be input to the K-means algorithm in a nice way so that the only transformation you need to do is convert that information to vectors. However, this is rarely the case with a data set from the real world. Usually you need an initial preprocessing stage to gather all the information, do some aggregation, and maybe fix some inconsistences.
The previous example used catMaybes from the Data.Maybe module. This function filters out every Nothing element in the list, and it’s convenient when working with a list of Maybe values.
Note
In the previous example and in the next examples in this section, I’ve factored out the code for accessing the database, which is not relevant to the current discussion. If you want to try the code, just include a simple return value. For example, purchasesByClientId could return [1,2,3], and numberItemsByPurchaseId, productIdByPurchaseId, and priceByProductId could return a constant value.
Clearly, this code is neither elegant nor maintainable. You have to write explicitly a waterfall of checks for Nothing or Just. Furthermore, in the event you want to add some new query in between the other ones, you would need to re-indent all the code you had already written. What you are going to do is to develop a combinator2 that will allow you to write better, more maintainable code.
The new code is definitely cleaner and much more maintainable. Furthermore, you have hidden the low-level operation of unwrapping Maybes into a combinator, leading to more reusability.
Note
Take some time to parse the previous function. The style of writing the argument to a function in a different line from the body is called hanging lambdas . It’s common when using function combinators such as your thenDo.
Thus, the newly defined combinator is strictly more powerful than fmap. It can be used to write a version of fmap for Maybe values because fmap cannot express the behavior of thenDo. The optional Exercise 6-4 asks you to verify that your new definition of fmap is indeed correct.
Exercise 6-4. Proving That Your fmap is Correct
Using the equational reasoning introduced in Chapter 3, prove that this implementation of fmap is correct. To do so, you should check that fmap as defined in this section works the same as the instance of Functor for Maybe values, which maps Just x to Just (f x) and Nothing to Nothing. Hint: Split the solution into cases, depending on the constructor for the Maybe value. In other words, start by using a case expression in which you pattern match on the two possible values of an expression of Maybe type, namely Nothing and Just v.
Combinators for State
Based on your success of building a combinator for chaining functions that may fail and return Nothing, you can think of doing the same to refactor a bit of your code for the K-means algorithm. It would be interesting to hide the management of the states found in the last version of the code.
Note
In the previous pieces of code I used the unit type, (). It’s a type that has only one element, the empty tuple, (). It’s customarily used when you need to return something in a function but don’t really have a good value for it.
Dissecting the Combinators
At the beginning of the section, I presented the way to deal with function chains involving Maybe values, and you learned that developers can benefit from a combinator called thenDo. You also successfully applied that idea to State values. Following the same approach used with functors, you should wonder whether this pattern can be abstracted into a type class.
The Maybe monad combines functions that may fail.
The State s monad combines functions that keep track of an internal state of type s.
Caution
The return function in Monad has nothing to do with the return keyword in C or Java. However, it was an unfortunate choice from the designers of this type class because it resembles imperative programming. Before continuing, try to free your mind from this idea. Monads have essentially no relation to imperative programming, state, or mutability (although specific Monad instances cover these use cases).
The role of (>>=) has already been explained, so let’s move to return. This function describes how to wrap a pure value using a monad. Usually, it also describes the simpler element you can get (just returning a value) for each kind of computation. At first, this might seem extremely vague, so let’s look at the implementation for your Maybe and State monads.
The specific type for the return implementation of State s is a -> State s a or, equivalently, a -> s -> (a,s). This is the only implementation I can think of that returns the value that was passed, with the internal state unchanged. This is the same purpose of the remain combinator in the previous section. It also complies with the idea of being the “simplest” computation with state – one that does not change the state at all.
For Maybe, the type of return looks like a -> Maybe a. So, you have two alternatives: either return the value wrapped in Just or return Nothing. In the definition of return, you already have a value to wrap, so it makes more sense to have return = Just. Furthermore, if you look at the final example in the section where incomplete data was discussed, you can see that in the last step you used Just, and now you could change it to a return.
The next function in the type class is (>>). As you can see from its definition, it combines two computations such that the second one doesn’t use the return value of the first one. This may sound strange, but you have already encountered such a situation. When you modify the state in your State s monad , you don’t use the return value of this operation (which is always the empty tuple, ()). Like in many other default implementations, this function is defined here because it’s expected that some instances could give a much faster definition for (>>) than the default one.
Note
Historically, the Monad type class also contained a fail method. As its name suggests, it allows you to define special behavior of the monad when some part of its computation fails. For example, failing into the Maybe monad should intuitively return Nothing. However, not all monads have sensible definitions for fail, State being a prime example. For that reason it has been decided to move this function to its own type class, called MonadFail.
Right now you have enough information for using a monad instead of a custom combinator in the previous examples. Exercise 6-5 shows you how to do so.
Exercise 6-5. Monads For Incomplete Data and K-means
All the parts that make up the Monad instance for Maybe have already been discussed. Write the instance declaration for it. Then, rewrite the purchaseValue function using (>>=) and return.
Indeed, this definition is equivalent to the previous handwritten definition. The good news is that this implementation works for any monad; that is, every Monad instance gives rise to a Functor instance by defining fmap as shown earlier. It’s included in the Control.Monad module of the base package, under the name liftM.
Note
If any Monad instance is also an instance of Functor, why is this relation not shown in the declaration of those classes? The truth is that in the library this relation exists but includes the Applicative type class in between. That is, Applicative is a superclass of Monad, and Functor is a superclass of Applicative. Chapter 10 contains a thorough description of the Applicative type class and its uses.
do Notation
The monad concept, brought from a branch of mathematics called category theory into Haskell by Phil Wadler (among others), is ubiquitous in Haskell libraries. Many computational structures have been found to be instances of Monad. Given its success, the Haskell designers decided to include special syntax for monads in the language: the so-called do notation .3
A do block starts with the do keyword and then is followed by a series of expressions. At compile time, those expressions are translated into regular code using (>>=), (>>), and fail. So, the best way to understand what this notation means is by looking at the possible ways you could use monadic functions and see how do notation approaches it.
Notice that you don’t have to write in after this kind of let expression.
In turn, this call to fail implies that the type of that piece of code does not only require a Monad, but the more restrictive MonadFail. Any time that you check the shape of the return value of a monadic computation, you should expect a MonadFail constraint to appear.
For the K-means implementation, you can stop using your home-baked data type and start using the State implementation that you can find in the Control.Monad.State module of the mtl package. mtl (from Monad Transformers Library) is one of the basic libraries, along with base or containers, that make up the Haskell Platform. It contains instances of many different monads and utility functions for all of them.
Since obtaining only part of the state in that way is used often, mtl includes a gets function for that task.
Monad Laws
Beware that not all definitions of (>>=) and return will make a true monad. As with functors, the Monad type class imposes some laws over the behavior of their instances. These laws are not checked by the compiler but must be satisfied if you don’t want the user or the compiler to introduce subtle errors in the code. Don’t worry if in a first read you don’t understand all the details. This information is useful only if designing new monads, but it’s not needed at all for their usage.
return a >>= f must be equivalent to f a, or in do notation, do { x <- return a; f x} must be equivalent to bare do { f a }. That is, nothing changes if you apply a computation to a value wrapped into the monad via return, or without it.
x >>= return must be equivalent to x, or in do notation, do { y <- m; return y } must be equivalent to do { m }. This means that return just unwraps and wraps again a value when bound from another computation.
Note The second law is important for good Haskell coding style. Remember that computing a value inside a monad to immediately call return is not needed; just include the value computation as an expression.
The final law makes explicit that the definition of fmap that was given based on a monad must indeed be the fmap of its Functor instance . That is, fmap f g must be equivalent to g >>= (x -> return $ f x).
Monads Everywhere
If you look at the available information about Haskell on the Internet, you will notice that there are a large number of tutorials devoted to monads. This might imply that monads are difficult to grasp, but they shouldn’t be.
Using monads is much more common than designing monads. You have already looked at the Maybe and State monads, and you will continue looking at more instances of this type class throughout the book. If you understand how to use each of them, you’ll be ready for real Haskell programming and on the path to fully understanding the concept of a monad.
Different Sorts of State
It’s important to know the most common instances of monads . In this section, you will look at those monads that have some relation to keeping or using an internal state. Two of them, Reader and Writer, could be seen as restricted versions of State. However, they have their own uses, and it’s interesting to know in which scenario you should apply each of them. Then the discussion will move to the ST monad, which is a special one that allows you to use mutable references (as variables in a impure language) but in a controlled way so you don’t surpass the purity of the language.
State and Lenses
Before going in-depth into the other monads, I will highlight a special feature of the micro lens library, among other lens libraries: its special combinators for using lenses inside the State monad. Using these combinators, code resembles a more sequential style of programming but keeps all the purity.
Instead of using get and then applying a lens with view , you can directly access part of a data structure with the function use. This function already gives the result in the State monad, so you don’t need to call any extra fmap or return to get the value.
Remember that when you used the update functions for lenses, you always had to write the structure to be applied by explicitly using either $ or &. But inside a State monad there’s always a special value to count on: the internal state. For each update function ending in tilde (such as .~, %~, or +~), we have a corresponding function ending in an equal sign (.=, %=, or += in the previous cases), which changes the internal state.
Reader, Writer, and RWS
In many cases the global state does not change through the execution of the code but contains a bunch of values that are taken as constants . For example, in the K-means algorithm, the number of clusters to make, the information in which the algorithm is executed, or the error threshold can be seen as constant for a concrete run. Thus, it makes sense to treat them differently than the rest of the state. You aren’t going to change it, so let’s ask the Haskell compiler to ensure that absence of modification for you.
ask retrieves the complete context, similarly to the get function for mtl’s State.
asks applies a function to the context and returns the result. This function is similar to the access function you developed for your handwritten State monad and to the gets function in mtl, and it’s useful for querying a specific field in a structure.
As happened with State, you also need a function to execute the monad, to which you give the context. In this case, it is called runReader and just takes as an argument the initial unchangeable state.
You have just seen functions that consume a state but don’t modify it. The other side of the coin comprises those functions that generate some state but never look back at it. This is the case of a logging library. You are always adding messages to the log, but you never look at the previous messages; you are interested only in increasing the log. For that you should use the Writer monad, as usually available in mtl.
- 1.
If you are building a log composed of strings, the monoid structure is that of the list type. The neutral element is the empty list, and the operation to combine two strings is their concatenation. So, if you want to build a log, you should use String as type parameter to Writer.
- 2.
Another place where some information can be seen as an output parameter is in the case of counting the number of iterations for the K-means algorithm. In that case, every time you perform some number of iterations, you want it to be added to the current value. So, the monoid structure is that of the integer with sum. Remember that since numbers have usually two monoidal structures (one for addition and another one for product), you need to wrap the values inside the Sum newtype to use addition as an operation.
Since the initial value for the output information must be taken as the neutral element of the corresponding monoid, you don’t need any extra argument to run a Writer monad value using runWriter, which returns a tuple with both the return value of the computation and the output information.
Writer is an example of a monad whose instance declaration is still accessible while learning. Exercise 6-6 asks you to do so, taking care of some tricks needed to write the correct types.
Exercise 6-6. Internals of The Writer Monad
Now you can write the declaration starting with instance Monoid m => MyWriter m. Also, provide a definition for the tell function. Remember to first write down the specific types of the return and (>>=) functions; it will make things a lot easier.
Haskell tries to carefully delimit how much power should be given to each function, making the compiler able to detect more kinds of errors than in other languages. This philosophy can be transported to the context or state of a particular function. You should give only read access to the information that should be seen as constant, write-only for output that won’t be queried, and read and write to the internal state that will be manipulated. It seems that in many cases what you need is a combination of the Reader, Writer, and State monads.
How monads can be combined is a topic for the next chapter, but for this specific case the mtl developers have designed the RWS monad (the acronym comes from the initial letter of each functionality it includes), which you can find in the Control.Monad.RWS module. A specific value of this monad takes three type parameters: one for the read-only context, one for the write-only output, and one for the mutable state. The operators needed to access each component remain the same: ask and asks get the Reader value, tell includes a new value in the Writer monad, and get, put, and modify are used to query and update the State value.
As you can see, RWS provides an elegant way to design your functions, separating explicitly the purpose of each piece of information. This monad is especially useful when porting algorithms that have been developed before in an imperative language without losing any purity in the process.
Mutable References with ST
You have seen how a clever combination of extra arguments to functions and combinators allows for easier descriptions of computations with state. Furthermore, these abstractions can be turned into monads, which enable you to use the do notation, making the code more amenable to reading. But apart from this, Haskell also provides true mutable variables, in the same sense of C or Java, using the ST monad.
Caution
There’s a chance that after reading this section you will start using the ST monad everywhere in your code. It’s interesting to know how this monad works, because it can lead to more efficient implementations of some algorithms and because it gives a glimpse of the full range of possibilities of the Haskell Platform.
One question that may come to mind is, does the use of ST destroy the purity of the language? The answer is that it does not. The reason is that the way ST is implemented restricts the mutable variables from escaping to the outside world. That is, when you use ST at a particular point, you can create new mutable variables and change them as much as you want. But at the end of that computation, all the mutable variables are destroyed, and the only thing that matters is the return value. Thus, for the outside world there’s no mutability involved. Furthermore, the Haskell runtime separates the mutable variables from different ST instances, so there’s a guarantee that mutable variables from different realms won’t influence each other.
Let’s present the actors in the ST play. The first one is, of course, the ST monad from the Control.Monad.ST module, which takes two type parameters, but only the second is important for practical use. It’s the type of the return value of the computation (following the same pattern as other state monads). The first argument is used internally by the compiler to assign a unique identifier that will prevent different ST computations from interfering. Once the computation is declared, it’s run simply by using it as an argument to the runST function.
Inside ST computations, you can create mutable variables, which have the type STRef a, from the Data.STRef module, where a is the type of the values that will be held in the cell. All the definitions and functions related to STRefs live in the Data.STRef module of the base package. Each new variable must be created with a call to newSTRef, which consumes the initial value for the variable (uninitialized variables are not supported). The result value is the identifier for that specific mutable variable, which will be used later to access and modify its contents.
The value of a variable can be queried using readSTRef, which just needs the variable identifier to perform its task. For updating a variable, as in the case of State, you have two different means. You can either specify the new value using the writeSTRef function; or you can specify a function that will mutate the current value of the STRef cell into a new value. For that matter, you can use modifySTRef. However, since modifySTRef is lazy on its application, there’s a strong recommendation against its use, because it may lead to memory leaks similar to the ones shown in the previous chapter. Use instead modifySTRef' , which is strict.
Note
You cannot use map of fold directly on the list because you are in a monadic context, and the types of those functions do not allow this. In the next chapter, you will see how monadic counterparts to these exist, such as mapM, foldM, and forM.
Exercise 6-7. K-means Using ST
Implement the K-means algorithm using the ST monad . In particular, you must create one STRef for holding the centroids that will be updated and another one for the number of iterations.
Summary
Several implementations of the K-means clustering algorithm were presented, starting with a handwritten one, then refining it using your own combinators, and finally creating versions using the State and RWS monads.
The chapter defined combinators for working with Maybe values in an easier way.
The chapter explained the monad, which is a way to combine computations with some special characteristic, such as being able to fail or having an internal state.
Monads are one of the most important constructions in Haskell and come with a custom syntax, called do notation, which you studied in depth in this chapter. This is the most used style of writing monadic code.
You saw several other monads: Reader, which holds a read-only context; Writer, which outputs a write-only value that is combined using a monoid structure; RWS, which combines the three Reader, Writer, and State monads; and ST, which implements controlled mutable variables.
Apart from monads, in this chapter lenses were introduced as a way to query and update data structures in a common and powerful way.
