You have seen how parametric polymorphism and higher-order functions help in the process of abstraction. In this chapter, I’ll introduce a new kind of polymorphism that sits in between parametric and the absence of polymorphism: ad hoc polymorphism. Using this feature, you can express that certain types exhibit a common behavior. Incidentally, you will also learn how Haskell makes it possible to use addition, (+), on different numeric types like Integer and Float while maintaining a strong type system.
Containers will be used in the examples throughout this chapter. A container is any data structure whose purpose is to hold elements of other types in it, such as lists or trees. In addition to writing your own implementation of binary trees with a caching mechanism, you will look at implementations that are available in Hackage and Stackage , the Haskell community’s package repositories. This will lead you deeper into the features of Cabal and how you can use it to manage not only projects but also their dependencies. In addition to repositories or libraries, the Haskell community provides a lot of ways to search for code and documentation; I’ll introduce the Hoogle tool in this chapter.
While using and implementing these containers, a lot of patterns will emerge. This will be the dominant situation from now on; after looking at some useful types, you will look at their commonalities. In particular, this chapter will introduce functors, foldables, and monoids.
Using Packages
Until this point you have been using functions and data types from the base package. However, a lot of functionality is available in other packages. In this section you will first learn how to manage packages, and add them as dependencies to your projects.
A package is the distribution unit of code understood by Cabal and Stack, the tools I have already introduced for building projects. Each package is identified by a name and a version number and includes a set of modules. Optionally, the package can include some metadata such as a description or how to contact the maintainer. In fact, the projects you created previously are all packages.
You can manipulate packages by hand, but there’s an easier way to obtain and install them in your system: to make your own projects depend on them. If Cabal finds out that a package is not available in your system, it contacts the Hackage package database ( which lives at http://hackage.haskell.org ) and downloads, compiles, and installs the corresponding package. Hackage started as a mere repository for hosting packages, but now it provides some extra features such as the ability to generate documentation. Anyone with an account is allowed to upload new packages to Hackage. This ability, combined with the active Haskell community, means a wide range of libraries are available.
When your use Stack to build your projects, Hackage is not consulted by default. Instead, packages are looked for in Stackage (which lives at https://www.stackage.org ). Stackage provides snapshots of Hackage (called resolvers) in which all packages are known to work well together. This provides a huge gain for reproducibility at the expense of not always containing the bleeding-edge version of the packages.
Tip
Go to the Hackage web page and click the Packages link. Take some time to browse the different categories and the packages available in each of them. Then, find the containers package in the Data Structures category and click it. Now go the Stackage web page and click the link of the latest LTS corresponding to your version of GHC. Try to find containers in the list of packages. Compare the version of this package to the latest one available in Hackage.
In both cases, you will see the list of modules that are exported, along with its documentation. It’s important that you become comfortable with these sites because they are the main entrance to the world of Haskell libraries.
Managing Dependencies
Package Versioning Policy
If any function, data type, type class, or instance has been changed or its type or behavior removed, the major version (i.e., the first two components) must be increased.
Otherwise, if only additions have been done, you can just increase the remaining components. This also holds for new modules, except in the case of a likely conflict with a module in another package.
In addition to these recommendations for package writers, the previously explained rule for specifying dependencies was introduced.
Note however that this versioning policy is a controversial issue within the Haskell community. You might find fierce arguments by defendants and opponents. But in practice, as a user of Haskell, tools work well enough even when not all packages in the repositories adhere to this practice.
Note
You may see some extra properties, such as cabal-version and build-type. Those are meant to be used when the developer needs to tweak the building system or maintain compatibility with older versions of Cabal. My suggestion is to leave those properties as they are initially created.
Building Packages
In Chapter 2 we looked very briefly at the steps required to build a package with either of the build tools of the Haskell ecosystem, namely Cabal and Stack. In this section we look at them in more detail and describe the underlying notions in their package systems.
Building Packages with Cabal
Cabal used to be one of the very few sources of mutability in a Haskell system. All packages, including dependencies, were installed in a global location. This made the state of a Haskell installation quite brittle, especially when different packages required different versions of the same package. Fortunately, this landscape changes with the introduction of sandboxes, which isolated the dependencies of each package being developed. For a long time, sandboxes have been opt-in, and global installation remained the default method. Not any more: if you use the Cabal commands starting with new-, you use an enhanced form of sandboxes. This is now the recommended way of dealing with Haskell packaging, and it’s the one we shall describe in this section.
Since the new- commands try to isolate the package being developed from the rest of the system state, they must be run in a folder in which a .cabal file exists. This is in contrast to the previous mode of operation, in which commands could be run anywhere since they affected the global environment.
If you get any error in this step, double check that the src folder exists.
In a first step, all the dependencies (in this example output, package exceptions version 0.10.0) are downloaded and built. Then, the package itself (in this case, chapter4) is configured and built. Of course, dependencies are only compiled in the first run, or whenever they change.
Then you can build one specific package by issuing the new-build command followed by the name of the package. The great benefit of using a cabal.project file is that if one of the packages depends on any other, Cabal knows where to find it. This solves one of the problems of the older behavior of Cabal, in which global mutation of the environment was the only way to develop several interdependent packages in parallel.
Building Packages with Stack
In my initial description of building packages with Stack, I hinted to the idea of resolvers. This is in fact a central idea for Stack: a resolver describes a set of packages with a specific version, and a specific compiler environment in which they work. In other words, a resolver is defined by giving a version of GHC and a version of all the packages belonging to that resolver. There are two types of resolvers: nightlies, which include newer versions but are less stable, and LTSs, which are guaranteed to work correctly. I recommend to always use an LTS for production environments.
In order to start using Stack with a Cabal project, you need to create a stack.yaml file. The main goal of that file is to specify which resolver to use. From that point on, Stack creates an isolated environment for your project, including a local version of GHC as specified by the resolver.
What a waste of space, I hear you muttering. GHC is not light, indeed, and having one copy per project would result in thousands of duplicated files. Fortunately, Stack tries to share as many compilation artifacts as possible, so the same compiler is used for all the packages using the same major LTS version.
With all this information, you are ready to create the package for the store. Follow Exercise 4-1, and try looking carefully at all the steps needed to bring a new package to life.
Exercise 4-1: Time Machine Store Package
Create a new package that will be the origin of Time Machine Store, using either Cabal or Stack. Since it will become a web application, make it an executable. Add containers and persistent as dependencies (remember to use the version rule) and then configure and build the project. Experiment with the different metadata fields.
In addition, create both a cabal.project and a stack.yaml file. Ensure that your package builds with both tools.
Obtaining Help
I already mentioned that the Hackage and Stackage websites contains documentation about all the packages available in their databases, including module, function, type, and class descriptions. It’s a great source of information for both when you want to find information about some specific function and when you want to get a broad overview of a module. Furthermore, all the packages in the Haskell Platform come with high-quality explanations and examples.
One really cool tool that helps in daily Haskell programming is Hoogle, available at www.haskell.org/hoogle/ . The powerful Hoogle search engine allows you to search by name but also by type. Furthermore, it understands Haskell idioms. For example, if you look for a function with a specific type, it may find a more general function using a type class that the types in the signature implement, or the order of the arguments may be swapped in the found version. This tool is available also as the command-line program hoogle, which you can obtain by running cabal install hoogle in the command line. Note that this will take some time, since it needs to download and compile all dependencies in addition to the executable. Before being able to issue any query, you must run hoogle generate at the console.
Containers: Maps, Sets, Trees, Graphs
They are much faster because they were specially developed for a particular pattern. For example, looking for the value associated to a key in a list involves searching the entire list, whereas in a map the time is almost constant.
Libraries implementing these structures provide functions that were created for the specific use cases of each of them. For example, you have functions for visiting nodes or getting the strongly connected components of a graph. These functions could be implemented if using lists but are not already available in the Haskell Platform.
All the containers I will talk about are provided by the containers package, so to try the examples, you need to include that package as a dependency, as in the previous section.
Maps
Let’s start with maps, which allow you to associate values with keys efficiently. No duplicate keys are allowed, so if you want to alter the value for a specific key, the new one will override the previous one. In contrast, with association lists, by implementing mappings as a list of tuples, you were responsible for maintaining such an invariant.
The type itself is Map k a. It takes as parameters the type k of the keys that will index values of type a. For example, a mapping between clients and the list of products that each client has bought will have type Map Client [Product]. In the examples you will work with simpler maps from strings to integers, which are much more concise.
You can completely ignore that old value and just replace it with the new one. This is achieved via the insert function, which takes just the new key and value, and the map where the association must be changed, in that order.
You can combine the old value with the new one. To do so, use insertWith, of the following type:
(a -> a -> a) -> k -> a -> Map k a -> Map k a
The first parameter is the combining function that will be called with the old and new values whenever the corresponding key is already present. In some cases, you will also want to have the key as a parameter of the combining function; in that case, you should use insertWithKey, whose first parameter is of type k -> a -> a -> a. This is an instance of a common pattern in the Data.Map module; each time that a function will be called with a value of the map, there’s an alternative function ending in WithKey that also gives the key to the function.
Notice how in the last step the pair ("hello",5) lived in the map and ("hello",7) was going to be inserted. You specified addition as the combinator, so you get ("hello",12) in the final map.
Note
If you come from an imperative language such as C or Java, you will be used to functions directly changing the contents of a container. By contrast, Haskell is pure, so all these functions return a new map with the corresponding change applied. However, the underlying implementation does not create a whole new copy of the data structure every time it’s changed, due to laziness (which will be explained in the next chapter). That way, performance is not compromised.
Exercise 4-2 asks you to check whether alter is a general form of the functions that were introduced earlier.
Exercise 4-2: Altering Your Maps
It’s common for Haskell libraries to contain a fully general function such as alter, which is later made more concrete in other functions. This makes it easier to work with the library. Put yourself for a moment in the place of a library designer and write the functions insert, delete, and adjust using alter.
I have already talked about converting from a list of tuples into a map using fromList. You can do the inverse transformation using assocs. You may have noticed that maps are always shown with their keys ordered. The map itself maintains that invariant, so it can easily access the maximal and minimal elements in the map. Indeed, functions such as findMin/findMax, deleteMin/deleteMax, and updateMin/updateMax take advantage of this fact and allow for fast retrieving, deleting, or updating of the values associated to those keys.
Sets
IntMap, IntSet, HashMap, AND HashSet
Maps can be made much more efficient if you use only integers as keys. The same happens for sets holding only integer values. For that reason, the containers library provides specific data types for that purpose, namely, IntMap and IntSet.
Alternatively, the keys on a map or the values on a set might not be integers but could be mapped almost uniquely to one integer. This mapping is called a hash of the original value. The types HashMap and HashSet in the unordered-containers package provide implementations of maps and sets whose keys and elements, respectively, can be hashed; this is much more efficient than the Map and Set types discussed in this section, if the type can to be hashed.
Like with any other value, the following containers can be nested one inside another: lists of sets, maps with string keys and values that are lists of numbers, and so on. In Exercise 4-3 you will use a map with sets as values to classify a list of clients in the store.
Exercise 4-3: Classifying Clients
The first should traverse the list element by element and perform on each element the classification, decide which map item to modify, and then add itself to the set.
The second should first create lists corresponding to the three different kinds and at the end convert those lists to sets and generate the mentioned map from them.
You can create a large client list and run the two implementations to compare which one behaves better in speed.
Trees
The type synonym and its expansion are interchangeable in all circumstances. That is, you can also write the type of filter as Predicate a -> [a] -> [a], and the compiler would be fine with it. In contrast, the other way to define alternative names, using newtype, doesn’t make the types equivalent. When should you use this second option will be covered later in the chapter.
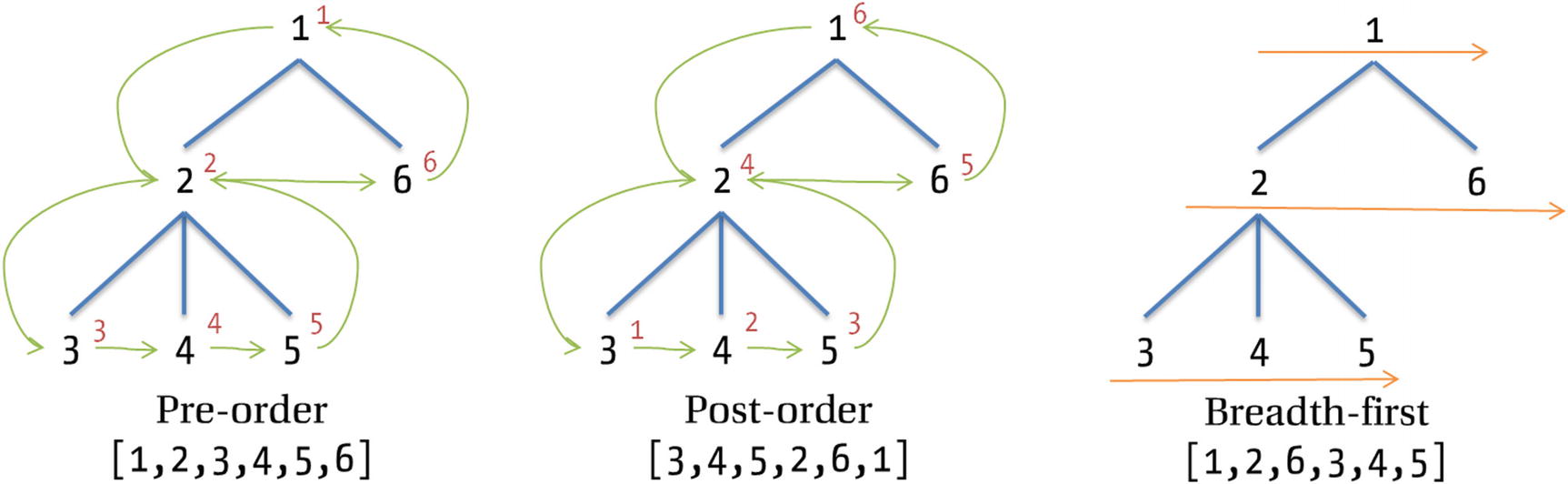
Traversing in pre-order, post-order, and breadth-first fashions
Graphs
Trees are just an instance of a more general data structure called a graph. A graph is composed of a set of vertices, joined via a set of edges. In the implementation in Data.Graph, nodes are always identified by an integer, and edges are directed (an edge from a to b does not imply an edge from b to a) and without weights.
You use graphFromEdges when you have a list of nodes; each of them is identified by a key and holds a value, and for each node you also have its list of neighbors – that is, the list of any other nodes that receive an edge from the former. In such a case, you call graphFromEdges, which takes a list of triples, (value, key, [key]), the latest component being the aforementioned list of neighbors. In return, you get a graph but also two functions. The first one of type Vertex -> (node, key, [key]) maps a vertex identifier from the graph to the corresponding information of the node, whereas the second one, with type key -> Maybe Vertex, implements the inverse mapping: from keys to vertex identifiers.
If you already have your graph in a form where you have integer identifiers, you can use buildG instead. This function takes as parameters a tuple with the minimal and maximum identifiers (its bounds) and a list of tuples corresponding to each directed edge in the graph.

Graphs about time machines
Ad Hoc Polymorphism: Type Classes
Notice how Ord k is separated from the rest of the type by => (not to be confused by the arrow -> used in the type of functions). The purpose of Ord k is to constrain the set of possible types that the k type variable can take. This is different from the parametric polymorphism of the list functions in the previous chapters. Here you ask the type to be accompanied by some functions. This kind of polymorphism is known as ad hoc polymorphism. In this case, the Ord type class is saying that the type must provide implementations of comparison operators such as < or ==. Thus, it formalizes the notion of default order that I talked about previously.
Declaring Classes and Instances
Caution
Type classes in Haskell should not be confused with classes in object-oriented (OO) programming. Actually, if you had to make a connection, you can think of type classes as interfaces in those languages, but they have many more applications, such as linking together several types in a contract (e.g., specifying that an IntSet holds elements of type Int). The word instance is also used in both worlds with very different meanings. In OO languages it refers to a concrete value of a class, whereas in Haskell it refers to the implementation of a class by a type. This points to a third difference: in OO the declaration of a class includes a list of all the interfaces it implements, whereas in Haskell the declaration of a type and its implementation of a type class are separated. Indeed, in some cases they are even in different modules (these instances are referred to as orphan ones).
Exercise 4-4 shows you how to use type classes and instances. It does so in the direction of fulfilling the main target: creating a powerful time machine store.
Exercise 4-4: Prices for the Store
Besides time machines, the web store will also sell travel guides and tools for maintaining the machines. All of them have something in common: a price. Create a type class called Priceable of types supporting a price, and make those data types implement it.
Be aware that the meaning of this signature may not match your intuition, especially if you are coming from an object-oriented programming background. When the compiler processes this code, it will look for a concrete type for the type variable p. This means it can work only with homogeneous lists. You can compute the price of a list of time machines, [TimeMachine], or a list of books, [Book]. But there’s no way to type or create a heterogeneous list containing both values of type TimeMachine and Book.
Nameable is similar to the Show type class, which provides a function called show to convert a value into a string . You have already met this type class in the definition of previous data types, but you haven’t written any instance for those data types. The reason is that Haskell can automatically write instances of a set of type classes, deriving them from the shape of the data type. This is called the deriving mechanism because the instances to generate are specified after the deriving keyword at the end of the data type definition.
Note
According to the standard, Haskell is able to derive instances for only some type classes, which are hard-coded in the compiler. However, there’s a field of functional programming, called generic programming, that provides ways to write functions that depend on the structure of data types. Chapter 14 provides an introduction to that topic.
There’s a dual class to Show , called Read , which performs the inverse function: converting a string representation into an actual value of a type, via the read function. The implementation of a Read instance is usually tricky since you must take care of spacing, proper handling of parentheses, different formats for numbers, and so forth. The good news is that Haskell also allows you to derive Read instances automatically, which are guaranteed to read back any value produced by the show function. If deriving both, you can be sure that read . show is the identity on the values of the data type; that is, the final value will be the same as the initial one.
Built-in Type Classes
I have spoken in the previous chapters about some list functions involving types having “default comparisons” and “default equivalences.” Now that you know about type classes, it is time to introduce the specific classes that encode those concepts, namely, Ord and Eq.
I mentioned that type classes include only the declaration of functions to be implemented, but here you find some code implementation. The reason is that those are default definitions: code for a function that works whenever some of the rest are implemented. For example, if you implement (==), there’s a straightforward way to implement (/=), as shown earlier. When instantiating a type class, you are allowed to leave out those functions with a default implementation.
This means that when implementing Eq, you may do it without any actual implementation because all functions have default implementations. In that case, any comparison will loop forever because (/=) calls (==), which then calls (/=), and so on, indefinitely. This may lead to the program crashing out of memory or just staying unresponsive until you force its exit. For preventing such cases, type classes in Haskell usually specify a minimal complete definition; in other words, which set of functions should be implemented for the rest to work without problems? For Eq, the minimal complete definition is either (==) or (/=), so you need to implement at least one.
Caution
Knowing the minimal complete definitions for a type class is important since it’s the only way to enforce that programs behave correctly. The GHC compiler is able to check that you have defined all necessary functions from version 7.8 on. However, because this feature was not present since the beginning in the compiler, some libraries do not explicitly mention the minimal complete definition in code. Thus, you should double-check by looking at the documentation of the type class.
Ease of instantiation: For some types it may be more natural to write the Eq instance by defining (==), whereas in others the code for (/=) will be easier to write. Being able to do it in both ways makes it easy for consumers to instantiate the type class. This may not be so apparent for Eq, but for more complex type classes it is important.
Performance: Having both functions in the type classes allows you to implement the two of them if desired. This is usually done for performance reasons; maybe your type has a faster way of checking for nonequality than trying to check equality and failing.
Let’s focus on the highlighted parts. First, there is the restriction on the elements that have been introduced using the same syntax as in functions. Then, the declaration uses a parametric [a] in the type name, with a type variable. In sum, this instance is applicable to lists of any type a that also is an Eq. The Haskell Platform already includes these declarations for many common containers, not only lists. Instances of Eq are specified for tuples, maps, sets, trees, Maybe, and so on.
As usual, the power of instantiating type classes by parametric types is not exclusive of a special set of built-in types, but it’s available for use in your own data types, as Exercise 4-5 shows.
Exercise 4-5: The Same Client
Implement Eq for the Person and Client i types introduced in the previous chapters so that it checks the equality of all the fields. Notice that for Client you may need to add some restrictions over the type of the identifiers.
The good news is that in daily work you don’t need to write those instances because Haskell can also derive Eq like it does with Show and Read .
Once again, it has a lot of members, but thanks to default definitions, the minimal complete one is either implementing compare or implementing <=. However, if you look at the code in compare, you may notice that it’s using (==), which is a member of Eq. Indeed, at the beginning of the definition of Ord there’s a prerequisite for its implementation. Every type belonging to the class Ord must also belong to the class Eq. The syntax is similar again to including restrictions in functions or in instance implementations: Eq a =>.
In this case, you say that Eq is a superclass of Ord. Once again, I must warn you against any possible confusion when comparing the concept with the one in object-oriented languages. A type class does not inherit anything from its superclass but the promise that some functions will be implemented in their instances. For all the rest, they are completely different type classes. In particular, type implementations will go in separate instance declarations.
Like with Eq, Haskell provides automatic derivation of Ord instances . When doing so, it will consider that different alternatives follow the same order as in the data declaration. For example, in the declaration of clients at the beginning of the section, government organizations will always precede companies, which will always precede individuals. Then, if two values have the same constructor, Haskell will continue looking along each field in declaration order. In this case, it means that after the kind of client, the next thing to compare is its identifier. However, this may not be the best behavior, as Exercise 4-6 points out.
Exercise 4-6: Ordering Clients
The automatically derived Ord instance for Clients doesn’t make much sense. As discussed, it checks the kind of client and then its identifier. Instead of that, write a new instance with the following properties: first, the instance should compare the name of the client. Then, if they coincide, it should put individuals first and then companies and government organizations at the end. You may need to add further comparisons in the rest of the fields to make the order correct (e.g., for two companies whose responsibility fields are different, so you must decide which one to put first).
Think beforehand whether you need to include some restriction in the instance.
Number-Related Type Classes
Type class | Parent class | Description |
|---|---|---|
Num | n/a | Basic number type. Supports addition (+), subtraction (-), multiplication (*), unary negation (negate), absolute value (abs), sign (signum), and conversion from an Integer value (fromInteger). |
Real | Num | Subclass supporting conversion to Rational values (using toRational). Integer is an instance of this class because integral values can be embedded as fractions with a denominator of 1. |
Integral | Real | Subclass for integer values that support integer division and integer modulus. Related functions come in triples: quot, rem, and quotRem compute the division, modulus, or both (truncating toward 0), whereas div, mod, and divMod do the truncating toward negative infinity (-∞). |
Fractional | Num | Subclass for fractional values. Supports division (/), taking the reciprocal (recip) and conversion from a Rational value (fromRational). |
Floating | Fractional | Subclass for floating-point values. Supports common values such as pi and e. Allows for square roots (sqrt), natural logarithms (log), exponentiation (exp for natural base and (**) for general base), and circular and hyperbolic trigonometric functions. |
As you can see, the constant itself is polymorphic. It may represent 1 in any type that instantiates Num. The reason for that is the fromInteger function, which allows you to extract a value from an integer constant.
Binary Trees for the Minimum Price
Until now you have saved all the information about clients in lists for this chapter. Even though you now know about where to look for already implemented types, this section is going to step back and look at the design of a custom container type that completely suits the needs of the application. In particular, the aim is to provide support for the discount module, which needs access to the cheapest elements in the container. In the process, you will see how type classes allow for a greater degree of generalization, thus increasing reusability.
Step 1: Simple Binary Trees
A first solution is to use bare lists. The greatest problem with them is that querying for elements in them is costly because the only option you have is to traverse the list element by element. In the worst case, you may need to traverse the entire list until you find an answer. A solution for this is to use binary trees, which have a better complexity in this task (in particular, logarithmic vs. linear).
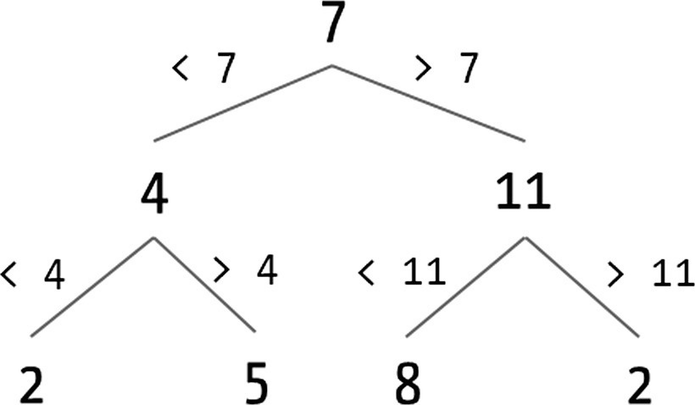
Graphical example of binary tree
Step 2: Polymorphic Binary Trees
Note
You may wonder whether you can encode the restriction on the class of elements that the binary tree may hold directly in the declaration of BinaryTree2. It’s indeed possible, but it’s not recommended. The best way is to encode the restriction in each of the operations that work on that structure, as has been done in this example. Be aware that in order to impose this restriction, you must hide the Node2 and Leaf2 constructors from public consumption.
The treeFind function has been generalized, but you still need to make some changes to the treeInsert function to make it fully general. Exercise 4-7 dives into this problem.
Exercise 4-7: More Operations on Generic Trees
Make the changes needed in treeInsert to work with the new BinaryTree2.
Also, try to implement concatenation of binary trees by repeatedly inserting all the elements in one of the binary trees.
Let’s assume now that ordering by price is used for the rest of the examples.
Step 3: Binary Trees with Monoidal Cache
At some point you may be told that in addition to minimum prices, the marketing team wants to have information about the average price of travel guides to analyze what percentage of people are buying books under and over the average. To do this, you need to create a new insertion function, which instead of the minimum computes the sum of all the prices, so you can later divide by the total number of guides. But altogether, the structure of the function remains the same.
For any two elements you need to find another one of the same type. That is, you need a function f of type c -> c -> c.
Also, depending on the way you have inserted elements in the tree, the structure may not be the same. But this should not matter for the final cached value. So, you need to be sure that the parentheses structure does not matter. In other words, the operation must be associative.
One last thing comes from the observation that when you concatenate two binary trees, you should be able to recover the new cached value for the root from the cached values from the initial roots. That means an empty tree, which contains no elements, should be assigned a value e such that f e x = f x e = x.
This means that you usually won’t write mappend; rather, you can use its synonym, (<>), coming from Semigroup .
Monoid is one of the type classes that may have multiple implementations for just one type, which has led to the creation of newtypes for some common types. Some of the most important ones are All, which implements the monoid structure of Bool under the operation (&&) with neutral element True; and All, which does the same with (||) and neutral element False. Numbers also admit two monoidal structures: Sum uses addition as an operation and 0 as a neutral element, whereas Product uses multiplication and 1.
Container-Related Type Classes
In many cases while developing an application you need to change the container you are using to handle the values. So, it might be interesting to step back and think about the commonalities between them because it may be possible to abstract from them and discover some useful type class.
Functors
You may notice a strange fact about the Functor class; in the definition of fmap , the type variable corresponding to the instance is applied to another type variable, instead of being used raw. This means that those types that are to be functors should take one type parameter. For example, IntSet, which takes none, cannot have such an instance (even though conceptually it is a functor).
The way in which the Haskell compiler checks for the correct application of type parameters is by the kind system. Knowing it may help you make sense of some error messages. Until now, you know that values, functions, and constructors have an associated type, but types themselves are also categorized based on the level of application. To start with, all basic types such as Char or Integer have kind *. Types that need one parameter to be fully applied, such as Maybe, have kind * -> *. This syntax resembles the one used for functions on purpose. If you now have Maybe Integer, you have a type of kind * -> *, which is applied to a type of kind *. So, the final kind for Maybe Integer is indeed *.
Functor is one of the most ubiquitous type classes in Haskell. Exercise 4-8 guides you in writing the corresponding instances for one of the basic types in Haskell, Maybe, and also for the binary trees that have been introduced in the previous section.
Exercise 4-8: Functor Fun!
Write the corresponding Functor instances for both Maybe and the binary trees from the previous section. The functor instance of Maybe is quite interesting because it allows you to shorten code that just applies a function when the value is a Just (a pattern matching plus a creation of the new value is just replaced by a call to map). You will need to create a new type for Maybe values in order to make the compiler happy.
From all the binary tree types shown so far, choose BinaryTree2 as the type for instantiating Functor. In this last case, remember that you must respect the order invariant of the tree, so the best way to write the map function may involve repeatedly calling treeInsert2 on an empty tree.
In this case, the concept behind the type class implementation is that of computational context. This adds to any expression an extra value of type r that can be used to control the behavior of such an expression. You will see in Chapter 6 how this mimics the existence of a constant of type r in your code.
Note
Set cannot be made an instance of Functor. The reason is that the mapping function for sets has the type Ord b => (a -> b) -> Set a -> Set b, which is not compatible with that of Functor, which doesn’t have any restriction. The Haskell language provides enough tools nowadays for creating another type class for functors that would allow Set inside it. However, this would make using the Functor type class much more complicated and would break a lot of already existing code. For that reason, the simpler version of Functor is the one included in the libraries.
Foldables
Like the list foldr, a fold takes an initial value and a combining function and starting with the initial value, applies the combining function to the current value and the next element in the structure.
You can see that a type with a binary function and some special value matches exactly the definition of a monoid. Furthermore, you have seen how combining functions in foldr should be associative, just like (<>) from Monoid is.
The rest of the operations correspond to default definitions that could be overridden for performance reasons. fold is a version of foldMap that just combines a container full of monoid values without previously applying any function. foldl corresponds to folding over the elements starting from the “other side” of the structure. You’ve already seen how the result of foldr and foldl are different if the combining function is not commutative. The versions ending with prime (') are strict versions of the functions; they will play a central role in the next chapter.
Foldables are also ubiquitous in Haskell code, like functors. Exercise 4-9 asks you to provide instances of this class for the same types you did in Exercise 4-8.
Exercise 4-9: Foldable Fun!
Maybe and binary trees can also be folded over. Write their corresponding Foldable instances. The warnings and hints from Exercise 4-8 also apply here.
As you saw in the previous chapter, a lot of different algorithms can be expressed using folds. The module Data.Foldable includes most of them, such as maximum or elem. One easy way to make your functions more general is by hiding the functions with names from the Prelude module and importing the similarly named ones using Foldable.
Note
You may wonder why Prelude includes specialized definitions for lists instead of the most general versions using Functor and Foldable. The reason is that, for a beginner, having the functions working only on [a] helps you understand the first error messages that Haskell may encounter because they don’t involve type classes. But now that you know about them, you should aim for the largest degree of abstraction that you can achieve.
In this section you wrote instances of Functor and Foldable for various data types. Because Functor and Foldable are so heavily used, the GHC developers also decided to include automatic derivation of these type classes. However, since this is not indicated in the Haskell Report, you need to enable some extensions, namely, DeriveFunctor and DeriveFoldable, for them to work. Note that if you have a type with several parameters, the one chosen for mapping or folding over is always the last one in the declaration.
Typeclassopedia
Several of the type classes discussed here, such as Monoid, Functor, and Foldable, are deeply documented in Typeclassopedia, the encyclopedia of Haskell type classes. You can find it online at wiki.haskell.org/Typeclassopedia . It’s an important source of information and examples.
Summary
You learned about how packages are specified as dependencies, and then used by either Cabal or Stack, allowing the reuse of many libraries already available in the repositories Hackage and Stackage.
Several new containers were introduced, including maps, sets, trees, and graphs. The quest for understanding their commonalities led to the discovery of the concepts of Functor and Foldable.
I covered the reason why (+) could work on several numeric types, namely, through ad hoc polymorphism and type classes. You learned both how to declare a new type class describing a shared concept between types and how to instantiate that class for a specific type. Furthermore, you saw how both classes and instances can depend on class constraints on other types or parameters.
You learned about the built-in classes Eq, describing equivalence; Ord, describing ordering; Num and its derivatives, describing numbers; and Default, describing default values for a data type.
I covered the design of a special binary tree with a cache, including how to incrementally improve the design of such a data type. In particular, you saw how type classes allow you to generalize the values it can take, looking specifically at the monoidal structure that is common in Haskell data types.
