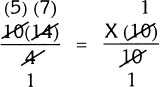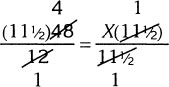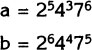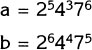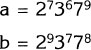XI.  Solving Mathematical Word Problems

Section 1  Introduction

People frequently express anxiety and even despair in dealing with mathematical word problems. Generally these feelings stem from unfortunate experiences in early math training. However, just as many people frightened of water have been taught to swim, this chapter has helped many people develop greater confidence and skill in mathematics.

The problems in this chapter are called mathematical word problems. But what does that mean? Simply this: Each problem describes a situation involving numerical relationships. The situation and relationships must first be interpreted and grasped. Then simple arithmetic computations need to be performed to get the answer.

Although these problems are called mathematical word problems, they really aren’t very different from the nonmathematical problems which you worked earlier. The computations are simple and the use of algebra or formulas is not required. Primarily the problems require that you understand and spell out precisely the situation that is being described. Once a problem has been set up properly, the arithmetic is easy. One of the main things you will learn in this chapter is that if you make a habit of thinking thoroughly and precisely, you can master mathematics. But before turning to the math problems, some general aspects of problem solving will be reviewed.

Section 2  An Expert’s Response

As you know, the problem solutions which follow the problems in this book summarize the steps that can be taken in reaching the answers. However, the problem solutions paint a somewhat idealized and perhaps misleading picture. They fail to show the many activities in which good problem solvers become engaged as they analyze a problem and gradually find their way to a solution. Shown on the next page is the actual response of a good problem solver as she solved a problem similar to one you worked earlier. Please read aloud both the comments on the left and the problem solver’s response on the right.

Original Problem

If deleting the letters R, I, and E from the word surmise leaves a meaningful 3-letter word, circle the first S in this word surmise. Otherwise circle the U in the word surmise where it appears for the third time in the exercise.

Problem Solver’s Response

Section 3  Another Problem Response

Here is the verbatim response which another problem solver made to a different problem you worked earlier. Again read it aloud, following the problem solver’s thoughts and logic.

Original Problem

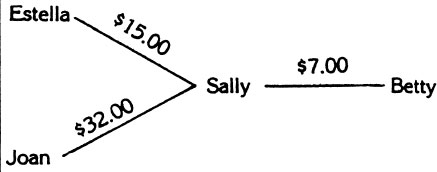
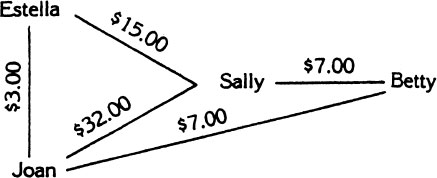
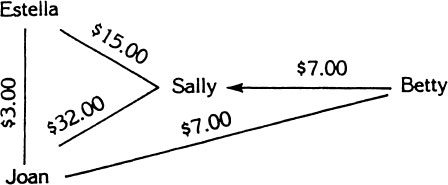
Sally loaned $7.00 to Betty. But Sally borrowed $15.00 from Estella and $32.00 from Joan. Moreover, Joan owes $3.00 to Estella and $7.00 to Betty. One day the girls got together at Betty’s house to straighten out their accounts. Which girl left with $18.00 more than she came with?

Hint: On your diagram, use arrows to show which person has to return money to which other person. Show the direction in which the money must be returned.

Problem Solver’s Response

Section 4  Concern for Accuracy, Step-by-Step Analysis and Subvocal Speech

Two characteristics of good problem solvers were evident in the responses you just read.

First is carefulness: the concern and quick retracking when ideas became confusing; the rechecking, reviewing, and rereading to be sure that errors hadn’t crept in, that nothing had been overlooked.

Second is the step-by-step approach. An important example of this was when the problem solvers restated ideas in their own words, in a form which was clearer or more useful to them. For instance, at one place in the last section the problem solver read “Sally loaned $7.00 to Betty.” He changed this to “That means Betty has to return money to Sally.” This shows that the problem solver went through two steps in representing the information in his diagram. First he translated the original statement to one which was closer to the form he needed for the diagram. Then he incorporated the new statement into his diagram. With the new statement he could more easily see that on the diagram he had to draw the arrow pointing toward Sally. Restating ideas is an important way in which good problem solvers use the step-by-step method to analyze the fine details of a problem.

While on this topic, it should be emphasized that restating ideas—and “talking to themselves” while thinking—is not something good problem solvers do only when they are asked to work a problem aloud. Studies using electronic amplifying equipment (to monitor speech muscle activity) reveal that good problem solvers talk to themselves while they solve problems. They repeat information, rephrase it, weigh it, compare different facts, express thoughts like “I better read the first sentence again,” and in general, clarify ideas for themselves. This talking, which is not done aloud, is called covert or subvocal speech.

Quiz Yourself

What is subvocal speech? What do good problem solvers talk to themselves about while solving problems?

Section 5 Sample Ratio Problem

Here is a simple ratio problem. If you are using this book in a class, one student should work the problem aloud.

This problem tells you the distance that the train travels in 3 minutes—and then asks you to compute the distance it travels in 6 minutes. Six minutes is twice as much time as 3 minutes. If the train travels for twice as much time, it will go twice as far.

This problem is called a ratio problem because you first compute the ratio of 6 minutes to 3 minutes. Once you see that 6 minutes is twice as long as 3 minutes, you use that information to calculate the answer.

Ratio problems can become more complicated than this one, and generally there is more than one way to solve them. The ability to solve ratio problems is important in many high school and college courses.

Section 6

Here is another ratio problem. In a class, one student should work it aloud at the chalkboard.

Section 7  Several Approaches

Here is the problem you were asked to solve in section 6:

There is more than one way to solve this problem. We will look at three ways, which we will call solutions 1, 2, and 3. Each solution can be viewed in terms of the underlying logic, and in terms of the mathematical computations. Looking at the solution in terms of the underlying logic is slower and less elegant. But in a sense it is more important. People who try to apply mathematical formulas without comprehending the underlying logic of a problem stand a good chance of using an incorrect formula and arriving at a wrong answer. Therefore we will begin with the logic and then look at the mathematical computations.

Solution 1

Logic of the Solution: Here is one way to look at the problem. If the train can travel 10 miles in 4 minutes, then it can travel 20 miles in 8 minutes, and 30 miles in 12 minutes. If it travels still another 2 minutes (to make a total of 14 minutes) it will go 5 more miles, for a total of 35 miles. This is shown below:

This is also represented in the following diagram:

Mathematical Solution of the Problem: Notice that in constructing the table above we counted off how many times 4 minutes goes into 14 minutes. We found that it does three times, with 2 minutes left over. At the same time we counted off the same number of 10-mile sections, and concluded that the train travels 35 miles in 14 minutes. We do the same thing arithmetically when we divide 4 minutes into 14 minutes and then multiply this by 10 miles. Thus:

The important thing to understand is that this procedure of dividing and then multiplying is really a shortcut method of spelling out the entire situation, as was done in the table and the diagram above. The diagram shows that we are thinking in terms of 4-minute intervals. In other words, 12 minutes is exactly three 4-minute intervals; and 2 minutes is one-half of a 4-minute interval. Moreover, the train travels 10 miles in each 4-minute interval, and 5 miles in one-half of a 4-minute interval. So it goes 35 miles total.

Solution 2

Logic of the Solution: Another way to solve the problem is to think in terms of ratios that are equal to each other. This approach requires more mathematical background and experience than the other two solutions. Don’t use this method with any of the later problems in this chapter unless you are absolutely certain you understand exactly what you are doing.

The logic of the solution is shown in the following diagram:

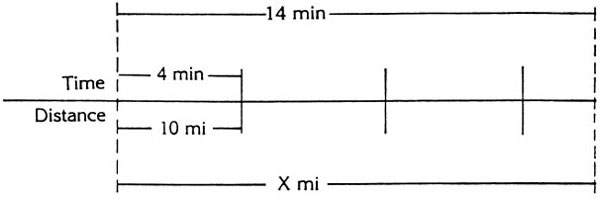
Note the X in the diagram. This is what the problem asks you to find, the distance traveled by the train in 14 minutes.

From the diagram you can see that since 14 minutes is 3½ times more than 4 minutes, the unknown distance X must be 3½ times larger than 10 miles. In other words; the ratio of 14 minutes to 4 minutes is equal to the ratio of X miles to 10 miles. With this idea in mind we can write the following equation:

On the left side of the equation we have the ratio of 14 minutes to 4 minutes. And on the right side we have the ratio of X miles to 10 miles. The equal sign means that these two ratios must be numerically equal.

Mathematical Solution: Once you have set up this equation of ratios, you find X by using simple arithmetic and algebra. Here are steps you could employ:

Solution 3

Logic of the Solution: A third approach begins by asking how many miles the train travels in I minute, and then multiplying this by 14 minutes to find the total distance traveled by the train. The following diagram shows that since the train travels 10 miles in 4 minutes, it must travel 2½ miles in 1 minute.

Once we know that the train travels 2½ miles in 1 minute, it is easy to find out how far it travels in 14 minutes. We just add up 14 of these intervals, as shown below.

Mathematical Solution: First you need to determine how many miles the train travels each minute:

Once you know that the train travels 2½ miles each minute, you can multiply this by 14 to find how far it travels in 14 minutes.

Summary

All three solutions are correct. They use different computational approaches and formulas, but they are based on basically the same picture of what happens as the train’s traveling time increases from 4 minutes to 14 minutes.

Procedure for Solving Math Word Problems

This section reviews the procedure for solving math word problems while using the thinking aloud pair problem solving technique with a partner.

1.Try to do all your thinking aloud. Read aloud and vocalize (think-aloud) all of your thoughts, decisions, analyses, and conclusions. Vocalize how you are starting the problem, questions you are asking yourself, steps you are taking in breaking the problem into parts, conclusions you are drawing— everything. If you have to add some numbers, add them aloud. If you perform any other mental operations (such as translating an unfamiliar word to a familiar word, or visualizing a picture of a relationship described in the text), perform these operations aloud. If you occasionally want to reread and think about something silently, explain your thoughts to your partner as soon as possible.

2.Adopt the step-by-step analytical procedure and the various other techniques that good problem solvers use. Break a problem into parts. Work one part accurately and then move on to the next part. Translate unfamiliar or unclear phrases into your own words. Visualize or make diagrams of relationships presented verbally. Simplify a problem by substituting easier numbers, making a table of successive computations, or referring to an earlier problem.

3.Be extremely accurate. Continually check your thinking. In the back of your mind there should always be the thought: “Is that entirely correct? & Is that completely accurate?” Never work so quickly that it leads to errors. Work everything slowly and carefully. Give sufficient time to all parts of the problem. Never just give up on a problem and guess an answer. Always try to reason the problem out.

4.While another student is working a problem, check his accuracy so that he will learn to think with more precision and thoroughness. In addition, in your own mind contrast his method with the way you might attack the same problem. How might you break the problem down more completely into subproblems? What other steps might you take? How might you visualize or diagram certain relationships? Would you work more carefully and accurately? In other words, try to imagine ways in which you might attack the problem more effectively.

Section 8 Sample Problem

Try this problem. It is in some ways similar, but in other ways different from the last one. In a class, one student should solve the problem aloud at the chalkboard, explaining his logic completely.

Section 9 Problem Solution

Original Problem

Problem Solution

A good way to begin this problem is to imagine yourself actually taking a ruler and measuring off 4 feet of string. You might picture a ball of string on a table and see yourself pulling out the string and laying off 1 foot at a time using the ruler.

The ruler is supposedly 12 inches long, and 12 inches is 1 foot. Each time you measure off a section of string equal to the length of the ruler, you supposedly have 1 foot of string. Since you want 4 feet, you will have to do this four times.

However, the ruler is warped, so each section of string is only 11½ inches long. Therefore when you measure off four sections of string, the total length is:

There are several alternate ways of doing this problem. In picturing yourself laying off four sections of string with the ruler, you might calculate how much your accumulated error is.

The ruler is 11½ inches, so each time you lay off a section of string with the ruler you are ½ inch short of the full 12 inches. When you lay off four sections of string with the ruler, you will be four times that short:

Since you are 2 inches short of the full 48 inches, your string will actually be 46 inches long.

A third way of approaching this problem is to look at it in terms of ratios. In the diagram below we let X inches be the unknown length of the string measured off with the warped ruler. The diagram shows that there are as many 12-inch sections in 48 inches as there are 11½ inch sections in X inches.

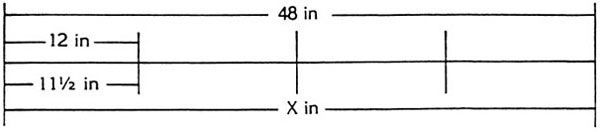
From the diagram we see that because 48 divided by 12 is four, we know that X divided by 11½ must also be four. The ratio of 48 to 12 is equal to the ratio of X to 11½. In mathematical symbols we write that this way:

To solve this equation you could employ the following steps:

Look back at problem 1 on page 232. In what ways is that problem similar to this one? In what ways is it different?

Section 10  Sample Problem

Some of the math word problems in this chapter are quite different from the ratio or rate problems you have just worked. Here is an example. In a class, one student should solve the problem aloud at the chalkboard.

Section 11 Problem Solution

Original Problem

Ted’s weekly income is $100.00 less than double Gary’s weekly income. If Ted makes $500.00 a week, what does Gary make?

Problem Solution

Whenever it is possible to represent the ideas of a math problem with a diagram, it is generally useful to do so. We will use a diagram to help keep track of the facts in this problem.

The first sentence says Ted’s weekly income is $100.00 less than double Gary’s weekly income. We’ll draw a line to represent income and then place Ted on it.

Since Ted’s income is $100.00 less than double Gary’s, it means that on the diagram Ted’s income should be below (less) double Gary’s income. Therefore we’ll place “double Gary’s income” above Ted’s income, separated by $100.00.

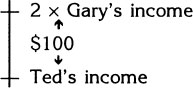
Check the diagram. Does it show what it is supposed to show, namely that Ted makes $100.00 less than double Gary?

Finally, the problem says that Ted makes $500.00. We’ll add that to the diagram.

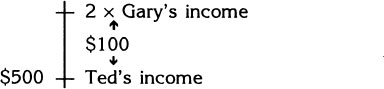
From the diagram we see that double Gary’s income is $100.00 more than Ted’s income—which means it is $600.00.

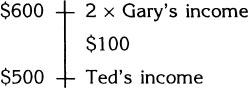
Since double Gary’s income is $600.00, his actual income must be one-half of that:

In working this problem there is a common error made, especially if a diagram is not used to help keep track of the relationships. As soon as beginners see the words “less than” they often automatically conclude that they should subtract. Their reasoning goes something like this: “Ted’s income is $100.00 less than double Gary’s income. Ted makes $500.00 a week: $100.00 less than that is $400.00. So double Gary’s income is $400.00 and ½ of that is $200.00.”

Do you see where the error was made in this train of thought? Before continuing, review and explain it in your own words.

This faulty reasoning comes from dealing carelessly or superficially with the words “less than,” rather than spelling out exactly which income is less than which. In all of the problems that follow, spell out fully and precisely the relationships among the facts. And whenever you feel a little doubtful or confused, try to use a diagram.

Now look back at problem 3 on page 47. In what ways are the two problems similar? In what ways are they different?

Section 12  Sample Problem

Work this problem by representing the facts of the first sentence in one diagram, and then the second sentence in a separate diagram. In a class, one student should work the problem aloud at the chalkboard.

Section 13 Sample Problem

Original Problem

Paul makes $25.00 a week less than the sum of what Fred and Carl together make. Carl’s weekly income would be triple Steven’s if he made $50.00 more a week. Paul makes $285.00 a week and Steven makes $75.00 a week. How much does Fred make?

Problem Solution

The first sentence says Paul makes $25.00 a week less than the incomes of Fred and Carl combined. So we’ll make a diagram with Paul placed $25.00 below Fred plus Carl.

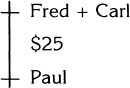
The second sentence says Carl’s weekly income would be triple Steven’s if he made $50.00 more a week. In other words, if we go up $50.00 from Carl’s income it will bring us to triple Steven’s income. This is shown in the diagram on the right.

The problem says Paul makes $285.00 a week. When we add that to the diagram, we see that Fred plus Carl combined make $310.00.

The problem also says that Steven makes $75.00 a week. Therefore triple Steven’s income is: 3 × $75 = $225. The diagram on the right shows that Carl makes $50.00 less than this, so Carl must make $175.00 a week.

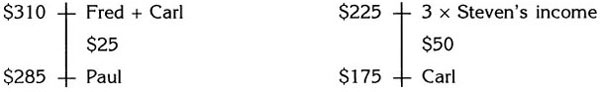
We now know that Carl’s income is $175.00 a week, and we also know that the sum of Fred’s plus Carl’s incomes is $310.00 a week. From this we can determine Fred’s income by subtraction.

Math Word Problems

Introduction

Your instructor may ask you to work in pairs, taking turns solving the following problems aloud. In working the problems, make sure you understand the underlying logic before you apply any formulas. First take some time to spell out in your mind (or in a table or diagram) what the actual situation is, and only then start to make your mathematical computations. This is the key to working mathematical word problems correctly.

Special Instruction for Listeners

If your partner performs computations or applies formulas that are inappropriate and lead to wrong answers—or has not spelled out situations with full understanding—insist that you be shown a table or diagram which illustrates, step-by-step, the relationships between the facts in the problem. Stopping your partner and requesting a full explanation of certain computations is your responsibility in helping both of you become good mathematical problem solvers.

Problem 1

John can run 7 ft in the time that Fred runs 5 ft. How far will John run in the time that Fred runs 15 ft?

Original Problem

John can run 7 ft in the time that Fred runs 5 ft. How far will John run in the time that Fred runs 15 ft?

Problem Solution

Logic of the Solution: If John can run 7 feet when Fred runs 5, then John can run 14 feet when Fred runs 10, and he can run 21 feet when John runs 15. This is shown in the table below.

Mathematical Solution:

Step 1.  When Fred runs 15 feet, how many times further does he run compared to when he runs only 5 feet? To answer this you divide:

Step 2.  If Fred runs three times as far, he must run three times as long.

Step 3.  When John also runs three times as long, how much distance does he cover? The answer is 7 × 3 = 21 feet.

This diagram shows that every time Fred runs 5 ft, John runs 7 ft.

When Fred runs 15 ft, John runs 21 ft.

Problem 2

A train travels 30 mi in the time a car travels 20 mi. At that rate, how far will the train travel when the car travels 90 mi?

Original Problem

A train travels 30 mi in the time a car travels 20 mi. At that rate, how far will the train travel when the car travels 90 mi?)

Problem Solution

Logic of the Solation: If the train travels 30 miles when the car travels 20, then the train travels 60 miles when the car travels 40, it travels 90 miles when the car travels 60, it travels 120 miles when the car travels 80, and it travels 135 miles when the car travels 90. This is shown below.

Mathematical Solution:

Step 1.  We need to know how many times as far the car travels when it goes 90 miles compared to when it goes 20 miles.

Step 2.  If the car travels 4.5 times as far in going 90 miles, it must travel 4.5 times as long. When the train travels 4.5 times as long, it goes this far: 4.5 × 30 miles.

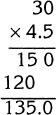
The train travels 135 miles when the car travels 90 miles.

Problem 3

Be careful to notice the difference between feet and yards in this problem.

If Fidel runs 4 yds in the time Sadam runs 9 ft, how many ft does Sadam run when Fidel runs 120 ft?

Original Problem

If Fidel runs 4 yds in the time Sadam runs 9 ft, how many ft does Sadam run when Fidel runs 120 ft?

Problem Solution

Step 1.  One yard is 3 feet. So 4 yards equals 12 feet.

The problem can be restated like this:

If Fidel runs 12 ft in the time Sadam runs 9 ft, how many ft does Sadam run when Fidel runs 120 ft?

Step 2.  We need to know how many times as far Fidel goes when he runs 120 feet compared to when he runs 12 feet.

Step 3.  If Fidel travels 10 times as far in going 120 feet, he must travel 10 times as long. During that same time Sadam would also run 10 times as far:

Problem 4

A man runs 1 mi in 10 min and a car goes 50 mi an hr. At these rates, how far does the man go when the car goes 150 mi?

Original Problem

A man runs 1 mi in 10 min and a car goes 50 mi an hr. At these rates, how far does the man go when the car goes 150 mi?

Problem Solution

Step 1.  One way to work this problem is to determine how much time the car takes to go 150 miles, and then find how far the man runs in the same time.

Step 2.  The car goes 150 miles, and it covers 50 miles each hour. Therefore the number of hours it travels is:

This means the man also runs for 3 hours.

Step 3.  The problem says the man runs 1 mile every 10 minutes. Since an hour has 60 minutes (which is 6 times as long as 10 minutes) he runs 6 miles an hour. Therefore in 3 hours he runs:

Problem 5

A car travels 40 mi an hr and a plane travels 10 mi a min. How far will the car travel while the plane travels 450 mi?

Original Problem

A car travels 40 mi an hr and a plane travels 10 mi a min. How far will the car travel while the plane travels 450 mi?

Problem Solution

Step 1.  We can work this problem by determining how much time the plane takes to go 450 miles, and then finding out how far the car goes in the same time.

Step 2.  Since the plane goes 450 miles, and it travels 10 miles each minute, it’s traveling time is:

Step 3.  This means the car also travels for 45 minutes. The problem says it travels 40 miles an hour. Let’s figure out how far it travels per minute. Since there are 60 minutes in an hour, the car will travel 1/60 of 40 miles in a minute.

Step 4.  The car travels 2/3 of a mile each minute. In 45 minutes it will go:

Problem 6

Clock A keeps perfect time whereas clock B runs fast. When clock A says 6 min have passed, clock B says 8 min have passed. How many minutes have really passed when clock B says 56 min have passed?

Original Problem

Clock A keeps perfect time whereas clock B runs fast. When clock A says 6 min have passed, clock B says 8 min have passed. How many minutes have really passed when clock B says 56 min have passed?

Problem Solution

Step 1.  The question is how many minutes have passed according to clock A (which is accurate) when clock B shows that 56 minutes have passed.

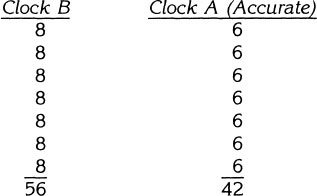
Step 2.  When clock B says 8 minutes have passed, actually only 6 minutes have passed. When clock B says 16 minutes have passed, only 12 minutes have passed.

Step 3.  It is necessary to find out how many 8-minute intervals there are in 56 minutes.

Step 4.  So the actual time that passed is 7 intervals of 6 minutes each.

Step 5.  The actual time that passed is 42 minutes.

Problem 7

Clock A keeps perfect time whereas clock B runs fast. When clock A says 4 min have passed, clock B says 6 min have passed. How many minutes have really passed when clock B says 27 min have passed?

Original Problem

Clock A keeps perfect time whereas clock B runs fast. When clock A says 4 min have passed, clock B says 6 min have passed. How many minutes have really passed when clock B says 27 min have passed?

Problem Solution

Step 1.  The question is how many minutes have passed according to clock A (which is accurate) when clock B shows that 27 minutes have passed.

Step 2.  When clock B says 6 minutes have passed, actually only 4 minutes have passed. When clock B says 12 minutes have passed, only 8 minutes have passed.

Step 3.  It is necessary to find out how many 6-minute intervals there are in 27 minutes.

Step 4.  So the actual time that passed is 4½ intervals of 4 minutes each.

Step 5.  The actual time that passed is 18 minutes.

Problem 8

A certain clock runs fast, gaining 6 min every hour. If it is set correctly at 3:00, what time will it show when the correct time is 7:30?

Original Problem

A certain clock runs fast, gaining 6 min every hour. If it is set correctly at 3:00, what time will it show when the correct time is 7:30?

Problem Solution

Step 1.  From 3:00 to 7:30 is 4½ hours.

Step 2.  The clock gains 6 minutes every hour. In 4 hours it will gain 24 minutes, and in ½ hour it will gain 3 minutes. So in 4½ hours it will gain 27 minutes.

Step 3.  7:30 plus 27 minutes is 7:57.

The clock will read 7:57.

Problem 9

A certain clock runs fast; it indicates 1 hr has passed when actually only 56 min have passed. If it is set correctly at 1:00, what is the correct time when it reads 6:30?

Original Problem

A certain clock runs fast; it indicates 1 hr has passed when actually only 56 min have passed. If it is set correctly at 1:00, what is the correct time when it reads 6:30?

Problem Solution

Step 1.  Every time the clock shows an hour having passed, actually 4 minutes less than an hour has passed. When the clock shows 2 o’clock, it is really 1:56. When it shows 3:00, it is really 2:52.

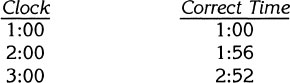
Step 2.  When the clock moves from 1:00 to 6:30, it moves 5½ hours. For each hour on the clock, the true time that passed is 4 minutes less than an hour. So when the clock says that 5½ hours have passed, the true time that passed is less than that by the amount:

Step 3.  When the clock reads 6:30, the true time is 22 minutes less than this:

Problem 10

Clock A loses 4 min every half hour, and clock B gains 5 min every 1 hrs. Both clocks are set correctly at 5:00 P.M. How many minutes apart are they when the true time is 9:00 P.M.?

Original Problem

Clock A loses 4 min every half hour, and clock B gains 5 min every 2 hrs. Both clocks are set correctly at 5:00 P.M. How many minutes apart are they when the true time is 9:00 P.M.?

Problem Solution

Step 1.  From 5:00 P.M. to 9:00 P.M. is a total period of 4 hours.

Step 2.  Clock A loses 4 minutes every half hour. That means it loses 8 minutes every hour. So in 4 hours it will be behind by this amount:

Step 3.  Clock B gains 5 minutes every 2 hours. Therefore in 4 hours it gains 10 minutes.

Step 4.  So far we have determined that clock A will be 32 minutes behind when the correct time is 9:00 P.M., and clock B will be 10 minutes ahead. That means they will be 42 minutes apart.

Problem 11

A 12-in ruler is poorly constructed and is really 12½ in long. You measure off what you believe is 5 yrds of string with this ruler. What is the true length of the string?

Original Problem

A 12-in ruler is poorly constructed and is really 12½ in long. You measure off what you believe is 5 yrds of string with this ruler. What is the true length of the string?

Problem Solution

Step 1.  Each time you measure off a section of string equal in length to the ruler, it is really 12½ inches long.

Step 2.  You want 5 yards of string. Since there are 3 feet in a yard, this is 15 feet of string.

Step 3.  When you measure off 15 sections of string, each equal to the length of the ruler, the total length of string is:

Problem 12

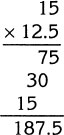
How many inches short would a piece of cloth be if you measure off 24 ft of cloth with a yardstick that is warped and is 2 in short?

Note: A yardstick is 1 yrd, and 1 yrd equals 3 ft.

Original Problem

How many inches short would a piece of cloth be if you measure off 24 ft of cloth with a yardstick that is warped and is 2 in short?

Note: A yardstick is 1 yrd, and 1 yrd equals 3 ft.

Problem Solution

Step 1. Each time you measure off a yardstick’s length of material it is 2 inches short. When you measure off 2 yards it is 4 inches short, when you measure off 3 yards it is 6 inches short.

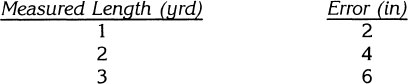
Step 2. It is necessary to determine how many times the yardstick would be used in measuring off 24 feet of material. One yard is 3 feet. Two yards is 6 feet. Three yards is 9 feet. Four yards is 12 feet. Five yards is 15 feet. Six yards is 18 feet. Seven yards is 21 feet. Eight yards is 24 feet.

So the yardstick will be applied eight times, and each time it is in error by 2 inches. Therefore, the total error will be:

Step 3. Thus, the piece of material would be 16 inches short.

Problem 13

Boris owns 6 suits, 3 less than Che and twice as many as Phylis. Gene owns 3 times as many suits as Che. How many suits each do Gene and Phylis own?

Note: Knowledge of algebra is not required in solving this problem or the ones that follow. All that is required is that you read the problem carefully, determine what it is asking, determine what information and what relationships are given, and then work through the relationships accurately.

Original Problem

Boris owns 6 suits, 3 less than Che and twice as many as Phylis. Gene owns 3 times as many suits as Che. How many suits each do Gene and Phylis own?

Problem Solution

Step 1. Boris owns 6 suits.

Step 2. Boris owns 3 suits less than Che. That means Che owns 3 more suits than Boris, so Che owns 9 suits.

Step 3. Boris owns twice as many suits as Phylis. This means Phylis owns only half as many suits as Boris. Since Boris owns 6 suits, Phylis owns 3 suits.

Step 4. Gene owns 3 times as many suits as Che. Che owns 9 suits, so Gene owns 27 suits.

Step 5. How many suits each do Gene and Phylis own?

Gene owns 27, Phylis owns 3.

Problem 14

The number of cows owned by farmer Smith is the number owned by farmer Thompson divided by the number owned by farmer Jones. If farmer Thompson, who owns 42 cows, had 14 more cows, he would own 8 times as many cows as farmer Jones. How many cows does farmer Smith own?

Original Problem

The number of cows owned by farmer Smith is the number owned by farmer Thompson divided by the number owned by farmer Jones. Farmer Thompson, who owns 42 cows, would own 8 times as many cows as farmer Jones if he owned 14 more cows. How many cows does farmer Smith own?

Problem Solution

Step 1. The problem asks how many cows farmer Smith owns.

Step 2. The number of cows owned by Smith is the number owned by Thompson divided by the number owned by Jones.

Step 3. Thompson has 42 cows.

Step 4. If Thompson owned 14 more cows he would own eight times as many cows as Jones.

Step 5. If Thompson owned 14 more cows he would own:

Step 6. So 56 cows is eight times as many cows as Jones owns.

Step 7. To find Jones’ cows divide 56 by 8.

Step 8. To get the number of cows owned by Smith, the division shown in step 2 must be carried out.

Step 9. Smith owns 6 cows.

Problem 15

If Bo’s weekly income doubled he would be making $500.00 a week more than Om. Bo’s weekly income is $700.00 more than one-half of Phi’s. Phi makes $1800.00 a week. How much does Om make?

Original Problem

If Bo’s weekly income doubled he would be making $500.00 a week more than Om. Bo’s weekly income is $700.00 more than one-half of Phi’s. Phi makes $1800.00 a week. How much does Om make?

Problem Solution

Step 1. Strategy for working this problem: The problem asks for Om’s income. It gives Phi’s income as $1800.00. It also tells how to get from Phi’s income to Bo’s income, and then from Bo’s income to Om’s income.

Step 2. It says Phi’s income is $1800.00 and it says Bo’s income is $700.00 more than one-half of this. So if Phi’s income is divided in half, and then $700.00 is added, we will have Bo’s income.

Step 3. Thus, Bo’s income is $1600.00 a week.

Step 4. It says that double Bo’s income is $500.00 more than Om’s. 2 × Bo’s income is $500.00 more than Om’s income.

Step 5. Double Bo’s income is: 2 × $1600 = $3200.

Step 6. So, $3200.00 is $500.00 more than Om’s income. Therefore, Om’s income is $3200 − $500 = $2700.

Problem 16

Pau owns 4 more than one-half as many books as Ete. Pau owns 32 books. How many books does Ete own?

Note: After you solve the problem, please read the problem solution—even if your answer is correct. The problem solution illustrates a principle which is used in the remaining four problems of the program.

Original Problem

Pau owns 4 more than one-half as many books as Ete. Pau owns 32 books. How many books does Ete own?

Problem Solution

Step 1. A diagram can be used to clarify the relationship between Pau’s books and Ete’s books. Starting at Ete’s books, we take one-half of them.

If we now add 4 books, we have Pau’s books (which the problem says is 32 books).

Step 2. To solve the problem work backwards. The diagram shows that if 4 books are taken from Pau he will have exactly one-half as many as Ete.

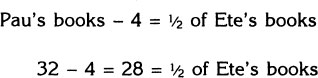
Step 3. One-half the number of books owned by Ete is 28. So Ete owns twice this number.

Step 4. Ete owns 56 books.

Problem 17

Leslie owns 1 more than 3 times as many dresses as Su. Leslie owns 28 dresses. How many dresses does Su own?

Note: Make a diagram in the space below if it helps your thinking.

Original Problem

Leslie owns 1 more than 3 times as many dresses as Su. Leslie owns 28 dresses. How many dresses does Su own?

Problem Solution

Step 1. The relationship between the number of dresses owned by Su and by Leslie is shown in the diagram.

Step 2. Leslie owns 28 dresses.

Step 3. Leslie owns one more than three times as many dresses as Su. So if one dress is taken from Leslie, she will have exactly three times as many dresses as Su.

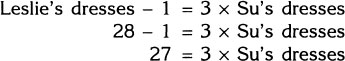
Step 4. Since 27 is three times as many dresses as Su owns, the number of dresses owned by Su can be obtained by dividing 27 by three.

Step 5. Su owns 9 dresses.

Problem 18

Jim’s weekly income is $100.00 less than triple John’s weekly income. Huey’s weekly income is $20.00 more than double John’s weekly income. Huey’s income is $120.00. What is Jim’s income?

Note: If you have difficulty you may find it helpful to follow these steps.

1.  Diagram the relationship between John’s and Huey’s income.

2.  Determine John’s income.

3.  Diagram the relationship between John’s and Jim’s income.

4.  Determine Jim’s income.

Original Problem

Jim’s weekly income is $100.00 less than triple John’s weekly income. Huey’s weekly income is $20.00 more than double John’s weekly income. Huey’s income is $120.00. What is Jim’s income?

Problem Solution (Diagrams are Shown Below)

Step 1.  The problem asks for Jim’s income. It gives Huey’s income as $120.00 and it tells how to get John’s income from Huey’s income and then Jim’s income from John’s income.

Step 2.  Huey’s income is $120.00. This is $20.00 more than double John’s income. So, if $20.00 is subtracted, it will be double John’s income. (See diagram)

Step 3.  Double John’s income is $100.00, so John’s income is one-half of $100.00.

Step 4.  Jim’s income is $100.00 less than triple John’s weekly income. So triple John’s income minus $100.00 is Jim’s income. (See diagram)

Step 5.  Jim’s income is $50.00.

Problem 19

The sum of the weekly income of Bill and his wife, Rachel, is $1300.00 less than triple Xudy’s income. Bill makes $400.00 less than double what his wife makes. Rachel makes $800.00. How much does Xudy make?

Original Problem

The sum of the weekly income of Bill and his wife, Rachel, is $1300.00 less than triple Xudy’s income. Bill makes $400.00 less than double what his wife makes. Rachel makes $800.00. How much does Xudy make?

Problem Solution

Step 1.  Bill’s wife makes $800.00.

Step 2.  Bill makes $400.00 less than double what his wife makes. So Bill’s income can be obtained by doubling Rachel’s income and subtracting $400.00.

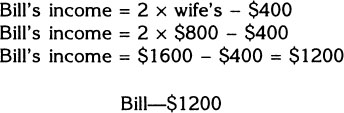
Step 3.  The sum of Bill’s and his wife’s income is $1300.00 less than triple Xudy’s income.

Step 4.  The sum of Bill’s and his wife’s income is: $1200 + $800 = $2000

Step 5.  So $2000.00 is $1300.00 less than triple Xudy’s income. This means that if $1300.00 is added to $2000.00 we will have triple Xudy’s income.

Step 6.  $3300.00 is triple Xudy’s income. So Xudy’s income can be obtained by dividing $3300.00 by 3.

Step 7.  Xudy’s income is $1100.00.

Problem 20

Double Pete’s weekly income is $50.00 less than the combined incomes of Joe and Sally. Patti, who makes $170.00 a week, makes $20.00 a week less than Sally but $40.00 more than Pete. How much does Joe make?

Original Problem

Double Pete’s weekly income is $50.00 less than the combined incomes of Joe and Sally. Patti, who makes $170.00 a week, makes $20.00 a week less than Sally but $40.00 more than Pete. How much does Joe make?

Problem Solution

Step 1.  The first sentence says that double Pete’s income is $50.00 less than the combined incomes of Joe and Sally. This is shown in the following diagram.

Step 2.  The second sentence says Patti, who makes $170.00 a week, makes $20.00 a week less than Sally.

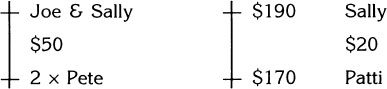
Step 3.  The sentence also says Patti makes $40.00 more than Pete.

Step 4.  If Pete’s income is $130.00 a week, then double his income must be $260.00. This fact is placed on the left diagram.

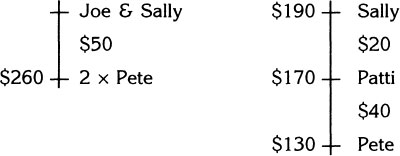
Step 5.  The diagram on the left now shows us that the combined income of Joe and Sally is $310.00.

Step 6.  We know that Sally makes $190.00 a week. Therefore Joe must make: $310 − $190 = $120 a week.

Problem 21

A stone statue was divided into 5 parts and packed in crates for shipping. The 5 full crates together weighed a total of 520 lbs, whereas each crate weighed 20 lbs empty. How much did the statue itself weigh?

Original Problem

A stone statue was divided into 5 parts and packed in crates for shipping. The 5 full crates together weighed a total of 520 lbs, whereas each crate weighed 20 lbs empty. How much did the statue itself weigh?

Problem Solution

Step 1.  Each empty crate weighs 20 pounds. Therefore the weight of 5 crates is:

Step 2.  The weight of the statue is the total weight minus the weight of the 5 crates.

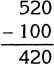
The statue weighs 420 pounds.

Problem 22

A metal statue was divided into 5 parts and packed in crates for shipping. Each full crate weighed 520 lbs, whereas it weighed 20 lbs empty. How much did the statue itself weigh?

Original Problem

A metal statue was divided into 5 parts and packed in crates for shipping. Each full crate weighed 520 lbs, whereas it weighed 20 lbs empty. How much did the statue itself weigh?

Problem Solution

Step 1.  Each crate weighed 520 pounds full and 20 pounds empty, so the weight of the piece of statue in each crate was:

Step 2.  There were 5 pieces of statue each weighing 500 pounds, so the total weight of the statue was:

Problem 23

Paul sold 160 sandwiches for $2.00 each. Each sandwich consisted of 4 oz of ham, 2 slices of bread, and mustard. Paul paid $3.00 a pound for the ham, 60¢ a loaf for the bread (20 slices per loaf) and used 8 jars of mustard at 50¢ each. How much profit did he make?

Original Problem

Paul sold 160 sandwiches for $2.00 each. Each sandwich consisted of 4 oz of ham, 2 slices of bread, and mustard. Paul paid $3.00 a pound for the ham, 60¢ a loaf for the bread (20 slices per loaf) and used 8 jars of mustard at 50¢ each. How much profit did he make?

Problem Solution

Step 1.  160 sandwiches require 320 slices of bread.

Step 2.  There are 20 slices of bread in a loaf, so the number of loaves is:

Step 3.  The cost of 16 loaves of bread is:

Step 4.  160 sandwiches require 640 ounces of ham.

Step 5.  There are 16 ounces in a pound, so the number of pounds of ham is:

Step 6.  The cost of 40 pounds of ham is:

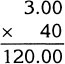
Step 7.  The cost of 8 jars of mustard at 50¢ each is:

Step 8.  The total cost for bread, ham and mustard is:

Step 9.  Paul sold 160 sandwiches for $2.00 each. So he collected:

Step 10.  Paul’s profit is the amount of money he collected minus the total cost:

Paul’s profit is $186.40.

Problem 24

Ornamental chain sells for $1.23 a foot. How much will farmer Jones have to spend for chain in order to enclose a 70′ × 30′ patch of ground, leaving a 4′ entrance in the middle of each of the 30′ sides?

Original Problem

Ornamental chain sells for $1.23 a foot. How much will farmer Jones have to spend for chain in order to enclose a 70′ × 30′ patch of ground, leaving a 4′ entrance in the middle of each of the 30′ sides?

Problem Solution

Step 1.  Farmer Jones’ garden is shown below with the 4′ entrances.

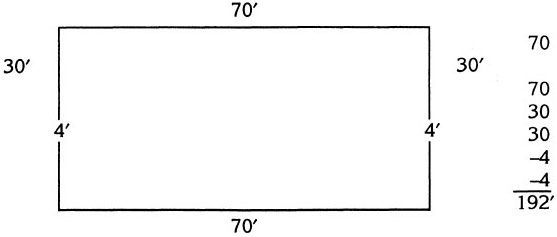
Step 2.  The length of chain needed is 192 ft.

Therefore the cost is $1.23 × 192 = $236.16.

Note: The remaining problems require familiarity with some terms in mathematics and operations with fractions and powers. If you are unfamiliar with these topics but have developed the skill of careful, analytical thinking, you can learn them readily by taking a course in basic math in high school, college, or an adult education program. A good textbook in this area is Developing Mathematical Skills: Computation, Problem Solving, and Basics for Algebra, by Whimbey and Lochhead, McGraw Hill, Inc., 1981.

Problem 25

A certain ball, when dropped from any height, bounces one-third of the original height. If the ball is dropped from 54 ft, bounces back up, and continues to bounce up and down, what is the total distance that the ball has traveled when it hits the ground for the fourth time? Remember to count both the ascending and descending portions of the ball’s path in computing the total distance.

Hint: make a diagram to represent the total path of the ball. You may want to show the ball bouncing at an angle, instead of straight up and down, in order to be able to see the ball’s entire path. The beginning of such a diagram is shown below.

Original Problem

A certain ball, when dropped from any height, bounces one-third of the original height. If the ball is dropped from 54 ft, bounces back up, and continues to bounce up and down, what is the total distance that the ball has traveled when it hits the ground for the fourth time?

Problem Solution

Step 1.  Ball drops from a height of 54 ft. So when it hits the ground it will have traveled 54 ft.

Step 2.  The ball bounces back up one-third of 54 ft: 54/3 = 18.

So, at that point it has travelled a total of 54 + 18 = 72 ft.

Step 3.  The ball continues to fall and bounces up one-third as high.

The first 4 bounces are shown in the following diagram. (Although the bounces may have been straight up, they are drawn slanted to the right so that they can all be seen.)

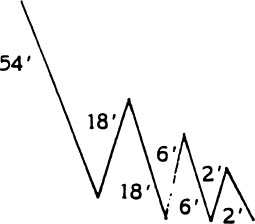
Step 4.  How far will it have traveled when it hits the ground for the fourth time?

The sum is 106 ft.

Problem 26

A car starts on a trip from city A to city B which is 60 miles away. It runs out of gas after it has gone one-third of the second half of the trip. How many miles still remain of the trip to city B?

Original Problem

A car starts on a trip from city A to city B which is 60 miles away. It runs out of gas after it has gone one-third of the second half of the trip. How many miles still remain of the trip to city B?

Problem Solution

Step 1.  The car ran out of gas after it went one-third of the second half of the trip. First the car went one-half of the trip. This is shown below.

Step 2.  Then the car went one-third of the second half.

Step 3.  The entire trip is 60 miles, so half the trip is 30 miles, and one-third of 30 miles is 10 miles.

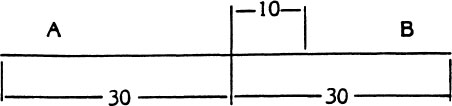
Step 4.  How many miles still remain of the trip to city B? There are 20 miles remaining to city B.

Problem 27

If the sum of two positive whole numbers is 10, what is their greatest possible product?

Note: When two numbers are multiplied together, the answer is called the “product.”

Original Problem

If the sum of two positive whole numbers is 10, what is their greatest possible product?

Problem Solution

Step 1.  The column labeled SUM shows all combinations of positive whole numbers whose sum is 10.

The column labeled PRODUCT shows the product for each combination.

Step 2.  The product is largest when the two numbers are equal:

Problem 28

Is the sum of any two even positive integers—each of which is less than 10—odd or even?

Original Problem

Is the sum of any two even positive integers—each of which is less than 10—odd or even?

Problem Solution

Step 1.  Here are the sums of all pairs of even positive integers, where each is less than 10:

Step 2.  All these sums are even.

See the end of this chapter for a more detailed discussion of this problem.

Problem 29

Note:4³ means 4 × 4 × 4 × 5 × 5

Original Problem

Problem Solution

Step 1.  

Step 2.  These products can be rewritten like this:

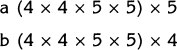
Step 3.  This shows that a is bigger.

Problem 30

Original Problem

Problem Solution

Step 1.  Note that .

Therefore:

Step 2.  Note that and .

Therefore:

Step 3.  We now have:

Step 4.  This shows that b is larger.

Problem 31

Here is how a number is multiplied by a fraction:

Using this procedure, multiply 5² times

Original Problem

Multiply 5² times

Problem Solution

Additional Problems

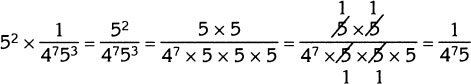
1.   In the time a car travels 4 mi, a plane travels 30 mi. When the car travels 60 mi, how far does the plane travel?

2.   Tarzan can swim 8 ft in the time a crocodile swims 10 ft. When Tarzan swims 20 ft, how far does the crocodile swim?

3.   Paul can run 12 ft in the time Bob runs 10 ft.

a.   When Paul runs 6 ft, how far does Bob run? _____ ft

b.   When Paul runs 3 ft, how far does Bob run? _____ ft

c.   When Paul runs 30 ft, how far does Bob run? _____ ft

d.   When Paul runs 246 ft, how far does Bob run? _____ ft

4.   A restaurant uses 2 pt of milk with 3 pt of cream to make coffee creamer. To make a larger quantity of the mixture, how many pints of cream should they use with 18 pt of milk?

5.   A warped 12-in ruler is only 11 in long. Unaware of this, Judy used the ruler to measure off 48 in of rope. What was the true length of the rope?

6.   A 5-in piece of cloth shrank to 4 in when it was washed. At that rate, how long would a 75-in piece of cloth measure after washing?

7.   A clock runs fast. It says 8 min have passed when only 5 min have passed. How much time has really passed when the clock says 20 min have passed?

8.   Yvette makes $20.00 a week less than double Celeste. Yvette makes $320.00 a week. How much does Celeste make?

9.   Bob and Fred together make $20.00 a week less than double John. John makes $110.00 a week and Bob makes $140.00 a week. How much does Fred make?

10.   Dero makes $70.00 a week more than double Willie. Also, Dero makes $15.00 a week less than Harry. Harry makes $185.00. How much does Willie make?

11.   Beverly makes $25.00 less than Jody and Hal combined. Jody makes $30.00 less than Hal. Hal makes $140.00. How much does Beverly make?

12.   If Joe’s weekly income doubled he would be making $70.00 a week more than Joan. Joe’s weekly income is $20.00 more than one-half of Bill’s. Bill makes $200.00 a week. How much does Joan make?

13.   If Tommy had three more books he would have twice as many as Helen. Tommy has 21 books. How many does Helen have?

14.   The number of dresses owned by Beth is the number owned by Julie divided by the number owned by J. E. Julie, who owns 28 dresses, would own five times as many dresses as J. E. if she had 7 more dresses. How many dresses does Beth have?

15.   Jack weighs 25 lbs less than Phil. Bill weighs 40 lbs more than Jack. Frank weighs 70 lbs less than Bill. A1 weighs 5 lbs less than Frank. Which man is heaviest? Which is lightest?

16.   Starting at one end of my street, my house is the third house. Starting at the other end, my house is the seventh one. Not counting my house, how many houses are on my side of the street?

17.   Starting at one end of a street, the police station is the fifth building. Starting at the other end, it is the ninth building. Including the police station, how many buildings are on that side of the street?

18.   Fred and Tom attended the same school. Fred lives 7 mi away and Tom lives 9 mi away.

a.   What is the greatest possible distance between their homes?

b.   What is the shortest possible distance between their homes?

19.   There are 15 books stacked in a single pile. How many books are between 2 other books?

Some of the following problems require familiarity with concepts and operations in mathematics such as fractions, decimals, percents, area, coordinates, negative numbers, and powers. If you are unfamiliar with these topics but have developed the skill of careful, analytical thinking, you can learn them by taking a course in basic mathematics in high school, college, or an adult education program. These problems are Included here to show you the types of questions you may encounter on standardized academic aptitude tests.

20.   A certain ball, when dropped from any height, bounces one-half the original height. If it was dropped from 80 ft and allowed to bounce freely, what was the total distance it traveled when it hit the ground for the third time?

21.   A mouse made a dash from the cellar door to his hole in the living room wall which was 90 ft away. The cat saw him after he had gone one-third of the second half of the distance. How far did the mouse still have to run for safety? Make a diagram showing the distances.

22.   A car started on a trip from city X to city Y which is 120 mi away. It ran out of gas one-quarter of the way through the last third of the trip. How many miles did it travel before running out of gas?

23.   Is the sum of any two positive odd integers—each of which is less than 10—odd or even? (See pages 332–333 for a detailed solution.)

24.   Is the sum of any odd and even positive integers—each of which is less than 10—odd or even?

25.   Is the sum of any 2 consecutive positive integers—each of which is less than 10—odd, even, or either?

26.   Is the sum of any 3 consecutive positive integers—each of which is less than 10—odd, even, or either?

27.   Is the sum of any 4 consecutive positive integers—each of which is less than 10—odd, even, or either?

28.   Is the sum of any 5 consecutive positive integers—each of which is less than 10—odd, even, or either?

29.   If the product of 2 positive equal numbers is 25, what is their sum?

30.   A rectangular park is .6 mile long and .5 mile wide.

a.   What is the area of the park? (Area = Length × Width)

b.   What is the perimeter of the park? (The perimeter is the total distance around the park.)

31.   A square park is 1.5 mi long on each side.

a.   What is the area of the park?

b.   What is the perimeter of the park?

32.   If the area of a rectangular park is 30 square mi and the width of the park is .5 mi, what is the length?

33.   If the perimeter of a square park is 1.2 square mi, what is the length of each side?

34.   A square is 3 ft long on each side. A rectangle is 2 ft long and 7 ft wide. What is the ratio of the perimeter of the square to the perimeter of the rectangle?

35.   One square is 6 in long on each side. Another square has sides which are only one-half as long. What is the ratio of the area of the small square to the large square?

36.   Eighty-eight pounds of a medicine was divided into 1000 equal parts. How much did each part weigh?

37.   Fred bought a car for $4000.00 and sold it 2 years later for 70% of what he paid.

a.   How much did he sell it for?

b.   How much less did he sell it for than he paid for it?

38.   A dealer bought a TV for $300.00, then sold it for 40% more than that price.

a.   How much profit did he make?

b.   How much did he sell it for?

39.   An art dealer bought a painting for $500.00 and sold it 2 years later for 350% of the price he paid. How much did he sell it for?

40.   The line below is marked off into 4 equal parts. If you start at point A and go 70% of the way to point E, between which 2 letters would you be? Hint: ¼ equals 25%.

41. a The line below is marked off into 5 equal parts. If you start at point U and go 150% of the distance to point V, between which two letters would you be?

42.   If you start at point U and go 380% of the distance to point V, between which two letters would you be?

43.   Perform each multiplication and reduce the answer to simplest terms.

a.   Multiply 20 times

b.   Multiply 30 times

c.   Multiply 5³ times

d.   Multiply 5² times

e.   Multiply 5³ times

f.   Multiply 5³ times

44.   Monthly Utility Bills For The Jones’ In 1998

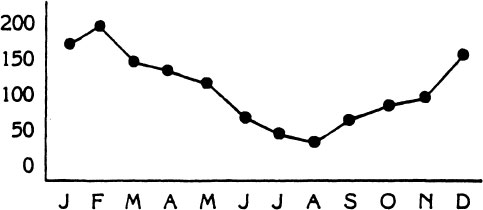
a.   Is the average of the monthly utility bills more or less than $150.00?

b.   Is the average of the monthly utility bills for January and February more or less than the total of the bills for November and December?

c.   How much higher was the utility bill in January than in June?

45. a. How many faces does the cube shown below have?

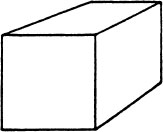
b.   If each edge of the cube is 6 in long, how many square inches of paper are required to cover all faces of the cube?

45. a. If the cube below is cut in half along the dotted line, how many total faces do the two pieces have?

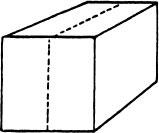
b.   If each edge of the original cube was 6 in long, how many square inches of paper would be required to cover all the faces of the two pieces produced by cutting the cube?

46.   If the cube below is cut into quarters along the dotted lines, how many total faces do the four pieces have?

47.   If each edge of the original cube was 6 in long, how many square inches of paper would be required to cover all the faces of the four pieces produced by cutting the cube?

48.   A company bought 60 gallons of soda for $30.00 and quart-size bottles for 5¢ each. How much total profit did they make if they sold all the soda for 50¢ a bottle? (One gallon equals 4 quarts.)

49.   A garden is 50 ft long and 25 ft wide. How many total fence posts would be required to place a fence post at each corner and additional fence posts every 5 ft?

50.   A field is 1500 ft long and 60 ft wide. How many total fence posts would be required to place a fence post at each corner and additional fence posts every 5 ft?

51.   Mr. Smith’s garden is 30 ft long and 21 ft wide and he would like to put a chain fence around it. The chain costs $5.00 a yard. He will support the chain by putting a metal post in each of the 4 corners and additional posts every 3 ft. The posts cost $2.00 each. What is the total cost of the chain and posts?

52.   Starting at one corner, a park runs 30 mi east, 15 mi north, 10 mi east, 25 mi south, 40 mi west, then back to the first corner.

a.   Make a diagram of the park.

b.   Compute the distance around the park. (This distance is called the perimeter.)

53.   Compute the area of the park described in problem 52 by dividing it into two rectangles and computing each part separately, then adding the two parts.

54.   Starting at one corner, a park runs 10 mi west, 8 mi south, 20 mi west, 18 mi north, 30 mi east, then back to the first corner.

a.   Make a diagram of the park.

b.   Compute the distance around the park.

55.   Compute the area of the park described in problem 54 by dividing it into two rectangles and computing each part separately, then adding the two parts.

56.   John had $4000.00 in the bank on January 1, 1990. Each year for the next several years he spent 1/2 of the money he had in the bank at the beginning of the year. How much did he have in the bank on January 1, 1995?

57.   Phil had $540.00 in the bank on January 1, 1991. Each year for the next several years he spent 1/3 of the money he had in the bank at the beginning of the year. How much did he have in the bank on January 1, 1994?

58.   Phil had $540.00 in the bank on January 1, 1991. Each year for the next several years he spent 1/3 of the money he had in the bank at the beginning of the year. How much had he spent by January 1, 1994?

59.   Jane deposited $2000.00 in an account which paid 10% interest per year. At the end of the first year she left the original $2000.00 and the interest in the account. How much was in the account at the end of the second year?

60.   

a.   What are the coordinates of the point a? What are the coordinates of the point b?

b.   Compute the distance between points a and b using this formula:

61.   If x − 8 is a positive number and x is a whole number, what is the smallest possible value of x?

62.   If x + 7 is a negative number and x is an integer, what is the largest possible value of x?

63.   If 5(2 + 1) = 20 + x, what is x?

64.   If r is the radius of a circle and d is the diameter, which is larger:

65.   If x − 7 = y + 9, which is larger, x or y?

Discussion for Problems 23–28

New knowledge in mathematics often results from a mathematician seeing a consistency and then showing theoretically why the consistency occurs. The process is similar to the steps you might use in solving this problem.

Is the sum of any two even integers odd or even?

Solution

Step 1.  We will try adding several pairs of even integers to see if the sums are odd or even. We attempt to avoid using only special cases for which a conclusion might be true even though it is not true for all cases.

Experimenting with a few concrete cases is a good way to start many math problems involving general formulas or statements.

Step 2.  All these sums are even numbers, so it appears that the sum of any two even integers is even.

Step 3.  To be sure that the sum of any pair of even integers is even, we will begin with the definition of an even integer.

When an even integer is divided by 2 the answer is an integer, not a fraction or a mixed number.

This means that if A and B are any even integers, then:

Step 4.  We want to show that if A and B are even integers, then their sum (A + B) is also an even integer.

This means we must show that is an integer, not a fraction or a mixed number.

Step 5.  From the rule for adding fractions we know that:

Step 6.  We know that and are both integers.

Also, the sum of two integers is itself an integer.

Therefore, is an integer.

Step 7.  This shows that the sum of any two even integers is also an even integer.

Here are some other problems that could be approached in the same way. Just remember that when 1 is divided by 2 the answer is ½, when −1 is divided by 2 the answer is − ½, and when other odd numbers are divided by 2 the answer is a mixed number with the fraction portion equal to ½. Furthermore, .

Is the sum of any two odd integers odd or even?

Is the sum of any odd and even integer odd or even?

Is the sum of any two consecutive integers odd or even?

Is the sum of any three consecutive integers odd, even, or either?