CHAPTER 1

Background Issues for Regression Analysis

Chapter 1 Preview

When you have completed reading this chapter you will:

• Realize that this is a practical guide to regression not a theoretical discussion.
• Know what is meant by cross-sectional data.
• Know what is meant by time-series data.
• Know to look for trend and seasonality in time-series data.
• Know about the three data sets that are used the most for examples in the book.
• Know how to differentiate between nominal, ordinal, interval, and ratio data.
• Know that you should use interval or ratio data when doing regression.
• Know how to access the “Data Analysis” functionality in Excel.

Introduction

The importance of the use of regression models in modern business and economic analysis can hardly be overstated. In this book, you will see exactly how such models can be developed. When you have completed the book you will understand how to construct, interpret, and evaluate regression models. You will be able to implement what you have learned by using “Data Analysis” in Excel to build basic mathematical models of business and economic relationships.

You will not know everything there is to know about regression; however, you will have a thorough understanding about what is possible and what to look for in evaluating regression models. You may not ever actually build such a model in your own work but it is very likely that you will, at some point in your career, be exposed to such models and be expected to understand models that someone else has developed.

Initial Data Issues

Before beginning to look at the process of building and evaluating regression models, first note that nearly all of the data used in the examples in this book are real data, not data that have been contrived to show some purely academic point. The data used are the kind of data one is faced with in the real world. Data that are used in business applications of regression analysis are either cross-sectional data or time-series data. We will use examples of both types throughout the text.

Cross-Sectional Data

Cross-sectional data are data that are collected across different observational units but in the same time period for each observation. For example, we might do a customer (or employee) satisfaction study in which we survey a group of people all at the same time (e.g., in the same month).

A cross-sectional data set that you will see in this book is one for which we gathered data about college basketball teams. In this data set, we have many variables concerning 82 college basketball teams all for the same season. The goal is to try to model what influences the conference winning percentage (WP) for such a team. You might think of this as a “production function” in which you want to know what factors will help produce a winning team.

Each of the teams represents one observation. For each observation, we have a number of potential variables that might influence (in a causal manner) a team’s winning percent in their conference games. In Figure 1.1, you see a graph of the conference winning percentage for the 82 teams in the sample. These teams came from seven major sport conferences: ACC, Big 12, Big East, Big 10, Mountain West, PAC 10, and SEC.

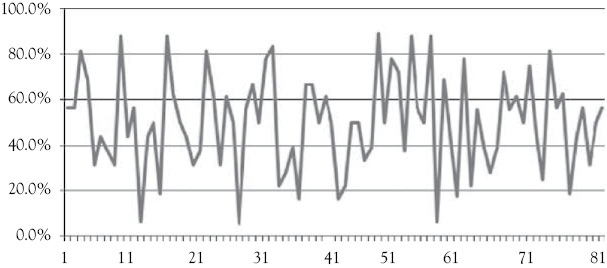
Figure 1.1 The conference winning percentage for 82 basketball teams: An example of cross-sectional data

Source: Statsheet at http://statsheet.com/mcb.

Time-series Data

Time-series data are data that are collected over time for some particular variable. For example, you might look at the level of unemployment by year, by quarter, or by month. In this book, you will see examples that use two primary sets of time-series data. These are women’s clothing sales in the United States and the occupancy for a hotel.

A graph of the women’s clothing sales is shown in Figure 1.2. When you look at a time-series graph, you should try to see whether you observe a trend (either up or down) in the series and whether there appears to be a regular seasonal pattern to the data. Much of the data that we deal with in business has either a trend or seasonality or both. Knowing this can be helpful in determining potential causal variables to consider when building a regression model.

The other time-series used frequently in the examples in this book is shown in Figure 1.3. This series represents the number of rooms occupied per month in a large independent motel. During the time period being considered, there was a considerable expansion in the number of casinos in the State, most of which had integrated lodging facilities. As you can see in Figure 1.3, there is a downward trend in occupancy. The owners wanted to evaluate the causes for the decline. These data are proprietary so the numbers are somewhat disguised as is the name of the hotel. But the data represent real business data and a real business problem.

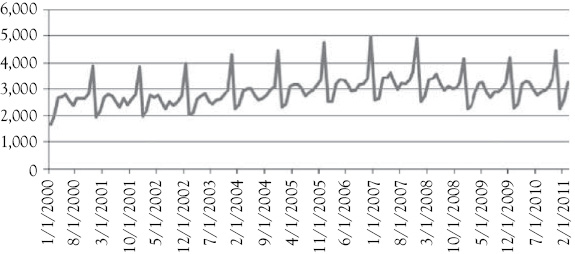
Figure 1.2 Women’s clothing sales per month in the United States in millions of dollars: An example of time-series data

Source: www.economagic.com.

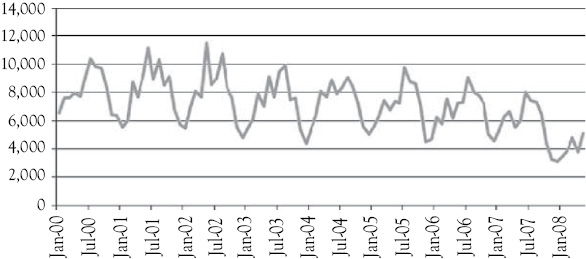
Figure 1.3 Stoke’s Lodge occupancy per month: A second example of time-series data.

Source: Proprietary.

To help you understand regression analysis, these three sets of data will be discussed repeatedly throughout the book. Also, in Chapter 10, you will see complete examples of model building for quarterly Abercrombie & Fitch sales and quarterly U.S. retail jewelry sales (both time-series data). These examples will help you understand how to build regression models and how to evaluate the results.

An Additional Data Issue

Not all data are appropriate for use in building regression models. This means that before doing the statistical work of developing a regression model you must first consider what types of data you have. One way data are often classified is to use a hierarchy of four data types. These are: nominal, ordinal, interval, and ratio. In doing regression analysis, the data that you use should be composed of either interval or ratio numbers.1 A short description of each will help you recognize when you have appropriate (interval or ratio) data for a regression model.

Nominal Data

Nominal data are numbers that simply represent a characteristic. The value of the number has no other meaning. Suppose, for example, that your company sells a product on four continents. You might code these continents as: 1 = Asia, 2 = Europe, 3 = North America, and 4 = South America. The numbers 1 through 4 simply represent regions of the world. Numbers could be assigned to continents in any manner. Some one else might have used different coding, such as: 1 = North America, 2 = Asia, 3 = South America, and 4 = Europe. Notice that arithmetic operations would be meaningless with these data. What would 1 + 2 mean? Certainly not 3! That is, Asia + Europe does not equal North America (based on the first coding above). And what would the average mean? Nothing, right? If the average value for the continents was 2.50 that number would be totally meaningless. With the exception of “dummy variables,” never use nominal data in regression analysis. You will learn about dummy variables in Chapter 8.

Ordinal Data

Ordinal data also represent characteristics, but now the value of the number does have meaning. With ordinal data the number also represents some rank ordering. Suppose you ask someone to rank their top three fast food restaurants with 1 being the most preferred and 3 being the least preferred. One possible set of rankings might be:

1 = Arby’s

2 = Burger King

3 = Billy’s Big Burger Barn (B4)

From this you know that for this person Arby’s is preferred to either Burger King or B4. But note that the distance between numbers is not necessarily equal. The difference between 1 and 2 may not be the same as the distance between 2 and 3. This person might be almost indifferent between Arby’s and Burger King (1 and 2 are almost equal) but would almost rather starve than eat at B4 (3 is far away from either 1 or 2). With ordinal or ranking data such as these arithmetic operations again would be meaningless. The use of ordinal data in regression analysis is not advised because results are very difficult to interpret.

Interval Data

Interval data have an additional characteristic in that the distance between the numbers is a constant. The distance between 1 and 2 is the same as the distance between 23 and 24, or any other pair of contiguous values. The Fahrenheit temperature scale is a good example of interval data. The difference between 32°F and 33°F is the same as the distance between 76°F and 77°F. Suppose that on a day in March the high temperature in Chicago is 32°F while the high in Atlanta is 64°F. One can then say that it is 32°F colder in Chicago than in Atlanta, or that it is 32°F warmer in Atlanta than in Chicago. Note, however, that we cannot say that it is twice as warm in Atlanta than in Chicago. The reason for this is that with interval data the zero point is arbitrary. To help you see this, note that a temperature of 0°F is not the same as 0°C (centigrade). At 32°F in Chicago it is also 0°C. Would you then say that in Atlanta it is twice as warm as in Chicago so it must be 0°C (2 × 0 = 0) in Atlanta? Whoops, it doesn’t work!

In business and economics, you may have survey data that you want to use. A common example is to try to understand factors that influence customer satisfaction. Often customer satisfaction is measured on a scale such as: 1 = very dissatisfied, 2 = somewhat dissatisfied, 3 = neither dissatisfied nor satisfied, 4 = somewhat satisfied, and 5 = very satisfied. Research has shown that it is reasonable to consider this type of survey data as interval data. You can assume that the distance between numbers is the same throughout the scale. This would be true of other scales used in survey data such as an agreement scale in which 1 = strongly agree to 5 = strongly disagree. The scales can be of various lengths such as 1–6 or 1–7 as well as the 5 point scales described previously. It is quite alright for you to use interval data in regression analysis.

Ratio Data

Ratio data have the same characteristics as interval data with one additional characteristic. With ratio data there is a true zero point rather than an arbitrary zero point. One way you might think about what a true zero point means is to think of zero as representing the absence of the thing that is being measured. For example, if a car dealer has zero sales for the day it means there were no sales. This is quite different from saying that 0°F means there is no temperature, or an absence of temperature.2 Measures of income, sales, expenditures, unemployment rates, interest rates, population, and time are other examples of ratio data (as long as they have not been grouped into some set of categories). You can use ratio data in regression analysis. In fact, most of the data you are likely to use will be ratio data.

Finding “Data Analysis” in Excel

In Excel, sometimes the “Data Analysis” functionality does not automatically appear. But it is almost always available to you if you know where to look for it and how to make it available all the time. In Figures 1.4, 1.5, and 1.6, you will see how to activate “Data Analysis” in three different versions of Excel (Excel 2003, Excel 2007, and Excel 2010-2013, respectively). Figure 1.7 illustrates where “Data Analysis” shows up in the Excel Sheet under the data tab.

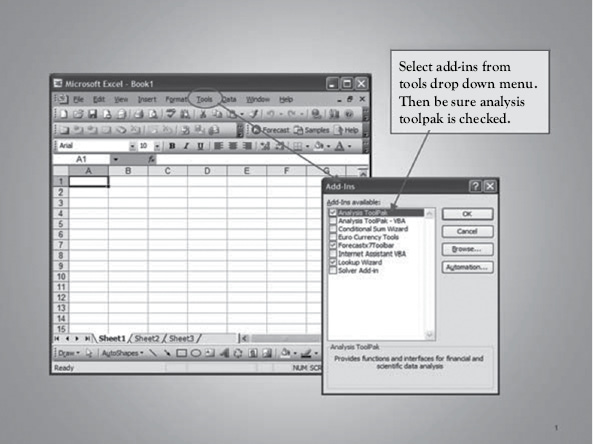
Figure 1.4 Getting “Data Analysis” in Excel 2003

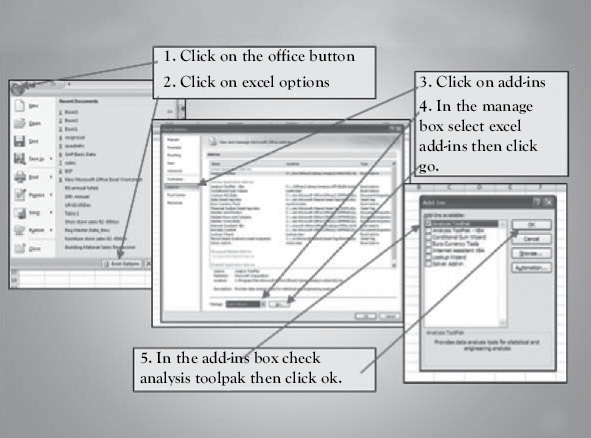
Figure 1.5 Getting “Data Analysis” in Excel 2007

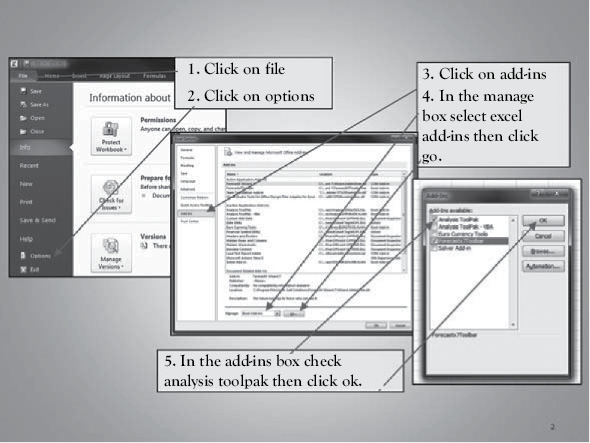
Figure 1.6 Getting “Data Analysis” in Excel 2010–2013

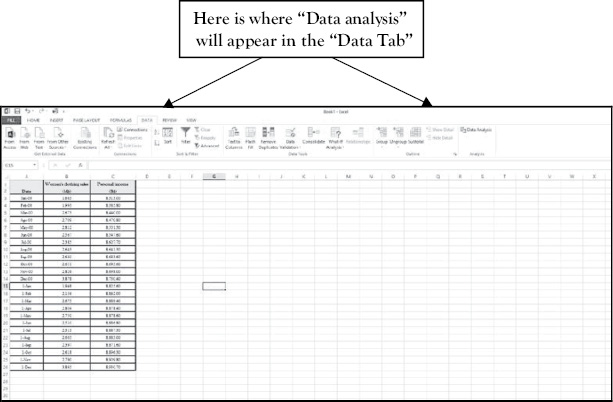
Figure 1.7 Where “Data Analysis” Now Shows Up in the Excel Sheet Under the Data Tab

What You Have Learned in Chapter 1

• You understand that this is a practical guide to regression, not a theoretical discussion.
• You know what is meant by cross-sectional data.
• You know what is meant by time-series data.
• You know to look for trend and seasonality in time-series data.
• You are familiar with the three data sets that are used for most of the examples in the remainder of the book.
• You know how to differentiate between nominal, ordinal, interval, and ratio data.
• You know that you should use interval or ratio data when doing regression (with the exception of “dummy variables”— see Chapter 8).
• You know how to access the “Data Analysis” functionality in Excel.