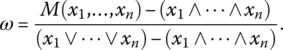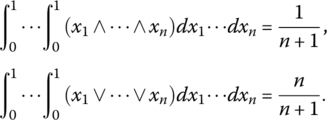2.1
Graded Logic as a Generalization of Classical Boolean Logic
This chapter introduces graded logic as a system of realistic models of observable properties of human aggregation reasoning. After an introduction to aggregation as the fundamental activity in evaluation logic, we discuss the relationships between graded evaluation logic and fuzzy logic. Then, we present a survey of classical bivalent Boolean logic and introduce evaluation logic as a weighted compensative generalization of the classical Boolean logic. At the end of this chapter, we present a brief history of graded logic.
Three of the most frequent words in this book are means, logic, and aggregators. If we have n real numbers ![]() , then according to common sense the mean value of these numbers is a value M(x1, …, xn), which is located somewhere between the smallest and the largest of the numbers:
, then according to common sense the mean value of these numbers is a value M(x1, …, xn), which is located somewhere between the smallest and the largest of the numbers:
This property of function M is called internality. In our case, x1, …, xn are degrees of truth, and they belong to the unit interval ![]() . So,
. So, ![]() and
and ![]() . We can also rewrite relation (2.1.1) as follows:
. We can also rewrite relation (2.1.1) as follows:
Therefore, means are functions between conjunction and disjunction, and relation (2.1.2) obviously suggests that means can be interpreted as logic functions (and indeed, they are logic functions, assuming that logic means modeling observable properties of human reasoning). In particular, relation (2.1.2) indicates that the mean M (as a logic function) can be linearly interpolated between AND and OR as follows:
The parameter ![]() defines the location of M in the space between conjunction and disjunction. More precisely, ω denotes the proximity of M to disjunction, or the similarity between M and disjunction, and it can be called the disjunction degree or similarity to OR, or orness. According to (2.1.3), the disjunction degree of mean M is
defines the location of M in the space between conjunction and disjunction. More precisely, ω denotes the proximity of M to disjunction, or the similarity between M and disjunction, and it can be called the disjunction degree or similarity to OR, or orness. According to (2.1.3), the disjunction degree of mean M is
Relations (2.1.3) and (2.1.4) indicate that each mean could be interpreted as a mix of disjunctive and conjunctive properties. From that standpoint, we are particularly interested in parameterized means. Such means have an adjustable parameter r(ω) that can be used to adjust the logic properties of mean and provide a continuous transition from AND to OR:
The function M(x1, …, xn; r(ω)) can be interpreted as a logic function: it has an adjustable degree of similarity to disjunction (or to conjunction) and represents a fundamental component for building a graded logic. We call this function the graded (or generalized [DUJ07a]) conjunction/disjunction (in both cases, the abbreviation is GCD).
The above short story and relations (2.1.1 to 2.1.5) exactly describe my initial reasoning in 1972–1973, when I started developing a logic based on functions that provide continuous transition from AND to OR. My goals were to generalize the classic Boolean logic, to model observable properties of human reasoning, and to apply that methodology in the area of evaluation. These are also the main goals of this book.
2.1.1 Aggregators and Their Classification
Our first step is to introduce logic aggregators, i.e., functions that aggregate two or more degrees of truth and return a degree of truth in a way similar to observable patterns of human reasoning. The meaning and role of inputs and outputs of logic aggregators can be used as the necessary restrictive conditions that filter those functions and properties that have potential to serve in mathematical models of human evaluation reasoning. Not surprisingly, a general goal of mathematical definitions is the ultimate generality. In the area of aggregators, the mathematical generality means that highly applicable logic aggregators are mixed with lots of unnecessary mathematical ballast. Consequently, it is useful to first briefly investigate the families of functions that are closely related to logic aggregators. Such families are means, general aggregation functions, and triangular norms.
2.1.1.1 Means
Means are fundamental logic functions that we use in graded logic. Let us again note that our logic is continuous, all variables belong to unit interval ![]() and all logic phenomena and their models occur inside the unit hypercube
and all logic phenomena and their models occur inside the unit hypercube ![]() . So, before we start using means as graded logic functions, it is necessary to have a definition of mean.
. So, before we start using means as graded logic functions, it is necessary to have a definition of mean.
Mathematics provides various definitions of means. According to Oscar Chisini [CHI29], the mean M(x1, …, xn) (known as Chisini mean) generates a mean value x of n components of vector (x1, …, xn) if the following holds:
Both Chisini and Gini [GIN58] considered this definition too general and not implying internality (2.1.1). For purposes of applicability in logic, the internality (2.1.1) is the fundamental assumption, and consequently, we can consider that (2.1.1) is the most important component of any definition of means, and such means satisfy (2.1.6). By inserting ![]() in (2.1.1) we have
in (2.1.1) we have ![]() and we directly get idempotency:
and we directly get idempotency:
All means are internal and idempotent. Similarly, all nondecreasing idempotent aggregation functions ![]() are internal, i.e., they are means [GRA09].
are internal, i.e., they are means [GRA09].
Another fundamental property of means is monotonicity: Means should be nondecreasing in each variable. More precisely, Mitrinović, Vasić, and Bullen [MIT77, BUL03] specify that a function f(x, y), in order to be considered a mean, should have the following fundamental properties:
- Continuity:
 .
. - Internality:
 .
. - Monotonicity:
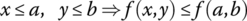 .
. - Idempotency (reflexivity):
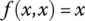 .
. - Symmetry:
 .
. - Homogeneity:
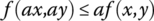 .
.
The above properties reflect the special case where all variables have the same weight. In a general case, we assume that symmetry is excluded because each argument may have a different degree of importance and commutativity is not desirable. More mathematical details about definitions and properties of means can be found in [CHI29, DEF31, GIN58, KOL30, NAG30, ACZ48, MIT77, MIT89, BUL88, BUL03, BEL16].
2.1.1.2 General Aggregation Functions
In addition to means, decision models also use the concept of aggregation functions on [0, 1] or general aggregators [FOD94, CAL02, GRA09, BEL07, MES15, BEL16]. We call these aggregators “general” to differentiate them from the subclass of logic aggregators that will be defined and used later.
According to (2.1.7), a general aggregator is defined less restrictively than a mean. Primarily, such aggregators do not need to support internality and idempotency. For example, ![]() is an aggregator, but it is not idempotent and not a mean, while
is an aggregator, but it is not idempotent and not a mean, while ![]() is both an aggregator and a mean. So, all means that we use are aggregators, but all aggregators are not means.
is both an aggregator and a mean. So, all means that we use are aggregators, but all aggregators are not means.
Graded logic decision models predominantly use idempotent aggregators (means) but sometimes may also use nonidempotent aggregators. As we already mentioned, all internal functions are idempotent, and all idempotent nondecreasing functions are internal. All means that we use in GL support internality and idempotency.
Aggregators have a diagonal section function ![]() that is defined as a value that an aggregator generates along the main diagonal of the unit hypercube. Obviously, all idempotent aggregators have the diagonal section function
that is defined as a value that an aggregator generates along the main diagonal of the unit hypercube. Obviously, all idempotent aggregators have the diagonal section function ![]() . For example, the idempotent aggregator
. For example, the idempotent aggregator ![]() has the diagonal section function
has the diagonal section function ![]() . The nonidempotent t‐norm aggregator
. The nonidempotent t‐norm aggregator ![]() has the diagonal section function
has the diagonal section function ![]() and its De Morgan dual, the t‐conorm
and its De Morgan dual, the t‐conorm ![]() has the diagonal section function
has the diagonal section function ![]() . Since
. Since ![]() , in this particular case we also have
, in this particular case we also have ![]() .
.
Mathematical literature [FOD94, BEL07, GRA09, MES15, BEL16] uses the following classification of aggregators:
- Conjunctive aggregators:
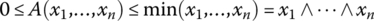 .
. - Disjunctive aggregators:
 .
. - Averaging aggregators:
 .
. - Mixed aggregators: aggregators that do not belong to groups (1), (2), (3).
Unfortunately, this classification is not oriented toward the logic interpretation of aggregators. Primarily, the variables x1, …, xn are not assumed to be degrees of truth of corresponding statements, and aggregators are not assumed to be functions of propositional calculus. In addition, the averaging aggregation is not interpreted as a continuum of conjunctive or disjunctive logic operations, but mostly as a statistical computation of mean values. Simultaneity (conjunctive aggregation) is recognized only in the lowest region of the unit hypercube, and substitutability (disjunctive aggregation) is recognized only in the highest region of the unit hypercube. This is not consistent with the propositional logic interpretation of aggregation functions ![]() . Therefore, we will not use the above definition and classification of general aggregators. We need a more restrictive definition of logic aggregators, as well as a different classification, outlined below and discussed in detail in subsequent sections.
. Therefore, we will not use the above definition and classification of general aggregators. We need a more restrictive definition of logic aggregators, as well as a different classification, outlined below and discussed in detail in subsequent sections.
2.1.1.3 Logic Aggregators
Our classification of logic aggregators will be based on the fact that basic logic aggregators are models of simultaneity or models of substitutability. In addition, the centroid of all logic aggregators is the logic neutrality, modeled as the arithmetic mean. Various degrees of predominant simultaneity can be modeled using aggregation functions that are located below neutrality. Various degrees of predominant substitutability can be modeled using aggregation functions that are located above neutrality. Therefore, assuming nonidentical arguments, we will use the following basic classification of logic aggregators:
- Neutral logic aggregator:
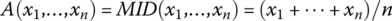 .
. - Conjunctive aggregators:
 .
. - Disjunctive aggregators:
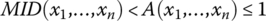 .
.
More specifically, conjunctive and disjunctive aggregators can be regular if they are means. On the other hand, all nonidempotent conjunctive logic aggregators that satisfy ![]() will be denoted as hyperconjunctive. Similarly, all nonidempotent disjunctive aggregators that satisfy
will be denoted as hyperconjunctive. Similarly, all nonidempotent disjunctive aggregators that satisfy ![]() will be denoted as hyperdisjunctive. A full justification of this classification, the definition of logic aggregators, and more details can be found in Sections 2.1.2 and 2.1.3.
will be denoted as hyperdisjunctive. A full justification of this classification, the definition of logic aggregators, and more details can be found in Sections 2.1.2 and 2.1.3.
2.1.1.4 Triangular Norms and Conorms
The areas of hyperconjunctive and hyperdisjunctive aggregators offer models of very high degrees of simultaneity and substitutability. These areas overlap with the areas of triangular norms (t‐norms) and triangular conorms (t‐conorms).
According to [FOD94] a t‐norm is a function ![]() that satisfies the following conditions:
that satisfies the following conditions:
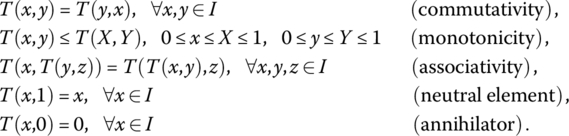
These properties indicate conjunctive behavior of t‐norms [MES15], i.e., the possibility to use some of t‐norms for modeling simultaneity. Particularly important in that direction are Archimedean t‐norms that satisfy ![]() . In other words, the diagonal section function of Archimedean t‐norms satisfies
. In other words, the diagonal section function of Archimedean t‐norms satisfies ![]() , showing that the surface of such t‐norm is located below the pure conjunction function:
, showing that the surface of such t‐norm is located below the pure conjunction function: ![]() . For example,
. For example, ![]() . Therefore, Archimedean t‐norms can be used as models of hyperconjunctive aggregators. The associativity of t‐norms permits the use of t‐norms in cases of more than two variables.
. Therefore, Archimedean t‐norms can be used as models of hyperconjunctive aggregators. The associativity of t‐norms permits the use of t‐norms in cases of more than two variables.
T‐conorms are defined using duality: ![]() . That yields the following properties of t‐conorms that are symmetric to the properties of t‐norms:
. That yields the following properties of t‐conorms that are symmetric to the properties of t‐norms:

Among a variety of t‐norms and t‐conorms the most frequently used t‐norms/conorms in literature are min/max (M), product (P), Łukasiewicz (L), and drastic (D), defined as follows:
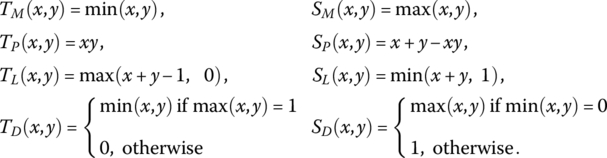
Among these aggregators, M and P are sometimes used in logic aggregation for modeling very high levels of simultaneity and substitutability. Others have rather low applicability, as discussed in [DUJ07c]. The primary reasons are the incompatibility with observable properties of human reasoning: the absence of idempotency (except for M), the absence of weights, discontinuities (L, D), insensitivity to improvements (M, L, D), and insufficient support for modeling simultaneity or substitutability (L). For example, ![]() , and there is absolutely no reward for the average satisfaction of inputs. This model might be called the “excess 50%” norm, because its main concern is to eliminate candidates who cannot make an average score of 50%. After that, TL(x, y) behaves similarly to the arithmetic mean, providing simple additive compensatory features. For example,
, and there is absolutely no reward for the average satisfaction of inputs. This model might be called the “excess 50%” norm, because its main concern is to eliminate candidates who cannot make an average score of 50%. After that, TL(x, y) behaves similarly to the arithmetic mean, providing simple additive compensatory features. For example, ![]() and in this case the decrement Δx is insufficiently penalized because it can be compensated with the increment having the same size:
and in this case the decrement Δx is insufficiently penalized because it can be compensated with the increment having the same size: ![]() . So, TL(x, y) shows inability to properly penalize the lack of simultaneity, which is a fundamental issue in all models of simultaneity.
. So, TL(x, y) shows inability to properly penalize the lack of simultaneity, which is a fundamental issue in all models of simultaneity.
Such properties are not useful in graded evaluation logic and were among reasons for defining logic aggregators in Section 2.1.3 in a way that excludes TL(x, y) and TD(x, y) from the status of logic aggregators, in an attempt to reduce mathematical ballast generated by too permissive (insufficiently restrictive) definition of general aggregators (Definition 2.1.0). The main restrictive concept of our approach is that logic aggregators must be applicable as models of human reasoning, and we try to focus only on mathematical infrastructure that supports that fundamental goal.
Duals of Archimedean t‐norms (Archimedean t‐conorms) can be used as models of hyperdisjunctive aggregators. For example, ![]() is a t‐norm and a hyperconjunctive aggregator and
is a t‐norm and a hyperconjunctive aggregator and ![]() is a t‐conorm and a hyperdisjunctive aggregator. On the other hand,
is a t‐conorm and a hyperdisjunctive aggregator. On the other hand, ![]() can be used as a hyperconjunctive aggregator but it is not a t‐norm. Its dual,
can be used as a hyperconjunctive aggregator but it is not a t‐norm. Its dual, ![]() can be used as a hyperdisjunctive aggregator, but is not a t‐conorm.
can be used as a hyperdisjunctive aggregator, but is not a t‐conorm.
Some of presented general aggregators are consistent and some are inconsistent with observable properties of human evaluation reasoning. Keeping in mind these basic types of aggregators and their properties, we can now focus on studying aggregation functions that are provably suitable for building models of evaluation reasoning.
2.1.2 How Do Human Beings Aggregate Subjective Categories?
The only way to answer this crucial question is to observe characteristic patterns of human aggregative reasoning and to identify necessary properties of aggregation. If we can identify a single case of an indisputably valid reasoning pattern, such a case is a sufficient proof of the existence of that reasoning pattern, as well as a proof that the mathematical models of logic reasoning must include and correctly quantitatively describe the properties of such reasoning.
Initial attempts to investigate human aggregation of subjective categories using empirical analysis based on experiments with human subjects can be found in [THO79, ZIM80, ZIM87, KOV92, ZIM96)]. These valuable efforts were restricted to the study of nonidempotent gamma aggregator ![]() ,
, ![]() and unfortunately remained isolated.
and unfortunately remained isolated.
In this section, we identify basic characteristic patterns of aggregation of subjective categories. For each pattern, we first define the characteristic property and then provide the proof of existence. Our analysis is focused on aggregation in the context of evaluation reasoning. We assume that a decision maker has input percepts of the suitability degrees ![]() of a group of
of a group of ![]() components of an evaluated object. The decision maker then aggregates input suitability degrees to create a composite percept of the output (fused) suitability of the analyzed group of n components of the evaluated object,
components of an evaluated object. The decision maker then aggregates input suitability degrees to create a composite percept of the output (fused) suitability of the analyzed group of n components of the evaluated object, ![]() ,
, ![]() . In most practical cases the evaluated objects are artifacts (products made by humans), but the evaluation can also include other forms of decision alternatives.
. In most practical cases the evaluated objects are artifacts (products made by humans), but the evaluation can also include other forms of decision alternatives.
There are two clearly visible types of aggregation of subjective categories: idempotent and nonidempotent. Idempotent aggregation is based on assumption that any object is as suitable as its components in all cases where all components have the same suitability.
Nonidempotent aggregation is based on the assumption that if all components of an evaluated object have the same value, then the overall value of the object can be less then or greater than the value of components [ZIM96, DUJ07c]. One of such aggregators (originating in probability theory) is ![]() . So, if the values of two components x and y are 50%, then the value of the whole object is 25%. Proponents of nonidempotent aggregation rarely relate aggregation with human reasoning and decision making. An exception is the nonidempotent gamma aggregator of Zimmermann and Zysno [ZIM80], which was empirically validated.
. So, if the values of two components x and y are 50%, then the value of the whole object is 25%. Proponents of nonidempotent aggregation rarely relate aggregation with human reasoning and decision making. An exception is the nonidempotent gamma aggregator of Zimmermann and Zysno [ZIM80], which was empirically validated.
In the context of evaluation, human beings aggregate subjective categories using observable reasoning patterns. This process is based on the following fundamental reasoning patterns that are further investigated in Section 2.1.8, as well as in Chapter 2.2.
Pattern 1. Idempotent Aggregation
This aggregation pattern is based on the assumption that the output (aggregated) suitability degree must be between the lowest and the highest input suitability degrees. This property is called internality. Consequently, if all input suitability degrees are equal, the output suitability must have the same value (typical idempotent operations include means, conjunction, disjunction, set union, and set intersection).
Proof of Existence
In all schools, the grade point average (GPA) reflects the overall satisfaction of educational requirements, and it is universally accepted as a valid percept of academic performance of students. Assuming a set of different individual grades, the GPA score is always higher than the lowest individual grade and lower than the highest individual grade. This reasoning is equally accepted by students, teachers, and schools as the most reasonable grade aggregation pattern.
Pattern 2. Nonidempotent Aggregation
This aggregation pattern is based on assumption that the aggregated suitability degree can be lower than the lowest or higher than the highest input suitability degree (![]() or
or ![]() ). This property is called externality.
). This property is called externality.
Proof of Existence
In situations where suitability can be interpreted as probability (or likelihood), it is possible to find cases where input suitability degrees reflect independent events and the overall suitability is a product of input suitability degrees. For example, biathlon athletes combine cross‐country skiing and rifle shooting. These two rather different skills can be considered almost completely independent. Consequently, if the performance of an athlete in cross‐country skiing is x1 and in rifle shooting is x2, then the overall suitability of such an athlete for biathlon competitions might be ![]() . This model becomes obvious if x1 and x2 are interpreted as two independent probabilities: x1 is the probability of winning in skiing and x2is the probability of winning is rifle shooting.
. This model becomes obvious if x1 and x2 are interpreted as two independent probabilities: x1 is the probability of winning in skiing and x2is the probability of winning is rifle shooting.
In a reversed case where x1 denotes patient’s motor impairment (disability) and x2 denotes patient’s visual impairment, it is not difficult to find unfortunate situations where the overall disability satisfies the condition ![]() .
.
In the area of evaluation the idempotent aggregation is significantly more frequent and more important than the nonidempotent aggregation. The reason for the high importance of idempotent aggregation is that objects of evaluation are most frequently human products (both physical and conceptual), human properties (like academic or professional performance), etc., where evaluation reasoning is similar as in the case of GPA: the overall suitability of an evaluated complex object cannot be higher than the suitability of its best component or less than the suitability of its worst component.
The industrial evaluation projects are predominantly focused on complex industrial products. Contrary to the assumption of fully independent components, all industrial products have components characterized by positively correlated suitability degrees. Indeed, all engineers develop products that have very balanced quality of components (positively correlated with the price of product). For example, if a typical car is driven 15,000 miles per year and typically lasts up to 200,000 miles, then it can be used approximately 14 years. It would be meaningless to install in such a car a windshield wiper mechanism that is designed to last 40 years. The design logic of engineering products is based on selected price range that is closely related to the expected overall quality degree. Consequently, the designers try to make all components as close as possible to the selected overall quality level. For example, an expensive car regularly has an expensive radio; a computer with a very fast processor usually has a very large main memory and large disk storage. Similarly, student grades on midterm exam are highly correlated with the grades on the final exam because both of them depend on student’s ability and effort. Obviously, the evaluated components are not independent, and usually they have highly correlated suitability degrees. In such cases, the result of evaluation is an overall suitability degree, acting as a kind of centroid of suitability degrees of all relevant components and located inside the [min, max] range. Such evaluation models must be based on the idempotent aggregation. Therefore, we next focus on evaluation reasoning patterns that are necessary and sufficient for idempotent aggregation.
Pattern 3. Noncommutativity
In human reasoning, each truth has its degree of importance. Commutative (symmetric) aggregators are either special cases, or unacceptable oversimplifications.
Proof of Existence
In the GPA aggregation example, the grade G4 of a course that has 4 hours of lectures per week cannot be equally important as the grade G2 of a course that has 2 hours of lectures per week (G4 should be two times more important than G2). For most car buyers, the car safety features are much more important than the optional heating of the front seats. For most homebuyers, the quality of a living room is not as important as the quality of a laundry room.
Pattern 4. Adjustable Simultaneity (Partial Conjunction)
This is the most frequent aggregation pattern. It reflects the condition for simultaneous satisfaction of two or more requirements. The degree of simultaneity (or the percept of importance of simultaneity) can vary in a range from low to high and must be adjustable. In some cases, a moderate simultaneity is satisfactory, and in other cases only the high simultaneity is acceptable. The degree of simultaneity is called andness.
Proof of Existence
A homebuyer simultaneously requires a good quality of home, and a good quality of home location, and an affordable price of home. A biathlon athlete must simultaneously be a good skier and a good rifle shooter.
Pattern 5. Adjustable Substitutability (Partial Disjunction)
This aggregation pattern reflects the condition where the satisfaction of any of two or more requirements significantly satisfies an evaluation criterion. The degree of substitutability (or the percept of importance of substitutability) can vary in a range from low to high and must be adjustable. In some cases a low or moderate substitutability can be satisfactory, and in other cases decision makers may require a high substitutability. The degree of substitutability is called orness.
Proof of Existence
A patient has a medical condition that combines motor impairments (decreased ability to move) and sensory symptoms (pain). Patient disability degree is the consequence of either sufficient motor impairments or sufficiently developed sensory problems, yielding disjunctive aggregation.
Pattern 6. The Use of Annihilators
Human evaluation reasoning is frequently based on aggregators that support annihilators. The annihilator is an extreme value of suitability (either 0 or 1) that is sufficient to decide the result of aggregation regardless of the values of other inputs [BEL07a]. In the case of necessary conditions the annihilator is 0: If any of mandatory requirements is not satisfied, the evaluated object is rejected (in other words, ![]() ). In a dual case of sufficient conditions the annihilator is 1: If any of sufficient requirements is fully satisfied, the evaluation criterion is fully satisfied (in other words,
). In a dual case of sufficient conditions the annihilator is 1: If any of sufficient requirements is fully satisfied, the evaluation criterion is fully satisfied (in other words, ![]() ). The aggregators that support annihilators 0 and 1 are called hard and aggregators that do not support annihilators are called soft.
). The aggregators that support annihilators 0 and 1 are called hard and aggregators that do not support annihilators are called soft.
Proof of Existence
In many schools, a failure grade in a single course is sufficient to annihilate the effect of all other course grades and produce the overall failure, forcing the student to repeat the whole academic year. This annihilator has dual interpretation:
- The overall failure is the failure in class #1 or the failure in class #2 or the failure in any other class (the annihilator is 1).
- The overall passing grade assumes the passing grade in class #1 and the passing grade in class #2, and the passing grades in all other classes (the annihilator is 0).
Pattern 7. Partial and Full Hard Simultaneity (Hard Partial Conjunction)
This pattern is encountered in situations where it is highly desirable to simultaneously satisfy two or more inputs, and the satisfaction of all inputs is mandatory. The percept of aggregated satisfaction of hard simultaneous requirements will automatically be zero if any of inputs has zero satisfaction. It is going to be nonzero only if all inputs are partially satisfied. In the extreme case of full hard simultaneity, the aggregated suitability is equal to the lowest input suitability. In extreme cases, the lowest suitability cannot be compensated by increasing suitability of other inputs. In a more frequent case of partial hard simultaneity, nonzero low inputs can be partially compensated by higher values of other inputs.
Proof of Existence
In the process of selecting a home location, a senior citizen who cannot drive a car needs to be in the proximity of public transportation and food stores. If any of these mandatory requirements is not satisfied, the aggregated percept of satisfaction with a home location is zero, and the corresponding home location is rejected. Home locations are acceptable if and only if all inputs are positive (partially satisfied). In an extreme case of full hard simultaneity, the stakeholder does not want to accept any low input (neither remote food stores nor remote public transport). In such cases, the lowest input cannot be compensated by other higher inputs, and the aggregated percept of suitability is affected solely by the lowest of input suitability degrees. Much more frequently, however, the percept of aggregated suitability depends on all mandatory inputs and not only the lowest input. In other words, an adjustable partial compensation of the lowest (but always positive) suitability degree is usually possible.
Pattern 8. Soft Simultaneity (Soft Partial Conjunction)
This pattern is encountered in situations where it is desirable to simultaneously satisfy two or more inputs, but none of the inputs is mandatory. The percept of aggregated satisfaction of soft simultaneous requirements will not automatically be zero if one of the inputs has zero satisfaction. It is going to be nonzero as long as at least one of inputs is partially satisfied.
Proof of Existence
In the process of selecting a home location, a senior citizen would like to live in the proximity of park, restaurants, and public library. The percept of satisfaction with a given location depends on simultaneous proximity to park, restaurants, and libraries, but the stakeholder is usually ready to accept situations where some (but not all) of the desired amenities are missing.
Pattern 9. Partial and Full Hard Substitutability (Hard Partial Disjunction)
This pattern is encountered in situations where it is desirable to satisfy two or more inputs that can partially or completely replace each other. Each input is sufficient to alone completely satisfy all requirements. The percept of aggregated satisfaction of hard substitutability requirements will automatically be complete if any of inputs is completely satisfied. In the case of incomplete satisfaction of input requirements, each input has the capability to partially compensate the lack of other inputs. The percept of aggregated suitability is nonzero as long as at least one of inputs is partially satisfied. In the extreme case of full hard substitutability, the aggregated suitability is equal to the highest input suitability, and lower suitability degrees do not affect the aggregated suitability. In a more frequent case of partial hard substitutability and incomplete satisfaction of requirements, low inputs can affect (decrease) the aggregated percept of suitability.
Proof of Existence
A homebuyer in an area with very poor (or nonexistent) street parking needs a parking solution, and the options are: a private garage or a shared garage or a reserved space in an outdoor parking lot. If any of these three options is completely satisfied, the homebuyer is fully satisfied. If the satisfaction with these options is incomplete (e.g., the homebuyer needs space for two cars but the available private garage has space for only one car), then the aggregated suitability of parking depends on all available options, or in an infrequent extreme case, it can depend only on the best option.
Pattern 10. Soft Substitutability (Soft Partial Disjunction)
This pattern is encountered in situations where it is desirable to satisfy two or more inputs that can partially replace each other, but none of them is sufficient to alone completely satisfy all requirements. The percept of aggregated satisfaction of soft substitutability requirements will not automatically be complete unless all inputs are completely satisfied. However, each input has the capability to partially compensate for the lack of other inputs. The percept of aggregated suitability is nonzero as long as at least one of inputs is partially satisfied.
Proof of Existence
A homebuyer with a very limited budget has a list of amenities (sport stadiums, restaurants, parks, etc.) that are desirable in the vicinity of home. None of the amenities is sufficient to completely satisfy the homebuyer, but a homebuyer who has a small number of choices is forced to be partially satisfied with any subset of them.
The patterns 6 to 10 are denoted in Fig. 2.1.1 as logically symmetric. In this context, the symmetry does not mean commutativity, but the fact that all inputs support (or do not support) annihilators in the same way. So, either all inputs are hard or all inputs are soft.

Figure 2.1.1 Types of aggregation and the classification of logic aggregators (bold frames).
Pattern 11. Asymmetric Simultaneity (Conjunctive Partial Absorption)
This pattern is encountered in situations where it is desirable to simultaneously satisfy a mandatory input requirement and an optional input requirement. This form of aggregation is conjunctive but asymmetric. The mandatory input supports the annihilator 0 (if it is not satisfied the percept of aggregated suitability is zero regardless the level of satisfaction of the optional input). The optional input does not support the annihilator 0. If the mandatory requirement is partially satisfied, the zero optional input decreases the output suitability below the level of the mandatory input, but does not yield the zero result, showing the asymmetry of this form of simultaneity. Similarly, if the optional input is perfectly satisfied, it will, to some extent, increase the output suitability above the level of the mandatory input.
Proof of Existence
A homebuyer who needs parking in a moderately populated urban area would like to have a private garage in the home and good street parking in front of the home. However, the private parking garage is mandatory, while good street parking for the homeowner and occasional visitors is optional, i.e., it is desirable but not mandatory. The home without a private garage will be rejected regardless of the availability of good street parking, while a nice home with a private garage but poor street parking will be acceptable.
Pattern 12. Asymmetric Substitutability (Disjunctive Partial Absorption)
This pattern is encountered in situations where it is desirable to satisfy a sufficient input requirement and/or an alternative optional input requirement. This form of aggregation is disjunctive but asymmetric. The sufficient input supports the annihilator 1 (if it is fully satisfied the percept of aggregated suitability is the full satisfaction regardless the level of satisfaction of the optional input). The optional input does not support the annihilator 1. If the sufficient requirement is completely not satisfied, then a positive degree of satisfaction of the optional input can partially compensate for the lack of sufficient input, but it cannot yield the full satisfaction. That shows the asymmetry of this form of substitutability. Similarly to the case of asymmetric simultaneity, if the sufficient requirement is partially satisfied, the zero optional input decreases the output suitability below the level of the sufficient input but does not yield the zero result. On the other hand, if the optional input is perfectly satisfied, it will to some extent increase the output suitability above the level of the sufficient input.
Proof of Existence
A homebuyer who needs parking in a highly populated urban area would like to have a private garage for two cars in the home or a good street parking in front of the home. A high‐quality two‐car private parking garage is sufficient to completely satisfy the parking requirements and in such a case the street parking becomes irrelevant. In the absence of private garage, a good street parking is acceptable as a nonideal (partial) solution of the parking problem. In addition, if a single‐car (i.e., medium suitability) private garage is available, then a good street parking can increment (improve) the overall percept of parking suitability, and the corresponding parking suitability score will be higher than the private garage score. Similarly, in the case of single‐car private garage, poor street parking can further decrement the overall percept of parking suitability and the parking suitability score, below the level of the medium suitability of the single‐car private garage. These suitability increments and decrements are called reward and penalty. They can be used to adjust desired properties of all partial absorption aggregators.
Pattern 13. Neutrality (The Centroid of Logic Aggregators)
In its extreme version, simultaneity means that an aggregation criterion is completely satisfied only if all input components are simultaneously completely satisfied. In the extreme case of substitutability, any single input can completely satisfy an aggregation criterion and compensate the absence of all other inputs. Not surprisingly, human reasoning uses extreme versions of simultaneity and substitutability only in extreme situations. In normal situations, simultaneity and substitutability are used as complementary components in the process of aggregation. Humans can continuously adjust degrees of simultaneity and substitutability, making a smooth continuous transition from extreme simultaneity to extreme substitutability. Along that path, there is a central point where conjunctive and disjunctive properties are perfectly balanced. This point can be denoted as neutrality, and it represents a kind of centroid of basic logic aggregators. In the case of idempotent aggregators, the middle point between conjunction and disjunction is the arithmetic mean, as indicated in the simplest case of two inputs: ![]() . It is most likely that neutrality is an initial default aggregator in human reasoning, which is subsequently adjusted (refined) moving in conjunctive or disjunctive direction, and using different weights of inputs. This is the reason why neutrality can be considered the centroid of all logic aggregators.
. It is most likely that neutrality is an initial default aggregator in human reasoning, which is subsequently adjusted (refined) moving in conjunctive or disjunctive direction, and using different weights of inputs. This is the reason why neutrality can be considered the centroid of all logic aggregators.
Proof of Existence
The logic behind using arithmetic mean as a school grade aggregator in computing the GPA score is the simultaneous presence and the perfect balance of two completely contradictory requirements: (1) excellent students must simultaneously have all excellent course grades (conjunctive property), and (2) any subset of good grades can partially compensate any subset of bad grades (disjunctive property). The logic neutrality reflects human ability to seamlessly combine and balance the effects of such diverse requirements.
Various patterns of human aggregation of subjective categories are summarized and classified in Fig. 2.1.1. There are nine idempotent and two nonidempotent aggregation patterns that are easily observable in human evaluation reasoning. These types of aggregation combined with negation are necessary and sufficient to model graded logic used in human reasoning, including evaluation and other applications of soft propositional logic. A detailed analysis supporting the concept of sufficiency is provided in subsequent sections.
In all presented reasoning patterns, exemplifying the characteristic property of reasoning is equivalent to proving that the property is necessary. Consequently, in the special case of idempotent logic aggregators, fundamental properties of aggregation can be specified as follows:
- There are nine fundamental necessary and sufficient idempotent logic aggregation patterns used in evaluation logic: soft and (full or partial) hard symmetric conjunctive and disjunctive patterns, neutrality, and asymmetric conjunctive and disjunctive patterns.
- If available aggregators do not explicitly support all the fundamental patterns of human aggregation of subjective categories, they cannot be used in logic aggregation models. Of course, there are many aggregators that can model only a subset of fundamental aggregation patterns, and such aggregators can be used if the aggregation problem does not need all aggregation patterns.
In the case of nonidempotent aggregators, we noticed their low applicability in the area of modeling human evaluation reasoning, but nevertheless, they are present in human reasoning. In the human mind, there is no switch for discrete transition from idempotent to nonidempotent aggregators. The transition from idempotent to nonidempotent aggregators and vice versa must be seamless, and logic aggregators must be developed to enable that form of transition. That is going to be one of our goals in the next chapters.
Let us again emphasize that in this book we are interested in logic aggregation (i.e., the aggregation of degrees of truth) and not in aggregation in the mathematical theoretical sense. Many aggregators that satisfy the extremely permissive aggregation function conditions (Definition 2.1.0) have properties that are obviously incompatible with properties of human reasoning (poor support for modeling simultaneity and substitutability, discontinuities of first derivatives, etc.). Therefore, the general study of aggregators is a much wider area than the study of logic aggregators. Logic aggregators satisfy the conditions (2.1.7), but they must satisfy a number of other restrictive conditions that reduce the number of possible aggregation function and restrictively specify their fundamental properties.
The basic logic reasoning patterns presented in this section are the point of departure for any study of evaluation logic reasoning. There are two “aggregation roads” diverging from this point of departure. One is to ignore the observable reasoning patterns and to build aggregation models as general (formal) mathematical structures; there are many travelers we can encounter along the aggregation theory road. The second option is to take “the road less traveled by” and to try to strictly follow, model, and further develop the observable reasoning patterns. If we want to reach the territory of professional evaluation applications, we must take the second road.
2.1.3 Definition and Classification of Logic Aggregators
Mathematical literature devoted to aggregators [GRA09, BEL07, BEL16] defines an aggregator A(x1, …, xn) as a function that is monotonically increasing in all arguments and satisfies two boundary conditions as shown in Definition 2.1.0. It is rather easy to note that the Definition 2.1.0 is extremely permissive, yielding various families of functions, which have properties not encountered in logic models, and not observable in human reasoning. Unfortunately, such functions are still called conjunctive or disjunctive, and these terms imply the proximity to logic and applicability in models of human reasoning. Therefore, it is useful to define the concept of logic aggregator in a more restrictive way, to exclude properties that are inconsistent with observable properties of human aggregative reasoning.
If aggregators are applied in evaluation logic, then we assume that input variables x1, …, xn have semantic identity as degrees of truth of value statements, and aggregators are functions of propositional calculus (also called sentential logic, sentential calculus, or propositional logic). Thus, undesirable properties of logic aggregators include the following:
- Discontinuities: natura non facit saltum (nature makes no leap) and logic aggregators should be continuous functions.
- If all arguments are to some extent true (i.e., positive), their aggregate cannot be false (0). To create aggregated falsity, at least one input argument must be false.
- If all arguments are not completely true, their aggregate cannot be completely true. To create a complete (perfect) aggregated truth, at least one input argument must be completely true.
- Discontinuities and/or oscillations of first derivatives are questionable properties, incompatible with human reasoning. They occur in special cases (e.g., as a consequence of using min and max functions), but not as a regular modus operandi in logic aggregation.
Taking into account these observations, we are going to use the following definition of logic aggregators.
Therefore, we restricted the general Definition 2.1.0 by requesting the continuity of logic aggregation functions and two additional logic conditions. For example, according to this definition, both Łukasiewicz and drastic t‐norms are not logic aggregators. Of course, in propositional logic we regularly use logic functions that are not classified as logic aggregators. In most cases, such functions use the standard negation (![]() ), which can destroy nondecreasing monotonicity and result in logic functions that are not aggregators. On the other hand, it is easy to note that from Definition 2.1.1 it follows that compound functions created using superposition of logic aggregators are again logic aggregators. In this book, we are interested only in logic aggregators and in functions created using logic aggregators and standard negation. Therefore, wherever we use the term aggregator we assume logic aggregators based on Definition 2.1.1 and not general aggregators based on Definition 2.1.0.
), which can destroy nondecreasing monotonicity and result in logic functions that are not aggregators. On the other hand, it is easy to note that from Definition 2.1.1 it follows that compound functions created using superposition of logic aggregators are again logic aggregators. In this book, we are interested only in logic aggregators and in functions created using logic aggregators and standard negation. Therefore, wherever we use the term aggregator we assume logic aggregators based on Definition 2.1.1 and not general aggregators based on Definition 2.1.0.
The central position in propositional logic is reserved for logic aggregators that are models of simultaneity (conjunction), substitutability (disjunction), and negation. The most frequent logic models are based on combining various forms of conjunction, disjunction, and negation to create logic functions of higher complexity. Methods for building such models belong to propositional calculus. Consequently, our first step is to investigate models of simultaneity and substitutability.
According to [DUJ74a] and the analysis presented in Section 2.1.1, the area of partial conjunction is located between the arithmetic mean and the pure conjunction ![]() , and the area of partial disjunction is located between the arithmetic mean and the pure disjunction
, and the area of partial disjunction is located between the arithmetic mean and the pure disjunction ![]() . Logic aggregators are characterized by their location in the space between the pure conjunction and the pure disjunction. The location of an aggregator can be quantified as the volume under the aggregator surface inside the unit hypercube. The intensity of partial conjunction is measured using the conjunction degree (or andness) α defined as follows1 [DUJ73a, DUJ74a]:
. Logic aggregators are characterized by their location in the space between the pure conjunction and the pure disjunction. The location of an aggregator can be quantified as the volume under the aggregator surface inside the unit hypercube. The intensity of partial conjunction is measured using the conjunction degree (or andness) α defined as follows1 [DUJ73a, DUJ74a]:
The intensity of partial disjunction is measured using the disjunction degree (or orness) ω defined as the complement of α:
Obviously, for idempotent aggregators, ![]() . In the case of pure conjunction, we have
. In the case of pure conjunction, we have ![]() , and in the case of pure disjunction we have
, and in the case of pure disjunction we have ![]() . In the case of arithmetic mean
. In the case of arithmetic mean ![]() the andness and orness are equal:
the andness and orness are equal:
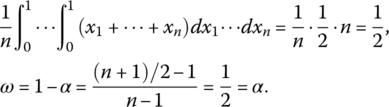
Therefore, the arithmetic mean is the central point (a centroid of logic aggregators) between the pure conjunction and the pure disjunction. Conjunctive aggregators are less than the arithmetic mean and therefore located in the area between the arithmetic mean and the pure conjunction where ![]() . Similarly, the disjunctive aggregators are greater than the arithmetic mean and therefore located in the area between the arithmetic mean and the pure disjunction where
. Similarly, the disjunctive aggregators are greater than the arithmetic mean and therefore located in the area between the arithmetic mean and the pure disjunction where ![]() .
.
Let us now investigate the basic means. The geometric mean ![]() is obviously a conjunctive logic function: It is less than the arithmetic mean2
is obviously a conjunctive logic function: It is less than the arithmetic mean2 ![]() , and for
, and for ![]() and
and ![]() it gives the same mapping as the pure conjunction:
it gives the same mapping as the pure conjunction: ![]() . Similar conjunctive logic function is the harmonic mean
. Similar conjunctive logic function is the harmonic mean ![]() . Since
. Since ![]() and
and ![]() , it follows
, it follows ![]() (the geometric mean g is located between a and h). In other words, the harmonic mean is more conjunctive than the geometric mean. However, the quadratic mean
(the geometric mean g is located between a and h). In other words, the harmonic mean is more conjunctive than the geometric mean. However, the quadratic mean ![]() is disjunctive. From
is disjunctive. From ![]() it follows that
it follows that ![]() . Since
. Since ![]() it follows
it follows ![]() and
and ![]() . Consequently, we have proved for two variables the inequality of basic conjunctive and disjunctive aggregators:
. Consequently, we have proved for two variables the inequality of basic conjunctive and disjunctive aggregators:
In this expression, the equality holds only if ![]() . Using more complex proving technique [BUL03], it is possible to show that the same inequality also holds for n variables, and in the general case of different normalized weights:
. Using more complex proving technique [BUL03], it is possible to show that the same inequality also holds for n variables, and in the general case of different normalized weights:

This interpretation of conjunctive and disjunctive aggregation is different from the interpretation used in mathematical literature about general aggregators [BEL07, GRA09]. Indeed, in propositional logic which is consistent with classical Boolean logic, the extreme logic aggregators are the pure conjunction (the min function) and the pure disjunction (the max function).
However, aggregation can sometimes go beyond the pure conjunction and the pure disjunction. For example, in the case of the nonidempotent t‐norm aggregator ![]() from (2.1.8) and (2.1.9) we have
from (2.1.8) and (2.1.9) we have
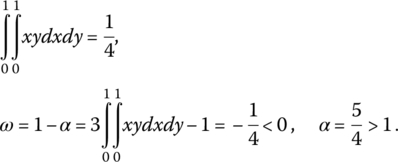
Similarly, for the t‐conorm ![]() we have
we have

Similar to drastic t‐norm/conorm, GL models of simultaneity and substitutability inside the unit hypercube [0, 1]n have limit cases called the drastic conjunction and the drastic disjunction. The drastic conjunction is the most conjunctive GL function: ![]() with exception
with exception ![]() . The drastic disjunction is the most disjunctive GL function:
. The drastic disjunction is the most disjunctive GL function: ![]() with exception
with exception ![]() . These limit cases, which are graded logic functions, but not aggregators according to Definition 2.1.1, are discussed in Section 2.1.7.6. So, from formulas (2.1.8) and (2.1.9) we get the minimum and maximum possible values of andness and orness:
. These limit cases, which are graded logic functions, but not aggregators according to Definition 2.1.1, are discussed in Section 2.1.7.6. So, from formulas (2.1.8) and (2.1.9) we get the minimum and maximum possible values of andness and orness:
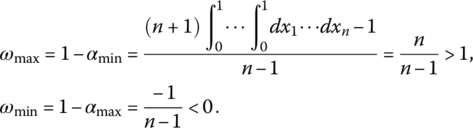
Therefore, in a general case of n variables, the ranges of global andness and orness of graded conjunctive and disjunctive logic functions are
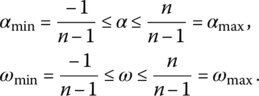
The values αmin, αmax, ωmin, ωmax correspond to the drastic conjunction and the drastic disjunction, which by Definition 2.1.1 are not logic aggregators. Thus, the range of andness/orness of logic aggregators is ![]() , and the range of andness/orness of GL functions is
, and the range of andness/orness of GL functions is ![]() .
.
For the minimum number of variables ![]() we have the largest range of andness and orness of GL functions:
we have the largest range of andness and orness of GL functions:
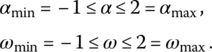
However, the range of andness and orness decreases as the number of variables increases. According to [DUJ73a], we have:
Let Vint denote the volume of the region inside the unit hypercube where internality and idempotency hold. Similarly, let Vext denote the volume of the region where externality and nonidempotency hold. According to (2.1.10), these regions can be compared as follows:
If the number of variables increases, then the region of internality increases, and the region of externality decreases. For example, for ![]() ,
, ![]() ,
, ![]() . Furthermore,
. Furthermore,
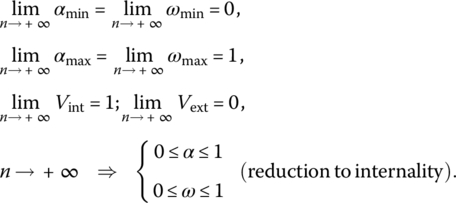
Taking into account these properties, the graded logic aggregators should be classified as follows:
- Neutral aggregator:
- The arithmetic mean:
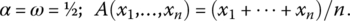
- The arithmetic mean:
- Conjunctive aggregators:
- Regular conjunctive aggregators:
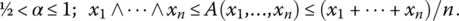
- Hyperconjunctive aggregators:

- Regular conjunctive aggregators:
- Disjunctive aggregators:
- Regular disjunctive aggregators:
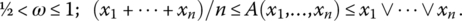
- Hyperdisjunctive aggregators:

- Regular disjunctive aggregators:
We assume that regular conjunctive and regular disjunctive aggregators are implemented as idempotent means. Hyperconjunctive and hyperdisjunctive aggregators are not idempotent. They can be implemented as t‐norms and t‐conorms, or as various other hyperconjunctive and hyperdisjunctive functions. Conjunctive models of simultaneity and disjunctive models of substitutability cover the maximum possible range of andness/orness ![]() shown in Fig. 2.1.2. The centroid of all logic aggregation models is the arithmetic mean, which is the model of conjunctive/disjunctive balance and neutrality.
shown in Fig. 2.1.2. The centroid of all logic aggregation models is the arithmetic mean, which is the model of conjunctive/disjunctive balance and neutrality.

Figure 2.1.2 Andness/orness‐based classification of logic aggregation functions used in the soft computing propositional logic.
In the area of evaluation logic, the idempotent regular conjunctive and regular disjunctive aggregators are much more frequent than the nonidempotent hyperconjunctive and hyperdisjunctive aggregators. For simplicity, in cases where only regular idempotent aggregators are used, we can omit the attribute regular, assuming that by default all conjunctive and disjunctive aggregators are regular.
2.1.4 Logic Bisection, Trisection, and Quadrisection of the Unit Hypercube
Let us now investigate the location of aggregators inside the unit hypercube [0, 1]n. Logic aggregators are distributed in two main regions of the unit hypercube: conjunctive and disjunctive. The border between the conjunctive area and the disjunctive area is the neutrality plane (i.e., the arithmetic mean). The bisection of unit hypercube for ![]() is shown in Fig. 2.1.3. All conjunctive aggregators, used as models of simultaneity, are located under the neutrality plane. All disjunctive aggregators, serving as models of substitutability, are located in the region above the neutrality plane. Not surprisingly, for any
is shown in Fig. 2.1.3. All conjunctive aggregators, used as models of simultaneity, are located under the neutrality plane. All disjunctive aggregators, serving as models of substitutability, are located in the region above the neutrality plane. Not surprisingly, for any ![]() , the volumes of the conjunctive region (Vc) and the volume of the disjunctive region (Vd) are the same:
, the volumes of the conjunctive region (Vc) and the volume of the disjunctive region (Vd) are the same: ![]() .
.

Figure 2.1.3 Bisection of unit cube using the neutrality plane  .
.
Two important classic aggregators are the pure (or full) conjunction (C) and the pure (or full) disjunction (D), shown in Fig. 2.1.4. They provide a trisection of the unit hypercube: The resulting regions are idempotent logic aggregators (ILA), hyperconjunctive aggregators (CC), and hyperdisjunctive aggregators (DD). For example, nonidempotent t‐norms are located in the CC area and nonidempotent t‐conorms are located in the DD area. According to formulas (2.1.10) and (2.1.11), in the case ![]() , the resulting three regions have the same size
, the resulting three regions have the same size ![]() . However, already in the case of three variables, the situation changes:
. However, already in the case of three variables, the situation changes: ![]() . In other words, as the number of variables n grows, the region of ILA is growing, and the regions of CC and DD are shrinking.
. In other words, as the number of variables n grows, the region of ILA is growing, and the regions of CC and DD are shrinking.

Figure 2.1.4 Trisection of the unit hypercube based on conjunction and disjunction.
If a logic aggregator A(x1, …, xn) has andness greater than 1 (or orness greater than one), it must be nonidempotent. Informal proof of this theorem for ![]() directly follows from Definition 2.1.1 and geometric properties of conjunction and disjunction shown in Fig. 2.1.4. If the andness is greater than 1, then the volume under the surface of aggregator A(x, y) must be less than the volume under the pure conjunction
directly follows from Definition 2.1.1 and geometric properties of conjunction and disjunction shown in Fig. 2.1.4. If the andness is greater than 1, then the volume under the surface of aggregator A(x, y) must be less than the volume under the pure conjunction ![]() . Obviously, there are only two ways to achieve such a property: either (1) the diagonal section function of such an aggregator must be below the idempotency line (i.e.,
. Obviously, there are only two ways to achieve such a property: either (1) the diagonal section function of such an aggregator must be below the idempotency line (i.e., ![]() ), or (2) we keep the idempotency line
), or (2) we keep the idempotency line ![]() and bend the surface of A(x, y) so that it is below the planar wings of the pure conjunction. So, if
and bend the surface of A(x, y) so that it is below the planar wings of the pure conjunction. So, if ![]() then
then ![]() , but if we want to increase the andness of A(x, y), then for
, but if we want to increase the andness of A(x, y), then for ![]() we must have
we must have ![]() . In other words, the aggregator A(x, y) must be decreasing in y and it would no longer be nondecreasing. Since the cost of higher andness is the loss of nondecreasing monotonicity (and the loss of the status of aggregator), the option (2) must be rejected, and the only way to increase the andness is to use the option (1), i.e., to sacrifice the idempotency, and to get nonidempotent monotonic aggregators of higher andness such as
. In other words, the aggregator A(x, y) must be decreasing in y and it would no longer be nondecreasing. Since the cost of higher andness is the loss of nondecreasing monotonicity (and the loss of the status of aggregator), the option (2) must be rejected, and the only way to increase the andness is to use the option (1), i.e., to sacrifice the idempotency, and to get nonidempotent monotonic aggregators of higher andness such as ![]() . Using duality, a similar reasoning can be applied in the case of orness greater than one, and in all cases where
. Using duality, a similar reasoning can be applied in the case of orness greater than one, and in all cases where ![]() . Therefore, the full conjunction min(x1, …, xn) is the most conjunctive idempotent aggregator, and the full disjunction max(x1, …, xn) is the most disjunctive idempotent aggregator. All ILA are means, and all means can be used (more or less successfully) as ILA.
. Therefore, the full conjunction min(x1, …, xn) is the most conjunctive idempotent aggregator, and the full disjunction max(x1, …, xn) is the most disjunctive idempotent aggregator. All ILA are means, and all means can be used (more or less successfully) as ILA.
The most important logic decomposition of the unit hypercube is the quadrisection shown in Fig. 2.1.5. The four regions of the unit hypercube are denoted as follows:
- DD: nonidempotent hyperdisjunctive logic aggregators
- DI: regular disjunctive idempotent logic aggregators
- CI: regular conjunctive idempotent logic aggregators
- CC: nonidempotent hyperconjunctive logic aggregators

Figure 2.1.5 Quadrisection of the unit hypercube and four regions of logic aggregators.
The volumes of these regions are:
In the case of three variables, ![]() . For
. For ![]() the regions of DI and CI continue to grow and the regions of hyperconjunctive and hyperdisjunctive aggregators decrease, as shown in the table in Fig. 2.1.5. These facts have practical consequences in evaluation, because all hyperconjunctive and all hyperdisjunctive aggregators belong to the relatively small regions with volume
the regions of DI and CI continue to grow and the regions of hyperconjunctive and hyperdisjunctive aggregators decrease, as shown in the table in Fig. 2.1.5. These facts have practical consequences in evaluation, because all hyperconjunctive and all hyperdisjunctive aggregators belong to the relatively small regions with volume ![]() and consequently, with increasing n, these aggregators must be rather similar. For example, if
and consequently, with increasing n, these aggregators must be rather similar. For example, if ![]() then
then ![]() and for
and for ![]() the values of Πxi quickly come close to 0, reducing the diversity of hyperconjunctive and hyperdisjunctive aggregators for all values of arguments except those that are close to 1.
the values of Πxi quickly come close to 0, reducing the diversity of hyperconjunctive and hyperdisjunctive aggregators for all values of arguments except those that are close to 1.
Further investigation of properties of aggregators located in four characteristic regions of the unit hypercube can be found in Sections 2.1.7 and 2.1.8.
2.1.5 Propositions, Value Statements, Graded Logic, and Fuzzy Logic
The meaning of logic permanently expands, including more and more human mental activities. A classic definition (e.g., one offered by the Webster’s encyclopedic unabridged dictionary) is that logic is the science that investigates the principles governing correct or reliable inference. The central point of all classic definitions of logic is the valid human reasoning and its use.
We are interested in evaluation reasoning as a human mental activity, and in logic as a discipline focused on mathematical models of observable human reasoning. Of course, many authors go far beyond this basic approach. One direction is logic as an area for building abstract mathematical formalisms, and another area is logic as an engineering discipline interested in hardware and software solutions that use some basic logic components or deal with imprecision, uncertainty, and fuzziness.
Human communication is based on natural languages and consists of linguistic sentences. Some sentences are truth bearers, i.e., they can be true or false (or partially true and partially false). In logic, such sentences are called propositions or statements. In addition to propositions, human communication also includes sentences that are not truth bearers (e.g., questions, requests, commands, etc.). Many sentences (both truth bearers and not truth bearers) may include fuzzy expressions. For our purposes, the linguistic sentences and related logics can be classified as shown in Fig. 2.1.6.

Figure 2.1.6 Simplified classification of various types of propositions and logics
In propositional logic, we study methods for correct use of propositions. Propositions can be crisp or graded, depending on the type of truth value they bear. Declarative sentences that express assertions that are either completely true (coded as 1) or completely false (coded as 0) are called crisp propositions or crisp statements. For example, the statement “a square has four sides” is a crisp proposition that is (completely) true. The classical logic (a propositional calculus from Aristotle to George Boole) deals with crisp propositions only. It is used to decide whether a statement is true or false.
The statement “Concorde is an ideal passenger jet airliner” is not crisp because it is neither completely true nor completely false. Of course, those who know history will agree that it is truer than the statement “Tu‐144 is an ideal passenger jet airliner.” These statements assert the value of evaluated object and their degree of truth is located between true and false. Such statements are called the value statements.
Truth comes in degrees. Graded propositions use degree of truth that can be continuously adjustable from false to true and coded in the interval [0,1]. Such a degree of truth can also be interpreted as the degree of membership in a fuzzy set where the full membership corresponds to the degree of truth 1, and no membership corresponds to the degree of truth 0. If a logic uses graded truth and process it using graded aggregators then we call it a graded logic (GL). Consequently, it is necessary to discuss relationships between GL and fuzzy logic. That brings us to the definition of fuzzy logic. The originator of the concept of fuzzy logic is Lotfi Zadeh and it is natural to accept his explanation of this concept. On 1/25/2013, after receiving the BBVA Award, Zadeh addressed the BISC community with the message entitled “What is fuzzy logic?” that contains the following short but very precise definitions of fuzzy logic concepts in the way seen by the originator of these concepts:
The BBVA Award has rekindled discussions and debates regarding what fuzzy logic is and what it has to offer. The discussions and debates brought to the surface many misconceptions and misunderstandings. A major source of misunderstanding is rooted in the fact that fuzzy logic has two different meanings – fuzzy logic in a narrow sense, and fuzzy logic in a wide sense. Informally, narrow‐sense fuzzy logic is a logical system which is a generalization of multivalued logic. An important example of narrow‐sense fuzzy logic is fuzzy modal logic. In multivalued logic, truth is a matter of degree. A very important distinguishing feature of fuzzy logic is that in fuzzy logic everything is, or is allowed to be, a matter of degree. Furthermore, the degrees are allowed to be fuzzy. Wide‐sense fuzzy logic, call it FL, is much more than a logical system. Informally, FL is a precise system of reasoning and computation in which the objects of reasoning and computation are classes with unsharp (fuzzy) boundaries. The centerpiece of fuzzy logic is the concept of a fuzzy set. More generally, FL may be a system of such systems. Today, the term fuzzy logic, FL, is used preponderantly in its wide sense. This is the sense in which the term fuzzy logic is used in the sequel. It is important to note that when we talk about the impact of fuzzy logic, we are talking about the impact of FL. Intellectually, narrow‐sense fuzzy logic is an important part of FL, but volume‐wise it is a very small part. In fact, most applications of fuzzy logic involve no logic in its traditional sense.
According to Zadeh’s dual (narrow/wide) classification, the wide‐sense fuzzy logic includes all intellectual descendants of the concept of fuzzy set.3 The narrow‐sense fuzzy logic includes logic systems where truth is a matter of degree. Zadeh’s classification is adopted in Fig. 2.1.6. According to this classification, GL is a generalization of classical bivalent and multivalued logic, as well as a fundamental component and refinement of the narrow-sense fuzzy logic.
The link between classical Boolean logic and GL in Fig. 2.1.6 shows that GL is a successor (and seamless generalization) of classical bivalent Boolean logic. All main properties of GL can be derived within the framework of classical logic, without explicitly using the concept of fuzzy set. On the other hand, the partial truth of a value statement can also be interpreted as a degree of membership of the evaluated object in a fuzzy set of maximum‐value objects. Consequently, we can link FL/N and GL, and relationships between GL and FL are discussed in several sections of this book, particularly in Chapter 2.2.
Fuzzy logic has specific areas that deal with various forms of imprecision and uncertainty, and includes type 1 fuzzy logic [WIK11b, ZAD89, ZAD94, KLI95], interval type 2 fuzzy logic [WU11, MEN01, CAS08], and others.
In the area of evaluation we are primarily interested in value statements (propositions that affirm or deny value, based on decision maker goals and requirements). Typical examples of value statements are “the area of home H completely satisfies all our needs,” “the location of airport A is perfectly suitable for city C,” and “student S deserves the highest grade.” All these statements can be partially true and partially false. The degree of truth of a value statement is a human percept, interpreted as the degree of satisfaction of stakeholder’s requirements. Generally, we define GL as follows.
According to this definition, GL is used for processing degrees of truth. The degree of truth of a value statement can be interpreted as the degree of suitability or the degree of preference. To have a compact notation we usually call these degrees simply “suitability” or “preference.” Of course, the degrees of truth are human percepts and GL can also be interpreted as a mathematical infrastructure for perceptual computing. So, the term suitability means the human percept of suitability. One of our main objectives is to compute the overall suitability of a complex object as a logic function of the suitability degrees of its components (attributes).
The most distinctive GL properties (and the most frequently used) are internality and idempotency of graded simultaneity (partial conjunction) and substitutability (partial disjunction) models. In addition, using interpolative aggregators [DUJ05c, DUJ14], GL provides seamless connectivity between idempotent and nonidempotent logic aggregators [DUJ16a], covering all regions of the unit hypercube (see Section 2.1.7 and Chapter 2.4).
Internality holds in all cases where the overall suitability of a complex object cannot be greater than the suitability of its best component, or less than the suitability of its worst component. Internality yields the possibility to interpret means as logic functions, located between the pure conjunction (the minimum function) and the pure disjunction (the maximum function). Based on this interpretation, the first form of graded (or generalized) conjunction/disjunction (GCD) was proposed in [DUJ73b] as a general logic function that provides a continuous transition from conjunction to disjunction by selecting a desired conjunction degree (andness), or the desired disjunction degree (orness). By making conjunction a matter of degree and disjunction a matter of degree, and using weights as degrees of importance of inputs we made an explicit move toward a graded logic, where everything is a matter of degree.
Relationships between the classical bivalent Boolean logic (BL), the graded logic (GL), the fuzzy logic in the narrow sense (FL/N) and the fuzzy logic in the wide sense (FL/W) are subset‐structured as follows: ![]() . BL is primarily a crisp bivalent propositional calculus. GL includes BL plus graded truth, graded idempotent conjunction/disjunction, weight‐based semantics, and (less frequently) nonidempotent hyperconjunction/hyperdisjunction (Section 2.1.7). GL also supports all nonidempotent basic logic functions (e.g., partial implication, partial equivalence, partial nand, partial nor, partial exclusive or, and others). All such functions are “partial” in the sense that they use adjustable degrees of similarity or proximity to their “crisp” equivalents in traditional bivalent logic. FL/N includes GL plus variety of forms of nonidempotent conjunction/disjunction, and other generalizations of multivalued logic. FL/W includes FL/N plus all a wide variety of models of reasoning and computation based on the concept of fuzzy set.
. BL is primarily a crisp bivalent propositional calculus. GL includes BL plus graded truth, graded idempotent conjunction/disjunction, weight‐based semantics, and (less frequently) nonidempotent hyperconjunction/hyperdisjunction (Section 2.1.7). GL also supports all nonidempotent basic logic functions (e.g., partial implication, partial equivalence, partial nand, partial nor, partial exclusive or, and others). All such functions are “partial” in the sense that they use adjustable degrees of similarity or proximity to their “crisp” equivalents in traditional bivalent logic. FL/N includes GL plus variety of forms of nonidempotent conjunction/disjunction, and other generalizations of multivalued logic. FL/W includes FL/N plus all a wide variety of models of reasoning and computation based on the concept of fuzzy set.
Because of its location between BL and FL/N, we can interpret GL as a descendant of both the classical bivalent logic, and the fuzzy logic. These two interpretations are complementary. In the case of logic interpretation, all variables represent suitability, i.e. the degrees of truth of value statements that assert the highest values of evaluated objects or their components. In the case of fuzzy interpretation, the variables represent the degrees of membership in corresponding fuzzy sets of highest‐value objects. In the case of bivalent logic, GL is a direct and natural seamless generalization of BL (in points {0, 1}n of hypercube [0, 1]n we have GL=BL). In the case of fuzzy logic, GL is a special case, even if the fuzzy logic is defined in a narrow sense, because GL excludes various fuzzy concepts and techniques that are not related to logic. Since GL is primarily a propositional calculus, it is more convenient and more natural to interpret GL as a weighted compensative generalization of classical bivalent Boolean logic, than to interpret GL as a relatively narrow subarea in a heterogeneous set of models of reasoning and computation derived from the concept of fuzzy set. However, contacts of GL and the area of fuzzy sets are frequent and natural, in particular because GL provides logic infrastructure in all cases where fuzzy models need to include human percepts and human logic reasoning.
2.1.6 Classical Bivalent Boolean Logic
Omne enuntiatum aut verum aut falsum est.
(Every statement is either true or false.)
—Marcus Tullius Cicero, De Fato, 44 BC
In this section we summarize a classical bivalent propositional calculus with crisp truth values formalized as a Boolean algebra. Let us assume that the only logic values are true (numerically coded as 1) and false (numerically coded as 0), and all logic variables, as well as andness and orness,4 belong to the set {0,1}. The basic logic functions are the pure conjunction (and function) ![]() , the pure disjunction (or function)
, the pure disjunction (or function) ![]() , and negation
, and negation ![]() . Obviously,
. Obviously, ![]() (involution),
(involution), ![]() ,
, ![]() ,
, ![]() . Under these assumptions a Boolean function of n variables
. Under these assumptions a Boolean function of n variables ![]() is defined using 2n combinations of input values (from 00…0 to 11…1). Consequently, there are
is defined using 2n combinations of input values (from 00…0 to 11…1). Consequently, there are ![]() different Boolean functions of n variables.
different Boolean functions of n variables.
If n=1 there are four Boolean functions shown in Table 2.1.1 and if n=2 there are 16 Boolean functions shown in Table 2.1.2. We always assume that conjunction has higher precedence than disjunction. For example, we can write basic logic expressions without parentheses: ![]() . Engineering literature frequently uses a simplified notation of logic expressions where the previous example is written as
. Engineering literature frequently uses a simplified notation of logic expressions where the previous example is written as ![]() (conjunction is interpreted as logic multiplication and denoted using concatenation, and disjunction is interpreted as logic addition and denoted using the plus sign). To avoid ambiguity we will use different symbols for conjunction/disjunction and arithmetic operations.
(conjunction is interpreted as logic multiplication and denoted using concatenation, and disjunction is interpreted as logic addition and denoted using the plus sign). To avoid ambiguity we will use different symbols for conjunction/disjunction and arithmetic operations.
Table 2.1.1 Boolean Functions 
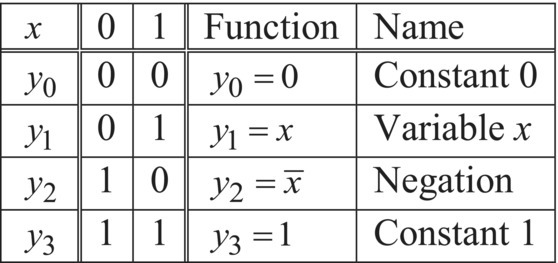
Table 2.1.2 Bivalent Boolean functions z = f(x,y).
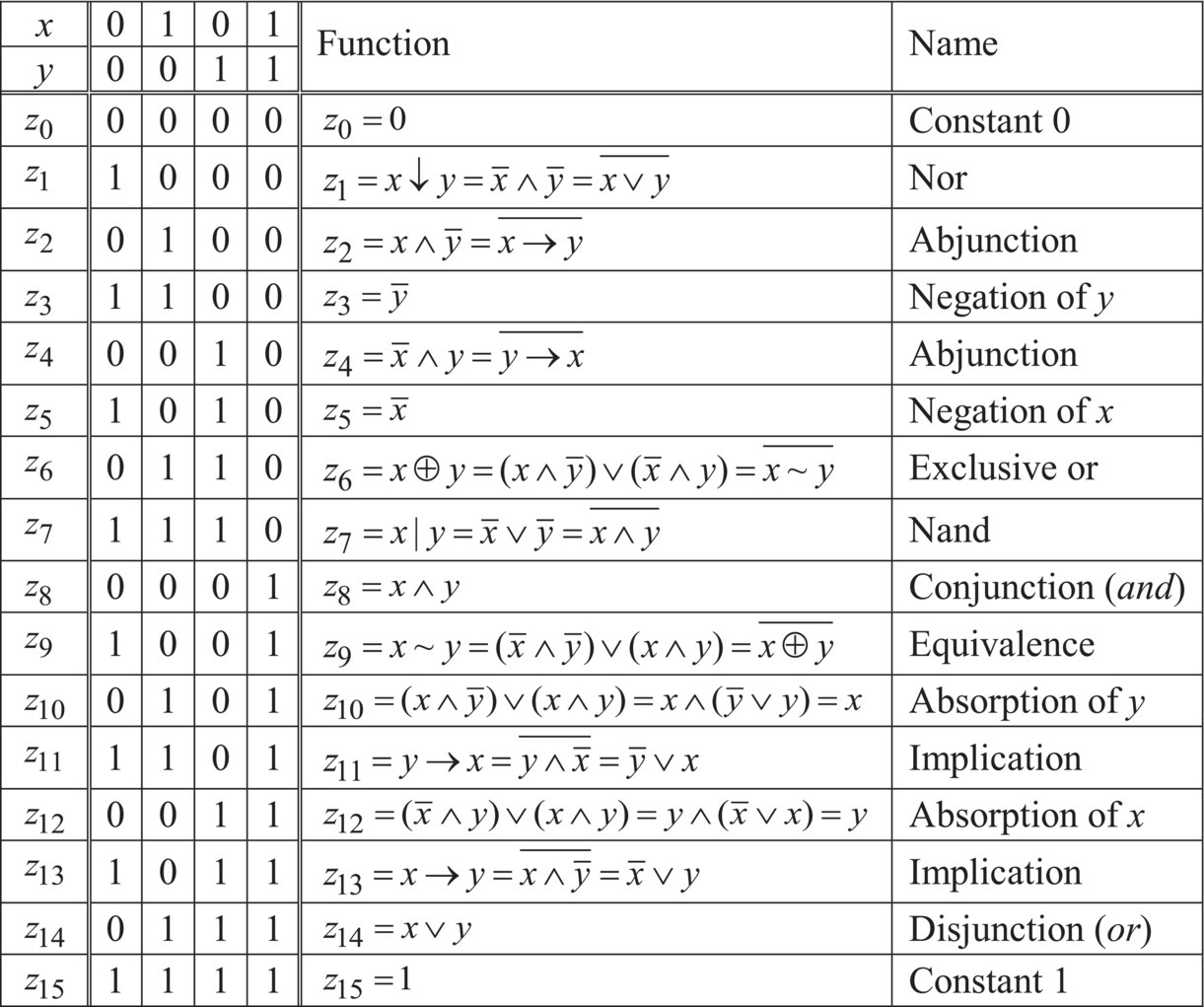
Pure conjunction and disjunction are idempotent, commutative, associative, and distributive; there are also neutral elements, annihilators, and inverse elements:

Since ![]() , it follows that 0 is the annihilator for conjunction and 1 is the annihilator for disjunction.
, it follows that 0 is the annihilator for conjunction and 1 is the annihilator for disjunction.
Using distributivity it is easy to show the following total absorption properties5 that completely eliminate (absorb) the impact of variable y:

These relations are the reason for calling the corresponding functions in Table 2.1.2 the total absorption. In addition, we frequently use the following simplification properties:

Table 2.1.2 can be used to identify two important properties of Boolean functions that are subsequently inherited in GL: monotonicity and idempotency. Monotonicity is the fundamental property of conjunction and disjunction: it means that an increase (i.e., the change from 0 to 1) of any input variable either increases the output or keeps it unchanged, but can never cause a decrease (the change from 1 to 0). Similarly, a decrease (i.e., the change from 1 to 0) of any input variable either decreases the output or keeps it unchanged, but can never cause an increase (the change from 0 to 1). For monotonic functions, the output values either remain unchanged or change in the same direction as input variables. All compound functions that are obtained as superposition of monotonic functions are also monotonic. Nonmonotonicity can be realized by using negation.
Considering the important property of idempotency, in Table 2.1.2 idempotent are those functions ![]() where
where ![]() , i.e., those functions that have 0 in the first column and 1 in the fourth column. So, the idempotency holds only for four functions: z8, z10, z12, z14 (conjunction, disjunction, and two absorptions). No other Boolean function of two variables satisfies the boundary conditions
, i.e., those functions that have 0 in the first column and 1 in the fourth column. So, the idempotency holds only for four functions: z8, z10, z12, z14 (conjunction, disjunction, and two absorptions). No other Boolean function of two variables satisfies the boundary conditions ![]() and
and ![]() . Since GL is a generalization of classical Boolean logic (obtained using the graded conjunction/disjunction instead of pure conjunction or pure disjunction), it follows that the only idempotent GL functions are the graded conjunction/disjunction and compound aggregation functions (e.g., partial absorption) obtained as a superposition of special cases of the graded conjunction/disjunction.
. Since GL is a generalization of classical Boolean logic (obtained using the graded conjunction/disjunction instead of pure conjunction or pure disjunction), it follows that the only idempotent GL functions are the graded conjunction/disjunction and compound aggregation functions (e.g., partial absorption) obtained as a superposition of special cases of the graded conjunction/disjunction.
Boolean functions that are listed in Table 2.1.2 sometimes appear in literature under different names. For example, the implication ![]() is also known as “material implication” and it means that if the antecedent x implies the consequent y, then it is not possible that x is satisfied and y is not satisfied. The negated implication
is also known as “material implication” and it means that if the antecedent x implies the consequent y, then it is not possible that x is satisfied and y is not satisfied. The negated implication ![]() is also known as material nonimplication, or abjunction. In the context of evaluation the abjunction is an elementary model of bipolarity because it aggregates a desired property x and an undesired property y. If
is also known as material nonimplication, or abjunction. In the context of evaluation the abjunction is an elementary model of bipolarity because it aggregates a desired property x and an undesired property y. If ![]() denotes implication, then
denotes implication, then ![]() is a converse implication. The total absorption of x and y are sometimes called projection functions.
is a converse implication. The total absorption of x and y are sometimes called projection functions.
For ![]() and an arbitrary Boolean function of n variables, we can use the following decomposition (separation of xi and other variables):
and an arbitrary Boolean function of n variables, we can use the following decomposition (separation of xi and other variables):

The above decomposition can be generalized. First, let us introduce a convenient notation ![]() ,
, ![]() . Then, we have the following decomposition theorem:
. Then, we have the following decomposition theorem:

The above disjunction includes 2k terms. For example, for ![]() we have
we have

If ![]() then we get a disjunctive normal form (disjunction of conjunctive clauses) of the function of two variables:
then we get a disjunctive normal form (disjunction of conjunctive clauses) of the function of two variables:
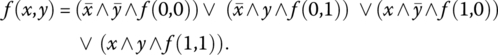
Obviously, the disjunctive normal form includes only those terms where ![]() (e.g.,
(e.g., ![]() ). Similar disjunctive normal forms can be easily written for any number of variables.
). Similar disjunctive normal forms can be easily written for any number of variables.
The negation of Boolean functions is based on De Morgan’s laws ![]() ,
, ![]() . These laws can be easily verified; if
. These laws can be easily verified; if ![]() , then we have
, then we have ![]() ,
, ![]() and if
and if ![]() then we have
then we have ![]() ,
, ![]() . De Morgan’s laws show the duality of conjunction and disjunction: if we have one of these operations, the other one can be obtained as a mirrored dual operation. To make conjunction from disjunction we use
. De Morgan’s laws show the duality of conjunction and disjunction: if we have one of these operations, the other one can be obtained as a mirrored dual operation. To make conjunction from disjunction we use ![]() and to make disjunction from conjunction we use
and to make disjunction from conjunction we use ![]() . De Morgan’s law can be written for general Boolean function
. De Morgan’s law can be written for general Boolean function ![]() as follows:
as follows:
For example, if ![]() then
then ![]() . This example illustrates that the generalized De Morgan’s law assumes a parenthesized notation of Boolean expressions, and during the replacement of variables and operators all parentheses must remain unchanged. In simple cases that is not visible. For example, the implication
. This example illustrates that the generalized De Morgan’s law assumes a parenthesized notation of Boolean expressions, and during the replacement of variables and operators all parentheses must remain unchanged. In simple cases that is not visible. For example, the implication ![]() is interpreted as follows: if from x follows y then it is not possible that x is satisfied and y is not satisfied. Consequently,
is interpreted as follows: if from x follows y then it is not possible that x is satisfied and y is not satisfied. Consequently, ![]() .
.
Frequently used functions of three variables are:

Here ![]() if two or more inputs are equal to 1;
if two or more inputs are equal to 1; ![]() if an odd number of inputs is equal to 1 (addition modulo 2);
if an odd number of inputs is equal to 1 (addition modulo 2); ![]() if all inputs are equivalent (either 0 or 1), i.e., f3(x, y, z) is the equivalence function.
if all inputs are equivalent (either 0 or 1), i.e., f3(x, y, z) is the equivalence function.
Classical Boolean logic can be derived in a deductive axiomatic way as a Boolean algebra using a set with two elements ![]() and binary internal operations
and binary internal operations ![]() (i.e.,
(i.e., ![]() ), using the following three axioms:
), using the following three axioms:
- A1. Binary operations
 are commutative and distributive:
are commutative and distributive:
- A2. On set B binary internal operations
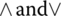 have two different neutral elements:
have two different neutral elements:

- A3. On set B each element x has a unique inverse element

Using these axioms, it is possible to prove various properties presented in this section (idempotency, involution, absorption, associativity, Dr Morgan’s laws, etc.). For example, the idempotency can be proved as follows:


An important property of a Boolean algebra, clearly visible from A1, A2, A3, and the above examples, is the concept of duality: all axioms are given in pairs, separately for operation ![]() and for operation
and for operation ![]() . In addition, these operations are symmetrical: if
. In addition, these operations are symmetrical: if ![]() is replaced by
is replaced by ![]() , and 1 by 0, then using an axiom for
, and 1 by 0, then using an axiom for ![]() we get the corresponding axiom for
we get the corresponding axiom for ![]() . According to duality, a dual of any Boolean expression can be derived by replacing
. According to duality, a dual of any Boolean expression can be derived by replacing ![]() by
by ![]() ,
, ![]() by
by ![]() , 0 by 1, and 1 by 0. Then, any theorem that can be proved is thus also proved for its dual. This property is visible (and useful) in all other relations of classical Boolean logic. For example, consider the following simplification:
, 0 by 1, and 1 by 0. Then, any theorem that can be proved is thus also proved for its dual. This property is visible (and useful) in all other relations of classical Boolean logic. For example, consider the following simplification:
The validity of this relation can be verified if we separately consider the cases ![]() (when both sides of the relation reduce to b) and
(when both sides of the relation reduce to b) and ![]() (when both sides of the relation reduce to a). Now, we can use duality to claim that the following holds:
(when both sides of the relation reduce to a). Now, we can use duality to claim that the following holds:
Similarly, a conjunctive normal form can be derived as a dual of the corresponding disjunctive normal form.
All Boolean logic functions can be derived by superposing a set of basic functions. The most frequent sets of such functions are:
 ,
,  ,
,  .
. .
.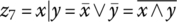 .
. ,
,  .
.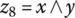 ,
,  .
. ,
,  ,
, 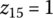 .
. ,
, 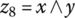 ,
, 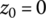 .
. ,
, 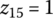 .
. ,
,  .
.
For example, cases #2 and #3 show that negation, conjunction, and disjunction can be expressed using nor and nand functions as follows:
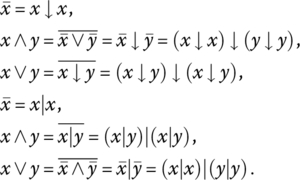
In case #9, we can express negation, disjunction, and conjunction, as follows:
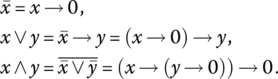
Note that ![]() , and the implication can also be combined with negation. If
, and the implication can also be combined with negation. If ![]() and
and ![]() , that means that x and y are equivalent:
, that means that x and y are equivalent: ![]() .
.
In case #6 from ![]() , we have
, we have ![]() ,
, ![]() and consequently
and consequently

If ![]() , then all basic binary Boolean functions can also be expressed using simple arithmetic operations of addition, subtraction, and multiplication, as follows:
, then all basic binary Boolean functions can also be expressed using simple arithmetic operations of addition, subtraction, and multiplication, as follows:

In classical Boolean logic, simultaneity and substitutability are not graded. Conjunction is the only model of simultaneity and disjunction is the only model of substitutability (replaceability). Conjunction and disjunction are dual based on De Morgan’s laws:

These laws are suitable for simplification of expressions, as in the following examples:

Axioms of Boolean algebra (A1, A2, A3) are not the only way to define Boolean algebra. They can be derived from, or replaced by, the Huntington axiom plus commutativity ![]() and associativity
and associativity ![]() , or by the Robbins axiom plus commutativity and associativity (i.e., the Huntington axiom is replaceable by the Robbins axiom).
, or by the Robbins axiom plus commutativity and associativity (i.e., the Huntington axiom is replaceable by the Robbins axiom).
A straightforward approach to propositional logic and propositional calculus consists of creating the models of simultaneity, substitutability, and negation, and then building all other compound functions by superposing these three fundamental components.
Tautologies are defined as formulas that are always true. Following are selected tautologies that are frequently used in bivalent logic reasoning.
The law of the excluded middle:
Modus ponens (if x is satisfied and x implies y, then that implies that y is also satisfied):
Syllogism (if x implies y and y implies z, then x implies z):

Reductio ad absurdum (if x implies both y and its negation ![]() , then x must be false):
, then x must be false):
Classical Boolean functions of n variables are defined only in 2n isolated vertices {0, 1}n of the unit hypercube [0, 1]n. In the case of Boolean function ![]() we have a binary value of function f defined in each vertex, yielding
we have a binary value of function f defined in each vertex, yielding ![]() different Boolean functions of n variables. As opposed to that, in the case of GL function of n variables
different Boolean functions of n variables. As opposed to that, in the case of GL function of n variables ![]() the degrees of truth belong to the whole interval [0,1], and the function F has a value from the unit interval in each and every point of the hypercube [0, 1]n. Consequently, GL expands logic models in the whole unit hypercube using six important expansions presented in the next section.
the degrees of truth belong to the whole interval [0,1], and the function F has a value from the unit interval in each and every point of the hypercube [0, 1]n. Consequently, GL expands logic models in the whole unit hypercube using six important expansions presented in the next section.
2.1.7 Six Generalizations of Bivalent Boolean Logic
Graded logic is used for modeling human reasoning and decision making in the area of evaluation. The goal of this section is to introduce fundamental GL concepts and properties by systematically expanding and generalizing corresponding properties of the classical bivalent Boolean logic (BL). All presented generalizations are motivated by the applicability of GL in modeling human decision making.
Most concepts in human evaluation logic reasoning (such as truth, importance, suitability, simultaneity, etc.) are a matter of degree. Consequently, that area of human logic reasoning is not reducible to zeros and ones, and it cannot be modeled only in the vertices of the hypercube {0, 1}n as in the case of classical bivalent BL. Since the truth is a matter of degree, it belongs to interval ![]() and all humanized models of logic reasoning must be applicable everywhere inside the hypercube [0, 1]n. Such models are observable in human evaluation reasoning and belong to GL.
and all humanized models of logic reasoning must be applicable everywhere inside the hypercube [0, 1]n. Such models are observable in human evaluation reasoning and belong to GL.
Regardless of significant applicability of BL in the area of computing, the expressive power of bivalent BL as an infrastructure for modeling human reasoning and decision making, particularly in the area of evaluation, is extremely modest. Indeed, BL can be used only for modeling insignificant extreme cases of reasoning where conjunction is reduced to the minimum function and disjunction is reduced to the maximum function. On the other hand, these extreme cases must also be available in GL. Consequently, GL must be a seamless generalization of BL and in the vertices {0, 1}n of the hypercube [0, 1]n GL and BL must be identical.
Another important distinction is that BL ignores semantic aspects of logic, such as the percept of importance, and compensative logic properties where most deficiencies of some inputs can be compensated by excesses of other inputs, while GL takes semantic aspects explicitly into account. More precisely, GL is a weighted compensative generalization of classical BL, and can sometimes be denoted as a weighted compensative logic [DUJ15a].
Observations of human evaluation reasoning indicate that GL must provide six fundamental expansions (generalizations) of BL that can be summarized as follows:
- Expansion of function domain: Boolean logic function domain is extended from {0,1}n to [0,1]n, and crisp values are replaced by graded values.
- Expansion of logic domain: The basic logic function, called graded (or generalized) conjunction/disjunction (GCD), must provide a parameterized continuous transition from conjunction to disjunction controlled by andness/orness.
- Expansion of annihilator adjustability: GCD must provide adjustable support for annihilators 1 and 0.
- Expansion of semantic domain: logic functions must provide the adjustability of degrees of importance of variables using weights.
- Expansion of compensative logic functions: To keep compatibility with the observable properties of human intuitive logic reasoning (i.e., the applicability in decision models), GL must support compensative properties of aggregation operators.
- Expansion of the range of andness/orness from drastic conjunction to drastic disjunction: GL provides a possibility to combine idempotent and nonidempotent logic aggregators, making a seamless transition from idempotent behavior to nonidempotent behavior inside the same aggregator and covering all regions of the unit hypercube from drastic conjunction
 to drastic disjunction
to drastic disjunction  .
.
Following is a detailed description and justification of these necessary expansions.
2.1.7.1 Expansion of Function Domain
The basic expansion of Boolean logic function domain from {0, 1}n to [0, 1]n is illustrated for ![]() in Fig. 2.1.7. The GL must be a seamless generalization of BL, i.e., GL and BL must be identical in {0, 1}n. In all points inside the hypercube [0, 1]n GL functions have values from the interval [0,1].
in Fig. 2.1.7. The GL must be a seamless generalization of BL, i.e., GL and BL must be identical in {0, 1}n. In all points inside the hypercube [0, 1]n GL functions have values from the interval [0,1].

Figure 2.1.7 Expansion of logic function domain from vertices to the whole unit hypercube.
From the standpoint of evaluation logic, the most important dichotomy of both BL and GL functions of two or more variables ![]() is the identification and separation of two fundamental categories of functions: idempotent functions
is the identification and separation of two fundamental categories of functions: idempotent functions ![]() and nonidempotent functions
and nonidempotent functions ![]() .
.
In the case of idempotent GL functions, the idempotency is present in all points of the idempotency line ![]() . Fig. 2.1.7 shows the dashed idempotency line connecting for
. Fig. 2.1.7 shows the dashed idempotency line connecting for ![]() the points
the points ![]() and (x, y, z)=(1, 1, 1). Thus, the idempotent partial conjunction, partial disjunction, and all compound functions obtained by superposition of idempotent partial conjunction and partial disjunction include (contain) the idempotency line, which connects the points 0, …, 0 and 1, …, 1.
and (x, y, z)=(1, 1, 1). Thus, the idempotent partial conjunction, partial disjunction, and all compound functions obtained by superposition of idempotent partial conjunction and partial disjunction include (contain) the idempotency line, which connects the points 0, …, 0 and 1, …, 1.
Idempotent BL functions satisfy the conditions ![]() and
and ![]() . For n=2, the only idempotent BL functions are conjunction
. For n=2, the only idempotent BL functions are conjunction ![]() , disjunction
, disjunction ![]() , conjunctive (total) absorption
, conjunctive (total) absorption ![]() and disjunctive (total) absorption
and disjunctive (total) absorption ![]() . Since GL and BL must be identical in 2nvertices {0, 1}n, for n=2 it follows that the only idempotent GL functions of two variables are conjunction, disjunction, and absorption. The terms conjunction and disjunction assume both the full and the partial versions of these functions, and the term absorption assumes both the total and the partial absorption (Chapter 2.6). These are the only functions that can be written without the use of negation. Both BL and GL functions of n variables are always a superposition of functions of two variables and negation (
. Since GL and BL must be identical in 2nvertices {0, 1}n, for n=2 it follows that the only idempotent GL functions of two variables are conjunction, disjunction, and absorption. The terms conjunction and disjunction assume both the full and the partial versions of these functions, and the term absorption assumes both the total and the partial absorption (Chapter 2.6). These are the only functions that can be written without the use of negation. Both BL and GL functions of n variables are always a superposition of functions of two variables and negation (![]() ). It is easy to verify the following properties that hold in both BL and GL:
). It is easy to verify the following properties that hold in both BL and GL:
- All functions made as a superposition of idempotent functions are idempotent.
- If nonidempotent functions are based on idempotent forms of partial conjunction and disjunction, they must contain negation.
- If a function
 is idempotent, then its De Morgan dual
is idempotent, then its De Morgan dual  is also idempotent.
is also idempotent. - Logic functions that contain negation can be either idempotent or nonidempotent.
To verify the property (I) the functions of two or more variables should be written in form of a tree where each node represents an idempotent function. If all leaves have the same value, then that value propagates through all nodes up to the root of the tree. To verify the property (II) we can consider the opposite case: if there is no negation involved, then the compound function must be a superposition of idempotent functions of conjunction, disjunction, and absorption, giving the idempotent function. Consequently, such nonidempotent functions must contain negation. To verify the property (III) let ![]() . Then
. Then ![]() ,
, ![]() . The property (IV) follows directly form (II) and (III): The idempotent dual of an idempotent function is obtained by inserting negation in all input branches and in the output (root) branch of the function tree (each GL aggregation structure can be represented as a tree where the nodes are aggregators, the leaves are input degrees of truth, and the root is the output degree of truth).
. The property (IV) follows directly form (II) and (III): The idempotent dual of an idempotent function is obtained by inserting negation in all input branches and in the output (root) branch of the function tree (each GL aggregation structure can be represented as a tree where the nodes are aggregators, the leaves are input degrees of truth, and the root is the output degree of truth).
2.1.7.2 Expansion of Logic Domain
Similarly to the percept of partial truth, human percepts of simultaneity and substitutability are also a matter of degree. Both simultaneity and substitutability are graded concepts: Decision makers sometimes require high degree of simultaneity an sometimes the degree of simultaneity can be low. The same holds for substitutability. Consequently, the basic GL function, GCD, must provide a continuous parameterized transition from the pure conjunction to the pure disjunction. The transition is controlled by two complementary parameters: the andness α and the orness ω ![]() . For
. For ![]() , that is illustrated in Fig. 2.1.8 where the pure conjunction (
, that is illustrated in Fig. 2.1.8 where the pure conjunction (![]() ) is denoted C and the pure disjunction (
) is denoted C and the pure disjunction (![]() ) is denoted D. The presented sequence of functions C, C+, CA, C–, A, D–, DA, D+ and D corresponds to the values of orness ω = 0, ⅛, ¼, ⅜, ½, ⅝, ¾, ⅞, 1, or to the values of andness
) is denoted D. The presented sequence of functions C, C+, CA, C–, A, D–, DA, D+ and D corresponds to the values of orness ω = 0, ⅛, ¼, ⅜, ½, ⅝, ¾, ⅞, 1, or to the values of andness ![]() . All functions contain the idempotency line
. All functions contain the idempotency line ![]() that connects the extreme points (0,0,0) and (1,1,1). In the middle of that sequence, as a logic centroid, is the arithmetic mean A (
that connects the extreme points (0,0,0) and (1,1,1). In the middle of that sequence, as a logic centroid, is the arithmetic mean A (![]() ) characterized by
) characterized by ![]() .
.
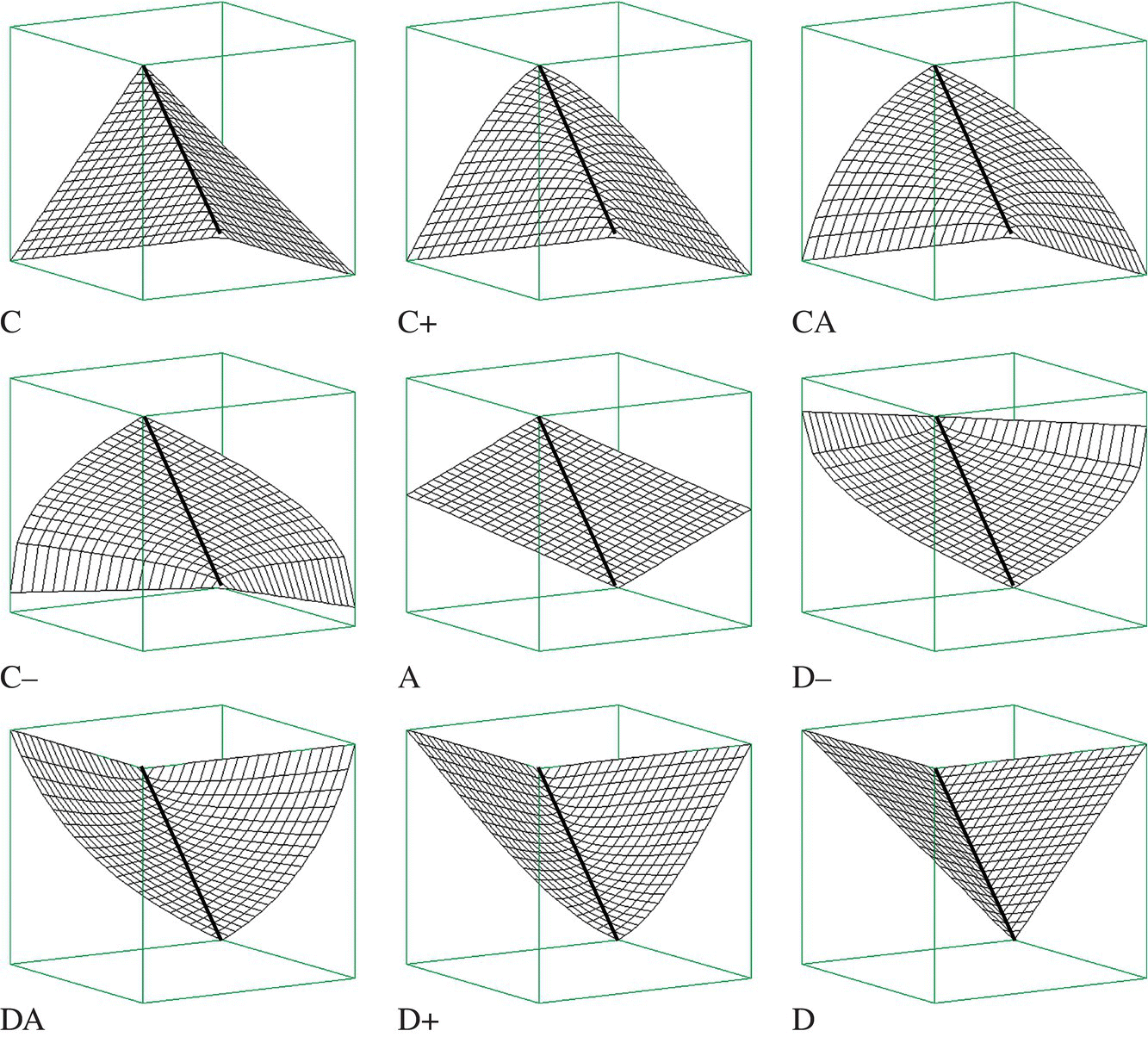
Figure 2.1.8 An example of continuous transition from conjunction (C) to disjunction (D) controlled by the adjustable parameters of andness or orness (the case of two variables).
The presented sequence of functions uses the andness/orness step 1/8. It can also use other steps, depending on the desired precision of andness/orness parameters. Fig. 2.1.8 shows that functions C+, CA and C– are similar to conjunction and respectively called strong, medium and weak partial conjunction. Similarly, functions D+, DA and D– are similar to disjunction and called strong, medium and weak partial disjunction. The partial conjunction and the full conjunction are models of simultaneity. Partial disjunction and the full disjunction are models of substitutability. Obviously, both the simultaneity and the substitutability are a matter of degree. All functions presented in Fig. 2.1.8 are idempotent, satisfy De Morgan’s laws, and include the idempotency line.
2.1.7.3 Expansion of Annihilator Adjustability
Annihilators 0 and 1 are present and easily visible in human evaluation reasoning, and consequently, they are necessary in GL. A GL function ![]() has the annihilator 0 if
has the annihilator 0 if ![]() ,
, ![]() . Similarly, f has the annihilator 1 if
. Similarly, f has the annihilator 1 if ![]() ,
, ![]() . The annihilator 0 is visible in all cases where human reasoning includes mandatory requirements. For example, if a homebuyer rejects buying both an excellent house located in an unacceptable location and an unacceptable house located in a perfect location, then both the quality of house and the quality of location are simultaneously necessary and represent mandatory requirements. Modeling of such requirements is impossible without support of annihilator 0.
. The annihilator 0 is visible in all cases where human reasoning includes mandatory requirements. For example, if a homebuyer rejects buying both an excellent house located in an unacceptable location and an unacceptable house located in a perfect location, then both the quality of house and the quality of location are simultaneously necessary and represent mandatory requirements. Modeling of such requirements is impossible without support of annihilator 0.
The use of annihilators in human reasoning can be more diversified, as illustrated in Table 2.1.3, where we compare three characteristic (annihilator‐different) criteria for quality of parking. The criterion C1 reflects the homebuyer who simultaneously needs both the garage in the house and the quality street parking in front of the house (e.g., for visitors/customers). So, both the house garage and the quality street parking are the mandatory requirements, and in such cases we need support for the annihilator 0. Such form of simultaneity is called a hard partial conjunction. The hard partial conjunction is a model of mandatory requirements.
Table 2.1.3 Three characteristic parking criteria.

The criterion C2 is different, and reflects a homebuyer who would like to have both the garage and street parking but can be partially satisfied if only one of them is available. The availability of garage is considered more important than the availability of street parking. Consequently, the criterion C2 reflects a visible simultaneity, but the annihilator 0 must not be supported. In other words, the criterion C2 specifies optional requirements. Such a form of simultaneity is called a soft partial conjunction. Generally, symmetric aggregators that support annihilators are called hard and those that do not support annihilators are called soft.
The criteria C1 and C2 are symmetric in the sense that all inputs either support or do not support the annihilator 0. This is not the case with the criterion C3, where we have the homebuyer for whom the garage is a mandatory requirement and the street parking in front of house is optional (i.e., not mandatory). This is obviously an asymmetric case where one input must support the annihilator 0 and the other must not support the annihilator. If a high‐quality garage is available, then the absence of street parking is penalized 30% and the overall suitability of such parking is 0.7. On the other hand, if the quality of garage is only 50% and the high quality street parking is always available, then the street parking yields the reward of 30% and the overall suitability of such parking is 0.65. The selected penalty and reward reflect homebuyer’s needs and can be different. Such an asymmetric aggregator is rather frequent. It is called the conjunctive partial absorption (an alternative name is the asymmetric partial conjunction). Note that from a formal standpoint, asymmetric aggregators do not support annihilators because the support is restricted to selected variable(s) and not available for optional variable(s). However, the use of asymmetric annihilators is frequent in human decision making, and consequently, it must be available in EL. Table 2.1.3 also shows sample idempotent analytic forms of criteria C1, C2, and C3, implemented using power means.
The use of annihilator 1 in models of substitutability is the De Morgan dual of the case of annihilator 0 in the area of simultaneity and all properties of annihilators 0 and 1 are symmetric. Fig. 2.1.8 shows a typical example of the presence and absence of annihilators in the case of GCD z(x, y). For andness ![]() GCD supports the annihilator 0, i.e.,
GCD supports the annihilator 0, i.e.,![]() , and such support is not available for
, and such support is not available for ![]() . For orness
. For orness ![]() GCD supports annihilator 1, i.e.,
GCD supports annihilator 1, i.e., ![]() , and such support is not available for
, and such support is not available for ![]() . The lowest andness that supports the annihilator 0 is called the threshold andness and denoted αθ. Similarly, the lowest orness that supports the annihilator 0 is called the threshold orness and denoted ωθ. The values of αθ and ωθ are adjustable parameters of GL. In the special case where
. The lowest andness that supports the annihilator 0 is called the threshold andness and denoted αθ. Similarly, the lowest orness that supports the annihilator 0 is called the threshold orness and denoted ωθ. The values of αθ and ωθ are adjustable parameters of GL. In the special case where ![]() , the hard and soft partial conjunction and partial disjunction have equal ranges and such a form of GCD is called the uniform GCD and denoted UGCD.
, the hard and soft partial conjunction and partial disjunction have equal ranges and such a form of GCD is called the uniform GCD and denoted UGCD.
It is important to note that the diversified use of annihilators is a fundamental property of human evaluation reasoning and one of fundamental properties of idempotent logic aggregators (ILA) in GL; this property is not available in BL. The parameterized adjustability of the presence or the absence of support for the annihilator 0 in simultaneity models and the annihilator 1 in substitutability models (hard and soft partial conjunction and disjunction) for ILA can be summarized as follows:
- Simultaneity models
- Symmetric simultaneity (symmetric annihilators characterized by
 )
)
- Mandatory requirements (annihilator 0 supported; high andness, hard partial conjunction)
- Nonmandatory or optional requirements (annihilator 0 not supported; low andness, soft partial conjunction)
- Adjustable location of threshold andness
- Asymmetric simultaneity (asymmetric annihilators)
- Adjustable penalty caused by low optional input
- Adjustable reward caused by high optional input
- Symmetric simultaneity (symmetric annihilators characterized by
- Substitutability models
- Symmetric substitutability (symmetric annihilators characterized by
 )
)
- Sufficient requirements (annihilator 1 supported; high orness, hard partial disjunction)
- Nonsufficient or optional requirements (annihilator 1 not supported; low orness, soft partial disjunction)
- Adjustable location of threshold orness
- Asymmetric substitutability (asymmetric annihilators)
- Adjustable penalty caused by low optional input
- Adjustable reward caused by high optional input
- Symmetric substitutability (symmetric annihilators characterized by
2.1.7.4 Expansion of Semantic Domain
Semantic components of human reasoning are those components that are related to the role and meaning of variables and statements, in the context of specific goals and interests of the decision maker (stakeholder). Generally, semantics is a branch of linguistics and logic concerned with meaning. In the context of GL, the most frequent semantic component is the percept of importance that is associated with the majority of variables in perceptual computing. In classical BL, semantic components are not present and the concept of importance is excluded from BL models. In GL, the semantic components are explicitly present in all decision models.
In the area of evaluation reasoning, decision makers select and use various attributes that contribute to the overall suitability of an evaluated object. Individual attributes and their groups regularly have different importance for the decision maker because they have different ability to contribute to the attainment of decision maker’s goals. The percept of overall suitability is predominantly affected by those attributes and groups of attributes that have high overall importance.
The overall importance of an attribute or a group of attributes is a compound percept. Both the high andness and the high orness of a group of attributes contribute to the percept of their importance. Indeed, if all attributes in a group must simultaneously be sufficiently satisfied, that means all of them are important to the decision maker. Similarly, high orness indicates that each attribute in a group is so important that satisfying only one of them is sufficient to create the percept of group satisfaction. On the other hand, in each group of attributes there is also the percept of relative importance: some attributes can be more important than other attributes. Consequently, the compound percept of the overall importance of each attribute in this context consists of two principal components: the relative importance and the level of andness (or orness), as illustrated for a GCD aggregator in Fig. 2.1.9.
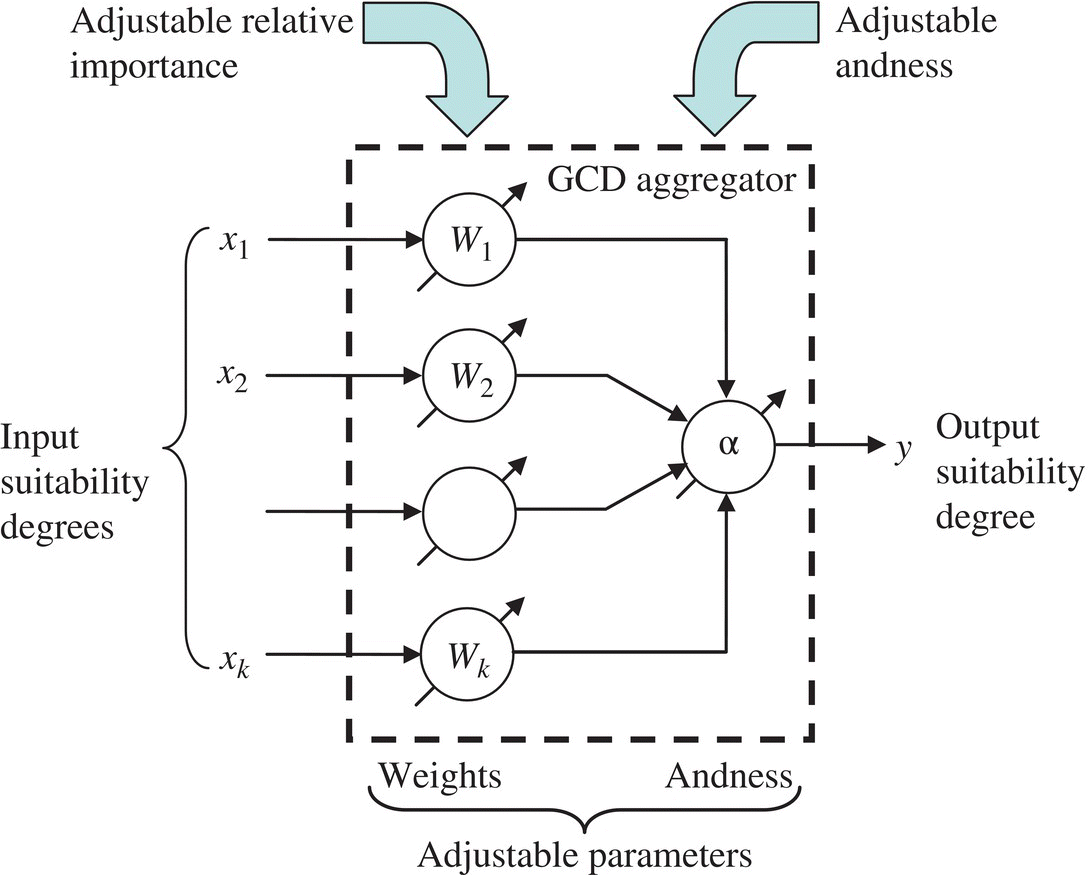
Figure 2.1.9 Adjustable semantic components of a GCD aggregator.
The relative importance is regularly expressed using adjustable normalized weights: ![]() ,
, ![]() . The group importance of attributes x1, …, xk is adjusted by selecting the degree of andness/orness. Then, the percept of overall importance that the decision maker intuitively creates for each of k input attributes is obtained by combining the group importance and the individual relative importance of attributes.
. The group importance of attributes x1, …, xk is adjusted by selecting the degree of andness/orness. Then, the percept of overall importance that the decision maker intuitively creates for each of k input attributes is obtained by combining the group importance and the individual relative importance of attributes.
The compound percept of the overall importance of individual inputs of GCD aggregators is the point of departure in creating the GCD aggregators. In other words, decision makers must decompose the percept of overall importance in order to adjust the weights and andness as illustrated in Fig. 2.1.9. This decomposition is a rather natural process, and decision makers can answer the questions about the desired degree of simultaneity/substitutability and the desired degrees of relative importance in any order. Rational and trained decision makers can specify the relative importance and the degree of simultaneity/substitutability in a way that is consistent with the percepts of overall importance of individual attributes. Not surprisingly, human reasoning can sometimes be inconsistent; an example is the request for high andness (i.e., high group importance) and simultaneously a very low weight (i.e., very low individual importance) of an attribute. For more detail, see Section 2.2.6.
2.1.7.5 Expansion of Compensative Logic Functions
The compatibility with observable properties of human intuitive logic reasoning requires the compensative properties of aggregators, where the deficiencies of specific inputs can be compensated by the excesses of other inputs. The pure conjunction and disjunction are not compensative, as illustrated in Fig. 2.1.10. Indeed, if ![]() and
and ![]() , then a decrement of x cannot be compensated by an increment of y. More precisely, z is insensitive to both increments and decrements of y as long as
, then a decrement of x cannot be compensated by an increment of y. More precisely, z is insensitive to both increments and decrements of y as long as ![]() . Similarly, if
. Similarly, if ![]() and
and ![]() , then decrement of y cannot be compensated by an increment of x. These are extreme properties, not frequently observable in human evaluation reasoning.
, then decrement of y cannot be compensated by an increment of x. These are extreme properties, not frequently observable in human evaluation reasoning.
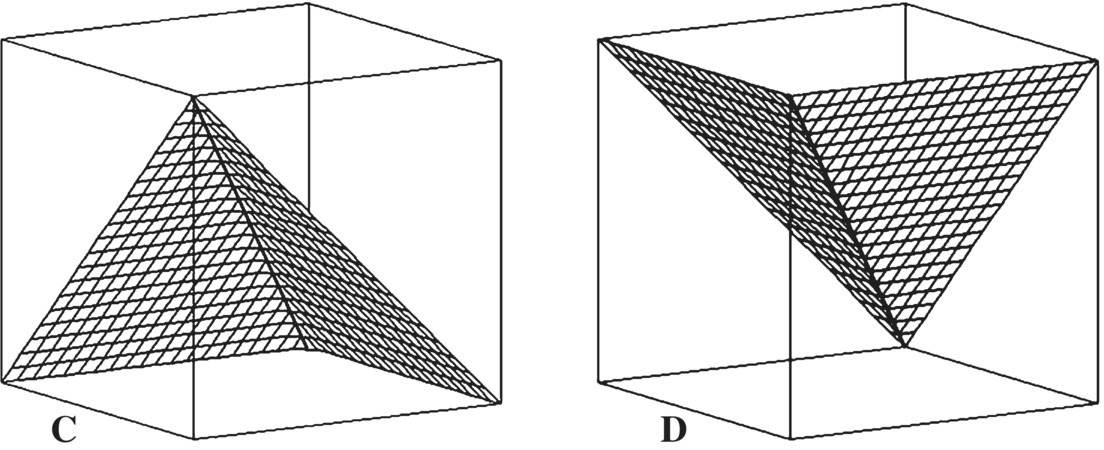
Figure 2.1.10 Pure conjunction C (the minimum function) and the pure disjunction D (the maximum function) in the case of two variables.
In human evaluation reasoning, we can easily observe the prevalence of compensative aggregation. For example, in all schools a bad grade in some class can be compensated by a good grade in another class. Similarly, most homebuyers are ready to compensate imperfections of house location by an increased house quality, and vice versa.
A soft computing aggregator f(x1, …, xn) is fully compensative if the deficiency of a selected input xi can be fully compensated by the excesses of other inputs:
Of course, there are always deficiencies that cannot be compensated. If the deficiency Δxi is larger than some threshold value it might be impossible to compensate it. Furthermore, if an input is mandatory, its absence can never be compensated. In addition, the compensation can sometimes be partial (incomplete). There are also cases where the deficiency Δxi can be compensated by a selected other (sufficiently important) input, or by any other input. In the extreme case of sufficient inputs, each such input can fully compensate any deficiency of all other inputs. Consequently, compensative properties can vary in a wide range, but some form of compensation is frequently visible in human evaluation reasoning.
Compensative properties of an aggregator are most visible in the case of the neutrality aggregator (the arithmetic mean) ![]() shown in Fig. 2.1.11. The obvious condition for compensation of deficiency Δx is
shown in Fig. 2.1.11. The obvious condition for compensation of deficiency Δx is ![]() , or
, or ![]() . So, the decrement
. So, the decrement ![]() is compensated by the increment
is compensated by the increment ![]() and the suitability z in points P and Q is the same. Except for the full conjunction and the full disjunction, all other suitability aggregators in GL have some compensative properties and generally the compensation is achieved using
and the suitability z in points P and Q is the same. Except for the full conjunction and the full disjunction, all other suitability aggregators in GL have some compensative properties and generally the compensation is achieved using ![]() . There are seven categories of compensative GL aggregators shown in Table 2.1.4 and described in the next section.
. There are seven categories of compensative GL aggregators shown in Table 2.1.4 and described in the next section.
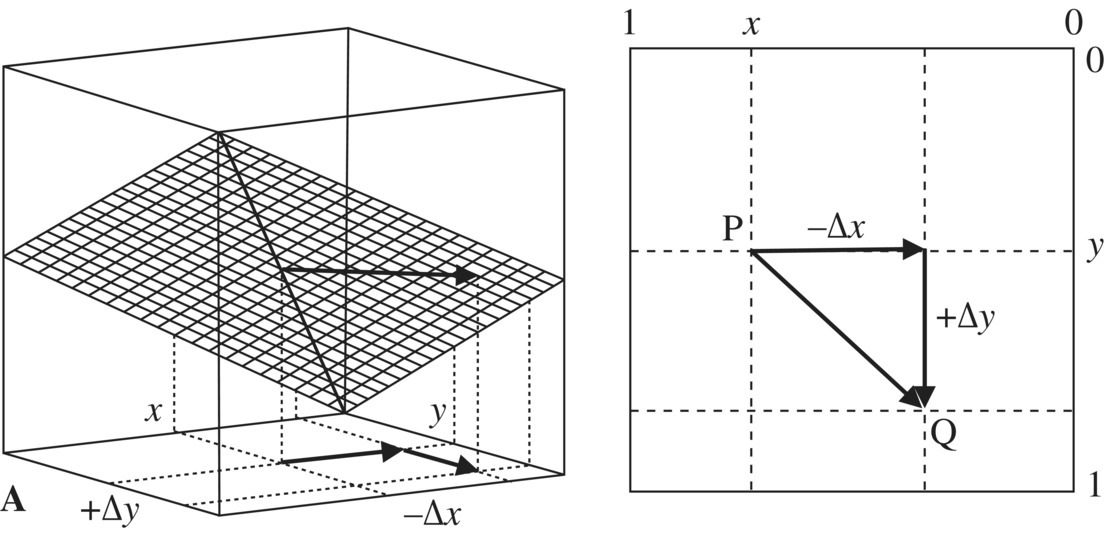
Figure 2.1.11 Conjunctive‐disjunctive neutrality (the arithmetic mean) and its compensative properties.
Table 2.1.4 Nine most significant idempotent aggregators in graded logic.
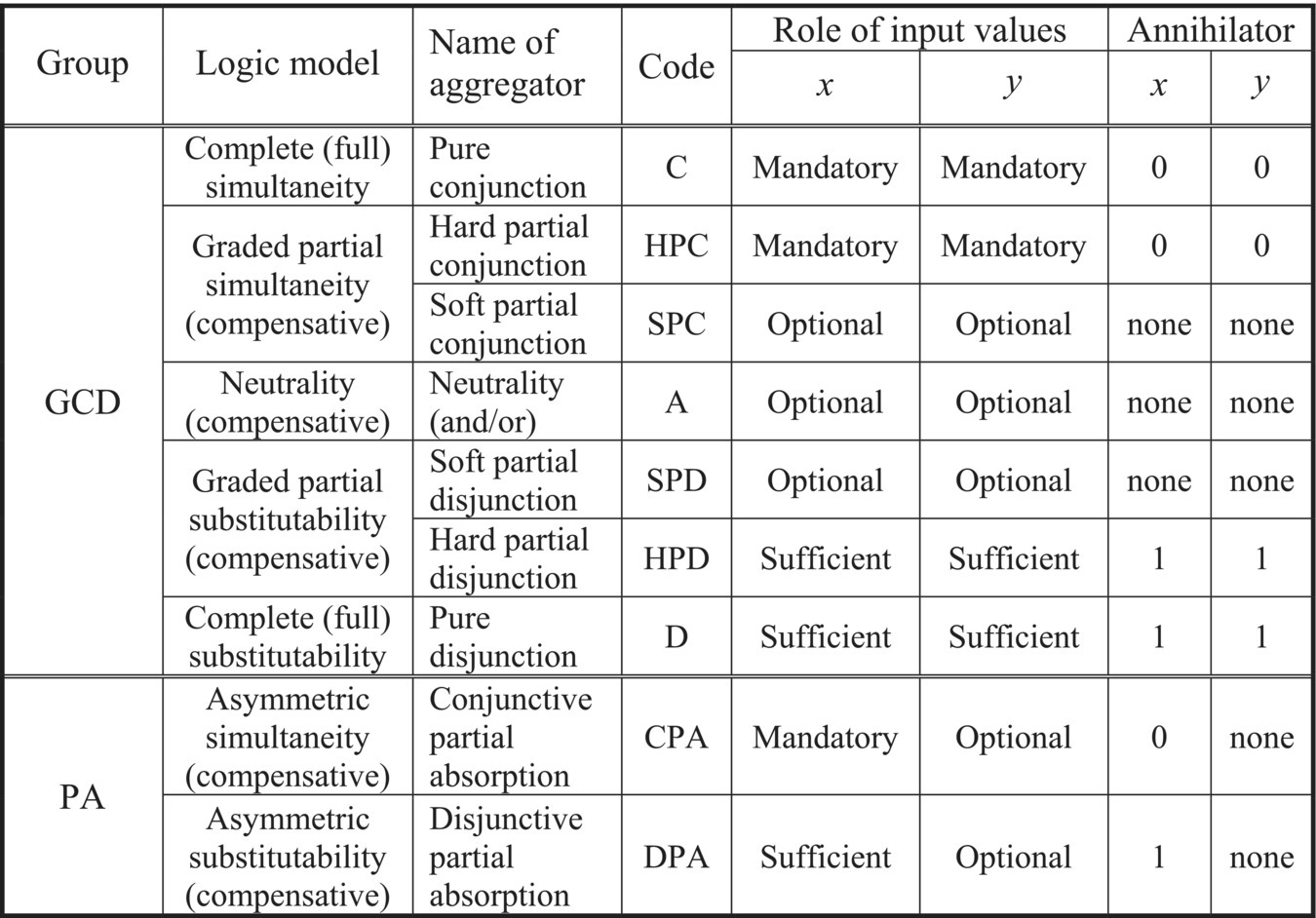
2.1.7.6 Expansion of the Range of Andness/Orness from Drastic Conjunction to Drastic Disjunction
Idempotent aggregators restrict the range of andness and orness to interval [0,1]. However, human reasoning sometimes includes nonidempotent aggregation where we use the logic functions of hyperconjunction (stronger simultaneity than the pure conjunction) or hyperdisjunction (stronger substitutability than the pure disjunction). Therefore, general models of human reasoning should be capable to expand the range of andness and orness beyond the standard interval [0,1], as shown in Fig. 2.1.2. For logic function A(x1, …, xn; α) the global andness α is based on the volume V under A(x1, …, xn; α):
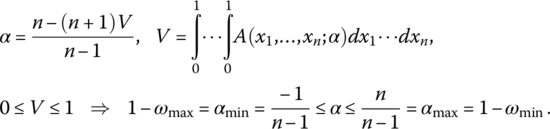
Now is the time to introduce the extreme logic functions, those that have the lowest and the highest andness. The highest andness corresponds to the minimum volume ![]() . The corresponding most conjunctive logic function that yields the zero volume is the drastic conjunction, defined as follows:
. The corresponding most conjunctive logic function that yields the zero volume is the drastic conjunction, defined as follows:
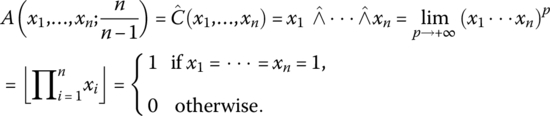
This is obviously the maximum possible degree of simultaneity. The drastic conjunction is satisfied only if all inputs are simultaneously perfectly satisfied. For example, in the case of student evaluation we accept only those candidates that have the GPA equal to the highest possible grade and all other candidates are rejected. Consequently, ![]() and
and ![]() . It is impossible to imagine a higher degree of simultaneity.
. It is impossible to imagine a higher degree of simultaneity.
The lowest andness corresponds to the maximum volume ![]() . The corresponding least conjunctive (and most disjunctive) logic function that yields the maximum volume is the drastic disjunction, defined as follows:
. The corresponding least conjunctive (and most disjunctive) logic function that yields the maximum volume is the drastic disjunction, defined as follows:

This is obviously the maximum possible degree of substitutability. The drastic disjunction is unsatisfied only if all inputs are simultaneously completely unsatisfied. For example, in the case of student evaluation, we reject only those student candidates that have the GPA equal to the lowest, failing grade. All other cases are fully acceptable, giving ![]() and the minimum andness
and the minimum andness ![]() . Even the slightest satisfaction of any input yields the maximum aggregated suitability. Obviously, it is not possible to imagine a higher degree of substitutability.
. Even the slightest satisfaction of any input yields the maximum aggregated suitability. Obviously, it is not possible to imagine a higher degree of substitutability.
The drastic conjunction and the drastic disjunction belong to conjunctive or disjunctive graded logic functions. However, according to Definition 2.1.1, the drastic conjunction and the drastic disjunction do not have the formal status of logic aggregator. As conjunctive/disjunctive functions, they have andness and orness either ![]() or
or ![]() . Since andness and orness are properties of conjunctive/disjunctive functions, we always specify andness and orness in the range
. Since andness and orness are properties of conjunctive/disjunctive functions, we always specify andness and orness in the range ![]() and not in the open range
and not in the open range ![]() that formally corresponds to functions defined as logic aggregators. More precisely, basic conjunctive/disjunctive graded logic functions include logic aggregators, plus the drastic conjunction and the drastic disjunction as the closest flanking neighbors of logic aggregators.
that formally corresponds to functions defined as logic aggregators. More precisely, basic conjunctive/disjunctive graded logic functions include logic aggregators, plus the drastic conjunction and the drastic disjunction as the closest flanking neighbors of logic aggregators.
The drastic conjunction and the drastic disjunction might look as abstract and unrealistic extreme cases. The reality can sometimes be different. Indeed, there are situations where only the best is acceptable and that is exactly the criterion expressed by the drastic conjunction (rejection of all suboptimal alternatives). Similarly, there are medical conditions where the patient is not sick only in cases where all serious symptoms are simultaneously absent. In all other cases the patient needs medical help. This type of criterion is expressed using a drastic disjunction.
In the case of two variables the drastic conjunction and the drastic disjunction are shown in Fig. 2.1.12. If we provide a continuous transition from the drastic conjunction to the drastic disjunction, so that all transitory functions along the path have acceptable logic properties, consistent with human reasoning, then we can traverse and cover all four regions defined by the logic quadrisection of the unit hypercube (Fig. 2.1.5). In other words, we can provide logic aggregators that are necessary and sufficient for modeling human logic criteria. That can be analytically achieved using the mean andness theorem [DUJ05c] and interpolative aggregators [DUJ14] presented in Sections 2.4.7 and 2.4.8.

Figure 2.1.12 Drastic conjunction and drastic disjunction in the case of two variables.
To exemplify the process of expansion of the range of andness/orness, let us use two aggregators, A1(x1, …, xn; α1) and A2(x1, …, xn; α2), which have increasing andness:

If ![]() then according to [DUJ14, DUJ15a], we can create an aggregator A(x1, …, xn; α) which linearly interpolates between A1(x1, …, xn; α1) and A2(x1, …, xn; α2) as follows:
then according to [DUJ14, DUJ15a], we can create an aggregator A(x1, …, xn; α) which linearly interpolates between A1(x1, …, xn; α1) and A2(x1, …, xn; α2) as follows:
Using this method, we can seamlessly expand GL aggregators from idempotent to nonidempotent domain [DUJ16a]. A detailed presentation of this technique can be found in Chapter 2.4. To illustrate the idea of interpolative logic aggregators in the simple case of two variables, we can perform a continuous andness‐directed transition from the drastic conjunction to the drastic disjunction using an interpolative aggregator ![]() , as follows:
, as follows:

The conjunctive aggregator F(x1, x2; α) is idempotent between the arithmetic mean and the pure conjunction and then seamlessly nonidempotent and hyperconjunctive between the pure conjunction and the drastic conjunction. This example illustrates the possibility to extend the domain of andness/orness beyond the standard [0,1] range. So, basic GCD aggregators in GL can have any desired value of andness and orness in the maximum possible range ![]() (Fig. 2.1.2). In this way, GCD can cover all regions inside the unit hypercube. Examples of hyperconjunctive and hyperdisjunctive aggregators of two variables are shown in Fig. 2.1.13. Comparing Figs. 2.1.10 and 2.1.13, it is easy to see that the hyperconjunctive aggregators are located visibly under the pure conjunction and the idempotency line. Similarly, the hyperdisjunctive aggregators are located visibly over the pure disjunction and the idempotency line. Note also that hyperconjunctive and hyperdisjunctive aggregators satisfy all conditions of logic aggregators specified in Definition 2.1.1. Therefore, the use of hyperconjunctive and hyperdisjunctive aggregators is a way to expand the expressive power of GL, covering all regions of the unit hypercube.
(Fig. 2.1.2). In this way, GCD can cover all regions inside the unit hypercube. Examples of hyperconjunctive and hyperdisjunctive aggregators of two variables are shown in Fig. 2.1.13. Comparing Figs. 2.1.10 and 2.1.13, it is easy to see that the hyperconjunctive aggregators are located visibly under the pure conjunction and the idempotency line. Similarly, the hyperdisjunctive aggregators are located visibly over the pure disjunction and the idempotency line. Note also that hyperconjunctive and hyperdisjunctive aggregators satisfy all conditions of logic aggregators specified in Definition 2.1.1. Therefore, the use of hyperconjunctive and hyperdisjunctive aggregators is a way to expand the expressive power of GL, covering all regions of the unit hypercube.

Figure 2.1.13 Sample highly hyperconjunctive and highly hyperdisjunctive aggregators of two variables close to the drastic conjunction and the drastic disjunction.
2.1.8 GL Conjecture: Ten Necessary and Sufficient GL Functions
Knowledge of components is a prerequisite for building systems. This holds for all kinds of systems. Hardware designers know (from the Charles Peirce theorem) that all digital logic circuitry can be built using either NOR or NAND gates. Software designers know (from Giuseppe Jacopini’s structure theorem) that all software can be built using a loop with conditional exit, a sequence, and some auxiliary flag variables (e.g., theoretically, there is no need for branches such as if‐then‐else, because they can be made using flags and while loops). In the case of mathematical objects and systems, the fundamental question is to find necessary and sufficient basic components that must be available for building compound objects of any complexity. In this context, a component is necessary if we cannot build a compound object without that component. A set of components is sufficient if it contains all components that are necessary for building a compound object. A set of components is necessary and sufficient if it contains the minimum set of necessary components; i.e., if we omit any component from that set, we cannot build desired compound objects. For example, in the case of Boolean logic, one of sets of necessary and sufficient basic functions includes AND, OR, and NOT. So, we have to answer the same question for GL, and specify basic logic functions that are necessary and sufficient for building compound GL functions.
Before answering this question, we must answer the question about the acceptable way of demonstrating that an operator is necessary, and a group of operators is sufficient. Since these operators are used in the context of human decision making and not in the context of a formal mathematical proof, the only way to show that an operator is necessary is to show the situation where human decision makers provably use the analyzed operator. Sufficiency can be demonstrated using the geometric properties of the unit hypercube and relationships with classical logic. The following conjecture offers an answer to the question of necessary and sufficient aggregators:
The graded logic conjecture. There are 10 necessary and sufficient graded logic functions: (1) neutrality, (2) soft partial conjunction, (3) soft partial disjunction, (4) hard partial conjunction, (5) hard partial disjunction, (6) full conjunction, (7) full disjunction, (8) hyperconjunction, (9) hyperdisjunction, and (10) negation. The functions (1) to (9) are graded logic aggregators that are special cases of the graded conjunction/disjunction (GCD). Except for negation, neutrality and full conjunction/disjunction, all other functions are logic categories with adjustable range of andness/orness.
Reasons that Support the Necessity
We assume that logic is derived from observing human intuitive decision making and logic aggregators provide quantitative models of human reasoning. Each of the 10 fundamental functions is provably present in human evaluation reasoning. For each of them we can present a proof of existence of a justifiable decision process which uses the selected operator (see Section 2.1.2 and Chapter 2.2). For example, a homebuyer simultaneously wants a high‐quality home located in a sufficiently convenient location. So, this is a conjunctive aggregator. Most homebuyers would reject all homes having unacceptable quality or unacceptable location. In addition, if the degrees of satisfaction with the home quality and location are the same, that would be interpreted as the overall satisfaction with the home. Consequently, the aggregator is conjunctive, hard, and idempotent, and the type of such aggregator is obviously the hard partial conjunction. This type of aggregator has a range of continuously adjustable andness/orness. There is not a slightest doubt that the idempotent hard partial conjunction is necessary in human reasoning and, consequently, it is a necessary component in basic logic models. The empirical fact that the hard partial conjunction is used in most home selection processes (as well as in countless similar situations) should be a sufficient proof that this type of aggregator is necessary. We can provide similar proofs of necessity for each of the 10 fundamental functions. The set of 10 basic functions is denoted B10.
Reasons that Support the Sufficiency
Logic neutrality, full conjunction, and full disjunction are operators that logically partition the unit hypercube in four regions: (1) soft and hard partial conjunction; (2) soft and hard partial disjunction; (3) hyperconjunction; and (4) hyperdisjunction, as shown in Fig. 2.1.5. Inside the unit hypercube there are no other regions and no space for other types of logic aggregators. Consequently, the nine non‐unary operators are sufficient to completely cover the unit hypercube. In addition, full conjunction, full disjunction, and negation are sufficient to secure the complete compatibility with classic Boolean logic, making graded logic a seamless generalization of Boolean logic. GCD and negation are necessary and sufficient graded logic functions in exactly the same way as conjunction, disjunction, and negation are necessary and sufficient for building the classic Boolean logic.
The presented reasoning about necessity and sufficiency of the 10 soft computing logic operators provides a strong empirical validation of the graded logic conjecture. In the context of perceptual computing, the empirical justification of the GCD conjecture seems to be equally appropriate as a formal proof based on a formal axiomatic theory.
The graded logic conjecture provides a convincing answer to Zimmermann’s question from [ZIM96]:
“How do human beings aggregate subjective categories, and which mathematical models describe this procedure adequately?”
Our answer is: “Human beings aggregate subjective categories using aggregation structures that are appropriate combinations of ten necessary and sufficient types of logic operators: nine aggregators that are special cases of the graded conjunction/disjunction and the standard negation. After selecting an appropriate type of aggregator humans regularly perform fine tuning of aggregator by additionally adjusting desired andness/orness.”
The fundamental 10 necessary and sufficient basic GL functions (called the basic group B10) and their symbolic notation are as follows:
- Full (or pure) conjunction (C):
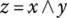 .
. - Hard partial conjunction (HPC):
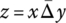 .
. - Soft partial conjunction (SPC):
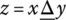 .
. - Neutrality (arithmetic mean) (A):
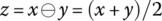 .
. - Soft partial disjunction (SPD):
 .
. - Hard partial disjunction (HPD):
 .
. - Full (or pure) disjunction (D):
 .
. - Hyperconjunction (CC):
 .
. - Hyperdisjunction (DD):
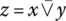 .
. - Standard negation (NOT):
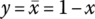 .
.
The list of 10 necessary and sufficient GL functions yields the following obvious corollary: All aggregation functions that do not support the presented seven idempotent and two nonidempotent types of aggregation cannot be used as general models of human reasoning. GCD aggregator must be designed so as to support all nine necessary types of aggregation. Except for GCD, all currently used aggregators (some of them rather popular) support only a small subset of the necessary nine types of aggregation.
There are seven basic idempotent GL functions (idempotent aggregators) shown in Table 2.1.4: three forms of conjunction, neutrality, and three forms of disjunction. Those are our “magnificent seven,” the most important and the most frequently used aggregators in evaluation: B7 = {C, HPC, SPC, A, SPD, HPD, D}. Then, B10 = B7 ∪ {NOT, CC, DD}.
Table 2.1.4 also contains two frequently used compound idempotent aggregators, denoted as partial absorption (PA): conjunctive partial absorption (CPA) and disjunctive partial absorption (DPA). CPA aggregates mandatory and optional inputs and DPA aggregates sufficient and optional inputs. These functions, introduced in [DUJ74a, DUJ75a, DUJ79a] are so frequent in applications that they must be included in the “inner circle” of the most important aggregators (the basic group B9). We study them in Chapter 2.2, and Chapter 2.6 is completely devoted to PA. PA functions are compound aggregators based on basic necessary and sufficient idempotent aggregators of partial conjunction, neutrality and partial disjunction. They are defined as follows:

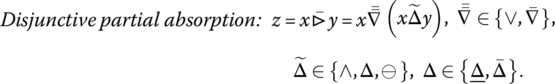
These functions are a generalization of classical BL absorption theorems ![]() and
and ![]() ; here x plays the role of primary variable and y is a secondary variable. The BL version completely absorbs the variable y (making it insignificant). The above GL version absorbs the secondary variable y only partially (making it optional, but not negligible). Except for the extreme cases of full conjunction and disjunction (inherited from BL), all GL functions in Table 2.1.4 are compensative.
; here x plays the role of primary variable and y is a secondary variable. The BL version completely absorbs the variable y (making it insignificant). The above GL version absorbs the secondary variable y only partially (making it optional, but not negligible). Except for the extreme cases of full conjunction and disjunction (inherited from BL), all GL functions in Table 2.1.4 are compensative.
Inputs of idempotent GL aggregators can be mandatory, or sufficient, or optional. Mandatory inputs must be satisfied to avoid zero output values. Sufficient inputs denote important features that are completely sufficient to satisfy given requirements regardless of the satisfaction of other inputs in a group. Optional inputs contribute to satisfying the requirements of the criterion that uses them; they are certainly desired, but neither mandatory nor sufficient. Optional inputs are used in all conjunctive criteria that can tolerate some (but not all) zero input values without producing the zero output. In the case of disjunctive criteria, optional inputs are used to model desirable inputs that are not so important that they alone can completely satisfy a criterion function.
2.1.9 Basic Idempotent GL Aggregators
The adjustable simultaneity is modeled using either soft or hard partial conjunction. The characteristic forms of soft and hard partial conjunctions, in the case of two variables, are illustrated in Fig. 2.1.14. In the case of soft partial conjunction, we have that the aggregation function touches the plane ![]() only in the point (0, 0). As opposed to that, the hard partial conjunction function touches the plane
only in the point (0, 0). As opposed to that, the hard partial conjunction function touches the plane ![]() in all points where
in all points where ![]() or
or ![]() . That makes x and y mandatory inputs. However, contrary to the pure conjunction and the pure disjunction, for all positive x and y, the functions shown in Fig. 2.1.14 are compensative.
. That makes x and y mandatory inputs. However, contrary to the pure conjunction and the pure disjunction, for all positive x and y, the functions shown in Fig. 2.1.14 are compensative.

Figure 2.1.14 Typical forms of the soft and hard partial conjunction.
The degree of simultaneity (andness) is an indicator that reflects the similarity between the partial conjunction and the pure conjunction, as discussed in Section 2.1.3. GCD functions perform continuous transition from conjunction to disjunction inside the unit hypercube. Consequently, the simplest way to characterize the overall degree of simultaneity of GCD function can be based on computing the volume Vol(GCD) under the function inside the unit hypercube, as shown in formula (2.1.8). For all aggregators in the GCD group, the andness α can be expressed as follows:
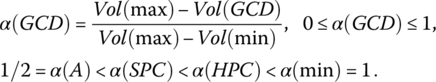
The andness ![]() for the arithmetic mean (A) is an obvious consequence of the fact that
for the arithmetic mean (A) is an obvious consequence of the fact that ![]() (see Fig. 2.1.3). The arithmetic mean is the “centroid of logic aggregators,” because it is located exactly in the middle between the pure conjunction and the pure disjunction:
(see Fig. 2.1.3). The arithmetic mean is the “centroid of logic aggregators,” because it is located exactly in the middle between the pure conjunction and the pure disjunction:
The adjustable substitutability is modeled using either soft or hard partial disjunction. The characteristic forms of soft and hard partial conjunctions are illustrated in Fig. 2.1.15. In the case of soft partial disjunction we have that the aggregation function touches the plane ![]() only in the point (1,1). As opposed to that, the hard partial disjunction function touches the plane
only in the point (1,1). As opposed to that, the hard partial disjunction function touches the plane ![]() in all points, where either
in all points, where either ![]() or
or ![]() . That makes x and y sufficient inputs: if one of them is fully satisfied then
. That makes x and y sufficient inputs: if one of them is fully satisfied then ![]() regardless the value of the other input.
regardless the value of the other input.

Figure 2.1.15 Typical forms of the soft and hard partial disjunction (compensative partial substitutability).
Similar to the case of partial conjunction, the functions shown in Fig. 2.1.15 are compensative. The degree of substitutability (orness) is an indicator that reflects the similarity between the partial disjunction and the pure disjunction. Using the same approach we used for defining the global andness, the global orness ω of all GCD aggregators can be expressed as follows:
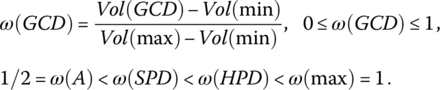
From Fig. 2.1.14 and Fig. 2.1.15, it is easy to see the symmetry between SPC and SPD, as well as the symmetry between HPC and HPD; most frequently these pairs are defined to be De Morgan duals: if one of them is f(x, y), then the other is ![]() . If we compare the GCD functions HPC, SPC, A, SPD, and HPD (e.g., see Fig. 2.1.8), it is easy to see that all of them contain the idempotency line
. If we compare the GCD functions HPC, SPC, A, SPD, and HPD (e.g., see Fig. 2.1.8), it is easy to see that all of them contain the idempotency line ![]() and consequently in the vicinity of the idempotency line all GCD aggregators behave similarly to the arithmetic mean.
and consequently in the vicinity of the idempotency line all GCD aggregators behave similarly to the arithmetic mean.
Compensative functions can be asymmetric. Fig. 2.1.16 shows the partial absorption function (PA), which has two versions: conjunctive and disjunctive. The conjunctive partial absorption, CPA (also called the asymmetric simultaneity) has one mandatory input (x) and one optional input (y) and combines the properties of HPC and SPC. If x>y, then CPA behaves as SPC, and if y>x, then CPA is similar to HPC. If the optional input is not satisfied (y=0), then the output z is equal to the value of the mandatory input x reduced for a desired value of penalty. However, if the mandatory input is not satisfied (x=0) then the output is z=0. Thus, the mandatory input supports the annihilator 0, and the asymmetric optional input does not support annihilators.
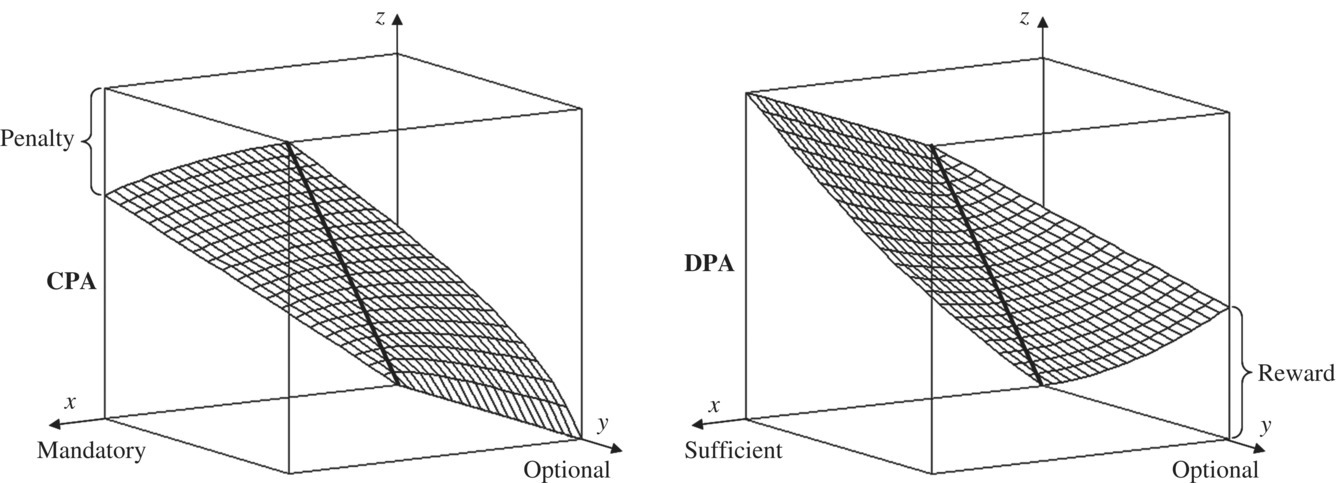
Figure 2.1.16 Typical forms of the conjunctive partial absorption (asymmetric simultaneity) and disjunctive partial absorption (asymmetric substitutability).
The disjunctive partial absorption, DPA (also called the asymmetric substitutability) has one sufficient input (x) and one optional input (y) and combines the properties of HPD and SPD. If x>y, then DPA behaves as HPD, and if y>x, then DPA is similar to SPD. If the optional input is fully satisfied (y=1), then the value of output z is equal to the value of the sufficient input x increased for a desired value of reward. However, if the sufficient input is fully satisfied (x=1), then the output is z=1. Thus, the sufficient input supports the annihilator 1, and the asymmetric optional input does not support annihilators.
CPA and DPA functions presented in Fig. 2.1.16 are obtained as generalizations of BL absorption theorems (![]() and
and ![]() ). However, taking into account that CPA is a mix of HPC and SPC, and DPA is a mix of HPD and SPD, it is also possible to interpret CPA as asymmetric conjunction, and DPA as asymmetric disjunction.
). However, taking into account that CPA is a mix of HPC and SPC, and DPA is a mix of HPD and SPD, it is also possible to interpret CPA as asymmetric conjunction, and DPA as asymmetric disjunction.
The classical bivalent Boolean logic provides models of the {0,1}‐type of reasoning, while humans actually use the [0,1]‐type of reasoning, as the theory of fuzzy systems clearly proves. GL extends the domain of logic functions from the vertices of the unit hypercube {0, 1}n to the complete volume of the unit hypercube [0, 1]n, and, in addition, it offers other important extensions discussed in Section 2.1.7. Naturally, these extensions must be seamless, and in vertices {0, 1}n the BL and GL must be identical. A direct benefit that GL derives from the relationship with BL is that the bivalent ancestor provides a sound background for deciding about the necessary and sufficient material for building graded logic models.
In GL, we use specific notation of basic graded logic functions, and this notation is related to the notation used in classical Boolean logic. We assume that all variables belong to the unit interval ![]() . Pure conjunction and pure disjunction are always realized as minimum and maximum:
. Pure conjunction and pure disjunction are always realized as minimum and maximum: ![]() ,
, ![]() ,
, ![]() . The negation is defined as the standard negation
. The negation is defined as the standard negation ![]() .
.
The graded conjunction/disjunction (GCD) is denoted using symbol ![]() , which combines the symbols of conjunction
, which combines the symbols of conjunction ![]() and disjunction
and disjunction ![]() . GCD is the most important GL function, and it can be realized in many different ways that have various desired features. The simplest possible implementation of GCD, in the case of two variables, is the following min‐max function:
. GCD is the most important GL function, and it can be realized in many different ways that have various desired features. The simplest possible implementation of GCD, in the case of two variables, is the following min‐max function:
The parameter α (introduced in Section 2.1.3) is called andness or the conjunction degree. The parameter ω is called orness or the disjunction degree. Andness and orness are complementary parameters. The high andness denotes that GCD is similar to conjunction, and the high orness denotes that GCD is similar to disjunction. We use ![]() as a symbolic notation of GCD, assuming that x1 has the same degree of importance as x2, and that aggregator
as a symbolic notation of GCD, assuming that x1 has the same degree of importance as x2, and that aggregator ![]() corresponds to a specific degree of andness/orness. By changing orness from 0 to 1, we can realize a continuous transition from conjunction to disjunction, as illustrated in Fig. 2.1.17.
corresponds to a specific degree of andness/orness. By changing orness from 0 to 1, we can realize a continuous transition from conjunction to disjunction, as illustrated in Fig. 2.1.17.
Figure 2.1.17 The simplest min‐max implementation of the GCD of two variables.
If ![]() , then GCD becomes similar to conjunction, and in such cases
, then GCD becomes similar to conjunction, and in such cases ![]() is called the partial conjunction and symbolically denoted x1Δx2. The aggregator Δ is called andor, and it is the symbol of partial conjunction. If
is called the partial conjunction and symbolically denoted x1Δx2. The aggregator Δ is called andor, and it is the symbol of partial conjunction. If ![]() , then GCD becomes similar to disjunction, and in such cases
, then GCD becomes similar to disjunction, and in such cases ![]() is called the partial disjunction and is denoted
is called the partial disjunction and is denoted ![]() . The aggregator
. The aggregator ![]() is called orand, and it is the symbol of partial disjunction. In a special case where
is called orand, and it is the symbol of partial disjunction. In a special case where ![]() we have that
we have that ![]() is called the neutrality function and is symbolically denoted x1⊖x2. Obviously, the neutrality function is located right in the middle between the pure conjunction and the pure disjunction, and it is implemented as the arithmetic mean:
is called the neutrality function and is symbolically denoted x1⊖x2. Obviously, the neutrality function is located right in the middle between the pure conjunction and the pure disjunction, and it is implemented as the arithmetic mean:
We use ![]() as a symbol of arithmetic mean or neutrality, indicating a perfectly balanced presence of conjunctive and disjunctive properties. Therefore, GCD has five major special cases and can be written as follows:
as a symbol of arithmetic mean or neutrality, indicating a perfectly balanced presence of conjunctive and disjunctive properties. Therefore, GCD has five major special cases and can be written as follows:

The presented GCD model assumes that all inputs (in this case, x1 and x2) are equally important. However, in human reasoning, that is an infrequent special case. In human evaluation logic, x1 can be more or less important than x2. The differences in importance are usually expressed as normalized weights, where W1 denotes the relative importance of x1 and W2 denotes the relative importance of x2, assuming ![]() , and
, and ![]() . In such cases, we have weighted GCD that can be symbolically written as follows:
. In such cases, we have weighted GCD that can be symbolically written as follows:

Again, this is a symbolic notation: W1x1 and W2x2 are not products, but symbols of the presence of different weights. Therefore, if the importance of inputs is the same, then the symbolic notation is ![]() . The notation without weights is a simplified notation that assumes equal importance of all inputs:
. The notation without weights is a simplified notation that assumes equal importance of all inputs: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
There are various functions that can be used as a model of weighted GCD. One of the frequently used functions is the weighted power mean (WPM) [GIN58, MIT69, BUL03]:
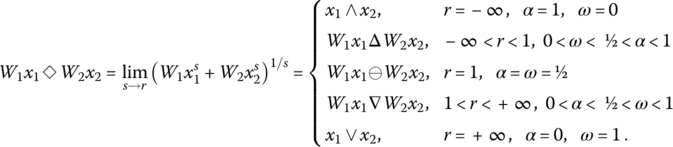
Consequently,

For example, popular special cases of partial conjunction are the weighted geometric mean ![]() (the case
(the case ![]() ) and the weighted harmonic mean
) and the weighted harmonic mean ![]() (the case
(the case ![]() ). A popular special case of partial disjunction is the weighted quadratic mean
). A popular special case of partial disjunction is the weighted quadratic mean ![]() (the case
(the case ![]() ).
).
Presented WPM aggregators are special cases of a family of aggregators based on quasi‐arithmetic means
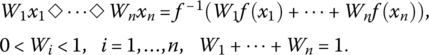
Here ![]() is a continuous and strictly monotonic function. In the case of weighted power means,
is a continuous and strictly monotonic function. In the case of weighted power means, ![]() . In the case of equal weights, the symbolic notation can be simplified:
. In the case of equal weights, the symbolic notation can be simplified: ![]() .
.
Generally, GL is the logic of partial truth and graded logic functions, used for modeling evaluation decisions. The graded logic functions are defined as logic functions where the andness α (the degree of simultaneity), the orness ω (the degree of substitutability), and the relative importance of inputs are elastic, i.e., graded and adjustable. Andness and orness, respectively, denote the conjunction degree and the disjunction degree. The term conjunction is mostly used for the full conjunction, ![]() , n > 1; it corresponds to the maximum andness of an idempotent aggregator, α=1. The term disjunction is mostly used for the full disjunction,
, n > 1; it corresponds to the maximum andness of an idempotent aggregator, α=1. The term disjunction is mostly used for the full disjunction, ![]() ; it corresponds to the maximum orness of an idempotent aggregator, ω =1.
; it corresponds to the maximum orness of an idempotent aggregator, ω =1.
The most frequently used GL functions are the partial conjunction and the partial disjunction. The partial conjunction is any function that is similar to conjunction, and its andness can be interpreted as the degree of similarity. The partial disjunction is any function that is similar to disjunction, and its orness can be interpreted as the degree of similarity. The inputs of partial conjunction and partial disjunction functions are assumed to have different and adjustable degrees of relative importance.
All idempotent logic aggregators are means. The most popular of all parameterized means is the weighted power mean ![]() because it is the parent of the most frequently used arithmetic, geometric, harmonic, and quadratic means. Looking at parameterized means from the GL perspective, we might ask the question, “What are means, and who needs them?” For example, is the weighted power mean a model of statistical averaging or a model of human logic aggregation?
because it is the parent of the most frequently used arithmetic, geometric, harmonic, and quadratic means. Looking at parameterized means from the GL perspective, we might ask the question, “What are means, and who needs them?” For example, is the weighted power mean a model of statistical averaging or a model of human logic aggregation?
The weighted power mean can obviously be used for both statistical averaging and for logic aggregation. However, only a few special cases of this model are widely used in averaging: The harmonic mean ![]() is used for averaging speeds, the geometric mean
is used for averaging speeds, the geometric mean ![]() is used for averaging performance ratios, and the arithmetic mean
is used for averaging performance ratios, and the arithmetic mean ![]() is used for averaging student grades and many other things (but not speeds and performance ratios!). The minimum
is used for averaging student grades and many other things (but not speeds and performance ratios!). The minimum ![]() and the maximum
and the maximum ![]() are legitimate extreme cases but not something that is useful as an average. In addition, in the area of averaging, equal weights are more frequent than unequal weights, and other exponents from the infinite range
are legitimate extreme cases but not something that is useful as an average. In addition, in the area of averaging, equal weights are more frequent than unequal weights, and other exponents from the infinite range ![]() have little practical use, interpretation and significance.
have little practical use, interpretation and significance.
As opposed to averaging, the weighted power mean can frequently be an appropriate model of idempotent human logic aggregation in the whole range from conjunction ![]() to disjunction
to disjunction ![]() and all exponents
and all exponents ![]() have applicability in modeling simultaneity and substitutability, which are pillars of human propositional logic. For selected segments of parameters, weighted power means can be incorporated in various interpolative aggregators and conjunctive aggregators can be defined as a De Morgan’s dual of disjunctive aggregators, and vice versa. In addition, unequal weights are suitable and necessary models of various degrees of importance, and the percept of importance is a cornerstone of semantics of human logic aggregation. So, as our contribution to highly controversial opinions, let us claim that means are more important as logic functions than as statistical averages. From the standpoint of GL, parameterized means are primarily logic functions used as models of idempotent human logic aggregation, and a few special cases of such means are also applicable in statistical averaging.
have applicability in modeling simultaneity and substitutability, which are pillars of human propositional logic. For selected segments of parameters, weighted power means can be incorporated in various interpolative aggregators and conjunctive aggregators can be defined as a De Morgan’s dual of disjunctive aggregators, and vice versa. In addition, unequal weights are suitable and necessary models of various degrees of importance, and the percept of importance is a cornerstone of semantics of human logic aggregation. So, as our contribution to highly controversial opinions, let us claim that means are more important as logic functions than as statistical averages. From the standpoint of GL, parameterized means are primarily logic functions used as models of idempotent human logic aggregation, and a few special cases of such means are also applicable in statistical averaging.
2.1.10 A Summary of Differences between Graded Logic and Bivalent Boolean Logic
The human mind should be a role model whenever we try to develop logic models. All trustworthy logic models (including GL models used in professional evaluation projects) must be compatible with observable properties of human reasoning; that requirement should be self‐evident in all applications. Intention to model the laws of thought is visible in the seminal books of De Morgan and Boole [DEM47, BOO47, BOO54].
Generally, mathematical logic does not have to be applied, and does not have to relate to observable properties of human reasoning. Recent mathematical research in fuzzy logic, and theoretical aggregation models almost never claim intentions to model human reasoning, and do not include experiments with human subjects. A valuable exception is the work of H.‐J. Zimmermann and his coauthors [ZIM79, THO79, ZIM87, ZIM96]. In most cases, including BL, mathematical logic is developed as a formal theory, where axioms are defined without any claim that they reflect some form of observable reality, and without any claim of usability. The goal of building such systems is to develop provably correct mathematical models consistent with their axiomatic roots.
In this section, we summarize the differences between GL and its ancestor BL. The classical logic is based on bivalence, which is the principle that no proposition is both true and false. In other words, every meaningful proposition is either true or false. The complete falsity and the complete truth are the only options for the degree of truth of any proposition; these are the only values that logic variables can take. In addition, the classical logic is based on the law of excluded middle that claims that every proposition is either true or not true. All propositions have the same importance, and the concept of relative importance does not exist in logic models. Logic functions have no adjustable parameters, and the absorption theorem provides a total absorption of the less significant input.
It is easy to note that basic classical logic concepts are a very simplified and incomplete model of clearly visible (both semantic and formal logic) properties of human logic reasoning. So, it is unbelievable that these concepts remained practically unchallenged from the time of Aristotle (i.e., for more than 23 centuries). The first significant challenges came in the twentieth century and culminated in Zadeh’s concept of fuzziness.
GL is a human‐centric generalization of BL. Following are the fundamental concepts of GL (as introduced in [DUJ73b, DUJ74a, DUJ75a, DUJ79a] and expanded in [DUJ05b, DUJ07a, DUJ07c, DUJ12, DUJ15a]) based on observable properties of human reasoning:
- Each value statement is a verbal approximation/interpretation of perceived reality. However, human value statements rarely reflect reality with perfect precision. Much more frequently, human statements reflect the reality only approximately, including imprecision, partial truth, fuzziness, inconsistencies, and errors. In general, value statements are only partially true, and not completely true or completely false.
- The degree of truth is an indicator of similarity between a proposition and the reality. For example, if in reality S is an average student, then the similarity between the statement “S deserves the highest grade” and the reality is around 50%. Partial truth and partial falsity are positive values less than 1.
- The maximum degree of truth is denoted by the numeric value 1 (or 100%), and it corresponds to value statements that are in perfect agreement with reality.
- The minimum degree of truth is denoted by the numeric value 0, and it corresponds to value statements that are a perfect negation of reality (completely opposite to reality).
- Let t be a degree of truth (
 ). The value statement “evaluated object completely satisfies all requirements” that has the degree of truth t is equivalent to the value statement “evaluated system satisfies the fraction t of the total requirements” that has the degree of truth 1.
). The value statement “evaluated object completely satisfies all requirements” that has the degree of truth t is equivalent to the value statement “evaluated system satisfies the fraction t of the total requirements” that has the degree of truth 1. - In the context of evaluation reasoning the aggregation of value statements assumes that each input value statement has a specific degree of relative importance. The relative importance varies from low (close to 0) to high (close to 1).
- Relative importance cannot be 0 (because irrelevant statements are excluded from evaluation) and cannot be 1 (because the ultimate relative importance of a value statement would exclude all other value statements). In other words, contrary to usual mathematical assumption, the relative importance always belongs to the interval ]0, 1[.
- Simultaneity and substitutability are the fundamental logic concepts. Both the simultaneity and the substitutability are partial (incomplete or graded), meaning that decision makers select adjustable degrees of penalizing incomplete simultaneity and incomplete substitutability. In evaluation reasoning, simultaneity and substitutability are opposite and complementary concepts (increasing the degree of simultaneity means decreasing the degree of substitutability and vice versa). Simultaneity and substitutability can be modeled using a single function called graded (or generalized) conjunction/disjunction (GCD).
- Graded simultaneity is modeled using a partial conjunction. The conjunction degree (andness) belongs to the interval [0,1] and the extreme value 1 denotes the full conjunction (the minimum function).
- Graded substitutability is modeled using a partial disjunction. The disjunction degree (orness) belongs to the interval [0,1] and the extreme value 1 denotes the full disjunction (the maximum function).
- In exceptional cases, the simultaneity can be stronger than the full conjunction and the substitutability can be stronger than the full disjunction. Such cases are called hyperconjunction and hyperdisjunction. The andness of hyperconjunction is greater than 1 and the orness of hyperconjunction is less than 0.
- GCD and the standard negation (
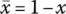 ) are the basic evaluation logic functions.
) are the basic evaluation logic functions.
Our presentation of GL in Part Two follows the above concepts. In that way we hope to keep both the process and the product of evaluation reasoning in agreement with reality. In addition, this approach contributes to the credibility of both the LSP evaluation models and the results of the LSP evaluation, comparison, and selection of complex systems. GL has both similarities and differences with BL. A summary of differences between BL and GL is shown in Table 2.1.5.
Table 2.1.5 Main differences between the classical bivalent Boolean logic and GL.

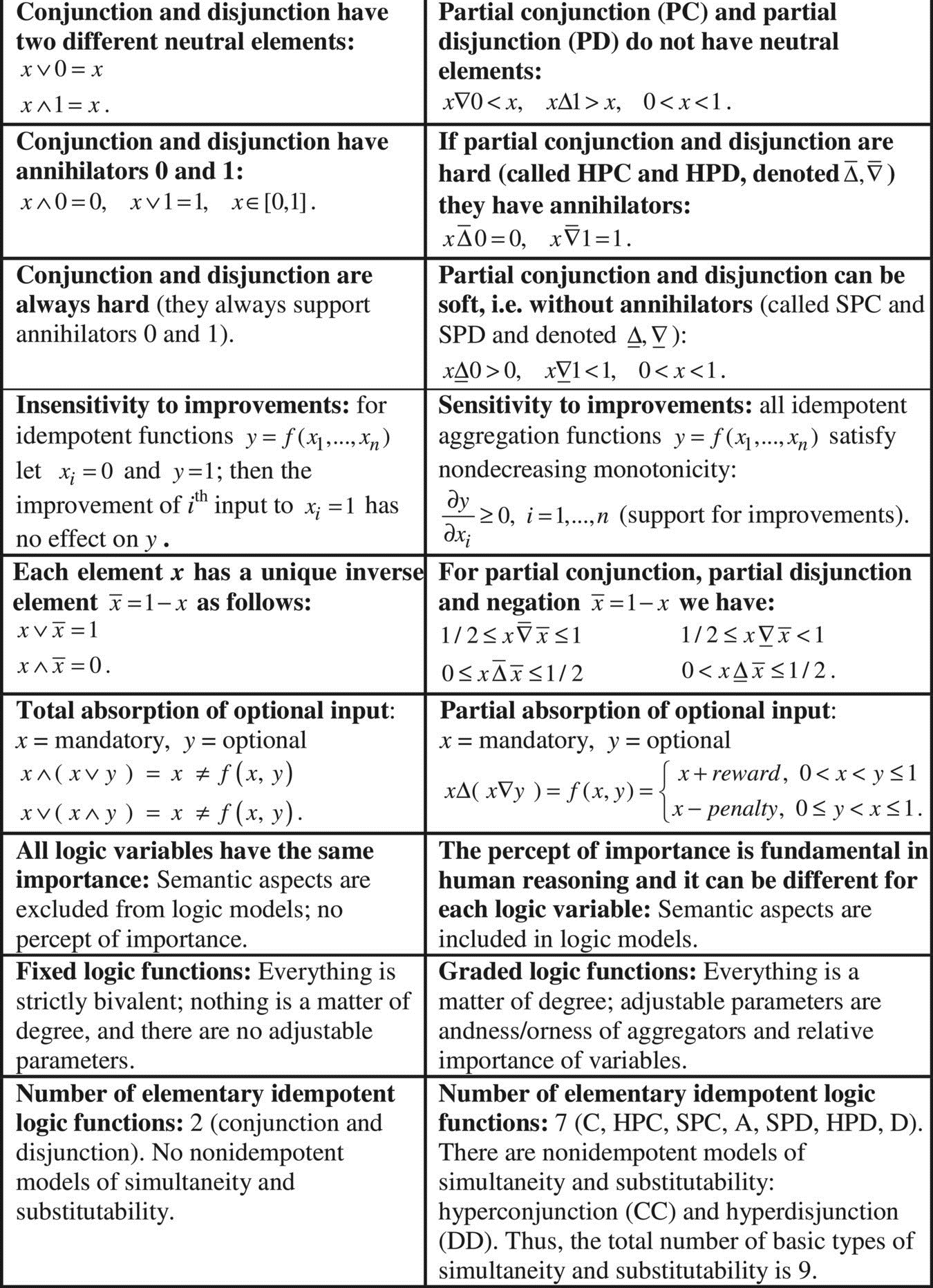
2.1.11 Relationships between Graded Logic, Perceptual Computing, and Fuzzy Logic
There is a significant difference between mathematical models of physical world and mathematical models of human logic reasoning. In the case of the physical world, all variables (e.g., speed, acceleration, length, voltage, current, force, temperature, etc.) have objective and measurable values. Mathematical models that predict the value of a variable under given conditions can always be justified by measuring the difference between the actual value and the value predicted by the mathematical model. In many cases (e.g., Ohm’s law, Kirchhoff’s circuit laws, and Maxwell’s equations in electrical engineering), the models of physical phenomena can be so precise that any difference between the measured and predicted values are normally interpreted as errors of measurement equipment and not as errors of an imprecise model.
As opposed to models of physical world the models of human evaluation reasoning do not deal with objectively measurable values. Obviously, the concept of value does not exist in the physical word, but only in the human mind. All variables that participate in human logic processes are objectively nonmeasurable and inherently imprecise perceptions. Indeed, human perceptions of value, importance, truth, suitability, satisfaction, simultaneity, substitutability, goals, requirements, and so on cannot be measured. All quantifications of their values can only come from a human subject in the form of imprecise verbalization using primarily a natural language. Computational models that process human perceptions are called perceptual computing [MEN10]. Of course, human perceptions are subjective judgments, and according to Jerry M. Mendel, who is the primary contributor to this area, mathematical models for solving perceptual computing problems should be identified as perceptual computers. From that standpoint our goal in this book is to build a perceptual computer for solving evaluation problems (Section 2.2.1), and GL is a mathematical infrastructure necessary for building such a computer.
In human evaluation reasoning, everything is a matter of degree. Human perception of value, and related cognition, reasoning, and communication regularly include imprecision, vagueness and partial truth. While various aspects of the concept of vagueness attract debates in philosophy [SMI08, WIL94, KEE97, DEE10], we are only interested in “quantifiable vagueness,” i.e., in percepts that can be precisely defined and quantitatively modeled as fuzziness or partial truth. Outside mathematics and related theoretical disciplines, it is difficult to find statements that are perfectly crisp, having the bivalent degree of truth. Most of human reasoning, perception, and communication are fuzzy, and truth comes in degrees. A typical statement that is partially true is, “Person P is tall.” This statement might be considered perfectly true for most professional basketball players and perfectly false for most professional jockeys, and for everybody else it would be partially true.
In the propositional calculus with crisp truth values (i.e., in the classical bivalent logic) the statement, “The glass is full,” is true only if the glass is completely full, and it is false immediately when a drop is missing. A more natural (i.e., obviously closer to human reasoning) approach to logic is to consider that each statement has a truth value, or the degree of truth going continuously from the complete falsity (denoted 0) to the complete truth (denoted 1). In other words, “Truth comes in degrees.” For example, the statement “the glass is full” can be perfectly false (if the glass is empty), perfectly true (if the glass is full), and partially true (in all other cases). So, if the reality is that the glass contains 75% of water, we can consider that the statement, “The glass is full,” is 75% true. Consequently, humans use approximate reasoning based on partial truth.
The partial truth in the above example can be interpreted as a quantitative indicator of the difference between a value statement and the objective reality. In some cases, the objective reality is known and measurable, like in the cases of the fullness of the glass of water, or the capacity of computer memory. In such cases, the partial truth is related to the error of an imprecise statement. Much more frequently, however, the partial truth is related to human perception of value, in cases where the objective reality is not measurable. For example, a homebuyer usually creates a list of attributes that affect the perception of the suitability of home, then evaluates (intuitively or quantitatively) all attributes and aggregates the attribute suitability degrees to get an overall suitability degree/score. This procedure is then applied to each competitive home. The resulting overall suitability score is an approximation of the degree of truth of the value statement, “The evaluated home completely satisfies all homebuyer’s requirements.” The value statement is partially true because of those requirements that are incompletely satisfied or not satisfied.
The objective reality of the values of competitive homes might be established if the homebuyer could buy all competitive homes, live in all of them at the same time, and eventually find the real truth about their suitability. This is not possible, and the human percept of the overall suitability used to select and buy a home is just an estimate (or a prediction) of the inherently unknown reality.
Once we accept partial truth, it is less obvious but equally natural that we also accept the partial conjunction and partial disjunction to express various degrees of simultaneity and substitutability, and partial absorption to express elastic aggregation of mandatory and optional, or sufficient and optional inputs. In addition, each input has its role and adjustable degree of importance, which is proportional to the level of supporting attainment of stakeholder goals and requirements.
Reasoning with elastic concepts that are a matter of degree was always present in human logic. Computing with such graded values belongs to the area of soft computing, and it can be contrasted to traditional hard computing with crisp values. For our purposes, soft computing can be simply defined as computing with variables that are a matter of degree (see also [ZAD94]). A variable that is a matter of degree can regularly be interpreted as the degree of membership in an appropriate fuzzy set. Such variables can also be interpreted as degrees of truth of appropriate statements [DUJ17]. Consequently, GL provides soft computing results that have dual interpretation: as degrees of truth or as degrees of fuzzy membership. That creates a relationship between GL and fuzzy logic.
In soft computing, everything is graded and adjustable (i.e., a matter of degree: conjunction, disjunction, absorption, relative importance, etc.). A characteristic question, “Are you satisfied with the object X that you currently evaluate and intend to use?” does not have only two answers: yes or no. These are only rare extreme cases, or imprecise approximations, where “yes” (numerically coded as 1) denotes an absolutely complete satisfaction and “no” (numerically coded as 0) denotes an absolutely complete dissatisfaction. What is much more frequent in real life is the partial satisfaction, a value that is between yes and no, or numerically between 0 and 1. In fact, “true” and “false” are extreme special cases of partial truth. Similarly, black and white are extreme special cases of gray.
Soft computing properties of GL models for evaluation of complex systems can have a large number of inputs and parameters. Most of them are defined as a matter of degree, as illustrated in Fig. 2.1.18 where all graded variables and parameters are based on human percepts. All input suitability degrees and the overall suitability are soft computing variables, (i.e., a matter of degree). Parameters of evaluation models are also soft: the relative importance is graded, and so are degrees of simultaneity and substitutability. Compound functions, such as the partial absorption also have soft parameters (degrees of penalty and reward, described in Chapter 2.6) that are used to control the degrees of absorption of optional inputs in mandatory/optional and sufficient/optional aggregators. Using GCD as a fundamental function, GL is established in a way that is both consistent with classical (bivalent or continuous) logic and represents its natural extension/generalization.

Figure 2.1.18 In soft computing evaluation models, everything is a matter of degree.
In the majority of evaluation problems, the fuzzy interpretation and the logic interpretation of evaluation results are equivalent. Indeed, we can interpret elementary attribute criteria (Figs. 1.2.2 to 1.2.7) as membership functions of individual attributes, i.e., the degrees of membership in fuzzy sets of objects that completely satisfy given attribute requirements. Furthermore, we can interpret the overall suitability as the compound degree of membership in the fuzzy set of objects that completely satisfy all stakeholders’ requirements.
On the other hand, the same concepts can be interpreted as logic concepts. Each attribute suitability score is a degree of truth of the statement claiming that a specific input completely satisfies user needs. The overall suitability is the degree of truth of the statement claiming that an evaluated system as a whole completely satisfies all stakeholders’ requirements. So, in the area of evaluation, the fuzzy and logic interpretations are equally acceptable, and all GL results can also be interpreted in the context of fuzzy sets and fuzzy logic [DUJ17].
Fuzziness and partial truth belong to the same family of graded concepts, which are the central concepts of soft computing. However, the scope of fuzzy logic (FL) is much wider than the scope of GL, as we discussed in Section 2.1.5. FL penetrates areas such as linguistics and automatic control, while GL focuses on a narrow field of evaluation decision models. Both FL and GL are derived from observable properties of human reasoning, but in different areas. The narrow focus of GL (infinitely valued propositional calculus) permits us to identify and rather correctly model a spectrum of specific properties of evaluation reasoning. From the very beginning in the early 1970s, GL was a soft logic based on GCD and means, and used primarily for evaluation. As opposed to that, both the propositional and the predicate fuzzy logics mostly belong to t‐norm fuzzy logics, where the emphasis is not on evaluation problems. FL evaluation models are not frequent and seem to be dominated by fuzzy weighted averages [KOS93, MEN10] without focus on specific needs of evaluation logic reasoning.
GL is a generalization of traditional Boolean logic based on concepts of graded conjunction, and graded disjunction. FL is based on the graded concept of fuzzy set, which is a generalization of the concept of traditional crisp set. GL provides aggregation models of finer granularity then FL, and it can be interpreted as a refinement of a specific segment of FL (Fig. 2.1.6). Readers interested in fuzzy sets, fuzzy logic (in a wide sense), and nonidempotent aggregation based of t‐norms and conorms should consult the rich literature in fuzzy sets and fuzzy logic, primarily [ZAD65, ZAD73, ZAD74, ZAD76, ZAD89, ZAD94, ZAD96, ZIM84, ZIM87, ZIM96, KLI95, KOS93, FOD94, CAR02, LEE05, TOR07, MEN01, MEN10, BEL07, GRA09, ROS10].
2.1.12 A Brief History of Graded Logic
Graded logic, as it is presented in this book (as a model of human logic aggregation and criteria used in evaluation reasoning) was born in the early 1970s in the School of Electrical Engineering at the University of Belgrade (Fig. 2.1.19). This section shows the chronology of early developments of GL from author’s personal point of view. In other words, I would like to present and comment on GL ideas not as an observer but as a developer. The goal is to show not only when GL ideas were introduced and initial results published, but also why and where that methodology for modeling the logic of evaluation reasoning became necessary.

Figure 2.1.19 School of Electrical Engineering at the University of Belgrade.
(reproduced by permission of PC Press, Belgrade, author Zoran Životić)
The reason for developing GL was not theoretical. My motivation was to solve decision engineering problems related to the evaluation, comparison, selection, and optimization of mainframe computer systems, where decisions in the late 1960s and the early 1970s were based on approximately 80–120 input attributes. That number of inputs and logic relationships among them clearly showed the inadequacy of both discriminant analysis [DUJ69] and simple additive weighted scoring [MIL66, MIL70, SCH69, SCH70, DUJ72a, DUJ72b] (see details in Chapter 1.3). My first professional mainframe computer evaluation and selection project in 1968–1969 (for a major Belgrade bank) used discriminant analysis (I‐distance, [IVA63, DUJ69]), and the second in 1970–1971 (for a utility company in Zagreb) used the additive weighted scoring. In both cases, there was a clear need for models of graded simultaneity and substitutability, and for making some requirements necessary and some optional, to use sufficient and desired inputs, and above all, to make mathematical models consistent with the intuitive reasoning of stakeholders. With existing (additive) methods, that was completely impossible, and I started to develop both the necessary mathematical infrastructure and the necessary software support, based on the theory of means [GIN58, MIT69]. Thus, my motivation for the development of GL, as well as the selection of necessary GL properties, came directly from the demands of decision engineering practice.
The interest in partial truth, multivalued logics, and reasoning with vague concepts emerged in logic in works of Bernard Russell, Jan Lukasiewicz, and Max Black in the early twentieth century [KOS93]. However, these ideas did not smoothly evolve in soft computing and engineering applications. The development of soft computing concepts originated in engineering as a response to practical needs for problem solving in decision engineering, computer science, and control engineering. The starting point of all engineering applications of soft computing concepts is 1965, when Lotfi Zadeh at the University of California Berkeley introduced fuzzy sets [ZAD65], the first successful step toward wide use of graded concepts in science, computing, and engineering. Important concepts of fuzzy logic (FL), namely linguistic variables and the calculus of fuzzy if‐then‐else rules, were introduced by Zadeh in 1973 [ZAD73] and 1974 [ZAD74].
GL was also introduced in 1973 [DUJ73b]. GL was developed independently from FL between 1970 and 1973 at the University of Belgrade and the Institute “M. Pupin,” and initially used for the development of comprehensive models for evaluation of analog, hybrid, and digital computers developed by the Institute. Practical evaluation problems generated the need for graded logic aggregators that can be used to model simultaneity and substitutability. The “aha! moment” occurred when I realized that logic functions are not only conjunction and disjunction but also everything that is between them; so, parameterized means can be naturally interpreted as logic functions and the continuous transition from conjunction to disjunction must be controlled by appropriate parameters. To achieve that goal, in 1973 I introduced concepts of the conjunction degree (andness) and the complementary disjunction degree (orness) [DUJ73b] and started to use new graded logic functions: partial conjunction, partial disjunction, and partial absorption. I found that partial conjunction and partial disjunction are appropriate logic aggregators, good models of adjustable simultaneity and substitutability, and above all, consistent with observable human evaluation reasoning. Stakeholders (in mainframe computer selection projects) accepted GL as a model of their evaluation reasoning, and I was able to involve them into selecting andness/orness and weights in GL criteria, and to formally confirm that the developed criteria correctly reflect their goals and requirements. The ease of accepting GL models by practitioners participating in evaluation projects showed that they recognize these logic models from their intuitive evaluation reasoning experience more than from my mathematical explanation. That was a decisive signal that the development of GL moves in the right direction. Early developments of GL and papers published in 1973, 1974, and 1975 were strictly located in the framework of graded logic and interpreted GL as a generalization of the classical Boolean logic. Of course, the need for idempotency naturally connected GL models and the theory of means.
My work in early 1970s benefited very much from the research on means and their inequalities performed by my math professors, and later friendly colleagues, D. S. Mitrinović and P. M. Vasić [MIT69, MIT70], a few doors from my office in the School of Electrical Engineering at the University of Belgrade (some of the impressive work of D. S. Mitrinović and P. M. Vasić in the areas of means and related inequalities is presented after their death in [BUL03]). So, I was extremely lucky to be directly exposed to the work of that world‐class group of mathematicians, and also to be stimulated (despite being an electronic engineer) to publish my work in their math journal and get valuable feedback. Following is a short survey of the initial GL publications.
The concepts of logic functions that provide a controlled continuous transition from conjunction to disjunction (graded conjunction/disjunction), as well as the adjustable andness/orness (both the local andness/orness and the mean local andness/orness), and corresponding logic aggregators, were introduced in [DUJ73b]. The LSP method, initially called Mixed Averaging by Levels (MAL) and renamed to LSP in 1987, is based on graded logic and soft computing aggregators controlled (initially) by the mean local andness. It was introduced in 1973 [DUJ73c] and was used for evaluation, comparison, and selection of analog, digital, and hybrid computer systems. The concept of global andness/orness, the sensitivity analysis of aggregation structures and sensitivity indicators, the system of 17 andness/orness levels of graded conjunction/disjunction, and the concept of asymmetric simultaneity and asymmetric substitutability aggregators (partial absorption function, with tables for computing parameters of the function) were introduced in 1974 [DUJ74b] and were applied to solving problems of computer evaluation [DUJ74d, DUJ75c] and optimization [DUJ74c].
All fundamental GL developments and corresponding applications in 1973 and 1974 were sponsored by the Laboratory for Computer Engineering of the Mihajlo Pupin Institute in Belgrade. The Institute was a manufacturer of analog, digital, and hybrid computers and evaluation models were used to verify the suitability of these products and for their comparison with other competitive products. The necessary software infrastructure for professional system evaluation consisted of a specialized System Evaluation Language SEL [DUJ76a] and a specialized criterion database support system [DUJ76b]. Most initial results were published in Serbo‐Croatian, and therefore their use in decision engineering practice remained limited to former Yugoslavia.
Early papers written in English that introduced GL and the corresponding evaluation methodology include [DUJ73a, DUJ74a, SLA74, DUJ75a, DUJ75b, DUJ76d, DUJ77a, DUJ77b, DUJ79a]. The global andness/orness (initially called the conjunction degree and the disjunction degree) was first presented in English in [DUJ74a]. It is interesting to note that the global andness and orness in [DUJ74a] were defined for the following mean:

Of course, this is the Bajraktarević mean, which includes as special cases the quasi‐arithmetic means, exponential means, Gini means, counter‐harmonic means, and weighted power means. So, the authors who claim that in [DUJ74a] the global andness and orness were introduced for the special case of power means are incorrect.
The term partial absorption function and the properties of asymmetric aggregators were first presented in English in [DUJ75a]; the first English paper fully devoted to mathematical details of the partial absorption function was [DUJ79a]. Except for [DUJ76d], all these papers were published in former Yugoslavia, and remained little known before [FOD94].
Starting in 1973, I was responsible for a sequence of more than 25 evaluation decision projects based on GL and the LSP method, for major governmental and corporate customers in former Yugoslavia. This industrial practice was the primary generator of theoretical advances. For example, the partial absorption function [DUJ74b] and asymmetric logic relationships (Chapter 2.6) were introduced in 1974 to satisfy the needs of the computer selection criterion for the Naftagas oil industry in Novi Sad. All logic models presented in this book originated in decision engineering practice, where the initial efforts were focused on evaluation and selection of mainframe digital computers [DUJ73c, DUJ74e, DUJ75c, DUJ76e, DUJ77b, DUJ78a, DUJ78b, DUJ79b, DUJ80], as well as analog computers [DUJ74d] and hybrid computers [DUJ76c, DUJ76d]. The first optimization method based on GL criteria was developed for optimizing computing units of analog and hybrid computers in [DUJ74c]. All theoretical GL results were first tested and used in industrial applications, and then published.
The first logic evaluation models of software systems, based on GL and the LSP method, were developed in 1979–1982, during my employment as a computer science faculty member at the University of Florida, Gainesville. The LSP method was used for a data management systems evaluation project for NIST in Washington, DC [DUJ82, SU82]. This work was later presented in a comprehensive paper [SU87].
Most fundamental concepts of GL and the LSP method were developed in the first half of the 1970s. In the 1980s, the LSP method was frequently used, and in 1987, it was presented as a rather complete and standardized industrial decision methodology in [DUJ87] and [SU87] under its current name, Logic Scoring of Preference. So, 1987 is the year that marks the end of early years (1973–1987) of GL and its applications.
Since 1987 there have been many new developments and publications related to GL and LSP (e.g., the first book chapter, [DUJ91]). These results are the basis of this book. In particular, in the 1990s and later, the GL applications expanded in a variety of new areas, such as advanced software systems, real estate, medical applications, ecology, geography, and others (see Part Four).
The logic concepts of andness, orness, and aggregators that realize a continuous transition from AND to OR, that the author introduced in 1973, are very natural and visible in human reasoning. So, it is not surprising that other people later independently created the same or similar ideas.
As a part of these early historic notes, let us mention that the graded logic functions, imprecision, partial truth, fuzziness, and similar soft computing concepts are easily visible in human reasoning, but their quantification and formalization found resistance in some academic circles, and the pioneers had to pay the price for taking “the road less traveled by.” A plausible explanation for this is the difference between modeling physical processes that are objectively measurable and modeling human perceptions that are not objectively measurable. Traditional scientific education focuses on modeling measurable physical phenomena. People trained in modeling measurable phenomena expect that all models can always be verified only by analyzing the difference between the model results and the measured reality. In early years, when such people first encountered soft computing models of human perceptions (which are quantifiable but not precisely objectively measurable), they would discover the lack of traditional objective measurable justification, and interpret it as the undesirable “subjectivity.” Consequently, they would sometimes aggressively distrust not only the quality of the models but also the very reason for their existence.