The Kaplan-Meier Method
In biomedicine, the Kaplan-Meier (KM) estimator is the most widely used method for estimating survivor functions. Also known as the product-limit estimator, this method had been in use for many years prior to 1958 when Kaplan and Meier showed that it was, in fact, the nonparametric maximum likelihood estimator. This gave the method a solid theoretical justification.
When there are no censored data, the KM estimator is simple and intuitive. Recall from Chapter 2, “Basic Concepts of Survival Analysis,” in the section Describing Survival Distributions, that the survivor function S(t) is the probability that an event time is greater than t, where t can be any nonnegative number. When there is no censoring, the KM estimator Ŝ(t) is just the sample proportion of observations with event times greater than t. Thus, if 75 percent of the observations have event times greater than 5, we have Ŝ(5) =.75.
The situation is also quite simple in the case of single right censoring, that is, when all the censored cases are censored at the same time c and all the observed event times are less than c. In that case, for all t ≤ c, Ŝ(t) is still the sample proportion of observations with event times greater than t. For t > c, Ŝ(t) is undefined.
Things get more complicated when some censoring times are smaller than some event times. In that instance, the observed proportion of cases with event times greater than t can be biased downward because cases that are censored before t may, in fact, have “died” before t without our knowledge. The solution is as follows. Suppose there are k distinct event times, t1 <t2 < ... <tk. At each time tj, there are nj individuals who are said to be at risk of an event. At risk means they have not experienced an event nor have they been censored prior to time tj. If any cases are censored at exactly tj, they are also considered to be at risk at tj. Let dj be the number of individuals who die at time tj. The KM estimator is then defined as
Equation 3.1
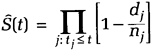
for t1 ≤ t ≤ tk. In words, this formula says that for a given time t, take all the event times that are less than or equal to t. For each of those event times, compute the quantity in brackets, which can be interpreted as the conditional probability of surviving to time tj+1, given that one has survived to time tj. Then multiply all of these conditional probabilities together. For t less than t1, (the smallest event time), Ŝ(t) is defined to be 1.0. For t greater than tk, the largest observed event time, the definition of Ŝ(t) depends on the configuration of the censored observations. When there are no censored times greater than tk, Ŝ(t) is set to 0 for t > tk. When there are censored times greater than tk, Ŝ(t) is undefined for t greater than the largest censoring time. For an explanation of the rationale for equation (3.1), see The Life-Table Method later in this chapter.
Here’s an example of how to get the KM estimator using PROC LIFETEST with the myelomatosis data shown in Output 2.1:
data myel; input dur status treat renal; datalines; 8 1 1 1 180 1 2 0 632 1 2 0 852 0 1 0 52 1 1 1 2240 0 2 0 220 1 1 0 63 1 1 1 195 1 2 0 76 1 2 0 70 1 2 0 8 1 1 0 13 1 2 1 1990 0 2 0 1976 0 1 0 18 1 2 1 700 1 2 0 1296 0 1 0 1460 0 1 0 210 1 2 0 63 1 1 1 1328 0 1 0 1296 1 2 0 365 0 1 0 23 1 2 1 run; proc lifetest data=myel; time dur*status(0); run;
The KM estimator is the default, so you do not need to request it. To be explicit, you can put METHOD=KM in the PROC LIFETEST statement. The syntax DUR*STATUS(0) is common to PROC LIFETEST, PROC LIFEREG, and PROC PHREG. The first variable is the time of the event or censoring; the second variable contains information on whether or not the observation was censored; and the number (or numbers) in parentheses are values of the second variable that correspond to censored observations. These statements produce the results shown in Output 3.1.
Output 3.1. Kaplan-Meier Estimates for Myelomatosis Data
Product-Limit Survival Estimates
Survival
Standard Number Number
DUR Survival Failure Error Failed Left
0.00 1.0000 0 0 0 25
8.00 . . . 1 24
8.00 0.9200 0.0800 0.0543 2 23
13.00 0.8800 0.1200 0.0650 3 22
18.00 0.8400 0.1600 0.0733 4 21
23.00 0.8000 0.2000 0.0800 5 20
52.00 0.7600 0.2400 0.0854 6 19
63.00 . . . 7 18
63.00 0.6800 0.3200 0.0933 8 17
70.00 0.6400 0.3600 0.0960 9 16
76.00 0.6000 0.4000 0.0980 10 15
180.00 0.5600 0.4400 0.0993 11 14
195.00 0.5200 0.4800 0.0999 12 13
210.00 0.4800 0.5200 0.0999 13 12
220.00 0.4400 0.5600 0.0993 14 11
365.00* . . . 14 10
632.00 0.3960 0.6040 0.0986 15 9
700.00 0.3520 0.6480 0.0970 16 8
852.00* . . . 16 7
1296.00 0.3017 0.6983 0.0953 17 6
1296.00* . . . 17 5
1328.00* . . . 17 4
1460.00* . . . 17 3
1976.00* . . . 17 2
1990.00* . . . 17 1
2240.00* . . . 17 0
* Censored Observation
Summary Statistics for Time Variable DUR
Point 95% Confidence Interval
Quantile Estimate [Lower, Upper)
75% . 220.00 .
50% 210.00 63.00 1296.00
25% 63.00 18.00 195.00
Mean 562.76 Standard Error 117.32
NOTE: The last observation was censored so the estimate of the mean
is biased.
Summary of the Number of Censored and Uncensored Values
Total Failed Censored %Censored
25 17 8 32.0000 |
Each line of numbers in Output 3.1 corresponds to one of the 25 cases, arranged in ascending order (except for the first line, which is for time 0). Censored observations are starred. The crucial column is the second—labeled Survival—which gives the KM estimates. At 180 days, for example, the KM estimate is .56. We say, then, that the estimated probability that a patient will survive for 180 days or more is .56. When there are tied values (two or more cases with the same event time), as we have at 8 days and 63 days, the KM estimate is reported only for the last of the tied cases. No KM estimates are reported for the censored times.
In fact, however, the KM estimator is defined for any time between 0 and the largest event or censoring time. It’s just that it only changes at an observed event time. Thus, the estimated survival probability for any time from 70 days up to (but not including) 76 days is .64. The one-year (365 days) survival probability is .44, the same as it was at 220 days. After 2240 days (the largest censoring time), the KM estimate is undefined.
The third column, labeled Failure, is just 1 minus the KM estimate, which is the estimated probability of a death prior to the specified time. The fourth column, labeled Survival Standard Error, is an estimate of the standard error of the KM estimate, obtained by the well-known Greenwood’s formula (Collett 1994, p. 23). You can use this estimated standard error to construct confidence intervals around the KM estimates.
The fifth column, labeled Number Failed, is just the cumulative number of cases that experienced events prior to and including each point in time. The column labeled Number Left is the number of cases that have neither experienced events nor been censored prior to each point in time. This is the size of the risk set for each time point. Below the main table, you find the estimated 75th, 50th, and 25th percentiles (labeled Quantiles). If these were not given, you could easily determine them from the Failure column. Thus, the 25th percentile (63 in this case) is the smallest event time such that the probability of dying earlier is greater than .25. No value is reported for the 75th percentile because the KM estimator for these data never reaches a failure probability greater than .70.
Of greatest interest is the 50th percentile, which is, of course, the median death time. Here, the median is 210 days, with a 95-percent confidence interval of 63 to 1296. An estimated mean time of death is also reported. As noted on the output, the mean is biased downward when there are censoring times greater than the largest event time. Even when this is not the case, the upper tail of the distribution will be poorly estimated when a substantial number of the cases are censored, and this can greatly affect estimates of the mean. Consequently, the median is usually a much preferred measure of central tendency for censored survival data.
You can get a plot of the estimated survivor function by requesting it in the PROC LIFETEST statement:
proc lifetest data=myel plots=(s) graphics; time dur*status(0); symbol1 v=none; run;
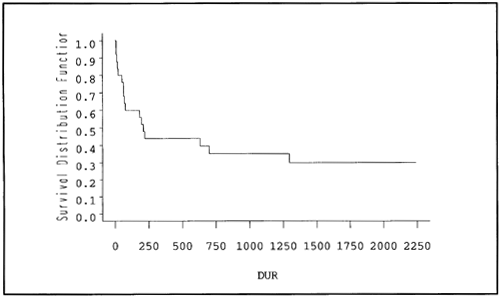
The GRAPHICS option requests high-resolution graphics rather than character-based graphics. The SYMBOL1 statement suppresses the symbols ordinarily placed at the data points on the graph. (The data points are apparent from the steps on the graph, and the default symbol (+) just adds clutter). Output 3.2 shows the resulting graph. At each death time, the curve steps down to a lower value. It stops at the highest censoring time (2240).
Output 3.2. Plot of the Survivor Function for Myelomatosis Data
To get confidence intervals around the survival probabilities, you can calculate them by hand using the standard errors reported in the table. However, it’s much easier to write the intervals to an output data set. You can do this using the OUTSURV= option in the PROC LIFETEST statement:
proc lifetest data=myel outsurv=a; time dur*status(0); run; proc print data=a; run;
Output 3.3 shows the printed data set. The two right-hand columns give the upper and lower limits for a 95-percent confidence interval around each survival probability. (To get 90-percent intervals, use ALPHA=.10 as an option in the PROC LIFETEST statement.)
Output 3.3. Data Set Produced by the OUTSURV= Option
OBS DUR _CENSOR_ SURVIVAL SDF_LCL SDF_UCL 1 0 0 1.00000 1.00000 1.00000 2 8 0 0.92000 0.81366 1.00000 3 13 0 0.88000 0.75262 1.00000 4 18 0 0.84000 0.69629 0.98371 5 23 0 0.80000 0.64320 0.95680 6 52 0 0.76000 0.59259 0.92741 7 63 0 0.68000 0.49715 0.86285 8 70 0 0.64000 0.45184 0.82816 9 76 0 0.60000 0.40796 0.79204 10 180 0 0.56000 0.36542 0.75458 11 195 0 0.52000 0.32416 0.71584 12 210 0 0.48000 0.28416 0.67584 13 220 0 0.44000 0.24542 0.63458 14 365 1 0.44000 . . 15 632 0 0.39600 0.20271 0.58929 16 700 0 0.35200 0.16192 0.54208 17 852 1 0.35200 . . 18 1296 0 0.30171 0.11498 0.48845 19 1296 1 0.30171 . . 20 1328 1 0.30171 . . 21 1460 1 0.30171 . . 22 1976 1 0.30171 . . 23 1990 1 0.30171 . . 24 2240 1 0.30171 . . |
It is important to realize that each of these confidence intervals applies only to a particular point in time. You may be tempted to interpret the entire series of confidence intervals as a confidence region such that you have 95-percent confidence that the whole survivor function falls within that region. This is misleading, however, because the probability that a single interval covers the true value may be much higher than the probability that all such intervals contain their respective true values. Harris and Albert (1991) describe methods for constructing confidence regions for the entire survivor function, and their book includes a disk containing SAS macros for those methods.
Another problem with confidence intervals is that the calculated intervals may extend outside the bounds of 0 or 1. The usual solution is to truncate the interval at 1 or 0, as with the upper confidence limits for lines 2 and 3 in Output 3.3. A preferable approach described by Collett (1994) is to find confidence intervals for the transformation log(–logŜ(t)) and then transform the limits back to the original metric.
