Appendix C

The Weak Law of Large Numbers

Let p be the mathematical probability of success and k/N be the actual success ratio. The question is how close is k/N to p? In modern notation, where ε represents any small positive number chosen,

converges to 1, as N grows large.

Using Chebyshev’s inequality and some simple algebra, we may prove the theorem. If we perform a binomial experiment N times, then (by definition of the probability) the expected ratio of successes is k/N, and the standard deviation of the ratio of successes (again by definition) is

where q = 1 – p. Now let

where L is some number we will choose later. We have

and so

By Chebyshev’s inequality, the probability is smaller than (or equal to) L²/N that the ratio of success, k/N, differs from p by

or more. Expressed more succinctly, this says:

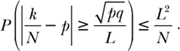
So if L²/N and

are both small, then our last sentence would translate as: the likelihood is small that the ratio of successes differs by more than a very small amount. Now here is the dazzling trick. Remember that we can choose L to be any number we wish. Choose L so that

is small. (Since p and q are already fixed, we can do that.) Then choose N large enough so that L²/N is as small as we need. This proves the weak law, for it says that for any ε and δ there is a large N, for which

holds, and that is precisely the weak law of large numbers.