Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

Chapter 7. Power Collections

Power Collections Plug-n-Play

Power Collections came into existence during 2005, followed by the introduction of the .NET Framework 2.0. Wintellect is the company that created Power Collections. At the time of writing, with the introduction of LINQ and some data structures in .NET 4.0, Power Collections look dated. However, there are some data structures, such as OrderedBag and Deque , and some great algorithms in Power Collections that become all the more easy to use with LINQ. To this day, this collection is being used.

In this chapter, we will discuss some of the algorithms available in this API that are difficult to reproduce with standard LINQ operators. In the latter half of this chapter, we will see how some of the algorithms that we had skipped can be reproduced through LINQ operators. It does make a lot of sense to make these algorithms as LINQ Standard Query Operators (LSQO)so that they can be used on all IEnumerable<T> implementations. Wintellect has shared the code as an open source project on http://powercollections.codeplex.com/.

Setting up the environment

First we need to get the binary files for the API. Go to http://powercollections.codeplex.com/ and download the API ZIP file. The DLL will be available under the PowerCollectionsBinaries folder after you unzip the file.

Now that we have the API, let's put it with LINQPad 4 (that we had used in Chapter 5, Observable Collections).

Open LINQPad 4.
Press F4. You will see the following screen:
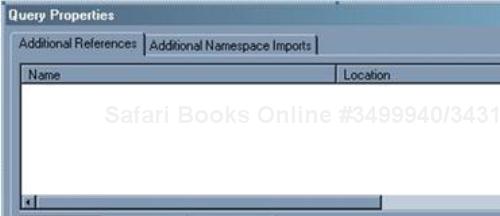
Click on Browse to locate the following binary file:
Once you add the file, it will be displayed in the list of Additional References, as follows:
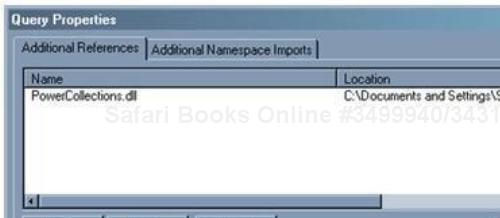
Click on OK to complete this process.
Click on the next tab, Additional Namespace Imports, and write Wintellect.PowerCollections in the textbox: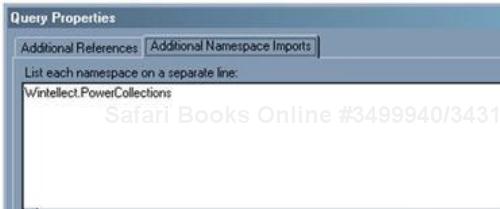

Every time you open LINQPad, you have to repeat step 4 and step 5 explained earlier. So, I recommend not to close your LINQPad instance when you are practicing.

Just change the Language drop-down value to C# Statement in the LINQPad editor header. We are now ready to play with all the power algorithms (if you will) in LINQPad.

Let's start exploring algorithms that I think are interesting and which Power Collections has to offer.

BinarySearch()

This query operator allows the user to search for an item from an IList<T> instance using the binary search algorithm. As you know, a prerequisite for a binary search is that the array must be sorted. The BinarySearch() method takes care of the sorting internally, so you don't have to actually sort the list.

There are three overloads of this generic method:

This overload takes a type of list and item to search for, and an index where the index of the sought item will be stored.

Time for action – finding a name from a list of names

Problem 1: Say we have a list of names and we want to find the index of a given name:

Copy the following code in LINQPad:

int index;
string[] names = {"Sam", "Pamela", "Dave", "Pascal", "Erik"};

Algorithms.BinarySearch(names, "Dave", out index);
index.Dump(""Dave" is found at");

Algorithms.BinarySearch(names, "Sam", out index);
index.Dump(""Sam" is found at");

Run the code snippet. Make sure C# Statements is selected in the Language drop-down, otherwise it will not work. Once successfully run, you should expect the following output:

What just happened?

The BinarySearch() method first sorts the provided list of elements. In this case, it sorts the string array in alphabetical order. So after sorting, the list would be as follows:

"Dave", "Erik", "Pamela", "Pascal", "Sam"

Now, a binary search algorithm is applied on this string array to find the index of a given element from the array. So, you see the index returned by the binary search is the index of the sought element in the sorted collection. Thus, when we searched for Dave, the index returned was 0 and when we searched for Sam, the index returned was 5, which should ideally be 4. So, when you use BinarySearch() to find the index, always check whether the index is within bounds before dereferencing the index.

CartesianProduct()

This generic method generates the Cartesian product of two given lists. The lists can have a different number of items in them. Let's see how this method can help in a real-life situation.

Time for action – generating names of all the 52 playing cards

Follow the given steps:

Copy the following code snippet as a query in LINQPad:

List<Pair<string, string>> deck = 

Algorithms.CartesianProduct
(
  new List<string>() {"Ace", "2", "3", "4", "5", "6", "7", "8", "9", "10", "Jack", "Queen", "King"},

  new List<string>() { "Spade", "Heart", "Diamond", "Club" }
)

.ToList();

List<string> cardNames = deck
  .Select(c => c.First + " of " + c.Second)
  .ToList ();

cardNames.Dump("Names of all the Playing Cards");

Run the query. You will get the list of all the 52 cards. A few of them are listed in the following screenshot:

What just happened?

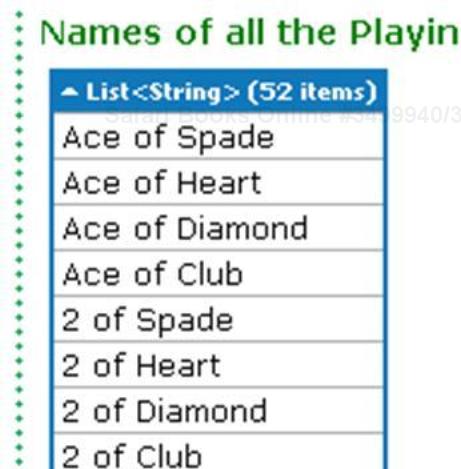
The CartesianProduct() method returns a list of Pair<string, string>. In this case, c.First refers to the first element of the pair and c.Second refers to the second element of the pair. Thus, the part of the code, c.First + " of " + c.Second, generates the output Ace of Heart. Using the Select()LINQ operator, we are converting each Pair<string, string> object in the final result.

RandomShuffle()

Now that we have created a deck of cards, it would be great to shuffle them. The RandomShuffle() method does that and returns a randomly shuffled list. The in-place version, RandomShuffleInPlace(), modifies the original list and stores the shuffled list.

Time for action – randomly shuffling the deck

Follow the given steps:

Copy the following code snippet as a query in LINQPad:

//Using the deck of cards we created earlier.
List<string> cardNames = deck.Select(c => c.First + " of " + c.Second)
  .ToList ();

cardNames.Take(13).Dump("Before Shuffling first 13 cards");
List<string> shuffledDeck = Algorithms.RandomShuffle(cardNames).ToList();

shuffledDeck.Take(13).Dump("After Shuffling first 13 cards");

Run the query. You will get the following output. The actual names of the card that appear may differ:

What just happened?

The RandomShuffle() method randomly shuffles the collections passed as an argument. This method internally uses a random number generator. However, there is another overloaded version of this method where you can specify a random number generator. However, it is not recommended to use any hardcoded random number generator as it will always produce the same result.

For example, the following code snippet:

Algorithms.RandomShuffle(cardNames, new Random(1)).ToList();

will always return the same list. However, you can pass new Random(), which is essentially the same as omitting it as an argument to the algorithm.

NCopiesOf()

Sometimes we want to create multiple copies of the same object or value. Suppose you have a class, creating an object of which is computationally very expensive.

The NCopiesOf() generic method comes in very handy when creating such a list.

Time for action – creating random numbers of any given length

Follow the given steps:

Copy the following code snippet as a query in LINQPad:

StringBuilder bigRandomNumber = new StringBuilder();
List<string> allRandomNumbers = new List<string>();

for (int i = 0; i < 5; i++)
{
  bigRandomNumber = new StringBuilder();
  Algorithms.NCopiesOf(10, new Random())
            .Select(c => c.Next(100).ToString("000"))
            .ToList()
            .ForEach
  (
    c => bigRandomNumber.Append(c.ToString())
  );

  allRandomNumbers.Add(bigRandomNumber.ToString());
  System.Threading.Thread.Sleep(20);
}

allRandomNumbers.Dump("5 Random Numbers");

Run the query. You will get an output similar to the following screenshot:

What just happened?

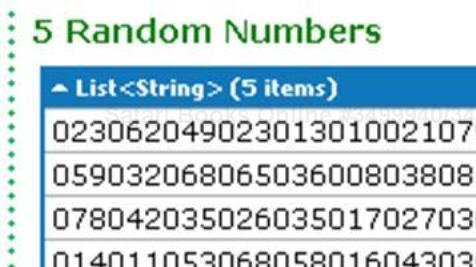
If you notice carefully, you will see that all of these numbers are of 30 digits. That's because they are a concatenation of 10 three digit random numbers generated from 10 copies of the Random class.

The following code:

Algorithms.NCopiesOf(10, new Random())

creates 10 Random objects. LINQ Standard Query Operator, Select(), is then used to format the numbers as three digit numbers. So, if the random number generated is 14, the Select() method will make it 014, because of the ToString("000") method call. So at this point, we have 10 random numbers of three digits each. Now, we have to stitch them together to create a 30 digit number. So, we convert this into a list of strings so that we can use the ForEach operator on list to concatenate the results on the StringBuilder object.

Once done, the number is added to the list of random numbers called allRandomNumbers.

Random number generators work with the system clock. A Thread.Sleep call is made to make sure that we don't get the same random numbers again.

Time for action – creating a custom random number generator

Now, let's take a step ahead and create a custom random number generator that can generate random numbers of any digit. As many people could use this, I thought it would be a nice idea to make this a web app. In this section, I will take you through the Windows clone:

Create a Windows app and place the controls as shown in the following screenshot:

Add the following code in the click event of the Generate Serials button:

private void btnGenerate_Click(object sender, EventArgs e)
{
  txtResult.Clear();
  int howManyDigit = Convert.ToInt16(digitCount.Value);
  int howManyNumbers = Convert.ToInt16(numCount.Value);
  int basicDigitCount = 3;
  int numberOfRandomInstances = howManyDigit / basicDigitCount;
  StringBuilder bigRandomNumber = new StringBuilder();
  List<string> allRandomNumbers = new List<string>();
  for (int i = 0; i < howManyNumbers;)
  {
    bigRandomNumber = new StringBuilder();
    Algorithms.ForEach(Algorithms.NCopiesOf(numberOfRandomInstances, new Random()).ToList().Select(c => c.Next(100).ToString("100")), c => bigRandomNumber.Append(c.ToString()));
    if(bigRandomNumber.ToString().Length < howManyDigit)
    {
      for (int k = 0; k <= howManyDigit - bigRandomNumber.ToString().Length; k++)
      bigRandomNumber.Append("0");
    }
    if(bigRandomNumber.ToString().Length > howManyDigit)
    {
      for (int k = bigRandomNumber.ToString().Length; k <= bigRandomNumber.ToString().Length - howManyDigit; k++)
      bigRandomNumber.Remove(k, 1);
    }
    if(!allRandomNumbers.Contains(bigRandomNumber.ToString()))
    {
      allRandomNumbers.Add(bigRandomNumber.ToString());
      i++;
    }
    System.Threading.Thread.Sleep(20);
  }
  int duplicates = allRandomNumbers.Count – allRandomNumbers.Distinct().Count();
  Algorithms.ForEach(allRandomNumbers, c => txtResult.Text = txtResult.Text + c + Environment.NewLine);
}

Following is the output of the program:

What just happened?

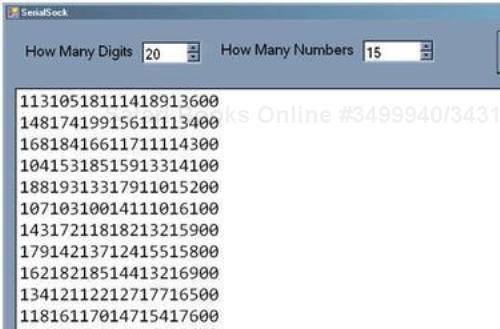
The program relies on the following code to generate random numbers:

Algorithms.ForEach
(
  Algorithms.NCopiesOf
  (
    numberOfRandomInstances
    ,new Random()
  )
  .ToList()
  .Select(c => c.Next(100).ToString("100"))
  ,c => bigRandomNumber.Append(c.ToString())
);

Calls to the method, Algorithms.NCopiesOf(), generates random numbers (with the maximum value 100). However, if there is a number less than 100, then it will prepend 1 before that number due to the method call: ToString("100"). For example, if the random number generated is 4 then it will become 104—this is because otherwise the numbers won't be of the same digit count.

ForEach() puts all these numbers together to the StringBuilder object. However, if there is a mismatch in the number of digits, zeros are either appended at the end of the number or some numbers are trimmed from the right end. These numbers are then put in a collection and added to the textbox.

You can find the web-based version at www.consulttoday.com/SerialSock.

ForEach()

In the previous example, we had to convert the result to a list so that we can use the ForEach() method of the List class to concatenate the numbers together. However, by using the ForEach() method, we can do that without converting the result to a list. Let's see how.

Time for action – creating a few random numbers of given any length

Follow the given steps:

Copy the following code snippet as a query in LINQPad:

StringBuilder bigRandomNumber = new StringBuilder();
List<string> allRandomNumbers = new List<string>();
for (int i = 0; i < 5; i++)
{
  bigRandomNumber = new StringBuilder();
  Algorithms.ForEach
  (
    Algorithms.NCopiesOf(10, new Random())
    .Select(c => c.Next(100).ToString("000")),
    c => bigRandomNumber.Append(c.ToString())
  );
  allRandomNumbers.Add(bigRandomNumber.ToString());
  System.Threading.Thread.Sleep(20);
}

Run the query. You will get an output similar to the following screenshot:

What just happened?

The ForEach() generic method takes two arguments. The first one is the collection through which to iterate and the second one is an Action delegate that is to be applied on each of the items in the collection:

The Action delegate can be replaced with a Func or a Lambda Expression at runtime. So, we replaced that with the following delegate:

c => bigRandomNumber.Append(c.ToString())

Rotate() and RotateInPlace()

Rotate() and RotateInPlace() algorithms can rotate a represented sequence, which implements IList<T> interface, to a given amount. This doesn't change the original sequence. However, the in-place cousin does so.

The second argument determines the amount of rotation. If 4 is given as the rotation amount then the fifth element in the current list becomes the first element in the rotated list; because what we are passing as a rotation amount is an index to rotate. On the other hand, if -4 is given as the rotation amount then the fourth element from the end of the collection becomes the first element in the rotated collection.

Time for action – rotating a word

Follow the given steps:

Copy the following code snippet as a query in LINQPad:

StringBuilder builder = new StringBuilder();
string word = "Generics";
word.Dump("Original Word");

List<char> wr = Algorithms.Rotate(word.ToList(), 4).ToList();

wr.ForEach(c => builder.Append(c.ToString()));
builder.ToString().Dump("After rotation is called with amountToRotate = 4");
builder = new StringBuilder();

List<char> wrr = Algorithms.Rotate(wr.ToList(), -4).ToList();
wrr.ForEach(c => builder.Append(c.ToString()));
builder.ToString().Dump("Going back to original one");

Run the query. You will get the following output:

What just happened?

In the first Rotate() method call, the word becomes ricsGene and the second Rotate() method call made it turn back to the original one Generics. As the fourth letter from the end of ricsGene is G, the second call returned Generics.

Time for action – creating a word guessing game

Using Rotate() and RandomShufflle() algorithms, I created a small game that asks the users to guess a randomly shuffled or rotated word. On successful guess, it loads a different word. The game has two options namely: Let Me Win and Bring It On.

Create a user interface and place the controls as follows:

Add the following variables in Form1.cs:

List<string> allWords = new List<string>();
int seconds = 0;
int rotated = 0;
string word;

Add a timer to the project. Leave its name as Timer1 and enable it. Change its Interval value to 1000 so that it ticks every second.

Add the following code in the Form_Load event:

StreamReader sr = new StreamReader("C:\T9.txt");
allWords.AddRange(sr.ReadToEnd().Split(new char[]{'','
','
'},StringSplitOptions.RemoveEmptyEntries));
sr.Close();
LoadNextWord();

Add the following method to load the next word:

private void LoadNextWord()
{
  lblWordRotated.Text = "";
  rotated = (new Random()).Next(100);
  word = allWords[(new Random()).Next(0, allWords.Count - 1)];
  if (radLetMeWin.Checked)
  {
    Algorithms.ForEach
    (
      Algorithms.Rotate(word.ToList(), rotated).ToList(),c => lblWordRotated.Text = lblWordRotated.Text + c.ToString()
    );
    if (lblWordRotated.Text.Equals(word))
    LoadNextWord();
  }
  else
  {
    Algorithms.ForEach
    (
      Algorithms.RandomShuffle(word.ToList()).ToList(),c => lblWordRotated.Text = lblWordRotated.Text + c.ToString()
    );
    if (lblWordRotated.Text.Equals(word))
    LoadNextWord();

  }
  timer1.Start();
}

Deal with the change as users attempt to guess the rotated or shuffled word:

private void txtUserInput_TextChanged(object sender, EventArgs e)
{
  if (txtUserInput.Text == word)
  {
    System.Media.SoundPlayer player = new System.Media.SoundPlayer(@"tada.wav");
    player.Play();
    lblTimer.Text = "";
    txtUserInput.Clear();
    LoadNextWord();
  }
}

Let's give the users an emotional stress. Let's show them a progress bar:

private void timer1_Tick(object sender, EventArgs e)
{
  lblTimer.Text = lblTimer.Text + " .";
  seconds++;
  if (seconds == 24)
  {
    lblTimer.Text = "";
    seconds = 0;
  }
}

Once you run the program, you will be presented with a screen similar to the following screenshot:

What just happened?

Can you guess the word in the preceding screenshot? It's affairs. The Let Me Win radio button uses the Rotate() method to generate a rotated version of the word, which is kind of easy to figure out. However, the Bring It On radio button uses the RandomShuffle() method to generate a more difficult version of the word.

The Algorithms.Rotate(word.ToList(), rotated) method returns an instance of IEnumerable<T> interface. Using the ToList() method, the instance is converted to a list so that the ForEach() method can iterate through the collection.

The following Lambda expression:

c => lblWordRotated.Text = lblWordRotated.Text + c.ToString()

appends each character generated from the rotation of the character list and puts them at the end of lblWordRotated.

Have a go hero

However, there could be a possible buggy situation for Bring It On when there are anagrams in the dictionary. For example, the words "DEAR" and "READ" both could become "AERD" when randomly shuffled. However, if the program picked "DEAR" and the user enters "READ" then the program will not be able to identify that as a correct response.

Can you provide a fix for this? Hint: You can use MultiDictionary described in Chapter 3, Dictionaries.

RandomSubset()

RandomSubset() is the method to sample a collection. If you want to randomly select a subset of a given set, this is the method for you. Let's see how it works.

Time for action – picking a set of random elements

Follow the given steps:

Copy the following code in LINQPad:

string[] names = { "Sam", "Pamela", "Dave", "Pascal", "Erik" };
string[] sub = Algorithms.RandomSubset(names, 3);
sub.Dump("A Random Sample of 3 names");

Run the query. You should get the following output:

What just happened?

The RandomSubset() method takes two arguments. The first one is the collection on which the method has to operate and the second one is the number of elements to be selected in the subset.

This method will come particularly handy in designing systems where the computer has to pick a handful from a haystack of elements.

Reverse()

This method is capable of reversing a collection of any type. Let's see how it works.

Time for action – reversing any collection

Follow the given steps:

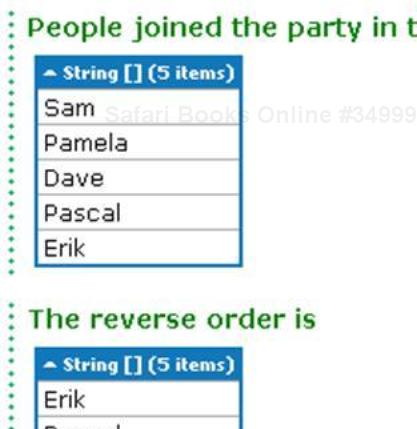
Copy the following code in LINQPad:

string[] names = { "Sam", "Pamela", "Dave", "Pascal", "Erik" };
names.Dump("People joined the party in this order");
string[] sub  = Algorithms.Reverse(names).ToArray();
sub.Dump("The reverse order is");

Run the query. It will generate the following output:

What just happened?

The Reverse() method returns a reversed collection which is just the opposite of the input sequence. Check the input. Sam appeared at the first index. In the output Sam appeared at the end. This is same as the Reverse operator in LINQ Operators.

EqualCollections()

The EqualCollections() method helps compare two collections. If two collections have exactly the same number of elements, then this method returns true. For the primitive type, it knows how to do the comparison of elements. However, for the user-defined type, it needs a comparer object or a binary predicate to do the comparison. The order in which elements appear in the collection is important. If the order is not the same and still both collections hold the same elements, even then they are not considered as equal collections.

Time for action – revisiting the palindrome problem

With the two methods, Reverse() and EqualCollections(), finding whether a sequence is palindromic or not becomes a single line of code. Let's see how:

Copy the following code in LINQPad:

string word = "rotor";
bool isPalindrome = 
Algorithms.EqualCollections(word.ToCharArray(), Algorithms.Reverse(word.ToCharArray()));
string status = word + " is ";
if (isPalindrome)
    status += "Palindromic";
else
    status += "Not Palindromic";
status.Dump();

Run the query. It will generate the following output:

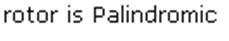
This method can work with any type of collection.

What just happened?

The Reverse() method is used to reverse the character array representation of the word "rotor". The following line:

Algorithms.EqualCollections(word.ToCharArray(),Algorithms.Reverse(word.ToCharArray()));

checks whether two collections, the character array representation of the word and its reverse, are equal or not. Two collections are said to be equal only if they contain the same elements in the same order. As "rotor" and its reversed version are the same, EqualCollections() returns true in this case.

DisjointSets()

Sometimes we need to check whether two collections contain the same element or not. However, that's a quadratic time operation at the least and .NET doesn't have any method to check that directly. Although you can convert any collection to a .NET set implementation and then do such a check. But that would be computationally expensive.

However, the DisjointSets() method does that. It considers each collection as a set and returns false if they have the same elements in any order; and true otherwise. Think of this method as the complementary method to the EqualCollections() method.

Time for action – checking for common stuff

Follow the given steps:

Copy the following code in LINQPad:

string[] cities = { "Boston", "Berlin", "Chicago" };
string[] otherCities = { "Berlin", "Chicago", "Boston" };

bool isDisjoint = Algorithms.DisjointSets(cities, otherCities);
isDisjoint.Dump();

Run the query. It will generate the following output:

What just happened?

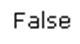
Because both the collections (arrays in this case) cities and otherCities have the same elements, though in different order, they turn out to be equal sets so they are not disjoint to each other. Thus, the method returns false. Unlike EqualCollections(), order in the sequence of elements in the collections is not important.

Time for action – finding anagrams the easiest way

As they say, if all you have is a hammer, every problem would seem like a nail. Finding an anagram is similar to finding whether two sorted character sets exactly match with each other or not. OrderedBag<T> collection from Power Collections is perfect for this job. I can't emphasize this more. Let's see how we can do it:

Create a Console Application project and call it AnaCheck.
Add PowerCollections.dll reference to the project.

Now add the following lines of code in the Main() method:

static void Main(string[] args)
{
  OrderedBag<char> first = new OrderedBag<char>("dad");
  OrderedBag<char> second = new OrderedBag<char>("add");
  bool isAna = Algorithms.EqualCollections(first, second);
  if(isAna)
  Console.Write(""dad" and "add" are anagrams");
}

Now, we are ready to run the application. When you run the application, you will see the following output:

What just happened?

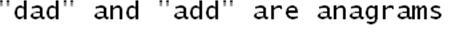
"dad" and "add" are anagrams as both of them have the same character set with the same frequency of occurrence of each character. If the characters are sorted, both words "add" and "dad" become "add". That's exactly what OrderedBag<char> does for us. It sorts the elements and doesn't care whether you pass duplicates, as I did in this case.

So internally, first and second, both the OrderedBag<char> instances hold "a", "d", and "d" as the characters are in that order. Thus, when we check whether the collections are the same or not, we get the answer as true. If you are familiar with C++, you would find the OrderedBag<T> class similar to the MultiMap<T, V> class.

Have a go hero

Create a generic anagramic sequence checker using the OrderedBag<T> class.

Creating an efficient arbitrary floating point representation

Scientists in number theory sometimes need to represent a floating point to some reasonably big decimal places, say to the 20,000th digit after the decimal. However, the largest available data type in .NET (decimal) supports only to the 28th digit after the decimal.

Following is what scientists want and what we can assume:

To be able to store as many digits after the decimal as possible.
To be able to know what the digit is after the decimal at any given index at constant time. This means, no matter which value they want to get at whichever index after the decimal, be it at index 0 or at index 100; it should take the same constant time. Users can't wait long.
To know which digit occurred most in the decimal places. Again they can't wait. So, the faster the better.
The floating point number will always be represented in the p/q format where p and q are integers within the System.Int32 range.

Let's see how we can help them.

Time for action – creating a huge number API

Follow the given steps:

Create a Class Library project and call it Huge.
Add PowerCollections.dll in the reference for this project.

Add the following class, HugeInteger, in this Class Library project:

public class HugeInteger
{
  /// <summary>
  /// Internal representation of the huge integer
  /// </summary>
  private Dictionary<int, BigList<decimal>> _huge;
  /// <summary>
  /// Creating such an empty huge integer
  /// </summary>
  public HugeInteger()
  {
    _huge = new Dictionary<int, BigList<decimal>>();
    Enumerable.Range(0, 10).ToList()
    .ForEach(i => _huge.Add(i, new BigList<decimal>()));
  }
  /// <summary>
  /// Length of the huge integer
  /// </summary>
  public decimal Length
  {
    get
    {
      //As it deals with zero based indexing
      //so the actual length would be one more.
      Dictionary<int, BigList<decimal>> temp = new Dictionary<int, BigList<decimal>>();
      Enumerable.Range(0, 10).ToList()
      .ForEach(i => temp.Add(i, new BigList<decimal>()));
      foreach (int k in _huge.Keys)
      temp[k] = _huge[k];
      return
      Algorithms.Maximum(new decimal[]{temp[0].LastOrDefault(), temp[1].LastOrDefault(), temp[2].LastOrDefault(), temp[3].LastOrDefault(), temp[4].LastOrDefault(), temp[5].LastOrDefault(), temp[6].LastOrDefault(), temp[7].LastOrDefault(), temp[8].LastOrDefault(), temp[9].LastOrDefault()}) + 1;
    }
  }
  /// <summary>
  /// Represents the huge integer as a string format
  /// </summary>
  public override string ToString()
  {
    StringBuilder builder = new StringBuilder();
    for (int i = 0; i < this.Length; i++)
    {
      builder.Append(this.huge.First(indices =>
      indices.Value.Contains(i)).Key.ToString());
    }
    return builder.ToString();
  }
  /// <summary>
  /// Adds a digit to the huge integer 
  /// </summary>
  /// <param name="digit">The digit</param>
  /// <param name="index">Where should we add it</param>
  public void AddDigit(int digit, decimal index)
  {
    _huge[digit].Add(index);
  }
}

Add the following class, HugeFloatingPoint, in the Class Library project:

/// <summary>
/// Class to represent floating point numbers 
/// </summary>
public class HugeFloatingPoint
{
  int IntegralPart;
  HugeInteger decimalPart;
  decimal digitsAfterDecimal;
  public HugeFloatingPoint(string floatingPoint)
  {
    IntegralPart = 
    Convert.ToInt32(floatingPoint.Split('.')[0].Trim());
    decimalPart = new HugeInteger(floatingPoint.Split('.')[1].Trim());
    digitsAfterDecimal = decimalPart.Length;
  }
  /// <summary>
  /// Create an Irrational number with arbitrary 
  /// number of digits after decimal. 
  /// </summary>
  /// <param name="numerator">The numerator or the p or p/q
  /// format</param>
  /// <param name="denominator">The denominator or the q or p/q
  /// format</param>
  /// <param name="digits">Requested number of digits after
  /// decimal</param>
  public HugeFloatingPoint(int numerator, int denominator, 
    decimal digits)
  {
    IntegralPart = numerator / denominator;
    digitsAfterDecimal = digits;
    decimalPart = new HugeInteger();
    decimal count = 0;
    do
    {
      int digit = numerator / denominator;
      int div = numerator % denominator;
      if (div < denominator)
      numerator = div * 10;
      if (digit > 9 || digit == IntegralPart)
      continue;
      decimalPart.AddDigit(digit, count);
      count++;
    } 
    while (count != digitsAfterDecimal);
  }
  /// <summary>
  /// Overridden ToString() to represent a the floating
  /// point number as a string.
  /// </summary>
  /// <returns></returns>
  public override string ToString()
  {
    return IntegralPart.ToString() + "." + decimalPart.ToString().Substring(1);
  }
}

Now we are ready to consume these classes and create an irrational number with an arbitrary number of digits after the decimal. Create a Console Application project in the same solution and call it HugeTest.

Stay in the HugeTest project. Set it as the StartUp Project by right-clicking on it. Add the following code in the Main() method:

static void Main(string[] args)
{
  //Square root of 3.
  //approximated as 97/56 as per Wikipedia
  //(http://en.wikipedia.org/wiki/Square_root_of_3)
  HugeFloatingPoint fp = new HugeFloatingPoint(97, 56, 60);
  string sqRoot3 = fp.ToString();
  Console.WriteLine(@"Square root of 3 approximated to 60 digits after decimal is");
  Console.WriteLine(sqRoot3);
  Console.ReadKey();
}

Ok! Now we are ready to run the application. As you run the application, you will get the following output:

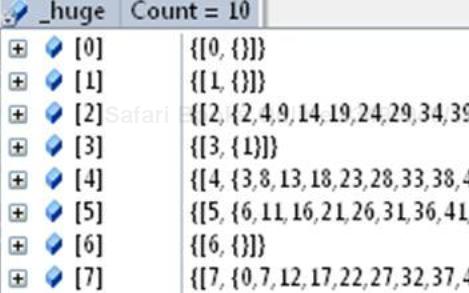
What just happened?

The arbitrary floating point is represented as a dictionary of integers and the indices where the integers occur in the given number. For example, the number 1230913233 will be stored, as shown in the following screenshot:

The keys of this dictionary would be 0 to 9 and where they occur in the number will be stored in the associated values, which is a BigList<T> instance.

To determine the length of the digit, it will be sufficient to find the maximum of the values stored as follows:

The preceding screenshot explains the logic of the Length property of the HugeInteger class. A HugeFloatingPoint class is just a combination of the following two parts:

An integral number.
A decimal part after decimal, which is also a HugeInteger class.

That's why in the constructor of the HugeFloatingPoint class, digits are being added to the huge number list through the AddDigit() method. Following is a screenshot showing how the internal dictionary, _huge, looks for the square root of 3, as previously approximated:

With .NET 4.0, a BigInteger class implementation is available from the System.Numerics namespace. However, that doesn't quite help to create a big floating point representation as we did in this section.

Have a go hero

I didn't add code to find the digit that occurs the maximum number of times after the decimal and the digit at any given index after the decimal. Both of these tasks are quite simple. Add these methods in the HugeFloatingPoint class.

Creating an API for customizable default values

LINQ Standard Query Operators: FirstOrDefault(), LastOrDefault(), or any operator that ends with "Default" in its name throws a useless null, as the default value, for user-defined objects.

Now, if you have several situations where you have to deal with such values, you would prefer to be able to set a default value of your choice to these collections.

Power Collections offer an algorithm called Fill and a range version called FillRange, which offer functionality to fill a collection or an array with a given default value.

I thought it would be really useful if we can use these two algorithms to brew some default value initialization framework using the LINQ extension method style. Suppose we have a List<string> with 10 entries and we want to set the first four to # and that's needed for our application. In such situations, we can use the framework that we are about to build.

Time for action – creating a default value API

Follow the given steps:

Create a Class Library project and call it DefaultValues.
Change the default name Class1 and rename it to DefaultValueMap.

Add the following code in the class:

public static  class DefaultValueMap
{
  public static Dictionary<string, object> DefaultValueMapping = null;
  /// <summary>
  /// Allows to add new default value at runtime.
  /// </summary>
  /// <param name="fullTypeName">Fully Qualified name of the object for which the default value is being set</param>
  /// <param name="value">The default value</param>
  public static void AddDefaultValue(string fullTypeName, object value)
  {
    if(!DefaultValueMapping.ContainsKey(fullTypeName))
    DefaultValueMapping.Add(fullTypeName, value);
  }
  /// <summary>
  /// Initializes the default values for the type we care about         
  /// Only once
  private static void InitDefaultValues()
  {
    //this check is to make sure that initialization happens only once.
    if (DefaultValueMapping == null)
    {
      DefaultValueMapping = new Dictionary<string, object>();
      DefaultValueMapping.Add("System.String", "*");
      DefaultValueMapping.Add("System.Int32", 10);
      DefaultValueMapping.Add("DefaultValues.Student", new Student(name: "new student", age: 10));
    }
    /// <summary>
    /// Sets a range of values in a collection by the pre-
    ///defined default value
    /// </summary>
    /// <typeparam name="T">Type of the collection</typeparam>
    /// <param name="list">The collection for which default 
    ///values have to be set</param>
    /// <param name="start">The starting index of the 
    ///range</param>
    /// <param name="count">Element count in the range</param>
    /// <returns></returns>
    public static IEnumerable<T> SetDefault<T>(this IEnumerable<T> list, int start, int count)
    {
      InitDefaultValues();
      T[] internalArray = list.ToArray();
      Algorithms.FillRange(internalArray, start, count, (T)DefaultValueMapping[list.ElementAt(0).GetType().FullName]);
      return internalArray.AsEnumerable();
    }

    /// <summary>
    /// Sets the first few values to default value for the type
    /// </summary>
    /// <typeparam name="T">The type of the 
    ///collection</typeparam>
    /// <param name="list">The collection for which the values 
    ///have to be set to default</param>
    /// <param name="tillThis">Till this item all the values 
    ///must be set to default</param>
    /// <returns></returns>
    public static IEnumerable<T> SetDefault<T>(this IEnumerable<T> list, int tillThis)
    {
      InitDefaultValues();
      IEnumerable<T> temp;
      try
      {
        temp = list.Take(tillThis);
      }
      catch
      {
        throw new ArgumentOutOfRangeException("There is not enough element to set to default");
      }
      T[] internalArray = temp.ToArray();
      Algorithms.Fill(internalArray, (T)DefaultValueMapping[list.ElementAt(0).GetType().FullName]);
      return internalArray.Concat(list.Skip(tillThis));
    }
  }
}

Create a new Console Application project to test this API and call it DefaultValuesTest.

Add the following code in the Main() method:

static void Main(string[] args)
{
  List<string> codes = new 
  List<string>(5){"a", "b", "c", "d", "e"};
  List<string> codes1 = codes.SetDefault(3).ToList();
  List<string> codes2 =  codes.SetDefault(1).ToList();
  List<string> codes3 = codes
    .SetDefault(codes.Count-2, 2).ToList();

  Console.WriteLine("Original List is ");
  codes.ForEach(Console.WriteLine);
  Console.WriteLine("First 3 values set to default as *");
  codes1.ForEach(Console.WriteLine);
  Console.WriteLine("First value set to default as *");
  codes2.ForEach(Console.WriteLine);
  Console.WriteLine("Last 2 value set to default as *");
  codes3.ForEach(Console.WriteLine);
  Console.ReadKey();
}

Now we are ready to run the application. As you run the application, you will get the following output:

What just happened?

This is a clever use of the Fill() and the FillRange() methods available in Power Collections. Both these methods operate on either IList<T> or T[] inputs. However, I wanted to make sure that the SetDefault<T>() method works on IEnumerable<T>, similar to all the LINQ Standard Query Operators.

The following line of code converts the input to an array by the projection LSQO ToArray():

T[] internalArray = temp.ToArray();

In the following line:

Algorithms.Fill(internalArray, (T)DefaultValueMapping[list.ElementAt(0).GetType().FullName]);

internalArray is being filled with the default value assigned for the type.

As the dictionary, DefaultValueMapping, stores the default value as an object, we must cast it to type T before we can use it in the Fill() or FillRange() algorithm, as they expect a strongly typed value of type T to be used as the default value.

The list.ElementAt(0).GetType() method returns the type of the collection and FullName property returns the fully qualified name of the type. For example, a collection List<string> returns System.String and a collection List<int> returns System.Int32.

In the end, LSQO Concat is used to concatenate the part filled with default values to the rest and then this combined collection is returned by the method SetDefault<T>().

Mapping data structure

Before we wrap this chapter, it would be great to know what Power Collections data structures brought to the table and how they can now be replaced with System.Collections.Generics collection classes:

Power Collections class	.NET Generics class	Comments
`Pair<TKey, TValue>`	`KeyValuePair<TKey, TValue>`
`Set<T>`	`HashSet<T>`
`MultiDictionary<TKey, TValue>`	Not available	You can use the `MultiDictionary` that we have created in Chapter 3, Dictionaries.
`OrderedSet<T>`	`SortedSet<T>`
`Bag<T>`	`List<T>`
`OrderedBag<T>`	Not available	This is basically a sorted list that allows duplication.
`Deque<T>`	`LinkedList<T>`	You can add/remove elements from both ends of a `LinkedList<T>`.
`Triple<T1, T2, T3>`	`Tuple<T1, T2, T3>`	This is a special case of `Tuple`.
`BigList<T>`	`List<T>`

Algorithm conversion strategy

As you might have noticed, we haven't covered all the algorithms that Power Collections has to offer. The reason is that the skipped set of algorithms can be easily constructed using several LSQOs.

For example, let's consider the following line of code:

public static ICollection<T> RemoveWhere<T> (ICollection<T> collection, Predicate<T> predicate);

First, we can use the Where() operator to filter the values and then call the Remove() method to delete them.

Algorithms in Power Collections use Predicate<T> and BinaryPredicate<T>. This is because Power Collections was written before Func came into existence. You can replace Predicate<T> with Func<T, bool> and BinaryPredicate<T> with Func<T, T, bool>.

In order to convert the input to these algorithms to be compatible with LSQOs, use the following projection operators ToArray(), ToList(), and AsEnumerable().

Summary

We have studied various algorithms and the OrderedBag and BigList data structures that Power Collections has to offer. Although most of the functionalities offered by these algorithms and data structures can be achieved otherwise, it still makes sense to know about them because these are still being used for the sheer simplicity it brings to the table.

If you are craving for more data structures and algorithms, hold on. In the next chapter, we will study another well-known and reputed generic collection API called C5, which is home to different great algorithms and data structures.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 7. Power Collections

Create new playlist

Sign In

Sign Up

Chapter 7. Power Collections

Setting up the environment

BinarySearch()

Time for action – finding a name from a list of names

What just happened?

CartesianProduct()

Time for action – generating names of all the 52 playing cards

What just happened?

RandomShuffle()

Time for action – randomly shuffling the deck

What just happened?

NCopiesOf()

Time for action – creating random numbers of any given length

What just happened?

Time for action – creating a custom random number generator

What just happened?

ForEach()

Time for action – creating a few random numbers of given any length

What just happened?

Rotate() and RotateInPlace()

Time for action – rotating a word

What just happened?

Time for action – creating a word guessing game

What just happened?

Have a go hero

RandomSubset()

Time for action – picking a set of random elements

What just happened?

Reverse()

Time for action – reversing any collection

What just happened?

EqualCollections()

Time for action – revisiting the palindrome problem

What just happened?

DisjointSets()

Time for action – checking for common stuff

What just happened?

Time for action – finding anagrams the easiest way

What just happened?

Have a go hero

Creating an efficient arbitrary floating point representation

Time for action – creating a huge number API

What just happened?

Have a go hero

Creating an API for customizable default values

Time for action – creating a default value API

What just happened?

Mapping data structure

Algorithm conversion strategy

Summary

Table of Contents for
7. Power Collections