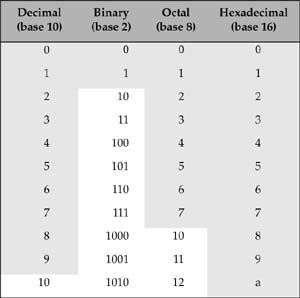
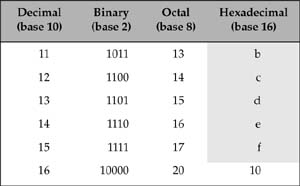
Table G.1 lists the integers from 0 to 16, showing their equivalents in the binary (base 2), octal (base 8), and hexadecimal (base 16) number systems. The shaded cells in each column show the digits in each number system.
In addition to the decimal literals, Java also allows integer literals to be specified in octal and hexadecimal number systems, but not in the binary number system. Octal and hexadecimal numbers are specified with 0 and 0x prefix, respectively. The prefix 0X can also be used for hexadecimal numbers. Note that the leading 0 (zero) digit is not the uppercase letter O. The hexadecimal digits from a to f can also be specified with the corresponding uppercase forms (A to F). Negative integers (e.g., -90) can be specified by prefixing the minus sign (-) to the magnitude, regardless of number system (e.g., -0132 or -0X5A). The actual memory representation of the integer values is discussed in Section G.4.
A binary number can be converted to its equivalent decimal value by computing the positional values of its digits. Each digit in the binary number contributes to the final decimal value by virtue of its position, starting with position 0 (units) for the right-most digit in the number. The positional value of each digit is given by
digit × baseposition
The number 1010012 corresponds to 4110 in the decimal number system:
1010012 = 1× 25 + 0× 24 + 1× 23 + 0× 22 + 0× 21 + 1× 20
= 32 + 0 + 8 + 0 + 0 + 1
= 4110
Similarly, octal (base 8) and hexadecimal (base 16) numbers can be converted to their decimal equivalents:
0132 = 1328 = 1× 82 + 3× 81 + 2× 80 = 64 + 24 + 2 = 9010 Octal → Decimal
0x5a = 5a16 = 5× 161 + a× 160 = 80 + 10 = 9010 Hex → Decimal
The same technique can be used to convert a number from any base to its equivalent representation in the decimal number system.
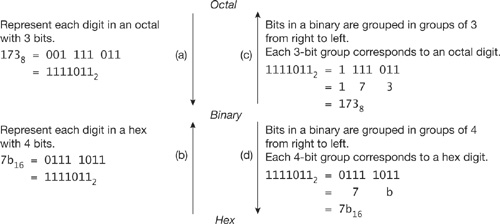
From Table G.1 we see that 3 bits are needed to represent any octal digit, and 4 bits to are needed to represent any hexadecimal digit. We can use this fact to convert between binary, octal, and hexadecimal systems, as shown in Figure G.1.
The procedure for converting an octal to a binary is shown by the arrow marked (a). We can prove that replacing each octal digit by its 3-bit equivalent binary value gives the right result:
1738 = 1× 82 + 7× 81 + 3× 80
= 1× (23)2 + 7× (23)1 + 3× (23)0
= 1× 26 + 7× 23 + 3
= (0012)× 26 + (1112)× 23 + (0112)
= (0× 22+0× 21+1× 20)× 26 + (1× 22+1× 21+1× 20)× 23 + (0× 22+1× 21+1× 20)
= 1× 26 + 1× 25+1× 24+1× 23 + 0× 22+1× 21+1× 20
= 1× 26 + 1× 25 + 1× 24 + 1× 23 + 0× 22 + 1× 21 + 1× 20
= 11110112
Analogously, we can convert a hexadecimal number to its equivalent binary number by replacing each digit in the hexadecimal number by its 4-bit equivalent binary value, as shown by the arrow marked (b).
To convert a binary to it octal equivalent, we reverse the procedure outlined earlier (see arrow marked (c) in Figure G.1). The bits in the binary number are grouped into 3-bit groups from right to left. Each such group is replaced by its equivalent octal digit. This corresponds to reversing the computation shown above. Analogously, we can convert a binary to a hexadecimal number by replacing each 4-bit group by its equivalent hex digit (see arrow marked (d) in Figure G.1).
In order to convert decimals to binaries, we reverse the process outlined in Section G.1 for converting a binary to a decimal.
4110 = 20×2 + 1 Dividing 41 by 2, gives the quotient 20 and remainder 1.
2010 = 10×2 + 0 We again divide the current quotient 20 by 2.
1010 = 5×2 + 0
510 = 2×2 + 1 We repeat this procedure until ...
210 = 1×2 + 0
110 = 0×2 + 1 ... the quotient is 0.
4110 = 1010012
The divisor used in the steps above is the base of the target number system (binary, base 2). The binary value, 1010012, is represented by the remainders, with the last remainder as the left-most bit. Back substitution of the quotient gives the same result:
4110 = (((((0×2 + 1)×2 + 0)×2 + 1)×2 + 0)×2 + 0)×2 + 1
= 1×25 + 0×24 + 1×23 + 0×22 + 0×21+ 1×20
= 1010012
Analogously, we can apply the above procedure for converting an octal to a binary. The conversion for the decimal number 90 can be done as follows:
9010 = 11×8 + 2
1110 = 1×8 + 3
110 = 0×8 + 1
9010 = 1328 = 0132
The remainder values represent the digits in the equivalent octal number: 1328. This can be verified by back substitution, which gives the following result:
9010 = ((0×8 + 1)×8 + 3)×8 + 2
= 1×82 + 3×81 + 2×80
= 1328 = 0132
Conversion to hexadecimal is analogous:
9010 = 5×16 + 10
510 = 0×16 + 5
9010 = 5a16 = 0x5a
The remainders represent the digits of the number in the hexadecimal system: 5a. Back substitution gives the same result:
9010 = (0×16+ 5)×16 +10
= 5×161 + a×160
= 5a16 = 0x5a
Integer data types in Java represent signed integer values, i.e., both positive and negative integer values. The values of char type can effectively be regarded as unsigned 16-bit integers.
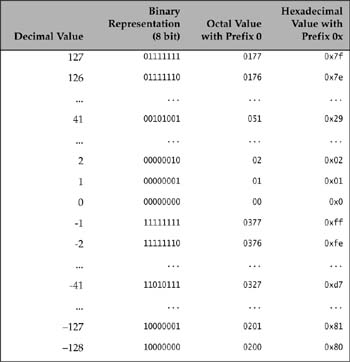
Values of type byte are represented as shown in Table G.2. A value of type byte requires 8 bits. With 8 bits, we can represent 28 or 256 values. Java uses 2’s complement (explained later) to store signed values of integer data types. For the byte data type, this means values are in the range −128 (−27) to +127 (27−1), inclusive.
Bits in an integral value are usually numbered from right to left, starting with the least significant bit 0 (also called the right-most bit). When applying bitwise operators, the number of the most significant bit (also called the left-most bit) is dependent on the integral type; bit 31 for byte, short, char, and int, and bit 63 for long. The representation of the signed types sets the most significant bit to 1, indicating negative values. Adding 1 to the maximum int value 2147483647 results in the minimum value -2147483648, i.e., the values wrap around for integers and no overflow or underflow is indicated.
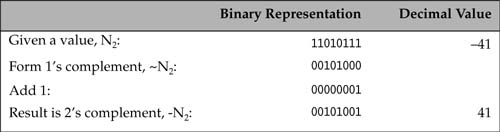
Before we look at 2’s complement, we need to understand 1’s complement. 1’s complement of a binary integer is computed by inverting the bits in the number. Thus, 1’s complement of the binary number 00101001 is 11010110. 1’s complement of a binary number N2 is denoted as ~N2. The following relations hold between a binary integer N2, its 1’s complement ~N2, and its 2’s complement −N2:
−N2 = ~N2 + 1
0 = −N2 + N2
If N2 is a positive binary integer, then −N2 denotes its negative binary value, and vice versa. The second relation states that adding a binary integer N2 to its 2’s complement −N2 equals 0.
Given a positive byte value, say 41, the binary representation of -41 can be found as follows:

Similarly, given a negative number, say -41, we can find the binary representation of 41:
Adding a number N2 to its 2’s complement −N2 gives 0, and the carry bit from the addition of the most significant bits (after any necessary extension of the operands) is ignored:

Subtraction between two integers is also computed as addition with 2’s complement:
N2 − M2 = N2 + (−M2)
For example, calculating 4110 − 310 (with the correct result 3810) is computed as follows:

The previous discussion on byte values applies equally to values of other integer types: short, int, and long. These types have their values represented by 2’s complement in 16, 32, and 64 bits, respectively.