In this chapter, I present the adaptive computation of important features for data representation and classification. I demonstrate the importance of these features in machine learning, data visualization, and data analytics. I also show the importance of these algorithms in multiple disciplines and present how these algorithms are obtained there. Finally, I present a common methodology to derive these algorithms. This methodology is of high practical value since practitioners can use this methodology to derive their own features and algorithms for their own use cases.
For these data features, I assume that the data arrives as a sequence, has to be used instantaneously, and the entire batch of data cannot be stored in memory.
In machine learning and data analysis problems such as regression, classification, enhancement, or visualization, effective representation of data is key. When this data is multi-dimensional and time varying, the computational challenges are more formidable. Here we not only need to compute the represented data in a timely manner, but also adapt to the changing input in a fast, efficient, and robust manner.
A well-known method of data compression/representation is the Karhunen-Loeve theorem [Karhunen–Loève theorem, Wikipedia] or eigenvector orthonormal expansion [Fukunaga 90]. This method is also known as principal component analysis (PCA) [principal component analysis, Wikipedia]. Since each eigenvector can be ranked by its corresponding eigenvalue, a subset of the “best” eigenvectors can be chosen as the most relevant features.
Data representation feature e1 that best represents the data from the two classes [Source: Chatterjee et al. IEEE Transactions on Neural Networks, Vol. 8, No. 3, pp. 663-678, May 1997]
In classification, however, you generally want to extract features that are effective for preserving class separability . Simply stated, the goal of classification feature extraction is to find a transform that maps the raw measurements into a smaller set of features, which contain all the discriminatory information needed to solve the overall pattern recognition problem.
Data classification feature e2 that leads to best class separability [Source: Chatterjee et al. IEEE Transactions on Neural Networks, Vol. 8, No. 3, pp. 663-678, May 1997]
- 1.
Commonly used features that are obtained by a linear transform of the data and are used with streaming data for edge applications
- 2.
Historical relevance of these features and how we derive them from different disciplines
- 3.
Why we want to use adaptive algorithms to compute these features
- 4.
How to create a common mathematical framework to derive adaptive algorithms for these features and many more
1.1 Commonly Used Features Obtained by Linear Transform
In this section, I discuss four commonly used features for data analytics and machine learning. These features are effective in data classification and representation, and can be easily obtained by a simple linear transform of the data. The simplicity and effectiveness of these features makes them useful for streaming data and edge applications.
In mathematical terms, let {xk} be an n-dimensional (zero mean) sequence that represents the data. We are seeking a matrix sequence {Wk} and a transform:
, (1.1)
such that the linear transform yk has properties of data representation and is our desirable feature. I discuss a few of these features later.
Definition: Define the data correlation matrix A of {xk} as
![$$ A=underset{k o infty }{lim }Eleft[{mathbf{x}}_k{mathbf{x}}_k^T
ight] $$](https://imgdetail.ebookreading.net/2023/10/9781484280171/9781484280171__9781484280171__files__images__522202_1_En_1_Chapter__522202_1_En_1_Chapter_TeX_IEq2.png)
. (1.2)
Data Whitening
Data whitening is a process of decorrelating the data such that all components have unit variance. It is a data preprocessing step in machine learning and data analysis to “normalize” the data so that it is easier to model. Here the linear transform yk of the data has the property ![$$ Eleft[{mathbf{y}}_k{mathbf{y}}_k^T
ight] $$](https://imgdetail.ebookreading.net/2023/10/9781484280171/9781484280171__9781484280171__files__images__522202_1_En_1_Chapter__522202_1_En_1_Chapter_TeX_IEq3.png)
=In (identity). I discuss in Chapter 3 that the optimal value of Wk=A–½.
Original correlated data is uncorrelated by the data whitening algorithm
Principal Components
Principal component analysis (PCA) is a well-studied example of the data representation model. From the perspective of classical statistics, PCA is an analysis of the covariance structure of multivariate data {xk}. Let yk=[yk1,…,ykp]T be the components of the PCA-transformed data. In this representation, the first principal component yk1 is a one-dimensional linear subspace where the variance of the projected data is maximal. The second principal component yk2 is the direction of maximal variance in the space orthogonal to the yk1 and so on.
It has been shown that the optimal weight matrix Wk is the eigenvector matrix of the correlation of the zero-mean input process {xk}. Let AΦ=ΦΛ be the eigenvector decomposition (EVD) of A, where Φ and Λ are respectively the eigenvector and eigenvalue matrices. Here Λ=diag(λ1,…,λn) is the diagonal eigenvalue matrix with λ1≥…≥λn>0 and Φ is orthonormal. We denote Φp∈ℜnXp as the matrix whose columns are the first p principal eigenvectors. Then optimal Wk=Φp.
- 1.
When p=n, the n components of yk are ordered according to maximal to minimal variance. This is the component analyzer that is used for data analysis.
- 2.
When p<n, the p components of yk have maximal information for data compression.
- 3.
For p<n, the n–p components of yk with minimal variance can be regarded as abnormal signals and reconstructed as (In–ΦpΦpT)xk to obtain a novelty filter.
Original correlated data is uncorrelated by PCA projection
Linear Discriminant Features
data correlation matrix B=E(xkxkT),
cross correlation matrix M=E(xkckT),
and A=MMT.
It is well known that the linear transform Wk (Eq 1.1) is the generalized eigen-decomposition (GEVD) [generalized eigenvector, Wikipedia] of A with respect to B. Here AΨ=BΨΔ where Ψ and Δ are respectively the generalized eigenvector and eigenvalue matrices. Furthermore, Ψp∈ℜnXp is the matrix whose columns are the first p≤n principal generalized eigenvectors.
Original correlated data is uncorrelated by linear discriminant analysis
Singular Value Features
Singular value decomposition (SVD) [singular value decomposition, Wikipedia] is a special case of a EVD problem as follows. Given the cross-correlation (n-by-m real) matrix M=E(xkckT) ∈ℜnXm, SVD computes two matrices Uk∈ℜnXn and Vk∈ℜmXm such that UkTMVk=Snxm, where Uk and Vk are orthonormal and S=diag(s1,...sr), r=min(m, n), with s1>=...>=sr>=0. By rearranging the vectors xk and ck we can make a nxm dimensional SVD problem into a (n+m)x(n+m) dimensional EVD problem.
Summary
.Statistical Property of yk and Matrix Property of Wk
Computation | Statistical Property of yk | Matrix Property of Wk |
|---|---|---|
Whitening |
| Wk = A–½ = ΦΛ–½ΦT |
PCA/EVD | Max | Wk = Φp and |
LDA/GEVD | Max | Wk = Ψp and |
![$$ Eleft[{mathbf{y}}_k{mathbf{y}}_k^T
ight]={I}_n $$](https://imgdetail.ebookreading.net/2023/10/9781484280171/9781484280171__9781484280171__files__images__522202_1_En_1_Chapter__522202_1_En_1_Chapter_TeX_IEq5.png)
![$$ Eleft[{mathbf{y}}_k^T{mathbf{y}}_k
ight] $$](https://imgdetail.ebookreading.net/2023/10/9781484280171/9781484280171__9781484280171__files__images__522202_1_En_1_Chapter__522202_1_En_1_Chapter_TeX_IEq6.png)
![$$ Eleft[{mathbf{y}}_k{mathbf{y}}_k^T
ight]={I}_p $$](https://imgdetail.ebookreading.net/2023/10/9781484280171/9781484280171__9781484280171__files__images__522202_1_En_1_Chapter__522202_1_En_1_Chapter_TeX_IEq8.png)
![$$ Eleft[{mathbf{y}}_k^T{mathbf{y}}_k
ight] $$](https://imgdetail.ebookreading.net/2023/10/9781484280171/9781484280171__9781484280171__files__images__522202_1_En_1_Chapter__522202_1_En_1_Chapter_TeX_IEq9.png)
![$$ Eleft[{mathbf{y}}_k{mathbf{y}}_k^T
ight]={I}_p $$](https://imgdetail.ebookreading.net/2023/10/9781484280171/9781484280171__9781484280171__files__images__522202_1_En_1_Chapter__522202_1_En_1_Chapter_TeX_IEq11.png)
1.2 Multi-Disciplinary Origin of Linear Features
In this section, I further discuss the importance of data representation and classification features by showing how multiple disciplines derive these features and compute them adaptively for streaming data. For each discipline, I demonstrate the use of these features on real data.
Hebbian Learning or Neural Biology
Hebb’s postulate of learning is the oldest and most famous of all learning rules. Hebb proposed that when an axon of cell A excites cell B, the synaptic weight W is adjusted based on f(x,y), where f(⋅) is a function of presynaptic activity x and postsynaptic activity y. As a special case, we may write the weight adjustment ΔW=ηxyT, where η>0 is a small constant.
Given an input sequence {xk}, we can construct its linear transform 
, where wk∈ℜn is the weight vector. We can describe a Hebbian rule [Haykin 94] for adjusting wk as wk+1=wk+ηxkyk. Since this rule leads to exponential growth, Oja [Oja 89] introduced a rule to limit the growth of wk by normalizing wk as follows:
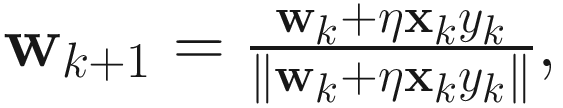(1.3)
Assuming small η and ‖wk‖=1, (1.3) can be expanded as a power series in η, yielding
(1.4)
Eliminating the O(η2) term, we get the constrained Hebbian algorithm (CHA) or Oja’s one-unit rule (Chapter 4, Sec 4.3). Indeed, this algorithm converges to the first principal eigenvector of A.
Note that adaptive PCA algorithms are commonly used on streaming data and some GitHubs exist. I create here a comprehensive repository of these algorithms and also present new ones in this book and the associated GitHub.
Adaptive PCA algorithm used on seasonal streaming data
Auto-Associative Networks
Auto-association is a neural network structure in which the desired output is same as the network input xk. This is also known as the linear autoencoder [autoencoder, Wikipedia]. Let’s consider a two-layer linear network with weight matrices W1 and W2 for the input and output layers, respectively, and p (≤n) nodes in the hidden layer. The mean square error (MSE) at the network output is given by
![$$ e=Eleft[{leftVert {mathbf{x}}_k-{W}_2^T{W}_1^T{mathbf{x}}_k
ightVert}^2
ight] $$](https://imgdetail.ebookreading.net/2023/10/9781484280171/9781484280171__9781484280171__files__images__522202_1_En_1_Chapter__522202_1_En_1_Chapter_TeX_IEq15.png)
. (1.5)
Due to p nodes in the hidden layer, a minimum MSE produces outputs that represent the best estimates of xk∈ℜn in the ℜp subspace. Since projection onto Φp minimizes the error in the ℜp subspace, we expect the first layer weight matrix W1 to be rotations of Φp. The second layer weight matrix W2 is the inverse of W1 to finally represent the “best” identity transform. This intuitive argument has been proven [Baldi and Hornik 89,95, Bourland and Kamp 88], where the optimum weight matrices are
W1 = ΦpR and 
, (1.6)
, then R is a unitary matrix and the input layer weight matrix W1 is orthonormal and spans the space defined by Φp, the p principal eigenvectors of the input correlation matrix A. See Figure 1-7.
Auto-associative neural network
Note that if we have a single node in the hidden layer (i.e., p=1), then we obtain e as the output sum squared error for a two-layer linear auto-associative network with input layer weight vector w and output layer weight vector wT. The optimal value of w is the first principal eigenvector of the input correlation matrix Ak.
The result in (1.6) suggests the possibility of a PCA algorithm by using a gradient correction only to the input layer weights, while the output layer weights are modified in a symmetric fashion, thus avoiding the backpropagation of errors in one of the layers. One possible version of this idea is
and W2(k + 1) = W1(k + 1)T. (1.7)
Denoting W1(k) by Wk, we obtain an algorithm that is the same as Oja’s subspace learning algorithm (SLA).
Convergence of the first two principal eigenvectors computed from multidimensional streaming data. Data is on the left and feature convergence (ideal value = 1) is on the right
Hetero-Associative Networks
Hetero-associative neural network
We consider a two-layer linear hetero-associative neural network with just a single neuron in the hidden layer and m≤n output units. Let w∈ℜn be the weight vector for the input layer and v∈ℜm be the weight vector for the output layer. The MSE at the network output is
e = E{‖d − vwTx‖2}. (1.8)
We further assume that the network has limited power, so wTBw=1. Hence, we impose this constraint on the MSE criterion in (1.8) as
J(w, v) = E{‖d − vwTx‖2} + μ(wTBw − 1), (1.9)
where μ is the Lagrange multiplier. This equation has a unique global minimum where w is the first principal eigenvector of the matrix pencil (A,B) and v=MTw. Furthermore, from the gradient of (1.9) with respect w, we obtain the update equation for w as
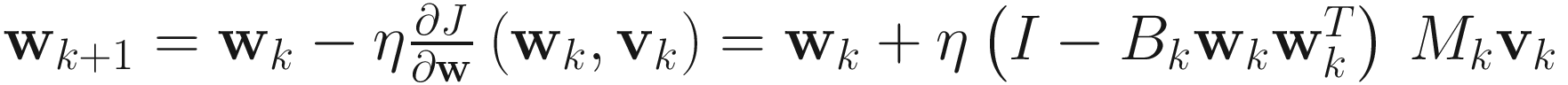. (1.10)
We can substitute the convergence value of v (1.10) and avoid the back-propagation of errors in the second layer to obtain
(1.11)
This algorithm can be used effectively to adaptively compute classification features from streaming data.
The original multi-dimensional e-shopping data on the left 2 figures.
The original data correlation on the right (3rd figure). The original data correlation matrix shows that the classes are indistinguishable in the original data.
The correlation matrix of the data transformed by algorithm (1.11) on the far right. The white and red blocks on the far right matrix show the two classes are clearly separated in the transformed data by the algorithm (1.11).
e-Shopping clickstream data on the left and uncorrelated class separable data on the right
Statistical Pattern Recognition
One special case of linear hetero-association is a network performing one-from-m classification, where input x to the network is classified into one out of m classes ω1,...,ωm. If x∈ωi then d=ei where ei is the ith standard basis vector. Unlike auto-associative learning, which is unsupervised, this network is supervised. In this case, A and B are scatter matrices. Here A is the between-class scatter matrix Sb, the scatter of the class means around the mixture mean, and B is the mixture scatter matrix Sm, the covariance of all samples regardless of class assignments. The generalized eigenvector decomposition of (A,B) is known as linear discriminant analysis (LDA), which was discussed in Section 1.1.
Information Theory
Another viewpoint of the data model (1.1) is due to Linsker [1988] and Plumbley [1993]. According to Linsker’s Infomax principle, the optimum value of the weight matrix W is when the information I(x,y) transmitted to its output y about its input x is maximized. This is equivalent to information in input x about output y since I(x,y)=I(y,x). However, a noiseless process like (1.1) has infinite information about input x in y and vice versa since y perfectly represents x. In order to proceed, we assume that input x contains some noise n, which prevents x from being measured accurately by y. There are two variations of this model, both inspired by Plumbley [1993].
In the first model, we assume that the output y is corrupted by noise due to the transform W. We further assume that average power available for transmission is limited, the input x is zero-mean Gaussian with covariance A, the noise n is zero-mean uncorrelated Gaussian with covariance N, and the transform noise n is independent of x. The noisy data model is
y = WTx + n. (1.12)
The mutual information I(y,x) (with Gaussian assumptions) is
I(y, x) = 0.5 log det(WTAW + N) − 0.5 log det(N). (1.13)
We define an objective function with power constraints as
J(W) = I(y, x) − 0.5tr(Λ(WTAW + N)), (1.14)
where Λ is a diagonal matrix of Lagrange multipliers. This function is maximized when W=ΦR, where Φ is the principal eigenvector matrix of A and R is a non-singular rotation matrix.
Optimization Theory
In optimization theory , various matrix functions are computed by evaluating the maximums and minimums of objective functions. Given a symmetric positive definite matrix pencil (A,B), the first principal generalized eigenvector is obtained by maximizing the well-known Raleigh quotient:
. (1.15)
Lagrange multiplier:
J(w) = − wTAw + α(wTBw − 1), (1.16)
Penalty function:
J(w) = − wTAw + μ(wTBw − 1)2, (1.17)
Augmented Lagrangian:
J(w) = − wTAw + α(wTBw − 1) + μ(wTBw − 1)2, (1.18)
where α is a Lagrange multiplier and μ > 0 is the penalty constant. Several algorithms based on this objective function are given in Chapters 4-7.
We obtain adaptive algorithms from these objective functions by using instantaneous values of the gradients and a gradient ascent technique, as discussed in the following chapters. One advantage of these objective functions is that we can use accelerated convergence methods such as steepest descent, conjugate direction, and Newton-Raphson. Chapter 6 discusses several such methods. The recursive least squares method has also been applied to adaptive matrix computations by taking various approximations of the inverse Hessian of the objective functions.
1.3 Why Adaptive Algorithms?
- 1.
The first set of solutions requires the relevant matrices to be known in advance.
- 2.
The second set of solutions requires a sequence of samples from which the matrix can be computed.
In this section, I explain the difference between batch and adaptive processing, benefits of adaptive processing on streaming data, and the requirements for adaptive algorithms.
Iterative or Batch Processing of Static Data
When the data is available in advance and the underlying matrices are known, we can use the batch processing approach. These algorithms have been used to solve a large variety of matrix algebra problems such as matrix inversion, EVD, SVD, and PCA [Cichocki et al. 92, 93]. These algorithms are solved in two steps: (1) using the pooled data to estimate the required matrices, and (2) using a numerical matrix algebra procedure to solve the necessary matrix functions.
For example, consider a simple matrix inversion problem for the correlation matrix A of a data sequence {xk}. We can calculate the matrix inverse A-1 after all of the data have been collected and A has been calculated. This approach works in a batch fashion. When a new sample x is added, it is not difficult to get the inverse of the new matrix Anew=(nA+xxT)/(n+1), where n is the total number of samples used to compute A. Although the computation for A is simple, all the computations for solving 
need to be repeated.
- 1.
First, the dimension of the samples may be large so that even if all the samples are available, performing the matrix algebra may be difficult or may take a prohibitively large amount of computational time. For example, eigenvector evaluation requires O(n3) computation, which is infeasible for samples of a large dimension (say 1,000) which occurs commonly in image processing and automatic control applications.
- 2.
Second, the matrix functions evaluated by conventional schemes cannot adapt to small changes in the data (e.g., a few incoming samples). If the matrix functions are estimated by conventional methods from K samples, then for each additional sample all of the computation has to be repeated.
These deficiencies make the batch schemes inefficient for real-time applications where the data arrives incrementally or in an online fashion.
My Approach: Adaptive Processing of Streaming Data
When we have a continuous sequence of data samples, batch algorithms are no longer useful. Instead, adaptive algorithms are used to solve matrix algebra problems. An immediate advantage of these algorithms is that they can be used on real-time problems such as edge computation, adaptive data compression [Le Gall 91], antenna array processing for noise analysis and source location [Owsley 78], and adaptive spectral analysis for frequency estimation [Pisarenko 73].
My approach is to offer computationally simple adaptive algorithms for matrix computations from streaming data. Note that adaptive algorithms are critical in environments where the data volume is large, the data has high dimensions, the data is time varying and has changing underlying statistics, and we do not have sufficient storage, compute, and bandwidth to process the data with low latency. One such environment is edge devices and computation.
wk is last value of the sentiment,
wk+1 is the latest updated value of the sentiment,
xk is the newest data used to calculate wk+1, and
f(.) is a simple function of wk and xk.
An example of this update rule is the well-known algorithm [Oja 82] to compute the first principal eigenvector of a streaming sequence {xk}:
, (1.19)
where η>0 is a small gain constant. In this algorithm, for each sample xk the update procedure requires simple matrix-vector multiplications, and the vector wk converges to the principal eigenvector of the data correlation matrix A. Clearly, this can be easily implemented in small CPUs.
e-Shopping clickstream data on the left and buyer sentiments computed by the update rule (1.19) on the right (ideal value = 1)
There are several advantages and disadvantages of adaptive algorithms over conventional iterative batch solutions.
While conventional solutions find all eigenvectors and eigenvalues, adaptive solutions compute the desired eigenvectors only. In many applications, we do not need eigenvalues. Hence, they should be more efficient.
Furthermore, computational complexity of adaptive algorithms depends on the efficiency of the matrix-vector product Ax. These methods can be even more efficient when the matrix A has a certain structure such as sparse, Hankel, or Toeplitz for which FFT can be used to speed up the computation.
Adaptive algorithms easily fit the framework of time-varying multidimensional processes such as adaptive signal processing, where the input process is continuously updated.
Adaptive algorithms produce an approximate value of the features for the current dataset whereas batch algorithms provide an exact value.
The adaptive approach requires a “ramp up” time to reach high accuracy as evidenced by the curves in Figure 1-10.
Requirements of Adaptive Algorithms
The algorithms should adapt to small changes in data, which is useful for real-time applications.
The estimates obtained from the algorithms should have known statistical properties.
The network architectures associated with the adaptive algorithms consist of linear units in one- or two-layer networks, such that the networks can be easily implemented with simple CPUs and no special hardware.
The computation involved in the algorithms is inexpensive such that the statistical procedure can process every data sample as they arrive.
The estimates obtained from the algorithms converge strongly to their actual values.
With these requirements, we proceed to design adaptive algorithms that solve the matrix algebra problems considered in this book. The objective of this book is to develop a variety of neuromorphic adaptive algorithms to solve matrix algebra problems.
Although I will discuss many adaptive algorithms to solve the matrix functions, most of the algorithms are of the following general form:
Wk + 1 = Wk + ηH(xk, Wk), (1.20)
where H(xk,Wk) follows certain continuity and regularity properties [Ljung 77,78,84,92], and η > 0 is a small gain constant. These algorithms satisfy the requirements outlined before.
Real-World Use of Adaptive Matrix Computation Algorithms and GitHub
In Chapter 8, I discuss several real-world applications of these adaptive matrix computation algorithms. I also published the code for these applications in a public GitHub [Chanchal Chatterjee GitHub].
1.4 Common Methodology for Derivations of Algorithms
- 1.
I present a common methodology to derive and analyze each adaptive algorithm.
- 2.
I present adaptive algorithms to a number of matrix algebra problems.
The literature for adaptive algorithms for matrix computation offers a wide range of techniques (including ad hoc methods) and various types of convergence procedures. In this book, I present a common methodology to derive and prove the convergence of the adaptive algorithms (all proofs are in the GitHub).
The advantage of adopting this is to allow the reader to follow the methodology and derive new adaptive algorithms for their use cases.
- 1.
Objective function
- 2.
Derive the adaptive algorithm
I derive an adaptive update rule for matrix W by applying the gradient descent technique on the objective function J(W;Ak). The adaptive gradient descent update rule is
Wk + 1 = Wk − ηk∇WJ(Wk, Ak) = Wk + ηkh(Wk, Ak), (1.21)
- 3.
Speed up the adaptive algorithm
- 4.
Show the algorithms converge to the matrix functions
In this book, I provide numerical experiments to demonstrate the convergence of these algorithms. The mathematical proofs are provided in a separate document in the GitHub [Chatterjee Github].
An important benefit of following this methodology is to allow practitioners to derive new algorithms for their own use cases.
Matrix Algebra Problems Solved Here
In the applications, I consider the data as arriving in temporal succession, such as in vector sequences {xk} or {yk}, or in matrix sequences {Ak} or {Bk}. Note that the algorithms given here can be used for non-stationary input streams.
Mean, correlation, and normalized mean of {xk}
Square root (A½) and inverse of the square root (A–½) of A from {xk} or {Ak}
Principal eigenvector of A from {xk} or {Ak}
Principal and minor eigenvector of A from {xk} or {Ak}
Generalized eigenvectors of A with respect to B from {xk} and {zk} or {Ak} and {Bk}
Singular value decomposition (SVD) of C from {xk} and {zk} or {Ck}
Adaptive computation of mean, covariance, and matrix inversion
Methods to accelerate the adaptive algorithms by techniques of nonlinear optimization
1.5 Outline of The Book
In the following chapters, I discuss in detail the formulation, derivation, convergence, and experimental results of many adaptive algorithms for various matrix algebra problems.
In Chapter 2, I discuss basic terminologies and methods used throughout the remaining chapters. This chapter also discusses adaptive algorithms mean, median, correlation, covariance, and inverse correlation/covariance computation for both stationary and non-stationary data. I further discusses novel adaptive algorithms for normalized mean computation.
In Chapter 3, I discuss three adaptive algorithms for the computation of the square root of a matrix sequence. I next discuss three algorithms for the inverse square root of the same. I offer objective functions and convergence proofs for these algorithms.
In Chapter 4, I discuss 11 algorithms, some of them new algorithms, for the adaptive computation of the first principal eigenvector of a matrix sequence or the online correlation matrix of a vector sequence. I offer best practices to choose the algorithm for a given application. I follow the common methodology of deriving and analyzing the convergence of each algorithm, supported by experimental results.
In Chapter 5, I present 21 adaptive algorithms for the computation of principal and minor eigenvectors of a matrix sequence or the online correlation matrix of a vector sequence. These algorithms are derived from 7 different types of objective functions, each under 3 different conditions. Each algorithm is derived, discussed, and shown to converge analytically and experimentally. I offer best practices to choose the algorithm for a given application.
Since I have objective functions for all of the adaptive algorithms, in Chapter 6, I deviate from the traditional gradient descent method of deriving the algorithms. Here I derive new computationally faster algorithms by using steepest descent, conjugate direction, Newton-Raphson, and recursive least squares on the objective functions. Experimental results and comparison with state-of-the-art algorithms show the faster convergence of these adaptive algorithms.
In Chapter 7, I discuss 21 adaptive algorithms for generalized eigen-decomposition from two matrix or vector sequences. Once again, I follow the common methodology and derive all algorithms from objective functions, followed by experimental results.
In Chapter 8, I present real-world applications of these algorithms with examples and code.
The bibliography is in Chapter 9.