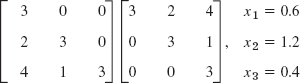
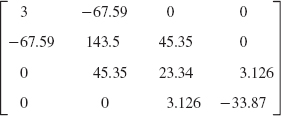
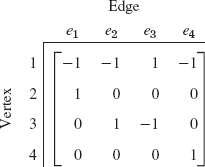
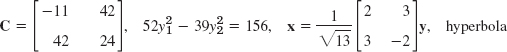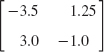APPENDIX 2

Answers to
Odd-Numbered Problems

Problem Set 1.1, page 8

• 1.
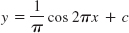
• 3. y = ce^x
• 5. y = 2e^−x(sin x − cos x + c
• 7.
• 9. y = 1.65e^−2x + 0.35
• 11.
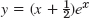
• 13. y = 1/(1 + 3e^x)
• 15. y = 0 and y = 1 because y′ = 0 for these y
• 17. exp, t = 10¹¹(1n 2)/1.4 [sec]
• 19. Integrate y″ g twice, y′(t) = gt + v₀, y′(0) = v₀ = 0 (start from rest), then , where y(0) = y₀ = 0

Problem Set 1.2, page 11

• 11. Straight lines parallel to the x-axis
• 13. y = x
• 15. mv′ = mg − bv², v′ = 9.8 − v², v(0) = 10, v′ = 0 gives the limit/9.8 = 3.1 [meter/sec]
• 17. Errors of steps 1, 5, 10: 0.0052, 0.0382, 0.1245, approximately
• 19. x₅ = 0.0286(error 0.0093), x₁₀ = 0.2196(error 0.0189)

Problem Set 1.3, page 18

• 1. If you add a constant later, you may not get a solution. Example: y′ = y, In |y| = x + c, 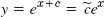but not e^x + c (with c ≠ 0)
• 3. cos²y dy = dx,
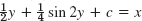
• 5. y² + 36x² = c, ellipses
• 7. y = x arctan (x₂ + c)
• 9. y = x/(c − x)
• 11. y = 24/x, hyperbola
• 13. dy/sin²y = dx/cosh²x, −cot y = tanh x + c, c = 0, y = −arccot (tanh x)
• 15. y² + 4x² = c = 25
• 17. y = x arctan (x³ − 1)
• 19. y0e^kt = 2y0, e^k = 2 (1 week), e^2k = 2²(2 weeks), e^4k = 2⁴
• 21. 69.6% of y₀
• 23. pV = c = const
• 25. T = 22 − 17e^−0.5306t = 21.9 [°C] when t = 9.68 min
• 27. , e^−kt0 − 0.01,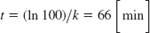
• 29. No. Use Newton's law of cooling.
• 31. y = ax, y′ = g(y/x) = a = const, independent of the point (x,y)
• 33. ΔS = 0.5SΔφ, ds/dφ = 0.15S, S = S_0e^0.15φ = 1000S₀, φ = (1/0.15) In 1000 = 7.3 · 2π. Eight times.

Problem Set 1.4, page 26

• 1. Exact, 2x = 2x, x²y = c,y = c/x²
• 3. Exact, y = arccos (c/cos x)
• 5. Not exact,
• 7.
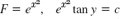
• 9. Exact, u = e^2x cos y + k(y), u_y = −e^2x sin y + k′, k′ = 0. Ans. e^2x cos y = 1
• 11. F = sinh x, sinh² x cos y = c
• 13. u = e^x + k(y), u_y = k′ = −1 + e^y, k = −y + e^y. Ans. e^x − y + e^y = c
• 15. b = k, ax² + 2kxy + ly² = c

Problem Set 1.5, page 34

• 3. y = ce^x − 5.2
• 5. y = (x + c)e^−kx
• 7. y = x²(c + e^x)
• 9. y = (x − 2.5/e)e^{cos x}
• 11. y = 2 + c sin x
• 13. Separate. y − 2.5 = c cosh⁴ 1.5x
• 15. (y₁ + y₂)′ + p(y₁ + y₂) = (y₁′ + py₂) = 0 + 0 = 0
• 17. (y₁ + y₂)′ + p(y₁ + y₂) = (y₁′ + py₂) = r + 0 = r
• 19. Solution of cy₁′ + pcy₁ + c(y′₁ + py₁) = cr
• 21. . Thus, y = uyh gives (4). We shall see that this method extends to higher-order ODEs (Secs. 2.10 and 3.3).
• 23.
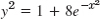
• 25. y = 1/u, u = ce^−3.2x + 10/3.2
• 27. dx/dy = 6e^y − 2x, x = ce^−2y + 2e^y
• 31. T = 240e^kt + 60, T(10) = 200, k = −0.0539, t = 102 min
• 33. y′ = A − ky, y(0) = 0, y = A(1 − e^−kt)/k
• 35. y′ = 175(0.0001 − y/450), y(0) = 450 · 0.0004 = 0.18, y = 0.135e^−0.3889t + 0.045 = 0.18/2, e^−0.3889t = (0.09 − 0.045)/0.135 = 1/3, t = (In 3)/0.3889 = 2.82. Ans. About 3 years
• 37. y′ = y − y² − 0.2y, y = 1/(1.25 − 0.75e^−0.8t), limit 0.8, limit 1
• 39.. y′ = By(y − A/B,A > 0,B > 0. Constant solutions y = 0, y = A/B, y′ > 0 if y > A/B (unlimited growth), y′ < 0 if 0 < y < A/B (extinction). y = A/(ce^At + B), y(0) > A/B if c < 0, y(0) < A/B if c > 0.

Problem Set 1.6, page 38

• 1. x²/(c² + 9) + Y²/c² m 1 = 0
• 3. y − cosh (x − c) − c = 0
• 5. 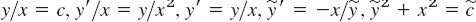, circles
• 7.
• 9.
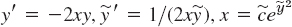
• 11.
• 13. y′ = −4x/9y. Trajectories 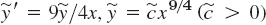. Sketch or graph these curves.
• 15. u = c, u_xdx + u_ydy = 0, y′ = −u_x/u_y. Trajectories. . Now , y′ = −_x/u_y. This agrees with the trajectory ODE in u if u_x = v_y (equal denominators) and u_y = −v_x(equal numerators). But these are just the Cauchy–Riemann equations.

Problem Set 1.7, page 42

• 1. y′ = f(x,y) = r(x) − ∂f/∂y = −p(x) is continuous and is thus bounded in the closed interval. |x − x₀| a.
• 3. In |x − x₀| < a; just take b in α = b/k large, namely, b = αk.
• 5. R has sides 2a and 2b and center (1, 1) since y(1) = 1. = 1. In R, f = 2y² 2(b + 1)² = K, α = b/K = b/(2(b + 1)²2), dα/db = 0 gives b = 1, and 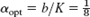. Solution by dy/y²2 = 2 dx, etc., y = 1/(3 − 2x).
• 7. |1 + y²| K = 1 + b², α = b/K, dα/db = 0, b = 1, .
• 9. No. At a common point (x₁,y₁) they would both satisfy the “initial condition” y(x₁) = y₁, violating uniqueness.

Chapter 1 Review Questions and Problems, page 43

• 11. y = cey−2x
• 13. y = 1/(cey−4x + 4)
• 15. y = ce^−x + 0.01 cos 10x + 0.1 sin 10x
• 17. y = ce^−2.5x + 0.640x − 0.256
• 19. 25y² − 4x² = c
• 21. F = x,x³e^y + x²y = c
• 23.
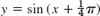
• 25.
• 27. e^k = 1.25, (In 2)/In 1.25 = 3.1, (In 3)/In 1.25 = 4.9 [days]
• 29. e^k = 0.9, 6.6 days. 43.7 days from e^kt = 0.5,e^kt = 0.01

Problem Set 2.1, page 53

• 1. F(x,z,z′) = 0
• 3. y = c₁e^2x + c₂
• 5. y = (c₁x + c₂)^−1/2
• 7.
• 9. y₂ = x³ In x
• 11.
• 13.
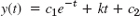
• 15. y = 3 cos 2.5x − sin 2.5x
• 17. y = −0.75x^3/2 − 2.25x^−1/2
• 19. y = 15e^−x − sin x

Problem Set 2.2, page 59

• 1.
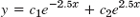
• 3.
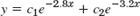
• 5.
• 7.
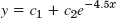
• 9.
• 11.
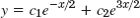
• 13.
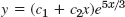
• 15.
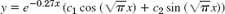
• 17.
• 19. y″ + 4y′ + 5y = 0
• 21. y = 4.6 cos 5x − 0.24 sin 5x
• 23. y = 6e^2x + 4e^−3x
• 25. y = 2e^−x
• 27. y = (4.5 − x)e^−πx
• 29.
• 31. Independent
• 33. In x = 0 with x = 1 gives c₁ = 0; then c₂ = 0 for x = 2, say.
• 35. Dependent since sin 2x = 2 sin x cos x
• 37. y₁ = e^−x, = y₂ = 0.001e^x + e^−x

Problem Set 2.3, page 61

• 1. 4e^2x, −e^−x + 8e^−2x, −cos x − 2 sin x
• 3. 0, 0, (D − 2I)(−4e^−2x = 8e^−2x + 8e^−2x
• 5.
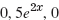
• 7.
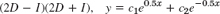
• 9.
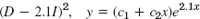
• 11.
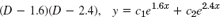
• 15. Combine the two conditions to get L(cy + kw) = L(cy) + L(kw) = cLy + kLw. The converse is simple.

Problem Set 2.4, page 69

• 1.. y′ = y₀ cos ω₀t + (v₀/ω₀) sin ω₀t. At integer t (if ω₀ = π), because of periodicity.
• 3. (i) Lower by a factor 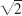(ii) higher by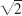
• 5.
• 7. mLθ″ = −mg sin θ ≈ −mgθ (tangential component of W = mg), .
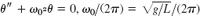• 9. , where m = 1 kg, ay = π · 0.01² · 2y meter³ is the volume of the water that causes the restoring force. aγy with γ = 9800 nt (= weight/meter³). 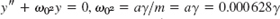. Frequency .
• 13.
• 15.
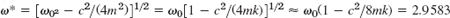
• 17. The positive solutions of tan t = 1, that is, π/4 (max), 5π/4 (min). etc
• 19.

Problem Set 2.5, page 73

• 3. y = (c₁ + c₂ In x)x^−1.8
• 5.
• 7.
• 9. y = (c₁ + c₂ In x)x^0.6
• 11.
• 13. y = x^−3/2
• 15. y = (3.6 + 4.0 In x)/x
• 17. y = cos (In x) + sin (In x)
• 19. y = −0.525x⁵ + 0.625x⁻³

Problem Set 2.6, page 79

• 3. W = −2.2e^−3x
• 5. W = −x⁴
• 7. W = a
• 9. y″ + 25y = 0, W = 5, y = 3 cos 5x − sin 5x
• 11. y″ + 5y + 6.34 = 0, W = 0.3e^−5x, 3e^−2.5cos 0.3x
• 13. y″ + 2y′ = 0, W = −2e^−2x, y = 0.5(1 + e^−2x
• 15. y″ − 3.24y = 0, W = 1.8, y = 14.2 cosh 1.8x + 9.1 sinh 1.8x

Problem Set 2.7, page 84

• 1.
• 3.
• 5.
• 7.
• 9.
• 11.
• 13.
• 17. y = e^−0.1x(1.5 cos 0.5x − sin 0.5x) + 2e^0.5x

Problem Set 2.8, page 91

• 3. y_p = 1.0625 cos 2t + 3.1875 sin 2t
• 5. y_p = −1.28 cos 4.5t + 0.36 sin 4.5t
• 7.
• 9. y = e^−1.5t(A cos t + B sin t) + 0.8 cos t + 0.4 sin t
• 11.
• 13. y = A cos t + B sin t − (cos ωt)/(ω² − 1)
• 15.
• 17.
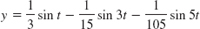
• 19.
• 25. CAS Experiment. The choice of needs experimentation, inspection of the curves obtained, and then changes on a trail-and-error basis. It is interesting to see how in the case of beats the period gets increasingly longer and the maximum amplitude gets increasingly larger as ω/(2π)approaches the resonance frequency.

Problem Set 2.9, page 98

• 1. RI′ + I/C = 0, I = ce^−t/(RC)
• 3. LI′ + RI = E, I = (E/R) + ce^Rt/L = 4.8 + ce^−40t
• 5. I = 2 (cos t − cos 20t)/399
• 7. I₀ is maximum when S = 0; thus, c = 1/(ω²L).
• 9. I = 0
• 11. I = 5.5 cos 10t + 16.5 sin 10t A
• 13. I = e^−5t(A cos 10t + B sin 10t) − 400 cos 25t + 200 sin 25t A
• 15.
• 17. E(0) = 600, I′(0) = 600, I = e^−3t (−100 cos 4t + 75 sin 4t) + 100 cos t
• 19. R = 2Ω, L = 1 H, C = 1/12 F, E = 4.4 sin 10t V

Problem Set 2.10, page 102

• 1.
• 3.
• 5.
• 7. y = (c₁ + c₂x)e^2x + x⁻²e^2x
• 9. y = (c1 + c₂x)e^x + 4x^7/2e^x
• 11. y = c₁x² + c₂x³ + 1/(2x⁴)
• 11. y = c₁x² + c₂x³ + 1/(2x⁴)
• 13. y = c₁x⁻³ + c₂x³ + 3x⁵

Chapter 2 Review Questions and Problems, page 102

• 7. y = c₁e^−4.5x + c₂e^−3.5x
• 9. y = e^−3x (A cos 5x + B sin 5x)
• 11. y = (c₁ + c₂x)e^0.8x
• 13. y = c₁x⁻⁴ + c₂x³
• 15. y = c₁e^2x + c₂e^−x/2 − 3x + x2
• 17. y = (c₁ + c₂x)e^1.5x + 0.25x²e^1.5x
• 19.
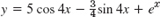
• 21. y = −4x + 2x³ + 1/x
• 23. I = −0.01093 cos 415t + 0.05273 sin 415t A
• 25.
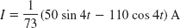
• 27. RLC − circuit with R = 20 Ω, L = 4 H, C = 0.1 F, E = −25 cos 4t V
• 29.

Problem Set 3.1, page 111

• 9. Linearly independent
• 11. Linearly independent
• 13. Linearly independent
• 15. Linearly dependent

Problem Set 3.2, page 116

• 1. y = c₁ + c₂ cos 5x + c₃ sin 5x
• 3. y = c₁ + c₂x + c₃ cos 2x + c₄ sin 2x
• 5. y = A1 cos x + B₁ sin x + A₂ cos 3x + B₂ sin 3x
• 7. y = 2.398 + e^−1.6x (1.002 cos 1.5x − 1.998 sin 1.5x)
• 9. y = 4e^−x + 5e^−x/2 cos 3x
• 11. y = cosh 5x − cos 4x
• 13. y = e^0.25x + 4.3e^−0.7x + 12.1 cos 0.1x − 0.6 sin 0.1x

Problem Set 3.3, page 122

• 1.
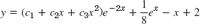
• 3. y = c₁ cos x + c₂ sin x + c₃ cos 3x + c₄ sin 3x + 0.1 sinh 2x
• 5.
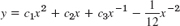
• 7.
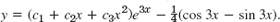
• 9.
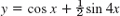
• 11. y = e^−3x (−1.4 cos x − sin x)
• 13. y = 2 − 2 sin x + cos x

Chapter 3 Review Questions and Problems, page 122

• 7. y = c₁ + e^−2x (A cos 3x + B sin 3x)
• 9. y = c₁ cosh 2x + c₂ sinh 2x + c3 cos 2x + c₄ sin 2x + cosh x
• 11. y = (c₁ + c₂x + c₃x²)e^−1.5x
• 13. y = (c1 + c₂x + c₃x²)e^−2x + x² − 3x + 3
• 15.
• 17. y = 2e^−2x cos 4x + 0.05 x − 0.06
• 19. y = 4e^−4x + 5e^5x

Problem Set 4.1, page 136

• 1. Yes
• 5. y′₁ = 0.02(−y₁ + y₂), y′₂ = 0.02(y₁ − 2y₂ + y3), y′₃ = 0.02(y2 − y₃)
• 7. c₁ = 1, c₂ = −5
• 9. c₁ = 10, c₂ = 5
• 11.
• 13. y′₁ = y₂, y′₂ = 24y₁ − 2y₂, y₁ = c₁e^4t + c₂e^−6t = y, y2 = y′
• 15. (a) For example, C = 1000 gives −2.39993, −. 0.000167. (b) −2.4, 0. gives the critical case. C about 0.18506.

Problem Set 4.3, page 147

• 1. y₁ = c₁e^−2t + c₂e^−2t, y₂ = −3c₁e^2t − c₂
• 3. y₁ = 2c₁e^2t + 2c₂, y₂ = c₁e^2t − c₂
• 5.
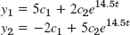
• 7.
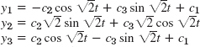
• 9.
• 11.
• 13. y₁ = 2 sinh t, y₂ = 2 cosh t
• 15.
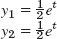
• 17.
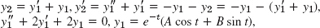
• 19. I₁ = c₁e^−t + 3c₂e^−3t, I₂ = −3c₁e^−t − c₂e^−3t

Problem Set 4.4, page 151

• 1. Unstable improper node, y₁ = c₁e^t, y₂ = c₂e^2t
• 3. Center, always stable, y₁ = A cos 3t + B sin 3t, y₂ = 3B cos 3t − 3A sin 3t
• 5. Stable spiral, y₁ = e^−2t(A cos 2t + B sin 2t), y₂ = e^−2t(B cos 2t − A sin 2t)
• 7. Saddle point, always unstable, y₁ = c₁e^−t + c₂e^3t, y₂ = c₁e^−t + c₂e^3t
• 9. Unstable node, y₁ = c₁e^6t + c₂e^2t, y₂ = 2c₁e^6t − 2c₂e^2t
• 11. y = e^−t (A cos t + B sin t). Stable and attractive spirals
• 15. p = 0.2 ≠ 0 (was 0) δ < 0, spiral point, unstable.
• 17. For instance,

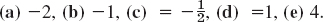
Problem Set 4.5, page 159

• 5. Center at (0, 0). At (2, 0) set 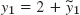. Then . Saddle point at (2, 0).
• 7. (0, 0), y′₁ = −y₁ + y₂, y′₂ = −y₁ m y₂, stable and attractive spiral point; (−2, 2), saddle point
• 9. (0, 0) saddle point, (−3, 0) and (3, 0) centers.
• 11. saddle points; centers. Use −cos
• 13.
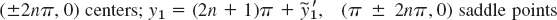
• 15. By multiplication, 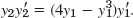By integration,

Problem Set 4.6, page 163

• 3. y₁ = c₁e^−t + c₂e^t, y₂ = −c₁e^−t + c₂e^t − e^3t
• 5. y₁ = c₁e^5t + c₂e^2t − 0.43t − 0.24, y₂ = c₁e^2t − 2c₂e^2t + 1.12t + 0.53.
• 7. y₁ = c₁e^t + 4c₂e^2t − 3t − 4 − 2e^−t − 5c₂e^2t + 5t + 7.5 + e^−t
• 9. The formula for v shows that these various choices differ by multiples of the eigenvector for λ = −2, which can be absorbed into, or taken out of c₁, in the general solution. y^(h)
• 11.
• 13. y₁ = cos 2t + sin 2t + 4 cos t, y₂ = 2 cos 2t − 2 sin 2t + sin t
• 15. y₁ = 3e^−t − 4e^t + e^2t, y₂ = −4e^−t + t
• 17.
• 19. c₁ = 17.948, c₂ = −67.948

Chapter 4 Review Questions and Problems, page 164

• 11. y₁ = c₁e^4t + c₂e^−4t, y₂ = 2c₁e^4t − 2c₂e^−4t. Saddle point.
• 13. asymptotically stable spiral point
• 15. y₁ = c₁e^−5t + c₂e^−t, y₂ = c₁e^−5t − c₂e^−t. Stable node
• 17. y₁ = e^−t(A cos 2t + B sin 2t), y₂ = e^−t(B cos 2t − A sin 2t). Stable and attractive spiral point
• 19. Unstable spiral point
• 21. y₁ = c₁e^−4t + c₂e^4t − 1 − 8t², y₂ = −c₁e^−4t + c₂e^4t − 4t
• 23. y₁ = 2c₁e^−t + 2c₂e^3t + cos t − sin t, y₂ = −c₁e^−t + c₂e^3t
• 25. I1′ + 2.5(I₁ − I₂) = 169 sin t, 2.5(I₂′ − I₂′ − I₁′) + 25I₂ = 0, I₁ = (19 + 32.5t)e^−5t − 19 cos t + 62.5 sin t, I₂ = (−6 − 32.5t)e^−5t + 6 cos t + 2.5 sin t
• 27. (0, 0) Saddle point; (−1, 0), (1, 0) centers
• 29. (nπ, 0) center when n is even and saddle point when n is odd

Problem Set 5.1, page 174

• 3.
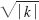
• 5.
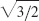
• 7.
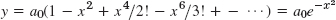
• 9.
• 11.
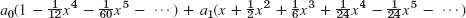
• 13.
• 15.
• 17.
• 19. 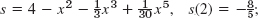but x = 2 is too large to give good values. Exact: y = (x − 2)²e^x

Problem Set 5.2, page 179

• 5.
• 11. Set x = az. y = c₁P_n(x/a) + c₂Q_n(x/a)
• 15.

Problem Set 5.3, page 186

• 3.
• 5. b₀ = 1, c₀ = 0, r² = 0, y₁ = e^−x, y² = e^−x In x
• 7.
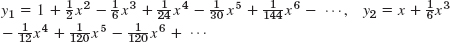
• 9.
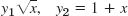
• 11. y₁ = e^x, y₂ = e^x/x
• 13. y₁ = e^x, y₂ = e^x In x
• 15.
• 17.
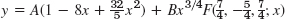
• 19.

Problem Set 5.4, page 195

• 3.
• 5.
• 7.
• 9.
• 13. 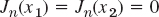implies 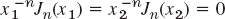and somewhere betweenx₁ and x₂ by Rolle's theorem. Now use (21b) to get J_n+1(x) = 0 there. Conversely, 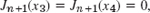thus implies J_n(x) = 0 in between by Roll's theorem and (21a) with v = n + 1.
• 15.By Rolle, J′_o = 0 at least once between two zeros of J₀. Use J′_o = −J₁ by (21b) with v = 0. Together J₁ = 0 at least once between two zeros of J_o. Also use (xJ₁)′ = xJ_o by (21a) with v = 1 and Rolle.
• 19. Use (21b) with v = 0, (21a) with v = 1, (21d) with v = 2, respectively.
• 21. Integrate (21a).
• 23. Use (21a) with v = 1, partial integration, (21b) with v = 0, partial integration.
• 25. Use (21d) to get

  

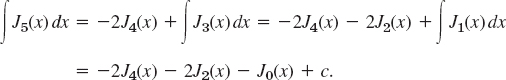
Problem Set 5.5, page 200

• 1. c₁J₄(x) + c₂Y₄(x)
• 3. c₁J_2/3(x₂) + c₂Y_2/3(x₂)
• 5.
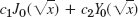
• 7.
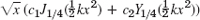
• 9. x₃(c₁J₃(x) + c₂Y₃(x))
• 11. Set H₍₁₎ = kH₍₂₎ and use (10).
• 13. Use (20) in Sec. 5.4.

Chapter 5 Review Questions and Problems, page 200

• 11. cos 2x, sin 2x
• 13.(x − 1)⁻⁵, (x − 1)⁷; Euler–Cauchy with x − 1 instead of x
• 15. J_/s(x), J_−/5(x)
• 17. e^x, 1 + x
• 19.

Problem Set 6.1, page 210

• 1. 3/s² + 12/s
• 3. s/(s² + π²)
• 5. 1/((s − 2)² − 1)
• 7. (ω cos θ + s sin θ)/(s² + ω²)
• 9.
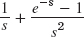
• 11.
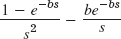
• 13.
• 15.
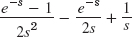
• 19. Use e^at = cosh at + sinh at.
• 23. Set ct = p. Then
• 25. 0.2 cos 1.8t + sin 1.8t
• 27.
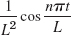
• 29. 2t³ − 1.9t⁵
• 31.
• 33.
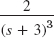
• 35.
• 37. πte^−πt
• 39.
• 41. e^−5πt sinh π t
• 43.
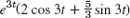
• 45. (k_o + k₁t)e_−at

Problem Set 6.2, page 216

• 1. y = 1.25e^−5.2t − 1.25 cos 2t + 3.25 sin 2t
• 3. (s − 3)(s + 2) = 11s + 28 − 11 = 11s + 17, y = 10/(s − 3) + 1/(s + 2), y = 10e^3t + e^−2t
• 5.
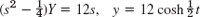
• 7.
• 11. (s + 1.5)²Y = s + 31.5 + 3 + 54/s⁴ + 64/s, Y = 1/(s + 1.5) + 1/(s + 1.5)² + 24/s⁴ + 32/s², y = (1 + t)e^−1.5t + 4t³ − 16t² + 32t
• 13.
• 15.
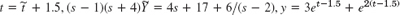
• 17.
• 19.
• 21. Answer: (s² − 2)/(s³ − 4a)
• 23. 12(1 − e^−t/4
• 25. (1 − cos ωt/ω²
• 27.
• 29.

Problem Set 6.3, page 223

• 3.
• 5.
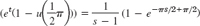
• 7.
• 9.
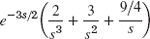
• 11. (se^−πs/2 + e^−πs)/(s² + 1)
• 13. 2[1 + u(t − π)]sin 3t
• 15. (t − 3)³u(t − 3)/6
• 17. e^−t cos t (0 < t < 2π)
• 19.
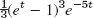
• 21.
• 23.
• 25. t − sin t(0 < < 1), cos (t − 1) + sin (t − 1) − sin t (t > 1)
• 27.
• 29. 0.1i′ + 25i = 490e^−5t[1 − u(t − 1)], i = 20(e^−5t − e^−250t) + 20u(t − 1)[−e^−5t + e^−250t+245]
• 31.
• 33.
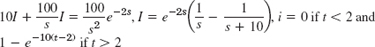
• 35. i = (10 sin 10t + 100 sin t)(u(t − π) − u(t − 3π))
• 37.
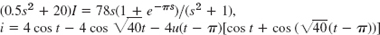
• 39.

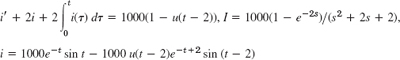
Problem Set 6.4, page 230

• 3.
• 5. sin t(0 < t < π);0(π < t < 2π);−sin t(t > 2)
• 7.
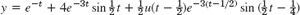
• 9. y = 0.1[e^t + e^−2t(−cos t + 7 sin t)] + 0.1u(t − 10)[−e^−t + e^2t+30(cos (t − 10) − 7 sin (t − 10))]
• 11.
• 15. ke^−ps/(s − se^−ps) (s > 0)

Problem Set 6.5, page 237

• 1. t
• 3. (e^t −e^−t)/2 = sinh t
• 5.
• 7. e^{t − t − 1}
• 9. y − 1 * y = 1, y = e^t
• 11. y = cos t
• 13.
• 17. e^4t − e^−1.5t
• 19. t sin πt
• 21. (ωt − sin ωt)/ω²
• 23. 4.5(cosh 3t − 1)
• 25. 1.5t sin 6t

Problem Set 6.6, page 241

• 3.
• 5.
• 7.
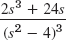
• 9.
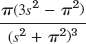
• 11.
• 15.
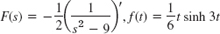
• 17. In s − In (s − 1);(−1 + e^t)/t
• 19. [In (s² + 1) − 2 In (s − 1)]′ = 2s/(s² + 1) − 2/(s − 1);2(−cos t + e^t)/t

Problem Set 6.7, page 246

• 3. y₁ = −e^−5t + 4e^2t, y₂ = e^−5t + 3e^2t
• 5. y₁ = −cos t + sin t + 1 + u(t − 1)[−1 + cos (t − 1)− sin (t − 1)] y₂ = cos t + sin t − 1 + u(t − 1)[1 − cos (t − 1) − sin (t − 1)]
• 7.
• 9. y₁ = (3 + 4t)e^3t, y₂ = (1 − 4t)e^3t
• 11. y₁ = e^t + e^2t, y₂ = e^2t
• 13. y₁ = −4e^t + sin 10t + 4 cos t, y₂ = 4e^t − sin 10t + 4 cos t
• 15. y₁ = e^t,y₂ = e^−t,y₃ = e^t − e^−t
• 19.

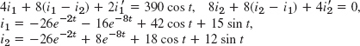
Chapter 6 Review Questions and Problems, page 251

• 11.
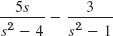
• 13.
• 15.
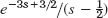
• 17. Sec. 6.6; 2s²/(s² + 1)²
• 19. 12/(s²(s + 3))
• 21. tu(t − 1)
• 23. sin (ωt + θ)
• 25. 3t² + t³
• 27. e^−t(3 cos t − 2 sin t)
• 29. y = e^−2t(13 cos t + 11 sin t) + 10t − 8
• 31. e^−t + u(t − π)[1.2 cos t − 3.6 sin t + 2e^−t+π − 0.8e^2t−2π]
• 33. 0 ≠ (0 t 2), 1 − 2e^−(t−2) (t > 2)
• 35. y₁ = 4e^t − e^−2t,y₂ = e^t − e^−2t
• 37.
• 39.
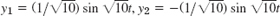
• 41. 1 − e^−t(0 < t < 4), (e⁴ − 1)e^{−t (t} > 4)
• 43.
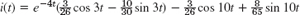
• 45.

Problem Set 7.1, page 261

• 3. 3 × 3, 3 × 4, 3 × 6, 2 × 2, 2 × 3, 3 × 2
• 5.
• 7. No, no, yes, no, no
• 9.
• 11.
• 13.
• 15.

Problem Set 7.2, page 270

• 5. 10, n(n + 1)/2
• 7.
• 11.
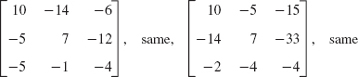
• 13.
• 15.
• 17.
• 19.
• 25. (d) AB = (AB)^T = B^TA^T = BA; etc. (e) Answer. If AB = −BA.
• 29. P = [85 62 30]^T, ν = [44,920 30,940]^T

Problem Set 7.3, page 280

• 1. x = −2, y = 0.5
• 3. x = 1, y = 3, z = −5
• 5. x = 6, y = −7
• 7. x = −3t, y = t arb., z = 2t
• 9. x = 3t − 1, y = −t + 4, z = t arb.
• 11. w = 1, x = t₁ arb., y = 2t₂ − t₁, z = t₂ arb.
• 13. w = 3, x = 0, y = 2, z = 6
• 17. I₁ = 2, I₂ = 6, I₃ = 8
• 19. I₁ = (R₁ + R₂)E₀/(R₁R₂)A, I₂ = E₀/R₁ A, I₃ = E₀/R₂ A
• 21 x₂ = 1600 − x₁, x₃ = 600 + x₁, x₄ = 1000 − − x₁. No
• 23. C:3x₁ − x₃ = 0, H:8x₁ − 2x₄ = 0, O:2₂ − 2x₃ − x₄ = 0, thus C₃H₈ + 5O₂ → 3CO₂ + 4H₂O

Problem Set 7.4, page 287

• 1. 1; [2 −1 3]; [2 −1]^T
• 3. 3; {[3 5 0], [0 3 5], [0 0 1]}
• 5. 3; {[2 −1 4], [0 1 −46], [0 0 1]}; {[2 0 1], [0 3 23], [0 0 1]}
• 7. 2; [8 0 4 0], [0 2 0 4]; [8 0 4], [0 2 0]
• 9. 3; [9 0 1 0], [0 9 8 9], [0 0 1 0]
• 11. (c) 1
• 17. No
• 19. Yes
• 21. No
• 23. Yes
• 25. Yes
• 27. 2, [−2 0 1], [0 2 1]
• 29. No
• 31. No
• 33.
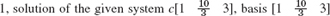
• 35.

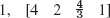
Problem Set 7.7, page 300

• 7. cos (α + β)
• 9. 1
• 11. 40
• 13. 289
• 15. −64
• 17. 2
• 19. 2
• 21. x = 3.5, y = −1.0
• 23. x = 0, y = 4, z = −1
• 25. w = 3, x = 0, y = 2, z = −2

Problem Set 7.8, page 308

• 1.
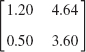
• 3.
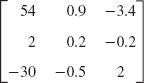
• 5.
• 7. A₋₁ = A
• 9.
• 11.
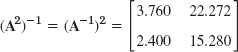
• 15. AA⁻¹ = I, (AA⁻¹)⁻¹ = (A⁻¹)⁻¹A⁻¹ = I. Multiply by A from the right.

Problem Set 7.9, page 318

• 1. [1 0]^T, [0 1]^T; [1 0]^T, [0 − 1]^T; [0 −1]^T; [1 1]^T, [−1 1]^T
• 3. 1, [1 11 −7]^T
• 5. No
• 7. Dimension 2, basis xe^−x, e^−x
• 9.
• 11. x₁ = 5y₁ − y₂, x₂ = 3y₁ − y₂
• 13. x₁ = 2y₁ − 3y₂, x₂ = −10y₁ + 16y₂ + y₃, x₃ = −7y₁ + 11y₂ + y₃
• 15.
• 17.
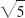
• 19. 1
• 21. k = −20
• 23.
• 25. a = [5 3 2]^T, b = [3 2 −1]^T, 90 + 14 = 2(38 + 14)

Chapter 7 Review Questions and Problems, page 318

• 11.
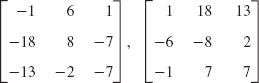
• 13. [21 −8 −31]^T, [21 −8 31]
• 15. 197, 0
• 17. −5, det A² = (det A)² = 25, 0
• 19.
• 21. x = 4, y = −2, z = 8
• 23. x= 6, y = 2t + 2, z = t arb.
• 25. x = 0.4, y = −1.3, z = 1.7
• 27. x = 10, y = −2
• 29. Ranks 2, 2, ∞
• 31. Ranks 2, 2, 1
• 33. I₁ = 16.5 A, I₂ = 11 A, I₃ = 5.5 A
• 35. I₁ = 4 A, I₂ = 5 A, I₃ = 1 A

Problem Set 8.1, page 329

• 1. 3, [1 0]^T; −0.6, [0 1]^T
• 3. −4, [2 9]^T; 3, [1 1]^T
• 5.
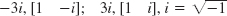
• 7. λ² = 0, [1 0]^T
• 9. 0.8 + 0.6i, [1 −i]^T; 0.8 − 0.6i, [1 i]^T
• 11. −(λ³ − 18λ² + 99λ − 162)/(λ − 3) = −(λ² − 15λ + 54); 3, [2 −2 1]^T; 6, [1 2 2]^T; 9, [2 1 −2]^T
• 13. −(λ − 9)³; 9, [2 −2 1]^T, defect 2
• 15. (λ + 1)²(λ² + 2λ − 15); −1, [1 0 0 0]^T, [0 1 0 0]^T; −5, [−3 −3 1 1]^T, 3, [3 −3 1 −1]^T
• 17. 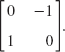Eigenvalues i, −i. Corresponding eigenvectors are complex, indicating that no direction is preserved under a rotation.
• 19. 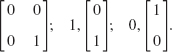A point onto the x₂-axis goes onto itself, a point on the x₁-axis onto the origin.
• 23. Use that real entries imply real coefficients of the characteristic polynomial.

Problem Set 8.2, page 333

• 1. 1.5, [1 −1]^T, −45°; 4.5, [1 1]^T, 45°
• 3.
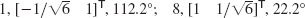
• 5. 0.5, [1 −1]^T; 1.5, [1 1]^T; directions −45° and 45°
• 7. [5 8]^T
• 9. [11 12 16]^T
• 11. 1.8
• 13. c[10 18 16]^T
• 15. X = (I − A)⁻¹y = [0.6747 0.7128 0.7543]^T
• 17. AX_j = λ_jX^j (X_j ≠ 0), (A − kI)X_j = λ_jX_j − kX_j = (λ_j − k)X_j.
• 19. From AX_j = λ_jX_j (X_j ≠ 0) and Prob. 18 follows and , integer). Adding on both sides, we see that has the eigenvalue . From this the statement follows.

Problem Set 8.3, page 338

• 1. 0.8 ± 0.6i, [1 ±i]^T; orthogonal
• 3. 2 ± 0.8i, [1 ±i]. Not skew-symmetric!
• 5. 1, [0 2 1]^T; 6, [1 0 0]^T, [0 1 −2]^T; symmetric
• 7. 0, ±25i, skew-symmetric
• 9. 1, [0 1 0]T; i [1 0 i]^T; −i, [1 0 −2]^T, orthogonal
• 15. No
• 17. A⁻¹ = (−A^T)⁻¹ = −(A⁻¹)^T
• 19. No since det A = det (A^T) = det (−A) = (−1)³det (A) = −det (A) = 0.

Problem Set 8.4, page 345

• 1.
• 3.
• 5.
• 9.
• 11.
• 13.
• 15.
• 17.
• 19.
• 21.
• 23.

Problem Set 8.5, page 351

• 1. Hermitian, 5, [−i 1]^T, 7, [i 1]^T
• 3. Unitary,
• 5. Skew-Hermitian, unitary, −i, [0 −1 1]^T, i, [1 0 0]^T, [0 1 1]^T
• 7. Eigenvalues −1, 1; eigenvectors [1 −1]^T, [1 1]^T; [1 −i]^T, [1 i]^T; [0 1]^T, [1 0]^T, resp.
• 9. Hermitian, 16
• 11. Skew-Hermitian, −6i
• 13.
• 15. (H Hermitian, S skew-Hermitian)
• 19.A^T − ^T A = (H + S)(H − S) − (H − S)(H + S) = 2(− HS + SH) = 0 if and only if HS = SH.

Chapter 8 Review Questions and Problems, page 352

• 11. 3, [1 1]^T; 2, [1 −1]^T
• 13. 3, [1 5]^T; 7, [1 1]^T
• 15. 0, [2 −2 1]^T; 9i, [−1 + 3i 1 + 3i 4]^T; −9i, [−1 − 3i 1 − 3i 4]^T
• 17.
• 19.
• 21.
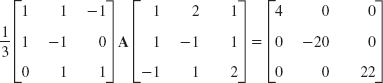
• 23.
• 25.

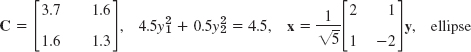
Problem Set 9.1, page 360

• 1. 5, 1, 0;
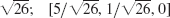
• 3. 8.5, −4.0, 1.7;
• 5. 2, 1, −2; 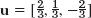, Position vector of Q
• 7.
• 9. Q: (0, 0, −8), |ν| = 8
• 11. [6, 4, 0], , [−3, −2, 0]
• 13. [1, 5, 8]
• 15. 7[9, −7, 8] = [63, −49, 56]
• 17. [12, 8, 0]
• 21. [4, 9, −3],
• 23. [0, 0, 5], 5
• 25.
• 27. P = [0, 0, −5]
• 29. V = [ν₁, ν₂, 3], ν₁, ν₂ arbitrary
• 31. k = 10
• 33. |p + q + u| 18. Nothing
• 35.
• 37. u + v + p = [−k, 0] + [l, l] + [0, −1000] = 0, −k + l + 0 = 0, 0 + l − 1000 = 0, l = 1000, k = 1000

Problem Set 9.2, page 367

• 1.44, 44, 0
• 3.
• 5.
• 7.
• 9. 300; CF. (5a) and (5b)
• 13. Use (1) and |cos γ| 1.
• 15. |a + b|² + |a − b|² = a · a + 2a · b + b · b + (a · a − 2a · b + b · b) = 2|a|² + 2|b|²
• 17. [2, 5, 0] · [2, 2, 2] = 14
• 19. [0, 4, 3] · [−3, −2, 1] = −5 is negative! Why?
• 21. Yes, because W = (p + q) · d = p · d + q · d.
• 23. arccos 0.5976 = 53.3°
• 27. β − α is the angle between the unit vectors a and b. Use (2).
• 29.
• 31.
• 33.
• 35. (a + b) · (a − b) = |a|² − |b|² = 0, |a| = |b|. A square.
• 37. 0. Why?
• 39. If |a| = |b| or if a and b are orthogonal.

Problem Set 9.3, page 374

• 5. −m instead of m, tendency to rotate in the opposite sense.
• 7. |v| = |[0, 20, 0] × [8, 6, 0]| = |[0, 0, −160]| = 160
• 9. Zero volume in Fig. 191, which can happen in several ways.
• 11. [0, 0, 7], [0, 0, −7], −4
• 13. [6, 2, 7], [−6, −2, −7]
• 15. 0
• 17. [−32, −58, 34], [−42, −63, 19]
• 19. 1, −1
• 21.
• 23. 0, 0, 13
• 25. m = [−2, −2, 0] × [2, 3, 0] = [0, 0, −10], m = 10 clockwise
• 27. [6, 2, 0] × [1, 2, 0] = [0, 0, 10]
• 29.
• 31. 3x + 2y − z = 5
• 33. 474/6 = 79

Problem Set 9.4, page 380

• 1. Hyperbolas
• 3. Parallel staraight lines (planes in space)
• 5. Circles, centers on the y-axis
• 7. Ellipses
• 9. Parallel planes
• 11. Elliptic cylinders
• 13. Paraboloids

Problem Set 9.5, page 390

• 1. Circle, center (3, 0), radius 2
• 3. Cubic parabola x = 0, z = y³
• 5. Ellipse
• 7. Helix
• 9. A “Lissajous curve”
• 11.
• 13. r = [2 + t, 1 + 2t, 3]
• 15. r = [t, 4t − 1, 5t]
• 17.
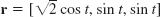
• 19.
• 21. Use sin (− α) = −sin α.
• 25. u = [−sin t, 0, cos t]. At p, r′ = [−8, 0, 6]. q(w) = [6 − 8w, i, 8 + 6w].
• 27.
• 29.
• 31.
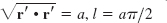
• 33. Start from r(t) = [t, f(t)].
• 35.
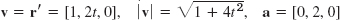
• 37. v(0) = (ω + 1) Ri, a(0) = −ω²Rj
• 39.
• 41.
• 43. 1 year = 365 · 86,400 sec, R = 30 · 365 · 86,400/2π = 151 · 10⁶¹ [km], |a| = ω²R = |v|^2/R = 5.98 · 10⁻⁶ [km/sec²]
• 45.
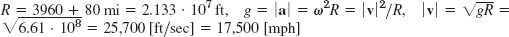
• 49. r(t) = [t, y(t), 0], r′ = [1, y′, 0] r · r′ = 1 p y′², etc.
• 51.
• 53. 3/(1 + 9t² + 9t⁴)

Problem Set 9.7, page 402

• 1. [2y − 1, 2x + 2]
• 3. [−y> x², 1> x]
• 5. [4x³, 4y³]
• 7. Use the chain rule.
• 9. Apply the quotient rule to each component and collect terms.
• 11. [y, x], [5, −4]
• 13. [2x/(x² + y²), 2y/(x² + y²)], [0.16, 0.12]
• 15. [8x, 18y, 2z], [40, −18, −22]
• 17. For P on the x- and y-axes.
• 19. [−1.25, 0]
• 21. [0, −e]
• 23. Points with y = 0, ±π, ±2π, ….
• 25. −ΔT(p) = [0, 4, −1]
• 31. Δf = [32x, −2y], δf(p) = [160, −2]
• 33. [12x, 4y, 2z], [60, 20, 10]
• 35. [−2x, −2y, 1], [−6, −8, 1]
• 37.
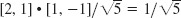
• 39.
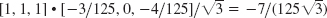
• 41.
• 43. f = xyz
• 45.

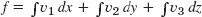
Problem Set 9.8, page 405

• 1. 2x + 8y + 18z; 7
• 3. 0, after simplification; solenoidal
• 5. 9x²y²z²; 1296
• 7. −2e^x (cos y)z
• 9. (b) (fν₁)x + (fν₂)y + (fν₃)z = f[(ν₁)_x + (ν2)_y + (ν3)_z] + f_xν₁ + f_yν₂ + f_zν₃, etc.
• 11. [ν₁, ν₂, ν₃] = r′ = [x′, y′, z′] = [y, 0, 0], z′ = 0, z = c₃, y′ = 0, y = c₂, and x′ = y = c₂, x = c₂t + c₁. Hence as t increases from 0 to 1, this “shear flow” transforms the cube into a parallelepiped of volume l.
• 13. div (w × r) = 0 because ν₁, ν₂ ν₃ do not depend on x, y, z, respectively.
• 15. −2 cos 2x + 2 cos 2y
• 17. 0
• 19. 2/(x² + y² + z²)²

Problem Set 9.9, page 408

• 3. Use the definitions and direct calculation.
• 5. [x(z² − y²), y(x² − z²), z(y² − x²)]
• 7. e^−x [cos y, sin y, 0]
• 9.
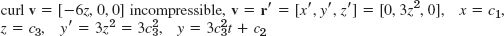
• 11.
• 13. curl v = 0, irrotational, div v = 1, compressible, r = [c₁e^t, c₂e^t, c₃e^−t]. Sketch it.
• 15. [−1, −1, −1], same (why?)
• 17. −yz −zx −xy, 0 (why?), −y − z − x
• 19. [−2z −y, −2x −z, −2y −x ], same (why?)

Chapter 9 Review Questions and Problems, page 409

• 11. −10, 1080, 1080, 65
• 13. [−10, −30, 0], [10, 30, 0], 0, 40
• 15. [−1260, −1830, −300], [−210, 120, −540], undefined
• 17. −125, 125, −125
• 19.
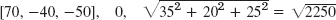
• 21. [−2, −6, −13]
• 23.
• 25. [5, 2, 0] · [4 − 1, 3 − 1, 0] = 19
• 27.
• 29. [0, 0, −14], tendency of clockwise rotation
• 31. 4
• 33. 1, −2y
• 35. 0, same (why?), 2(y² + x² − zx)
• 37. [0, −2, 0]
• 39.

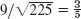
Problem Set 10.1, page 418

• 3. 4
• 5. r = [2 cos t, 2 sin t],
• 7. “Exponential helix,” (e^6π − 1)/3
• 9. 23.5, 0
• 11.
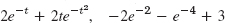
• 15.
• 17. [4 cos t, + sin t, sin t, 4 cos t], [2, 2, 0]
• 19. 144t⁴, 1843.2

Problem Set 10.2, page 425

• 3.
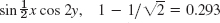
• 5. e^xy sin z, e − 0
• 7. cosh 1 − 2 = −0.457
• 9. e^x cosh y + e^z sinh y, e − (cosh 1 + sinh 1) = 0
• 13.
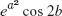
• 15. Dependent, x² ≠ −4y², etc.
• 17. Dependent, 4 ≠ 0, etc.
• 19. sin (a² + 2b² + c²)

Problem Set 10.3, page 432

• 3. 8y³/3, 54
• 5.
• 7.
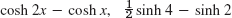
• 9. 36 + 27y², 144
• 11. z = 1 − r², dx dy = r dr dθ, Answer: π/2
• 13.
• 15.
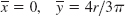
• 17. T_x = bh³/12, I_y = b³h/4
• 19. I_x = (a + b)h³/24, I_y = h(a⁴ − b⁴)/(48(a − b))

Problem Set 10.4, page 438

• 1. (−1 −1) · π/4 = −π/2
• 3.
• 5.
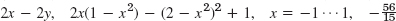
• 7. 0. Why?
• 9.
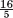
• 13.
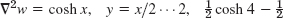
• 15. Δ²w = 6xy, 3x(10 − x²)² − 3x, 486
• 17. Δ²w = 6x − 6y, − 38.4
• 19.

Problem Set 10.5, page 442

• 1. Straight lines, k
• 3. 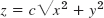, circles, straight lines, [−cu cos ν, −cu sin ν u]
• 5. z = x² + y², circles, parabolas, [−2u² cos ν, −2u² sin ν, u]
• 7. x²/a² + y²/b² + z²/c² = 1, [bc cos² ν cos u, ac cos² ν sin u, ab sin ν cos ν], ellipses
• 11.
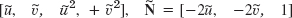
• 13. Set x = and y = ν.
• 15. [2 + 5 cos u, −1 + 5 sin u, ν], [5 cos u, 5 sin u, 0]
• 17. [a cos ν cos u, −2.8 + a cos ν sin u, 3.2 + a sin ν], a = 1.5; [a² cos² ν cos u, a² cos² ν sin u, a² cos ν sin ν]
• 19. [cosh u, sinh u, ν], [cosh u, −sinh u, 0]

Problem Set 10.6, page 450

• 1. F(r) • N = [−u², ν², 0] · [−3, 2, 1] = 3u² + 2ν², 29.5
• 3. F(r) • N = cos³ ν cos u sin u from (3), Sec. 10.5. Answer:
• 5. F(r) • N = −u³, −128π
• 7.
• 9.
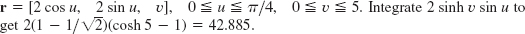
• 13.
• 15. G(r) = (1 + 9u⁴)^3/2, |N| = (1 + 9u⁴)^1/2, Answer: 54.4
• 21.
• 23. [u cos ν, u sin ν, u],
• 25. [cos u cos ν, cos u sin ν, sin u], dA = (cos u) du dν, B the z-axis, I_B = 8ν/3, I_K = I_B + 1² · 4π = 20.9.

Problem Set 10.7, page 457

• 1. 224
• 3. −e^−1−x + e^−y−x, −2e^−1−x + e^−x, 2e⁻³ − e⁻² − 2e⁻¹ + 1
• 5.
• 7. [r cos u cos ν, cos u sin ν, r sin u], dV = r² cos u dr du dv, σ = ν, 2π²a³/3
• 9. div F = 2x + 2z, 48
• 11. 12(e − 1/e) = 24 sinh 1
• 13. div F = −sin z, 0
• 15.
• 17. h⁴π/2
• 19. 8abc(b² + c²)/3
• 21. (a⁴/4) · 2π · h = ha⁴π/2
• 23. h⁵π/10
• 25. Do Prob. 20 as the last one.

Problem Set 10.8, page 462

• 1. x = 0, y = 0, z = 0, no contributions. x = a: ∂f/∂n = ∂f/∂x = −2x = −2a, etc. Integrals. x = a: (−2a)bc. y = b: (−2b)ac, z = c: (4c) ab. Sum 0
• 3. The volume integral of . The surface integral of f∂g/∂n = f · 2x = 2f = 8y² over x = 1 is . Others 0.
• 5. The volume integral of 6y² · 4 − 2x² · 12 is 0; 8(x = 1), −8(y = 1), others 0.
• 7. F = [x, 0, 0], div F = 1, use (2*), Sec. 10.7, etc.
• 9.
• 10.

Problem Set 10.9, page 468

• 1. S: z = y (0 x 1, 0 y 4), [0, 2z, −2z] · [0, −1, 1], ±20
• 3.
• 5.
• 7. [−e^x, −e^x, −e^y] · [−2x, 0, 1], ±(e⁴ − 2e + 1)
• 9. The sides contribute a, 3a²/2, −a, 0.
• 11. −2π; curl F = 0
• 13. 5k, 80π
• 15.
• 17. r = [cos u, sin u, ν], [−3ν², 0, 0] · [cos u, sin u, 0], −1
• 19. r = [u cos ν, u sin ν, u], 0 u 1, 0 ν π/2, [−e^x, 1, 0] · [−u cos ν −u sin ν, u]. Answer: 1/2

Chapter 10 Review Questions and Problems, page 469

• 11. r = [4 − 10t, 2 + 8t], F(r) · dr = [2(4 − 10t)², −4(2t + 8t²)] · [−10, 8] dt; −4528/3. Or using exactness.
• 13. Not exact, curl F = (5 cos x)k, ±10
• 15. 0 since curl F = 0
• 17. By Stokes, ±18π
• 19. F = grad (y² + xz), 2π
• 21.
• 23.
• 25.
• 29. div F = 20 + 6z². Answer: 21
• 31. 24 sinh 1 = 28.205
• 33. Direct integration,
• 35. 72π

Problem Set 11.1, page 482

• 1.
• 5. There is no smallest p > 0.
• 13.
• 15.
• 17.
• 19.
• 21.

Problem Set 11.2, page 490

• 1. Neither, even, odd, odd, neither
• 3. Even
• 5. Even
• 9.
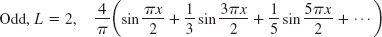
• 11.
• 13.
• 15.
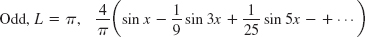
• 17.
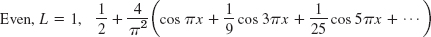
• 19.
• 23.
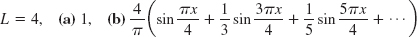
• 25.
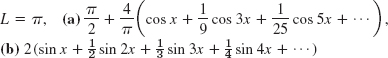
• 27.
• 29.

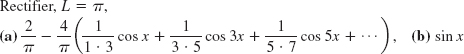
Problem Set 11.3, page 494

• 3. The output becomes a pure cosine series.
• 5. For A_n this is similar to Fig. 54 in Sec. 2.8, whereas for the phase shift B_n the sense is the same for all n.
• 7. y = C₁ cos ωt + C₂ sin ωt + a(ω) sint, a(ω) = 1/(ω² − 1) = −1.33, −5.26, 4.76, 0.8, 0.01. Note the change of sign.
• 11.
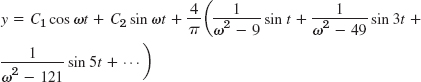
• 13.
• 15.
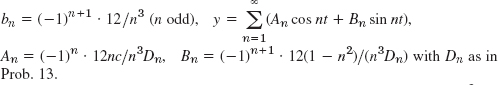
• 17.
• 19.

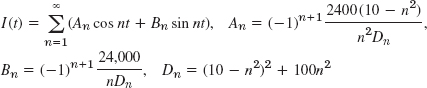
Section 11.4, page 498

• 3.
• 5.
• 7.

Section 11.5, page 503

• 3. Set x = ct + k.
• 5. x = cos θ, dx = −sin θ dθ, etc.
• 7. λ_m = (mπ/10)², m = 1, 2, …; y_m = sin (mπx/10)
• 9. λ = [(2m + 1)π/(2L)]², m = 0, 1, …, y_m = sin ((2m + 1)πx/(2L))
• 11. λ_m = m², m = 1, 2, …, y_m = x sin (m In |x|)
• 13. p = e^8x, q = 0, r = e^8x, λ_m = m², y_m = e^−4x sin mx, m = 1, 2, …

Section 11.6, page 509

• 1. 8(p₁(x) − p₃(x) + p₅(x))
• 3.
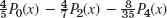
• 9. −0.4775p₁(x) − 0.6908p₃(x) + 1.844p₅(x) − 0.8236p₇(x) + 0.1658p₉(x) + …, m₀ = 9. Rounding seems to have considerable influence in Probs. 8–13.
• 11. 0.7854P₀(x) − 0.3540P₂(x) + 0.0830P₄(x) − …, m₀ = 4
• 13. 0.1212P₀(x) − 0.7955P₂(x) + 0.9600P₄(x) − 0.3360P₆(x) + …, m0 = 8
• 15.

Section 11.7, page 517

• 1. (see Example 3), etc.
• 3.
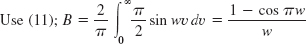
• 5.
• 7.
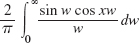
• 9.
• 11.
• 15. For n = 1, 2, 11, 12, 31, 32, 49, 50 the value of Si (nπ) − p/2 equals 0.28, −0.15, 0.029, − 0.026, 0.0103, −0.0099, 0.0065, −0.0064 (rounded).
• 17.
• 19.

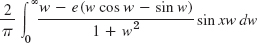
Section 11.8, page 522

• 1.
• 3.
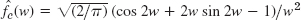
• 5.
• 7. Yes. No
• 9.
• 11.
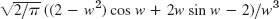
• 13.

Problem Set 11.9, page 533

• 3.
• 5.
• 7.
• 9.
• 11.
• 13. 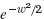by formula 9
• 17. No, the assumptions in Theorem 3 are not satisfied.
• 19. [f₁ + f₂ + f₃ + f₄, f₁ − if₂ − f₃ + if₄, f₁ − f₂ + f₃ − f₄, f₁ + if₂ − f₃ − if₄]
• 21.

Chapter 11 Review Questions and Problems, page 537

• 11.
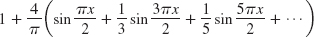
• 13.
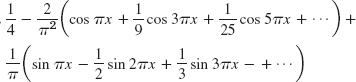
• 15. cosh x, sinh x (−5 < x < 5), respectively
• 17. Cf. Sec. 11.1.
• 19.
• 21.
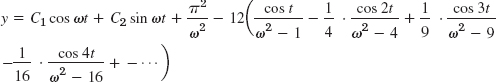
• 23. 0.82, 0.50, 0.36, 0.28, 0.23
• 25. 0.0076, 0.0076, 0.0012, 0.0012, 0.0004
• 27.
• 29.

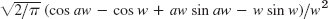
Problem Set 12.1, page 542

• 1. L(c₁u₁ + c₂u₂) = c₁L(u₁) + c₂L(u₂) = c₁ · 0 + c₂ · 0 = 0
• 3. c = 2
• 5. c = a/b
• 7. Any c and ω
• 9. c = π/25
• 15. u = 110 − (110/In 100) In (x² + y²)
• 17. u = a(y) cos 4πx + b(y) sin 4πx
• 19.
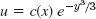
• 21. u = e^−3y (a(x) cos 2y + b(x) sin 2y) + 0.1e^3y
• 23. u = c₁(y)x + c₂(y)/x² (Euler–Cauchy)
• 25. u(x,y) = axy + bx + cy + k; a, b, c, k arbitrary constants

Problem Set 12.3, page 551

• 5. k cos 3πt sin 3πx
• 7.
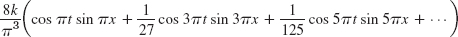
• 9.
• 11.
• 13.
• 17.
• 19. (a) u(0, t) = 0, (b) u(L, t) = 0, (c) u_x(0,t) = 0, (d) u_x(L, t) = 0. C = −A, D = −B from (a), (c). Insert this. The coefficient determinant resulting from (b), (d) must be zero to have a nontrivial solution. This gives (22).

Problem Set 12.4, page 556

• 3. c² = 300/[0.9/(2 · 9.80)] = 80.83² [m²/sec²]
• 9. Elliptic, u = f₁(y + 2ix) + f₂(y − 2ix)
• 11. Parabolic, u = xf₁(x − y) + f₂(x − y)
• 13. Hyperbolic, u = f₁(y − 4x) + f₂(y − x)
• 15. Hyperbolic,
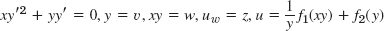
• 17. Elliptic, u = f₁(y − (2 − i)x) + f₂(y − (2 + i)x). Real or imaginary parts of any function u of this form are solutions. Why?

Problem Set 12.6, page 566

• 3. u₁ = sin x e^−t, u₂ = sin 2x e^−4t, u₃ = sin 3x e^−9t differ in rapidity of decay.
• 5.
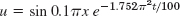
• 7.
• 9. u = u_I + u_II, where u_II = u − u_I satisfies the boundary conditions of the text, so that
• 11. F = A cos px + B sin px, F′ (0) = Bp = 0, B = 0, F′ (L) = −Ap sin pL = 0, p = nπ/L, etc.
• 13. u = 1
• 15.
• 17.
• 19.
• 21.
• 23.
• 25.

Problem Set 12.7, page 574

• 3.
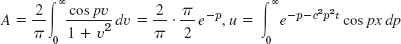
• 5.
• 7.
• 9. Set w = −ν in (21) to get erf (−x) = −erf x.
• 13. In (12) the argument 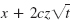is 0 (the point where f jumps) when ). This gives the lower limit of integration.
• 15. Set 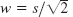in (21).

Problem Set 12.9, page 584

• 1. (a), (b) It is multiplied by . (c) Half
• 5. B_mn = (−1)ⁿ⁺¹8/(mnπ²) if m odd, 0 if m even
• 7. B_mn = (−1)^m+n4ab/(mnπ²)
• 11.
• 13.
• 17. (corresponding eigenfundtions F_4,16 and F_16,14), etc.
• 19.

Problem Set 12.10, page 591

• 5.
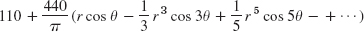
• 7.
• 11. Solve the problem in the disk r < a subject to u₀ (given) on the upper semicircle and −u₀ on the lower semicircle.

  

• 13. Increase by a factor
• 15.
• 17. No
• 25. α₁₁/(2π) = 0.6098; See Table A1 in App. 5.

Problem Set 12.11, page 598

• 5. A₄ = A₆ = A₈ = A₁₀ = 0, A₅ = 605/16, A₇ = −4125/128, A₉ = 7315/256
• 9.
• 13. u = 320/r + 60 is smaller than the potential in Prob. 12 for 2 < r < 4.
• 17. u = 1
• 19.
• 25. Set 1/r = ρ. Then u(ρ, θ, ø) = rν(r, θ, ø), u_ρ = (ν + rν_r)(−1/ρ²), u_ρρ = (2ν_r + rν_rr(1/ρ⁴) + (ν + rν_r)(2/ρ³), u_ρρ + (2/ρ)u_ρ = r⁵(ν_rr + (2/r)ν_r). Substitute this and u_øø etc. into (7) [written in terms of ρ] and divide by r_r5.

Problem Set 12.12, page 602

• 5.
• 7.
• 11. Set x²/(4c²π) = z². Use z as a new variable of integration. Use erf (∞) = 1.

Chapter 12 Review Questions and Problems, page 603

• 17. u = c₁(x)e^−3y + c₂(x)e^2y −3
• 19. Hyperbolic, f₁(x) + f₂(y + x)
• 21. Hyperbolic, f₁(y + 2x) + f₂(y − 2x)
• 23.
• 25.
• 29. 100 cos 2x e^−4t
• 39. u = (u₁ − u₀)(In r)/In (r₁/r₀) + (u₀ In r₁ − u₁ In r₀)/In (r₁/r₀)

Problem Set 13.1, page 612

• 1. 1/i = i/i² = −i, 1/i³ = i/i⁴ = i
• 3. 4.8 − 1.4i
• 5. x − iy = −(x + iy), x = 0
• 9. − 117, 4
• 11. −8 − 6i
• 13. − 120 − 40i
• 15. 3 − i
• 17. −4x²y²
• 19. (x² − y²)/(x² + y²), 2xy/(x² + y²)

Problem Set 13.2, page 618

• 1.
• 3.
• 5.
• 7.
• 9. 3π/4
• 11.
• 13. −1024. Answer: π
• 15. −3i
• 17. 2 + 2i
• 21.
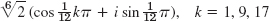
• 23.
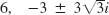
• 25.
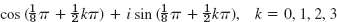
• 27.
• 29. i, −1 − i
• 31. ±(1 − i), ±(2 + 2i)
• 33.
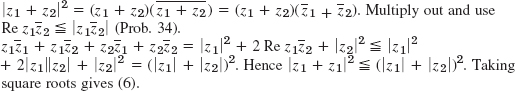
• 35.

Problem Set 13.3, page 624

• 1. Closed disk, center − 1 + 5i, radius
• 3. Annulus (circular ring), center 4 − 2i, radii π and 3π
• 5. Domain between the bisecting straight lines of the first quadrant and the fourth quadrant.
• 7. Half-plane extending from the vertical straight line x = −1 to the right.
• 11.
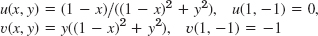
• 15.
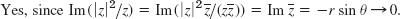
• 17. Yes, because Re z = r cos θ → 0 and 1 − |z| → 1 as r → 0.
• 19. f′(z) = 8(z − 4i)⁷. Now z − 4i = 3, hence f′ (3 + 4i) = 8 · 3⁷ = 17,496.
• 21. n(1 − z)⁻ⁿ⁻¹i, ni
• 23. 3iz²/(z + i)⁴, −3i/16

Problem Set 13.4, page 629

• 1. r_x = x/r = cos θ, r_y = sin θ, θ_x = −(sin θ)/r, θ_y = (cos θ)/r (a) 0 = u_x − ν_y = u_r cos θ + u_θ(−sin θ)/r − νr sin θ − ν_θ(cos θ)/r (b) 0 = u_y + ν_x = u_r sin θ + u_θ(cos θ)/r + ν_r cos θ + ν_θ(−sin θ)/r Multiply (a) by cos θ, (b) by sin θ, and add. Etc.
• 3. Yes
• 5.
• 7. Yes, when z ≠ 0. Use (7).
• 9. Yes, when z ≠ 0, −2πi, 2πi
• 11. Yes
• 13.
• 15. f(z) = 1/z + c (c real)
• 17. f(z) = z² + z + c (c real)
• 19. No
• 21. a = π, ν = e^πx sin πy
• 23.
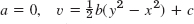
• 27. f = u + iv implies if = −ν + iu.
• 29. Use (4), (5), and (1).

Problem Set 13.5, page 632

• 3. e^2πie^−2π = 0.001867
• 5. e²(−1) = −7.389
• 7.
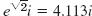
• 9. 5e^{i arctan (3/4)} = 5e^0.644i
• 11. 6.3e^πi
• 13.
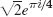
• 15. exp (x² − y²) cos 2xy, exp (x² − y²) sin 2xy
• 17. Re (exp (z³)) = exp (x³ − 3xy²) cos (3x²y − y³)
• 19. z = 2nπi, n = 0, 1, …

Problem Set 13.6, page 636

• 1. Use (11), then (5) for e^iy, and simplify.
• 7. cosh 1 = 1.543, i sinh 1 = 1.175i
• 9. Both −0.642 − 1.069i. Why?
• 11. i sinh π = 11.55i, both
• 15. Insert the definitions on the left, multiply out, and simplify.
• 17. z = ±(2n + 1)i/2
• 19. z = ±nπi

Problem Set 13.7, page 640

• 5. In 11 + πi
• 7.
• 9. i arctan (0.8/0.6) = 0.927i
• 11. In e + πi/2 = 1 + πi/2
• 13. ±2nπi, n = 0, 1, …
• 15.
• 17. In (i²) = In (−1) = (1 ± 2n)πi, 2 In i = (1 ± 4n)±i, n = 0, 1, …
• 19. e⁴⁻³ⁱ = e⁴ (cos 3 − i sin 3) = −54.05 − 7.70i
• 21. e^0.6e^0.4i = e^0.6 (cos 0.4 + i sin 0.4) = 1.678 + 0.710i
• 23.
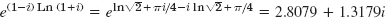
• 25. e^{(3−i)(In 3+πi)} = 27e^π(cos (3π − In 3) + i sin (3π − In 3)) = −284.2 + 556.4i
• 27. e^{(2−i)Ln(−1)} = e^(2−i)πi = e^π = 23.14

Chapter 13 Review Questions and Problems, page 641

• 1. 2 − 3i
• 3. 27.46e^0.9929i
• 11. −5 + 12i
• 13. 0.16 − 0.12i
• 15. i
• 17.
• 19. 15e^−πi/2
• 21. ±3, ±3i
• 23.
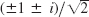
• 25. f(z) = −iz²/2
• 27. f(z) = e^−2z
• 29.
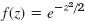
• 31. cos 3 cosh 1 + i sin 3 sinh 1 = −1.528 + 0.166i
• 33. i tanh 1 = 0.7616i
• 35. cosh π cos π + i sinh π sin π = −11.592

Problem Set 14.1, page 651

• 1. Straight segment from (2, 1) to (5, 2.5).
• 3. Parabola y = x² from (1, 2) to (2, 8).
• 5. Circle through (0, 0), center (3, − 1), radius , oriented clockwise.
• 7. Semicircle, center 2, radius 4.
• 9. Cubic parabola y = x³ (−2 x 2)
• 11. z(t) = t + (2 + t)i (−1 t 1)
• 13. z(t) = 2 − i + 2e^it (0 t π)
• 15. z(t) = 2 cosh t + i sinh t (− ∞ < t < ∞)
• 17. Circle z(t) = −a − ib + re^−it (0 t 2π)
• 19.
• 21. z(t) = (1 + i)t (1 t 3), Re z = t, z′ (t) = 1 + i. Answer: 4 + 4i
• 23. e^2πi − e^πi = 1 − (−1) = 2
• 25.
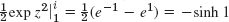
• 27.
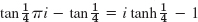
• 29.
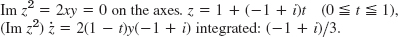
• 35.

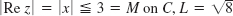
Problem Set 14.2, page 659

• 1. Use (12), Sec. 14.1, with m = 2.
• 3. Yes
• 5. 5
• 7. (a) Yes. (b) No, we would have to move the contour across ±2i.
• 9. 0, yes
• 11. πi, no
• 13. 0, yes
• 15. −π, no
• 17. 0, no
• 19. 0, yes
• 21. 2πi
• 23. 1/z + 1/(z −1), hence 2πi + 2πi = 4πi.
• 25. 0 (Why?)
• 27. 0 (Why?)
• 29. 0

Problem Set 14.3, page 663

• 1.
• 3. 0
• 5.
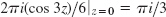
• 7. 2πi(i/2)³/2 = π/8
• 11.
• 13.
• 15. 2πi cosh (−π² − πi) = −2πi cosh π² = −60,739i since cosh πi = cos π = −1 and sinh πi = i sin π = 0.
• 17.
• 19. 2πie²ⁱ/(2i) = πe²ⁱ

Problem Set 14.4, page 667

• 1. (2πi/3!)(−cos 0) = −πi/3
• 3. (2πi/(n − 1)!)e⁰
• 5.
• 7.
• 9.
• 11.
• 13.
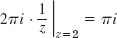
• 15. 0. Why?
• 17. 0 by Cauchy's integral theorem for a doubly connected domain; see (6) in Sec. 14.2.
• 19.

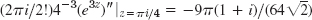
Chapter 14 Review Questions and Problems, page 668

• 21.
• 23. 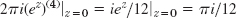by cauchy's integral formula.
• 25.
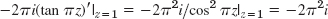
• 27.
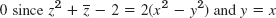
• 29. −4πi

Problem Set 15.1, page 679

• 1. z_n = (2i/2)ⁿ; bounded, divergent, ±1, ±i
• 3. by algebra; convergent to −πi/2
• 5. Bounded, divergent, ±1 + 10i
• 7. Unbounded, hence divergent
• 9. Convergent to 0, hence bounded
• 17. Divergent; use 1/In n > 1/n.
• 19. Convergent; use ∑ 1/n².
• 21. Convergent
• 23. Convergent
• 25. Divergent
• 29. By absolute convergence and Cauchy's convergence principle, for given 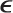> 0 we have for every n > N(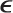) and p = 1, 2, …

  

  hence 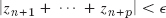by (6*), Sec. 13.2, hence convergence by Cauchy's principle.

Problem Set 15.2, page 684

• 1. No! Nonnegative integer powers of z (or z − z₀) only!
• 3. At the center, in a disk, in the whole plane
• 5.
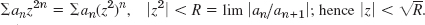
• 7. π/2, ∞
• 9.
• 11.
• 13.
• 15. 2i, 1
• 17.

Problem Set 15.3, page 689

• 3.
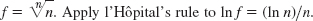
• 5. 2
• 7.
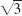
• 9.
• 11.
• 13. 1
• 15.

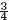
Problem Set 15.4, page 697

• 3.
• 5.
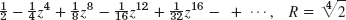
• 7.
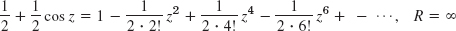
• 9.
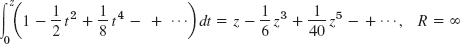
• 11. z³/(1!3) − z⁷/(3!7) + z¹¹/(5!11) − + …, R = ∞
• 13.
• 17. Team Project. (a) (Ln (1 + z))′ = 1 − z + z² − + … = 1/(1 + z). (c) Use that the terms of (sin iy)/(iy) are all positive, so that the sum cannot be zero.
• 19.
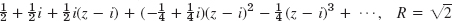
• 21.
• 23.
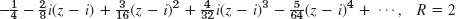
• 25.

Problem Set 15.5, page 704

• 3.
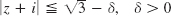
• 5.
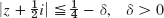
• 7. Nowhere
• 9. |z − 2i| 2 − ∂, ∂ > 0
• 11. |zⁿ| 1 ∑ 1/n² converges. Use Theorem 5.
• 13. |sinⁿ |z|| 1 for all z, and ∑ 1/n² converges. Use Theorem 5.
• 15. R = 4 by Theorem 2 in Sec. 15.2; use Theorem 1.
• 17.

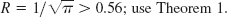
Chapter 15 Review Questions and Problems, page 706

• 11. 1
• 13. 3
• 15.
• 17. ∞, e^2x
• 19. ∞, cosh
• 21.
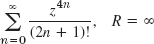
• 23.
• 25.
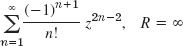
• 27.
• 29.

Problem Set 16.1, page 714

• 1.
• 3.
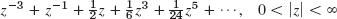
• 5.
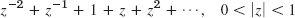
• 7.
• 9.
• 11.
• 13.
• 15.
• 19.
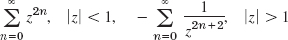
• 21.
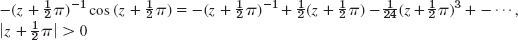
• 23. z⁸ + z¹² + z¹⁶ + …, |z| < 1, −z⁴ − 1 − z⁻⁴ − z⁻⁸ − …, |z| > 1
• 25.

Section 16.2, page 719

• 1. 0 ± 2π, ±4π, …, fourth order
• 3. −81i, fourth order
• 5. ±1, ±2, …, second order
• 7. ±(2 + 2i), ±i, simple
• 9.
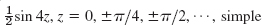
• 11. f(z) = (z − z₀)ⁿ g(z), g(z₀) ≠ 0, hence f²(z) = (z − z₀)²ⁿ g²(z).
• 13. Second-order poles at i and −2i
• 15. Simple pole at ∞, essential singularity at 1 + i
• 17. Fourth-order poles at ±nπi, n = 0, 1, …, essential singularity at ∞
• 19. e^x(1 − e^x) = 0, e^z = 1, z = ±2nπi simple zeros. Answer: at simple poles ±2nπi, essential singularity at ∞
• 21. 1, ∞ essential singularities, ±2nπi, simple poles

Section 16.3, page 725

• 3.
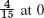
• 5.
• 7. 1/π at 0, ±1, …
• 9. −1 at ±2nπi
• 11.
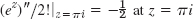
• 15. Simple poles at 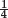inside C, residue −1/(2π). Answer: −i
• 17. Simple poles at π/2, residue e^π/2/(−sin π /2), and at −π/2, residue e^−π/2/sin π/2 = e^−π/2. Answer: −4πi sinh π/2
• 19.
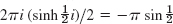
• 21. z⁻² cos πz = … + π⁴/(4!z) − + …. Answer: 2π⁵i/24
• 23.
• 25.

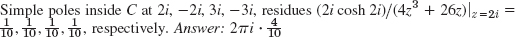
Problem Set 16.4, page 733

• 1.
• 3.
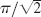
• 5. 5π/12
• 7.
• 9. 0. Why? (Make a sketch.)
• 11. π/2
• 13.0. Why?
• 15. π/3
• 17.0. Why?
• 19. Simple poles at
• 21. Simple poles at 1 and ±2πi, residues i and −. Answer:
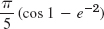
• 23. −π/2
• 25. 0
• 27. Let q(z) = (z − a₁)(z − a₂)…(z − a_k). Use (4) in Sec. 16.3 to form the sum of the residues 1/q′(a₁) + … + 1/q′(a_k and show that this sum is 0; here k > 1.

Chapter 16 Review Questions and Problems, page 733

• 11. 6πi
• 13. 2πi(− 10 − 10)
• 15.
• 17.0 (n even), (−1)^(n−1)/22πi/(n − 1)!(n odd)
• 19.π/6
• 21. π/60
• 23.0. Why?
• 25.

Problem Set 17.1, page 741

• 5. Only in size
• 7. x = c, w = −y + ic; y = k, w = −k = ix
• 9. Parallel displacement; each point is moved 2 to the right and 1 up.
• 11.
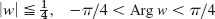
• 13. −5 Re z −2
• 15. u 1
• 17.
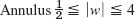
• 19. 0 < u < In 4, π/4 < v 3π/4
• 21.
• 23.
• 25. sinh z = 0 at z = 0, ±πi, ±2πi, …
• 29. M = |z| = 1 on the unit circle, J = |z|²
• 31. |w′| = 1/|z|² on the unit circle, J = 1/|z|⁴
• 33. M = e^x = 1 for the x = 0, y-axis, J = e^2x
• 35. M = 1/|z| = on the unit circle, J = 1/|z|²

Problem Set 17.2, page 745

• 7.
• 9.
• 11. z = 0, 1/(a + ib)
• 13.
• 15. z = i, 2i
• 17.
• 19.

Problem Set 17.3, page 750

• 3. Apply the inverse g of f on both sides of z₁ = f(z₁) to get g(z₁) = g(f(z₁)) = z₁.
• 9. w = iz, a rotation. Sketch to see.
• 11. w = (z + i)/(z − i)
• 13. w = 1/z, almost by inspection
• 15. w = 1/z − 1
• 17. w = (2z − i)/(−iz − 2)
• 19. w = (z⁴ − i)(−iz⁴ + 1)

Problem Set 17.4, page 754

• 1. Circle |w| = e^c
• 3.
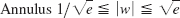
• 5. w-plane without w = 0
• 7. < |w| < e,v > 0
• 9. ±(2n + 1)π/2, n = 0, 1, …
• 11. u²/cosh² 2 + v²/sinh² 2 < 1, u > 0,v > 0
• 13. Elliptic annulus bounded by u²/cosh² 1 + v²/sinh² 1 = 1 and u²/cosh²3 + v^2/sinh2 3 = 1
• 15.
• 17.
• 19. Hyperbolas u²/cos² c v²/sin² c − sinh² c − sinh² c = 1 when c ≠ 0, π, and u²/cos² c − v²/sin² c = cosh² c − sinh² c = 1 when c = 0, π.
• 21. Interior of u²/cosh² 2 + v²/sinh² 2 = 1 in the fourth quadrant, or map π/2 < x < π, 0 < y < 2 by w = sin z (why?).
• 23. v < 0
• 25. The images of the five points in the figure can be obtained directly from the function w.

Problem Set 17.5, page 756

• 1. w moves once around the circle
• 3. Four sheets, branch point at z = −1
• 5. −,i/4, three sheets
• 7. z₀, n sheets
• 9. 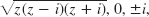two sheets

Chapter 17 Review Questions and Problems, page 756

• 11. 1 < |w| < 4, |arg w| < π/4
• 13. Horizontal strip −8 < v < 8
• 15. , same (why?)
• 17. |w| > 1
• 19.
• 21. w = 1 + iv, v < 0
• 23.
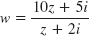
• 25. Rotation w = iz
• 27. w = 1/z
• 29. z = 0
• 31.
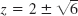
• 33. z = 0, ±i, ±3i
• 35. w = e^4x
• 37. w = iz² + 1
• 39. w = z²/(2c)

Problem Set 18.1, page 762

• 1. 2.5 mm = 0.25 cm; Φ = Re 110 (1 + (Ln z)/ln 4)
• 3.
• 5. Φ(x) = Re(375 + 25z)
• 7. Φ(r) = Re (32 − z)
• 13. Use Fig. 391 in Sec. 17.4 with the z- and w- planes interchanged and cos z = sin .
• 15. Φ 220 (x³ − 3xy²) Re (220z³)

Problem Set 18.2, page 766

• 3.
• 5. (b) x² − y² = c, xy = c, e^x cos y = c
• 7. See Fig. 392 in Sec. 17.4. Φ = Re(sin² z), sin²x)y = 0), sin² x cosh² 1 − cos² x sinh² 1(y = 1), −sinh² y(x = 0, π).
• 9. Φ (x, y) = cos² x cosh² y − sin² x sinh² y; cosh² y (x = 0), −sinh y 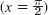cos² x (y = 0), cos² x cosh² 1 − sin² x sinh² 1 (y = 1)
• 13. Corresponding rays in the w-plane make equal angles, and the mapping is conformal.
• 15. Apply w = z².
• 17. z = (2z − i)/(−iZ − 2)(by (3) in Sec. 17.3.
• 19.

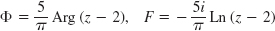
Problem Set 18.3, page 769

• 1. (80/d)y + 20. Rotate through π/2.
• 5.
• 7.
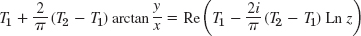
• 9.
• 11.
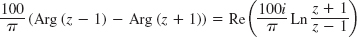
• 13.
• 15.
• 17. Re F(z) = 100 + (200/π) Re (arcsin z)

Problem Set 18.4, page 776

• 1.V (z) continuously differentiable.
• 3. |F′(iy)| = 1 + 1/y², |y| 1, is maximum at y = ±1, namely, 2.
• 5. Calculate or note that ∇² = div grad and curl grad is the zero vector; see Sec. 9.8 and Problem Set 9.7.
• 7. Horizontal parallel flow to the right.
• 9. F(z) = z⁴
• 11. Uniform parallel flow upward,
• 13. F(z) = z³
• 15. F(z) = z/r₀ + r₀/z
• 17. Use that w = arccos z gives z = cos w and interchanging the roles of the z- and w-planes.
• 19. y/(x² + y²) = c or x² + (y − k)² = k²

Problem Set 18.5, page 781

• 5.
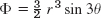
• 7.
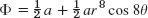
• 9. Φ = 3 − 4r² cos 2θ + r⁴ cos 4θ
• 11.
• 13.
• 15.
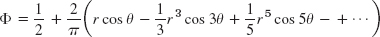
• 17.

Problem Set 18.6, page 784

• 1.
• 3. Use (2). F(z⁰ + e^ix) = (2 + 3e^ix)², etc. F(4) = 100
• 5. No, because |z| is not analytic.
• 7.
• 9.
• 13. |F(z)| = [cos² x + sinh² y]^1/2, z = ±i, Max = [1 + sinh² 1]^1/2 = 1.543
• 15. |F(z)|² = sinh² 2x cos² 2y + cosh² 2x sin² 2y = sinh² 2x + 1 · sin² 2y, z = 1, Max = sinh 2 = 3.627
• 17. |F(z)|² = 4(2 − 2cos 2θ), z = π/2, 3π/2, Max = 4
• 19. No. Make up a counterexample.

Chapter 18 Review Questions and Problems, page 785

• 11. Φ = 10(1 − x + y), F = 10 − 10(1 + i)z
• 13.
• 17. 2(1 − (2/π)Arg z)
• 19. 30(1 − (2/π)Arg (z − 1))
• 21.
• 23. T(x,y) = x(2y + 1) = const
• 25.

Problem Set 19.1, page 796

• 1. 0.84175 · 10², −0.52868 · 10³, 0.92414 · 10⁻3, −0.36201 · 10⁶
• 3.6.3698, 6.794, 8.15, impossible
• 5. Add first, then round.
• 7. 29.9667, 0.0335; 29.9667, 0.0333704 (6S-exact)
• 9. 29.97, 0.035; 29.97, 0.03337; 30, 0.0; 30, 0.033
• 11.
• 13.
• 15. (a) 1.38629 − 1.38604 = 0.00025, (b) ln 1.00025 = 0.000249969 is 6S-exact.
• 19. In the present case, (b) is slightly more accurate than (a) (which may produce nonsensical results; cf. Prob. 20).
• 21. c₄ · 2⁴ + … + c₀ · 2⁰ = (1 0 1 1 1.)₂, NOT (1 1 1 0 1.)₂
• 23. The algorithm in Prob. 22 repeats 0011 infinitely often.
• 25. n = 26. The beginning is 0.09375 (n = 1).
• 27. I₁₄ = 0.1812 (0.1705 4S-exact), I₁₃ = 0.1812 (0.1820), I₁₂ = 0.1951 (0.1951), I₁₁ = 0.2102 (0.2103), etc.
• 29. −0.126 · 10⁻², −0.402 · 10⁻³; −0.266 · 10⁻⁶, −0.847 − 10⁻⁷

Problem Set 19.2, page 807

• 3. g = 0.5 cos x, x = 0.450184 (= x₁₀, exact to 6S)
• 5. Convergence to 4.7 for all these starting values;
• 7. x = x/(e^x sin x); 0.5, 0.63256, …converges to 0.58853 (5S-exact) in 14 steps.
• 9. x = x⁴ − 0.12; x₀ = 0, x₃ = −0.119794(6S-exact)
• 11. g = 4/x + x₃/16 − x⁵/576; x₀ = 2, x_n = 2.39165 (n 6), 2.405 4S-exact
• 13. This follows from the intermediate value theorem of calculus.
• 15. x₃ = 0.450184
• 17. Convergence to x = 4.7, 4.7, 0.8, −0.5, respectively. Reason seen easily from the graph of f.
• 19.
• 21. 1.834243 (= x₄), 0.656620(= x₄), −2.49086 (= x₄)
• 23. x₀ = 4.5, x₄ = 4.73004 (6S-exact)
• 25. (a) ALGORITHM BISECT (f, a₀,b₀, N) Bisection Method

  This algorithm computes the solution c of f(x) = 0 (f continuous) within the tolerance 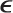, given an initial interval [a₀,b₀] such that f(a0)f(b0) < 0.

  

  Note that [a_N, b_N] gives (a_N + b_N)/2 as an approximation of the zero and (b_N − a_N)/2 as a corresponding error bound.

  (b) 0.739085; (c) 1.30980, 0.429494

• 27. x₂ = 1.5, x₃ = 1.76471, …, x₇ = 1.83424 (6S-exact)
• 29.0.904557 (6S-exact)

Problem Set 19.3, page 819

• 1. L₀(x) = −2x + 19, L₁(x) = 2x − 18, p₁(9.3) = L₀(9.3) · f₀ + L₁(9.3) · f₁ = 0.1086 · 9.3 + 1.230 = 2.2297
• 3.
• 5. 0.8033 (error −0.0245), 0.4872 (error −0.0148); quadratic; 0.7839 (−0.0051), 0.4678 (0.0046)
• 7. p₂(x) = 1.1640x − 0.337x²; −0.5089(error 0.1262), 0.4053(−0.0226), 0.9053(0.0186), 0.9911(−0.0672)
• 9. p₂(x) = −0.44304x² + 1.30896x − 0.023220, p₂(0.75) = 0.70929 (5S-exact 0.71116)
• 11.
• 13. 2x² − 4x + 2
• 15. p₃(x) = 2.1972 + (x − 9) · 0.1082 + (x − 9)(x − 9.5) · 0.005235
• 17.

Problem Set 19.4, page 826

• 9. [−1.39 (x − 5)² + 0.58(x − 5)³]″ = 0.004 at x = 5.8 (due to roundoff; should be 0).
• 11.
• 13. 1 − x₂, −2(x − 1) − (x − 1)² + 2(x − 1)³, −1 + 2(x − 2) + 5(x − 2)²
• 15. 4 + x² − x³, −8(x − 2) − 5(x − 2)² + 5(x − 2)³, 4 + 32(x − 4) + 25(x − 4)² − 11(x − 4)³
• 17. Use the fact that the third derivative of a cubic polynomial is constant, so that g″′ is piecewise constant, hence constant throughout under the present assumption. Now integrate three times.
• 19. Curvature f^″/(1 + f^′2)^3/2 ≈ f″ if |f′| is small.

Problem Set 19.5, page 839

• 1. 0.747131, which is larger than 0.746824. Why?
• 3. 0.5, 0.375, 0.34375, 0.335 (exact)
• 5. 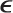^0.5 ≈ 0.03452 (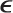_0.5 = 0.03307), 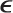_0.25 ≈ 0.00829 (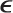_0.25 = 0.00820)
• 7. 0.693254 (6S-exact 0.693147)
• 9. 0.073930 (6S-exact 0.073928)
• 11. 0.785392 (6S-exact 0.785398)
• 13. (0.785398126 − 0.785392156)/15 = 0.39792 · 10₋₆
• 15. (a) M₂ = 2; |KM₂| = 2/(12n²) = 10⁻⁵/2,n = 183. (b) f^iv = 24/x⁵,M₄ = 24, |CM₄| = 24/(180) · (2m⁴) = 10⁻ⁿ⁵/2, 2m = 12.8, hence 14.
• 17. 0.94614588, 0.94608693 (8S-exact 0.94608307)
• 19. 0.9460831 (7S-exact)
• 21. 0.9774586 (7S-exact 0.9774377)
• 23.
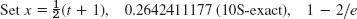
• 25.
• 27. 0.08, 0.32, 0.176, 0.256 (exact)
• 29.

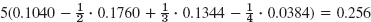
Chapter 19 Review Questions and Problems, page 841

• 17. 4.375, 4.50, 6.0, impossible
• 19. 44.885 s 44.995
• 21. The same as that of .
• 23. 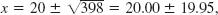x₁ = 39.95, x₂ = 0.05, x₂ = 2/39.95 = 0.05006 (erroe less than 1 unit of the last digit)
• 25. x = x⁴ − 0.1, −0.1, −0.9999, −0.99900399
• 27. 0.824
• 29. −x + x³, 2(x − 1) + 3(x − 1)² − (x − 1)³
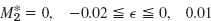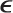
• 31. 0.26, M₂ = 6, , −0.02 0, 0.01
• 33. 0.90443, 0.90452 (5S-exact 0.90452)
• 35. (a) (0.4³ − 2 · 0.2³ + 0)/0.04 = 1.2, (b) (0.3³ − 2 · 0.2³ + 0.1³)/0.01 = 1.2 (exact)

Problem Set 20.1, page 851

• 1. x₁ = 7.3, x₂ = −3.2
• 3. No solution
• 5. x₁ = 2, x₂ = 1
• 7.
• 9.
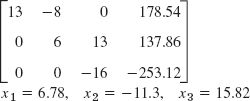
• 11.
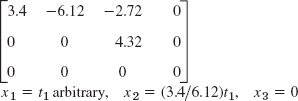
• 13.
• 15.

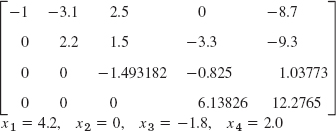
Problem Set 20.2, page 857

• 1.
• 3.
• 5.
• 7.
• 9.
• 11.
• 13. No, since x^T (−A)X = −X^T Ax < 0; yes; yes; no
• 15.
• 17.
• 19.

Problem Set 20.3, page 863

• 5. Exact 0.5, 0.5, 0.5
• 7. x₁ = 2, x₂ = −4, x3 = 8
• 9. Exact 2, 1, 4
• 11. (a) x^(3)T = [0.49983 0.50001 0.500017], (b) x^(3)T = [0.50333 0.49985 0.49968]
• 13. 8, −16, 43, 86 steps; spectral radius 0.09, 0.35, 0.72, 0.85, approximately
• 15. [1.99934 1.00043 3.99684]^T (Jacobi, Step 5); [2.00004 0.998059 4.00072]^T (Gauss–Seidel)
• 19.

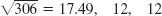
Problem Set 20.4, page 871

• 1. 18, 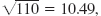8, [0.125 −0.375 1 0 −0.75 0]
• 3.
• 5.
• 7. ab + bc + ca = 0
• 9.
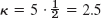
• 11.
• 13. k = 19 · 13 = 247; ill-conditioned
• 15. k = 20 · 20 = 400; ill-conditioned
• 17. 167 21 · 15 = 315
• 19. [− 4]^T, [−144.0 184.0]^T, k = 25,921 extremely ill-conditioned
• 21. Small residual [0.145 0.120], but large deviation of .
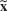• 23. 27, 748, 28,375, 943,656, 29,070,279

Problem Set 20.5, page 875

• 1. 1.846 − 1.038x
• 3. 1.48 + 0.09x
• 5. s = 90t − 675, v_av = 90 km/hr
• 9. −11.36 + 5.45x − 0.589x²
• 11. 1.89 − 0.739x + 0.207x²
• 13. 2.552 + 16.23x, −4.114 + 13.73x + 2.500x², 2.730 + 1.466x − 1.778x² + 2.852x³

Problem Set 20.7, page 884

• 1. 5, 0, 5; radii 6, 5, 6. Spectrum {−1, 4, 9}
• 3. Centers 0; radii 0.5, 0.7, 0.4. Skew-symmetric, hence λ = iμ, −0.7 μ 0.7.
• 5.
• 7. t₁₁ = 100, t₂₂ = t₃₃ = 1
• 9. They lie in the intervals with endpoints a_jj ± (n − 1) · 10⁻⁵. Why?
• 11.
• 13.
• 15.
• 17. Show that A^T = ^TA.
• 19. 0 lies in no Gerschgorin disk, by (3) with >; hence det A = λ₁…λ_n ≠ 0.

Problem Set 20.8, page 887

• 1. q = 10, 10.9908, 10.9999; |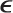| 3, 3028, 0.0275
• 3. q ± δ = 4 ± 1.633, 4.786 ± 0.619, 4.917 ± 0.398
• 5. Same answer as in Prob. 3, possibly except for small roundoff errors.
• 7. q = 5.5, 5.5738, 5.6018; |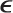| 0.5, 0.3115, 0.1899; eigenvalues (4S) 1.697, 3.382, 5.303, 5.618
• 9. y = Ax = λx, y^Tx = λx^Tx, y^Ty = λ²x^Tx, 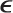² ≤ y^Ty/x^Tx − (y^Tx/x^Tx)² = λ² − λ² = 0
• 11. q = 1, …, −2.8993 approximates −3 (0 of the given matrix), |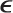| 1.633, …, 0.7024 (Step 8)

Problem Set 20.9, page 896

• 1.
• 3.
• 5.
• 7. Eigenvalues 16, 6, 2

  

• 9. Eigenvalues (4S) 141.4, 68.64, −30.04

  

Chapter 20 Review Questions and Problems, page 896

• 15. [3.9 4.3 1.8]^T
• 17. [−2 0 5]^T
• 19.
• 21.
• 23.
• 25.
• 27. 30
• 29. 5
• 31. 115 · 0.4458 = 51.27
• 33.
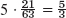
• 35. 1.514 + 1.129x −0.214x²
• 37. Centers 15,35,90; radii 30,35,25, respectively, Eigenvalues (3S) 2.63, 40.8, 96.6
• 39. Centers 0, −1, −4; radii 9, 6, 7, respectively; eigenvalues 0. 4.446, −9.446

Problem Set 21.1, page 910

• 1. y = se^−0.2x, 0.00458, 0.00830 (errors of y₅, y₁₀)
• 3. y = x − tanh x (set y − x = u), 0.00929, 0.01885 (errors of y₅, y₁₀)
• 5. y = e^x, 0.0013, 0.0042 (errors of y₅, y₁₀)
• 7. y = 1/(1 − x²/2), 0.00029, 0.01187 (errors of y₅, y₁₀)
• 9. Errors 0.03547 and 0.28715 of and y₅ and y₁₀ much larger
• 11. y = 1/(1 − x²/2); error −10⁻⁸, −4 · 10⁻⁸, …, −6 · 10⁻⁷, +9 · 10⁻⁶; 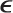= 0.0002/15 = 1.3 · 10⁻⁵ (use RK with h = 0.2)
• 13. y = tan x; error 0.83 · 10⁻⁷, 0.16 · 10⁻⁶, …, −0.56 · 10⁻⁶, +0.13 · 10⁻⁵
• 15. y = 3 cos x − 2 cos² x; error · 10⁷: 0.18, 0.74, 1.73, 3.28, 5.59, 9.04, 14.3, 22.8, 36.8, 61.4
• 17. y′ = 1/(2 − x⁴); error · 10⁹: 0.2, 3.1, 10.7, 23.2, 28.5, −32.3, −376, −1656, −3489, +80444
• 19. Errors for Euler–Cauchy 0.02002, 0.06286, 0.05074; for improved Euler–Cauchy −0.000455, 0.012086 0.009601; for Runge–Kutta. 0.0000011, 0.000016, 0.000536

Problem Set 21.2, page 915

• 1.
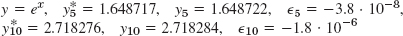
• 3. y = tan x, y⁴, …, y¹⁰ (error · 10⁵) 0.422798 (−0.49), 0.546315 (−1.2), 0.684161 (−2.4), 0.842332 (−4.4), 1.029714 (−7.5), 1.260288 (−13), 1.557626 (−22)
• 5. RK error smaller in absolute value, error · 10⁵ = 0.4, 0.3, 0.2, 5.6 (for x = 0.4, 0.6, 0.8, 1.0)
• 7. y = exp (x³) − 1, y⁴, …, y¹⁰ (error · 10¹⁰) 0.008032 (−4), 0.015749 (− 10), 0.027370 (− 17), 0.043810 (− 26), 0.066096 (− 39), 0.095411 (− 54), 0.133156 (− 74)
• 13. y = exp (x²). Errors · 10² from x = 0.3 to 0.7: −5, −11, −19, −31, −41
• 15. (a) 0, 0.02, 0.0884, 0.215848, y⁴ = 0.417818, y⁵ = 0.708887 (poor) (b) By 30−50%

Problem Set 21.3, page 922

• 1. y¹ = −e^−2x + 4e^x errors of y₁ (of y²) from 0.002 to 0.5 (from −0.01 to 0.1), monotone
• 3.
• 5. 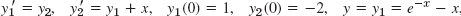, y = 0.8 (error 0.005), 0.61 (0.01), 0.429 (0.012), 0.2561 (0.0142), 0.0905 (0.0160)
• 7. By about a factor 10⁵. 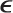ⁿ (y₁) · 10⁶ = −0.082, …, −0.27, 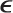ⁿ(y²) · 10⁶ = 0.08, …, 0.27
• 9. Errors of (of y₁ (of y²) from 0.3 · 10⁻⁵ to 1.3 · 10⁻⁵ (from 0.3 · 10⁻⁵ to 0.6 · 10⁻⁵)
• 11. (y₁, y²) = (0, 1), (0.20, 0.98), (0.39, 0.92), …, (−0.23, −0.97), (−0.42, −0.91), (−0.59), (−0.81); continuation will give an “ellipse.”

Problem Set 21.4, page 930

• 3. −3u₁₁ + u₁₂ = −200, u₁₁ − 3u₁₂ = −100
• 5. 105, 155, 105, 115; Step 5: 104.94, 154.97, 104.97, 114.98
• 7. 0, 0, 0, 0. All equipotential lines meet at the corners (why?). Step 5: 0.29298, 0.14649, 0.14649, 0.073245
• 9. 0.108253, 0.108253, 0.324760, 0.324760; Step 10: 0.108538, 0.108396, 0.324902, 0.324831
• 11. (a). u₁₁ = −u¹² = −66. (b) Reduce to 4 equations by symmetry.

  

• 13. u₁₂ = u₃₂ = 31.25, u₂₁ = u₂₃ = 18.75, u_jk = 25 at the others
• 15. u₂₁ = u₂₃ = 0.25, u₁₂ = u₃₂ = 0.25, u_jk = 0 otherwise
• 17. 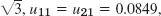u₁₂ = u₂₂ = 0.3170. (0.1083, 0.3248 are 4S-values of the solution of the linear system of the problem.)

Problem Set 21.5, page 935

• 5. u₁₁ = 0.766, u₂₁ = 1.109, u₁₂ = 1.957, u₂₂ = 3.293
• 7. A, as in Example 1, right sides −220, −220, −220, −220. Solution u₁₁ = u₂₁ = 125.7, u₂₁ = u₂₂ = 157.1
• 13.
• 15. b = [−200, −100, −100, 0]^T; u₁₁ = 73.68, u₂₁ = u₁₂ = 47.37, u₂₂ = 15.79 (4S)

Problem Set 21.6, page 941

• 5. 0, 0.6625, 1.25, 1.7125, 2, 2.1, 2, 1.7125, 1.25, 0.6625, 0
• 7. Substantially less accurate, 0.15, 0.25 (t = 0.04), 0.100, 0.163 (t = 0.08)
• 9. Step 5 gives 0, 0.06279, 0.09336, 0.08364, 0.04707, 0.
• 11. Step 2: 0 (exact 0), 0.0453 (0.0422), 0.0672 (0.0658), 0.0671 (0.0628), 0.0394 (0.0373), 0 (0)
• 13. 0.3301, 0.5706, 0.4522, 0.2380 (t = 0.04), 0.06538, 0.10603, 0.10565, 0.6543 (t = 0.20)
• 15. 0.1018, 0.1673, 0.1673, 0.1018 (t = 0.04), 0.0219, 0.0355, …(t = 0.20)

Problem Set 21.7, page 944

• 1. u(x, 1) = 0, −0.05, −0.10, −0.15, −0.20, 0
• 3. For x = 0.2, 0.4 we obtain 0.24, 0.40 (t = 0.2), 0.08 0.16 (t = 0.4), −0.08, −0.16 (t = 0.6), etc.
• 5. 0, 0.354, 0.766, 1.271, 1.679, 1.834, … (t = 0.1); 0, 0.575, 0.935, 1.135, 1.296, 1.357, … (t = 0.2)
• 7. 0.190, 0.308, 0.308, 0.190, (3S-exact: 0.178, 0.288, 0.288, 0.178)

Chapter 21 Review Questions and Problems, page 945

• 17. y = e^x, 0.038, 0.125 (errors of y₅ and y₁₀)
• 19. y = tan x; 0 (0), 0.10050 (−0.00017), 0.20304 (−0.00033), 0.30981 (−0.00048), 0.42341 (−0.00062), 0.54702 (−0.00072), 0.68490 (−0.00076), 0.84295 (−0.00066), 1.0299 (−0.0002), 1.2593 (0.0009), 1.5538 (0.0039)
• 21. 0.1003346(0.8 · 10⁻⁷)0.2027099 (1.6 · 10⁻⁷), 0.3093360 (2.1 · 10⁻⁷), 0.4227930 (2.3 · 10⁻⁷), 0.5463023 (1.8 · 10⁻⁷)
• 23. y = sin x, y_0.8 = 0.717366, y_1.0 = 0.841496 (errors − 1.0 · 10⁻⁵, −2.5 · 10⁻⁵)
• 25.
• 27.
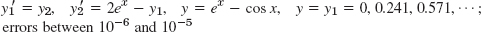
• 29. 3.93, 15.71, 58.93
• 31. 0, 0.04, 0.08, 0.12, 0.15, 0.16, 0.15, 0.12, 0.08, 0.04, 0 (t = 0.3 3 time steps)
• 33. u(p₁₁) = u(p₃₁) = 270, u(p₂₁) = u(p₁₃) = u(p₂₃) = u(p₃₃) = 30., u(p₁₂) = u(p₃₂) = 90, u(p₂₂) = 60
• 35. 0.043330, 0.077321, 0.089952, 0.058488 (t = 0.04), 0.010956, 0.017720, 0.017747, 0.010964 (t = 0.20)

Problem Set 22.1, page 953

• 3. f(x) = 2(x₁ − 1)² + (x₂ + 2)² − 6; Step 3; (1.037, −1.926), value −5.992
• 9. Step 5: (0.11247, −0.00012), value 0.000016

Problem Set 22.2, page 957

• 7. No
• 9. x₃,x₄ is the unused time on M₁, M₂, respectively.
• 11. f(2.5, 2.5) = 100
• 13.
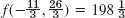
• 15. f(9,6) = 360
• 17. 0.5x₁ + 0.75x₂ 45 (copper), 0.5_x1 + 0.25x₂ 30, f = 120x₁ + 100x₂, f_max = f(45,30) = 8400
• 19. f = x₁ + x₂, 2x₁ + 3x₂ 1200, 4x₁ + 2x₂ 1600, f_max = f(300,200) = 500
• 21. x₁/3 + x₂/2 100, x₁/3 + x₂/6 80,f = 150x₁ + 100x₂,f_max = f(210, 60) = 37,500

Problem Set 22.3, page 961

• 3. f(120/11, 60/11) = 480/11
• 5. Eliminate in Coloumn 3, so that 20 goes.
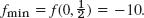
• 7.
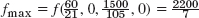
• 9. f_max = 6 on the segment from (3, 0, 0) to (0, 0, 2)
• 11. We minimize! The augmented matrix is

  

  The pivot is 600. The calculation gives

  

  

  Hence −f has the maximum value −13.5, so that f has the minimum value 13.5, at the point

  

• 13. f_max = f (5, 4, 6) = 478

Problem Set 22.4, page 968

• 1. f(6, 3) = 84
• 3. f(20, 20) = 40
• 5. f(10, 5) = 5500
• 7. f(1, 1, 0) = 13
• 9.

Chapter 22 Review Questions and Problems, page 968

• 9. Step 5: [0.353 −0.028]^T. Slower. Why?
• 11. Of course! Step 5: [−1.003 1.897]^T
• 17. f(2, 4) = 100
• 19. f(3, 6) = −54

Problem Set 23.1, page 974

• 9.
• 11.
• 13.
• 15.
• 17. If G is complete.
• 19.

Problem Set 23.2, page 979

• 1. 5
• 3. 4
• 5. The idea is to go backward. There is a v_k-1 adjacent to v_k and labeled k − 1, etc. Now the only vertex labeled 0 is s. Hence λ(v₀) = 0 implies v₀ = s, so thatv_o − v₁ − … − v_k-1 − v_k is a path s → u_k that has length k.
• 15. Delete the edge (2, 4).
• 17. No

Problem Set 23.3, page 983

• 1. (1, 2), (2, 4), (4, 3); L₂ = 12, L₃ = 36, L₄ = 28
• 5. (1, 2), (2, 4), (3, 4), (3, 5); L₂ = 2, L₃ = 4, L₄ = 3, L₅ = 6
• 7. (1, 2), (2, 4), (3, 4); L₂ = 10, L₃ = 15, L₄ = 13
• 9. (1, 5), (2, 3), (2, 6), (3, 4), (3, 5); L₂ = 9, L₃ = 7, L₄ = 8, L₅ = 4, L₆ = 14

Problem Set 23.4, page 987

• 1.
• 3.
• 5.
• 9. Yes
• 11.
• 13. New York–Washington–Chicago–Dalles–Denver–Los Angeles
• 15.G is connected. If G were not a tree, it would have a cycle, but this cycle would provide two paths between any pair of its vertices, contradicting the uniqueness.
• 19. If we add an edge (u, v) to T, then since T is connected, there is a path (u → v) in T which, together with (u, v), forms a cycle.

Problem Set 23.5, page 990

• 1. If G is a tree.
• 3. A shortest spanning tree of the largest connected graph that contains vertex 1.
• 7. (1, 4), (1, 3), (1, 2), (2, 6), (3, 5); L = 32
• 9. (1, 4), (4, 3), (4, 2), (3, 5); L = 20
• 11. (1, 4), (4, 3), (4, 5), (1, 2); L = 12

Problem Set 23.6, page 997

• 1. {3, 6}, 11 + 3 = 14
• 3. {4, 5, 6}, 10 + 5 + 13 = 28
• 5. {3, 6, 7}, 8 + 4 + 4 = 16
• 7. S {1, 4}, 8 + 6 = 14
• 9. One is interested in flows from s to t, not in the opposite direction.
• 13. Δ₁₂ = 5, Δ₂₄ = 8, Δ₄₅ = 2; Δ₁₂ = 5, Δ₂₅ = 3; Δ₁₃ = 4, Δ₃₅ = 9 P₁: 1 − 2 − 4 − 5, Δf = 2; P₂: 1 − 2 − 5, Δf = 3; P₃: 1 − 3 − 5, Δf = 4
• 15. 1 − 2 − 5, Δf = 2; 1 − 4 − 2 − 5, Δf = 2, etc.
• 17. f₁₃ = f₃₅ = 8, f₁₄ = f₄₅ = 5, f₁₂ = f₂₄ = f₄₆ = 4, f₅₆ = 13, f = 4 + 13 = 17, is f = 17 is unique.
• 19. For instance, f₁₂ = 10, f₂₄ = f₄₅ = 7, f₁₃ = f₂₅ = 5, f₃₅ = 3, f₃₂ = 2, f = 3 + 5 + 7 = 15, f = 15 is unique.

Problem Set 23.7, page 1000

• 3. (2, 3) and (5, 6)
• 5. By considering only edges with one labeled end and one unlabeled end
• 7. 1 − 2 − 5, Δ_t 2; 1 − 4 − 2 − 5, Δ_t 1; f = 6 + 2 + 1 = 9, where 6 is the given flow
• 9. 1 − 2 − 4 − 6, Δ_t 2; 1 − 3 − 5 − 6, Δ_t 1; f = 4 + 2 + 1 = 7, where 4 is the given flow
• 15. S = {1, 2, 4, 5}, T = {3, 6}, cap(S, T) = 14

Problem Set 23.8, page 1005

• 1. No
• 3. No
• 5. Yes, S = {1, 4, 5, 8}
• 7. Yes, S = {1, 3, 5}
• 11. 1 − 2 − 3 − 7 − 5 − 4
• 13. 1 − 2 − 3 − 7 − 5 − 4 is augmenting and gives 1 − 2 − 3 − 7 − 5 − 4 and is of maximum cardinality.
• 15. 1 − 4 − 3 − 6 − 7 − 8 is augmenting and gives 1 − 4 − 3 − 6 − 7 − 8 and (1, 4), (3, 6), (7, 8) is of maximum cardinality.
• 19. 3
• 21. 2
• 23. 3
• 25. K₄

Chapter 23 Review Questions and Problems, page 1006

• 11.
• 13.
• 15.
• 17.
• 19. (1, 2), (1, 4), (2, 3); L₂ = 2, L₃ = 5, L₄ = 5
• 23. (1, 6), (4, 5), (2, 3), (7, 8)

Problem Set 24.1, page 1015

• 1. qL = 19, qM = 20, qU = 20.5
• 3. qL = 138, qM = 144, qU = 154
• 5. qL = 199, qM = 201, qU = 201
• 7. qL = 1.3, qM = 1.4, qU = 1.45
• 9. qL = 89.9, qM = 91.0, qU = 91.8
• 11.
• 13.
• 15.
• 17. 3.54, 1.29

Problem Set 24.2, page 1017

• 1. 2³ outcomes: RRR, RRL, RLR, LRR, RLL, LRL, LLR, LLL
• 3. 6² = 36 outcomes (1, 1), (1, 2), …, (6, 6) first number (second number) referring to the first die (second die)
• 5. Infinitely many outcomes H TH TTH TTTH … (H = Head, T = Tail)
• 7. The space of ordered pairs of numbers
• 9. 10 outcomes: D ND NND … NNNNNNNNND
• 11. Yes
• 17. A ∪ B = B implies A ⊆ B by the definition of union. Conversely. A ⊆ B implies that A ∪ B = B because always B ⊆ A ∪ B, and if A ⊆ B, we must have equality in the previous relation.

Problem Set 24.3, page 1024

• 1. 1 − 4/216 = 98315%, by Theorem 1
• 3.
• 5.
• 7. Small sample from a large population containing many items in each class we are interested in (defectives and nondefectives, etc.)
• 9.
• 11.
• 13. 1 − 0.96³ = 11.5%
• 15. 1 − 0.8754 = 0.4138 < 1 − 0.75² = 0.4375 < 0.5 (c < b < a)
• 17. A = B∪(A∩B^c)hence p^A = p(B) + p(A∩B^c) p (B) by disjointedness of B and A∩B^c

Problem Set 24.4, page 1028

• 1. In 10! = 3,628,800 ways
• 3.
• 5.
• 7. 210, 70, 112, 28
• 9. In 6!/6 = 120 ways
• 11. 9 · 8 = 72
• 13. (b) 1/(12n)
• 15.P (No two people have a birthday in common) = 365 · 364 … 346/365²⁰ = 0.59. Answer: 41%, which is surprisingly large.

Problem Set 24.5, page 1034

• 1.
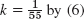
• 3.
• 5. No, because of (6)
• 7.
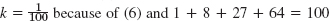
• 9. k = 5; 50%
• 11. 0.5³ = 12.5%
• 13.
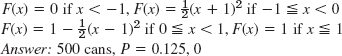
• 15. X > b, X b, X c, etc.

Problem Set 24.6, page 1038

• 1.
• 3. μ = π, σ² = π²/3; cf. Example 2
• 5.
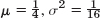
• 7.
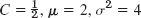
• 9. 750, 1, 0.002
• 11. c = 0.073
• 13. $643.50
• 15.
• 17. X = Product of the 2 numbers. E(X) = 12.25, 12 cents
• 19. (0 + 1 · 3 + 3 · 8 + 1 · 27)/8 = 54/8 6 · 75

Problem Set 24.7, page 1044

• 3. 38%
• 5.
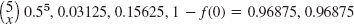
• 7. 0.265
• 9. f(x) = 0.5^xe^−0.5/x!,f(0) + f(1) = e^−0.5(1.0 + 0.5) = 0.91. Answer: 9%
• 11.
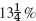
• 13. 42%, 47.2%, 10.5%, 0.3%
• 15. 1 − e^−0.2 = 18%

Problem Set 24.8, page 1050

• 1. 0.1587, 0.5, 0.6915, 0.6247
• 3. 45.065, 56.978, 2.022
• 5. 15.9%
• 7. 31.1%, 95.4%
• 9. About 58%
• 11. t = 1084 hours
• 13. About 683 (Fig. 521a)

Problem Set 24.9, page 1059

• 1.
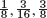
• 3.
• 5. f²(y) = 1/(β₂ − α₂) if α₂ < y lt; β²
• 7. 27.45 mm, 0.38 mm
• 11.25.26 cm, 0.0078 cm
• 13. 50%
• 15. The distributions in Prob. 17 and Example 1
• 17. No

Chapter 24 Review Questions and Problems, page 1060

• 11. Q_L = 110, Q_M = 112, Q_U = 115
• 13.
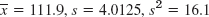
• 21. x_min x_j x_max. Sum over j from 1.
• 17.
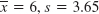
• 19.
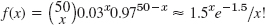
• 21. f(x) = 2^−x, x = 1, 2, …
• 23.
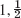
• 25. 0.1587, 0.6306, 0.5, 0.4950

Problem Set 25.2, page 1067

• 1. In Example 1,
• 3.
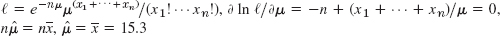
• 5.
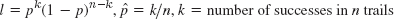
• 7. 7/12
• 9.
• 11.
• 13.
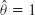
• 15. Variability larger than perhaps expected

Problem Set 25.3, page 1077

• 3. Shorter by a factor
• 5. 4, 16
• 7.
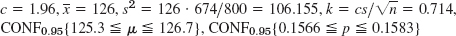
• 9. CONF_0.99{63.72 μ 66.28}
• 11.
• 13. CONF_0.95{0.023 σ² 0.085}
• 15. n − 1 = 99 degrees of freedom. F(c¹) = 0.025, c₁ = 74.2, F(c₂) = 0.975, c₂ = 129.6. Hence k₁ = 12.41, k₂ = 7.10. CONF_0.95 {7.10 σ² 12.41}.
• 17. CONF_0.95{0.74 σ² 5.19}
• 19. Z = X + Y is normal with mean 105 and variance 1.25. Answer: P(104 Z 106) = 63%

Problem Set 25.4, page 1086

• 3.
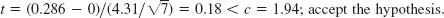
• 5. c = 6090 > 6019: do not reject the hypothesis.
• 7. σ²/n = 1.8, c = 57.8, accept the hypothesis.
• 9. μ < 58.69 or μ > 61.31
• 11.
• 13.
• 15. 19 · 1.0²/0.8² = 29.69 < c = 30.14 (Table A10. Appendix 5), accept the hypothesis
• 17.

Problem Set 25.5, page 1091

• 1. LCL = 1 − 2.58 · 0.02/2 = 0.974, UCL = 1.026
• 3. 27
• 5. Choose 4 times the original sample size
• 9.
• 11.
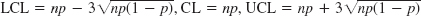
• 13. In about 30% (5%) of the cases
• 15.

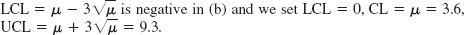
Problem Set 25.6, page 1095

• 1. 0.9825, 0.9384, 0.4060
• 3. 0.8187, 0.6703, 0.1353
• 5. e^−25θ(1 + 25θ), P(A; 1.5) = 94.5, α = 5.5%
• 7. 19.5%, 14.7%
• 9. (1 − θ)ⁿ + nθ(1 − θ)ⁿ⁻¹
• 11.
• 13.
• 15.

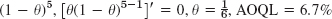
Problem Set 25.7, page 1099

• 3.
• 5.
• 7.
• 9. 42 even digits, accept.
• 13.
• 15. Combining the last three nonzero values, we have K − r − 1 = 9 (r = 1 since we estimated the mean, Accept the hypothesis.

Problem Set 25.8, page 1102

• 3. is the probability that 7 cases in 8 trials favor A under the hypothesis that A and B are equally good. Reject.
• 5.
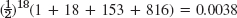
• 7. 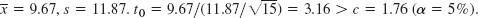Hypothesis rejected.
• 9.
• 11. Consider
• 13. n = 8;4 transpositions, P(T 4) = 0.007, Assert that fertilizing increases yield.
• 15. P(T) 2) = 2.8%. Assert that there is an increase.

Problem Set 25.9, page 1111

• 1. y = 0.98 + 0.495x
• 3. y = −11,457.p + 43.2x
• 5. y = −10 + 0.55x
• 7. y = 0.5932 + 0.1138x, R = 1/0.1138
• 9. y = 0.32923 + 0.00032x, y(66) = 0.35035
• 13. c = 3.18 (Table A9), k₁ = 43.2, q₀ = 54,878, K = 1.502, CONF_0.95{41.7 K₁} 44.7}.
• 15.

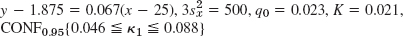
Chapter 25 Review Questions and Problems, page 1111

• 15.
• 17. CONF_0.99{27.94 μ 34.81}
• 19.
• 21.
• 23. α = 1 − (1 − θ)⁶ = 5.85%, when θ = 0.01. For θ = 15% we obtain β = (1 − θ)⁶ = 37.7%. If n increases, so does α, whereas β decreases.
• 25. y = 3.4 − 1.85x