Chapter 6. Torsion of Prismatic Bars

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

Chapter 6. Torsion of Prismatic Bars

6.1 Introduction

In this chapter, consideration is give to stresses and deformations in prismatic members subject to equal and opposite end torques. In general, these bars arne assumed to be free of end constraint. Usually, members that transmit torque, such as propeller shafts and torque tubes of power equipment, are circular or tubular in cross section. For circular cylindrical bars, the torsion formulas are readily derived by employing the method of mechanics of materials, as illustrated in the next section. In Sec. 6.6.2, we will observe that a shaft having a circular cross section is most efficient compared to a shaft having an arbitrary cross section.

Slender members with other-than-circular cross sections are also often used. In treating noncircular prismatic bars, cross sections that are initially plane (Fig. 6.1a) experience out-of-plane deformation or warping (Fig. 6.1b), and the basic kinematic assumptions of the elementary theory are no longer appropriate. Consequently, the theory of elasticity, a general analytic approach, is employed, as discussed in Section 6.4. The governing differential equations derived using this method are applicable to both the linear elastic and the fully plastic torsion problems. The latter is treated in Section 12.10.

Figure (a) illustrates a rectangular bar before loading. Figure (B) shows a rectangular bar after torque is applied. The section perpendicular to the axis of the beam wraps around when torque acts in opposite directions on either end of the beams. — Figure 6.1. *Rectangular bar: (a) before loading; (b) after a torque is applied.*

For cases that cannot be conveniently solved analytically, the governing expressions are used in conjunction with the membrane and fluid flow analogies, as discussed in Sections 6.6 through 6.9. Computer-oriented numerical approaches (Chapter 7) are also very efficient for such situations. This chapter concludes with discussions of warping of thin-walled open cross sections and combined torsion and bending of curved bars.

6.2 Elementary Theory of Torsion of Circular Bars

Consider a torsion bar or shaft of circular cross section (Fig. 6.2). Assume that the right end twists relative to the left end so that longitudinal line AB deforms to AB′. This results in a shearing stress τ and an angle of twist or angular deformation ϕ. As an earlier study of mechanics of materials [Ref. 6.1] revealed, the following basic assumptions underlie the formulations for the torsional loading of circular bars:

All plane sections perpendicular to the longitudinal axis of the bar remain plane following the application of torque; that is, points in a given cross-sectional plane remain in that plane after twisting.
Subsequent to twisting, cross sections are undistorted in their individual planes; that is, the shearing strain γ varies linearly from zero at the center to a maximum on the outer surface.

The preceding assumptions hold for both elastic and inelastic material behavior. In the elastic case, the following condition also applies:
The material is homogeneous and obeys Hooke’s law; hence, the magnitude of the maximum shear angle γ_max must be less than the yield angle.

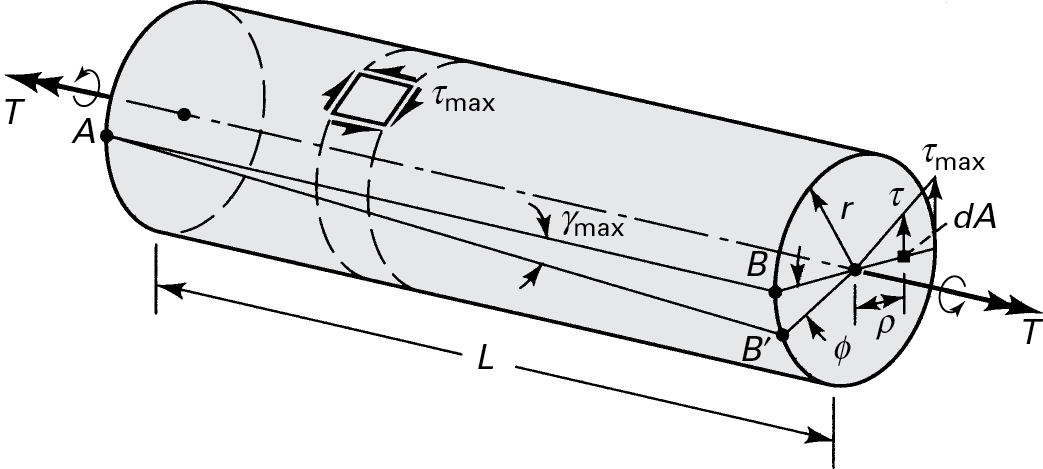
A figure shows the variation of stress and angular rotation of a circular member in torsion. — Figure 6.2. *Variation of stress and angular rotation of a circular member in torsion.*

A figure illustrates a circular shaft of length l and radius r. An externally applied torque T acts on either end of the shaft in the opposite direction. Due to the change in the angle of rotation along the length, AB deforms to AB prime at an angle of phi. The shearing angle gamma maximum varies from zero in the axis to a maximum at the outside surface of the shaft. A small cross-sectional area dA is considered. The maximum torque acts at area dA. The shaft has a square cross-section with the shear forces acting all along its surfaces.

We now derive the elastic stress and deformation relationships for circular bars in torsion in a manner similar to the most fundamental equations of the mechanics of materials: by employing the previously considered procedures and the foregoing assumptions. In the case of these elementary formulas, there is complete agreement between the experimentally obtained and the computed quantities. Moreover, their validity can be demonstrated through application of the theory of elasticity (see Example 6.4).

6.2.1 Shearing Stress

On any bar cross section, the resultant of the stress distribution must be equal to the applied torque T (Fig. 6.2). That is,

$T = \int ρ (τ d A) = \int ρ (\frac{ρ}{r} τ_{\max}) d A$

where the integration proceeds over the entire area of the cross section. At any given section, the maximum shearing stress τ_max and the distance r from the center are constant. Hence, the preceding expression can be written

$\begin{matrix} T = \frac{τ_{\max}}{r} \int ρ^{2} d A & (a) \end{matrix}$

where ∫ρ²dA = J is the polar moment of inertia of the circular cross section (Section C.2). For circle of radius r, J = π r⁴/2. Thus,

$\begin{matrix} τ_{\max} = \frac{T r}{J} & (6.1) \end{matrix}$

This is the well-known torsion formula for circular bars. The shearing stress at a distance ρ from the center is

$\begin{matrix} τ = \frac{T ρ}{J} & (6.2) \end{matrix}$

The transverse shearing stress obtained by Eq. (6.1) or (6.2) is accompanied by a longitudinal shearing stress of equal value, as shown on a surface element in Fig. 6.2.

When a shaft is subjected to torques at several points along its length, the internal torques will vary from section to section. A graph showing the variation of torque along the axis of the shaft is called the torque diagram. Such a diagram represents a plot of the internal torque T versus its position x along the shaft length. As a sign convention, T will be positive if its vector is in the direction of a positive coordinate axis. However, the torque diagram is rarely used, because in practice, only a few variations in torque occur along the length of a given shaft.

6.2.2 Angle of Twist

According to Hooke’s law, γ_max = τ_max/G; introducing the torsion formula, γ_max = Tr/JG, where G is the modulus of elasticity in shear. For small deformations, tan γ_max = γ_max, and we may write γ_max = rϕ/L (Fig. 6.2). These expressions lead to the angle of twist—that is, the angle through which one cross section of a circular bar rotates with respect to another:

$\begin{matrix} ϕ = \frac{T L}{J G} & (6.3) \end{matrix}$

Angle ϕ is measured in radians. The product JG is termed the torsional rigidity of the member.

Note that Eqs. (6.1) through (6.3) are valid for both solid and hollow circular bars; this follows from the assumptions used in the derivations. For a circular tube of inner radius r_i and outer radius r₀, we have $J = π (r_{0}^{4} - r_{i}^{4}) / 2$ .

Example 6.1 Stress and Deformation in an Aluminum Shaft

A hollow aluminum alloy 6061-T6 shaft of outer radius c = 40 mm, inner radius b = 30 mm, and length L = 1.2 m is fixed at one end and subjected to a torque T at the other end, as shown in Fig. 6.3. If the shearing stress is limited to τ_max = 140 MPa, find (a) the largest value of the torque; (b) the corresponding minimum value of shear stress; and (c) the angle of twist that will create a shear stress τ_min = 100 MPa on the inner surface.

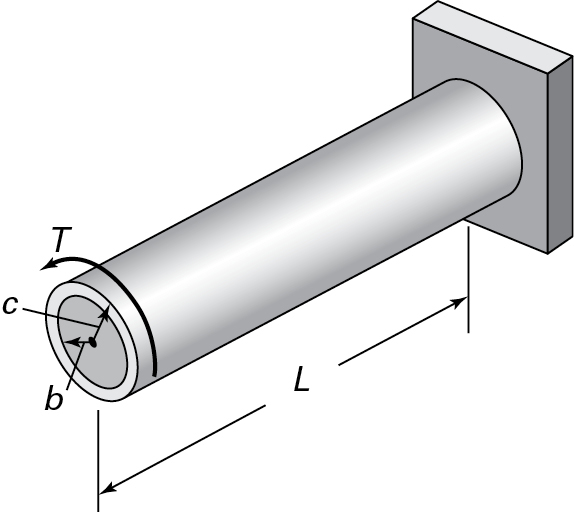
A figure represents a tubular circular bar of length l. One of the ends of the bar is fixed rigidly. Another end of the bar is subjected to torque in the anti-clockwise direction. The bar has an inner radius b and the outer radius c. — Figure 6.3. *Example 6.1. A tubular circular bar in torsion.*

Solution From Table D.1, we have the shear modulus of elasticity G = 72 GPa and τ_yp = 220 MPa.

In as much as τ_max < τ_yp, we can apply Eq. (6.1) with r = c to obtain

$\begin{matrix} T = \frac{J τ_{\max}}{c} & (b) \end{matrix}$

By Table C.1, the polar moment of inertia of the hollow circular tube is

$J = \frac{π}{2} (c^{4} - b^{4}) = \frac{π}{2} (40^{4} - 30^{4}) = 2.749 (10^{6}) {mm}^{4}$

Inserting J and τ_max into Eq. (b) results in

$T = \frac{2.749 (10^{- 6}) (140 \times 10^{6})}{0.04} = 9.62 kN \cdot m$
The smallest value of the shear stress is found on the inner surface of the shaft, and τ_min and τ_max are proportional to b and c, respectively. Therefore,

$τ_{\min} = \frac{b}{c} τ_{\max} = \frac{30}{40} = 105 MPa$
Through the use of Eq. (2.27), the shear strain on the inner surface of the shaft is equal to

$γ_{\min} = \frac{τ_{\min}}{G} = \frac{105 \times 10^{6}}{72 \times 10^{9}} = 1458 μ$

Referring to Fig. 6.2,

$ϕ = \frac{L γ_{\min}}{b} = \frac{1200}{30} (1458 \times 10^{- 6}) = 58.3 \times 10^{- 3} rad$

or

ϕ = 3.34°.

Example 6.2 Redundantly Supported Shaft

Given: A solid circular shaft AB fixed to rigid walls at both ends and subjected to a torque T at section C, as shown in Fig. 6.4a. The shaft diameters are d_a and d_b for segments AC and CB, respectively.

A figure illustrates the circular shaft. — Figure 6.4. *Example 6.2. (a) A fixed-ended circular shaft in torsion; (b) free-body diagram of the entire shaft.*

Figure (a) shows a circular shaft AB of length l. The shaft is fixed to rigid walls at A and B, respectively. The circular shaft contains two segments AC and CB of length a and b, respectively. The shaft is subjected to torque at C in an anti-clockwise direction. The diameters of the segment AC is d subscript and the segment BC is d subscript b. Figure (b) depicts the free body diagram of the entire shaft. The shaft is subjected to torque T subscript A and T subscript B at both ends in the same direction. The torque T at C rotates in an anti-clockwise direction.

Find: The lengths a and b if the maximum shearing stress in both shaft segments is to be the same for d_a = 20 mm and d_b = 12 mm and L = 600 mm.

Solution From the free-body diagram of Fig. 6.4a, we observe that the problem is statically indeterminate to the first degree; the one equation of equilibrium available is not sufficient to obtain the two unknown reactions T_A and T_B.

Condition of Equilibrium. Using the free-body diagram of Fig. 6.4b,

$\begin{matrix} \begin{matrix} \sum T = 0, & T_{A} + T_{B} = T \end{matrix} & (c) \end{matrix}$

Torque-Displacement Relations. The angle of twist at section C is expressed in terms of the left and right segments of the solid shaft, respectively, as

$\begin{matrix} ϕ_{a} = \frac{T_{A} a}{J_{a} G}, ϕ_{b} = \frac{T_{B} b}{J_{b} G} & (d) \end{matrix}$

Here, the polar moments of inertia are $J_{a} = π d_{a}^{4} / 32$ and $J_{b} = π d_{b}^{4} / 32$ .

Condition of Compatibility. The two segments must have the same angle of twist where they join. Thus,

$\begin{matrix} \begin{matrix} ϕ_{a} = ϕ_{b} & or & \frac{T_{A} a}{J_{a} G} = \frac{T_{B} b}{J_{b} G} \end{matrix} & (e) \end{matrix}$

Equations (c) and (e) can be solved simultaneously to yield the reactions

$\begin{matrix} T_{A} = \frac{T}{1 + (a J_{b} / b J_{a})}, T_{B} = \frac{T}{1 + (b J_{a} / a J_{b})} & (f) \end{matrix}$

The maximum shearing stresses in each segment of the shaft are obtained from the torsion formula:

$\begin{matrix} τ_{a} = \frac{T_{A} d_{a}}{2 J_{a}}, τ_{b} = \frac{T_{B} d_{b}}{2 J_{b}} & (g) \end{matrix}$

For the case under consideration τ_a = τ_b, or

$\frac{T_{A} d_{a}}{J_{a}} = \frac{T_{B} d_{b}}{J_{b}}$

Introducing Eqs. (f) into this expression and simplifying, we obtain

$\frac{a}{b} = \frac{d_{a}}{d_{b}}$

from which

$\begin{matrix} a = \frac{d_{a} L}{d_{a} + d_{b}}, b = \frac{d_{b} L}{d_{a} + d_{b}} & (h) \end{matrix}$

where L = a + b. Inserting the given data results in

$a = \frac{200 (600)}{20 + 12} = 375 mm, b = \frac{12 (600)}{20 + 12} = 225 mm$

Comment For a prescribed value of torque T, we can now compute the reactions, angle of twist at section C, and maximum shearing stress from Eqs. (f), (d), and (g), respectively.

6.2.3 Axial and Transverse Shear Stresses

In the preceding discussion, we considered shear stresses acting in the plane of a cut perpendicular to the axis of the shaft, defined by Eqs. (6.1) and (6.2). Their directions coincide with the direction of the internal torque T on the cross section (Fig. 6.2). These stresses must be accompanied by equal shear stresses occurring on the axial planes of the shaft, since equal shear stresses always exist on mutually perpendicular planes.

Now consider the state of stress depicted in Fig. 6.5a. Note that τ is the only stress component acting on this element removed from the bar; the element is in the state of pure shear. Observe that τ = τ_xz = τ_zx denotes the shear stresses in the tangential and axial directions. So, the internal torque develops not only a transverse shear stress along radial lines or in the cross section, but also an associated axial shear stress distribution along a longitudinal plane. The variation of these stresses on the mutually perpendicular planes is illustrated in Fig. 6.5b, where a portion of the shaft has been removed for illustration purposes. Consequently, if a material is weaker in shear axially than laterally (such as wood), the failure in a twisted bar occurs longitudinally along axial planes.

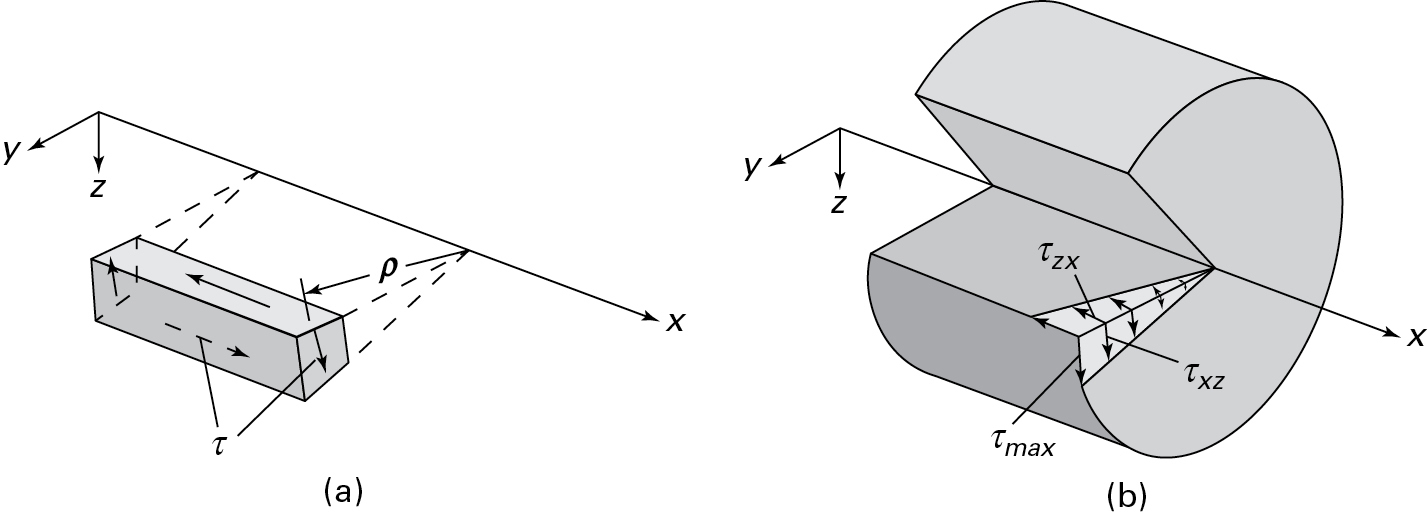
A figure shows the shaft element and shaft segment in pure shear. — Figure 6.5. *Shearing stresses on transverse (xz) and axial (zx) planes of a shaft (Fig. 6.2): (a) shaft element in pure shear; (b) shaft segment in pure shear*

Figure (a) depicts the shaft element in pure shear. The element lies along the x-axis and rho is a distance along the cross-section of element. The shearing stresses tau acts on the transverse (x z) and axial planes (z x). Figure (b) represents the shaft segment about the x-axis. The maximum shear stress occurs on the outer surface of the shaft where the tangential stress (tau z x) equals the axial stress (tau x z).

6.3 Stresses on Inclined Planes

Our treatment thus far has been limited to shearing stresses on planes at a point parallel or perpendicular to the axis of a shaft, defined by the torsion formula. This state of stress is depicted acting on a surface element on the left of the shaft in Fig. 6.6a. Alternatively, representation of the stresses at the same point may be given on an infinitesimal two-dimensional wedge whose outer normal (x′) on its oblique face makes an angle θ with the axial axis (x), as shown in Fig. 6.6b.

A figure presents the stresses acting on the surface elements of a shaft in torsion. — Figure 6.6. (*a) Stresses acting on the surface elements of a shaft in torsion; (b) free-body diagram of wedge cut from the shaft; (c) Mohr’s circle for torsional loading.*

Figure (a) shows a shaft of radius r. The shaft is subjected to external torque T in the equal and opposite direction. The state of stress from the surface of the plane at a point parallel to the axis of a shaft contains maximum stress acting all along the surfaces. The origin of the coordinate system is set at the midspan of the plane where theta is the angle formed between x and x prime (represented in dashed lines). The stresses on the surface element are sigma 1 and sigma 2. The stress element sigma 2 is oriented 45 degrees from the horizontal. Figure (b) depicts a free body diagram of the wedge cut from the shaft. The x prime and y prime axes are obtained by rotating the x and y-axes counterclockwise through an angle theta with the maximum torque. The torque tau x prime y prime and sigma x prime acts on the surfaces of the element. Figure (c) presents a Mohr's circle for torsional building. It consists of a set of coordinate axes with sigma representing the horizontal axis and tau representing the vertical axis. Locating point A on positive tau axis and B on negative tau axis. Similarly, the point A1 and B1 are located on sigma axis. Here, the points A and B are at opposite ends of the diameter A1 and B1. The circle passes through all the four points. The angle 2 theta locates the points A prime and B prime on the circle. The point B prime gives the stresses on the face of y element and point A prime gives the stresses on the face of x element. The maximum stress occurs between A and A1.

6.3.1 Stress Transformation

In this section, we will analyze the stresses σ_x′ and τ_x′y′ that must act on the inclined plane to keep the isolated body, as discussed in Sections 1.7 and 1.9. The equilibrium conditions of forces in the x′ and y′ directions, given by Eqs. (1.18a) and (1.18b) with σ_x = σ_y = 0 and, τ_xy = -τ_max yield

$\begin{matrix} σ_{x^{'}} = - τ_{\max} \sin 2 θ & (a) \end{matrix}$

$\begin{matrix} τ_{x^{'} y^{'}} = - τ_{\max} \cos 2 θ & (b) \end{matrix}$

These are the equations of transformation for stress in a shaft under torsion.

Figure 6.6c, a Mohr’s circle for torsional loading, provides a convenient way of checking the preceding results. Observe that the center C of the circle is at the origin of the coordinates σ and τ. Now recall that points A′ and B′ define the states of stress about any other set of x′ and y′ planes relative to the set through an angle. Similarly, the points and A(0, τ_max) and B(0, τ_min) are located on the τ axis, while A₁ and B₁ define the principal planes and the principal stresses. The radius of the circle is equal to the magnitude of the maximum shearing stress.

The variation in the stresses σ_x′ and σ_x′y′, given by Eqs. (a) and (b), with the orientation of the inclined plane is demonstrated in Fig. 6.7. Notice that τ_max = τ and τ_x′y′ = 0 when θ = 45° and σ_min = -τ and τ_x′y′ = 0 when θ = 135°. That is, the maximum normal stress equals σ₁ = Tr/J and the minimum normal stress equals σ₂ = Tr/J, acting in the directions shown in Fig. 6.6a. Also, no shearing stress greater than τ is developed.

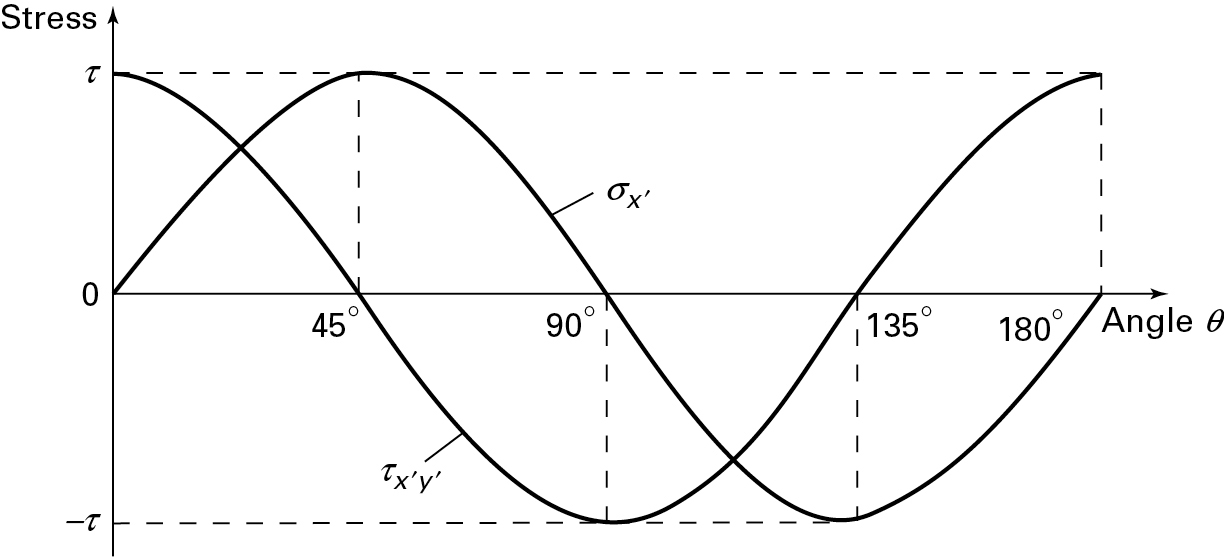
A graph of stress versus angle of the inclined plane is shown. — Figure 6.7. *Graph of normal stress σ_x′ and shear stress τ_x′y′ versus angle θ of the inclined plane.*

A graph represents the normal stress and shear stress with respect to angle theta. The curve representing normal stress (sigma x prime) starts at zero, which reaches its peak value of tau at 45 degrees and decreases to attain its lowest value of tau at 135 degrees. The curve representing the shear stress starts at tau, decreases rapidly to 90 degrees. Again it rises to its highest value of tau at 180 degrees.

For a brittle material such as cast iron, which is weaker in tension than in shear, failure occurs in tension along a helix as indicated by the dashed lines in Fig. 6.6a. Ordinary chalk behaves in the same manner. Conversely, shafts made of ductile materials that are weak in shearing strength (for example, mild steel) break along a line perpendicular to the axis. This behavior is consistent with the types of tensile failures discussed in Section 2.7.

6.3.2 Transmission of Power by Shafts

The power in kilowatts (kW) transmitted by a rotating shaft is of keen interest in the study of machines. As found from first principles,

$\begin{matrix} T= \frac{9549 kW}{n} & (6.4 a) \end{matrix}$

Here T = torque (N · m) and n = shaft speed (rpm). Since 1 horsepower (hp) equals 0.7457 kW, the preceding equation may be written as

$\begin{matrix} h p = \frac{F V}{745.7} = \frac{T n}{7121} & (6.4b) \end{matrix}$

where F is the tangential force (N) and V represents the velocity (m/s). More will be said about rotating shafts, disks, and flywheels in Chapter. 8.

In the design of circular slender shafts that transmit power at a specified speed, the material and the dimensions of the cross section are selected to not exceed the permissible shearing stress or a limiting angle of twist when rotating. A designer thus needs to know the torque acting on the power-transmitting shaft. Equations (6.4) may be used to convert the power supplied to the shaft into a constant torque exerted on it during rotation. After having determined the torque to be transmitted, the design of circular shafts to meet strength requirements can be accomplished by using the process outlined in Section 1.3.1.

Example 6.3 Design of a Shaft

A solid circular shaft of radius r is to transmit 400 kW at n = 1000 rpm without exceeding the yield strength in shear of τ_ys or a twisting through more than 5° in a length of 2 m.

Find: The required diameter of the shaft.

Given: The shaft is made of steel having τ_ys = 310 MPa and G = 80 GPa. A safety factor of 1.6 is used.

Solution Using Eq. (6.4a), we find the torque:

$T = \frac{9549 (400)}{1000} = 3820 N \cdot m$

Strength Specification. Equation (6.1) with a factor of safety of 1.6 leads to

$\frac{π}{2} r^{3} = \frac{3820 (1.6)}{310 (10^{6})}$

Solving, r = 23.2 mm.

Distortion Specification. We now determine the size of the shaft by applying Eq. (6.3):

$\begin{matrix} \frac{Φ_{all}}{L} = \frac{T}{G J} & (c) \end{matrix}$

Inserting the given numerical values,

$\frac{5 ° (π / 180)}{2} = \frac{3820}{(80 \times 10^{9}) π r^{4} / 2}$

This results in r = 28.9 mm.

Comment The minimum allowable diameter of the shaft must be 57.8 mm. Thus, a 58-mm shaft diameter should be used.

6.4 General Solution of the Torsion Problem

Consider a prismatic bar of constant arbitrary cross section subjected to equal and opposite twisting moments applied at the ends, as shown in Fig. 6.8a. The origin of x, y, and z in the figure is located at the center of twist of the cross section, about which the cross section rotates during twisting. The center of twist is also sometimes defined as the point at rest in every cross section of a bar in which one end is fixed and the other twisted by a couple. At this point, u and the x and y displacements are all zero.

A figure presents the torsion member of arbitrary cross-section. — Figure 6.8. *Torsion member of arbitrary cross section.*

Figure (a) shows a cylindrical bar. The bar is subjected to end torque T in the equal and opposite direction. Figure (b) depicts the partial end view of the bar. Points P and P prime are located r distance from the twist center A. The angle between P and P prime makes theta z. A slope is formed on the arbitrary line connecting P and P prime. The angle between P prime and x-axis is alpha.

The location of the center of twist is a function of the shape of the cross section. Note that while the center of twist is referred to in the derivations of the basic relationships, it is not dealt with explicitly in the solution of torsion problems (see Prob. 6.25). The z axis passes through the centers of twist of all cross sections.

6.4.1 Geometry of Deformation

In general, the cross sections warp, as already noted. We now explore the problem of torsion with free warping, by applying the Saint-Venant semi-inverse method [Refs. 6.2 and 6.3]. As a fundamental assumption, the warping deformation is taken to be independent of axial location; that is, it is identical for any cross section:

$\begin{matrix} w = f (x, y) & (a) \end{matrix}$

It is also assumed that the projection on the xy plane of any warped cross section rotates as a rigid body and that the angle of twist per unit length of the bar, θ, is constant.

We refer now to Fig. 6.8b, which shows the partial end view of the bar (and could represent any section). An arbitrary point on the cross section, point P(x, y), located a distance r from center of twist A, has moved to P′(x − u, y + υ) as a result of torsion. Assuming that no rotation occurs at end z = 0 and that θ is small, the x and y displacements of P are, respectively,

$\begin{matrix} \begin{matrix} u & = - (r θ z) \sin α = - y θ z \\ υ & = (r θ z) \cos α = x θ z \end{matrix} & (b) \end{matrix}$

Here the angular displacement of AP at a distance z from the left end is θz; then x, y, and z are the coordinates of point P, and α is the angle between AP and the x axis. Clearly, Eqs. (b) specify the rigid body rotation of any cross section through a small angle θz. By substituting Eqs. (a) and (b) into Eq. (2.4), we have

$\begin{matrix} \begin{matrix} ε_{x} = γ_{x y} = ε_{y} = ε_{z} = 0 \\ \begin{matrix} γ_{z x} = \frac{\partial w}{\partial x} - y θ, & γ_{z y} = \frac{\partial w}{\partial y} + x θ \end{matrix} \end{matrix} & (c) \end{matrix}$

Combining Equation (2.36) with these expressions leads to the following:

$\begin{matrix} σ_{x} = σ_{y} = σ_{z} = τ_{x y} = 0 & (d) \end{matrix}$

$\begin{matrix} \begin{matrix} τ_{z x} = G (\frac{\partial w}{\partial x} - y θ) \\ τ_{z y} = G (\frac{\partial w}{\partial y} + x θ) \end{matrix} & (e) \end{matrix}$

6.4.2 Equations of Equilibrium

By now substituting Eq. (d) into the equations of equilibrium (1.14), and assuming negligible body forces, we obtain

$\begin{matrix} \begin{matrix} \frac{\partial τ_{z x}}{\partial z} = 0, & \frac{\partial τ_{z y}}{\partial z} = 0, & \frac{\partial τ_{z x}}{\partial x} + \frac{\partial τ_{z y}}{\partial y} = 0 \end{matrix} & (6.5) \end{matrix}$

6.4.3 Equations of Compatibility

Differentiating the first equation of Eqs. (e) with respect to y and the second equation with respect to x, and subtracting the second from the first, we obtain an equation of compatibility:

$\begin{matrix} \frac{\partial τ_{z x}}{\partial y} - \frac{\partial τ_{z y}}{\partial x} = H & (6.6) \end{matrix}$

where

$\begin{matrix} H = - 2 G θ & (6.7) \end{matrix}$

Thus, the stress in a bar of arbitrary section may be determined by solving Eqs. (6.5) and (6.6) along with the given boundary conditions.

6.5 Prandtl’s Stress Function

As in the case of beams, the torsion problem is commonly solved by introducing a single stress function. If a function Φ(x, y) known as the Prandtl stress function, is assumed to exist, such that

$\begin{matrix} \begin{matrix} τ_{z x} = \frac{\partialΦ}{\partial y}, & τ_{z y} = - \frac{\partialΦ}{\partial x} \end{matrix} & (6.8) \end{matrix}$

then the equations of equilibrium (6.5) are satisfied. The equation of compatibility (6.6) becomes, upon substitution of Eq. (6.8),

$\begin{matrix} \frac{\partial^{2} Φ}{\partial x^{2}} + \frac{\partial^{2} Φ}{\partial y^{2}} = H & (6.9) \end{matrix}$

The stress function Φ must therefore satisfy Poisson’s equation if the compatibility requirement is to be satisfied.

6.5.1 Boundary Conditions

We are now prepared to consider the boundary conditions, treating first the load-free lateral surface. Recall from Section 1.5 that τ_xz is a z-directed shearing stress acting on a plane whose normal is parallel to the x axis—that is, the yz plane. Similarly, τ_zx acts on the xy plane and is x-directed. By virtue of the symmetry of the stress tensor, we have τ_xz = τ_zx and τ_yz = τ_zy. Therefore, the stresses given by Eq. (e) may be indicated on the xy plane near the boundary, as shown in Fig. 6.9. The boundary element is associated with arc length ds. Note that ds increases in the counterclockwise direction. When ds is zero, the element represents a point at the boundary. Then, referring to Fig. 6.9 together with Eq. (1.48), which relates the surface forces to the internal stress, and noting that the cosine of the angle between z and a unit normal n to the surface is zero [that is, cos(n, z) = 0], we have

$\begin{matrix} τ_{z x} l + τ_{z y} m = 0 & (a) \end{matrix}$

Illustration of arbitrary cross-section S in an x y plane is depicted. — Figure 6.9. *Arbitrary cross section of a prismatic member in torsion.*

A figure presents the arbitrary cross-section S in an x y plane. A slope of dy over negative d x is considered in the cross-section. The shearing stress tau z x is x-directed and tau z y is y directed. The unit normal n acts between the y and z plane. Similarly, the torque acts between y-axis and the unit normal.

According to Eq. (a), the resultant shear stress τ must be tangent to the boundary (Fig. 6.9). From the figure, it is clear that

$\begin{matrix} \begin{matrix} l = \cos (n, x) = \frac{d y}{d s}, & m = \cos (n, y) = - \frac{d x}{d s} \end{matrix} & (b) \end{matrix}$

As we proceed in the direction of increasing s, x decreases and y increases. This accounts for the algebraic sign in front of dx and dy in Fig. 6.9. Substituting Eqs. (6.8) and (b) into Eq. (a) yields

$\begin{matrix} \frac{\partial Φ}{\partial y} \frac{d y}{d s} + \frac{\partial Φ}{\partial x} \frac{d x}{d s} = \frac{d Φ}{d s} = 0 & (on the boundary) & (6.10) \end{matrix}$

This expression states that the directional deviation along a boundary curve is zero. Thus, the function Φ(x, y) must be an arbitrary constant on the lateral surface of the prism. Examination of Eq. (6.8) indicates that the stresses remain the same regardless of additive constants; that is, if Φ + constant is substituted for Φ, the stresses will not change. For solid cross sections, we are therefore free to set Φ equal to zero at the boundary.

In the case of multiply connected cross sections, such as hollow or tubular members, an arbitrary value may be assigned at the boundary of only one of the contours s₀, s₁,...., s_n. For such members, however, we must extend the mathematical formulation presented in this section. In Section 6.8, we consider solutions for thin-walled, multiply connected cross sections by applying the membrane analogy.

Returning to the member of solid cross section, we finish our discussion of the boundary conditions by considering the ends, at which the normals are parallel to the z axis and therefore cos(n, z) = n = ±1, l = m = 0. Equation (1.48) now gives, for p_z = 0,

$\begin{matrix} \begin{matrix} p_{x} = \pm τ_{z x}, & p_{y} = \pm τ_{z y} \end{matrix} & (c) \end{matrix}$

where the algebraic sign depends on the relationship between the outer normal and the positive z direction. For example, it is negative for the end face at the origin in Fig. 6.8a.

6.5.2 Force and Torque over the Ends

We now confirm that the summation of forces over the ends of the bar is zero:

$\begin{matrix} \begin{matrix} \iint p_{x} d x d y & = \iint τ_{z x} d x d y = \iint \frac{\partial Φ}{\partial y} d x d y \\ = \int d x \int_{y_{1}}^{y_{2}} \frac{\partial Φ}{\partial y} d y = \int {Φ |}_{y_{1}}^{y_{2}} d x = \int (Φ_{2} - Φ_{1}) d x = 0 \end{matrix} \end{matrix}$

Here y₁ and y₂ represent the y coordinates of points located on the surface. Because Φ = constant on the surface of the bar, the values of Φ corresponding to y₁ and y₂ must be equal to a constant, Φ₁ = Φ₂ = constant. Similarly, it may be shown that

$\iint τ_{z y} d x d y = 0$

The end forces, while adding to zero, must nevertheless provide the required twisting moment or externally applied torque about the z axis:

$\begin{matrix} T & = \iint (x τ_{z y} - y τ_{z x}) d x d y = - \iint x \frac{\partial Φ}{\partial x} d x d y - \iint y \frac{\partial Φ}{\partial y} d x d y \\ = - \int d y \int x \frac{\partial Φ}{\partial x} d x - \int d x \int y \frac{\partial Φ}{\partial y} d y \end{matrix}$

Integrating by parts, we have

$T = - \int x Φ_{x_{1}}^{x_{2}} d y + \iint Φ d x d y - \int y Φ_{y_{1}}^{y_{2}} d x + \iint Φ d x d y$

Since Φ = constant at the boundary and x₁, x₂, y₁, and y₂, denote points on the lateral surface, it follows that

$\begin{matrix} T = 2 \iint Φ d x d y & (6.11) \end{matrix}$

As Φ(x, y) has a value at each point on the cross section, it is clear that Eq. (6.11) represents twice the volume beneath the Φ surface.

The result of applying this approach is a set of equations satisfying all the conditions of the prescribed torsion problem. Equilibrium is governed by Eqs. (6.8), compatibility by Eq. (6.9), and the boundary condition by Eq. (6.10). Torque is related to stress by Eq. (6.11). To ascertain the distribution of stress, it is necessary to determine a stress function that satisfies Eqs. (6.9) and (6.10), as is demonstrated in the following example.

Example 6.4 Analysis of an Elliptical Torsion Bar

Consider a solid bar of elliptical cross section (Fig. 6.10a). Determine the maximum shearing stress and the angle of twist per unit length. Also, derive an expression for the warping w(x, y).

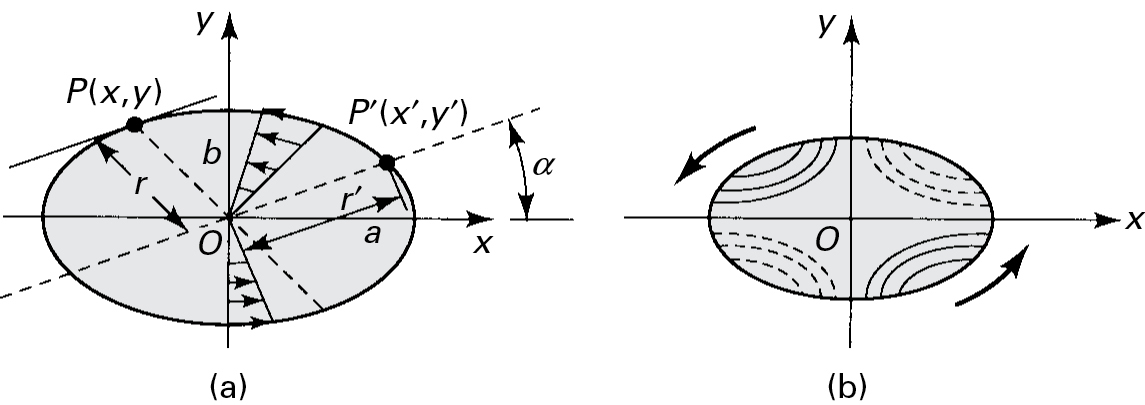
A figure illustrates the elliptical torsion bar. — Figure 6.10. *Example 6.4. Elliptical cross section: (a) shear stress distribution; (b) out-of-plane deformation or warping.*

Figure (a) shows the elliptical cross-section in the x y plane. Here, a and b are semi-axis dimensions. Two dashed lines representing p prime (x prime, y prime) and P (x, y) are drawn through the origin. The angle between the x-axis and p prime (x prime, y prime) makes alpha. The distance between p prime (x prime, y prime) and P (x, y) is r and r prime is the distance of p prime (x prime, y prime) from the origin. The tensile forces are distributed uniformly over the cross-section. Figure (b) represents the out-of-plane deformation or warping in the x y plane. The deformation is represented in the form of a semicircle pattern at each corner of the cross-section.

Solution Equations (6.9) and (6.10) are satisfied by selecting the stress function

$Φ = k (\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} - 1)$

where k is a constant. Substituting this expression into Eq. (6.9), we obtain

$k = \frac{a^{2} b^{2}}{2 (a^{2} + b^{2})} H$

Hence,

$\begin{matrix} Φ = \frac{a^{2} b^{2} H}{2 (a^{2} + b^{2})} (\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} - 1) & (d) \end{matrix}$

and Eq. (6.11) yields

$\begin{matrix} T & = \frac{a^{2} b^{2} H}{a^{2} + b^{2}} (\frac{1}{a^{2}} \iint x^{2} d x d y + \frac{1}{b^{2}} \iint y^{2} d x d y - \iint d x d y) \\ = \frac{a^{2} b^{2} H}{a^{2} + b^{2}} (\frac{1}{a^{2}} I_{y} + \frac{1}{b^{2}} I_{x} - A) \end{matrix}$

Here A is the cross-sectional area. Inserting the expressions for I_x, I_y and A (Table C.1) results in

$\begin{matrix} T = \frac{a^{2} b^{2} H}{a^{2} + b^{2}} (\frac{1}{a^{2}} \frac{π b a^{3}}{4} + \frac{1}{b^{2}} \frac{π a b^{3}}{4} - π a b) = \frac{- π a^{3} b^{3} H}{2 (a^{2} + b^{2})} & (e) \end{matrix}$

from which

$\begin{matrix} H = - \frac{2 T (a^{2} + b^{2})}{π a^{3} b^{3}} & (f) \end{matrix}$

The stress function is now expressed as

$Φ = - \frac{T}{π a b} (\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} - 1)$

and the shearing stresses are found readily from Eq. (6.8):

$\begin{matrix} \begin{matrix} τ_{z x} & = \frac{\partial Φ}{\partial y} = - \frac{2 T y}{π a b^{3}} = - \frac{T y}{2 I_{x}} \\ τ_{z y} & = - \frac{\partial Φ}{\partial x} = \frac{2 T x}{π a^{3} b} = \frac{T x}{2 I_{y}} \end{matrix} & (g) \end{matrix}$

The ratio of these stress components is proportional to y/x and, therefore, constant along any radius of the ellipse:

$\frac{τ_{z x}}{τ_{z y}} = - \frac{y}{x} \frac{a^{2}}{b^{2}} = - \frac{y}{x} \frac{I_{y}}{I_{x}}$

The resultant shearing stress,

$\begin{matrix} τ_{z α} = {(τ_{z x}^{2} + τ_{z y}^{2})}^{1 / 2} = \frac{2 T}{π a b} {(\frac{x^{2}}{a^{4}} + \frac{y^{2}}{b^{4}})}^{1 / 2} & (h) \end{matrix}$

has a direction parallel to a tangent drawn at the boundary at its point of intersection with the radius containing the point under consideration. Note that α represents an arbitrary angle (Fig. 6.10a).

To determine the location of the maximum resultant shear, which from Eq. (g) is somewhere on the boundary, consider a point P′(x′, y′) located on a diameter conjugate to that containing P(x, y) (Fig. 6.10a). Note that OP′ is parallel to the tangent line at P. The coordinates of P and P′ are related by

$\begin{matrix} x = \frac{a}{b} y^{'}, & y = \frac{b}{a} x^{'} \end{matrix}$

Substituting these expressions into Eq. (h), we have

$\begin{matrix} τ_{z α} = \frac{2 T}{π a^{2} b^{2}} {({x^{'}}^{2} + {y^{'}}^{2})}^{1 / 2} = \frac{2 T}{π a^{2} b^{2}} r^{'} & (i) \end{matrix}$

Clearly, τ_zα will have its maximum value corresponding to the largest value of the conjugate semidiameter r′. This occurs where r′ = a or r = b. The maximum resultant shearing stress thus occurs at P(x, y), corresponding to the extremities of the minor axis as follows: x = 0, y = ±b. From Eq. (i),

$\begin{matrix} τ_{\max} = \frac{2 T}{π a b^{2}} & (6.12a) \end{matrix}$

The angle of twist per unit length is obtained by substituting Eq. (f) into Eq. (6.7):

$\begin{matrix} θ = \frac{(a^{2} + b^{2}) T}{π a^{3} b^{3} G} & (6.12b) \end{matrix}$

The factor by which the twisting moment is divided to determine the twist per unit length is called the torsional rigidity, commonly denoted C. It is equal to

$\begin{matrix} C = \frac{T}{θ} & (6.13) \end{matrix}$

The torsional rigidity for an elliptical cross section, from Eq. (6.12b), is thus

$C = \frac{π a^{3} b^{3}}{a^{2} + b^{2}} G = \frac{G}{4 π^{2}} \frac{{(A)}^{4}}{J}$

where A = πab and J = πab(a²+b²)/4 are the area and polar moment of inertia of the cross section, respectively.

The components of displacement u and υ are then found from Eq. (b) of Section 6.4. To obtain the warpage w(x, y), consider Eq. (e) of Section 6.4, in which the previously derived relations for τ_zx, τ_zy and θ are substituted:

$\begin{matrix} τ_{z x} & = - \frac{2 T y}{π a b^{3}} = G [\frac{\partial w}{\partial x} - \frac{y (a^{2} + b^{2}) T}{π a^{3} b^{3} G}] \\ τ_{z y} & = \frac{2 T x}{π a^{3} b} = G [\frac{\partial w}{\partial y} + \frac{x (a^{2} + b^{2}) T}{π a^{3} b^{3} G}] \end{matrix}$

Integration of these equations leads to identical expressions for w(x, y), except that the first also yields an arbitrary function of y, f (y), and the second an arbitrary function of x, f (x). Since w(x, y) must give the same value for a given P(x, y), we conclude that f (x) = f (y) = 0; what remains is

$\begin{matrix} w (x, y) = \frac{T}{G} \frac{(b^{2} - a^{2}) x y}{π a^{3} b^{3}} & (6.14) \end{matrix}$

Comment The contour lines, obtained by setting w = constant, are the hyperbolas shown in Fig. 6.10b. The solid lines indicate the portions of the section that become convex, and the dashed lines indicate the portions of the section that become concave when the bar is subjected to a torque in the direction shown.

6.5.3 Circular Cross Section

The results obtained in this example for an elliptical section may readily be reduced to the case of a circular section by setting a and b equal to the radius of a circle r (Fig. 6.6a). Equations (6.12a and b) thus become

$\begin{matrix} τ_{\max} = \frac{2 T}{π r^{3}} = \frac{T r}{J}, & ϕ = θ L = \frac{T L}{J G} \end{matrix}$

where J = πr⁴/2 is the polar moment of inertia. Similarly, Eq. (6.14) gives w = 0, verifying assumption (1) of Section 6.2.

Example 6.5 Equilateral Triangle Bar Under Torsion

An equilateral cross-sectional solid bar is subjected to pure torsion (Fig. 6.11). What are the maximum shearing stress and the angle of twist per unit length?

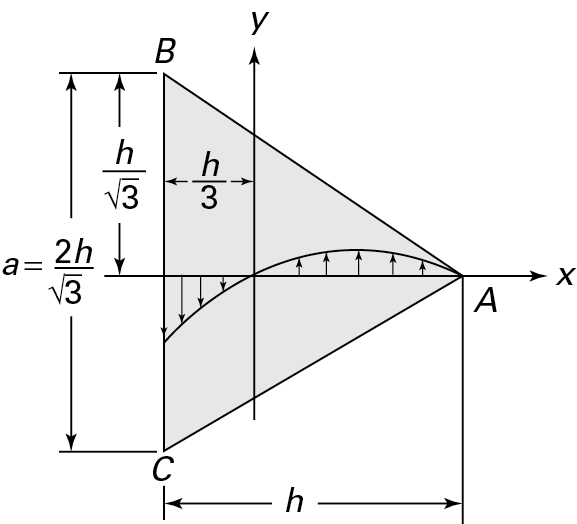
A figure shows the cross-section of the equilateral triangle ABC. — Figure 6.11. *Example 6.5. Equilateral triangle cross section.*

The side BC of the triangle is a equals 2 h over the square root of 3. The slant height of AC is h. The height h is the distance of B from the origin to the top. The side BC is located h over 3 distance from the y-axis. The shearing stress is distributed uniformly over the triangle.

Solution The equations of the boundaries are expressed as

$\begin{matrix} x + \frac{h}{3} = 0 & on B C \\ \frac{x}{\sqrt{3}} + y - \frac{2 h}{3 \sqrt{3}} = 0 & on A B \end{matrix}$

$\begin{matrix} \frac{x}{\sqrt{3}} - y - \frac{2 h}{3 \sqrt{3}} = 0 & on A C \end{matrix}$

Therefore, the stress function that vanishes at the boundary may be written in the form

$\begin{matrix} Φ = k (x + \sqrt{3} y - \frac{2 h}{3}) (x - \sqrt{3} y - \frac{2 h}{3}) (x + \frac{h}{3}) & (j) \end{matrix}$

in which k is constant.

Proceeding as in Example 6.4, we can readily see (see Prob. 6.29) that the largest shearing stress at the middle of the sides of the triangle is equal to

$\begin{matrix} τ_{\max} = \frac{15 \sqrt{3} T}{2 h^{3}} & (k) \end{matrix}$

At the corners of the triangle, the shearing stress is zero, as shown in Fig. 6.11. The angle of twist per unit length is given by

$\begin{matrix} θ = \frac{15 \sqrt{3} T}{h^{4} G} & (I) \end{matrix}$

The torsional rigidity is therefore $C = T / θ = h^{4} G / 15 \sqrt{3}$ . Note that, for an equilateral triangle of sides a, we have $a = 2 h / \sqrt{3}$ (Fig. 6.11).

Example 6.6 Rectangular Bar Subjected to Torsion

A torque T acts on a bar having rectangular cross section of sides a and b (Fig. 6.12). Outline the derivations of the expressions for the maximum shearing stress τ_max and the angle of twist per unit length θ.

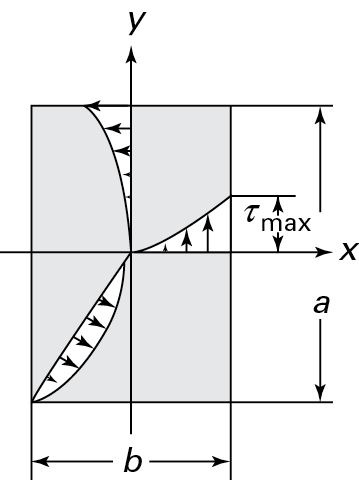
The rectangular cross-section of a torsion bar is illustrated. The rectangle is centered at the origin. The length and breadth of the rectangle is a and b, respectively. The shear stress (tau maximum) is distributed uniformly over the rectangle — Figure 6.12. *Example 6.6. Shear stress distribution in the rectangular cross section of a torsion bar.*

Solution The indirect method employed in the preceding examples does not apply to the rectangular cross sections, and mathematical solution of the problem is a lengthy process. For situations that cannot be conveniently solved by applying the theory of elasticity, the governing equations are used in conjunction with the experimental methods, such as membrane analogy [Ref. 6.4]. Finite element analysis is also very efficient for this purpose.

The shear stress distribution along three radial lines initiating from the center of a rectangular section of a bar in torsion is shown in Fig. 6.12, where the largest stresses occur along the center line of each face. The difference in this stress distribution compared with that of a circular section is very clear. For the latter, the stress reaches a maximum at the most remote point, but for the former, the stress is zero at the most remote point. The values of the maximum shearing stress τ_max in a rectangular cross section and the angle of twist per unit length θ are given in the next section (see Table 6.2 later in that section).

Comments Interestingly, a corner element of the cross section of a rectangular shaft under torsion does not distort at all, so that the shear stresses are zero at the corners, as illustrated in Fig. 6.13. This is possible because outside surfaces are free of all stresses. The same considerations can be applied to the other points on the boundary. The shear stresses acting on three outermost cubic elements isolated from the bar are illustrated in the figure, with the stress-free surfaces being shaded. Observe that all shear stressesτ_xy and τ_xz in the plane of a cut near the boundaries act on them.

Figure (a) presents the deformation and stress in a rectangular bar segment under torsion. The bar is subjected to external torque T in the equal and opposite directions. The bar lies along the z-axis. Three cubic elements are taken out from the bar. The cubical element contains the stresses such as tau x z, tau y x on its faces. The stress-free surface is shaded. — Figure 6.13. *Example 6.6. Deformation and stress in a rectangular bar segment under torsion. Note that the original plane cross sections have warped out of their own plane.*

6.6 Prandtl’s Membrane Analogy

In this section, we demonstrate that the differential equation for the stress function, Eq. (6.9), has the same form as the equation describing the deflection of a membrane or soap film subject to pressure. Hence, an analogy exists between the torsion and membrane problems, which serves as the basis for a number of experimental techniques. Consider an edge-supported homogeneous membrane, whose its boundary contour is defined by a hole cut in a plate (Fig. 6.14a). The shape of the hole is the same as that of the twisted bar to be studied; the sizes need not be identical.

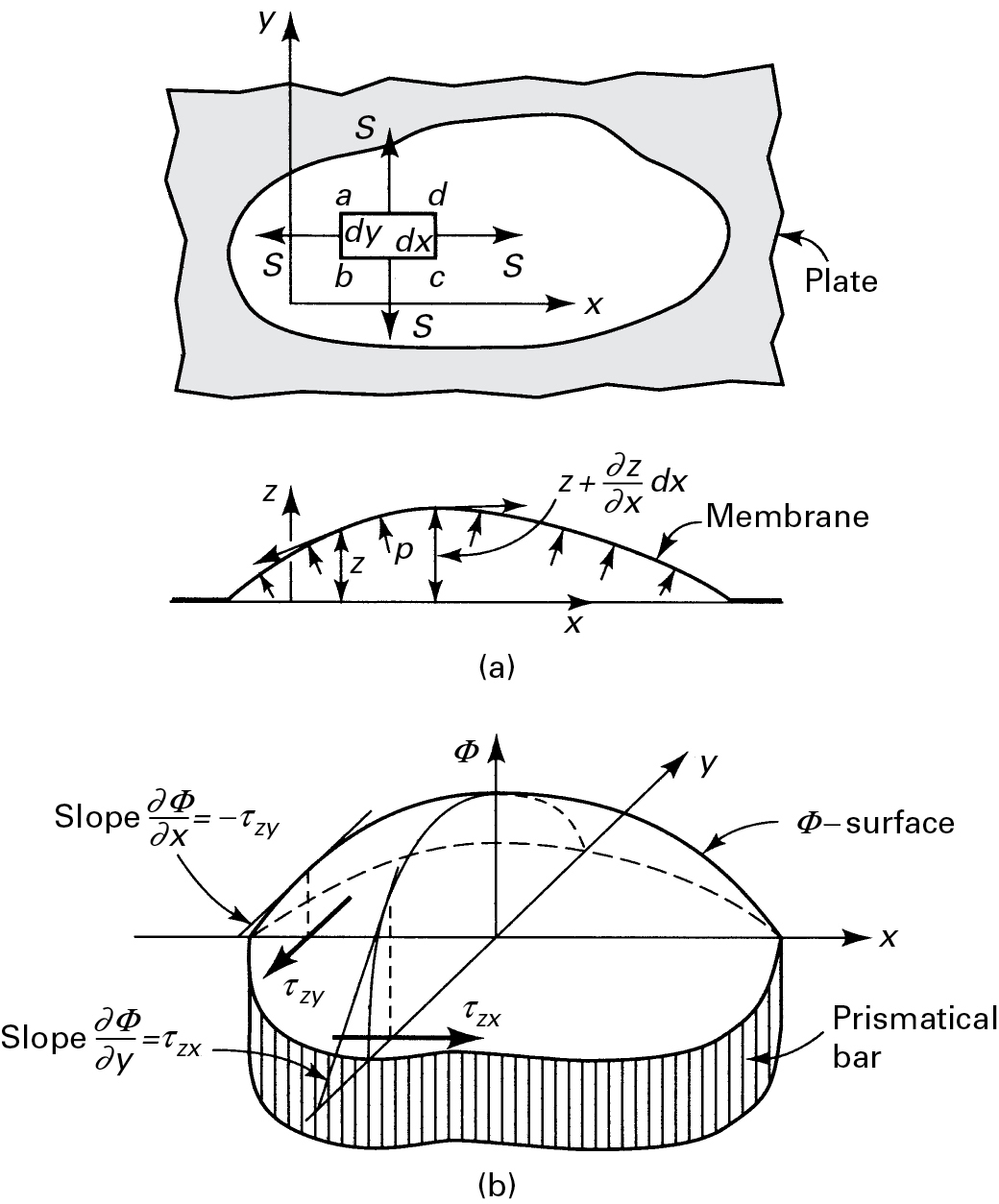
A figure depicts the membrane analogy for torsion members of the solid cross-section. — Figure 6.14. *Membrane analogy for torsion members of solid cross section.*

Figure (a) shows a plate. A hole is cut out from the plate. An isolated element abcd of the hole is considered in the x y plane. The membrane has a tensile force S, in all directions. The side view of the membrane is shown in the x z plane. It depicts the uniform distribution of stress p in the membrane. The height of the plane is z plus dho z over dho x times dx. The height of the membrane at any point is represented as z. The bulged region is represented as phi surface. Figure (b) represents the membrane analogy of prismatic bar in x y plane. Due to the shear force in x z and y z plane, the bar bulges which is represented by phi. The slope of tau in y z plane is slope times dho phi over dho x equals negative tau z y. The slope of z x plane is slope times dho phi over dho y equals tau z x.

6.6.1 Equation of Equilibrium

The equation describing the z deflection of the membrane is derived from considerations of equilibrium applied to the isolated element abcd. Let the tensile forces per unit membrane length be denoted by S. From a small z deflection, the inclination of S acting on side ab may be expressed as β ≈ ∂z/∂x. Since z varies from point to point, the angle at which S is inclined on side dc is

$β + \frac{\partial β}{\partial x} d x \approx \frac{\partial z}{\partial x} + \frac{\partial^{2} z}{\partial x^{2}} d x$

Similarly, on sides ad and bc, the angles of inclination for the tensile forces are ∂z/∂y and ∂z/∂y + (∂²z/∂y²)dy, respectively.

In the development that follows, S is regarded as a constant, and the weight of the membrane is ignored. For a uniform lateral pressure p, the equation of vertical equilibrium is then

$- (S d y) \frac{\partial z}{\partial x} + S d y (\frac{\partial z}{\partial x} + \frac{\partial^{2} z}{\partial x^{2}} d x) - (S d x) \frac{\partial z}{\partial y} + (S d x) (\frac{\partial z}{\partial y} + \frac{\partial^{2} z}{\partial y^{2}} d y) + p d x d y = 0$

leading to

$\begin{matrix} \frac{\partial^{2} z}{\partial x^{2}} + \frac{\partial^{2} z}{\partial y^{2}} = - \frac{p}{S} & (6.15) \end{matrix}$

This is again Poisson’s equation. Comparing Eq. (6.15) with Eqs. (6.9) and (6.8), we see that the quantities shown in Table 6.1 are analogous. The membrane, subject to the conditions outlined, then represents the Φ surface (Fig. 6.14b). In view of the derivation, the restriction with regard to smallness of slope must be borne in mind.

Table 6.1. Analogy between Membrane and Torsion Problems

Membrane Problem	Torsion Problem
z	Φ
$\frac{1}{S}$	G
p	2θ
$- \frac{\partial z}{\partial x}, \frac{\partial z}{\partial y}$	τ_zy, τ_zx
2 · (volume beneath membrane)	T

6.6.2 Shearing Stress and Angle of Twist

Next, we outline one method by which the foregoing theory can be reduced to a useful experiment. In two thin, stiff plates, bolted together, are cut two adjacent holes; one hole conforms to the outline of the irregular cross section and the other is circular. The plates are then separated and a thin sheet of rubber stretched across the holes (with approximately uniform and equal tension). Finally, the assembly is bolted together.

Subjecting one side of the membrane to a uniform pressure p causes a different distribution of deformation for each cross section, with the circular hole providing calibration data. The measured geometric quantities associated with the circular hole, together with the known solution, provide the needed proportionalities between pressure and angle of twist, slope and stress, volume and torque. These are then applied to the irregular cross section, for which the measured slopes and volume yield τ and T. This approach obviates the need for precise information concerning the membrane stress.

The membrane analogy provides more than a useful experimental technique. As is demonstrated in the next section, it also serves as the basis for obtaining approximate analytical solutions for bars of narrow cross section as well as for members of open thin-walled section.

For reference purposes, Table 6.2 presents the shearing stress and angle of twist for a number of commonly encountered shapes [Ref. 6.4]. Note that the values of coefficients α and β depend on the ratio of the length of the long side or depth a to the width b of the short side of a rectangular section. For thin sections, where a is much greater than b, their values approach 1/3. In all cases, the maximum shearing stresses occur at a point on the edge of the cross section that is closest to the center axis of the shaft. A circular shaft is the most efficient; it is subjected to both smaller maximum shear stress and a smaller angle of twist than the corresponding noncircular shaft of the same cross-sectional area and carrying the same torque.

The maximum shear stress and angle of twist per unit length of an ellipse, equilateral triangle, rectangle, rectangular tube, circular tube, and hexagon are listed in the table. — Table 6.2. *Shear Stress and Angle of Twist of Various Members in Torsion*

A table presents the shear stress and angle of twist of various members in torsion. A cross section of an ellipse is shown with an xy plane drawn in it. The horizontal length of the circle is marked 2a and the vertical length is marked as 2b. The maximum shearing stress (tau subscript A) is given as 2T over pi a b squared and the angle of twist per unit length (theta) is given as (a squared plus b squared), T over pi a cubed b cubed G. A cross-section of the equilateral triangle is shown with a point "A" marked in the center of one of its legs. The length of the leg is marked "a." The maximum shearing stress (tau subscript A) is given as 20T over a cubed. The angle of twist per unit length (theta) is given as 46.2 T over a power 4 G. A cross-section of the rectangle is shown with an xy plane drawn in its center. The length of the rectangle is marked "a" and breadth of the rectangle is marked "b." A point "A" is marked in the center of the lower base of the rectangle. The maximum shearing stress of the rectangle is (tau subscript A) is given as T over alpha a b squared. The angle of twist per unit length (theta) is given as T over beta a b cubed G. A cross-section of the rectangular tube is shown with an xy plane drawn in its center. The length of the rectangular tube is marked "a" and its breadth is marked "b." Points "A" and "B" are marked at the center of the base and sides. The thickness of the side tubes are marked "t" and the thickness of upper and lower tubes are marked "t subscript 1." The maximum shearing stress at A (tau subscript A) is given as T over 2ab t subscript 1. The maximum shearing stress at B (tau subscript B) is given as T over 2abt. The angle of twist per unit length (theta) is given as (at plus b t subscript 1), T over 2t t subscript 1,a squared, b squared G. A cross section of an elliptical tube with an xy plane drawn in its center is shown. The horizontal length of the circular tube is marked 2a and the vertical length is marked 2b. The thickness of the tube is marked t. A point "A" is marked at the upper center of the elliptical tube. The maximum shearing stress at A (tau subscript A) is given as T over 2 pi abt. The angle of twist per unit length (theta) equals the whole square root of 2 (a squared plus b squared), T over 4 pi a squared b squared t G. A cross-section of the hexagon is shown with a point "A" marked on one of its sides. The height of the hexagon is marked "a." The maximum shearing stress at A (tau subscript A) is given as 5.7 T over a cubed. The angle of twist per unit length (theta) is given as 8.8 T over a power 4 G.

Example 6.7 Analysis of a Stepped Bar in Torsion

A rectangular bar of width b consists of two segments: one with depth a₁ = 60 mm and length L₁ = 2.5 m, and the other with depth a₂ = 45 mm and length L₂ = 1.5 m (Fig. 6.15). The bar is to be designed using an allowable shearing stress τ_all = 50 MPa and an allowable angle of twist per unit length θ_all = 1.5° per meter.

A figure shows a rectangular bar AB of width b. — Figure 6.15. *Example 6.7. A stepped rectangular torsion bar.*

The torque T acts on either end of the bar in the opposite directions. The bar consists of two segments AC and CB. The length of each segment is L1 and L2, respectively. The diameter of the segment is a 1 and a 2.

Find: (a) The maximum permissible applied torque T_max assuming b = 30 mm and G = 80 GPa; (b) the corresponding angle of twist between the end sections, ϕ_max.

Solution The values of the torsion parameters from Table 6.2 are

$\begin{matrix} \begin{matrix} For segment A C (\frac{a_{1}}{b} = 2) : & α_{1} = 0.246 & \begin{matrix} and & β_{1} = 0.229 \end{matrix} \end{matrix} \\ \begin{matrix} For segment C B (\frac{a_{2}}{b} = 1.5) : & α_{2} = 0.231 & and & β_{2} = 0.196 \end{matrix} \end{matrix}$

Segment BC governs the torque because it is of smaller depth. The permissible torque T based on the allowable shearing stress is obtained from τ_max = T/α ab² Thus,

$T = α_{2} a_{2} b^{2} τ_{\max} = 0.231 (0.045) {(0.03)}^{2} (50 \times 10^{6}) = 468 N \cdot m$

The allowable torque T corresponding to the allowable angle of twist per unit length is determined from θ = T/βab³G:

$T = β_{2} a_{2} b^{3} G θ_{all} = 0.196 (0.045) {(0.03)}^{3} (80 \times 10^{9}) (\frac{1.5 π}{180}) = 499 N \cdot m$

The maximum permissible torque, equal to the smaller of the two preceding values, is T_max = 468 N · m.
The angle of twist is equal to the sum of the angles of twist for the two segments:

$\begin{matrix} ϕ_{\max} & = \frac{T_{\max}}{b^{3} G} (\frac{L_{1}}{β_{1} a_{1}} + \frac{L_{2}}{β_{2} a_{2}}) \\ = \frac{468}{({0.03}^{3}) (80 \times 10^{9})} [\frac{2.5}{0.229 (0.06)} + \frac{1.5}{0.196 (0.045)}] \\ = 0.0763 rad = 4.37 ° \end{matrix}$

Comment Clearly, had the allowable torque been based on the angle of twist per unit length, we would have found that ϕ_max = θ_all(L₁ + L₂) = 1.5(4) = 6°.

6.7 Torsion of Narrow Rectangular Cross Section

In applying the analogy to a bar of narrow rectangular cross section, it is usual to assume a constant cylindrical membrane shape over the entire dimension b (Fig. 6.16). Subject to this approximation, ∂z/∂y = 0, and Eq. (6.15) reduces to d²z/dx² = −p/S, which is twice integrated to yield the parabolic deflection

$\begin{matrix} z = \frac{1}{2} \frac{p}{S} [{(\frac{t}{2})}^{2} - x^{2}] & (a) \end{matrix}$

To arrive at Eq. (a), the boundary conditions that dz/dx = 0 at x = 0 and that z = 0 at x = t/2 have been employed. The volume bounded by the parabolic cylindrical membrane and the xy plane is given by V = pbt^3/12S.

According to the analogy, p is replaced by 2θ and 1/S by G, and consequently $T = 2 V = \frac{1}{3} b t^{3} G θ$ . The torsional rigidity for a thin rectangular section is therefore

$\begin{matrix} C = \frac{T}{θ} = \frac{1}{3} b t^{3} G = J_{e} G & (6.16) \end{matrix}$

where J_e represents the effective polar moment of inertia of the section. The analogy also requires that

$\begin{matrix} τ_{z y} = - \frac{\partial z}{\partial x} = 2 G θ x & (b) \end{matrix}$

The angle of twist per unit length is, from Eq. (6.16),

$\begin{matrix} θ = \frac{3 T}{b t^{3} G} & (6.17) \end{matrix}$

Maximum shear, which occurs at ± t/2, is

$\begin{matrix} τ_{\max} = G θ t = \frac{3 T}{b t^{2}} & (6.18) \end{matrix}$

$\begin{matrix} T = \frac{1}{3} b t^{2} τ_{\max} & (6.19) \end{matrix}$

Equation (b) shows that, the shearing stress is linear in x, as in Fig. 6.9, producing a twisting moment T about z given by

$T = 2 (\frac{1}{2} τ_{\max} \frac{t}{2}) (\frac{t}{3}) (b) = \frac{1}{6} b t^{2} τ_{\max}$

This is exactly one-half the torque given by Eq. (6.19). The remaining applied torque is evidently resisted by the shearing stresses τ_zx, which was neglected in the original analysis in which the membrane is taken as cylindrical. The membrane slope at y = ±b/2 is smaller than that at x = ±t/2 or, equivalently, (τ_zx)_max < (τ_zy)_max. It is clear, therefore, that Eq. (6.18) represents the maximum shearing stress in the bar, of a magnitude unaffected by the original approximation. The fact that the lower τ_zx stresses can provide a resisting torque equal to that of the τ_zy stresses is explained on the basis of the longer moment arm for the stresses near y = ±bl2.

6.7.1 Thin-Walled Open Cross Sections

Equations (6.17) and (6.18) are also applicable to thin-walled open sections such as those shown in Fig. 6.17. Because the previously given expressions neglect stress concentration, the points of interest should be reasonably distant from the corners of the section (Figs. 6.17b and c). The validity of the foregoing approach depends on the degree of similarity between the membrane shape of Fig. 6.16 and that of the geometry of the component section.

A figure represents the membrane analogy for a torsional member of narrow rectangular cross-sections. — Figure 6.16. *Membrane analogy for a torsional member of narrow rectangular cross section: (a) contours; (b) side view of membrane.*

Figure (a) show the stresses in a rectangular cross-section of width t and length b. The reference line x y is drawn at the center of the cross-section. The stresses in the x z and y z planes is distributed throughout the section in an anti-clockwise direction. The side view of the membrane with thickness t is shown individually. The distribution of the stress is represented inside the downward curve s.

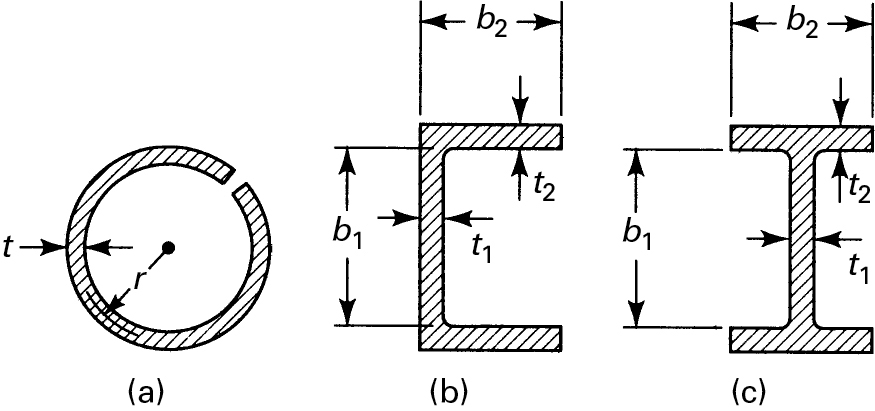
Illustration of thin-walled open sections is shown. — Figure 6.17. *Thin-walled open sections.*

Figure (a) depicts the thin-walled split circular ring of radius r and thickness t. Figure (b) presents a channel section. The thicknesses of the vertical section is t 1 and horizontal section is t 2. The width of the horizontal and vertical section is b 1 and b 2, respectively. Figure (c) represents an I-beam. The flange is labeled b 2. The height of the web is labeled b 1. The thicknesses of web and flange is t 2 and t, respectively.

Consider, for example, the I-section of Fig. 6.17c. Because the section is of varying thickness, the effective polar moment of inertia is written as

$\begin{matrix} J_{e} = \sum \frac{1}{3} b t^{3} & (6.20) \end{matrix}$

$J_{e} = \frac{1}{3} b_{1} t_{1}^{3} + \frac{2}{3} b_{2} t_{2}^{3}$

We thus have

$\begin{matrix} θ = \frac{T}{J_{e} G} = \frac{3 T}{G} \frac{1}{b_{1} t_{1}^{3} + 2 b_{2} t_{2}^{3}} & (6.21 a) \end{matrix}$

$\begin{matrix} τ_{\max} = G θ t_{i} = \frac{3 T t_{i}}{b_{1} t_{1}^{3} + 2 b_{2} t_{2}^{3}} & (6.21 b) \end{matrix}$

where t_i is the larger of t₁ and t₂. The effect of the stress concentrations at the corners is examined in Section 6.9.

6.8 Torsion of Multiply Connected Thin-Walled Sections

The membrane analogy may be applied to good advantage to analyze the torsion of thin tubular members, provided that some care is taken. Consider the deformation that would occur if a membrane subject to pressure were to span a hollow tube of arbitrary section (Fig. 6.18a). Since the membrane surface is to describe the stress function (and its slope, the stress at any point), arc ab cannot represent a meaningful stress function.

A figure represents the membrane analogy for tubular torsion members. — Figure 6.18. *Membrane analogy for tubular torsion members: (a) and (b) one-cell section; (c) two-cell section.*

Figure (a) shows the thin tubular member a b. The outer thickness of the membrane is t. Figure (b) depicts a membrane nnmm of height h . The slope S at the left edge of the plane is h (opposite side) and t (adjacent side). The cross-section of the plane represents a circular ring of thickness t. The element ds on the ring is considered. The plane nn is subjected to a uniform loading P. Figure (c) shows two membranes nnmp of height h1 and nmpp of height h2. The cross-section of the membrane represents two merged circular rings of thicknesses t 1 and t 2. The area of the two cells are A 1 and A 2, respectively. The shear forces tau 12, tau 2, and tau 3 acts through the outer section of the circular ring.

In the region ab, the stress must be zero, because no material exists there. If the curved surface ab is now replaced by a plane representing constant Φ, the zero-stress requirement is satisfied. For bars containing multiply connected regions, each boundary is also a line of constant Φ of different value. The absolute value of Φ is meaningless. Thus, at one boundary, Φ may arbitrarily be equated to zero and the others adjusted accordingly.

6.8.1 Shearing Stress

Based on the previous discussion, the membrane analogy may be extended to a thin tubular member (Fig. 6.18b), in which the fixed plate to which the membrane is attached has the same contour as the outer boundary of the tube. The membrane is also attached to a “weightless” horizontal plate having the same shape as the inner boundary nn of the tube, thereby bridging the inner and outer contours over a distance t.

The inner horizontal plate, made “weightless” by a counterbalance system, is permitted to seek its own vertical position but is guided so as not to experience sideward motion. Because we have assumed the tube to be thin walled, the membrane curvature may be disregarded; that is, lines nn may be considered straight. We are thus led to conclude that the slope is constant over a given thickness t, and consequently the shearing stress is likewise constant; it is given by

$\begin{matrix} τ = \frac{h}{t} or h = τ t & (a) \end{matrix}$

where h is the membrane deflection and t the tube thickness. Note that the tube thickness may vary circumferentially.

The dashed line in Fig. 6.18b indicates the mean perimeter, which may be used to determine the volume bounded by the membrane. Letting A represent the area enclosed by the mean perimeter, the volume mnnm is simply Ah, and the analogy gives

$\begin{matrix} T = 2 A h or h = \frac{T}{2 A} & (b) \end{matrix}$

Combining Eqs. (a) and (b), we have

$\begin{matrix} τ = \frac{T}{2 A t} & (6.22) \end{matrix}$

The application of Eq. (6.22) is limited to thin-walled members displaying no abrupt variations in thickness and no reentrant corners in their cross sections.

6.8.2 Angle of Twist

To develop a relationship for the angle of twist from the membrane analogy, we again consider Fig. 6.18b, in which h ≪ t and consequently tan(h/t) ≈ h/t = τ. Vertical equilibrium therefore yields

$p A = \oint (\frac{h}{t} S) d s = \oint τ S d s$

in which s is the length of the mean perimeter of the tube. Since the membrane tension is constant, h is independent of S. The preceding expression can therefore be written as

$\frac{p}{S} = \frac{1}{A} \oint τ d s = \frac{h}{A} \oint \frac{d s}{t} = 2 G θ$

where the last term follows from the analogy. The angle of twist per unit length is now found directly:

$\begin{matrix} θ = \frac{h}{2 A G} \oint \frac{d s}{t} = \frac{1}{2 A G} \oint τ d s & (6.23) \end{matrix}$

Equations (6.22) and (6.23) are known as Bredt’s formulas.

In Eqs. (a), (b), and (6.23), the quantity h possesses the dimensions of force per unit length, representing the resisting force per unit length along the tube perimeter. For this reason, h is referred to as the shear flow.

Example 6.8 Rectangular Torsion Tube

An aluminum tube of rectangular cross section (Fig. 6.19a) is subjected to a torque of 56.5 KN · m along its longitudinal axis. Determine the shearing stresses and the angle of twist. Assume G = 28 GPa.

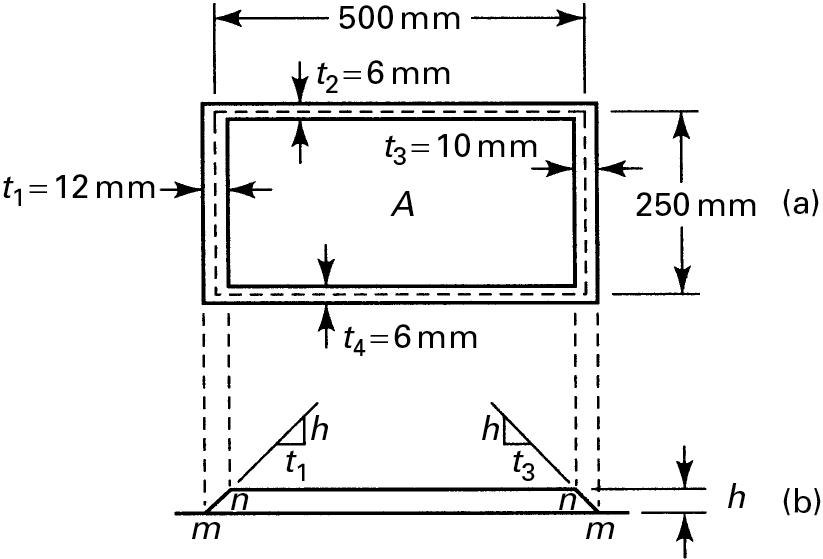
A figure shows a membrane with the corners labeled n, n, m, and m. — Figure 6.19. *Example 6.8. (a) Cross section; (b) membrane.*

The membrane is in the form of a trapezoid. The slope at the right edge of the membrane is h (opposite side) and t 3 (adjacent side). The slope at the left edge of the membrane is h (opposite side) and t 1 (adjacent side). The cross-section of the membrane represents the rectangle with varying thicknesses. The length and width of the section measure 500 millimeters and 250 millimeters, respectively. The thicknesses of the rectangular section are as follows: t1 equals 12 millimeters; t2 equals 6 millimeters; t 3 equals 10 millimeters; and t 4 equals 6 millimeters.

Solution Referring to Fig. 6.19b, which shows the membrane surface mnnm (representing Φ), the applied torque is, according to Eq. (b),

$T = 2 A h = 2 (0.125 h) = 56,500 N \cdot m$

from which h = 226,000 N/m. The shearing stresses are found from Eq. (a) as follows:

$\begin{matrix} τ_{1} & = \frac{h}{t_{1}} = \frac{226,000}{0.012} = 18.83 MPa \\ τ_{2} & = \frac{h}{t_{2}} = \frac{h}{t_{4}} = \frac{226,000}{0.006} = 37.67 MPa \\ τ_{3} & = \frac{h}{t_{3}} = \frac{226,000}{0.01} = 22.6 MPa \end{matrix}$

Applying Eq. (6.23), the angle of twist per unit length is

$\begin{matrix} θ = \frac{h}{2 A G} \oint \frac{d s}{t} & = \frac{226, 000}{2 \times 28 \times 10^{9} \times 0.125} (\frac{0.25}{0.012} + 2 \frac{0.5}{0.006} + \frac{0.25}{0.01}) \\ = 0.00686 rad/m \end{matrix}$

If multiply connected regions exist within a tubular member, as in Fig. 6.18c, the previously described techniques are again appropriate. As before, the thicknesses are assumed small, so lines such as mn, np, and pm are regarded as straight. The stress function is then represented by the membrane surface mnnppm. As in the case of a simple hollow tube, lines nn and pp are straight by virtue of flat, weightless plates with contours corresponding to the inner openings. Referring to the figure, the shearing stresses are

$\begin{matrix} τ_{1} = \frac{h_{1}}{t_{1}}, τ_{2} = \frac{h_{2}}{t_{2}} & (c) \end{matrix}$

$\begin{matrix} τ_{3} = \frac{h_{1} - h_{2}}{t_{3}} = \frac{t_{1} τ_{1} - t_{2} τ_{2}}{t_{3}} & (d) \end{matrix}$

The stresses are produced by a torque equal to twice the volume beneath surface mnnppm,

$\begin{matrix} T = 2 A_{1} h_{1} + 2 A_{2} h_{2} & (e) \end{matrix}$

or, after substituting Eqs. (c),

$\begin{matrix} T = 2 A_{1} t_{1} τ_{1} + 2 A_{2} t_{2} τ_{2} & (f) \end{matrix}$

Assuming the thicknesses t₁, t₂, and t₃ remain constant, application of Eq. (6.23) yields

$\begin{matrix} τ_{1} s_{1} + τ_{3} s_{3} = 2 G θ A_{1} & (g) \end{matrix}$

$\begin{matrix} τ_{2} s_{2} - τ_{3} s_{3} = 2 G θ A_{2} & (h) \end{matrix}$

where s₁, s₂, and s₃ represent the paths of integration indicated by the dashed wof stress, and the direction in which integration proceeds. Thus, there are four equations [(d), (f), (g), and (h)] containing four unknowns: τ₁, τ₂, τ₃ and θ.

If Eq. (d) is now written in the form

$\begin{matrix} τ_{1} t_{1} = τ_{2} t_{2} + τ_{3} t_{3} & (i) \end{matrix}$

we see that the shear flow h = τt is constant and distributes itself in a manner analogous to a liquid circulating through a channel of shape identical with that of the tubular bar. This analogy proves very useful when we are writing expressions for shear flow in tubular sections of considerably greater complexity.

Example 6.9 Three-Cell Torsion Tube

A multiply connected steel tube (Fig. 6.20) resists a torque of 12 KN · m. The wall thicknesses are t₁ = t₂ = t₃ = 6 mm and t₄ = t₅ = 3 mm. Determine the maximum shearing stresses and the angle of twist per unit length. Let G = 80 GPa. Dimensions are given in millimeters.

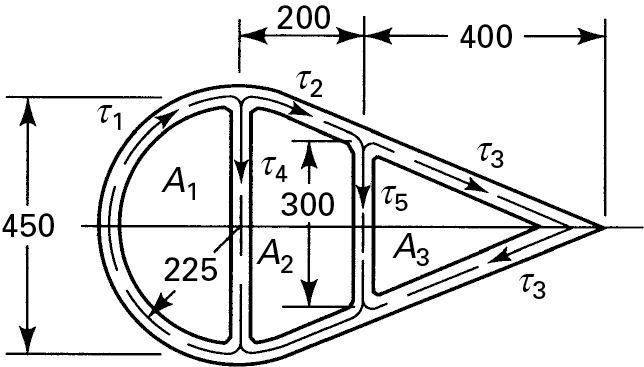
A figure shows a three cell torsion tube along with the dimensions. — Figure 6.20. *Example 6.9. Three-cell section.*

The cross-section represents an idealized airfoil structure for which the curved portion is the leading edge. The curved surface includes A 1. The following straight segments from the edge of the airfoil structure includes two cells A 2 and A 3. The dimensions of A 1, A 2, and A 3 are 450 millimeters, 200 millimeters, and 400 millimeters, respectively. The height of A 2 is 300 millimeters. The dimension across the structure A 1 is 225 millimeters.

Solution Assuming the shearing stresses are directed as shown in Fig. 6.20, analysis of the shear flow yields

$\begin{matrix} τ_{1} t_{1} = τ_{2} t_{2} + τ_{4} t_{4}, τ_{2} t_{2} = τ_{5} t_{5} + τ_{3} t_{3} & (j) \end{matrix}$

The torque associated with the shearing stresses must resist the externally applied torque, and an expression similar to Eq. (f) is obtained:

$\begin{matrix} T = 2 A_{1} t_{1} τ_{1} + 2 A_{2} t_{2} τ_{2} + 2 A_{3} t_{3} τ_{3} = 12,000 N \cdot m & (k) \end{matrix}$

Three more equations are available through application of Eq. (6.23) over areas A₁, A₂, and A₃:

$\begin{matrix} \begin{matrix} τ_{1} s_{1} + τ_{4} s_{4} & = 2 G θ A_{1} \\ - τ_{4} s_{4} + 2 τ_{2} s_{2} + τ_{5} s_{5} & = 2 G θ A_{2} \\ - τ_{5} s_{5} + 2 τ_{3} s_{3} & = 2 G θ A_{3} \end{matrix} & (I) \end{matrix}$

where s₁ = 0.7069 m, s₂ = 0.2136 m, s₃ = 0.4272 m, s₄ = 0.45 m, s₅ = 0.3 m, A₁ = 0.079522 m², A₂ = 0.075 m², and A₃ = 0.06 m². There are six equations describe the five unknown stresses and the angle of twist per unit length.

Thus, simultaneous solution of Eqs. (j), (k), and (l) leads to the following rounded values: τ₁ = 4.902 MPa, τ₂ = 5.088 MPa, τ₃ = 3.809 MPa, τ₄ = −0.373 MPa, τ₅ = 2.558 MPa, and θ = 0.0002591 rad/m. The positive values obtained for τ₁, τ₂, τ₃, and τ₅ indicate that the directions of these stresses are correctly depicted in Fig. 6.20. The negative sign of τ₄ means that the direction initially assumed was incorrect; that is, τ₄ is actually upward directed.

6.9 Fluid Flow Analogy and Stress Concentration

Examination of Eq. 6.8 suggests a similarity between the stress function Φ and the stream function ψ of fluid mechanics:

$\begin{matrix} \begin{matrix} τ_{z x} = \frac{\partial Φ}{\partial y}, \\ υ_{x} = \frac{\partial ψ}{\partial y}, \end{matrix} \begin{matrix} τ_{z y} = - \frac{\partial Φ}{\partial x} \\ υ_{y} = - \frac{\partial ψ}{\partial x} \end{matrix} & (6.24) \end{matrix}$

In Eqs. (6.24), υ_x and υ_y represent the x and y components of the fluid velocity υ. Recall that, for an incompressible fluid, the equation of continuity may be written as

$\frac{\partial υ_{x}}{\partial x} + \frac{\partial υ_{y}}{\partial y} = 0$

In turn, continuity is satisfied when ψ(x, y) is defined as in Eqs. (6.24). For two-dimensional flow, the vorticity $ω = \frac{1}{2} (\nabla \times υ)$ is

$ω = \frac{1}{2} (- \frac{\partial υ_{x}}{\partial y} + \frac{\partial υ_{y}}{\partial x})$

where ∇ = (∂/∂x)i + (∂/∂y)j. In terms of the stream function, we obtain

$\begin{matrix} \frac{\partial^{2} ψ}{\partial y^{2}} + \frac{\partial^{2} ψ}{\partial x^{2}} = - 2 ω & (6.25) \end{matrix}$

This expression is clearly analogous to Eq. (6.9), albeit with −2ω replacing −2Gθ. The completeness of the analogy is assured if it can be demonstrated that ψ is constant along a streamline (and hence on a boundary), just as Φ is constant over a boundary. Since the equation of a streamline in two-dimensional flow is

$\frac{d y}{d x} = \frac{υ_{y}}{υ_{x}} or υ_{x} d y - υ_{y} d x = 0$

in terms of the stream function, we have

$\begin{matrix} \frac{\partial ψ}{\partial y} d y + \frac{\partial ψ}{\partial x} d x = 0 & (6.26) \end{matrix}$

This is simply the total differential dψ and, therefore, ψ is constant along a streamline.

Based on the foregoing, experimental techniques have been developed that successfully exploit the analogy between the motion of an ideal fluid of constant vorticity and the torsion of a bar. The tube in which the fluid flows and the cross section of the twisted member are identical in these experiments—a factor that is useful in visualizing stress patterns in torsion. Moreover, a vast body of literature deals with flow patterns around bodies of various shapes, and the results presented are often directly applicable to the torsion problem.

The fluid flow or hydrodynamic analogy is especially valuable in dealing with stress concentration in shear, which we have heretofore neglected. In this regard, consider first the torsion of a circular bar containing a small circular hole (Fig. 6.21a). Figure 6.21b shows the analogous flow pattern produced by a solid cylindrical obstacle placed in a circulating fluid. From hydrodynamic theory, it is found that the maximum velocity (at points a and b) is twice the value in the undisturbed stream at the respective radii. In turn, a small hole has the effect of doubling the shearing stress normally found at a given radius.

A figure depicts the analogy of fluid flow in a circular shaft. — Figure 6.21. (*a) Circular shaft with hole; (b) fluid-flow pattern around small cylindrical obstacle; (c) circular shaft with keyway.*

Figure (a) illustrates a circular shaft with a hole. The shaft is fully shaded. Figure (b) depicts the pattern of fluid flow towards the back side of the shaded cylindrical obstacle. The obstacle is placed inside a revolving fluid. The direction of rotation of the fluid is in an anti-clockwise direction. Points a and b are marked on the obstacle. Figure (c) presents a circular shaft with rectangular keyway which is approximated at the top section. The keyway is represented by a and b, respectively. Theoretically, zero stress acts at A and infinite stress acts at B.

Also of great importance is the shaft keyway shown in Fig. 6.21c. On the one hand, according to the hydrodynamic analogy, the points a in the figure ought to have zero stress, since they are stagnation points of the fluid stream. In this sense, the material in the immediate vicinity of points a is excess. On the other hand, the velocity at the points b is theoretically infinite and, by analogy, so is the stress. It comes as no surprise, then, that most torsional fatigue failures have their origins at these sharp corners, with the salient point being that it is profitable to round such corners.

6.10 Torsion of Restrained Thin-Walled Members of Open Cross Section

In previous sections of this chapter, all cross sections of a bar subject to torques applied at the ends were assumed to suffer free warpage. As a consequence, the torque was expected to be produced by pure shearing stresses distributed over the ends as well as all other cross sections of the member. In this way, the stress distribution was obtained from Eq. (6.9) and satisfied the boundary conditions, Eq. (6.10).

If any section of the bar is held rigidly, however, both the rate of change of the angle of twist and the warpage will vary in the longitudinal direction. In such a case, the longitudinal fibers become subject to tensile or compressive stresses. Equations (6.9) and (6.10) are, in this instance, applied with satisfactory results in regions away from the restrained section of the bar. While this restraint has negligible influence on the torsional resistance of members having a solid section, such as rectangles and ellipses, it is significant when dealing with open thin-walled sections such as channels of I-beams.

Consider, for example, the case of a cantilever I-beam, shown in Fig. 6.22a. The applied torque causes each cross section to rotate about the axis of twist (z), thereby resulting in bending of the flanges. According to beam theory, the associated bending stresses in the flanges are zero at the juncture with the web. Consequently, the web does not depart from a state of simple torsion. In resisting the bending of the flanges or the warpage of a cross section, considerable torsional stiffness can, however, be imparted to the beam.

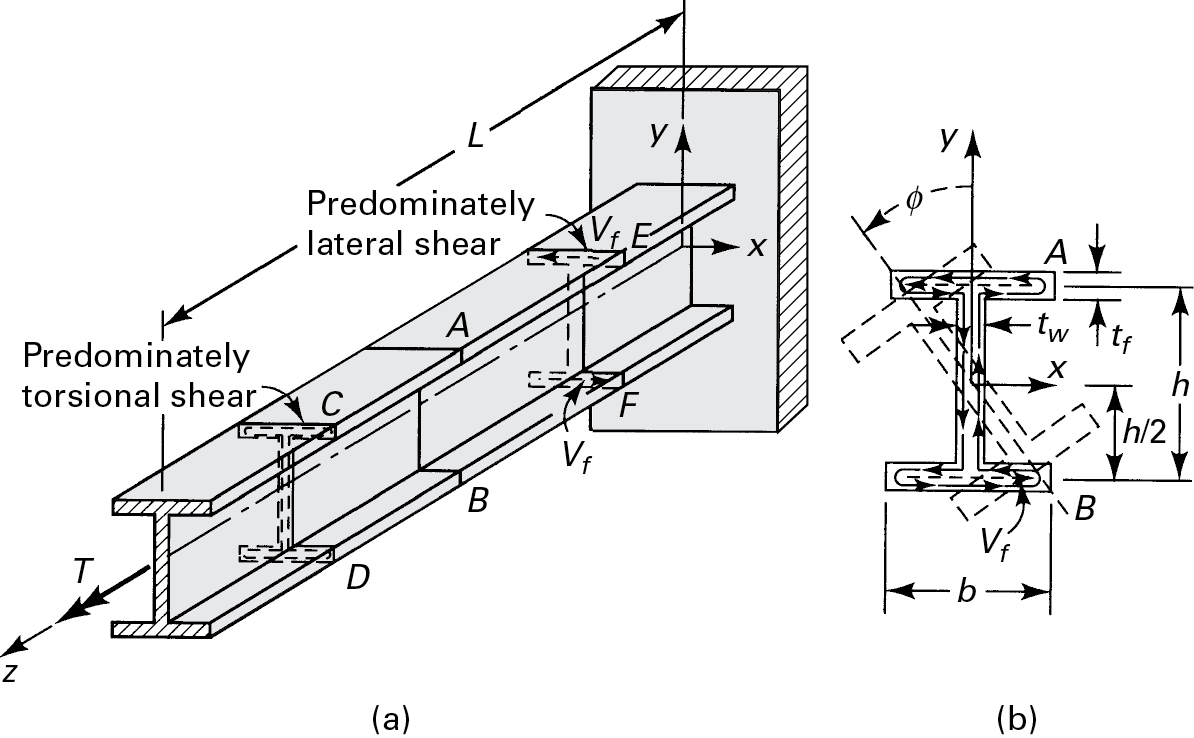
An I-section torsion member is shown. — Figure 6.22. *I-section torsion member: (a) warping is prevented for the section at *x = 0;* (b) partly lateral shear and partly torsional shear at arbitrary cross section AB.*

A figure shows an I-shaped member fixed at one end and free at the other end. The length of the member is L. The member is subjected to torsion at the free end in the z-axis. Three arbitrary cross sections are drawn on the member. The cross sections CD and EF are drawn closer to the free end and the fixed end. The cross section AB is present between the other two sections. The member is subjected to torsional shear at the cross sections CD and EF. The lateral shear (V subscript f) takes place at the section AB. Another figure shows the enlarged view of the cross section AB. The length of the flange is b and the width is t subscript f. The width of the web portion is t subscript w. The height of the cross section AB is h. The section is tilted to an angle phi with the vertical axis drawn from the center of the I-section. The lateral shear (V subscript f) acts along the lateral surface of the section.

6.10.1 Torsional and Lateral Shears

In Fig. 6.22a, the applied torque T is balanced in part by the action of torsional shearing stresses and in part by the resistance of the flanges to bending. At the representative section AB (Fig. 6.22b), consider the influence of torques T₁ and T₂. The former is attributable to pure torsional shearing stresses in the entire cross section, assumed to occur as though each cross section were free to warp. Torque T₁ is thus related to the angle of twist of section AB by the expression

$\begin{matrix} T_{1} = C \frac{d ϕ}{d z} & (a) \end{matrix}$

in which C is the torsional rigidity of the beam. The right-hand rule should be applied to furnish the sign convention for both torque and angle of twist. A pair of lateral shearing forces owing to bending of the flanges acting through the moment arm h gives rise to torque T₂:

$\begin{matrix} T_{2} = V_{f} h & (b) \end{matrix}$

An expression for v_f may be derived by considering the x displacement, u. Because the beam cross section is symmetrical and the deformation is small, we have u = (hl2)ϕ, and

$\begin{matrix} \frac{d u}{d z} = \frac{h}{2} \frac{d ϕ}{d z} & (c) \end{matrix}$

Thus, the bending moment M_f and shear V_f in the flange are

$\begin{matrix} M_{f} = E I_{f} \frac{d^{2} u}{d z^{2}} = \frac{E I_{f} h}{2} \frac{d^{2} ϕ}{d z^{2}} & (d) \end{matrix}$

$\begin{matrix} V_{f} = - E I_{f} \frac{d^{3} u}{d z^{3}} = \frac{E I_{f} h}{2} \frac{d^{3} ϕ}{d z^{3}} & (e) \end{matrix}$

where I_f is the moment of inertia of one flange about the y axis. Now Eq. (b) becomes

$\begin{matrix} T_{2} = - \frac{E I_{f} h^{2}}{2} \frac{d^{3} ϕ}{d z^{3}} & (f) \end{matrix}$

The total torque is then

$\begin{matrix} T = T_{1} + T_{2} = C \frac{d ϕ}{d z} - \frac{E I_{f} h^{2}}{2} \frac{d^{3} ϕ}{d z^{3}} & (6.27) \end{matrix}$

6.10.2 Boundary Conditions

The conditions appropriate to the flange ends are

${(\frac{d ϕ}{d z})}_{z = 0} = 0, {(\frac{d^{2} ϕ}{d z^{2}})}_{z = L} = 0$

indicating that the slope and the bending moment are zero at the fixed and free ends, respectively. When these conditions are satisfied, the solution of Eq. (6.27) is

$\begin{matrix} \frac{d ϕ}{d z} = \frac{T}{C} [1 - \frac{\cosh α (L - z)}{\cosh α L}] & (g) \end{matrix}$

where

$\begin{matrix} α = {(\frac{2 C}{E I_{f} h^{2}})}^{1/2} & (6.28) \end{matrix}$

6.10.3 Long Beams Under Torsion

For a beam of infinite length, Eq. (g) reduces to

$\begin{matrix} \frac{d ϕ}{d z} = \frac{T}{C} (1 - e^{- α z}) & (h) \end{matrix}$

By substituting Eq. (h) into Eqs. (a) and (f), we obtain the following expressions:

$\begin{matrix} \begin{array}{l} T_{1} = T (1 - e^{- α z}) \\ T_{2} = T e^{- α z} \end{array} & (6.29) \end{matrix}$

Thus, at the fixed end (z = 0), T₁ = 0 and T₂ = T. At this end, the applied torque is counterbalanced by the effect of shearing forces only, which from Eq. (b) are given by V_f = T₂/h = T/h. The torque distribution, Eq. (6.29), indicates that sections such as EF, close to the fixed end, contain predominantly lateral shearing forces (Fig. 6.22a). Sections such as CD, near the free end, contain mainly torsional shearing stresses (as Eq. 6.29 indicates for z → ∞).

The flange bending moment, obtained from Eqs. (d) and (h), is at a maximum at z = 0:

$\begin{matrix} M_{f, \max} = \frac{E I_{f} h α}{2 C} T & (i) \end{matrix}$

The maximum bending moment, occurring at the fixed end of the flange, is found by substituting Eq. (6.28) into Eq. (i):

$\begin{matrix} M_{f, \max} = \frac{T}{α h} & (6.30) \end{matrix}$

6.10.4 Angle of Twist

An expression for the angle of twist is determined by integrating Eq. (h) and satisfying the condition ϕ = 0 at z = 0:

$\begin{matrix} ϕ = \frac{T}{C} [z + \frac{1}{α} (e^{- α z} - 1)] & (j) \end{matrix}$

For relatively long beams, for which e^–αz may be neglected, the total angle of twist at the free end is, from Eq. (j),

$\begin{matrix} ϕ_{z = L} = \frac{T}{C} (L - \frac{1}{α}) & (6.31) \end{matrix}$

In this equation, the term 1/α indicates the influence of flange bending on the angle of twist. Since for pure torsion, the total angle of twist is given by ϕ = TL/C, it is clear that end restraint increases the stiffness of the beam in torsion.

Example 6.10 Analysis of an I-Beam Under Torsion

A cantilever I-beam with the idealized cross section shown in Fig. 6.22 is subjected to a torque of 1.2 kN · m. Determine (a) the maximum longitudinal stress and (b) the total angle of twist, ϕ. Take G = 80 GPa and E = 200 GPa. Let t_f = 10 mm, t_w = 7 mm, b = 0.1 m, h = 0.2 m, and 2.4 m.

Solution

The torsional rigidity of the beam is, from Eq. (6.21a),

$\begin{matrix} C & = \frac{T}{θ} = (b_{1} t_{1}^{3} + 2 b_{2} t_{2}^{3}) \frac{G}{3} = (0.19 \times {0.007}^{3} + 2 \times 0.1 \times {0.01}^{3}) \frac{G}{3} \\ = 8.839 \times 10^{- 8} G \end{matrix}$

The flexural rigidity of one flange is

$I_{f} E = \frac{0.01 \times {0.1}^{3}}{12} E = 8.333 \times 10^{- 7} E$

Hence, from Eq. (6.28) we have

$\frac{1}{α} = h \sqrt{\frac{E I_{f}}{2C}} = h \sqrt{\frac{200 \times 10^{9} \times 8333 \times 10^{- 7}}{8839 \times 10^{- 8} \times 2}} = 3.43 h$

From Eq. (6.30), the bending moment in the flange is found to be 3.43 times larger than the applied torque, T. Thus, the maximum longitudinal bending stress in the flange is

$σ_{f, \max} = \frac{M_{f, \max^{X}}}{I_{f}} = \frac{3.43 T \times 0.05}{8333 \times 10^{- 7}} = 0.2058 \times 10^{6} T = 247 MPa$
Since e^–αL = 0.03, we can apply Eq. (6.31) to calculate the angle of twist at the free end:

$\begin{matrix} ϕ & = \frac{T}{C} (L - \frac{1}{α}) = \frac{1200}{8.839 \times 10^{- 8} \times 80 \times 10^{9}} (2.4 - 3.43 \times 0.2) \\ = 0.2908 rad \end{matrix}$

Comment If the ends of the beam were both free, the total angle of twist would be ϕ = TL/C = 0.4073 rad, and the beam would experience ϕ_free/ϕ_fixed = 1.4 times more twist under the same torque.

6.11 Torsion Bar Springs

A torsion bar is a straight hollow or solid rod fixed at one end and twisted at the other, in which it is supported. It represents the simplest of all spring shapes, as depicted by the part AB in Figure 6.23a. Common applications of such members include counterbalancing for automobile hoods and trunk lids. Interestingly, a torsion bar with splined ends (Fig. 6.23b) is used for a vehicle suspension spring or sway bar. Often, one end fits into a socket on the chassis, and the other into the pivoted end of an arm. The arm is part of a linkage, permitting the wheel to rise and fall in approximately parallel motion. In a passenger car, the bar may have about ¾ m length, 25 mm diameter, and twist 30°–45°.

Two figures are shown. Figure (a) shows a torsion bar spring rod with bent ends. Figure (b) shows a torsion bar spring rod with splined ends. — Figure 6.23. *Torsion bar spring: (a) rod with bent ends; (b) rod with splined ends.*

Two figures of torsion bar spring are shown. Figure (a) shows a rod with bent ends A and B. The bar is labeled with the diameter, d and length, L. The angle of twist of the ends are labeled, phi. The moment arm and the axial load subjected to the ends are labeled, R and P, respectively. Figure (b) shows a rod with splined ends of length, L and bar diameter, d.

The stress in a torsion bar is basically that of torsional shear. Thus, the equations for torque, angular displacement, and stiffness, referring to Fig. (6.23a), are given as

$T = P R δ = ϕ R k = \frac{T}{ϕ}$

Here the angle of twist ϕ = TL/GJ. For the solid circular torsion bar, the moment of inertia is J = πd⁴/32. We thus have the formulas

$\begin{matrix} τ = \frac{16 P R}{π d^{3}} & (6.32) \end{matrix}$

$\begin{matrix} δ = \frac{T L R}{G J} = \frac{32 P L R^{2}}{π d^{4} G} & (6.33) \end{matrix}$

$\begin{matrix} k = \frac{π d^{4} G}{32 L} & (6.34) \end{matrix}$

where

τ = torsional shear stress

P = load

δ = relative displacement between ends

d = bar diameter

R = moment arm

L = bar length

k = spring rate

G = modulus of rigidity

These basic equations are supplemented, for torsion springs with noncircular cross sections, by Table 6.2. At the end parts of the spring that do not lie between supports A and B, there is a shear load P and an corresponding direct shear stress taking place on cross-sectional areas. Often, the effects of the curvature and of bending are neglected at these parts of the bar. When designing a torsion bar, the required diameter d is found by Eq. (6.32). On the basis of the allowable shear strength, then, Eq. (6.33) results in the bar length L necessary to provide the required deflection δ.

6.12 Curved Circular Bars

The assumptions of Section 6.2 are also valid for a curved, circular bar, provided that the radius r of the bar is small in comparison with the radius of curvature R. When $r / R = \frac{1}{12}$ , for example, the maximum stress computed on the basis of the torsion formula, τ = Tr/J, is approximately 5% too low. In contrast, if the diameter of the bar is large relative to the radius of curvature, we must take the length differential of the longitudinal surface elements into consideration, and an area of stress concentration occurs at the inner point of the bar.

We are concerned here with the torsion of slender curved members for which r/R ≪ 1 Frequently, a curved bar is subjected to loads that at any cross section produce both a twisting moment and a bending moment. Expressions for the strain energy in torsion and bending have already been developed in this text (Sections 2.14 and 5.12), and application of Castigliano’s theorem (Section 10.4) leads readily to the displacements.

Consider the case of a cylindrical rod or bar bent into a quarter-circle of radius R, as shown in Fig. 6.24a. The rod is fixed at one end and loaded at the free end by a twisting moment T. The bending and twisting moments at any section are (Fig. 6.24b)

$\begin{matrix} M_{θ} = T \sin θ, T_{θ} = - T \cos θ & (a) \end{matrix}$

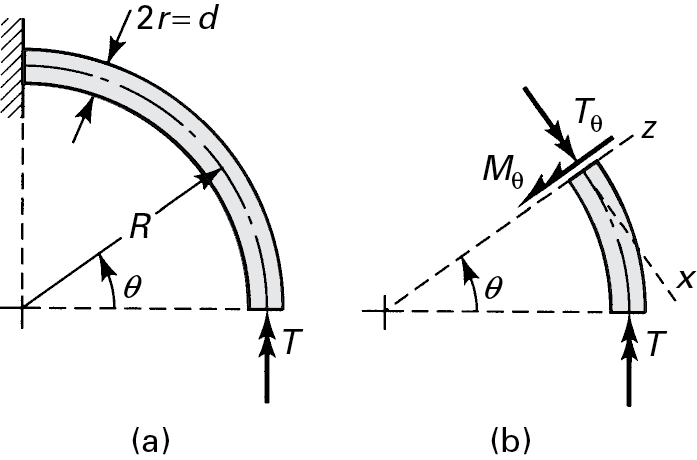
Two curved circular bars are shown to illustrate the twisting of the bar with bending and twisting moments. — Figure 6.24. *Twisting of a curved, circular bar.*

Two curved circular bars are shown. Figure (a) shows a rod, bent into a quarter circle along the XY plane. The radius of the rod is labeled, R, diameter, 2r equal to d, and angle, theta. The top end of the rod is fixed and the bottom end is free which is subjected to a twisting moment, T. Figure (b) shows a bent rod along the x and z-axes. The rod is bent at an angle, theta along the z-axis. The bottom end of the rod is applied with a twisting moment, T. The top end is subjected to both the twisting moment, T theta and bending moment, M theta.

Substituting these quantities into Eqs. (2.63) and (2.61), together with dx = ds = Rdθ, yields

$\begin{matrix} U = \frac{1}{2} \int (\frac{M_{θ}^{2}}{E I} + \frac{T_{θ}^{2}}{G J}) d s & (b) \end{matrix}$

$U = \frac{1}{2} T^{2} R \int_{0}^{π /2} (\frac{\sin^{2} θ}{E I} + \frac{\cos^{2} θ}{G J}) d θ$

where J = πd⁴/32 = 2I. The strain energy in the entire rod is obtained by integrating:

$\begin{matrix} U = \frac{8 (2 + ν) R}{d^{4} E} T^{2} & (6.35) \end{matrix}$

Upon application of ϕ = ∂U/∂T, it is found that

$\begin{matrix} ϕ = \frac{16 (2 + ν) R}{d^{4} E} T & (6.36) \end{matrix}$

for the angle of twist at the free end.

6.12.1 Helical Springs

Springs are used to exert forces or torques in a mechanism or (mainly) to store the energy of impact load. A notable deflection is essential to most spring applications. These flexible members usually operate with high values for the ultimate stresses and with varying loads. Helical springs consist of round or rectangular wire, and flat springs (cantilever or simply supported beams) are widely used. Springs come in a number of other types, such as disk, ring, and torsion bar.

In the design of springs manufactured from curved bars or wires, deflection is as important as strength. Springs are employed to apply forces or torques in a mechanism or to absorb the energy owing to suddenly applied loads.*

*For an extensive discussion of springs, see Refs. 6.5 and 6.6.

A helical tension or compression spring provides a push or pull force and is capable of large deflection. The standard form (that is, the most common spring configuration) has constant coil diameter, pitch (axial distance between coils), and spring rate. Variable-pitch, barrel, and hourglass springs are used to minimize resonant surging and vibration.

Case Study 6.1 discusses a helical spring, produced by wrapping a wire around a cylinder in such a way that the wire forms a helix of uniformly spaced turns, as typifies a curved bar.

Case Study 6.1 Analysis of a Helical Spring

An open-coiled helical spring wound from wire of diameter d, with pitch angle α and N number of coils of radius R, is extended by an axial load P (Fig. 6.25). (a) Develop expressions for the maximum stress and deflection. (b) Redo part (a) for a closely coiled spring. (c) Find the spring rate for closely coiled spring.

An open- coiled helical spring is shown. — Figure 6.25. *Case Study 6.1. Helical spring under tension.*

A helical spring with open coil shows a rigid hook on the left end and a loop on the other end, subjected to the axial load, P. The cross-section along the coils is marked, A. The coil diameter is marked, d with a pitch angle, alpha, and radius of curvature, 2R.

Assumption: Load is applied steadily at a rigid hook and loop at ends.

Solution An element of the spring located between two adjoining sections of the wire may be treated as a straight circular bar in torsion and bending. This is because a tangent to the coil at any point such as A is not perpendicular to the load. At cross section A, components P cos α and P sin α produce the following torque and moment:

$\begin{matrix} T = P R \cos α, M = P R \sin α & (c) \end{matrix}$

The stresses, from Eq. (4.7), are given by

$σ_{1,2} = \frac{16}{π d^{3}} (M ± \sqrt{M^{2} + T^{2}}), τ_{\max} = \frac{16}{π d^{3}} \sqrt{M^{2} + T^{2}}$

The maximum normal stress and the maximum shear stress are thus

$\begin{matrix} σ_{\max} = \frac{16 P R}{π d^{3}} (1 + \sin α) & (6.37 a) \end{matrix}$

$\begin{matrix} τ_{\max} = \frac{16 P R}{π d^{3}} & (6.37 b) \end{matrix}$

The deflection is computed by applying Castigliano’s theorem together with Eqs. (b) and (c):

$δ = \int_{0}^{L} (\frac{P R^{2} \sin^{2} α}{E I} + \frac{P R^{2} \cos^{2} α}{J G}) d s$

where the length of the coil L = 2πRN. It follows that the relationship

$δ = 2 π P R^{3} N (\frac{\sin^{2} α}{E I} + \frac{\cos^{2} α}{J G})$

or

$\begin{matrix} δ = \frac{128 P R^{3} N}{d^{4}} (\frac{\sin^{2} α}{E} + \frac{\cos^{2} α}{2 G}) & (6.38) \end{matrix}$

defines the axial end deflection of an open-coil helical spring.
For a closely coiled helical spring, the angle of pitch α of the coil is very small. The deflection is now produced entirely by the torsional stresses induced in the coil. To derive expressions for the stress and deflection, let α = sin α = 0 and cosα = 1 in Eqs. (6.37a) and (6.37b). In so doing, we obtain

$\begin{matrix} τ_{\max} = σ_{\max} = \frac{16 P R}{π d^{3}} & (6.39) \end{matrix}$

$\begin{matrix} δ = \frac{64 P R^{3} N}{G d^{4}} & (6.40) \end{matrix}$
The elastic behavior of a spring may be expressed conveniently by the slope of its force–deflection curve or spring rate k. Through the use of Eq. 6.40, we obtain

$\begin{matrix} k = \frac{P}{δ} = \frac{G d^{4}}{64 R^{3} N} & (6.41) \end{matrix}$

Also known as the spring constant or spring scale, the spring rate has units of N/m in SI and lb/in. in the U.S. Customary System.

The standard helical spring has a spring rate k that is mainly linear over most of its operating range. The first and last few percent of its deflection have a nonlinear rate. Usually, in spring design, the spring rate is defined between approximately 15% and 85% of its total and working deflections.

Comment The approximate results obtained in this case study are applicable to both tension and compression helical springs, the wire diameters of which are small in relation to coil radius.

References

6.1. UGURAL, A. C. Mechanics of Materials Hoboken, NJ: Wiley, 2008.

6.2. TODHUNTER, I., and PEARSON, K. History of the Theory of Elasticity and the Strength of Materials, Vols. I and II. New York: Dover, 1960.

6.3. TIMOSHENKO, S. P., and GOODIER, J. N. Theory of Elasticity, 3rd ed. New York: McGraw-Hill, 1970.

6.4. YOUNG, W. C., BUDYNAS, R. G., and SADEGH, A. M. Roark’s Formulas for Stress and Strain, 8th ed. New York: McGraw-Hill, 2011.

6.5. UGURAL, A. C. Mechanical Design of Machine Components, 2nd ed. Boca Raton, FL: CRC Press, Taylor & Francis Group, 2016.

6.6. WAHL, A. M. Mechanical Springs. New York: McGraw-Hill, 1963.

Problems

Sections 6.1 through 6.3

6.1. A hollow steel shaft of outer radius c = 35 mm is fixed at one end and subjected to a torque T = 3 kN · m at the other end. Calculate the required inner radius b, knowing that the average shearing stress is limited to 100 MPa.

6.2. A solid shaft of 40-mm diameter is to be replaced by a hollow circular tube of the same material, resisting the same maximum shear stress and the same torque. Find the outer diameter D of the tube for the case in which its wall thickness is t = D/25.

6.3. A solid shaft of diameter d and a hollow shaft of outer diameter D = 60 mm and thickness t = D/4 are to transmit the same torque at the same maximum shear stress. What is the required diameter d the shaft?

6.4. Figure P6.4 shows four pulleys, attached to a solid stepped shaft, transmit the torques. Find the maximum shear stress for each shaft segment.

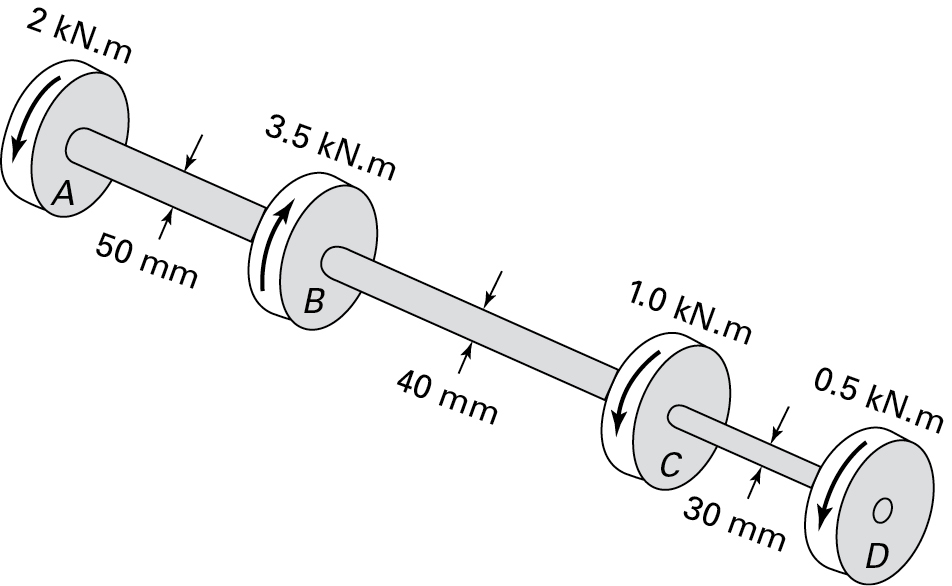
A illustration shows the torque acting on the four pulleys attached to a shaft. — Figure P6.4.

A figure shows four pulleys "A", B, C, and D attached to a stepped shaft. The diameter of the shaft: between the pulleys, "A" and B is 50 millimeters; between the pulleys, B and C is 40 millimeters; and between the pulleys, C and D is 30 millimeter. Torques 2-kilonewton meters and 1-kilonewton meters act in the anticlockwise direction on the pulleys "A" and C respectively. Torques 3.5-kilonewton meters and 0.5-kilonewton meters act in the clockwise direction on the pulleys B and D respectively.

6.5. Re-solve Prob. 6.4 for the case in which a hole of 16-mm diameter is drilled axially through the shaft to form a tube.

6.6. As seen in Fig. P6.6, a stepped shaft ABC with built-in end at A is subjected to the torques T_B = 3 kN · m and T_c = 1 kN · m at sections B and C, respectively. Based on a stress concentration factor K = 1.6 at the step B, what is the maximum shearing stress in the shaft? Given: d₁ = 50 mm and d₂ = 40 mm.

6.7. A brass rod AB (G_b = 42 GPa) is bonded to an aluminum rod BC (G_d = 28 GPa), as illustrated in Fig. P6.6. Determine the angle of twist at C, for the case in which T_B = 2T_c = 8 KN · m, d₁ = 2d₂ = 100 mm, and L₁ = 2L₂ = 0.7 m.

6.8. A hollow shaft is made by rolling a metal plate of thickness t into a cylindrical form and welding the edges along the helical seams oriented at an angle of ϕ to the axis of the member (Fig. P6.8). Calculate the maximum torque that can be applied to the shaft. Assumption: The allowable tensile and shear stresses in the weld are 120 MPa and 50 MPa, respectively. Given: D = 100 mm, t = 5 mm, and ϕ = 50°.

6.9. Re-solve Prob. 6.8 for the case in which the helical seam is oriented at an angle of ϕ = 35° to the axis of the member (Fig. P6.8).

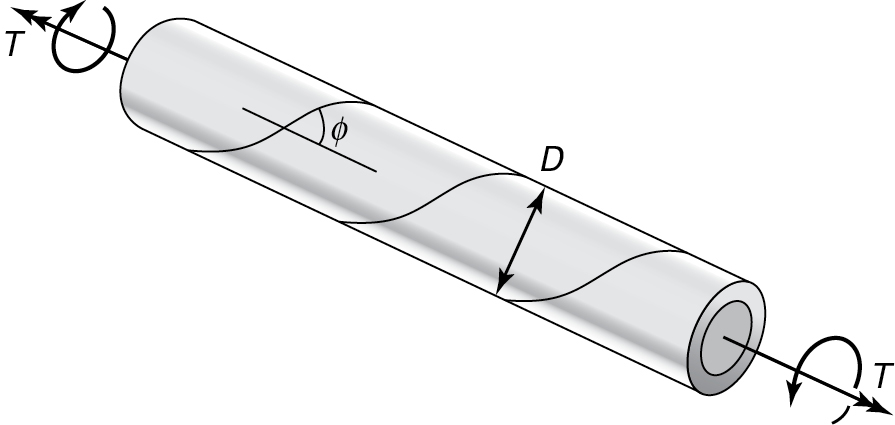
A hollow cylindrical shaft of diameter D made by rolling a metal plate is shown. This plate is attached to the edges of the shaft and makes an angle phi with the centerline of the shaft. Torque T acts in the opposite direction at both ends. — Figure P6.8.

6.10. What is the required diameter d₁ for the segment AB of the shaft illustrated in Fig. P6.6 if the permissible shear stress is τ_all = 50 MPa and the total angle of twist between A and C is limited to ϕ = 0.02 rad? Given: G = 39 GPa, T_B = 3 KN · m, T_c = 1 KN · m, L₁ = 2 m, L₂ = 1 m, and d₂ = 25 mm.

A illustration shows the torque acting on a stepped shaft. — Figure P6.6.

A stepped shaft ABC is shown. The side "A" is fixed to a square plate. The length of AB is L1 and the diameter of AB is d1. The shaft AB is made up of brass. The length of BC is L2 and the diameter of BC is d2. The shaft BC is made up of aluminum. Torque T subscript B acts in the clockwise direction at the point B and torque T subscript C acts in the anticlockwise direction at the point C.

6.11. Re-solve Prob. 6.10 for the case in which the torque applied at B is T_B = 2 KN · m and T_C = 0.5 KN · m

6.12. A stepped shaft of diameters D and d is under a torque T, as shown in Fig. P6.12. The shaft has a fillet of radius r (see Fig. D.4). Determine (a) the maximum shear stress in the shaft for r = 1.0 mm and (b) the maximum shear stress in the shaft for r = 5 mm. Given: D = 60 mm, d = 50 mm, and T = 2 KN · m.

An illustration of a stepped shaft subjected to torque T. — Figure P6.12.

A stepped shaft is shown. The diameter of the wider part is upper case D and the diameter of the other part is lower case d. The filleted radius is r. Torque T acts in the clockwise direction at the wider end and in the anticlockwise direction at the other end.

6.13. Two steel shafts are connected by gears and carry a torque T (Fig. P6.13). Find: (a) The angle of rotation in degrees at D; (b) the maximum shearing stress in shaft AB. Given: G = 80 GPa, T = 600 N · m, d₁ = 50 mm, d₂ = 40 mm.

A figure illustrates two steel shafts connected by gears and the torque T acting on it. — Figure P6.13.

A shaft AB of length 1.5 meters and diameter d1 is fixed at the end "A". At the end B, a gear of length 380 millimeters is attached to the shaft. A shaft of length 2 meters and diameter d2, is attached to a gear of length 250 millimeters. In this shaft, shaft sleeve is at the points C and D. The distance from the gear to the shaft sleeve D is 2 meters. The two gears are merged. Torque T acts in the anticlockwise direction at D.

6.14. A 33-kW motor, using a set of gears, drives a shaft at a speed n (Fig. P6.14). (a) Design, on the basis of a safety factor of 2.2, solid shafts AC and BC. (b) Calculate the total angle of twist between A and B. Given: G = 82 GPa, τ_yp = 210 MPa, n = 1500 rpm.

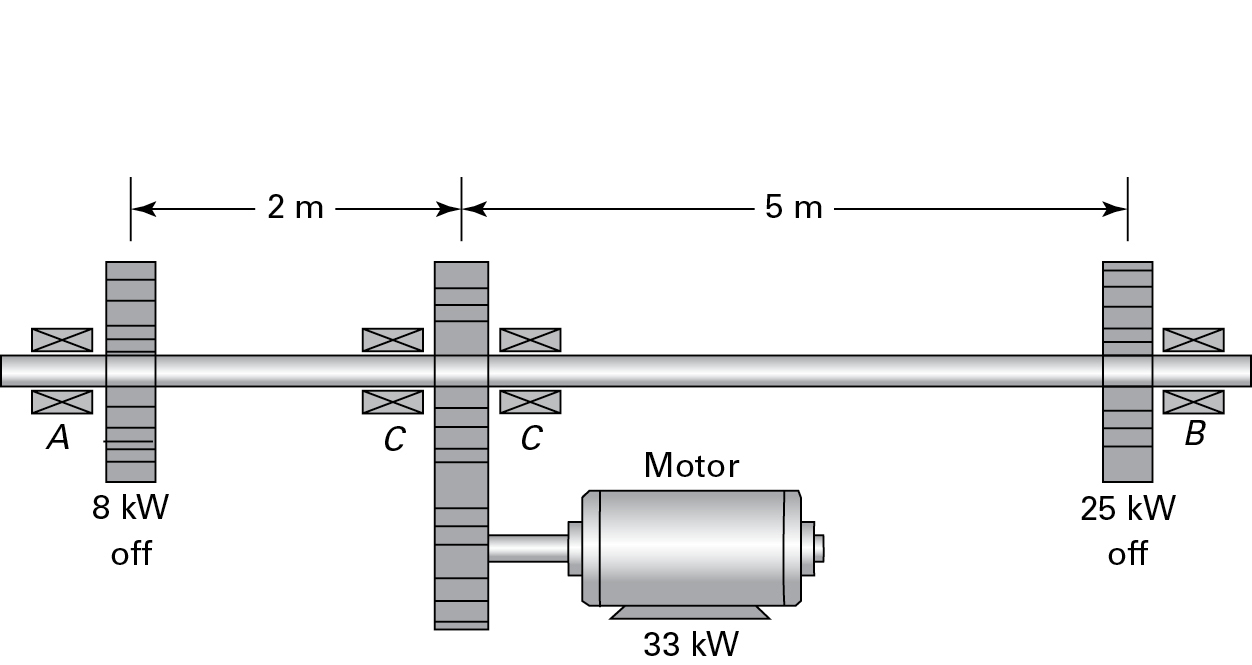
A 33-kilowatt motor is attached to a gear. The gear is connected to the shafts AC and CB at C. The length of AC is 2 meters and the length of CB is 5 meters. Shaft AC consists of an 8 kilowatt (off) gear at "A" and shaft CB consists of a 25 kilowatt (off) gear at B. — Figure P6.14.

6.15. A solid steel shaft of diameter D supports end loads P, M, and T. Find the factor of safety n, assuming that failure occurs according to the following criteria: (a) maximum shearing stress; (b) maximum energy of distortion. Given: τ_yp = 250 MPa, d = 80 mm, P = 40 kN, M = 4 kN · m, T = 8 kN · m.

6.16. Design a solid shaft for a 12-kW motor running at a speed n. Given: G = 80 GPa, τ_yp = 140 MPa, n = 3000 rpm. The angle of twist is not to exceed 1.8° per meter length. Assumptions: The shaft is made of steel. A factor of safety of 2.5 is used.

6.17. An outboard motor delivers 10 hp at 6000 rpm to the drive shaft of length L, as depicted in Fig. P6.17. The shaft is made of brass with modulus of elasticity G and an allowable shear stress τ_all. Find: (a) The required diameter d of the shaft; (b) the angle of twist ϕ of the shaft. Given: L = 0.6 m, G = 39 GPa, τ _all = 70 MPa.

A sketch of a drive shaft of an outboard motor is shown. — Figure P6.17.

The mid-section and the lower unit of an outboard motor are shown. The vertical drive shaft is present inside the housing and is rotated in the clockwise direction. The length of the drive shaft is L. The mounting flange is placed at the top of the mid-section. The propeller blades are fixed to the lower unit of the outboard motor.

6.18. A stepped shaft having solid circular parts with diameters D and d is in pure torsion (Fig. P6.12). The two parts are joined with a fillet of radius r (see Fig. D.4). If the shaft is made of brass with allowable shear strength 80 MPa, determine the largest torque capacity of the shaft. Given: D = 100 mm, d = 50 mm, r = 10 mm.

6.19. Consider two bars, one having a circular section of radius b, the other an elliptic section with semiaxes a, b (Fig. P6.19). (a) For equal angles of twist, which bar experiences the larger shearing stress? (b) For equal allowable shearing stresses, which bar resists a larger torque?

A figure shows a circular section of radius b in an x-y plane. Another figure shows an elliptical section in the x-y plane. The semi-axes of the elliptical section are a and b. — Figure P6.19.

6.20. A hollow (r_j = b, r₀ = c) and a solid (r₀ = a) cylindrical shaft are constructed of the same material. The shafts are of identical length and cross-sectional area, and both are subjected to pure torsion. Find the ratio of the largest torques that may be applied to the shafts for c = 1.4b: (a) if the allowable stress is τ_a and (b) if the allowable angle of twist is θ_a.

6.21. A solid circular shaft AB, held rigidly at both ends, has two different diameters (Fig. 6.4a). For a maximum permissible shearing stress τ_all = 150 MPa, calculate the allowable torque T that may be applied at section C. Use d_a = 20 mm, d_b = 15 mm, and a = 2b = 0.4 m.

6.22. Re-solve Prob. 6.16 for τ_all = 70 MPa, d_a = 25 mm, d_b = 15 mm, and a = 1.6b = 0.8 m.

Sections 6.4 through 6.7

6.23. The stress function appropriate to a solid bar subjected to torques at its free ends is given by

$Φ = k (a^{2} - x^{2} + b y^{2}) (a^{2} + b x^{2} - y^{2})$

where a and b are constants. Determine the value of k.

6.24. Figure P6.24 shows the cross section a × a of a cylinder resists a torque. Given: A stress function as follows:

$\begin{matrix} Φ = k (\frac{x^{2}}{a^{2}} - 1) (\frac{y^{2}}{a^{2}} - 1) & (p6.24) \end{matrix}$

A rectangular cross-section is shown. A vertical line (y) and a horizontal line (x) are drawn from the center (O) of the rectangle. The length of the rectangle is 2a and the breadth is 2b. — Figure P6.24.

in which k is a constant. Determine whether Eq. (P6.24) satisfies the required condition for a Prandtl’s stress function.

6.25. Show that Eqs. (6.6) through (6.11) are not altered by a shift of the origin of x, y, z from the center of twist to any point within the cross section defined by x = a and y = b, where a and b are constants. [Hint: The displacements are now expressed as u = −θz(y − b), υ = θz(x − a) and w = w(x, y).]

6.26. Rederive Eq. (6.11) for the case in which the stress function Φ = c on the boundary, where c is a nonzero constant.

6.27. A thin circular ring of cross-sectional radius r, shown in Fig. P6.27, is subjected to a distributed torque per unit length, Tθ = T cos²θ. Determine the angle of twist at sections A and B in terms of T, a, and r. Assume that the radius a is large enough to permit the effect of curvature on the torsion formula to be neglected.

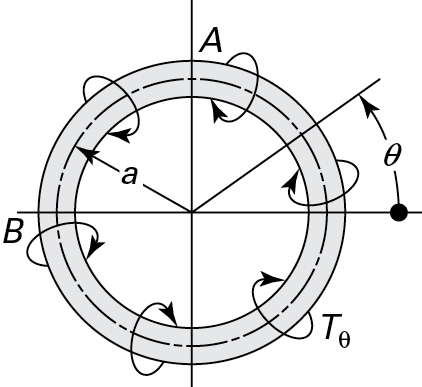
A figure shows a circular ring. — Figure P6.27.

A circular ring of radius a is shown. A vertical line and a horizontal line are drawn which passes through the center of the circular ring. The vertical line intersects the circular ring at point A, and the horizontal line intersects the ring at point B. A distributed torque T subscript theta acts in the clockwise direction at different portions of the ring.

6.28. Consider two bars of the same material: one circular of radius c, the other of rectangular section with dimensions a × 2a. Determine the radius c so that, for an applied torque, both the maximum shear stress and the angle of twist will not exceed the corresponding quantities in the rectangular bar.

6.29. The torsion solution for a cylinder of equilateral triangular section (Fig. 6.11) is derivable from the stress function, Eq. (j) of Section 6.5:

$Φ = k (x - \sqrt{3} y - \frac{2}{3} h) (x + \sqrt{3} y - \frac{2}{3} h) (x + \frac{2}{3} h)$

Derive expressions for the maximum and minimum shearing stresses and the twisting angle.

6.30. The torsional rigidity of a circle, an ellipse, and an equilateral triangle (Fig. 6.11) are denoted by C_C, C_e, and C_t, respectively. If the cross-sectional areas of these sections are equal, demonstrate that the following relationships exist:

$C_{e} = \frac{2 a b}{a^{2} + b^{2}} C_{c}, C_{t} = \frac{2 π \sqrt{3}}{15} C_{c}$

where a and b are the semiaxes of the ellipse in the x and y directions.

6.31. Two thin-walled circular tubes—one having a seamless section, the other (Fig. 6.17a) a split section—are subjected to the action of identical twisting moments. Both tubes have equal outer diameter d_o, inner diameter d_i, and thickness t. Determine the ratio of their angles of twist.

6.32. A steel bar of slender rectangular cross section (5 mm × 125 mm) is subjected to twisting moments of 80 N · m at the ends. Calculate the maximum shearing stress and the angle of twist per unit length. Take G = 80 GPa.

6.33. The torque T produces a rotation of 15° at the free end of the steel bar shown in Fig. P6.33. Use a = 24 mm, b = 16 mm, L = 400 m, and G = 80 GPa. What is the maximum shearing stress in the bar?

A figure shows a rectangular steel shaft of length L, breadth b, and width a. The shaft is fixed at one end and free at the other end. A horizontal force T acts from the free end of the shaft. — Figure P6.33.

6.34. Determine the largest permissible b×b square cross section of a steel shaft of length L = 3 m for which the shearing stress does not exceed 120 MPa and the shaft is twisted through 25° (Fig. P6.33). Take G = 75 GPa.

6.35. A steel bar (G = 200 GPa), whose cross section is shown in Fig. P6.35, is subjected to a torque of 500 N · m. Determine the maximum shearing stress and the angle of twist per unit length. The dimensions are b₁ = 100 mm, b₂ = 125 mm, t₁ = 10 mm, andt₂ = 4 mm.

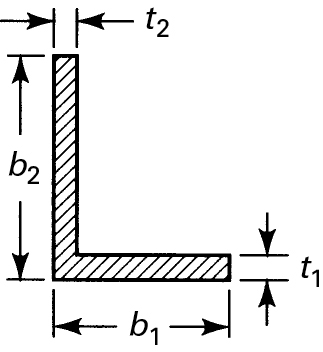
A figure shows the cross-section of an L-shaped steel bar. The length and thickness of the horizontal portion of the bar are b1 and t1 respectively. Similarly, the length and thickness of the vertical portion of the bar are b2 and t2 respectively. — Figure P6.35.

6.36. Re-solve Example 6.7 for the case in which segments AC and CB of torsion member AB have as a cross section an equilateral triangular of sides a₁ = 60 mm, and a₂ = 45 mm, respectively.

6.37. Derive an approximate expression for the twisting moment in terms of G, θ, b, and t_o for the thin triangular section shown in Fig. P6.37. Assume that at any y the expression for the stress function Φ corresponds to a parabolic membrane appropriate to the width at that y: Φ = Gθ [(t/2)² − x²].

A figure shows a triangular section of height b and base length t0. The vertical axis represents x and the horizontal axis represents y. The base of the triangle lies on the vertical axis (x). — Figure P6.37.

6.38. Consider the following sections: (a) a hollow tube of 50-mm outside diameter and 2.5-mm wall thickness; (b) an equal-leg angle, having the same perimeter and thickness as in (a); and (c) a square box section with 50-mm sides and 2.5-mm wall thickness. Compare the torsional rigidities and the maximum shearing stresses for the same applied torque.

6.39. The cross section of a 3-m-long steel bar is an equilateral triangle with 50-mm sides. The bar is subjected to end twisting couples, causing a maximum shearing stress equal to two-thirds of the elastic strength in shear (τ_yp = 420 MPa). Using Table 6.2, determine the angle of twist between the ends. Let G = 80 GPa.

Sections 6.8 through 6.12

6.40. Show that when Eq. (6.2) is applied to a thin-walled tube, it reduces to Eq. (6.22).

6.41. A torque T is applied to a thin-walled tube of a cross section in the form of a regular hexagon of constant wall thickness t and mean side length a. Derive relationships for the shearing stress τ and the angle of twist θ per unit length.

6.42. Re-solve Example 6.8 with a 0.01-m-thick vertical wall at the middle of the section.

6.43. The cross section of a thin-walled aluminum tube is an equilateral triangular section of mean side length 50 mm and wall thickness 3.5 mm. If the tube is subjected to a torque of 40 N · m, what are the maximum shearing stress and angle of twist per unit length? Let G = 28 GPa.

6.44. A square thin-walled tube of mean dimensions a × a and a circular thin-walled tube of mean radius c, both of the same material, length, thickness t, and cross-sectional area, are subjected to the same torque. Determine the ratios of the shearing stresses and the angle of twist of the tubes.

6.45. A hollow, multicell aluminum tube (cross section shown in Fig. P6.45) resists a torque of 4 kN · m. The wall thicknesses are t₁ = t₂ = t₄ = t₅ = 0.5 mm and t₃ = 0.75 mm. Determine the maximum shearing stresses and the angle of twist per unit length. Let G = 28 GPa.

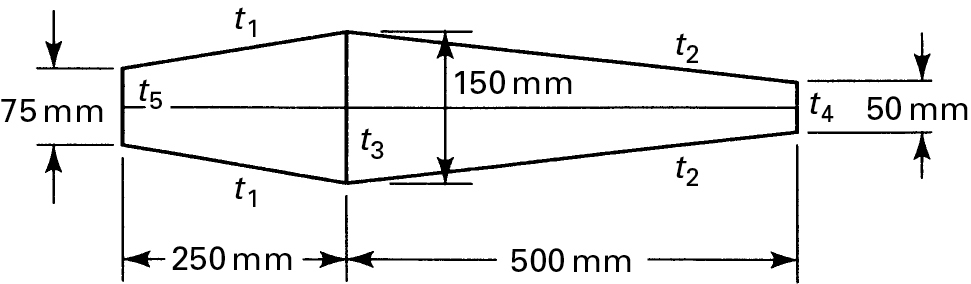
A figure shows a multi-cell aluminum tube. — Figure P6.45.

A cross-section of a multi-cell aluminum tube is shown. The length of the tube is 750 millimeters. The tube consists of two sections which are tapered. Initially, in the first section of the tube, the diameter of the tube is 75 millimeters and the thickness of the wall is t5. Then, the tube is tapered out up to a distance of 250 millimeters. The diameter and the wall thickness at this point are 150 millimeters and t3 respectively. The thickness of the tapered portion is t1. Further, the tube gets tapered in for a distance of 500 millimeters. The diameter and the wall thickness at this point are 50 millimeters and t4 respectively. Here, the wall thickness of the tapered portion is t2.

6.46. A thin-walled tube of length L and constant wall thickness t with a multicell cross section resists a torque T (Fig. P6.46). Find the shearing stress and total angle of twist in terms of T, L, G, a, and t, as required.

A figure shows a rectangular structure curved on the left and hollow in the middle. The length of the rectangle is 3 a and the breadth is 2 a. The radius of the curved portion is a. The thickness of the wall is t. — Figure P6.46.

6.47. A steel torsion bar is used as a counterbalance spring for the trunk lid of a car (Fig. 6.24a). If one end of the bar rotates 75° relative to the other end, find (a) the change in torque and (b) the change in shearing stress. Given: L = 1.5 m, d = 10 mm, G = 79 GPa.

6.48. A steel torsion bar is subjected to a load of 2.4 kN with a moment arm R = 180 mm (Fig. 6.24a). Find: (a) The wire diameter; (b) the length for a deflection of 45 mm. Given: n = 2, τ_yp = 340 MPa, G = 79 GPa.

6.49. A high-strength steel torsion bar (G = 79 GPa) with splined ends (illustrated in Fig. 6.24b) has a length L = 1.1 m and a diameter d = 10 mm. Calculate, when relative rotation between the ends is changed by 15°, the torque and the shear stress.

6.50. Consider two closely coiled helical springs—one made of steel, the other of copper. Each spring is 0.01 m in wire diameter, and one fits within the other. Each has an identical number of coils, N = 20, and ends constrained to deflect the same amount. The steel outer spring has a diameter of 0.124 m, and the copper inner spring has a diameter of 0.1 m. Determine (a) the total axial load the two springs can jointly sustain if the shear stresses in the steel and the copper are not to exceed 500 and 300 MPa, respectively, and (b) the ratio of spring constants. For steel and copper, use shear moduli of elasticity G_s = 79 GPa and G_c = 41 GPa respectively.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for Chapter 6. Torsion of Prismatic Bars

Create new playlist

Sign In

Sign Up

Chapter 6. Torsion of Prismatic Bars

6.1 Introduction

6.2 Elementary Theory of Torsion of Circular Bars

6.2.1 Shearing Stress

6.2.2 Angle of Twist

6.2.3 Axial and Transverse Shear Stresses

6.3 Stresses on Inclined Planes

6.3.1 Stress Transformation

6.3.2 Transmission of Power by Shafts

6.4 General Solution of the Torsion Problem

6.4.1 Geometry of Deformation

6.4.2 Equations of Equilibrium

6.4.3 Equations of Compatibility

6.5 Prandtl’s Stress Function

6.5.1 Boundary Conditions

6.5.2 Force and Torque over the Ends

6.5.3 Circular Cross Section

6.6 Prandtl’s Membrane Analogy

6.6.1 Equation of Equilibrium

6.6.2 Shearing Stress and Angle of Twist

6.7 Torsion of Narrow Rectangular Cross Section

6.7.1 Thin-Walled Open Cross Sections

6.8 Torsion of Multiply Connected Thin-Walled Sections

6.8.1 Shearing Stress

6.8.2 Angle of Twist

6.9 Fluid Flow Analogy and Stress Concentration

6.10 Torsion of Restrained Thin-Walled Members of Open Cross Section

6.10.1 Torsional and Lateral Shears

6.10.2 Boundary Conditions

6.10.3 Long Beams Under Torsion

6.10.4 Angle of Twist

6.11 Torsion Bar Springs

6.12 Curved Circular Bars

6.12.1 Helical Springs

References

Problems

Sections 6.1 through 6.3

Sections 6.4 through 6.7

Sections 6.8 through 6.12

Table of Contents for
Chapter 6. Torsion of Prismatic Bars