Appendix C. Moments of Composite Areas
C.1 Centroid
The plane area characteristics have special significance in various relationships governing stress and deflection of beams, columns, and shafts. Geometric properties for most areas encountered in practice are listed in numerous reference works [Ref. C.1]. Table C.1 presents several typical cases.
Table C.1. Properties of Some Plane Areas
1. Rectangle
|
|
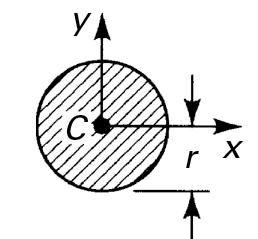
5. Circle
|
2. Right triangle 
|
|
6. Semicircle 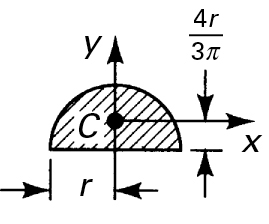
|
3. Ellipse 
|
|
7. Thin tube
|
4. Isosceles triangle 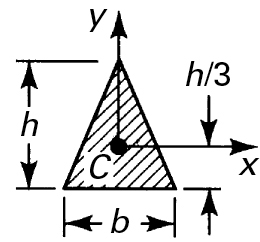
|
|
8. Half of thin tube 
|
The first step in evaluating the characteristics of a plane area is to locate the centroid of the area. The centroid is the point in the plane about which the area is equally distributed. For area A shown in Fig. C.1, the first moments about the x and y axes, respectively, are given by

Figure C.1. Plane area A with centroid C.
These properties are expressed in cubic meters or cubic millimeters in SI units and in cubic feet or cubic inches in U.S. Customary Units. The centroid of area A is denoted by point C, whose coordinates and satisfy the following relations:
When an axis possesses an axis of symmetry, the centroid is located on that axis, as the first moment about an axis of symmetry equals zero. When there are two axes of symmetry, the centroid lies at the intersection of the two axes. If an area possesses no axes of symmetry but does have a center of symmetry, the centroid coincides with the center of symmetry.
Frequently, an area can be divided into simple geometric shapes (for example, rectangles, circles, and triangles) whose areas and centroidal coordinates are known or easily determined. When a composite area is considered as an assemblage of n elementary shapes, the resultant or total area is the algebraic sum of the separate areas, and the resultant moment about any axis is the algebraic sum of the moments of the component areas. Thus, the centroid of a composite area has the coordinates
where and represent the coordinates of the centroids of the component areas, Ai(i = 1,2,...,n).
In applying Eqs. (C.3), it is important to sketch the simple geometric forms into which the composite area is resolved, as shown in Example C.1.
Example C.1 Centroid of an Angle
Locate the centroid of the angle section depicted in Fig. C.2. The dimensions are given in millimeters.

Figure C.2. Example C.1. Area consisting of two parts.
Solution The composite area is divided into two rectangles, A1 and A2, for which the centroids are known (Fig. C.2). Taking the X,Y axes as reference, Eqs. (C.3) are applied to calculate the coordinates of the centroid. The computation is conveniently carried out in the following tabular form. Note that when an area is divided into only two parts, the centroid C of the entire area always lies on the line connecting the centroids C1 and C2 of the components, as indicated in Fig. C.2.
No. |
Ai (mm2) |
(mm) |
(mm) |
(mm3) |
(mm3) |
|---|---|---|---|---|---|
1 |
20(140) = 2800 |
10 |
70 |
28 × 103 |
196 × 103 |
2 |
20(100) = 2000 |
70 |
130 |
140 × 103 |
260 × 103 |
|
ΣAi = 4800 |
|
|
||
|
|||||
C.2 Moments of Inertia
We now consider the second moment or moment of inertia of an area (a relative measure of the manner in which the area is distributed about any axis of interest). The moments of inertia of a plane area A with respect to the x and y axes, respectively, are defined by the following integrals:
where x and y are the coordinates of the element of area dA (Fig. C.1).
Similarly, the polar moment of inertia of a plane area A with respect to an axis through O perpendicular to the area is given by
where p is the distance from point O to the element dA, and p2 = x2 + y2. The product of inertia of a plane area A with respect to the x and y axes is defined as
In this expression, each element of area dA is multiplied by the product of its coordinates (Fig. C.1). The product of inertia of an area about any pair of axes is zero when either of the axes is an axis of symmetry.
From Eqs. (C.4) and (C.5), it is clear that the moments of inertia are always positive quantities because coordinates x and y are squared. Their dimensions are length raised to the fourth power; typical units are meters4, millimeters4, and inches4. The dimensions of the product of inertia are the same as for the moments of inertia; however, the product of inertia can be positive, negative, or zero depending on the values of the product xy.
The radius of gyration is a distance from a reference axis or a point at which the entire area of a section may be considered to be concentrated but still possesses the same moment of inertia as the original area. Therefore, the radii of gyration of an area A about the x and y axes and the origin O (Fig. C.1) are defined as the quantities rx, ry, and ρ = ro, respectively:
Substituting Ix, Iy, and Jo from Eqs. (C.7) into Eq. (C.5) results in
The radius of gyration has the dimension of length, expressed in meters.
C.2.1 Parallel Axis Theorem
The moment of inertia of an area with respect to any axis is related to the moment of inertia around a parallel axis through the centroid by the parallel-axis theorem, sometimes called the transfer formula. It is useful for determining the moment of inertia of an area composed of several simple shapes.
To develop the parallel-axis theorem, consider the area A depicted in Fig. C.3. Let and represent the centroidal axes of the area, parallel to the axes x and y, respectively. The distances between the two sets of axes and the origin are dx, dy and do The moment of inertia with respect to the x axis is
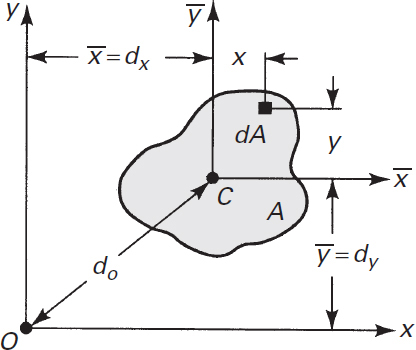
Figure C.3. Plane area for deriving the parallel-axis theorem.
The first integral on the right side equals the moment of inertia about the axis. As y is measured from the centroid axis is zero. Hence,
Similarly,
The parallel-axis theorem is thus stated as follows: The moment of inertia of an area with respect to any axis is equal to the moment of inertia around a parallel centroidal axis, plus the product of the area and the square of the distance between the two axes.
In a like manner, a relationship may be developed connecting the polar moment of inertia Jo of an area about an arbitrary point O and the polar moment of inertia Jc about the centroid of the area (Fig. C.3):
It can be shown that the product of inertia of an area Ixy with respect to any set of axes is given by the transfer formula
where denotes the product of inertia around the centroidal axes. Note that the parallel-axis theorems, Eqs. (C.9) through (C.11), may be employed only if one of the two axes involved is a centroidal axis.
For elementary shapes, the integrals appearing in the equations of this and preceding sections can usually be evaluated easily and the geometric properties of the area obtained (Table C.1). Cross-sectional areas employed in practice can often be broken into a combination of these simple shapes.
Example C.2 Moment of Inertia for a T Section
Determine the moment of inertia of the T section shown in Fig. C.4a around the horizontal axis passing through its centroid. The dimensions are given in millimeters.
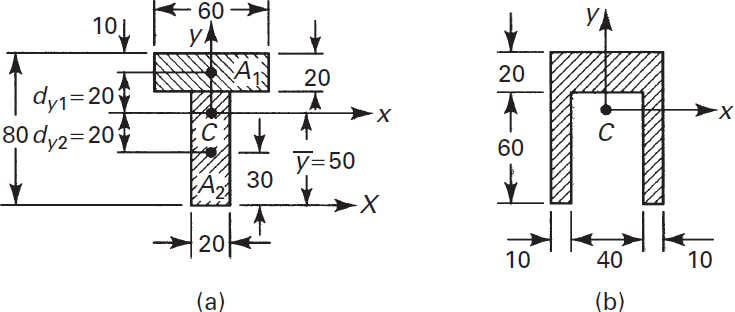
Figure C.4. Example C.2. (a) T section; (b) channel section.
Solution Location of Centroid: The area is divided into component parts A1 and A2, for which the centroids are known (Fig. C.4a). Because the y axis is an axis of symmetry, and
Centroidal Moment of Inertia: Application of the transfer formula to Fig. C.4a results in
Comment Interestingly, the properties of this T section about the centroidal x axis are the same as those of the channel (Fig. C.4b). Both sections possess an axis of symmetry.
C.2.2 Principal Moments of Inertia
The moments of inertia of a plane area depend not only on the location of the reference axis, but also on the orientation of the axes about the origin. The variation of these properties with respect to axis location are governed by the parallel-axis theorem, as described in Section C.2.1. We now derive the equations for transformation of the moments and product of inertia at any point of a plane area.
The area shown in Fig C.5 has the moments and product of inertia Ix, Iy, Ixy with respect to the x and y axes defined by Eqs. (C.4) and (C.6). We need to determine the moments and product of inertia Ix′, Iy′ and Ix′y′ about axes x′, y′ making an angle θ with the original x, y axes. The new coordinates of an element dA can be expressed by projecting x and y onto the rotated axes (Fig. C.5):
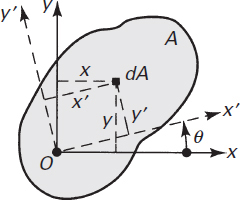
Figure C.5. Rotation of axes.
Then, by definition,
Upon substituting Eqs. (C.4) and (C.6), this expression becomes
The moment of inertia Iy′ may be readily found by substituting θ + π/2 for in the expression for Ix′. Similarly, using the definition Ix′y′ = ∫A x′y′ dA, we obtain
The transformation equations for the moments and product of inertia may be rewritten by introducing double-angle trigonometric relations in the following form:
Comparing the expressions here and in Chapter 1, we observe that moments of inertia (Ix, Iy, Ix′, Iy′) correspond to the normal stresses (σx, σy, σx′, σy), the negatives of the products of inertia (–Ixy, –Ix′y′) correspond to the shear stresses (τxy, τx′y′), and the polar moment of inertia (Jo) corresponds to the sum of the normal stresses (σx + σy). Thus, Mohr’s circle analysis and the characteristics for stress apply to these properties of area.
The angle θ at which the moment of inertia Ix′ of Eq. (C.12a) assumes an extreme value may be obtained from the condition dIx′ / dθ = 0:
Then
The quantity θp represents the two values of θ that locate the principal axes about which the principal or maximum and minimum moments of inertia occur.
When we compare Eq. (C.12c) with Eq. (d), it becomes clear that the product of inertia is zero for the principal axes. If the origin of axes is located at the centroid of the area, they are referred to as the centroidal principal axes. In Section C.2, we noted that the products of inertia relative to the axes of symmetry are zero. Thus, an axis of symmetry coincides with a centroidal principal axis.
The principal moments of inertia are determined by introducing the two values of θp into Eq. (C.12a). The sine and cosine of angles 2θp defined by Eq. (C.13) are
where . When these expressions are inserted into Eq. (C.12a), we obtain
in which I1 and I2 denote the maximum and minimum principal moments of inertia, respectively.
Example C.3 Principal Moments of Inertia for an Angular Section
Calculate the centroidal principal moments of inertia for the angular section shown in Fig. C.6a. The dimensions are given in millimeters.

Figure C.6. Example C.3. (a) Angle section; (b) Mohr’s circle for moments of inertia.
Solution Location of Centroid: The x, y axes are the reference axes through the centroid C (Fig. C.6a), whose location was determined in Example C.1. Again, the area is divided into rectangles A1 and A2.
Moments of Inertia: Applying the parallel-axis theorem, with reference to the x and y axes, we have
The product of inertia about the xy axes is obtained as described in Section C.2:
Principal Moments of Inertia: Equation (C.13) yields
Thus, the two values of θp are –35.54° and –125.54°. Using the first of these values, Eq. (C.12a) results in Ix′ = 1184(104) mm4. The principal moments of inertia are, from Eq. (C.14),
or I1 = Ix′ = 1184(104) mm4 and I2 = Iy′ = 296(104) mm4. The principal axes are indicated in Fig. C.6a as the x′ and y′ axes.
Comments The principal moments of inertia may also be determined readily by means of Mohr’s circle, following a procedure similar to that described in Section 1.11, as shown in Fig. C.6b. Note that the quantities indicated are expressed in cm4 and the results are obtained analytically from the geometry of the circle.
Example C.4 General Formulation of Moments of Inertia for an Angle Section
Derive general expressions for the centroidal moments and product of inertia for the angle section shown in Fig. C.6a. Write a computer program to obtain the centroidal principal moments of inertia.
Solution Using the X,Y axes as reference (Fig. C.6a), Eqs. (C.3) yield
The transfer formula, Eq. (C.9a), results in
Similarly,
For convenience in programming, we employ the notation
and
Equations (h), (i), (j), (C.13), and (C.14) are thus
The required C program is presented in Table C.2, along with input data (from Example C.3) and output values. The program was written and tested on a digital computer.
Table C.2. C Program for Moments of Inertia
/* C Program for Moments of Inertia*/
#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#define pi 3.14159265
void main()
{
FILE *fin, *fout;
float xbar, ybar, theta_p, float a, b, t;
float C1, C2, C3, C4, C5, C6, C7, C8, Ix, Iy, Ixy, D, E, F, I1, I2;
fin=fopen( "m_inertia.d", "r" );
fout=fopen( "m_inertia.o", "w" );
fscanf(fin, "%f%f%f", &a, &b, &t);
fprintf(fout,"input:
");
fprintf(fout,"a=%10.5f b=%10.5f t=%10.5f
", a, b, t);
xbar=(pow(b,2)-pow(t,2)+a*t)/(2.*(a+b-t));
ybar=((b-t)*(2.*a-t)+pow(a,2))/(2.*(a+b-t));
C1=t*(pow(a,3)+b*pow(t,2)-pow(t,3))/12.;
C2=b*t-t*t;
C3=ybar-(a-t/2.);
C4=a*t;
C5=ybar-a/2.;
C6=t*(pow((b-t),3)+a*pow(t,2))/12.;
C7=xbar-(b+t)/2.;
C8=xbar-t/2.;
Ix=C1+C2*pow(C3,2)+C4*pow(C5,2);
Iy=C6+C2*pow(C7,2)+C4*pow(C8,2);
Ixy=C2*C3*C7+C4*C5*C8;
D=(Ix+Iy)/2.;
E=(Ix-Iy)/2.;
F=-Ixy;
I1=D+sqrt(pow(E,2)+pow(F,2));
I2=D-sqrt(pow(E,2)+pow(F,2));
if(Iy != Ix) theta_p=(atan(F/E)/2.)*(180./pi);
if(Iy == Ix) theta_p=45.;
fprintf(fout,"output:
");
fprintf(fout,"xbar=%16.5f
ybar=%16.5f
Ix=%18.5f
Iy=%18.5f
", bar, ybar, Ix, Iy);
fprintf(fout,"Ixy=%17.5f
I1=%18.5f
I2=%18.5f
theta_p=%13.5f
", Ixy, I1, I2,
theta_p); fclose(fin);
fclose(fout);
}
input:
a= 140.00000 b= 120.00000 t= 20.00000
output:
xbar= 35.00000
ybar= 95.00000
Ix= 8840000.00000
Iy= 5960000.00000
Ixy= 4200000.00000
I1= 11840000.00000
I2= 2960000.00000
theta_p= –35.53768
Reference
C.1. YOUNG, W. C., BUDYNAS, R. G., and SADEGH, A. M. Roark’s Formulas for Stress and Strain, 8th ed. New York: McGraw-Hill, 2011.