Chapter 1 Analysis of Stress

1.1 Introduction

The basic structure of matter is characterized by nonuniformity and discontinuity attributable to its various subdivisions: molecules, atoms, and subatomic particles. Our concern in this text is not with the particulate structure, however, and it will be assumed that the matter with which we are concerned is homogeneous and continuously distributed over its volume. There is the clear implication in such an approach that the smallest element cut from the body possesses the same properties as the body. Random fluctuations in the properties of the material are thus of no consequence. This approach is that of continuum mechanics, in which solid elastic materials are treated as though they are continuous media, rather than composed of discrete molecules. Of the states of matter, we are here concerned only with the solid, with its ability to maintain its shape without the need of a container and to resist continuous shear, tension, and compression.

In contrast with rigid-body statics and dynamics, which treat the external behavior of bodies (that is, the equilibrium and motion of bodies without regard to small deformations associated with the application of load), the mechanics of solids is concerned with the relationships of external effect (forces and moments) to internal stresses and strains. Two different approaches used in solid mechanics are the mechanics of materials or elementary theory (also called the technical theory) and the theory of elasticity. The mechanics of materials focuses mainly on the more or less approximate solutions of practical problems. On the other hand, the theory of elasticity concerns itself largely with more mathematical analysis to determine the “exact” stress and strain distributions in a loaded body. The difference between these approaches is primarily in the nature of the simplifying assumptions used, described in Sec. 3.1.

External forces acting on a body may be classified as surface forces and body forces. A surface force is of the concentrated type when it acts at a point; a surface force may also be distributed uniformly or nonuniformly over a finite area. Body forces are associated with the mass of a body, rather than its surfaces, and are distributed throughout the volume of a body. Gravitational, magnetic, and inertia forces are all body forces. They are specified in terms of force per unit volume. All forces acting on a body, including the reactive forces caused by supports and body forces, are considered to be external forces. Internal forces are the forces that hold together the particles forming the body. Unless otherwise stated, we assume in this text that body forces can be neglected and that forces are applied steadily and slowly. The latter is referred to as static loading.

In the International System of Units (SI), force is measured in newtons (N). Because the newton is a small quantity, the kilonewton (kN) is often used in practice. In the U.S. Customary System, force is expressed in pounds (lb) or kilopounds (kips). We shall define all important quantities in both systems of units. However, in numerical examples and problems, SI units will be used throughout the text consistent with international convention. (Table D.2 compares the two systems.)

The study of the behavior of members in tension, compression, and bending began with Galileo Galilei (1564–1642), although Robert Hooke (1635–1703) was the first to point out that a body is deformed subject to the action of a force. Since then many engineers, physicists, and mathematicians in the field of stress analysis have contributed to the basic knowledge on which modern methods are based.^* The literature dealing with various aspects of solid mechanics is voluminous. For those seeking more thorough treatment, selected references are identified in brackets and compiled at the end of the text.

*Historical reviews of mechanics of materials and the theory of elasticity are given in Refs. 1.1 through 1.4.

1.2 Scope of Treatment

The usual objective of mechanics of materials and theory of elasticity is the examination of the load-carrying capacity of a body from three standpoints, strength, stiffness (deformation characteristics), and stability, by using the fundamental principles outlined in Sec. 3.2 and employed throughout the text. These are the laws of forces, the laws of material deformation, and the conditions of geometric compatibility. The principal topics under the general heading of mechanics of solids may be summarized as follows:

1. Analysis of the stresses and deformations within a body subject to a prescribed system of forces. This is accomplished by solving the governing equations that describe the stress and strain fields (theoretical stress analysis). It is often advantageous, where the shape of the structure or conditions of loading preclude a theoretical solution or where verification is required, to apply the laboratory techniques of experimental stress analysis.

2. Determination by theoretical analysis or by experiment of the limiting values of load that a structural element can sustain without suffering damage, failure, or compromise of function.

3. Determination of the body shape and selection of the materials that are most efficient for resisting a prescribed system of forces under specified conditions of operation such as temperature, humidity, vibration, and ambient pressure. This is the design function and, more particularly, that of optimum design. Efficiency may be gauged by such criteria as minimum weight or volume, minimum cost, or any criterion deemed appropriate.

The design function, item 3, clearly relies on the performance of the theoretical analyses under items 1 and 2, and it is to these that this text is directed. The role of analysis in design is observed in examining the following rational procedure in the design of a load-carrying member:

1. Evaluate the most likely modes of failure of the member. Failure criteria that predict the various modes of failure under anticipated conditions of service are discussed in Chapter 4.

2. Determine the expressions relating applied loading to such effects as stress, strain, and deformation. Often, the member under consideration and conditions of loading are so significant or so amenable to solution as to have been the subject of prior analysis. For these situations, textbooks, handbooks, journal articles, and technical papers are good sources of information. Where the situation is unique, a mathematical derivation specific to the case at hand is required.

3. Determine the maximum usable value of stress, strain, or energy. This value is obtained either by reference to compilations of material properties or by experimental means such as simple tension test and is used in connection with the relationship derived in step 2.

4. Select a design factor of safety. This is to account for uncertainties in a number of aspects of the design, including those related to the actual service loads, material properties, or environmental factors. An important area of uncertainty is connected with the assumptions made in the analysis of stress and deformation. Also, we are not likely to have a secure knowledge of the stresses that may be introduced during machining, assembly, and shipment of the element. The design factor of safety also reflects the consequences of failure; for example, the possibility that failure will result in loss of human life or injury or in costly repairs or danger to other components of the overall system. For the aforementioned reasons, the design factor of safety is also sometimes called the factor of ignorance. The uncertainties encountered during the design phase may be of such magnitude as to lead to a design carrying extreme weight, volume, or cost penalties. It may then be advantageous to perform thorough tests or more exacting analysis, rather to rely on overly large design factors of safety.

The true factor of safety, usually referred to simply as the factor of safety, can only be determined after the member is constructed and tested. This factor is the ratio of the maximum load the member can sustain under severe testing without failure to the maximum load actually carried under normal service conditions, the working load. When a linear relationship exists between the load and the stress produced by the load, the factor of safety n may be expressed as

(1.1)

Maximum usable stress represents either the yield stress or the ultimate stress. The allowable stress is the working stress. The factor of safety must be greater than 1.0 if failure is to be avoided. Values for factor of safety, selected by the designer on the basis of experience and judgment, are 1.5 or greater. For the majority of applications, appropriate factors of safety are found in various construction and manufacturing codes.

The foregoing procedure is not always conducted in as formal a fashion as may be implied. In some design procedures, one or more steps may be regarded as unnecessary or obvious on the basis of previous experience.

We conclude this section with an appeal for the reader to exercise a degree of skepticism with regard to the application of formulas for which there is uncertainty as to the limitations of use or the areas of applicability. The relatively simple form of many formulas usually results from rather severe restrictions in its derivation. These relate to simplified boundary conditions and shapes, limitations on stress and strain, and the neglect of certain complicating factors. Designers and stress analysts must be aware of such restrictions lest their work be of no value or, worse lead to dangerous inadequacies.

In this chapter, we are concerned with the state of stress at a point and the variation of stress throughout an elastic body. The latter is dealt with in Secs. 1.8 and 1.16 and the former in the balance of the chapter.

1.3 Definition of Stress

Consider a body in equilibrium subject to a system of external forces, as shown in Fig. 1.1a. Under the action of these forces, internal forces will be developed within the body. To examine the latter at some interior point Q, we use an imaginary plane to cut the body at a section a-a through Q, dividing the body into two parts. As the forces acting on the entire body are in equilibrium, the forces acting on one part alone must be in equilibrium: This requires the presence of forces on plane a-a. These internal forces, applied to both parts, are distributed continuously over the cut surface. The aforementioned process, referred to as the method of sections, will be relied on as a first step in solving all problems involving the investigation of internal forces.

Figure 1.1 (a) Sectioning of a body; (b) free body with internal forces; (c) enlarged area ΔA with components of the force ΔF.

Figure 1.1b shows the isolated left part of the body. An element of area ΔA, located at point Q on the cut surface is acted on by force ΔF. Let the origin of coordinates be placed at point Q, with x normal and y, z tangent to ΔA. In general, ΔF does not lie along x, y, or z. Decomposing ΔF into components parallel to x, y, and z (Fig. 1.1c), we define the normal stress σ_x and the shearing stresses τ_xy and τ_xz:

(1.2)

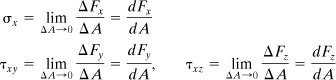
These definitions provide the stress components at a point Q to which the area ΔA is reduced in the limit. Clearly, the expression ΔA → 0 depends on the idealization discussed in the first paragraph of Sec. 1.1. Our consideration is with the average stress on areas, which, while small as compared with the size of the body, is large compared with interatomic distances in the solid. Stress is thus defined adequately for engineering purposes. As shown in Eq. (1.2), the intensity of force perpendicular, or normal, to the surface is termed the normal stress at a point, while the intensity of force parallel to the surface is the shearing stress at a point.

The values obtained in the limiting process of Eq. (1.2) differ from point to point on the surface as ΔF varies. The stress components depend on not only ΔF, however, but also on the orientation of the plane on which it acts at point Q. Even at a given point, therefore, the stresses will differ as different planes are considered. The complete description of stress at a point thus requires the specification of the stress on all planes passing through the point.

Because the stress (σ or τ) is obtained by dividing the force by area, it has units of force per unit area. In SI units, stress is measured in newtons per square meter (N/m²), or pascals (Pa). As the pascal is a very small quantity, the megapascal (MPa) is commonly used. When U.S. Customary System units are used, stress is expressed in pounds per square inch (psi) or kips per square inch (ksi).

1.4 Components of Stress: Stress Tensor

It is verified in Sec. 1.12 that in order to enable the determination of the stresses on an infinite number of planes passing through a point Q, thus defining the stresses at that point, we need only specify the stress components on three mutually perpendicular planes passing through the point. These three planes, perpendicular to the coordinate axes, contain three hidden sides of an infinitesimal cube (Fig. 1.2). We emphasize that when we move from point Q to point Q′ the values of stress will, in general, change. Also, body forces can exist. However, these cases will not be discussed here (see Sec. 1.8), as we are now merely interested in establishing the terminology necessary to specify a stress component.

Figure 1.2. Element subjected to three-dimensional stress. All stresses have positive sense.

The general case of a three-dimensional state of stress is shown in Fig. 1.2. Consider the stresses to be identical at points Q and Q′ and uniformly distributed on each face, represented by a single vector acting at the center of each face. In accordance with the foregoing, a total of nine scalar stress components defines the state of stress at a point. The stress components can be assembled in the following matrix form, wherein each row represents the group of stresses acting on a plane passing through Q(x, y, z):

(1.3)

This array represents a tensor of second rank (refer to Sec. 1.12) requiring two indexes to identify its elements or components. A vector is a tensor of first rank; a scalar is of zero rank.

The double subscript notation is interpreted as follows: The first subscript indicates the direction of a normal to the plane or face on which the stress component acts; the second subscript relates to the direction of the stress itself. Repetitive subscripts will be avoided in this text, so the normal stresses τ_xx, τ_yy, and τ_zz will be designated σ_x, σ_y, and σ_z, as indicated in Eq. (1.3). A face or plane is usually identified by the axis normal to it; for example, the x faces are perpendicular to the x axis.

Sign Convention

Referring again to Fig. 1.2, we observe that both stresses labeled τ_yx tend to twist the element in a clockwise direction. It would be convenient, therefore, if a sign convention were adopted under which these stresses carried the same sign. Applying a convention relying solely on the coordinate direction of the stresses would clearly not produce the desired result, inasmuch as the τ_yx stress acting on the upper surface is directed in the positive x direction, while τ_yx acting on the lower surface is directed in the negative x direction. The following sign convention, which applies to both normal and shear stresses, is related to the deformational influence of a stress and is based on the relationship between the direction of an outward normal drawn to a particular surface and the directions of the stress components on the same surface.

When both the outer normal and the stress component face in a positive direction relative to the coordinate axes, the stress is positive. When both the outer normal and the stress component face in a negative direction relative to the coordinate axes, the stress is positive. When the normal points in a positive direction while the stress points in a negative direction (or vice versa), the stress is negative. In accordance with this sign convention, tensile stresses are always positive and compressive stresses always negative. Figure 1.2 depicts a system of positive normal and shear stresses.

Equality of Shearing Stresses

We now examine properties of shearing stress by studying the equilibrium of forces acting on the cubic element shown in Fig. 1.2. As the stresses acting on opposite faces (which are of equal area) are equal in magnitude, but opposite in direction, translational equilibrium in all directions is assured; that is, ΣF_x = 0, ΣF_y = 0, and ΣF_z = 0. Rotational equilibrium is established by taking moments of the x-, y-, and z-directed forces about point Q, for example. From ΣM_z = 0,

(−τ_xydydz)dx + (τ_yxdxdz)dy = 0

Simplifying,

(1.4a)

Likewise, from ΣM_y = 0 and ΣM_x = 0, we have

(1.4b,c)

Hence, the subscripts for the shearing stresses are commutative, and the stress tensor is symmetric. This means that shearing stresses on mutually perpendicular planes of the element are equal. Therefore, no distinction will hereafter be made between the stress components τ_xy and τ_yx, τ_xz and τ_zx, or τ_yz and τ_zy. In Sec. 1.8, it is shown rigorously that the foregoing is valid even when stress components vary from one point to another.

Indicial Notation

Many equations of elasticity become unwieldy when written in full, unabbreviated form; see, for example, Eq. (1.24). As the complexity of the situation described increases, so does that of the formulations, tending to obscure the fundamentals in a mass of symbols. For this reason, the more compact indicial notation or tensor notation described in Appendix A is sometimes found in technical publications. A stress tensor is written in indicial notation as τ_ij where i and j each assume the values x, y, and z as required by Eq. (1.3). Generally, such notation is not employed in this text.

1.5. Some Special Cases of Stress

Under particular circumstances, the general state of stress (Fig. 1.2) reduces to simpler stress states as briefly described here. These stresses, which are commonly encountered in practice, will be given detailed consideration throughout the text.

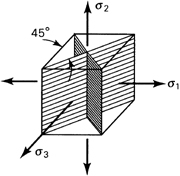
a. Triaxial Stress. We shall observe in Sec. 1.13 that an element subjected to only stresses σ₁, σ₂ and σ₃ acting in mutually perpendicular directions is said to be in a state of triaxial stress. Such a state of stress can be written as

(a)

The absence of shearing stresses indicates that the preceding stresses are the principal stresses for the element. A special case of triaxial stress, known as spherical or dilatational stress, occurs if all principal stresses are equal (see Sec. 1.14). Equal triaxial tension is sometimes called hydrostatic tension. An example of equal triaxial compression is found in a small element of liquid under static pressure.

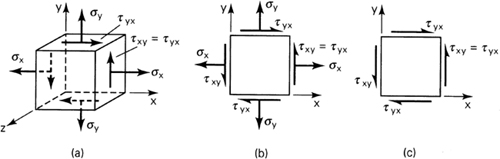
b. Two-dimensional or Plane Stress. In this case, only the x and y faces of the element are subjected to stress, and all the stresses act parallel to the x and y axes as shown in Fig. 1.3a. The plane stress matrix is written

Figure 1.3. (a) Element in plane stress; (b) two-dimensional presentation of plane stress; (c) element in pure shear.

(1.5)

Although the three-dimensional nature of the element under stress should not be forgotten, for the sake of convenience we usually draw only a two-dimensional view of the plane stress element (Fig. 1.3b). When only two normal stresses are present, the state of stress is called biaxial. These stresses occur in thin plates stressed in two mutually perpendicular directions.

c. Pure Shear. In this case, the element is subjected to plane shearing stresses only, for example, τ_xy and τ_yx (Fig. 1.3c). Typical pure shear occurs over the cross sections and on longitudinal planes of a circular shaft subjected to torsion.

d. Uniaxial Stress. When normal stresses act along one direction only, the one-dimensional state of stress is referred to as a uniaxial tension or compression.

1.6. Internal Force-Resultant and Stress Relations

Distributed forces within a member can be represented by a statically equivalent system consisting of a force and a moment vector acting at any arbitrary point (usually the centroid) of a section. These internal force resultants, also called stress resultants, exposed by an imaginary cutting plane containing the point through the member, are usually resolved into components normal and tangent to the cut section (Fig. 1.4). The sense of moments follows the right-hand screw rule, often represented by double-headed vectors, as shown in the figure. Each component can be associated with one of four modes of force transmission:

Figure 1.4. Positive forces and moments on a cut section of a body and components of the force dF on an infinitesimal area dA.

1. The axial force P or N tends to lengthen or shorten the member.

2. The shear forces V_y and V_z tend to shear one part of the member relative to the adjacent part and are often designated by the letter V.

3. The torque or twisting moment T is responsible for twisting the member.

4. The bending moments M_y and M_z cause the member to bend and are often identified by the letter M.

A member may be subject to any or all of the modes simultaneously. Note that the same sign convention is used for the force and moment components that is used for stress; a positive force (or moment) component acts on the positive face in the positive coordinate direction or on a negative face in the negative coordinate direction.

A typical infinitesimal area dA of the cut section shown in Fig. 1.4 is acted on by the components of an arbitrarily directed force dF, expressed using Eqs. (1.2) as dF_x = σ_x dA, dF_y = τ_xy dA, and dF_z = τ_xz dA. Clearly, the stress components on the cut section cause the internal force resultants on that section. Thus, the incremental forces are summed in the x, y, and z directions to give

(1.6a)

In a like manner, the sums of the moments of the same forces about the x, y, and z axes lead to

(1.6b)

where the integrations proceed over area A of the cut section. Equations (1.6) represent the relations between the internal-force resultants and the stresses. In the next paragraph we illustrate the fundamental concept of stress and observe how Eqs. (1.6) connect internal force resultants and the state of stress in a specific case.

Consider a homogeneous prismatic bar loaded by axial forces P at the ends (Fig. 1.5a). A prismatic bar is a straight member having constant cross-sectional area throughout its length. To obtain an expression for the normal stress, we make an imaginary cut (section a-a) through the member at right angles to its axis. A free-body diagram of the isolated part is shown in Fig. 1.5b, wherein the stress is substituted on the cut section as a replacement for the effect of the removed part. Equilibrium of axial forces requires that P = ∫ σ_x dA or P = Aσ_x. The normal stress is therefore

Figure 1.5. Prismatic bar in tension.

(1.7)

where A is the cross-sectional area of the bar. Because V_y, V_z, and T all are equal to zero, the second and third of Eqs. (1.6a) and the first of Eqs. (1.6b) are satisfied by τ_xy = τ_xz = 0. Also, M_y = M_z = 0 in Eqs. (1.6b) requires only that σ_x be symmetrically distributed about the y and z axes, as depicted in Fig. 1.5b. When the member is being extended as in the figure, the resulting stress is a uniaxial tensile stress; if the direction of forces were reversed, the bar would be in compression under uniaxial compressive stress. In the latter case, Eq. (1.7) is applicable only to chunky or short members owing to other effects that take place in longer members.^*

*Further discussion of uniaxial compression stress is found in Sec. 11.5, where we take up the classification of columns.

Similarly, application of Eqs. (1.6) to torsion members, beams, plates, and shells will be presented as the subject unfolds, following the derivation of stress–strain relations and examination of the geometric behavior of a particular member. Applying the method of mechanics of materials, we shall develop other elementary formulas for stress and deformation. These, also called the basic formulas of mechanics of materials, are often used and extended for application to more complex problems in advanced mechanics of materials and the theory of elasticity. For reference purposes to preliminary discussions, Table 1.1 lists some commonly encountered cases. Each equation presented in the table describes a state of stress associated with a single force, torque, moment component, or pressure at a section of a typical homogeneous and elastic structural member. When a member is acted on simultaneously by two or more load types, causing various internal-force resultants on a section, it is assumed that each load produces the stress as if it were the only load acting on the member. The final or combined stress is then determined by superposition of the several states of stress, as discussed in Sec. 2.2.

Table 1.1. Commonly Used Elementary Formulas for Stress^a

^aDetailed derivations and limitations of the use of these formulas are discussed in Secs. 1.6, 5.7, 6.2, and 13.13.

The mechanics of materials theory is based on the simplifying assumptions related to the pattern of deformation so that the strain distributions for a cross section of the member can be determined. It is a basic assumption that plane sections before loading remain plane after loading. The assumption can be shown to be exact for axially loaded prismatic bars, for prismatic circular torsion members, and for prismatic beams subjected to pure bending. The assumption is approximate for other beam situations. However, it is emphasized that there is an extraordinarily large variety of cases in which applications of the basic formulas of mechanics of materials lead to useful results. In this text we hope to provide greater insight into the meaning and limitations of stress analysis by solving problems using both the elementary and exact methods of analysis.

1.7 Stresses on Inclined Planes in an Axially Loaded Member

We now consider the stresses on an inclined plane b-b of the bar in uniaxial tension shown in Fig. 1.5a, where the normal x′ to the plane forms an angle θ with the axial direction. On an isolated part of the bar to the left of section b−b, the resultant P may be resolved into two components: the normal force P_x′ = P cos θ and the shear force P_y′ = −P sin θ, as indicated in Fig. 1.6a. Thus, the normal and shearing stresses, uniformly distributed over the area A_x′ = A/cos θ of the inclined plane (Fig. 1.6b), are given by

Figure 1.6. Isolated part of the bar shown in Fig. 1.5.

(1.8a)

(1.8b)

The negative sign in Eq. (1.8b) agrees with the sign convention for shearing stresses described in Sec. 1.4. The foregoing process of determining the stress in proceeding from one set of coordinate axes to another is called stress transformation.

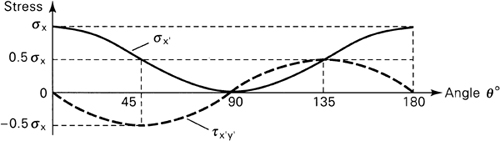
Equations (1.8) indicate how the stresses vary as the inclined plane is cut at various angles. As expected, σ_x′ is a maximum (σ_max) when θ is 0° or 180°, and τ_x′y′ is maximum (τ_max) when θ is 45° or 135°. Also, . The maximum stresses are thus

(1.9)

Observe that the normal stress is either maximum or a minimum on planes for which the shearing stress is zero.

Figure 1.7 shows the manner in which the stresses vary as the section is cut at angles varying from θ = 0° to 180°. Clearly, when θ > 90°, the sign of τ_x′y′ in Eq. (1.8b) changes; the shearing stress changes sense. However, the magnitude of the shearing stress for any angle θ determined from Eq. (1.8b) is equal to that for θ + 90°. This agrees with the general conclusion reached in the preceding section: Shearing stresses on mutually perpendicular planes must be equal.

Figure 1.7. Variation of stress at a point with the inclined section in the bar shown in Fig. 1.5.

We note that Eqs. (1.8) can also be used for uniaxial compression by assigning to P a negative value. The sense of each stress direction is then reversed in Fig. 1.6b.

Example 1.1

Compute the stresses on the inclined plane with θ = 35° for a prismatic bar of a cross-sectional area 800 mm², subjected to a tensile load of 60 kN (Fig. 1.5a). Then determine the state of stress for θ = 35° by calculating the stresses on an adjoining face of a stress element. Sketch the stress configuration.

Solution The normal stress on a cross section is

Introducing this value in Eqs. (1.8) and using θ = 35°, we have

σ_x′ = σ_x cos²θ = 75(cos 35°)² = 50.33 MPa

τ_x′y′ = −σ_x sin θ cos θ = −75(sin 35°)(cos35°) = −35.24 MPa

The normal and shearing stresses acting on the adjoining y′ face are, respectively, 24.67 MPa and 35.24 MPa, as calculated from Eqs. (1.8) by substituting the angle θ + 90° = 125°. The values of σ_x′ and τ_x′y′ are the same on opposite sides of the element. On the basis of the established sign convention for stress, the required sketch is shown in Fig. 1.8.

Figure 1.8. Example 1.1.

1.8 Variation of Stress within a Body

As pointed out in Sec. 1.3, the components of stress generally vary from point to point in a stressed body. These variations are governed by the conditions of equilibrium of statics. Fulfillment of these conditions establishes certain relationships, known as the differential equations of equilibrium, which involve the derivatives of the stress components.

Consider a thin element of sides dx and dy (Fig. 1.9), and assume that σ_x, σ_y, τ_xy and τ_yx are functions of x, y but do not vary throughout the thickness (are independent of z) and that the other stress components are zero. Also assume that the x and y components of the body forces per unit volume, F_x and F_y, are independent of z and that the z component of the body force F_z = 0. This combination of stresses, satisfying the conditions described, is the plane stress. Note that because the element is very small, for the sake of simplicity, the stress components may be considered to be distributed uniformly over each face. In the figure they are shown by a single vector representing the mean values applied at the center of each face.

Figure 1.9. Element with stresses and body forces.

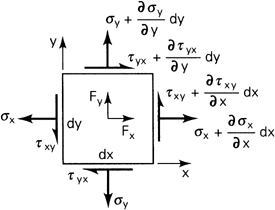
As we move from one point to another, for example, from the lower-left corner to the upper-right corner of the element, one stress component, say σ_x, acting on the negative x face, changes in value on the positive x face. The stresses σ_y, τ_xy, and τ_yx similarly change. The variation of stress with position may be expressed by a truncated Taylor’s expansion:

(a)

The partial derivative is used because σ_x is a function of x and y. Treating all the components similarly, the state of stress shown in Fig. 1.9 is obtained.

We consider now the equilibrium of an element of unit thickness, taking moments of force about the lower-left corner. Thus, ΣM_z = 0 yields

Neglecting the triple products involving dx and dy, this reduces to τ_xy = τ_yx. In a like manner, it may be shown that τ_yz = τ_zy and τ_xz = τ_zx, as already obtained in Sec. 1.4. From the equilibrium of x forces, ΣF_x = 0, we have

(b)

Upon simplification, Eq. (b) becomes

(c)

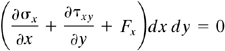
Inasmuch as dx dy is nonzero, the quantity in the parentheses must vanish. A similar expression is written to describe the equilibrium of y forces. The x and y equations yield the following differential equations of equilibrium for two-dimensional stress:

(1.10)

The differential equations of equilibrium for the case of three-dimensional stress may be generalized from the preceding expressions as follows:

(1.11)

A succinct representation of these expressions is given by Eq. (A.1). As the two equilibrium relations of Eqs. (1.10) contain three unknowns (σ_x, σ_y, τ_xy) and the three expressions of Eqs. (1.11) involve the six unknown stress components, problems in stress analysis are internally statically indeterminate.

In a number of practical applications, the weight of the member is the only body force. If we take the y axis as upward and designate by ρ the mass density per unit volume of the member and by g, the gravitational acceleration, then F_x = F_z = 0 and F_y = −ρg in Eqs. (1.10) and (1.11). The resultant of this force over the volume of the member is usually so small compared with the surface forces that it can be ignored, as stated in Sec. 1.1. However, in dynamic systems, the stresses caused by body forces may far exceed those associated with surface forces so as to be the principal influence on the stress field.^*

*In this case, the body is not in static equilibrium, and the inertia force terms −ρa_x, −ρa_y, and −ρa_z (where a_x, a_y and a_z are the components of acceleration) must be included in the body force components F_x, F_y, and F_z respectively, in Eqs. (1.11).

Application of Eqs. (1.10) and (1.11) to a variety of loaded members is presented in sections employing the approach of the theory of elasticity, beginning with Chapter 3. The following sample problem shows the pattern of the body force distribution for an arbitrary state of stress in equilibrium.

Example 1.2

The stress field within an elastic structural member is expressed as follows:

(d)

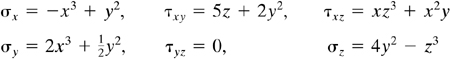
Determine the body force distribution required for equilibrium.

Solution Substitution of the given stresses into Eq. (1.11) yields

(−3x²) + (4y) + (3xz²) + F_x = 0

(y) + (0) + (0) + F_y = 0

(−3z²) + (z³ + 2xy) + (0) + F_z = 0

The body force distribution, as obtained from these expressions, is therefore

(e)

The state of stress and body force at any specific point within the member may be obtained by substituting the specific values of x, y, and z into Eqs. (d) and (e), respectively.

1.9 Two-Dimensional Stress at a Point

A two-dimensional state of stress exists when the stresses and body forces are independent of one of the coordinates, here taken as z. Such a state is described by stresses σ_x, σ_y, and τ_xy and the x and y body forces. Two-dimensional problems are of two classes: plane stress and plane strain. In the case of plane stress, as described in the previous section, the stresses σ_z, τ_xz, and τ_yz and the z-directed body forces are assumed to be zero. In the case of plane strain, the stresses τ_xz and τ_yz and the body force F_z are likewise taken to be zero, but σ_z does not vanish^* and can be determined from stresses σ_x and σ_y.

*More details and illustrations of these assumptions are given in Chapter 3.

We shall now determine the equations for transformation of the stress components σ_x, σ_y, and τ_xy at any point of a body represented by an infinitesimal element (Fig. 1.10a). The z-directed normal stress σ_z even if it is nonzero, need not be considered here.

Figure 1.10. Elements in plane stress.

Consider an infinitesimal wedge cut from the loaded body shown in Fig. 1.10a, b. It is required to determine the stresses σ_x′ and τ_x′y′, which refer to axes x′, y′ making an angle θ with axes x, y as shown in the figure. Let side AB be normal to the x′ axis. Note that in accordance with the sign convention, σ_x′ and τ_x′y′ are positive stresses as shown in the figure. If the area of side AB is taken as unity, then sides QA and QB have area cos θ and sin θ, respectively.

Equilibrium of forces in the x and y directions requires that

(1.12)

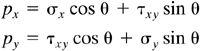
where p_x and p_y are the components of stress resultant acting on AB in the x and y directions, respectively. The normal and shear stresses on the x′ plane (AB plane) are obtained by projecting p_x and p_y in the x′ and y′ directions:

(a)

From the foregoing it is clear that . Upon substitution of the stress resultants from Eq. (1.12), Eqs. (a) become

(1.13a)

(1.13b)

The stress σ_y′ may readily be obtained by substituting θ + π/2 for θ in the expression for σ_x′:

(1.13c)

Equations (1.13) can be converted to a useful form by introducing the following trigonometric identities:

The transformation equations for stress now become

(1.14a)

(1.14b)

(1.14c)

The foregoing expressions permit the computation of stresses acting on all possible planes AB (the state of stress at a point) provided that three stress components on a set of orthogonal faces are known.

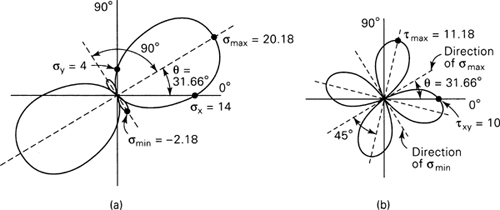
Consider, for example, the possible states of stress corresponding to σ_x = 14 MPa, σ_y = 4 MPa, and τ_xy = 10 MPa. Substituting these values into Eq. (1.14) and permitting θ to vary from 0° to 360° yields the data upon which the curves shown in Fig. 1.11 are based. The plots shown, called stress trajectories, are polar representations: σ_x′ versus θ (Fig. 1.11a) and τ_x′y′ versus θ (Fig. 1.11b). It is observed that the direction of each maximum shear stress bisects the angle between the maximum and minimum normal stresses. Note that the normal stress is either a maximum or a minimum on planes at θ = 31.66° and θ = 31.66° + 90°, respectively, for which the shearing stress is zero. The conclusions drawn from this example are valid for any two-dimensional (or three-dimensional) state of stress and will be observed in the sections to follow. It can be verified that, Cartesian representations of Eq. (1.14), which may be sketched similar to what is shown in Fig. 1.7, lead to the same results [Ref. 1.5].

Figure 1.11. Polar representations of σ_x′ and τ_x′y′ (in megapascals) versus θ.

1.10 Principal Stresses and Maximum Shear Stress in Two Dimensions

The transformation equations for two-dimensional stress indicate that the normal stress σ_x′ and shearing stress τ_x′y′ vary continuously as the axes are rotated through the angle θ. To ascertain the orientation of x′y′ corresponding to maximum or minimum σ_x′, the necessary condition dσ_x′/dθ = 0 is applied to Eq. (1.14a). In so doing, we have

(a)

This yields

(1.15)

Inasmuch as tan 2θ = tan(π + 2θ), two directions, mutually perpendicular, are found to satisfy Eq. (1.15). These are the principal directions, along which the principal or maximum and minimum normal stresses act. Two values of θ_p, corresponding to the σ₁ and σ₂ planes, are represented by and respectively.

When Eq. (1.14b) is compared with Eq. (a), it becomes clear that τ_x′y′ = 0 on a principal plane. A principal plane is thus a plane of zero shear. The principal stresses are determined by substituting Eq. (1.15) into Eq. (1.14a):

(1.16)

Note that the algebraically larger stress given here is the maximum principal stress, denoted by σ₁. The minimum principal stress is represented by σ₂. It is necessary to substitute one of the values θ_p into Eq. (1.14a) to determine which of the two corresponds to σ₁.

Similarly, employing the preceding approach and Eq. (1.14b), we determine the planes of maximum shearing stress. Thus, setting dτ_x′y′/dθ = 0, we now have (σ_x − σ_y)cos 2θ + 2τ_xy sin 2θ = 0 or

(1.17)

The foregoing expression defines two values of θ_s that are 90° apart. These directions may again be denoted by attaching a prime or a double prime notation to θ_s. Comparing Eqs. (1.15) and (1.17), we also observe that the planes of maximum shearing stress are inclined at 45° with respect to the planes of principal stress. Now, from Eqs. (1.17) and (1.14b), we obtain the extreme values of shearing stress as follows:

(1.18)

Here the largest shearing stress, regardless of sign, is referred to as the maximum shearing stress, designated τ_max. Normal stresses acting on the planes of maximum shearing stress can be determined by substituting the values of 2θ_S from Eq. (1.17) into Eqs. (1.14a) and (1.14c):

(1.19)

The results are illustrated in Fig. 1.12. Note that the diagonal of a stress element toward which the shearing stresses act is called the shear diagonal. The shear diagonal of the element on which the maximum shearing stresses act lies in the direction of the algebraically larger principal stress as shown in the figure. This assists in predicting the proper direction of the maximum shearing stress.

Figure 1.12. Planes of principal and maximum shearing stresses.

1.11 Mohr’s Circle for Two-Dimensional Stress

A graphical technique, predicated on Eq. (1.14), permits the rapid transformation of stress from one plane to another and leads also to the determination of the maximum normal and shear stresses. In this approach, Eqs. (1.14) are depicted by a stress circle, called Mohr’s circle.^* In the Mohr representation, the normal stresses obey the sign convention of Sec. 1.4. However, for the purposes only of constructing and reading values of stress from Mohr’s circle, the sign convention for shear stress is as follows: If the shearing stresses on opposite faces of an element would produce shearing forces that result in a clockwise couple, as shown in Fig. 1.13c, these stresses are regarded as positive. Accordingly, the shearing stresses on the y faces of the element in Fig. 1.13a are taken as positive (as before), but those on the x faces are now negative.

*After Otto Mohr (1835–1918), professor at Dresden Polytechnic. For further details, see Ref. 1.5, Sec. 4.5, for example.

Figure 1.13. (a) Stress element; (b) Mohr’s circle of stress; (c) interpretation of positive shearing stresses.

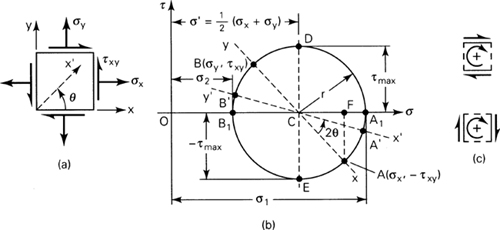
Given σ_x, σ_y, and τ_xy with algebraic sign in accordance with the foregoing sign convention, the procedure for obtaining Mohr’s circle (Fig. 1.13b) is as follows:

1. Establish a rectangular coordinate system, indicating +τ and +σ. Both stress scales must be identical.

2. Locate the center C of the circle on the horizontal axis a distance (σ_x + σ_y) from the origin.

3. Locate point A by coordinates σ_x and −τ_xy. These stresses may correspond to any face of an element such as in Fig. 1.13a. It is usual to specify the stresses on the positive x face, however.

4. Draw a circle with center at C and of radius equal to CA.

5. Draw line AB through C.

The angles on the circle are measured in the same direction as θ is measured in Fig. 1.13a. An angle of 2θ on the circle corresponds to an angle of θ on the element. The state of stress associated with the original x and y planes corresponds to points A and B on the circle, respectively. Points lying on diameters other than AB, such as A′ and B′, define states of stress with respect to any other set of x′ and y′ planes rotated relative to the original set through an angle θ.

It is clear that points A₁ and B₁ on the circle locate the principal stresses and provide their magnitudes as defined by Eqs. (1.15) and (1.16), while D and E represent the maximum shearing stresses, defined by Eqs. (1.17) and (1.18). The radius of the circle is

(a)

where

Thus, the radius equals the magnitude of the maximum shearing stress. Mohr’s circle shows that the planes of maximum shear are always located at 45° from planes of principal stress, as already indicated in Fig. 1.12. The use of Mohr’s circle is illustrated in the first two of the following examples.

Example 1.3

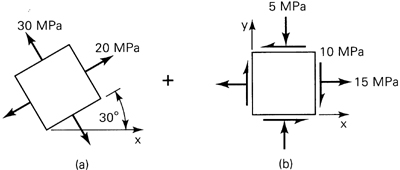
At a point in the structural member, the stresses are represented as in Fig. 1.14a. Employ Mohr’s circle to determine (a) the magnitude and orientation of the principal stresses and (b) the magnitude and orientation of the maximum shearing stresses and associated normal stresses. In each case, show the results on a properly oriented element; represent the stress tensor in matrix form.

Figure 1.14. Example 1.3.

Solution Mohr’s circle, constructed in accordance with the procedure outlined, is shown in Fig. 1.14b. The center of the circle is at (40 + 80)/2 = 60 MPa on the σ axis.

a. The principal stresses are represented by points A₁ and B₁. Hence, the maximum and minimum principal stresses, referring to the circle, are

or

σ₁ = 96.05 MPa and σ₂ = 23.95 MPa

The planes on which the principal stresses act are given by

and

Hence

= 28.15°       and        = 118.15°

Mohr’s circle clearly indicates that locates the σ₁ plane. The results may readily be checked by substituting the two values of θ_p into Eq. (1.14a). The state of principal stress is shown in Fig. 1.14c.

b. The maximum shearing stresses are given by points D and E. Thus,

It is seen that (σ₁ − σ₂)/2 yields the same result. The planes on which these stresses act are represented by

and

As Mohr’s circle indicates, the positive maximum shearing stress acts on a plane whose normal x′ makes an angle with the normal to the original plane (x plane). Thus, +τ_max on two opposite x′ faces of the element will be directed so that a clockwise couple results. The normal stresses acting on maximum shear planes are represented by OC, σ′ = 60 MPa on each face. The state of maximum shearing stress is shown in Fig. 1.14d. The direction of the τ_max’S may also be readily predicted by recalling that they act toward the shear diagonal. We note that, according to the general sign convention (Sec. 1.4), the shearing stress acting on the x′ plane in Fig. 1.14d is negative. As a check, if and the given initial data are substituted into Eq. (1.14b), we obtain τ_x′y′ = −36.05 MPa, as already found.

We may now describe the state of stress at the point in the following matrix forms:

These three representations, associated with the θ = 0°, θ = 28.15°, and θ = 73.15° planes passing through the point, are equivalent.

Note that if we assume σ_z = 0 in this example, a much higher shearing stress is obtained in the planes bisecting the x′ and z planes (Problem 1.37). Thus, three-dimensional analysis, Sec. 1.15, should be considered for determining the true maximum shearing stress at a point.

Example 1.4

The stresses acting on an element of a loaded body are shown in Fig. 1.15a. Apply Mohr’s circle to determine the normal and shear stresses acting on a plane defined by θ = 30°.

Figure 1.15. Example 1.4.

Solution Mohr’s circle of Fig. 1.15b describes the state of stress given in Fig. 1.15a. Points A₁ and B₁ represent the stress components on the x and y faces, respectively. The radius of the circle is (14 + 28)/2 = 21. Corresponding to the 30° plane within the element, it is necessary to rotate through 60° counterclockwise on the circle to locate point A′. A 240° counterclockwise rotation locates point B′. Referring to the circle,

	σx′ = 7 + 21 cos 60° = 17.5 MPa
	σy′ = −3.5 MPa
and	τx′y′ = ± 21 sin 60° = ± 18.19 MPa

Figure 1.15c indicates the orientation of the stresses. The results can be checked by applying Eq. (1.14), using the initial data.

Example 1.5

A thin-walled cylindrical pressure vessel of 250-mm diameter and 5-mm wall thickness is rigidly attached to a wall, forming a cantilever (Fig. 1.16a). Determine the maximum shearing stresses and the associated normal stresses at point A of the cylindrical wall. The following loads are applied: internal pressure p = 1.2 MPa, torque T = 3 kN · m, and direct force P = 20 kN. Show the results on a properly oriented element.

Figure 1.16. Example 1.5. Combined stresses in a thin-walled cylindrical pressure vessel: (a) side view; (b) free body of a segment; (c) and (d) element A (viewed from top).

Solution The internal force resultants on a transverse section through point A are found from the equilibrium conditions of the free-body diagram of Fig. 1.16b. They are V = 20 kN, M = 8 kN · m, and T = 3 kN · m. In Fig. 1.16c, the combined axial, tangential, and shearing stresses are shown acting on a small element at point A. These stresses are (Tables 1.1 and C.1)

We thus have σ_x = 47.6 MPa, σ_y = 30 MPa, and τ_xy = −6.112 MPa. Note that, for element A, Q = 0; hence, the direct shearing stress τ_d = τ_xz = VQ/Ib = 0.

The maximum shearing stresses are, from Eq. (1.18),

Equation (1.19) yields

To locate the maximum shear planes, we use Eq. (1.17):

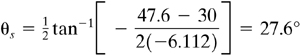and 117.6°

Applying Eq. (1.14b) with the given data and 2θ_s = 55.2°, τ_x′y′ = −10.71 MPa. Hence, , and the stresses are shown in their proper directions in Fig. 1.16d.

1.12 Three-Dimensional Stress at a Point

Equations governing the transformation of stress in the three-dimensional case may be obtained by the use of a similar approach to that used for the two-dimensional state of stress.

Consider a small tetrahedron isolated from a continuous medium (Fig. 1.17a), subject to a general state of stress. The body forces are taken to be negligible. In the figure, p_x, p_y, and p_z are the Cartesian components of stress resultant p acting on oblique plane ABC. It is required to relate the stresses on the perpendicular planes intersecting at the origin to the normal and shear stresses on ABC.

Figure 1.17. Stress components on a tetrahedron.

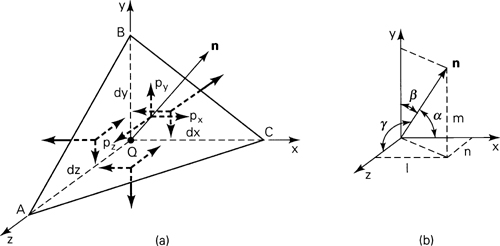
The orientation of plane ABC may be defined in terms of the angles between a unit normal n to the plane and the x, y, and z directions (Fig. 1.17b). The direction cosines associated with these angles are

(1.20)

The three direction cosines for the n direction are related by

(1.21)

The area of the perpendicular plane QAB, QAC, QBC may now be expressed in terms of A, the area of ABC, and the direction cosines:

A_QAB = A_x = A·i = A(li + mj + nk) · i = Al

The other two areas are similarly obtained. In so doing, we have altogether

(a)

Here i, j, and k are unit vectors in the x, y, and z directions, respectively.

Next, from the equilibrium of x, y, z-directed forces together with Eq. (a), we obtain, after canceling A,

(1.22)

The stress resultant on A is thus determined on the basis of known stresses σ_x, σ_y, σ_z, τ_xy, τ_xz and τ_yz and a knowledge of the orientation of A. In the limit as the sides of the tetrahedron approach zero, plane A contains point Q. It is thus demonstrated that the stress resultant at a point is specified. This in turn gives the stress components acting on any three mutually perpendicular planes passing through Q as shown next. Although perpendicular planes have been used there for convenience, these planes need not be perpendicular to define the stress at a point.

Consider now a Cartesian coordinate system x′, y′, z′, wherein x′ coincides with n and y′, z′ lie on an oblique plane. The x′y′z′ and xyz systems are related by the direction cosines: l₁ = cos(x′, x), m₁ = cos(x′, y), and so on. The notation corresponding to a complete set of direction cosines is shown in Table 1.2. The normal stress σ_x′ is found by projecting p_x, p_y, and p_z in the x′ direction and adding:

Table 1.2

(1.23)

Equations (1.22) and (1.23) are combined to yield

(1.24a)

Similarly, by projecting p_x, p_y and p_z in the y′ and z′ directions, we obtain, respectively,

(1.24b)

(1.24c)

Recalling that the stresses on three mutually perpendicular planes are required to specify the stress at a point (one of these planes being the oblique plane in question), the remaining components are found by considering those planes perpendicular to the oblique plane. For one such plane, n would now coincide with the y′ direction, and expressions for the stresses σ_y′, τ_y′x′, and τ_y′z′ would be derived. In a similar manner, the stresses σ_z′, τ_z′x′ and τ_z′y′ are determined when n coincides with the z′ direction. Owing to the symmetry of the stress tensor, only six of the nine stress components thus developed are unique. The remaining stress components are as follows:

(1.24d)

(1.24e)

(1.24f)

Equations (1.24) represent expressions transforming the quantities σ_x, σ_y, σ_z, τ_xy τ_xz and τ_yz, which, as we have noted, completely define the state of stress. Quantities such as stress (and moment of inertia, Appendix C), which are subject to such transformations, are tensors of second rank. Mohr’s circle is thus a graphical representation of a tensor transformation. Equations (1.24) are succinctly expressed by Eq. (A.3).

It is interesting to note that, because x′, y′, and z′ are orthogonal, the nine direction cosines must satisfy trigonometric relations of the following form:

(1.25a)

and

(1.25b)

From Table 1.2, observe that Eqs. (1.25a) are the sums of the squares of the cosines in each row, and Eqs. (1.25b) are the sums of the products of the adjacent cosines in any two rows.

1.13. Principal Stresses in Three Dimensions

For the three-dimensional case, it is now demonstrated that three planes of zero shear stress exist, that these planes are mutually perpendicular, and that on these planes the normal stresses have maximum or minimum values. As has been discussed, these normal stresses are referred to as principal stresses, usually denoted σ₁, σ₂, and σ₃. The algebraically largest stress is represented by σ₁, and the smallest by σ₃.

We begin by again considering an oblique x′ plane. The normal stress acting on this plane is given by Eq. (1.24a):

(a)

The problem at hand is the determination of extreme or stationary values of σ_x′. To accomplish this, we examine the variation of σ_x′ relative to the direction cosines. Inasmuch as l, m, and n are not independent, but connected by l² + m² + n² = 1, only l and m may be regarded as independent variables. Thus,

(b)

Differentiating Eq. (a) as indicated by Eqs. (b) in terms of the quantities in Eq. (1.22), we obtain

(c)

From n² = 1 − l² − m², we have ∂n/∂l = −l/n and ∂n/∂m = −m/n. Introducing these into Eq. (c), the following relationships between the components of p and n are determined:

(d)

These proportionalities indicate that the stress resultant must be parallel to the unit normal and therefore contains no shear component. It is concluded that, on a plane for which σ_x′ has an extreme or principal value, a principal plane, the shearing stress vanishes.

It is now shown that three principal stresses and three principal planes exist. Denoting the principal stresses by σ_p, Eq. (d) may be written as

(e)

These expressions, together with Eq. (1.22), lead to

(1.26)

A nontrivial solution for the direction cosines requires that the characteristic determinant vanish:

(1.27)

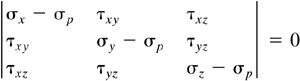
Expanding Eq. (1.27) leads to

(1.28)

where

(1.29a)

(1.29b)

(1.29c)

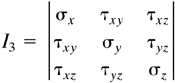
The three roots of the stress cubic equation (1.28) are the principal stresses, corresponding to which are three sets of direction cosines, which establish the relationship of the principal planes to the origin of the nonprincipal axes. The principal stresses are the characteristic values or eigenvalues of the stress tensor τ_ij. Since the stress tensor is a symmetric tensor whose elements are all real, it has real eigenvalues. That is, the three principal stresses are real [Ref. 1.6]. The direction cosines l, m, and n are the eigenvectors of τ_ij.

It is clear that the principal stresses are independent of the orientation of the original coordinate system. It follows from Eq. (1.28) that the coefficients I₁, I₂, and I₃ must likewise be independent of x, y, and z, since otherwise the principal stresses would change. For example, we can demonstrate that adding the expressions for σ_x′, σ_y′, and σ_z′ given by Eq. (1.24) and making use of Eq. (1.25a) leads to I₁ = σ_x′ + σ_y′ + σ_z′ = σ_x + σ_y + σ_z. Thus, the coefficients I₁, I₂, and I₃ represent three invariants of the stress tensor in three dimensions or, briefly, the stress invariants. For plane stress, it is a simple matter to show that the following quantities are invariant (Prob. 1.11):

(1.30)

Equations (1.29) and (1.30) are particularly helpful in checking the results of a stress transformation, as illustrated in Example 1.7.

If now one of the principal stresses, say σ₁ obtained from Eq. (1.28), is substituted into Eq. (1.26), the resulting expressions, together with l² + m² + n² = 1, provide enough information to solve for the direction cosines, thus specifying the orientation of σ₁ relative to the xyz system. The direction cosines of σ₂ and σ₃ are similarly obtained. A convenient way of determining the roots of the stress cubic equation and solving for the direction cosines is presented in Appendix B, where a related computer program is also included (see Table B.1).

Example 1.6

A steel shaft is to be force fitted into a fixed-ended cast-iron hub. The shaft is subjected to a bending moment M, a torque T, and a vertical force P, Fig. 1.18a. Suppose that at a point Q in the hub, the stress field is as shown in Fig. 1.18b, represented by the matrix

Figure 1.18. Example 1.6.

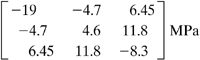
Determine the principal stresses and their orientation with respect to the original coordinate system.

Solution Substituting the given stresses into Eq. (1.28) we obtain from Eqs. (B.2)

σ₁ = 11.618MPa, σ₂ = −9.001 MPa, σ₃ = −25.316 MPa

Successive introduction of these values into Eq. (1.26), together with Eq. (1.25a), or application of Eqs. (B.6) yields the direction cosines that define the orientation of the planes on which σ₁, σ₂, and σ₃ act:

l1 = 0.0266,	l2 = −0.6209,	l3 = 0.7834
m1 = −0.8638,	m2 = 0.3802,	m3 = 0.3306
n1 = −0.5031,	n2 = −0.6855,	n3 = −0.5262

Note that the directions of the principal stresses are seldom required for purposes of predicting the behavior of structural members.

Example 1.7

The stress tensor at a point in a machine element with respect to a Cartesian coordinate system is given by the following array:

(f)

Determine the state of stress and I₁, I₂, and I₃ for an x′, y′, z′ coordinate system defined by rotating x, y through an angle of θ = 45° counterclockwise about the z axis (Fig. 1.19a).

Figure 1.19. Example 1.7.

Solution The direction cosines corresponding to the prescribed rotation of axes are given in Fig. 1.19b. Thus, through the use of Eq. (1.24) we obtain

(g)

It is seen that the arrays (f) and (g), when substituted into Eq. (1.29), both yield I₁ = 100 MPa, I₂ = 1400 (MPa)², and I₃ = −53,000 (MPa)³, and the invariance of I₁, I₂, and I₃ under the orthogonal transformation is confirmed.

1.14 Normal and Shear Stresses on an Oblique Plane

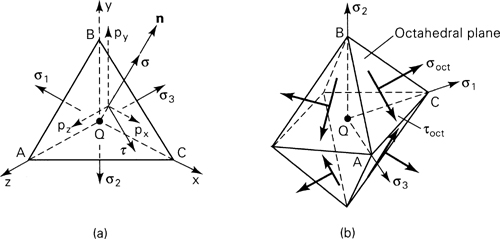
It is sometimes required to determine the shearing and normal stresses acting on an arbitrary oblique plane of a tetrahedron, as in Fig. 1.20a, given the principal stresses or triaxial stresses acting on perpendicular planes. In the figure, the x, y, and z axes are parallel to the principal axes. Denoting the direction cosines of plane ABC by l, m, and n, Eqs. (1.22) with σ_x = σ₁, τ_xy = τ_xz = 0, and so on, reduce to

Figure 1.20. (a) Element in triaxial stress; (b) stresses on an octahedron.

(a)

Referring to Fig. 1.20a and definitions (a), the stress resultant p is related to the principal stresses and the stress components on the oblique plane by the expression

(1.31)

The normal stress σ on this plane, from Eq. (1.24a), is found as

(1.32)

Substitution of this expression into Eq. (1.31) leads to

(1.33)

Expanding and using the expressions 1 − l² = m² + n², 1 − n² = l² + m², and so on, the following result is obtained for the shearing stress τ on the oblique plane:

(1.34)

This clearly indicates that if the principal stresses are all equal the shear stress vanishes, regardless of the choices of the direction cosines.

For situations in which shear as well as normal stresses act on perpendicular planes (Fig. 1.20a), we have p_x, p_y, and p_z defined by Eqs. (1.22). Then, Eq. (1.32) becomes

(1.35)

Hence,

(1.36)

where σ is given by Eq. (1.35). Formulas (1.32) through (1.36) represent the simplified transformation expressions for the three-dimensional stress.

It is interesting to note that substitution of the direction cosines from Eqs. (a) into Eq. (1.21) leads to

(1.37)

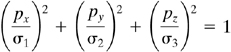
which is a stress ellipsoid having its three semiaxes as the principal stresses (Fig. 1.21). This geometrical interpretation helps to explain the earlier conclusion that the principal stresses are the extreme values of the normal stress. In the event that σ₁ = σ₂ = σ₃, a state of hydrostatic stress exists, and the stress ellipsoid becomes a sphere. In this case, note again that any three mutually perpendicular axes can be taken as the principal axes.

Figure 1.21. Stress ellipsoid.

Example 1.8

Determine the stresses acting on a plane of particular importance in failure theory, represented by face ABC in Fig. 1.20a with QA = QB = QC.

Solution The normal to this oblique face thus has equal direction cosines relative to the principal axes. Since l² + m² + n² = 1, we have

(b)

Plane ABC is clearly one of eight such faces of a regular octahedron (Fig. 1.20b). Equations (1.34) and (b) are now applied to provide an expression for the octahedral shearing stress, which may be rearranged to the form

(1.38)

Through the use of Eqs. (1.32) and (b), we obtain

(1.39)

The normal stress acting on an octahedral plane is thus the average of the principal stresses, the mean stress. The orientations of σ_oct and τ_oct are indicated in Fig. 1.20b. Another useful form of Eq. (1.38) is developed in Sec. 2.13.

1.15 Mohr’s Circle for Three-Dimensional Stress

It has been demonstrated that, given the magnitudes of the direction cosines of the principal stresses, the stresses on any oblique plane may be ascertained through the application of Eqs. (1.32) and (1.34). This may also be accomplished by means of a graphical technique due to Mohr, in which the aforementioned equations are represented by three circles of stress [Refs. 1.7 and 1.8]. In stress analysis, Mohr’s circles in three dimensions have great utility as a heuristic device. Inasmuch as all stresses in their various transformations may play a role in causing either yield or fracture of a material, it is often instructive to plot these circles.

Consider the element shown in Fig. 1.22a, resulting from the cutting of a small cube by an oblique plane. The element is subjected to principal stresses σ₁, σ₂, and σ₃ represented as coordinate axes with the origin at Q. We are interested in determining the normal and shear stresses acting at point G on the slant face (plane abcd). This plane is oriented so as to be tangent at G to a quadrant of a spherical surface inscribed within a cubic element as shown. Note that QG, running from the origin of the principal axis system to point G, is the line of intersection of the shaded planes (Fig. 1.22a), the inclination of plane QA₂GB₃ relative to the σ₁ axis is given by the angle θ (measured in the σ₁, σ₂ plane), and that of plane QA₃GB₁, by the angle ϕ (measured in the σ₁, σ₂ plane). Circular arcs A₁B₁A₂ and A₁B₃A₃ are located on the cube faces. It is clear that angles θ and ϕ unambiguously define the orientation of QG with respect to the principal axes.

Figure 1.22. (a) Element in triaxial stress; (b) Mohr’s circles for triaxial stress.

To determine σ and τ given σ₁, σ₂, σ₃, the following procedure is applied (refer to Fig. 1.22b):

1. Establish a Cartesian coordinate system, indicating +σ and +τ as shown. Lay off the principal stresses (to scale) along the σ axis, with σ₁ > σ₂ > σ₃ (algebraically).

2. Draw three Mohr semicircles centered at C₁, C₂, and C₃ (referred to as circles c₁, c₂, c₃) with diameters A₁A₂, A₂A₃, and A₁A₃.

3. At point C₁ draw line C₁B₁ at angle 2ϕ; at C₃, draw C₃B₃ at angle 2ϕ. These lines cut circles c₁ and c₃ at points B₁ and B₃, respectively.

4. By trial and error, draw arcs through points A₃ and B₁ and through A₂ and B₃, with their centers on the σ axis. The intersection of these arcs locates point G on the σ, τ plane.

In connection with the foregoing construction, several points are of particular interest:

a. Point G will be located within the shaded area or along the circumference of circles c₁, c₂, or c₃, for all combinations of θ and ϕ.

b. For the particular case θ = ϕ = 0, G coincides with A₁ in Fig. 1.22a and b.

c. For the case θ = 45° and ϕ = 0°, the shearing stress is a maximum located as the highest point on circle c₃ (2θ = 90°). The value of the maximum shearing stress is therefore

(1.40)

acting on the planes bisecting the planes of maximum and minimum principal stress, as indicated in Fig. 1.23. It is noted that the planes of maximum shear may also be ascertained by substituting n² = 1 − l² − m² into Eq. (1.33), differentiating with respect to l and m, and equating the resulting expressions to zero (Prob. 1.61).

Figure 1.23. Planes of maximum shearing stress.

d. For θ = ϕ = 45°, line QG will make equal angles with the principal axes. The oblique plane is, in this case, an octahedral plane, and the stresses acting on the plane, the octahedral stresses. Recall that Eqs. (1.38) and (1.39) provide algebraic expressions for these stresses.

Example 1.9

Given the state of stress described in Fig. 1.24a, use Mohr’s circle to determine (a) the principal stresses, and (b) the octahedral and maximum shearing stresses.

Figure 1.24. Example 1.9.

Solution

a. First, Mohr’s circle for the transformation of stress in the xy plane is sketched in the usual manner as shown, centered at C₂ with diameter A₂A₃ (Fig. 1.24b). Next, we complete the three-dimensional Mohr’s circle by drawing two additional semicircles of diameters A₁A₂ and A₁A₃ in the figure. Referring to the circle, the principal stresses are σ₁ = 100 MPa, σ₂ = 40 MPa, and σ₃ = −60MPa. Angle , as tan . The results are sketched on a properly oriented element in Fig. 1.24c.

b. Now, applying steps 3 and 4 of the general procedure given for θ = ϕ = 45°, the octahedral stresses are obtained graphically (Fig. 1.24b):

σ_oct = 26.7 MPa, τ_oct = 66 MPa

Note that, from Eqs. (1.39) and (1.38), we can readily calculate these stresses as 26.67 and 66 MPa, respectively.

The maximum shearing stress, point B₃, equals the radius of circle c₃ of diameter A₁A₃. Thus,

The maximum shearing stresses occur on the planes 45° from the y′ and z faces of the element of Fig. 1.24c.

1.16. Boundary Conditions in Terms of Surface Forces

We now consider the relationship between the stress components and the given surface forces acting on the boundary of a body. The equations of equilibrium that must be satisfied within a body are derived in Sec. 1.8. The distribution of stress in a body must also be such as to accommodate the conditions of equilibrium with respect to externally applied forces. The external forces may thus be regarded as a continuation of the internal stress distribution.

Consider the equilibrium of the forces acting on the tetrahedron shown in Fig. 1.17a, and assume that oblique face ABC is coincident with the surface of the body. The components of the stress resultant p are thus now the surface forces per unit area, or surface tractions, p_x, p_y, and p_z. The equations of equilibrium for this element, representing boundary conditions, are, from Eqs. (1.22),

(1.41)

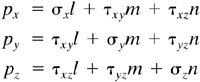
For example, if the boundary is a plane with an x-directed surface normal, Eqs. (1.41) give p_x = σ_x, p_y = τ_xy, and p_z = τ_xz; under these circumstances, the applied surface force components p_x, p_y, and p_z are balanced by σ_x, τ_xy, and τ_xz, respectively.

It is of interest to note that, instead of prescribing the distribution of surface forces on the boundary, the boundary conditions of a body may also be given in terms of displacement components. Furthermore, we may be given boundary conditions that prescribe surface forces on one part of the boundary and displacements on another. When displacement boundary conditions are given, the equations of equilibrium express the situation in terms of strain, through the use of Hooke’s law and subsequently in terms of the displacements by means of strain–displacement relations (Sec. 2.3). It is usual in engineering problems, however, to specify the boundary conditions in terms of surface forces as in Eq. (1.41), rather than surface displacements. This practice is adhered to in this text.

Problems

Secs. 1.1 through 1.8

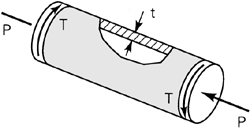
1.1. Two prismatic bars of 50 mm by 75 mm rectangular cross section are glued as shown in Fig. P1.1. The allowable normal and shearing stresses for the glued joint are 700 and 560 kPa, respectively. Assuming that the strength of the joint controls the design, what is the largest axial load P that may be applied?

Figure P1.1.

1.2. A prismatic steel bar of 50-mm by 50-mm square cross section is subjected to an axial tensile load P = 125 kN (Fig. 1.5a). Calculate the normal and shearing stresses on all faces of an element oriented at (a) θ = 20°, and θ = 45°.

1.3. A prismatic bar is under an axial load, producing a compressive stress of 75 MPa on a plane at an angle θ = 30° (Fig. P1.3). Determine the normal and shearing stresses on all faces of an element at an angle of θ = 50°.

Figure P1.3.

1.4. A square prismatic bar of 1300-mm² cross-sectional area is composed of two pieces of wood glued together along the x′ plane, which makes an angle θ with the axial direction (Fig. 1.5a). The normal and shearing stresses acting simultaneously on the joint are limited to 20 and 10 MPa, respectively, and on the bar itself, to 56 and 28 MPa, respectively. Determine the maximum allowable axial load that the bar can carry and the corresponding value of the angle θ.

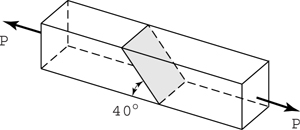
1.5. A cylindrical pipe of 160-mm outside diameter and 10-mm thickness, spirally welded at an angle of ϕ = 40° with the axial (x) direction, is subjected to an axial compressive load of P = 150 kN through the rigid end plates (Fig. P1.5). Determine the normal σ_x′ and shearing stresses τ_{x′ y′} acting simultaneously in the plane of the weld.

Figure P1.5.

1.6. The following describes the stress distribution in a body (in megapascals):

σx = x2 + 2y,	σy = xy − y2z,	τxy = − xy2 + 1
τyz = 0,	τxz = xz −2x2y,	σz = x2 − z2

Determine the body force distribution required for equilibrium and the magnitude of its resultant at the point x = −10 mm, y = 30 mm, z = 60 mm.

1.7. Given zero body forces, determine whether the following stress distribution can exist for a body in equilibrium:

σx = −2c1xy,	σy = c2z2,	σz = 0
τxy = c1(c2 − y2) + c3xz,	τxy = −c3y,	τyz = 0

Here the c’s are constants.

1.8. Determine whether the following stress fields are possible within an elastic structural member in equilibrium:

(a) 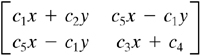, (b)

The c’s are constant, and it is assumed that the body forces are negligible.

1.9. For what body forces will the following stress field describe a state of equilibrium?

σx = −2x2 + 3y2 − 5z,	τxy = z + 4xy − 7
σy = −2y2,	τxz = −3x + y + 1
σz = 3x + y + 3z − 5,	τyz = 0

Secs. 1.9 through 1.11

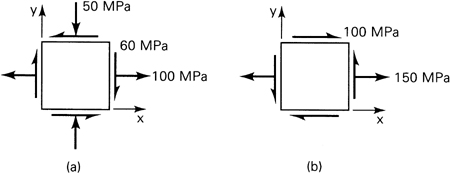
1.10. The states of stress at two points in a loaded beam are represented in Fig. P1.10a and b. Determine the following for each point: (a) The magnitude of the maximum and minimum principal stresses and the maximum shearing stress; use Mohr’s circle. (b) The orientation of the principal and maximum shear planes; use Mohr’s circle. (c) Sketch the results on properly oriented elements. Check the values found in (a) and (b) by applying the appropriate equations.

Figure P1.10.

1.11. By means of Mohr’s circle, verify the results given by Eqs. (1.30).

1.12. An element in plane stress (Fig. 1.3b) is subjected to stresses σ_x = 50MPa, σ_y = −190 MPa, and τ_xy = −70MPa. Determine the principal stresses and show them on a sketch of a properly oriented element.

1.13. For an element in plane stress (Fig. 1.3b) the normal stresses are σ_x = 60 MPa and σ_y = −100 MPa. What is the maximum permissible value of shearing stress τ_xy if the shearing stress in the material is not to exceed 140 MPa?

1.14. The state of stress on an element oriented at θ = 60° is shown in Fig. P1.14. Calculate the normal and shearing stresses on an element oriented at θ = 0°.

Figure P1.14.

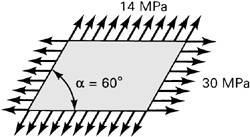
1.15. A thin skewed plate is subjected to a uniform distribution of stress along its sides as shown in Fig. P1.15. Calculate (a) the stresses σ_x, σ_y, τ_xy, and (b) the principal stresses and their orientations.

Figure P1.15.

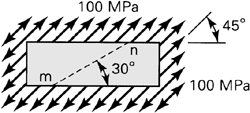
1.16. The stress acting uniformly over the sides of a rectangular block is shown in Fig. P1.16. Calculate the stress components on planes parallel and perpendicular to mn. Show the results on a properly oriented element.

Figure P1.16.

1.17. Redo Prob. 1.15 for the stress distribution shown in Fig. P1.17.

Figure P1.17.

1.18. A thin-walled cylindrical tank of radius r is subjected simultaneously to internal pressure p and a compressive force P through rigid end plates. Determine the magnitude of force P to produce pure shear in the cylindrical wall.

1.19. A thin-walled cylindrical pressure vessel of radius 120 mm and a wall thickness of 5 mm is subjected to an internal pressure of p = 4 MPa. In addition, an axial compression load of P = 30π kN and a torque of T = 10π kN · m are applied to the vessel through the rigid end plates (Fig. P1.19). Determine the maximum shearing stresses and associated normal stresses in the cylindrical wall. Show the results on a properly oriented element.

Figure P1.19.

1.20. A pressurized thin-walled cylindrical tank of radius r = 60 mm and wall thickness t = 4 mm is acted on by end torques T = 600 N · m and tensile forces P (Fig. P1.19 with sense of P reversed). The internal pressure is p = 5 MPa. Calculate the maximum permissible value of P if the allowable tensile stress in the cylinder wall is 80 MPa.

1.21. A hollow generator shaft of 180-mm outer diameter and 120-mm inner diameter carries simultaneously a torque T = 20 kN · m and axial compressive load P = 700 kN. What is the maximum tensile stress?

1.22. A cantilever beam of thickness t is subjected to a constant traction τ₀ (force per unit area) at its upper surface as shown in Fig. P1.22. determine, in terms of τ₀, h, and L, the principal stresses and the maximum shearing stress at the corner points A and B.

Figure P1.22.

1.23. A hollow shaft of 60-mm outer diameter and 30-mm inner diameter is acted on by an axial tensile load of 50 kN, a torque of 500 N · m, and a bending moment of 200 N · m. Use Mohr’s circle to determine the principal stresses and their directions.

1.24. Given the stress acting uniformly over the sides of a thin flat plate (Fig. P1.24), determine (a) the stresses on planes inclined at 20° to the horizontal and (b) the principal stresses and their orientations.

Figure P1.24.

1.25. A steel shaft of radius r = 75 mm is subjected to an axial compression P = 81 kN, a twisting couple T = 15.6 kN · m, and a bending moment M = 13 kN · m at both ends. Calculate the magnitude of the principal stresses, the maximum shear stress, and the planes on which they act in the shaft.

1.26. A structural member is subjected to a set of forces and moments. Each separately produces the stress conditions at a point shown in Fig. P1.26. Determine the principal stresses and their orientations at the point under the effect of combined loading.

Figure P1.26.

1.27. Redo Prob. 1.26 for the case shown in Fig. P1.27.

Figure P1.27.

1.28. Redo Prob. 1.26 for the case shown in Fig. P1.28.

Figure P1.28.

1.29. The shearing stress at a point in a loaded structure is τ_xy = 40 MPa. Also, it is known that the principal stresses at this point are σ₁ = 40 MPa and σ₂ = −60 MPa. Determine σ_x (compression) and σ_y and indicate the principal and maximum shearing stresses on an appropriate sketch.

1.30. Acting at a point on a horizontal plane in a loaded machine part are normal stress σ_y = 20 MPa and a (negative) shearing stress. One principal stress at the point is 10 MPa (tensile), and the maximum shearing stress is of magnitude 50 MPa. Find, by the use of Mohr’s circle, (a) the unknown stresses on the horizontal and vertical planes and (b) the unknown principal stress. Show the principal stresses on a sketch of a properly oriented element.

1.31. For a state of stress at a point in a structure, certain stress components are given for each of the two orientations (Fig. P1.31). Applying transformation equations, calculate stress components σ_y′ and τ_{x′ y′} and the angle θ₁ between zero and 90°.

Figure P1.31.

1.32. A solid shaft 200 mm in diameter rotates at f = 20 rps and is subjected to a bending moment of 21π kN · m. Determine the torque T and power P than can also act simultaneously on the shaft without exceeding a resultant shearing stress of 56 MPa and a resultant normal stress of 98 MPa. (With f expressed in rps and torque in N · m, P = 2πf · T in watts.)

1.33. The cylindrical portion of a compressed-air tank is made of 5-mm-thick plate welded along a helix at an angle of ϕ = 60° with the axial direction (Fig. P1.33). The radius of the tank is 250 mm. If the allowable shearing stress parallel to the weld is 30 MPa, calculate the largest internal pressure p that may be applied.

Figure P1.33.

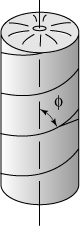
1.34. A thin-walled cylindrical tank is subjected to an internal pressure p and uniform axial tensile load P (Fig. P1.34). The radius and thickness of the tank are r = 0.45 m and t = 5 mm. The normal stresses at a point A on the surface of the tank are restricted to σ_x′ = 84 MPa and σ_y′ = 56 MPa, while shearing stress τ_{x′ y′} is not specified. Determine the values of p and P. Use θ = 30°.

Figure P1.34.

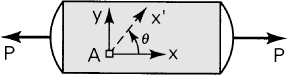
1.35. For a given state of stress at a point in a frame, certain stress components are known for each of the two orientations shown in Fig. P1.35. Using Mohr′s circle, determine the following stress components: (a) τ_xy and (b) τ_{x′ y′} and σ_y′.

Figure P1.35.

1.36. The state of stress at a point in a machine member is shown in Fig. P1.36. The allowable compression stress at the point is 14 MPa. Determine (a) the tensile stress σ_x and (b) the maximum principal and maximum shearing stresses in the member. Sketch the results on properly oriented elements.

Figure P1.36.

1.37. In Example 1.3, taking σ_Z = 0, investigate the maximum shearing stresses on all possible (three-dimensional) planes.

1.38. A thin-walled pressure vessel of 60-mm radius and 4-mm thickness is made from spirally welded pipe and fitted with two rigid end plates (Fig. P1.38). The vessel is subjected to an internal pressure of p = 2 MPa and a P = 50 kN axial load. Calculate (a) the normal stress perpendicular to the weld; (b) the shearing stress parallel to the weld.

Figure P1.38.

1.39. A thin-walled cylindrical pressure vessel of 0.3-m radius and 6-mm wall thickness has a welded spiral seam at an angle of ϕ = 30° with the axial direction (Fig. P1.5). The vessel is subjected to an internal gage pressure of p Pa and an axial compressive load of P = 9π kN applied through rigid end plates. Find the allowable value of p if the normal and shearing stresses acting simultaneously in the plane of welding are limited to 21 and 7 MPa, respectively.

Secs. 1.12 and 1.13

1.40. The state of stress at a point in an x, y, z coordinate system is

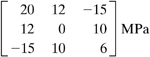
Determine the stresses and stress invariants relative to the x′, y′, z′ coordinate system defined by rotating x, y through an angle of 30° counterclockwise about the z axis.

1.41. Redo Prob. 1.40 for the case in which the state of stress at a point in an x, y, z coordinate system is

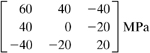
1.42. The state of stress at a point relative to an x, y, z coordinate system is given by

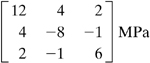
Calculate the maximum shearing stress at the point.

1.43. At a point in a loaded member, the stresses relative to an x, y, z coordinate system are given by

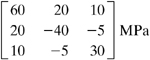
Calculate the magnitude and direction of maximum principal stress.

1.44. For the stresses given in Prob. 1.40, calculate the maximum shearing stress.

1.45. At a specified point in a member, the state of stress with respect to a Cartesian coordinate system is given by

Calculate the magnitude and direction of the maximum principal stress.

1.46. At a point in a loaded structure, the stresses relative to an x, y, z coordinate system are given by

Determine by expanding the characteristic stress determinant: (a) the principal stresses; (b) the direction cosines of the maximum principal stress.

1.47. The stresses (in megapascals) with respect to an x, y, z coordinate system are described by

At point (3, 1, 5), determine (a) the stress components with respect to x′, y′, z′ if

l₁ = 1, , , ,

and (b) the stress components with respect to x″, y″, z″ if , , and n₃ = 1. Show that the quantities given by Eq. (1.29) are invariant under the transformations (a) and (b).

1.48. Determine the stresses with respect to the x′, y′, z′ axes in the element of Prob. 1.45 if

,	,	l3 = 0
,	m2 = ,	m3 = 0
n1 = 0,	n2 = 0,	n3 = 1

1.49. For the case of plane stress, verify that Eq. (1.28) reduces to Eq. (1.16).

1.50. Obtain the principal stresses and the related direction cosines for the following cases:

(a) , (b)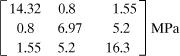

Secs. 1.14 through 1.16

1.51. The stress at a point in a machine component relative to an x, y, z coordinate system is given by

Referring to the parallelepiped shown in Fig. P1.51, calculate the normal stress σ and the shear stress τ at point Q for the surface parallel to the following planes: (a) CEBG, (b) ABEF, (c) AEG. [Hint: The position vectors of points G, E, A and any point on plane AEG are, respectively, r_g = 3i, r_e = 4j, r_a = 2k, r = xi + yj + zk. The equation of the plane is given by

(P1.51)

Figure P1.51.

from which

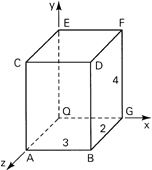
The direction cosines are then

1.52. Re-solve Prob. 1.51 for the case in which the dimensions of the parallelepiped are as shown in Fig. P1.52.

Figure P1.52.

1.53. The state of stress at a point in a member relative to an x, y, z coordinate system is

Determine the normal stress σ and the shearing stress τ on the surface intersecting the point and parallel to the plane: 2x + y − 3z = 9.

1.54. For the stresses given in Prob. 1.43, calculate the normal stress σ and the shearing stress τ on a plane whose outward normal is oriented at angles 35°, 60°, and 73.6° with the x, y, and z axes, respectively.

1.55. At a point in a loaded body, the stresses relative to an x, y, z coordinate system are

Determine the normal stress σ and the shearing stress τ on a plane whose outward normal is oriented at angles of 40°, 75°, and 54° with the x, y, and z axes, respectively.

1.56. Determine the magnitude and direction of the maximum shearing stress for the cases given in Prob. 1.50.

1.57. The stresses at a point in a loaded machine bracket with respect to the x, y, z axes are given as

Determine (a) the octahedral stresses; (b) the maximum shearing stresses.

1.58. The state of stress at a point in a member relative to an x, y, z coordinate system is given by

Calculate (a) the principal stresses by expansion of the characteristic stress determinant; (b) the octahedral stresses and the maximum shearing stress.

1.59. Given the principal stresses σ₁, σ₂, and σ₃ at a point in an elastic solid, prove that the maximum shearing stress at the point always exceeds the octahedral shearing stress.

1.60. Determine the value of the octahedral stresses of Prob. 1.45.

1.61. By using Eq. (1.33), verify that the planes of maximum shearing stress in three dimensions bisect the planes of maximum and minimum principal stresses. Also find the normal stresses associated with the shearing plane by applying Eq. (1.32).

1.62. Consider a point in a loaded body subjected to the stress field (megapascals) represented in Fig. P1.62. Determine, using only Mohr’s circle, (a) the principal stresses and their orientation with respect to the original system and (b) the normal and shear stresses on an oblique plane defined by θ = 30° and ϕ = 60°.

Figure P1.62.

1.63. Re-solve Prob. 1.62 for the case of a point in a loaded body subjected to the following nonzero stress components: σ_x = 80 MPa, σ_z = − 60 MPa, and τ_xy = 40 MPa.

1.64. The state of stress at a point in a loaded structure is represented in Fig. P1.64. Determine (a) the principal stresses; (b) the octahedral stresses and maximum shearing stress.

Figure P1.64.

1.65. The principal stresses at a point in a structural member are σ₁ = 20 MPa, σ₂ = 15 MPa, and σ₃ = −10 MPa. Use Mohr’s circle to determine the normal and shear stresses on an inclined plane defined by θ = 45° and ϕ = 60°.

1.66. The principal stresses at a point in a solid are σ₁ = 56 MPa, σ₂ = 35 MPa, and σ₃ = 14 MPa. Using Mohr’s circle, obtain (a) the maximum shearing stress and (b) the normal and shearing stresses on the octahedral planes.

1.67. Employ Mohr’s circle to find the normal and shearing stresses on an oblique plane defined by θ = 60° and ϕ = 30°. The principal stresses are σ₁ = 35 MPa, σ₂ = −14 MPa, and σ₃ = −28 MPa. Apply Eqs. (1.32) and (1.34) to check the values thus determined. If this plane is on the boundary of a structural member, what should be the values of surface forces, p_x, p_y, and p_x on the plane?

1.68. Redo Prob. 1.67 for θ = ϕ = 45°, σ₁ = 40MPa, σ₂ = 15 MPa, and σ₃ = 25 MPa.