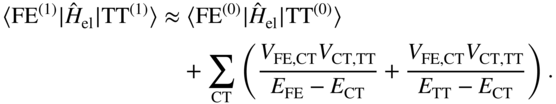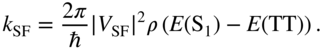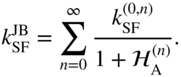Electronic Structure and Dynamics of Singlet Fission in Organic Molecules and Crystals
Timothy C. Berkelbach
Department of Chemistry and The James Franck Institute, The University of Chicago, Chicago, IL, 60637, USA
Contents
- I. Introduction
- II. Electronic Structure of Low-Lying Excited States
- III. Measuring Charge-Transfer Character
- IV. Charge-Transfer Implications for Singlet Fission
- V. Theory of Spectroscopy, Reaction Rates, and Singlet Fission Dynamics
- VI. Conclusions and Outlook
- Acknowledgments
- References
I. Introduction
Classic work has laid the foundation for our modern understanding of molecular excitons [1–6]. In this sense, much of the phenomenological theory is quite mature and leads to a satisfactory understanding of electronic interactions, as well as the important role played by molecular vibrations and crystalline phonons. And yet, these materials continue to provide fertile ground for new research, which is perhaps a testament to their genuinely complex optoelectronic properties. In general, this chapter is concerned with the renewed interest in a photophysical phenomenon known as singlet exciton fission (defined in the following). The recent intense study of this specific problem has prompted the field to revisit classic topics with modern tools and motivations.
On the experimental side, ultrafast time-resolved and nonlinear spectroscopies in particular have allowed for a richer and more detailed understanding of excited-state dynamics in a host of material systems, including not only organic molecules and crystals but of course also gas-phase molecules, liquids, nanocrystals, and light-harvesting complexes. On the theoretical side, modern computational tools are enabling predictive calculations that can in some cases supersede the semiempirical and phenomenological calculations that were necessarily employed to establish the field. Time-dependent density functional theory (TD-DFT) [7, 8], Green's function-based many-body perturbation theory [9, 10], and the density matrix renormalization group [11, 12] are just three examples of relatively new and powerful tools that are being brought to bear on the electronic structure of organic molecules and crystals. Techniques and capabilities of quantum dynamics, in particular related to reduced density matrix techniques, have also only more recently evolved to produce nonperturbative results for large, multichromophore systems.
The recent interest in organic materials in particular has been driven by a number of potential applications including organic solar cells, light-emitting diodes, and field-effect transistors. From a practical point of view, the advantages of organic materials are twofold. First, the raw materials are cheap and robust, ideally requiring no heavy atoms or special handling. Second, chemical functionalization is mature and should enable for precise control of structural, electronic, and optical properties. Although these advantages have always been recognized, it is only in recent years that such materials have really been employed in consumer technologies. Most relevant, the pressing need for clean energy has encouraged new efforts toward cheap and efficient solar cells. The organic-based solar cells have always trailed their inorganic counterparts in efficiency (admittedly, at lower cost), but “unconventional” light-harvesting technologies might help close that gap. In this vein, the phenomenon of singlet exciton fission has captured the attention of many scientists.
Singlet exciton fission (henceforth, “singlet fission”) is a version of carrier multiplication or multiple exciton generation but is unique to the organic semiconductors. Unlike the inorganic semiconductors, organics exhibit a large electron–hole exchange interaction, which is responsible for low-energy triplet states. In a single molecule, the transition from an excited singlet state to a triplet state is spin-forbidden (intersystem crossing) and, therefore, slow unless mediated by strong spin–orbit interactions. However, when two molecules are brought together, a new spin-singlet state is born, which has the character of a triplet excited state on each molecule – that is, it is a multiexciton state. This multiple-excitation character leads to a small oscillator strength and so the state is spectroscopically dark (in linear order). But for sufficiently low-energy triplets, the multiexciton energy may fall within the manifold of low-lying bright singlets and configuration interaction (CI) coupled with nuclear rearrangements could act to populate the multiexciton state following photoexcitation.
Because all involved states are of spin-singlet character, there is reason to believe that the singlet fission process could be fast (compared with fluorescence, intersystem crossing, and other nonradiative recombination mechanisms). If, on a longer timescale, this multiexciton singlet state evolves into some (non-spin-pure) state representing separated triplets, then multiple exciton generation has been achieved: a single photon has produced two (triplet) excitons. With an appropriate tandem or sensitization strategy, singlet fission can improve solar cell efficiencies and even (in principle) surpass the Shockley–Queisser limit [13–15].
The possibility of singlet fission was first discussed in 1965, by Singh et al., while investigating the delayed fluorescence of anthracene [16]. The suggestion was motivated as the reverse process of triplet-triplet (TT) annihilation to generate emissive singlets, which had been recently observed and investigated [17–19]. A few years later in 1968, Swenberg and Stacy invoked singlet fission to explain the quenched fluorescence yield in tetracene crystals [20]. Even in this very early proposition, the authors recognized the potential importance of the so-called charge-transfer (CT) configurations, which had only recently been highlighted in the context of molecular crystals by Rice et al. [2, 21, 22]. Borrowing their theoretical estimates of the relevant matrix elements, energy differences, and the density of states, Swenberg and Stacy performed a golden rule evaluation of the singlet fission rate and found ![]() –
–![]() s
s![]() or
or ![]() –25 ps. This timescale is significantly shorter than the fluorescence lifetime of the smaller acenes and thus gave credence to the notion that singlet fission was the dominant relaxation pathway for photoexcited singlet excited states in tetracene (ultrafast time-resolved spectroscopy would later show the singlet fission time constant in tetracene to be on the order of 10–100 ps [23–26]). The singlet fission proposal would quickly be verified via magnetic field effects, which unambiguously implicate intermediate triplet states [27, 28]. Subsequent theoretical work was focused on kinetic models of the process, including the interplay between singlet fission, triplet diffusion, and pairwise annihilation [29, 30].
–25 ps. This timescale is significantly shorter than the fluorescence lifetime of the smaller acenes and thus gave credence to the notion that singlet fission was the dominant relaxation pathway for photoexcited singlet excited states in tetracene (ultrafast time-resolved spectroscopy would later show the singlet fission time constant in tetracene to be on the order of 10–100 ps [23–26]). The singlet fission proposal would quickly be verified via magnetic field effects, which unambiguously implicate intermediate triplet states [27, 28]. Subsequent theoretical work was focused on kinetic models of the process, including the interplay between singlet fission, triplet diffusion, and pairwise annihilation [29, 30].
As discussed earlier, singlet fission was largely forgotten for 35 years until it was revived in the context of solar energy conversion [14, 31]. The subsequent 10 years, and especially the most recent 5 years, have seen a flurry of activity aimed at the investigation and characterization of various singlet fission materials. In general, materials systems of interest can be broken up into covalently bound dimers [32–37], thin films, and single crystals [12, 24, 25, 38–42], and more recently into solution [43], polymers [44, 45], and nanocrystals [46].
Although I will occasionally make reference to recent experiments, this chapter is about the theoretical and computational description of excitons and their dynamics, in organic molecules and crystals with a focus on singlet fission in the oligoacenes. More specifically, this work aims to connect theoretical results published over many years and in many different fields. Ultimately, I hope to demonstrate a (perhaps surprising) degree of consistency and harmony, the recognition and understanding of which should help advance the field toward new and challenging problems. A number of other reviews on singlet fission have recently appeared, which are less theoretically oriented than the present one [15, 47–49].
The layout of the chapter is as follows. First in Section II, I introduce the weak-coupling CI theory of low-lying states in organic molecules such as the oligoacenes and make connections to more accurate computational techniques. This overview establishes the electronic structure language relevant for singlet fission and introduces the notion of CT configurations, whose importance was recognized very early on in the field of molecular excitons. In Section III, I discuss the difficulties and techniques associated with the quantification of CT character in low-lying excited states. Having established the generic presence of CT states, I discuss the implications for singlet fission in Section IV. This leads to a discussion of reaction rates and more general singlet fission dynamics in Section V, before concluding in Section VI.
II. Electronic Structure of Low-Lying Excited States
Organic molecular crystals inherit their properties from their molecular constituents; therefore, most are conventional band insulators with ground states that are stable against symmetry breaking. Nonetheless, the electronic structure of the single-molecule ground state can be shockingly complex, especially for the longer oligoacenes. In particular, strong electronic correlation in the valence orbitals leads to a nontrivial multireference ground state with an increasing biradical (or even polyradical) character [50, 51]. These correlations extend to the low-lying excited states, where competing interactions lead to nearly degenerate states with mixed electronic character – that is, excitons.
The notion of excitons as a genuine quasiparticle originated in the field of inorganic semiconductors and evolved to describe any excited state where the Coulombic electron–hole interaction yields states that are significantly lower in energy than that of a noninteracting electron–hole pair. This behavior is almost trivially relevant in single molecules, where the difference between the ionization potential (IP) and the electron affinity (EA) is typically many electronvolts larger than the first few peaks in linear absorption. More interesting and rich behavior emerges when multiple molecules are brought together to form dimers, aggregates, and molecular crystals. In this case, the favorable kinetic energy due to charge delocalization competes with the potential energy of electron–hole localization. The excited-state properties can thus be very complex, depending on the strong intramolecular electron correlation as well as the intermolecular interactions and environmental effects, such as dielectric properties and crystal polymorphism. In terms of their optoelectronic properties, molecular crystals are, therefore, intermediate between small single molecules and conventional inorganic semiconductors. For reference, Fig. 1 shows the four-ring oligoacene (tetracene) as a single molecule and in the herringbone crystal structure that is typical of all the oligoacenes.
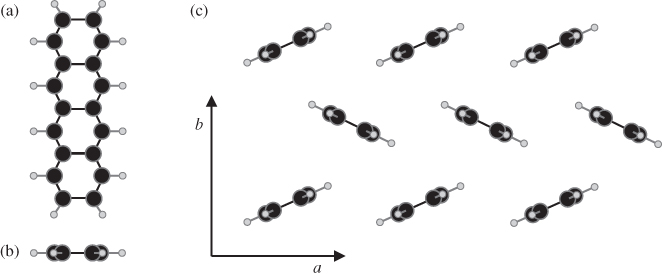
Figure 1 The prototypical herringbone crystal structure of the oligoacenes. Here, a cartoon of tetracene is shown for the single molecule from above (a), from the side (b), and for the crystal (c). The in-plane short and long axes of the crystal are denoted by  and
and  , respectively.
, respectively.
To a first approximation, the low-lying excited states of a single acene molecule involve only the highest occupied and lowest unoccupied molecular orbitals (HOMO and LUMO), that is, two electrons in two spatial orbitals. The same picture for ![]() molecules leads to
molecules leads to ![]() electrons in
electrons in ![]() spatial orbitals, which in the crystal phase becomes the HOMO- and LUMO-derived valence and conduction bands, respectively. As a purely first-principles approach, this approximation would lead to a CI theory within a minimal active space, which I now describe.
spatial orbitals, which in the crystal phase becomes the HOMO- and LUMO-derived valence and conduction bands, respectively. As a purely first-principles approach, this approximation would lead to a CI theory within a minimal active space, which I now describe.
A. Weak-Coupling Configuration Interaction Theory
In the modern context of singlet fission, this minimal active space approach was first presented by Smith and Michl for the case of two molecules [15], and by myself, Hybertsen, and Reichman for the case of clusters and crystals [52]; however, the model and its ingredients are of course very common and have been used for a variety of problems related to excitons in organic chromophores [17, 22, 53–56]. The theory is simple and intentionally so. Although quantitatively inaccurate (discussed later), this formalism immediately exposes the purely electronic aspects of singlet fission, including two mechanistic “pathways.” For two interacting molecules, the simple theory identifies five potentially low-lying electronic (spin-adapted) configurations, as shown in Fig. 2. I use the notation ![]() , where
, where ![]() denotes the electronic character of monomer
denotes the electronic character of monomer ![]() in the dimer wavefunction. The two intramolecular Frenkel excitations (FEs),
in the dimer wavefunction. The two intramolecular Frenkel excitations (FEs), ![]() and
and ![]() , have one molecule in the first singlet excited state
, have one molecule in the first singlet excited state ![]() , while the other is in the ground state
, while the other is in the ground state ![]() . The intermolecular CT (or ion-pair) excitations,
. The intermolecular CT (or ion-pair) excitations, ![]() and
and ![]() have one molecule in a cation state C and the other in an anion state A. The TT double excitation
have one molecule in a cation state C and the other in an anion state A. The TT double excitation ![]() is a correlated triplet-pair or multiexciton state, with both molecules in the lowest triplet state
is a correlated triplet-pair or multiexciton state, with both molecules in the lowest triplet state ![]() . I discuss the quantum mechanical properties of these states in order in the following.
. I discuss the quantum mechanical properties of these states in order in the following.
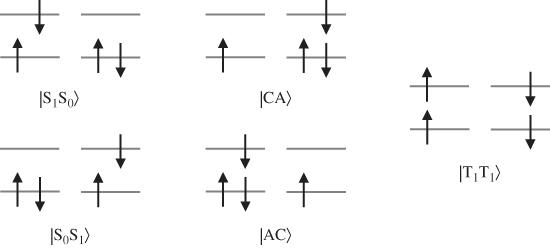
Figure 2 The five electronic configurations required for a minimal representation of the low-energy singlet excited states in organic molecules and crystals. Only the HOMO and LUMO orbitals of nearest-neighbor molecules are shown, and in practice the spin-adapted electronic configurations are used. The five states consist of intramolecular Frenkel-type excitations (two leftmost), intermolecular charge-transfer excitations (two center), and the triplet-pair double excitation (rightmost).
Intramolecular Frenkel-type excitations: The two intramolecular excitations form the starting point of conventional theories of molecular excitons. Indeed, in many molecular crystals, these states constitute a sufficient basis and comprise Frenkel's theory of excitons [57, 58].
Within the HOMO–LUMO picture, the excitation energy (i.e., the diagonal matrix element) of one such configuration is

where ![]() and
and ![]() are the orbital energies of the LUMO and HOMO of molecule A and two-electron integrals are given by
are the orbital energies of the LUMO and HOMO of molecule A and two-electron integrals are given by
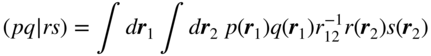
(for simplicity, I assume real orbitals). Physically, the excitation energy is the “bare” orbital energy difference (i.e., the charge or band gap, which can be related to the IP and EA) lowered by the attractive electron–hole Coulomb interaction ![]() and increased by twice the electron–hole exchange interaction
and increased by twice the electron–hole exchange interaction ![]() . These latter two “corrections” to the orbital energy difference can be thought of as a single-molecule exciton binding energy. For future reference, note that the energy of the single-molecule triplet is identical, but has no exchange repulsion,
. These latter two “corrections” to the orbital energy difference can be thought of as a single-molecule exciton binding energy. For future reference, note that the energy of the single-molecule triplet is identical, but has no exchange repulsion,
The interaction between intramolecular excitations is given by
The aforementioned matrix element physically represents the Coulomb interaction between each molecule's transition charge density, ![]() . For large intermolecular separation, a multipole expansion yields as the leading-order term a transition dipole–dipole interaction of the Förster form,
. For large intermolecular separation, a multipole expansion yields as the leading-order term a transition dipole–dipole interaction of the Förster form,

where the transition dipole moment is given by
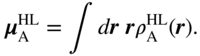
Using only the many-body basis of intramolecular excitons, the eigenstates have a dispersion with bandwidth proportional to ![]() (details depend on the lattice). For a periodic system and rigid lattice, these FEs are completely delocalized in space but have a vanishing electron–hole separation. However, at least two important mechanisms can act to localize FEs: energetic disorder (especially in low dimensions) and coupling to molecular vibrations and phonons. With increasing localization, the exciton dynamics will exhibit a crossover between band-like and hopping transport [59, 60].
(details depend on the lattice). For a periodic system and rigid lattice, these FEs are completely delocalized in space but have a vanishing electron–hole separation. However, at least two important mechanisms can act to localize FEs: energetic disorder (especially in low dimensions) and coupling to molecular vibrations and phonons. With increasing localization, the exciton dynamics will exhibit a crossover between band-like and hopping transport [59, 60].
Intermolecular CT excitations: The two intermolecular excited configurations arise from the excitation of an electron from the HOMO of one molecule to the LUMO of the other. These individual CT configurations have a nonvanishing dipole moment. However, for certain highly symmetric assemblies, the eigenstates (after CI) will exhibit a mixture of equal but opposite CT configurations and thus possess a vanishing dipole moment (see Section III). For this reason, it may be more transparent (but formally identical) to work with the “charge-resonance” basis states [61], ![]() .
.
The excitation energy of a CT configuration is approximately given by
where the intermolecular exchange integral has been neglected [21, 52]. The CT exciton binding energy is thus equal to the Coulomb integral ![]() . Because the CT electron–hole pair separation is larger than that of the intramolecular excitation, the former has a smaller Coulomb attraction, and thus
. Because the CT electron–hole pair separation is larger than that of the intramolecular excitation, the former has a smaller Coulomb attraction, and thus ![]() . However, especially in larger acenes and crystalline environments, it can happen that
. However, especially in larger acenes and crystalline environments, it can happen that ![]() , that is, the exciton binding energies (and thus the total excitation energies) of the intramolecular and CT excitons are approximately the same. In this limit, the two classes of states will mix, as was first predicted by Rice et al. for triplet [21] and singlet [2] excitons in aromatic molecular crystals. Equation (7) can clearly be compared with the classical CT energy expression
, that is, the exciton binding energies (and thus the total excitation energies) of the intramolecular and CT excitons are approximately the same. In this limit, the two classes of states will mix, as was first predicted by Rice et al. for triplet [21] and singlet [2] excitons in aromatic molecular crystals. Equation (7) can clearly be compared with the classical CT energy expression
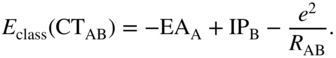
The CT configurations considered here are only for nearest-neighbor pairs; in principle, non-nearest-neighbor pairs could also be included, which would allow for larger exciton sizes and coupling into the manifold of dissociated exciton states (i.e., free electron–hole pairs). In principle, singlet fission to create triplets must out-compete exciton dissociation (among other radiative and nonradiative processes); however, the exciton binding energy in organic molecular crystals is typically much larger than thermal energy and so exciton dissociation (in the bulk) is quite rare. Nonetheless, within this generalization, there is a clear similarity to the Wannier theory of excitons [58, 62, 63]. Although the latter is conventionally applied to inorganic semiconductors with high dielectric constants, the increasing dispersion and polarizability of larger acenes necessitates this first-order Wannier-like addition to the localized basis of FE states.
Triplet-pair excitations: Finally, the target configuration of singlet fission (on the ultrafast timescale) is the multiexciton triplet-pair state ![]() . When two triplet (
. When two triplet (![]() ) excitations interact, they produce nine spin states: five quintets, three triplets, and one singlet. Only the latter couples significantly with other singlets, because the electronic nonrelativistic Hamiltonian is spin-preserving. Only the weaker spin–orbit terms will mix states of different spin multiplicity. Again, while this is not important at short times, it is crucial for the proper theoretical description of separation into individual triplets [15, 64, 65]. When properly spin-adapted, the spin-singlet triplet-pair state is given by
) excitations interact, they produce nine spin states: five quintets, three triplets, and one singlet. Only the latter couples significantly with other singlets, because the electronic nonrelativistic Hamiltonian is spin-preserving. Only the weaker spin–orbit terms will mix states of different spin multiplicity. Again, while this is not important at short times, it is crucial for the proper theoretical description of separation into individual triplets [15, 64, 65]. When properly spin-adapted, the spin-singlet triplet-pair state is given by

In principle, nothing prohibits the triplets in this state from occupying non-nearest neighbor molecules. Indeed, triplet diffusion from the nearest-neighbor pair to larger separations is surely required to realize the separation into independent triplets, although biexciton binding and entanglement effects are important topics that have only received minimal attention [66]. However, the reverse process of singlet fission, TT annihilation, has a longer history in the context of light-emitting diodes and (more recently) photon upconversion in solar cells. A theoretical picture of TT annihilation clearly requires a unified description of non-nearest neighbor triplet pairs, triplet exciton diffusion, and the full spin manifold.
To lowest order, the energy of the singlet multiexciton triplet-pair state is the sum of the single-molecule triplet energies, that is, ![]() for a homodimer. These simple considerations have led to one of the earliest design rules for singlet fission chromophores,
for a homodimer. These simple considerations have led to one of the earliest design rules for singlet fission chromophores, ![]() [15], which is a powerfully simple notion. Nonetheless, such a picture neglects the importance of the electronic coupling between bright singlet and dark triplet-pair states, as well as the important role played by vibrations and phonons. These latter finite-temperature effects can ultimately facilitate endoergic (uphill) singlet fission (as in tetracene) or even inhibit strongly exoergic (downhill) singlet fission (as in hexacene) – see Section V.
[15], which is a powerfully simple notion. Nonetheless, such a picture neglects the importance of the electronic coupling between bright singlet and dark triplet-pair states, as well as the important role played by vibrations and phonons. These latter finite-temperature effects can ultimately facilitate endoergic (uphill) singlet fission (as in tetracene) or even inhibit strongly exoergic (downhill) singlet fission (as in hexacene) – see Section V.
On the use of diabatic states: In the simplest sense, the relative energies and interactions between configurations dictate the relevant character of the low-lying electronic eigenstates. For fixed nuclei, the configuration basis and the eigenstate basis are trivially related; as the nuclei move, the matrix elements in the configuration basis will change, causing a concomitant change in the electronic character of the eigenstates. The configuration basis is therefore an approximate diabatic basis, that is, a basis whose members have a fixed electronic character (in this case, essentially by construction); the eigenstate basis at each nuclear configuration is precisely the adiabatic basis. For technical reasons [67], only the latter can be rigorously defined; however, the diabatic basis constitutes a conceptual cornerstone in modern chemical and condensed matter physics and a variety of approximate diabatization techniques are well-known in the literature [67, 68]. In principle, the adiabatic basis carries the same information (in the context of singlet fission, see the appendix of Ref. [69]), and the quantum dynamics mediated by the nonadiabatic coupling matrix elements could be simulated by surface hopping [70, 71], quantum-classical [72], or wavepacket-based methods [73]. However, in addition to its clearer interpretation, the diabatic basis is also the simplest one in which to formulate simple rate theories and more complex quantum dynamics, as discussed in Section V. For these reasons my coauthors and I advocated for the development of diabatic approaches to singlet fission electronic structure and dynamics in our first report, Ref. [52]. Later works demonstrated the ability of constructing more accurate dimer Hamiltonians in the diabatic basis, as discussed in the next section.
Another important aspect of the localized diabatic basis concerns the approximate construction of Hamiltonians for larger aggregates. Somewhat analogous to fragment-based approaches in quantum chemistry, an aggregate Hamiltonian can be straightforwardly constructed from potentially high-accuracy dimer Hamiltonians, as discussed in the next section. Of course, the subsequent electronic structure will neglect important environmental effects due to delocalization and screening. As such, this approach requires some adjustment of the energies and couplings that enter the final aggregate Hamiltonian [69]. Comparison with crystalline band structure and linear spectroscopy (see Section V) provides an important test of this procedure.
B. More Accurate Wavefunction-Based Methods
As warned earlier, the direct implementation of the minimal active space CI method is expected to yield poor excitation energies. Therefore, higher accuracy wavefunction-based methods have been more recently employed for the study of singlet fission. The excited-state electronic structure of the acenes is especially challenging because it (ideally) requires a combined treatment of static correlation (i.e., multireference character) in the valence orbitals as well as dynamical correlation (i.e., orbital relaxation and beyond) in the remaining orbitals. For molecular dimers, the restricted active space two spin-flip method [74, 75], which has been applied to singlet fission [76, 77], targets the same HOMO–LUMO active space with single excitations into and out of the active space to allow for orbital relaxation and improves upon the energies of the simple CI treatment described earlier. Higher accuracy requires larger active spaces and dynamical correlation. Very early work on singlet fission in pentacene [78] employed such a method (CASSCF, followed by multireference perturbation theory), which was also used and refined by Ananth et al. in their study of the low-lying states of pentacene dimers with crystal-like geometry [79].
The philosophy of few-state, low-energy effective Hamiltonians has a long history in quantum chemistry [80, 81] and is also embodied in semiempirical Hamiltonians, such as the Pariser–Parr–Pople model of conjugated molecules [55]. In such procedures, the one- and two-electron matrix elements in a small model subspace should be understood as ones that incorporate screening effects, which have been “folded in” from excitations to and among the neglected orbitals. More modern, first-principles approaches to construct effective Hamiltonians include canonical transformation approaches [82, 83] and the active space decomposition of Shiozaki et al. [84, 85]. The latter approach in particular aims to directly construct a many-body diabatic basis, without diabatization from an adiabatic calculation, and represents a powerful ab initio approach to generating chemically intuitive Hamiltonians. A similar approach to diabatic states via configuration restrictions has recently been given by Casanova and Krylov [86] and one based on spin and charge constraints to density functional theory was used by van Voorhis et al. [41].
Two important conclusions (regarding the electronic structure) emerge from the work of Ananth et al. [79] and Shiozaki et al. [85]: (i) the HOMO–LUMO active space provides an excellent qualitative and in some cases quantitative description of the excited-state structure of the tetracene and pentacene dimers; (ii) correlated diabatic wavefunctions can be directly constructed or obtained via diabatization of high-quality adiabatic wavefunctions to yield a highly accurate five-state basis, which is physically like the one described earlier. These two observations justify the use and explain the success of the minimal CI picture [15, 47, 52, 87]. Remarkably, Shiozaki et al. report that the absolute minimal two-orbital-per-molecule active space with no dynamical correlation yields off-diagonal couplings that are only different by 20–25%. Unsurprisingly, the diagonal energies are much more sensitive and are shifted by as much as 0.8 eV. Anticipating this result, my coauthors and I originally calculated the couplings in the simple CI theory (i.e., as one-electron matrix elements) and investigated the dynamical consequences of shifting the diagonal energies [87].
C. Mechanisms for Singlet Fission
At the dimer level, the simple theory espoused earlier suggests two mechanisms for singlet fission under the assumption that the relevant configuration following photoexcitation is an intramolecular Frenkel excitation ![]() (or some linear combination of such states). The first mechanism has been called the “direct” one and is enabled by the electronic coupling (CI) between
(or some linear combination of such states). The first mechanism has been called the “direct” one and is enabled by the electronic coupling (CI) between ![]() and
and ![]() . While the magnitude of this interaction is highly system dependent, essentially all calculations for unsubstituted acenes with crystal-like intermolecular separations find that this interaction is very small (roughly 1–5 meV) [76, 79, 85, 87, 88].
. While the magnitude of this interaction is highly system dependent, essentially all calculations for unsubstituted acenes with crystal-like intermolecular separations find that this interaction is very small (roughly 1–5 meV) [76, 79, 85, 87, 88].
The second mechanism has been called the “mediated” one, where mediation takes place via CT states. The interest in CT states originates from the observation that their interactions with the other states, that is, ![]() and
and ![]() , are large (on the order of 100 meV); however, their energy can be quite high. Therefore, depending on the relative energies of the diabatic states, the participation of CT states can take many different forms, depending in part on the finite-temperature dynamics of the nuclei. In the remainder of this chapter, I focus on the CT component of this story, including how the mediated mechanism has been studied and verified. There will no doubt be singlet fission systems for which the “direct” mechanism is dominant; two anticipated examples are when the mediated mechanism is symmetry-forbidden and when the chromophores are very far apart. However, the crystalline acenes are classical singlet fission materials, and they exhibit some of the largest fission rates; the evidence is now quite strong that the diabatic CT states are controlling singlet fission in these important prototypical materials [49, 69, 87–89].
, are large (on the order of 100 meV); however, their energy can be quite high. Therefore, depending on the relative energies of the diabatic states, the participation of CT states can take many different forms, depending in part on the finite-temperature dynamics of the nuclei. In the remainder of this chapter, I focus on the CT component of this story, including how the mediated mechanism has been studied and verified. There will no doubt be singlet fission systems for which the “direct” mechanism is dominant; two anticipated examples are when the mediated mechanism is symmetry-forbidden and when the chromophores are very far apart. However, the crystalline acenes are classical singlet fission materials, and they exhibit some of the largest fission rates; the evidence is now quite strong that the diabatic CT states are controlling singlet fission in these important prototypical materials [49, 69, 87–89].
III. Measuring Charge-Transfer Character
In the context of singlet fission, early work to move away from the dimer model employed a TD-DFT description of excited states in tetracene and pentacene clusters [76]. TD-DFT typically provides reasonable excited-state accuracy, given its low computational cost. However, previous work on single oligoacene molecules demonstrated that standard exchange–correlation functionals consistently underestimate (intramolecular) excitation energies by 0.3–0.7 eV [90]. For intermolecular excitations and more general CT-type excitations, TD-DFT is known to overestimate excitation energies [91], however, long-range corrections can significantly alleviate this problem [92, 93]. Studying a 10-molecule cluster of tetracene and pentacene and employing a more modern ![]() B97X-D functional, the authors of Ref. [76] found
B97X-D functional, the authors of Ref. [76] found ![]() excitation energies of 2.88 and 2.13 eV, in reasonable agreement with experiment: about 2.4 and 1.9 eV, respectively.
excitation energies of 2.88 and 2.13 eV, in reasonable agreement with experiment: about 2.4 and 1.9 eV, respectively.
An analysis of the aforementioned data based on the static dipole moment assigned a negligible CT character to the low-energy excited states, which was corroborated with an analysis based on natural transition orbitals (NTOs) (discussed later). This finding was in stark contrast to a contemporary study from Spano and coworkers [94], who employed a model-based (semiempirical) treatment of the excited-state electronic structure. At the time, the latter authors were not targeting singlet fission but rather the polarization dependence of linear absorption in oligoacene single crystals. In particular, the authors found that an excited-state basis lacking CT states was qualitatively unable to reproduce a spectroscopic observable known as the Davydov shift, in agreement with much earlier theory developed by Petelenz et al. [95]. Defined empirically, the Davydov shift is simply the signed energy difference between the lowest-lying absorption peaks in orthogonally polarized spectra. Following the notation of Fig. 1, the Davydov shift is given by ![]() . When only intramolecular excitations are included, the long-axis polarization (
. When only intramolecular excitations are included, the long-axis polarization (![]() ) always exhibits a lower energy peak than the short-axis one (
) always exhibits a lower energy peak than the short-axis one (![]() ), such that the Davydov shift is negative (and small), whereas experiment conclusively shows it to be positive (and large). However, an expanded basis with coupling to CT states was able to quantitatively reproduce the Davydov shift in crystalline tetracene (≈ 75 meV) and, importantly, produced a set of low-lying excited states with significant CT character. In fact, the authors of Ref. [94] found that as the number of oligoacene rings increases, the CT character of the lowest-lying excited state increases and the magnitude of the (positive) Davydov shift increases.
), such that the Davydov shift is negative (and small), whereas experiment conclusively shows it to be positive (and large). However, an expanded basis with coupling to CT states was able to quantitatively reproduce the Davydov shift in crystalline tetracene (≈ 75 meV) and, importantly, produced a set of low-lying excited states with significant CT character. In fact, the authors of Ref. [94] found that as the number of oligoacene rings increases, the CT character of the lowest-lying excited state increases and the magnitude of the (positive) Davydov shift increases.
In the present context, the motivation and identification of CT character in the excited states originates from the simple CI theory outlined in Section IIA. When working on such a basis, the characterization of eigenstates in terms of their CT components is simple. Similarly, any semiempirical [94, 96] or ab initio [85] formalism that works in (or leads to) an explicit many-body basis can also quantify the CT character of the eigenstates. For more general electronic structure techniques that generally work in the adiabatic basis, this characterization is not so straightforward, and thus for a brief period of time the field was divided over the CT character in the excitons of oligoacene crystals. In principle, a variety of diabatization techniques can transform many-body adiabatic wavefunctions into (approximate) diabatic states, as discussed earlier; analysis of the eigenstates in terms of this diabatic basis thereby provides means to quantify the CT character in low-lying excited states. But even more challenging, techniques based on the density [76], density matrix [51, 97], or many-body Green's function [10, 98] intrinsically have no access to the full wavefunction, and so quantification in terms of electronic configurations is impossible. These observations call for a suite of characterization techniques with broad applicability; ideal characterization would be completely method agnostic.
Perhaps the most straightforward measure of CT character is the dipole moment. Many molecules have both ground and excited states with a finite, static dipole moment. A common example of such excitations concerns ligated metal complexes; a typical low-lying excitation promotes an electron from the metal into the ligand shell (or vice versa). Such metal-to-ligand or ligand-to-metal CT excitations can indeed be quantified via the dipole moment (note that for charged molecules or polar ground states, the difference between the excited-state and ground-state dipole moments is typically used [99]). However, the dipole-based analysis can frequently break down: excitations of high-symmetry clusters can uniformly place electron density on the surrounding ligands, yielding a vanishing dipole moment.
The analogy with organic molecular crystals should be clear: even when CT configurations contribute to the excited-state wavefunction, the inversion symmetry of a uniform crystal requires weights that are equal in magnitude and oppositely directed. The static dipole moment of all excited states in an inversion-symmetric crystal, including oligoacenes such as tetracene and pentacene, is zero; only finite model clusters that do not respect the natural symmetries of the crystal can exhibit excited-state dipole moments. In fact, this important observation was made almost 30 years ago, by Petelenz and Smith [100] who were interested in calculating the electroabsorption spectrum of oligoacene crystals. Earlier experimental work by Bässler et al. had implicated CT excitons through a nontrivial electroabsorption spectrum [101], and the conventional interpretation was based on coupling to a static dipole moment in the excited states. Petelenz and Smith recognized that “[t]he eigenstates of the Hamiltonian …had to be superpositions of the two configurations of the charges …with equal weights. Since the dipole moments of each configuration have the same lengths but are oppositely directed, the resulting average dipole moment was bound to be zero” [100]. The authors proposed an alternative mechanism for electroabsorption, and later semiempirical calculations, employing interacting Frenkel and CT states coupled to vibrations, produced excellent agreement with experiment [96]. In the past few years, this behavior was investigated and confirmed at different levels of theory by Petelenz and Pac [102], Sharifzadeh et al. [103], and myself, Hybertsen and Reichman [69].
This class of excitations, with a vanishing dipole moment due to symmetry, is sometimes better described using NTOs [104]. The NTO formalism is most straightforwardly applied to the single-excitation theories, although it is applicable for any class of wavefunctions. In short, the approach diagonalizes the (nonsquare) transition density matrix,
via a singular value decomposition (as usual ![]() and
and ![]() denote occupied and unoccupied orbitals, respectively). The ordered singular values quantify the “most important” electron–hole excitations, and the corresponding left and right singular vectors give a single-particle (orbital) representation of the hole and electron, respectively. In the previous example of metal-to-ligand CT excitations, the NTO approach very successfully quantifies the character of the low-lying excitations and goes beyond the simple dipole moment, by providing a spatial and chemical interpretation of the electron and hole [104]. One must be very careful in applying this formalism to crystals, this time because of translation invariance. For a rigid lattice, essentially all single-particle-like transitions are between completely delocalized electron and hole orbitals, thus containing no information about the size of the exciton or its electronic character.
denote occupied and unoccupied orbitals, respectively). The ordered singular values quantify the “most important” electron–hole excitations, and the corresponding left and right singular vectors give a single-particle (orbital) representation of the hole and electron, respectively. In the previous example of metal-to-ligand CT excitations, the NTO approach very successfully quantifies the character of the low-lying excitations and goes beyond the simple dipole moment, by providing a spatial and chemical interpretation of the electron and hole [104]. One must be very careful in applying this formalism to crystals, this time because of translation invariance. For a rigid lattice, essentially all single-particle-like transitions are between completely delocalized electron and hole orbitals, thus containing no information about the size of the exciton or its electronic character.
A class of methods that I have not discussed until now are those based on Green's functions via many-body perturbation theory. Specifically, the one-particle Green's function calculated in the GW approximation [9, 105] provides accurate charged excitations (i.e., band gaps and band structure), while the two-particle Green's function calculated via the Bethe–Salpeter equation (BSE) [10] yields accurate neutral excitations (i.e., excitons and optical absorption). This GW+BSE program has been applied quite successfully to molecular crystals over the past 10 years [98, 106, 107] and especially recently by Neaton et al. [103, 108, 109]. In practice, the BSE leads to a single-excitation theory with dynamically screened Coulomb interactions calculated in the random-phase approximation. The exciton (electron–hole) wavefunction can be interpreted as a two-point correlation function, leading to a common analysis tool emerging from that community but applicable to any single-excitation theory with a two-particle wavefunction,

![]() is again the transition density matrix Eq. (10). For a fixed hole position
is again the transition density matrix Eq. (10). For a fixed hole position ![]() , the exciton wavefunction yields the probability amplitude to find the electron at position
, the exciton wavefunction yields the probability amplitude to find the electron at position ![]() or generally at a distance of
or generally at a distance of ![]() from the hole. In this real-space picture, if the hole is fixed on one molecule, then any electron amplitude on neighboring molecules is a direct confirmation of CT character, as defined earlier. By contrast, a pure FE would only exhibit electron amplitude on the same molecule.
from the hole. In this real-space picture, if the hole is fixed on one molecule, then any electron amplitude on neighboring molecules is a direct confirmation of CT character, as defined earlier. By contrast, a pure FE would only exhibit electron amplitude on the same molecule.
This analysis performed on the results of a GW+BSE calculation always shows significant CT character in the low-lying singlet states of crystalline pentacene [98, 103, 107]. In Ref. [69], we confirmed that our own excited-state calculations based on a diabatic model Hamiltonian (similar to that of Spano et al. [89, 94]) yield exciton structure that is completely in agreement with this picture. Furthermore, because we work in such a many-body diabatic basis, we can directly correlate the percentage of CT character in a given wavefunction to its real-space electron–hole wavefunction.
The results of these calculations are shown schematically in Fig. 3, along with the CI between Frenkel and CT components leading to the exciton eigenstates. For singlet excitons, a combination of the single-particle dispersion, screening, and polarizability of the crystal yields FE configurations with an energy similar to that of CT configurations, resulting in an efficient mixing of the two; this creates a roughly 50%/50% mixture in pentacene. Graphically, when the hole is fixed on a certain molecule, the electron density is found to be located partially on the same molecule (FE character) and partially on neighboring molecules (CT character). By contrast, triplet excitons have no exchange repulsion, which is strongest for the Frenkel component. This keeps the Frenkel configurations out of resonance with the CT configurations, leading to triplets that are predominantly intramolecular FEs.

Figure 3 Configuration interaction diagram (top) and schematic real-space structure (bottom) of singlet (a) and triplet (b) excitons in oligoacene crystals. The configuration interaction diagrams show the evolution, starting from the noninteracting band gap  , of the Frenkel exciton (FE) from the left and the charge-transfer exciton (CT) from the right. The exciton hole is fixed and indicated by a blue circle, and the conditional electron probability distribution is indicated by red circles.
, of the Frenkel exciton (FE) from the left and the charge-transfer exciton (CT) from the right. The exciton hole is fixed and indicated by a blue circle, and the conditional electron probability distribution is indicated by red circles.
Recent work by Plasser et al. has essentially unified many of the pictures discussed here, including the notion of excitons and electron–hole wavefunctions via both many-body theory as well as density matrices in quantum chemistry [110, 111]. This work provides a useful link from the solid-state picture discussed earlier to simple dimers and aggregates. In fact, many of the conceptual difficulties discussed here and associated with measuring CT character are less problematic in symmetry-breaking dimers and aggregates. Even in a pentacene dimer with a crystal-like geometry, the CT states have different energies, and so they do not appear in low-lying eigenstates with equal weight [79]. Conventional quantum chemistry techniques such as the dipole moment should indeed reflect the CT character in these cases. Other tools have recently been developed for quantifying the electronic character in small aggregates of coupled chromophores, such as the use of charge and spin cumulants [61].
IV. Charge-Transfer Implications for Singlet Fission
Having established the role of CT states in the low-lying excitons of organic molecules and crystals, I now return to the problem of singlet fission. While the current understanding of bright states in terms of their FE and CT components is in accord with classic work in the field, the multiexciton triplet-pair states have not historically been considered in such detail. In this section, I outline two qualitatively different regimes in which CT states can mediate the singlet fission process through their strong interaction with triplet-pair states.
A. High-Energy CT Configurations and the Superexchange Picture
For CT states with very high energies, the CT component of the low-lying eigenstates is very small; this limit can lead to a second-order superexchange-like mechanism [52, 87]. In the superexchange picture, one considers the first-order perturbed diabatic wavefunctions, due to the coupling with CT configurations:
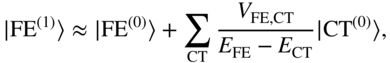

The total interaction between these states then has two parts: a first-order direct coupling and a second-order superexchange coupling [20, 87],
This effective interaction is the result of integrating-out the high-energy CT states, to yield a simpler few-state picture of the singlet fission process. It is perhaps worth emphasizing that superexchange contains no physics that cannot be obtained from a full diagonalization of the Hamiltonian into its exact eigenstates. Rather, the superexchange concept is a physical one that qualitatively distinguishes between a small (“virtual”) mixing of CT character and a large (“physical”) mixing of CT character into the low-lying eigenstates. Superexchange describes the former case: to a high accuracy, one can define a new set of diabatic states that excludes the CT configurations while retaining their electronic character; the small CT mixing produces a second-order coupling between the (otherwise weakly interacting) intramolecular excitation and the TT state.
The superexchange picture in singlet fission is almost completely analogous to the case of magnetic interactions in transition metal oxides, where the superexchange idea was first proposed by Kramers [112]. In that case, the same second-order coupling leads to a magnetic interaction between next-nearest-neighbor transition metal atoms. The high-energy CT state is a double-occupancy configuration arising due to CT from the transition metal onto a bridging oxygen atom; the double occupancy is expensive, and so the configuration is high in energy. This picture was further investigated by Anderson [113]. The same exact insight leads to (in a very formal sense) the so-called ![]() –
–![]() model after projecting out high-energy double-occupancy (CT) configurations in the Hubbard model [114]. Since these early works in condensed matter physics, superexchange has been found to be a useful and ubiquitous picture of mediated electronic interactions. A few important examples of superexchange in chemical physics include the electron transfer mechanism of biological donor–bridge–acceptor complexes [115, 116], charge transport through single-molecule junctions [117], and non-Förster excitation energy transfer [54, 56].
model after projecting out high-energy double-occupancy (CT) configurations in the Hubbard model [114]. Since these early works in condensed matter physics, superexchange has been found to be a useful and ubiquitous picture of mediated electronic interactions. A few important examples of superexchange in chemical physics include the electron transfer mechanism of biological donor–bridge–acceptor complexes [115, 116], charge transport through single-molecule junctions [117], and non-Förster excitation energy transfer [54, 56].
Whether a superexchange picture is meaningful obviously depends on the energetics of a given material system. On the basis of a simple CI calculation, my coauthors and I previously advocated that isolated molecular acene dimers and small oligomers would have an energetic ordering that supports superexchange [87]. This finding was strongly corroborated by Shiozaki and coworkers [85], whose active space decomposition yields diabatic CT states, which are approximately 1 eV higher in energy than the FE or TT states. The smaller oligoacenes can also be thought of as exhibiting singlet fission through a superexchange mechanism, because the CT mixing is relatively minor and the excitons are predominantly of Frenkel character. However, the triplet-pair state in crystals of smaller acenes is usually much higher in energy than the low-lying singlets, which precludes efficient singlet fission.
At this stage, note that the superexchange concept only provides an interaction between the purported initial and final states of the (early-time) singlet fission process; it says nothing yet about the rate. A microscopic rate expression can only be derived when considering the finite-temperature dynamics of the nuclei and their coupling to the excited-state electronic structure. This aspect of the problem is discussed in Section V, after a detailed discussion of the electronic aspects of singlet fission in crystals.
B. Low-Energy CT Configurations and Physical Mixing
As discussed earlier, the handful of theoretical treatments for excited states in true crystalline environments indicate an increasingly non-negligible CT character in the low-lying eigenstates. In this regime, superexchange is no longer relevant: the interaction with diabatic CT configurations is nonperturbative. Instead, the intramolecular FE and intermolecular CT configurations are all nearly degenerate and thus strongly interacting, leading to eigenstates with truly mixed character. If one first diagonalizes the “singles” excited-state manifold, that is, the part of the crystal Hamiltonian containing FE and CT configurations, this leads to a set of singlet eigenstates with high oscillator strength, which I simply call ![]() , and so on.
, and so on.
Upon photoexcitation near the absorption edge, the system is prepared in some combination of the aforementioned mixed eigenstates, ![]() . The fraction of CT character determines the coupling strength with the triplet-pair TT state. Schematically,
. The fraction of CT character determines the coupling strength with the triplet-pair TT state. Schematically,
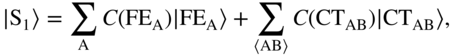
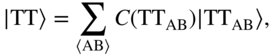
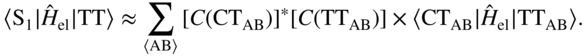
In reality, the overall effect is subtle due to crystal geometries and interfering pathways, but the result immediately suggests that the rate of singlet fission increases with increasing CT character in the photoexcited states. Again, I emphasize that this interpretation is only valid for those materials with (i) low-energy CT configurations and (ii) interactions with CT states that are stronger than those between FE and TT. These criteria appear to be satisfied in the larger oligoacene crystals such as tetracene, pentacene, and hexacene [42, 69, 94, 118].
Despite the increased singlet fission coupling, an increased CT character has other implications for the low-energy excited states. The first is related to the earlier discussion, concerning the Davydov shift. It appears to be the case that the energy of CT configurations falls faster than that of intramolecular excitations with increasing acene length. This gives rise to the increasingly larger CT character in the eigenstates, and the concomitant increase in the Davydov shift. The changing eigenstate ![]() energy necessarily alters the energy alignment between
energy necessarily alters the energy alignment between ![]() and TT, which substantially alters the singlet fission rate, as is discussed in Section V.
and TT, which substantially alters the singlet fission rate, as is discussed in Section V.
The second implication of increased CT character is a decreased oscillator strength. The intramolecular oscillator strength is significantly larger than the intermolecular one: the oscillator strength is roughly proportional to the overlap between the HOMO and LUMO involved in the transition. In the highly simplified limit where only intramolecular excitations carry oscillator strength and CT excitations are completely forbidden, the brightness of a given eigenstate depends on the balance of FE and CT character. In other words, the CT component borrows oscillator strength from the bright FE states. With this interpretation, we observe that increasing CT character in low-energy states diminishes the relative oscillator strength. With too much CT character, the states could become essentially dark.
Note that this observation is in fact very analogous to the situation in the Wannier theory of excitons in inorganic semiconductors, mentioned in Section A. In that case, the exciton envelope wavefunction ![]() , where
, where ![]() is the electron–hole separation, satisfies a hydrogen-like Schrödinger equation, leading to states with angular momentum character s, p, d, and so on. The absorption coefficient can be written as [58]
is the electron–hole separation, satisfies a hydrogen-like Schrödinger equation, leading to states with angular momentum character s, p, d, and so on. The absorption coefficient can be written as [58]
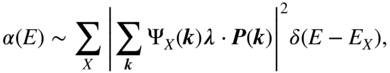
where ![]() is the photon polarization,
is the photon polarization, ![]() is the single-particle momentum matrix element, and
is the single-particle momentum matrix element, and ![]() is the exciton energy. The usual approximation is to take
is the exciton energy. The usual approximation is to take ![]() to be independent of
to be independent of ![]() , that is, completely local in space; this is analogous to assuming that only intramolecular excitations are dipole-allowed. After this approximation, the absorption coefficient becomes
, that is, completely local in space; this is analogous to assuming that only intramolecular excitations are dipole-allowed. After this approximation, the absorption coefficient becomes
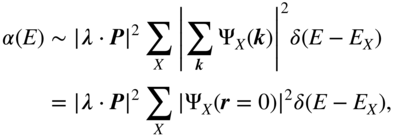
leading to the classic result that only s-type excitons are absorbing in linear spectroscopy. All states with ![]() , that is, all purely CT excitons, are dark. Even within the s-type manifold, the intensity is directly proportional to the probability of the electron and hole occupying the same site (
, that is, all purely CT excitons, are dark. Even within the s-type manifold, the intensity is directly proportional to the probability of the electron and hole occupying the same site (![]() ), which is equivalent to the fraction of on-site (non-CT) excitation character. (A minor caveat: in the Wannier picture, the exciton wavefunction is understood to be coarse–grained over one or more unit cells, so the “local” excitations are not strictly intra-atomic; this is to be expected because the valence electron and hole bandwidth in inorganic semiconductors is roughly an order of magnitude larger than in organics. In any event, the physical picture is the same: local excitations are bright, and nonlocal excitations are dark.)
), which is equivalent to the fraction of on-site (non-CT) excitation character. (A minor caveat: in the Wannier picture, the exciton wavefunction is understood to be coarse–grained over one or more unit cells, so the “local” excitations are not strictly intra-atomic; this is to be expected because the valence electron and hole bandwidth in inorganic semiconductors is roughly an order of magnitude larger than in organics. In any event, the physical picture is the same: local excitations are bright, and nonlocal excitations are dark.)
V. Theory of Spectroscopy, Reaction Rates, and Singlet Fission Dynamics
A. The Electronic–Vibrational Hamiltonian and Reduced Dynamics
To go beyond the static electronic structure picture of excitons requires a time-dependent treatment of the quantum dynamics of singlet fission. For a fully microscopic theory, we employ an explicit consideration of the vibrational degrees of freedom. In particular, we can write the total electronic-plus-vibrational Hamiltonian as
Here, ![]() is the diabatic electronic Hamiltonian discussed earlier, which can have as few as five states (for singlet fission dimers) or many more states (for clusters and crystals). Quite generally, the vibrational Hamiltonian can be taken as the collective normal modes of molecular vibrations, crystal phonons, and/or solvent polarization fluctuations (all indexed by
is the diabatic electronic Hamiltonian discussed earlier, which can have as few as five states (for singlet fission dimers) or many more states (for clusters and crystals). Quite generally, the vibrational Hamiltonian can be taken as the collective normal modes of molecular vibrations, crystal phonons, and/or solvent polarization fluctuations (all indexed by ![]() ),
),

Here, ![]() is the vibrational frequency,
is the vibrational frequency, ![]() and
and ![]() are the mass-weighted momentum and coordinate, and
are the mass-weighted momentum and coordinate, and ![]() and
and ![]() are bosonic creation and annihilation operators. The electronic–vibrational interaction can be written generically in the diabatic basis
are bosonic creation and annihilation operators. The electronic–vibrational interaction can be written generically in the diabatic basis ![]() as
as

The character of excitation energies in the diabatic basis is predominantly “intramolecular,” and so the nuclear dependence of the diagonal terms ![]() will be dominated by high-frequency intramolecular vibrations (in the crystal phase). The electronic coupling in the same basis is significantly more “intermolecular,” and so the nuclear dependence of off-diagonal terms
will be dominated by high-frequency intramolecular vibrations (in the crystal phase). The electronic coupling in the same basis is significantly more “intermolecular,” and so the nuclear dependence of off-diagonal terms ![]() will involve low-frequency intermolecular vibrations. In other words, the intramolecular vibrations modulate the “energies,” and the intermolecular vibrations modulate the “couplings”; these are only physically motivated observations, which may be highly system dependent. However, this separation into “Holstein” and “Peierls” couplings seems to hold well for single-particle states and charge transport [119].
will involve low-frequency intermolecular vibrations. In other words, the intramolecular vibrations modulate the “energies,” and the intermolecular vibrations modulate the “couplings”; these are only physically motivated observations, which may be highly system dependent. However, this separation into “Holstein” and “Peierls” couplings seems to hold well for single-particle states and charge transport [119].
At finite-temperature, the statistical ensemble averaging demands use of the density operator, as opposed to the wavefunction. The total density operator ![]() , an operator in the electronic-plus-vibrational Hilbert space, obeys the Liouville equation
, an operator in the electronic-plus-vibrational Hilbert space, obeys the Liouville equation
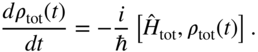
For many (but not all) observables of interest, we are only be concerned with dynamics in the electronic state space, averaged over the nuclear degrees of freedom. This leads to the reduced electronic density operator, obtained by tracing over the vibrational degrees of freedom, ![]() . The reduced density operator obeys the equation of motion
. The reduced density operator obeys the equation of motion
In the absence of coupling to vibrations, the diagonalization of ![]() yields the exact adiabatic eigenstates at the ground-state geometry,
yields the exact adiabatic eigenstates at the ground-state geometry,
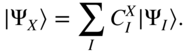
This basis is frequently referred to as the “exciton” basis, as opposed to the adiabatic Basis, which diagonalizes the Born–Oppenheimer Hamiltonian at each nuclear configuration. Lowest order perturbation theory in the electron–vibration interaction leads to the well-known (here, time-local) Redfield equations in the exciton basis [56, 120, 121],
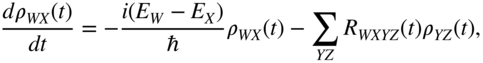
although other perturbative and numerically exact solutions of Eq. (24) are possible, which is discussed later. Detailed expressions for the Redfield tensor elements ![]() can be found in the literature [52, 56], but suffice to say this tensor is responsible for the vibrationally induced population relaxation
can be found in the literature [52, 56], but suffice to say this tensor is responsible for the vibrationally induced population relaxation ![]() and decoherence
and decoherence ![]() . The density matrix approach provides access to rates through the diagonal population elements, but also provides access to spectroscopies (in the presence of vibrations) through the off-diagonal coherence matrix elements [56].
. The density matrix approach provides access to rates through the diagonal population elements, but also provides access to spectroscopies (in the presence of vibrations) through the off-diagonal coherence matrix elements [56].
B. Validating the Hamiltonian Through Spectroscopy
The parameterization or calculation of all vibrational degrees of freedom and their coupling to the electronic excited states is a very demanding program. However, for a given model of the electronic–vibrational interaction, we can compare with experimental linear absorption spectroscopy to validate both the electronic and vibrational treatment in the Hamiltonian.
For single oligoacene molecules, the CC 1400 cm![]() vibration is known to be the most strongly coupled to the electronic transitions. To treat the dynamics in this limit, we only include two electronic states (the ground state and the
vibration is known to be the most strongly coupled to the electronic transitions. To treat the dynamics in this limit, we only include two electronic states (the ground state and the ![]() excited state), coupled via a dipole operator
excited state), coupled via a dipole operator ![]() , where
, where ![]() denotes the Hermitian conjugate. The vibrational coupling is taken to be diagonal and linear in the normal mode coordinate,
denotes the Hermitian conjugate. The vibrational coupling is taken to be diagonal and linear in the normal mode coordinate,
where ![]() is the exciton–vibration coupling strength and
is the exciton–vibration coupling strength and ![]() is the dimensionless Huang–Rhys factor. For this description, the time-local Redfield equation, that is, the second-order time-local cumulant, provides the exact solution to this nonperturbative pure-dephasing problem [122]. The so-calculated single-molecule absorption spectrum is shown in Fig. 4(a) and compared with the experimental one taken from Ref. [123]. The classical vibronic progression is clearly seen with a spacing of 1400 cm
is the dimensionless Huang–Rhys factor. For this description, the time-local Redfield equation, that is, the second-order time-local cumulant, provides the exact solution to this nonperturbative pure-dephasing problem [122]. The so-calculated single-molecule absorption spectrum is shown in Fig. 4(a) and compared with the experimental one taken from Ref. [123]. The classical vibronic progression is clearly seen with a spacing of 1400 cm![]() meV. The vertical excitation energy in this calculation is 2.25 eV and the reorganization energy of 120 meV (
meV. The vertical excitation energy in this calculation is 2.25 eV and the reorganization energy of 120 meV (![]() ) is responsible for the lowered absorption onset of the 0–0 transition at around 2.13 eV. It is important to note that this calculation does not require the explicit treatment of the vibrational Hilbert space; the vibrational effects are captured implicitly through the time dependence of the reduced density operator.
) is responsible for the lowered absorption onset of the 0–0 transition at around 2.13 eV. It is important to note that this calculation does not require the explicit treatment of the vibrational Hilbert space; the vibrational effects are captured implicitly through the time dependence of the reduced density operator.

Figure 4 Comparison of absorption spectra between experiment and the theory described in the text, for a single pentacene molecule in solution (a) and for a pentacene crystal (b). The theoretically predicted crystal spectrum is also divided into its polarized  and
and  components, where the onset energy difference yields the Davydov shift of approximately 150 meV.
components, where the onset energy difference yields the Davydov shift of approximately 150 meV.
When intermolecular couplings are added to the Hamiltonian, the time-local resummation is no longer an exact treatment of linear electronic–vibrational coupling; however, its Markovian limit provides a vibration-induced finite-temperature linewidth. Furthermore, in the crystal phase, phonons, anharmonicities, and other differences in the local environment can also modify the distribution of vibrational frequencies leading to a broadened vibrational density of states (discussed later). By extending the diabatic dimer Hamiltonian to aggregates and crystals, as described at the end of Section IIA, we can perform such quantum dynamics simulations to validate the Hamiltonian via polarized linear absorption [69]. The results are shown in Fig. 4(b) and compared with the polycrystalline experimental absorption from Ref. [40]. Even in the absence of explicit vibronic effects, the results are clearly quite good and capture the main features as well as the sign and magnitude of the Davydov shift, discussed earlier. For pentacene considered here, the Davydov shift is 150 meV, twice as large as in tetracene, indicative of the increased CT character in the low-lying excited states. Recent work from Spano et al. has performed a similar calculation with an enlarged (non-nearest-neighbor) CT exciton basis and explicit vibronic states, which leads to excellent agreement with both components of the polarized absorption [118]. In the absence of vibronic effects, that work finds a spectrum that is very similar to the one shown in Fig. 4(b); the major effect of explicit vibrations is an H-aggregate-like vibronic structure at energies above 2 eV. The combined results shown in Fig. 4 suggest that we have a highly accurate electronic–vibrational Hamiltonian and appropriate treatment of its quantum dynamics.
Simulating the dynamics of singlet fission requires only the addition of the triplet-pair manifold of states. Interestingly, including the coupling to these TT states only slightly changes the absorption because the CT-mediated coupling is not sufficient to overcome the non-negligible energy difference between the bright Frenkel component and the dark TT component.
C. Rate Theories
Before discussing the results of explicitly time-dependent quantum dynamics simulations, we first discuss the applicability of various microscopic rate theories. These rate theories can be derived in perturbative limits of the full quantum master equation, Eq. (24). In any situation where the explicit inclusion of CT states can be neglected – either due to a strong direct coupling, the appropriate use of a superexchange coupling, or when the initial ![]() state is understood to be a mixture of Frenkel and CT excitons – we can write the electronic excited-state Hamiltonian in a schematic two-state picture,
state is understood to be a mixture of Frenkel and CT excitons – we can write the electronic excited-state Hamiltonian in a schematic two-state picture,

Again, exact diagonalization will yield the eigenstates; however, we can gain some preliminary insight from a golden rule evaluation of the singlet fission rate constant,
The Franck–Condon-weighted density of states ![]() depends on the temperature and the detailed form of the coupling to molecular vibrations, phonons, or solvent nuclei. Note that when the physical CT mixing is not large, then the first two contributing terms to the coupling matrix element
depends on the temperature and the detailed form of the coupling to molecular vibrations, phonons, or solvent nuclei. Note that when the physical CT mixing is not large, then the first two contributing terms to the coupling matrix element ![]() are precisely those given in Eq. (14). When Eq. (14) is inserted in the rate expression Eq. (29), we find essentially the exact formula given in the early proposal of singlet fission by Swenberg and Stacy [20]. Only more recently have atomistic calculations been performed to more precisely quantify the terms contributing to this rate expression. A particular case of interest concerns the coherent addition of many different terms contributing to the total effective coupling, as in Eq. (14). Each term carries a sign and thus constructive or destructive interference can occur to enhance or suppress the singlet fission process [15, 47, 87].
are precisely those given in Eq. (14). When Eq. (14) is inserted in the rate expression Eq. (29), we find essentially the exact formula given in the early proposal of singlet fission by Swenberg and Stacy [20]. Only more recently have atomistic calculations been performed to more precisely quantify the terms contributing to this rate expression. A particular case of interest concerns the coherent addition of many different terms contributing to the total effective coupling, as in Eq. (14). Each term carries a sign and thus constructive or destructive interference can occur to enhance or suppress the singlet fission process [15, 47, 87].
Historical work has shown that in the limit of large interactions ![]() , the rate becomes independent of
, the rate becomes independent of ![]() . This marks a transition from a nonadiabatic rate process to an adiabatic rate process. This limit of large
. This marks a transition from a nonadiabatic rate process to an adiabatic rate process. This limit of large ![]() is of course beyond the perturbative limit of the golden rule. Early work in this area was motivated by electron transfer in polar solvents, where the solvent dynamics was assumed to be slow and classical [124–126]. The unification of nonadiabatic and adiabatic dynamics in the presence of a high-frequency intramolecular vibration requiring a quantum mechanical treatment was first achieved by Jortner and Bixon [127]. In the context of singlet fission, this rate equation takes the form
is of course beyond the perturbative limit of the golden rule. Early work in this area was motivated by electron transfer in polar solvents, where the solvent dynamics was assumed to be slow and classical [124–126]. The unification of nonadiabatic and adiabatic dynamics in the presence of a high-frequency intramolecular vibration requiring a quantum mechanical treatment was first achieved by Jortner and Bixon [127]. In the context of singlet fission, this rate equation takes the form
The sum is over vibrational energy levels of the high-frequency mode, which occurs at ![]() meV (
meV (![]() 1400 cm
1400 cm![]() ) in the oligoacenes. The golden rule (nonadiabatic) rate constant appears in the numerator,
) in the oligoacenes. The golden rule (nonadiabatic) rate constant appears in the numerator,

and the Franck–Condon-weighted adiabaticity parameter appears in the denominator,
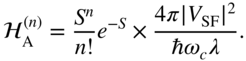
Here, ![]() is the Huang–Rhys factor of the intramolecular vibration and
is the Huang–Rhys factor of the intramolecular vibration and ![]() and
and ![]() are the characteristic frequency (inverse relaxation time) and reorganization energy of the remaining nuclear degrees of freedom. This approach was recently employed by van Voorhis and coworkers [41] to explain the measured singlet fission rate constants in a large class of crystal-phase pentacene derivatives. The derivatives contained side chains of varying size, to ultimately tune the intermolecular separation and thus the singlet fission electronic coupling
are the characteristic frequency (inverse relaxation time) and reorganization energy of the remaining nuclear degrees of freedom. This approach was recently employed by van Voorhis and coworkers [41] to explain the measured singlet fission rate constants in a large class of crystal-phase pentacene derivatives. The derivatives contained side chains of varying size, to ultimately tune the intermolecular separation and thus the singlet fission electronic coupling ![]() [41]. The study found that the nonadiabatic to adiabatic transition in pentacene derivatives occurs around
[41]. The study found that the nonadiabatic to adiabatic transition in pentacene derivatives occurs around ![]() meV. The take-home message is crucial: increased coupling is good for fast fission but has diminishing returns beyond a certain threshold.
meV. The take-home message is crucial: increased coupling is good for fast fission but has diminishing returns beyond a certain threshold.
D. Full Quantum Dynamics
With a large aggregate diabatic Hamiltonian including coupling to the triplet-pair states (totaling up to thousands of quantum states), we have recently performed Redfield dynamics calculations of singlet fission in pentacene [69]. The calculations use the same single-excitation manifold of states that produced the absorption spectrum shown in Fig. 4(b) and similarly parameterized triplet-pair states, with a coupling to vibrations appropriate for the condensed phase. Results of these simulations predict a singlet fission timescale of about 300 fs, which compares quite favorably with the experimental timescale of about 80–120 fs. Minor changes in the Hamiltonian can easily reproduce this timescale, though we choose not to pursue this degree of empiricism. Analysis of the population dynamics shows an overall incoherent kinetics for the total state populations, although individual quantum states localized throughout the crystal show highly oscillatory transient dynamics. For related reasons, different treatments of the exciting laser pulse (i.e., the initial condition) yield interesting and sometimes complex dynamics at very short times in the order of 5–10 fs.
The overall incoherent dynamics can partially be attributed to our treatment of the intramolecular vibrations and crystal phonons. In particular, we employed a coupling to an environmental reaction coordinate, which has a linear response and fluctuation correlations that decay exponentially in time [128, 129]. This is equivalent to linear coupling to a bath of harmonic oscillators characterized by an Ohmic spectral density with Lorentzian cutoff (also known as a Debye spectral density or the overdamped Brownian oscillator model) [130]. Specifically, we employed the diagonal interaction
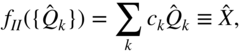
where ![]() is the reaction coordinate with fluctuations characterized by the autocorrelation function
is the reaction coordinate with fluctuations characterized by the autocorrelation function
where ![]() and
and ![]() are the reorganization energy and the characteristic vibrational frequency, as mentioned before. For a few-state model of singlet fission, Tao used the same Hamiltonian and performed semiclassical quantum dynamics [131], which in general embody an entirely different set of approximations compared with Redfield theory. However, the results were found to be in excellent agreement, suggesting that both methods are giving an accurate description of the dynamics generated by the model Hamiltonian.
are the reorganization energy and the characteristic vibrational frequency, as mentioned before. For a few-state model of singlet fission, Tao used the same Hamiltonian and performed semiclassical quantum dynamics [131], which in general embody an entirely different set of approximations compared with Redfield theory. However, the results were found to be in excellent agreement, suggesting that both methods are giving an accurate description of the dynamics generated by the model Hamiltonian.
Since our original treatment of the dynamics in models of singlet fission dimers [87], there have been a number of important extensions to other dimer systems, including more accurate treatments of the vibrational coupling. In particular, Beljonne et al. performed a first-principles calculation of the electronic structure and vibrational couplings in pentacene and rubrene dimers and trimers [132]. These authors then used the numerically exact multiconfigurational time-dependent Hartree approach to simulate the singlet fission dynamics. For pentacene, these results corroborated the superexchange-like pathway in small aggregates, and the overall decay dynamics are quite similar to those from Redfield theory but with additional transient vibrational oscillations. In another recent work, Fujihashi and Ishizaki analyze the possibility and implications of correlated vibrational fluctuations within a few-state model of singlet fission [133] and again find that the long-time decay dynamics are essentially unchanged from our Redfield simulations; however, the short-time dynamics can look quite different based on the assumed correlations or anticorrelations in the coupling to the reaction coordinate.
I conclude this section by highlighting two of the nontrivial predictions achieved with the microscopic approach presented here. First, our early work on model singlet fission dimers investigated the validity of the superexchange rate theory embodied in Eqs (14) and (29). Because the Redfield approach is completely nonperturbative in the electronic degrees of freedom (i.e., it works in the electronic eigenstate basis), it is capable of capturing higher order effects in ![]() beyond the golden rule. In Ref. [87], we demonstrated that the nonadiabatic rate theory breaks down around
beyond the golden rule. In Ref. [87], we demonstrated that the nonadiabatic rate theory breaks down around ![]() meV, and the dynamics simulations show a turnover to reduced singlet fission rates. As discussed earlier, this nonadiabatic to adiabatic transition was later demonstrated with an experimental tour de force covering six pentacene derivatives and two to three orders of magnitude in the couplings and the rates [41]. Those results were interpreted in the framework of the Jortner–Bixon rate theory, Eq. (30), with electronic parameters calculated using constrained density functional theory. The agreement between our simulations and this rate expression is especially encouraging and suggests a consistent physical understanding. Figure 5(a) compares the results of our dynamical theory (using the electronic couplings calculated in Ref. [41]) to the experimental singlet fission rates.
meV, and the dynamics simulations show a turnover to reduced singlet fission rates. As discussed earlier, this nonadiabatic to adiabatic transition was later demonstrated with an experimental tour de force covering six pentacene derivatives and two to three orders of magnitude in the couplings and the rates [41]. Those results were interpreted in the framework of the Jortner–Bixon rate theory, Eq. (30), with electronic parameters calculated using constrained density functional theory. The agreement between our simulations and this rate expression is especially encouraging and suggests a consistent physical understanding. Figure 5(a) compares the results of our dynamical theory (using the electronic couplings calculated in Ref. [41]) to the experimental singlet fission rates.

Figure 5 The singlet fission rate in the oligoacene family as a function of two important electronic variables: the effective electronic coupling (a) and the energy difference or exoergicity (b). At large electronic coupling, a nonadiabatic to adiabatic transition takes place (a) and at large exoergicity, multiphonon effects are necessary to describe the smaller, but nonzero rate of singlet fission (b). The theory described in the text is shown as solid black lines, while the corresponding simpler lowest order results are shown as dashed red lines.
The final example concerns a nonperturbative effect in the vibrational degrees of freedom, rather than in the electronic coupling. In particular, my collaborators and I were motivated to extend the family of oligoacenes exhibiting singlet fission to include hexacene. A synthesis of unsubstituted crystalline hexacene was reported for the first time only recently, in 2012 [134]. The microscopic theory described here predicts strongly exoergic singlet fission like in hexacene to be a multiphonon process. For a model with linear coupling to phonons, the lowest order (Redfield-like) 1-phonon relaxation rate actually predicts a vanishing singlet fission rate. Physically, the large excess energy of singlet fission in hexacene cannot be taken on by a single phonon, because no such high-frequency phonons exist in the material. However, with a lower probability, multiple simultaneous phonon excitations can occur to accommodate this large excess energy. From a theoretical point of view, higher order perturbation theory with linear coupling or lowest order perturbation theory with a nonlinear coupling can both realize this behavior [135]. In Ref. [42], we applied the latter formalism, that is, still using the Redfield framework but with an electronic–vibrational interaction of the form
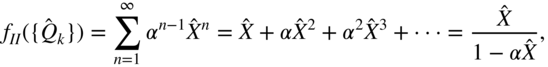
where clearly ![]() recovers the conventional linear-coupling expression. With this form, we provided a rate expression for multiphonon singlet fission, and the results are shown in Fig. 5(b) and compared with experimental values for tetracene, pentacene, and hexacene. Via transient absorption spectroscopy, the singlet fission time of hexacene was observed to be 530 fs [42], roughly five times slower than in pentacene, and in good agreement with the prediction of the theory. It is important to recognize that singlet fission in hexacene is not faster than in pentacene simply because it is “more downhill” in energy; this is essentially the physics embodied in exponential energy gap laws [136, 137] and (in a less precise sense) the inverted regime of Marcus theory [138].
recovers the conventional linear-coupling expression. With this form, we provided a rate expression for multiphonon singlet fission, and the results are shown in Fig. 5(b) and compared with experimental values for tetracene, pentacene, and hexacene. Via transient absorption spectroscopy, the singlet fission time of hexacene was observed to be 530 fs [42], roughly five times slower than in pentacene, and in good agreement with the prediction of the theory. It is important to recognize that singlet fission in hexacene is not faster than in pentacene simply because it is “more downhill” in energy; this is essentially the physics embodied in exponential energy gap laws [136, 137] and (in a less precise sense) the inverted regime of Marcus theory [138].
The intermolecular interactions and vibrational degrees of freedom mediating singlet fission are relatively similar across the (unsubstituted) acenes, and so the energy difference is (in general) the only remaining material property that can explain the variations in the rate. Indeed, the theory described here ascribes the comparatively slow singlet fission in tetracene to the endoergicity, which also leads to a predicted temperature dependence. Although early studies reported such a temperature dependence [39], later experiments demonstrated temperature-independent singlet fission down to very low temperature [23–25]. However, more recent work from Bardeen et al. has identified a significant difference in the singlet fission behavior of tetracene films and single crystals [48], with the latter showing the expected activated temperature dependence.
VI. Conclusions and Outlook
In this chapter, I have discussed the historical and modern aspects of theoretical descriptions of excitons in organic molecules and crystals. The current picture of bright excitons is entirely consistent with classic works [21, 22, 95] and emphasizes the importance of CT excitons in longer oligoacenes. Spectroscopically dark triplet-pair excitons have only more recently been investigated in the context of singlet fission, motivated by photovoltaic technologies. A simple theoretical picture presents a powerful qualitative and sometimes quantitative description of the singlet fission event. Most importantly, it establishes the language and frames the discussion surrounding the electronic structure and dynamical mechanism of singlet fission. Modern computational tools developed in quantum chemistry and condensed matter physics communities are being employed to fine-tune this theory and provide quantitative, predictive power.
Ultrafast time-resolved spectroscopies are now enabling the precise determination of singlet fission rates and even more complex real-time dynamics. This experimental observation encourages the development and implementation of predictive rate theories and quantum dynamics simulations with which to compare. Our early perturbative reduced density matrix simulations have employed a fully microscopic Hamiltonian to predict singlet fission rates and trends, which are in good agreement with experiment [42, 69, 87], although further work is needed to probe the precise details and implications of the vibrational degrees of freedom. Nonetheless, the current set of tools appears to be sufficiently accurate to enable studies of new molecular assemblies and complex crystalline environments. In particular, the molecular details associated with sample quality, including defects and grain boundaries, would be an important application of large-scale quantum dynamics simulations.
Having established the importance of CT excitons for singlet fission in a variety of dynamical regimes, it seems appropriate to pursue engineered CT states. Environmental effects could be particularly effective in achieving this goal to improve singlet fission performance. Along these lines, an important topic for future research concerns the experimental determination of CT character. Although it seems clear that we need to include CT configurations to reproduce relevant experimental observables such as the absorption spectrum, it would be useful to have experimental probes that can unambiguously report on CT character. To the extent that the complex features seen in linear absorption of larger oligoacenes seem to arise from oscillator strength borrowing from bright FEs to dark CT excitons, then nonlinear spectroscopies might be able to identify cross peaks that shed light on this excitonic mixing.
Acknowledgments
I thank many colleagues for discussions related to this material, including Garnet Chan, Pierre Darancet, Josef Michl, Sahar Sharifzadeh, Omer Yaffe, and Xiaoyang Zhu. I am especially grateful to Mark Hybertsen and David Reichman, with whom I collaborated on much of the work described here. This chapter was written while I was supported as a fellow at the Princeton Center for Theoretical Science.
References
- Knox, R.S. (1963) Theory of Excitons, Academic Press, New York.
- 2. Silbey, R.J., Jortner, J., and Rice, S.A. (1965) J. Chem. Phys., 42, 1515.
- 3. Robinson, G.W. (1970) Annu. Rev. Phys. Chem., 21, 429.
- 4. Davydov, A.S. (1971) Theory of Molecular Excitons, Plenum Press, New York.
- 5. Salcedo, J.R., Siegman, A.E., Dlott, D.D., and Fayer, M.D. (1978) Phys. Rev. Lett., 41, 131.
- 6. Pope, M. and Swenberg, C.E. (1982) Electronic Processes in Organic Crystals, Oxford University Press, New York.
- 7. Petersilka, M., Grossman, U.J., and Gross, E.K.U. (1996) Phys. Rev. Lett., 76, 1212.
- 8. Casida, M.E. (2009) J. Mol. Struct. THEOCHEM, 914, 3.
- 9. Hybertsen, M.S. and Louie, S.G. (1986) Phys. Rev. B, 34, 4927.
- 10. Rohlfing, M. and Louie, S.G. (2000) Phys. Rev. B, 62, 4927.
- 11. White, S.R. (1992) Phys. Rev. Lett., 69, 2863.
- 12. Chan, G.K.-L. and Sharma, S. (2011) Annu. Rev. Phys. Chem., 62, 465.
- 13. Shockley, W. and Queisser, H.J. (1961) J. Appl. Phys., 32, 510.
- 14. Hanna, M.C. and Nozik, A.J. (2006) J. Appl. Phys., 100, 074510.
- 15. Smith, M.B. and Michl, J. (2010) Chem. Rev., 110, 6891.
- 16. Singh, S., Jones, W.J., Siebrand, W., Stoicheff, B.P., and Schneider, W.G. (1965) J. Chem. Phys., 42, 330.
- 17. Sternlicht, H., Nieman, G.C., and Robinson, G.W. (1963) J. Chem. Phys., 38, 1326.
- 18. Avakian, P., Abramson, E., Kepler, R.G., and Caris, J.C. (1963) J. Chem. Phys., 39, 1127.
- 19. Jortner, J., Choi, S.-I., Katz, J.L., and Rice, S.A. (1963) Phys. Rev. Lett., 11, 323.
- 20. Swenberg, C.E. and Stacy, W.T. (1968) Chem. Phys. Lett., 2, 327.
- 21. Choi, S.-I., Jortner, J., Rice, S.A., and Silbey, R.J. (1964) J. Chem. Phys., 41, 3294.
- 22. Jortner, J., Rice, S.A., Katz, J.L., and Choi, S.-I. (1965) J. Chem. Phys., 42, 309.
- 23. Burdett, J.J., Gosztola, D., and Bardeen, C.J. (2011) J. Chem. Phys., 135, 214508.
- 24. Chan, W.-L., Ligges, M., and Zhu, X.-Y. (2012) Nat. Chem., 4, 840.
- 25. Wilson, M.W.B., Rao, A., Johnson, K., Gélinas, S., di Pietro, R., Clark, J., and Friend, R.H. (2013) J. Am. Chem. Soc., 135, 16680.
- 26. Birech, Z., Schwoerer, M., Schmeiler, T., Pflaum, J., and Schwoerer, H. (2014) J. Chem. Phys., 140, 114501.
- 27. Geacintov, N., Pope, M., and Vogel, F.E. III (1969) Phys. Rev. Lett., 22, 593.
- 28. Merrifield, R.E., Avakian, P., and Groff, R.P. (1969) Chem. Phys. Lett., 3, 386.
- 29. Johnson, R.C. and Merrifield, R.E. (1970) Phys. Rev. B, 1, 896.
- 30. Suna, A. (1970) Phys. Rev. B, 1, 1716.
- 31. Paci, I., Johnson, J.C., Chen, X., Rana, G., Popović, D., David, D.E., Nozik, A.J., Ratner, M.A., and Michl, J. (2006) J. Am. Chem. Soc., 128, 16546.
- 32. Müller, A.M., Avlasevich, Y.S., Müllen, K., and Bardeen, C.J. (2006) Chem. Phys. Lett., 421, 518.
- 33. Müller, A.M., Avlasevich, Y.S., Schoeller, W.W., Müllen, K., and Bardeen, C.J. (2007) J. Am. Chem. Soc., 129, 14240.
- 34. Johnson, J.C., Nozik, A.J., and Michl, J. (2010) J. Am. Chem. Soc., 132, 16302.
- 35. Zirzlmeier, J., Lehnherr, D., Coto, P.B., Chernick, E.T., Casillas, R., Basel, B.S., Thoss, M., Tykwinski, R.R., and Guldi, D.M. (2014) Proc. Natl. Acad. Sci. U.S.A., 112, 5325.
- 36. Sanders, S.N., Kumarasamy, E., Pun, A.B., Trinh, M.T., Choi, B., Xia, J., Taffet, E.J., Low, J.Z., Miller, J.R., Roy, X., Zhu, X.-Y., Steigerwald, M.L., Sfeir, M.Y., and Campos, L.M. (2015) J. Am. Chem. Soc., 137, 8965.
- 37. Korovina, N.V., Das, S., Nett, Z., Feng, X., Joy, J., Krylov, A.I., Bradforth, S.E., and Thompson, M.E. (2016) J. Am. Chem. Soc., 138, 617.
- 38. Marciniak, H., Fiebig, M., Huth, M., Schieger, S., Nickel, B., Selmaier, F., and Lochbrunner, S. (2007) Phys. Rev. Lett., 99, 176402.
- 39. Thorsmolle, V.K., Averitt, R.D., Demsar, J., Smith, D.L., Tretiak, S., Martin, R.L., Chi, X., Crone, B.K., Ramirez, A.P., and Taylor, A.J. (2009) Phys. Rev. Lett., 102, 017401.
- 40. Wilson, M.W.B., Rao, A., Ehrler, B., and Friend, R.H. (2013) Acc. Chem. Res., 46, 1330.
- 41. Yost, S.R., Lee, J., Wilson, M.W.B., Wu, T., McMahon, D.P., Parkhurst, R.R., Thompson, N.J., Congreve, D.N., Rao, A., Johnson, K., Sfeir, M.Y., Bawendi, M., Swager, T.M., Friend, R.H., Baldo, M.A., and van Voorhis, T. (2014) Nat. Chem., 6, 492.
- 42. Busby, E., Berkelbach, T.C., Kumar, B., Chernikov, A., Zhong, Y., Zhu, X.-Y., Heinz, T.F., Hybertsen, M.S., Sfeir, M.Y., Reichman, D.R., Nuckolls, C., and Yaffe, O. (2014) J. Am. Chem. Soc., 136, 10654.
- 43. Walker, B.J., Musser, A.J., Beljonne, D., and Friend, R.H. (2013) Nat. Chem., 5, 1019.
- 44. Busby, E., Xia, J., Wu, Q., Low, J.Z., Song, R., Miller, J.R., Zhu, X.-Y., Campos, L.M., and Sfeir, M.Y. (2015) Nat. Mater., 14, 426.
- 45. Kasai, Y., Tamai, Y., Ohkita, H., Benten, H., and Ito, S. (2015) J. Am. Chem. Soc., 137, 15980.
- 46. Pensack, R.D., Tilley, A.J., Parkin, S.R., Lee, T.S., Payne, M.M., Gao, D., Jahnke, A.A., Oblinksy, D.G., Li, P.-F., Anthony, J.E., Seferos, D.S., and Scholes, G.D. (2015) J. Am. Chem. Soc., 137, 6790.
- 47. Smith, M.B. and Michl, J. (2013) Annu. Rev. Phys. Chem., 64, 361.
- 48. Piland, G.B., Burdett, J.J., Dillon, R.J., and Bardeen, C.J. (2014) J. Phys. Chem. Lett., 5, 2312.
- 49. Monahan, N.R. and Zhu, X.-Y. (2015) Annu. Rev. Phys. Chem., 66, 601.
- 50. Hachmann, J., Dorando, J.J., Avilés, M., and Chan, G.K.-L. (2007) J. Chem. Phys., 127, 134309.
- 51. Gidofalvi, G. and Mazziotti, D.A. (2008) J. Chem. Phys., 129, 134108.
- 52. Berkelbach, T.C., Hybertsen, M.S., and Reichman, D.R. (2013) J. Chem. Phys., 138, 114102.
- 53. Král, K. (1972) Czech. J. Phys. B, 22, 566.
- 54. Harcourt, R.D., Scholes, G.D., and Ghiggino, K.P. (1994) J. Chem. Phys., 101, 10521.
- 55. Barford, W. (2005) Electronic and Optical Properties of Conjugated Polymers, Oxford University Press, Oxford.
- 56. May, V. and Kühn, O. (2011) Charge and Energy Transfer Dynamics in Molecular Systems, Wiley-VCH Verlag GmbH, Weinheim.
- 57. Frenkel, J. (1931) Phys. Rev., 37, 17.
- 58. Bassani, F. and Pastori-Parravicini, G. (1975) Electronic States and Optical Transitions in Solids, Pergamon Press, New York.
- 59. Grover, M. and Silbey, R.J. (1971) J. Chem. Phys., 42, 1515.
- 60. Silbey, R.J. (1976) Annu. Rev. Phys. Chem., 27, 203.
- 61. Luzanov, A.V., Casanova, D., Feng, X., and Krylov, A.I. (2015) J. Chem. Phys., 142, 224104.
- 62. Wannier, G. (1937) Phys. Rev., 52, 191.
- 63. Sham, L.J. and Rice, T.M. (1966) Phys. Rev., 144, 708.
- 64. Burdett, J.J. and Bardeen, C.J. (2012) J. Am. Chem. Soc., 134, 8597.
- 65. Scholes, G.D. (2015) J. Phys. Chem. A, 119, 12699.
- 66. Teichen, P. and Eaves, J.D. (2015) J. Chem. Phys., 143, 044118.
- 67. van Voorhis, T., Kowalczyk, T., Kaduk, B., Wang, L.-P., Cheng, C.-L., and Wu, Q. (2010) Annu. Rev. Phys. Chem., 61, 149.
- 68. Nakamura, H. and Truhlar, D.G. (2002) J. Chem. Phys., 117, 5576.
- 69. Berkelbach, T.C., Hybertsen, M.S., and Reichman, D.R. (2014) J. Chem. Phys., 141, 074705.
- 70. Tully, J.C. (1990) J. Chem. Phys., 93, 1061.
- 71. Prezhdo, O.V. and Rossky, P.J. (1997) J. Chem. Phys., 107, 825.
- 72. Kapral, R. and Ciccotti, G. (1999) J. Chem. Phys., 110, 8919.
- 73. Ben-Nun, M. and Martinez, T.J. (2002) Adv. Chem. Phys., 121, 439.
- 74. Casanova, D. and Head-Gordon, M. (2009) Phys. Chem. Chem. Phys., 11, 9779.
- 75. Zimmerman, P.M., Bell, F., Goldey, M., Bell, A.T., and Head-Gordon, M. (2012) J. Chem. Phys., 137, 164110.
- 76. Zimmerman, P.M., Bell, F., Casanova, D., and Head-Gordon, M. (2011) J. Am. Chem. Soc., 133, 19944.
- 77. Feng, X., Luzanov, A.V., and Krylov, A.I. (2013) J. Phys. Chem. Lett., 4, 3845.
- 78. Zimmerman, P.M., Zhang, Z., and Musgrave, C.B. (2010) Nat. Chem., 2, 648.
- 79. Zeng, T., Hoffmann, R., and Ananth, N. (2014) J. Am. Chem. Soc., 136, 5755.
- 80. Freed, K. (1974) J. Chem. Phys., 60, 1765.
- 81. Durand, P. and Malrieu, J.-P. (1987) Adv. Chem. Phys., 321, 412.
- 82. Neuscamman, E., Yanai, T., and Chan, G.K.-L. (2010) Int. Rev. Phys. Chem., 29, 231.
- 83. Yanai, T. and Shiozaki, T. (2012) J. Chem. Phys., 136, 084107.
- 84. Parker, S.M., Seideman, T., Ratner, M.A., and Shiozaki, T. (2013) J. Chem. Phys., 139, 021108.
- 85. Parker, S.M., Seideman, T., Ratner, M.A., and Shiozaki, T. (2014) J. Phys. Chem. C, 118, 12700.
- 86. Casanova, D. and Krylov, A.I. (2016) J. Chem. Phys., 144, 014102.
- 87. Berkelbach, T.C., Hybertsen, M.S., and Reichman, D.R. (2013) J. Chem. Phys., 138, 114103.
- 88. Havenith, R.W.A., de Grier, H.D., and Broer, R. (2012) Mol. Phys., 110, 2445.
- 89. Beljonne, D., Yamagata, H., Brédas, J.L., Spano, F.C., and Olivier, Y. (2013) Phys. Rev. Lett., 110, 226402.
- 90. Kadantsev, E.S., Scott, M.J., and Rubio, A. (2006) J. Chem. Phys., 124, 134901.
- 91. Dreuw, A., Weisman, J.L., and Head-Gordon, M. (2003) J. Chem. Phys., 119, 2943.
- 92. Baer, R. and Neuhauser, D. (2005) Phys. Rev. Lett., 94, 043002.
- 93. Jacquemin, D., Perpéte, E.A., Scuseria, G.E., Ciofini, I., and Adamo, C. (2007) J. Chem. Theory Comput., 4, 123.
- 94. Yamagata, H., Norton, J., Hontz, E., Olivier, Y., Beljonne, D., Brédas, J.L., Silbey, R.J., and Spano, F.C. (2011) J. Chem. Phys., 134, 204703.
- 95. Petelenz, B., Petelenz, P., Shurvell, H.F., and Smith, V.H. (1988) Chem. Phys., 119, 25.
- 96. Petelenz, P., Slawik, M., Yokoi, K., and Zgierski, M.Z. (1996) J. Chem. Phys., 105, 4427.
- 97. Sand, A.M. and Mazziotti, D.A. (2015) J. Chem. Phys., 143, 134110.
- 98. Tiago, M.L., Northrup, J.E., and Louie, S.G. (2003) Phys. Rev. B, 67, 115212.
- 99. Shin, Y.K., Brunschwig, B.S., Creutz, C., and Sutin, N. (1995) J. Am. Chem. Soc., 117, 8668.
- 100. Petelenz, P. and Smith, V.H. (1989) Chem. Phys., 131, 409.
- 101. Sebastian, L., Weiser, G., and Bässler, H. (1981) Chem. Phys., 61, 125.
- 102. Petelenz, P. and Pac, B. (2013) J. Am. Chem. Soc., 135, 17379.
- 103. Sharifzadeh, S., Darancet, P., Kronik, L., and Neaton, J.B. (2013) J. Phys. Chem. Lett., 4, 2197.
- 104. Martin, R.L. (2003) J. Chem. Phys., 118, 4775.
- 105. Hedin, L. (1965) Phys. Rev., 139, A796, doi: 10.1103/PhysRev.139.A796.
- 106. Hummer, K. and Ambrosch-Draxl, C. (2005) Phys. Rev. B, 71, 081202(R).
- 107. Cudazzo, P., Gatti, M., and Rubio, A. (2013) Phys. Rev. B, 86, 195307.
- 108. Sharifzadeh, S., Biller, A., Kronik, L., and Neaton, J.B. (2012) Phys. Rev. B, 85, 125307.
- 109. Rangel, T., Berland, K., Sharifzadeh, S., Brown-Altvater, F., Lee, K., Hyldgaard, P., Kronik, L., and Neaton, J.B. (2016) Phys. Rev. B, 93, 115206.
- 110. Plasser, F., Wormit, M., and Dreuw, A. (2014) J. Chem. Phys., 141, 024106.
- 111. Bäppler, S.A., Plasser, F., Wormit, M., and Dreuw, A. (2014) Phys. Rev. A, 90, 052521.
- 112. Kramers, H.A. (1934) Physica, 1, 182.
- 113. Anderson, P.W. (1950) Phys. Rev., 79, 350.
- 114. Chao, K.A., Spalek, J., and Oles, A.M. (1977) J. Phys. C: Solid State Phys., 10, L271.
- 115. Pollard, W.T. and Friesner, R.A. (1994) J. Chem. Phys., 100, 5054.
- 116. Skourtis, S.S. and Beratan, D.N. (1999) Adv. Chem. Phys., 106, 377.
- 117. Nitzan, A. (2006) Chemical Dynamics in Condensed Phases, Oxford University Press, Oxford, New York.
- 118. Hestand, N.J., Yamagata, H., Xu, B., Sun, D., Zhong, Y., Harutyunyan, A.R., Chen, G., Dai, H.-L., Rao, Y., and Spano, F.C. (2015) J. Phys. Chem. C, 119, 22137.
- 119. Girlando, A., Grisanti, L., Masino, M., Brillante, A., Della Valle, R.G., and Venuti, E. (2011) J. Chem. Phys., 135, 084701.
- 120. Redfield, A.G. (1965) Adv. Magn. Reson., 1, 1.
- 121. Blum, K. (1981) Density Matrix Theory and Applications, Plenum Press, New York.
- 122. Reichman, D., Silbey, R.J., and Suárez, A. (1996) J. Chem. Phys., 105, 10500.
- 123. Hinderhofer, A., Heinemeyer, U., Gerlach, A., Kowarik, S., Jacobs, R.M.J., Sakamoto, Y., Suzuki, T., and Schreiber, F. (2007) J. Chem. Phys., 127, 194705.
- 124. Zusman, L.D. (1980) Chem. Phys., 49, 295.
- 125. Zusman, L.D. (1983) Chem. Phys., 80, 29.
- 126. Garg, A., Onuchic, J.N., and Ambegaokar, V. (1985) J. Chem. Phys., 83, 4491.
- 127. Jortner, J. and Bixon, M. (1988) J. Chem. Phys., 1, 167.
- 128. Chandler, D. (1991) in Les Houches. Part I. Liquids, Freezing and the Glass Transition (eds J.P. Hansen, D. Levesque, and J. Zinn-Justin), Elsevier Science Publishers B.V..
- 129. Zwanzig, R. (2001) Nonequilibrium Statistical Mechanics, Oxford University Press.
- 130. Mukamel, S. (1995) Principles of Nonlinear Optical Spectroscopy, Oxford University Press.
- 131. Tao, G. (2014) J. Phys. Chem. C, 118, 17299.
- 132. Tamura, H., Huix-Rotllant, M., Burghardt, I., Olivier, Y., and Beljonne, D. (2014) Phys. Rev. Lett., 115, 107401.
- 133. Fujihashi, Y. and Ishizaki, A. (2016) J. Phys. Chem. Lett., 7, 363.
- 134. Watanabe, M., Chang, Y.J., Liu, S.-W., Chao, T.-H., Goto, K., Islam, M.M., Yuan, C.-H., Tao, Y.-T., Shinmyozu, T., and Chow, T.J. (2012) Nat. Chem., 4, 574.
- 135. Egorov, S.A. and Skinner, J.L. (1995) J. Chem. Phys., 103, 1533.
- 136. Englman, R. and Jortner, J. (1970) Mol. Phys., 18, 145.
- 137. Singh, J. (1978) J. Phys. Chem. Solids, 39, 1207.
- 138. Marcus, R.A. (1964) Annu. Rev. Phys. Chem., 15, 155.