B COMPOUND INTEREST AND THE NUMBER e
If you have some money, you may decide to invest it to earn interest. The interest can be paid in many different ways—for example, once a year or many times a year. If the interest is paid more frequently than once per year and the interest is not withdrawn, there is a benefit to the investor since the interest earns interest. This effect is called compounding. You may have noticed banks offering accounts that differ both in interest rates and in compounding methods. Some offer interest compounded annually, some quarterly, and others daily. Some even offer continuous compounding.
What is the difference between a bank account advertising 8% compounded annually (once per year) and one offering 8% compounded quarterly (four times per year)? In both cases 8% is an annual rate of interest. The expression 8% compounded annually means that at the end of each year, 8% of the current balance is added. This is equivalent to multiplying the current balance by 1.08. Thus, if $100 is deposited, the balance, B, in dollars, will be

The expression 8% compounded quarterly means that interest is added four times per year (every three months) and that ![]() of the current balance is added each time. Thus, if $100 is deposited, at the end of one year, four compoundings have taken place and the account will contain $100(1.02)4. Thus, the balance will be
of the current balance is added each time. Thus, if $100 is deposited, at the end of one year, four compoundings have taken place and the account will contain $100(1.02)4. Thus, the balance will be
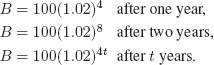
Note that 8% is not the rate used for each three-month period; the annual rate is divided into four 2% payments. Calculating the total balance after one year under each method shows that
![]()
Thus, more money is earned from quarterly compounding, because the interest earns interest as the year goes by. In general, the more often interest is compounded, the more money will be earned (although the increase may not be very large).
We can measure the effect of compounding by introducing the notion of effective annual rate. Since $100 invested at 8% compounded quarterly grows to $108.24 by the end of one year, we say that the effective annual rate in this case is 8.24%. We now have two interest rates that describe the same investment: the 8% compounded quarterly and the 8.24% effective annual rate. We call the 8% the nominal rate (nominal means “in name only”). However, it is the effective rate that tells you exactly how much interest the investment really pays. Thus, to compare two bank accounts, simply compare the effective annual rate. The next time you walk by a bank, look at the advertisements, which should (by law) include both the nominal rate and the effective annual rate.
Using the Effective Annual Yield
| Example 1 | Which is better: Bank X paying a 7% annual rate compounded monthly or Bank Y offering a 6.9% annual rate compounded daily? |
| Solution | We find the effective annual rate for each bank.
Bank X: There are 12 interest payments in a year, each payment being 0.07/12 = 0.005833 times the current balance. If the initial deposit were $100, then the balance B would be
To find the effective annual rate, we look at one year, or 12 months, giving B = 100(1.005833)12 = 100(1.072286), so the effective annual rate ≈ 7.23%. Bank Y: There are 365 interest payments in a year (assuming it is not a leap year), each being 0.069/365 = 0.000189 times the current balance. Then the balance is
so at the end of one year we have multiplied the initial deposit by
so the effective annual rate for Bank Y ≈ 7.14%. Comparing effective annual rates for the banks, we see that Bank X is offering a better investment, by a small margin. |
If interest at an annual rate of r is compounded n times a year, then r/n times the current balance is added n times a year. Therefore, with an initial deposit of P, the balance t years later is
![]()
Note that r is the nominal rate; for example, r = 0.05 when the annual rate is 5%.
Increasing the Frequency of Compounding: Continuous Compounding
Let us look at the effect of increasing the frequency of compounding. How much effect does it have?
| Example 3 | Find the effective annual rate for a 7% annual rate compounded
(a) 1000 times a year. (b) 10,000 times a year. |
| Solution | (a) In one year, a deposit is multiplied by
giving an effective annual rate of about 7.25056%. (b) In one year, a deposit is multiplied by
giving an effective annual yield of about 7.25079%. |
Notice that there's not a great deal of difference—7.25056% versus 7.25079%—between compounding 1000 times each year (about three times per day) and 10,000 times each year (about 30 times per day). What happens if we compound more often still? Every minute? Every second? Surprisingly, the effective annual rate does not increase indefinitely, but tends to a finite value. The benefit of increasing the frequency of compounding becomes negligible beyond a certain point.
For example, computing the effective annual rate on a 7% investment compounded n times per year for values of n larger than 100,000 gives
![]()
So the effective annual rate is about 7.25082%. Even if you take n = 1,000,000 or n = 1010, the effective annual rate does not change appreciably. The value 7.25082% is an upper bound that is approached as the frequency of compounding increases.
When the effective annual rate is at this upper bound, we say that the interest is being compounded continuously. (The word continuously is used because the upper bound is approached by compounding more and more frequently.) Thus, when a 7% nominal annual rate is compounded so frequently that the effective annual rate is 7.25082%, we say that the 7% is compounded continuously. This represents the most one can get from a 7% nominal rate.
Where Does the Number e Fit In?
It turns out that e is intimately connected to continuous compounding. To see this, use a calculator to check that e0.07 ≈ 1.0725082, which is the same number we obtained by compounding 7% a large number of times. So you have discovered that for very large n
![]()
As n gets larger, the approximation gets better and better, and we write
![]()
meaning that as n increases, the value of (1 + 0.07/n)n approaches e0.07.
If P is deposited at an annual rate of 7% compounded continuously, the balance, B, after t years, is given by
![]()
If interest on an initial deposit of P is compounded continuously at an annual rate r, the balance t years later can be calculated using the formula
![]()
In working with compound interest, it is important to be clear whether interest rates are nominal rates or effective rates, as well as whether compounding is continuous or not.
| Example 4 | Find the effective annual rate of a 6% annual rate, compounded continuously. |
| Solution | In one year, an investment of P becomes Pe0.06. Using a calculator, we see that
So the effective annual rate is about 6.18%. |
| Example 5 | You invest money in a certificate of deposit (CD) for your child' education, and you want it to be worth $120,000 in 10 years. How much should you invest if the CD pays interest at a 9% annual rate compounded quarterly? Continuously? |
| Solution | Suppose you invest P initially. A 9% annual rate compounded quarterly has an effective annual rate given by (1 + 0.09/4)4 = 1.0930833, or 9.30833%. So after 10 years you have
Therefore, you should invest
On the other hand, if the CD pays 9% per year, compounded continuously, after 10 years you have
So you would need to invest
Notice that to achieve the same result, continuous compounding requires a smaller initial investment than quarterly compounding. This is to be expected since the effective annual rate is higher for continuous than for quarterly compounding. |
Problems for Appendix B
1. A department store issues its own credit card, with an interest rate of 2% per month. Explain why this is not the same as an annual rate of 24%. What is the effective annual rate?
2. A deposit of $10,000 is made into an account paying a nominal yearly interest rate of 8%. Determine the amount in the account in 10 years if the interest is compounded:
(a) Annually
(b) Monthly
(c) Weekly
(d) Daily
(e) Continuously
3. A deposit of $50,000 is made into an account paying a nominal yearly interest rate of 6%. Determine the amount in the account in 20 years if the interest is compounded:
(a) Annually
(b) Monthly
(c) Weekly
(d) Daily
(e) Continuously
4. Use a graph of y = (1 + 0.07/x)x to estimate the number that (1 + 0.07/x)x approaches as x → ∞. Confirm that the value you get is approximately e0.07.
5. (a) Find (1 + 0.04/n)n for n = 10,000, and 100,000, and 1,000,000. Use the results to predict the effective annual rate of a 4% annual rate compounded continuously.
(b) Confirm your answer by computing e0.04.
6. Find the effective annual rate of a 6% annual rate, compounded continuously.
7. What nominal annual interest rate has an effective annual rate of 5% under continuous compounding?
8. What is the effective annual rate, under continuous compounding, for a nominal annual interest rate of 8%?
9. (a) Find the effective annual rate for a 5% annual interest rate compounded n times/year if
(i) n = 1000
(ii) n = 10,000
(iii) n = 100,000
(b) Look at the sequence of answers in part (a), and predict the effective annual rate for a 5% annual rate compounded continuously.
(c) Compute e0.05. How does this confirm your answer to part (b)?
10 A bank account is earning interest at 6% per year compounded continuously.
(a) By what percentage has the bank balance in the account increased over one year? (This is the effective annual rate.)
(b) How long does it take the balance to double?
(c) For a continuous interest rate r, find a formula for the doubling time in terms of r.
11. Explain how you can match the interest rates (a)–(e) with the effective annual rates I–V without calculation.
(a) 5.5% annual rate, compounded continuously.
(b) 5.5% annual rate, compounded quarterly.
(c) 5.5% annual rate, compounded weekly.
(d) 5% annual rate, compounded yearly.
(e) 5% annual rate, compounded twice a year.
I. 5%
II. 5.06%
III. 5.61%
IV. 5.651%
V. 5.654%
Countries with very high inflation rates often publish monthly rather than yearly inflation figures, because monthly figures are less alarming. Problems 12–13 involve such high rates, which are called hyperinflation.
12. In 1989, US inflation was 4.6% a year. In 1989 Argentina had an inflation rate of about 33% a month.
(a) What is the yearly equivalent of Argentina's 33% monthly rate?
(b) What is the monthly equivalent of the US 4.6% yearly rate?
13. Between December 1988 and December 1989, Brazil's inflation rate was 1290% a year. (This means that between 1988 and 1989, prices increased by a factor of 1 + 12.90 = 13.90.)
(a) What would an article which cost 1000 cruzados (the Brazilian currency unit) in 1988 cost in 1989?
(b) What was Brazil's monthly inflation rate during this period?


