How Support Vector Machines Work

First, why are they called support vector machines? The purpose of an SVM classifier is the same as any other classifier: to find a decision boundary that cleanly separates the classes. SVMs do this by finding a line in 2D space, a plane in 3D space, or a hyperplane in higher-dimensional space that allows them to distinguish between different classes with the greatest certainty possible. In the example in Figure 5-1, there are an infinite number of lines you can draw to separate the two classes, but the best line is the one that produces the widest margin (the one shown on the right). The width of the margin is the distance between the points closest to the boundary in each class along a line perpendicular to the boundary. These points are called support vectors and are circled in red.

Figure 5-1. Maximum-margin classification

Of course, real data rarely lends itself to such clean separation. Overlap between classes inevitably prevents a perfect fit. To accommodate this, SVMs support a regularization parameter usually referred to as C that can be adjusted to loosen or tighten the fit. Lower values of C produce a wider margin with more errors on either side of the decision boundary, as shown in Figure 5-2. Higher values yield a tighter fit to the training data with a correspondingly thinner margin and fewer errors. If C is too high, the model might not generalize well. The optimum value varies by dataset. Data scientists typically try different values of C to determine which one performs the best against test data.

All of the aforementioned is true, but none of it explains why SVMs are so good at what they do. SVMs aren’t the only models that mathematically look for boundaries separating the classes. What makes SVMs special are kernels, some of which add dimensions to data to find boundaries that don’t exist at lower dimensions. Consider Figure 5-3. You can’t draw a line that completely separates the red dots from the purple dots. But if you add a third dimension as shown on the right—a z dimension whose value is based on a point’s distance from the center—then you can slide a plane between the purples and the reds and achieve 100% separation. In this example, data that isn’t linearly separable in two dimensions is linearly separable in three dimensions. The principle at work is Cover’s theorem, which states that data that isn’t linearly separable might be linearly separable if projected into higher-dimensional space using a nonlinear transform.

Figure 5-2. Effect of C on margin width

Figure 5-3. Adding dimensions to achieve linear separability

The kernel transformation used in this example, which projects two-dimensional data to three dimensions by adding a z to every x and y, works well with this particular dataset. But for SVMs to be broadly useful, you need a kernel that isn’t tied to the shape of a specific dataset.

Kernels

Scikit-Learn has several general-purpose kernels built in, including the linear kernel, the RBF kernel,¹ the polynomial kernel, and the sigmoid kernel. The linear kernel doesn’t add dimensions. It works well with data that is linearly separable out of the box, but it doesn’t perform very well with data that isn’t. Applying it to the problem in Figure 5-3 produces the decision boundary on the left in Figure 5-4. Applying the RBF kernel to the same data produces the decision boundary on the right. The RBF kernel projects the x and y values into a higher-dimensional space and finds a hyperplane that cleanly separates the purples from the reds. When projected back to two dimensions, the decision boundary roughly forms a circle. Similar results can be achieved on this dataset with a properly tuned polynomial kernel, but generally speaking, the RBF kernel can find decision boundaries in nonlinear data that the pol⁠y­nomial kernel cannot. That’s why RBF is the default kernel type in Scikit if you don’t specify otherwise.

A logical question to ask is, did the RBF kernel add a z to every x and y? The short answer is no. It effectively projected the data points into a space with an infinite number of dimensions. The key word is effectively. Kernels use mathematical shortcuts called kernel tricks to measure the effect of adding new dimensions without actually computing values for them. This is where the math for SVMs gets hairy. Kernels are carefully designed to compute the dot product between two n-dimensional vectors in m-dimensional space (where m is greater than n and can even be infinite) without generating all those new dimensions, and ultimately, the dot products are all an SVM needs to compute a decision boundary. It’s the mathematical equivalent of having your cake and eating it too, and it’s the secret sauce that makes SVMs awesome. SVMs can take a long time to train on large datasets, but one of the benefits of an SVM is that it tends to do better on smaller datasets with fewer rows or samples than other learning algorithms.

Figure 5-4. Linear kernel versus RBF kernel

Kernel Tricks

Want to see an example of how kernel tricks are used to compute dot products in high-dimensional spaces without computing values for the new dimensions? The following explanation is completely optional. But if you, like me, learn better from concrete examples, then you might find this section helpful.

Let’s start with the two-dimensional circular dataset presented earlier, but this time let’s project it into three-dimensional space with the following equations:

$x^{\text{'}}=x^2$
$y^{\text{'}}=y^2$
$z=x·y·\sqrt{2}$

In other words, we’ll compute x and y in three-dimensional space (x′ and y′ ) by squaring x and y in two-dimensional space, and we’ll add a z that’s the product of the original x and y and the square root of 2. Projecting the data this way produces a clean separation between purples and reds, as shown in Figure 5-5.

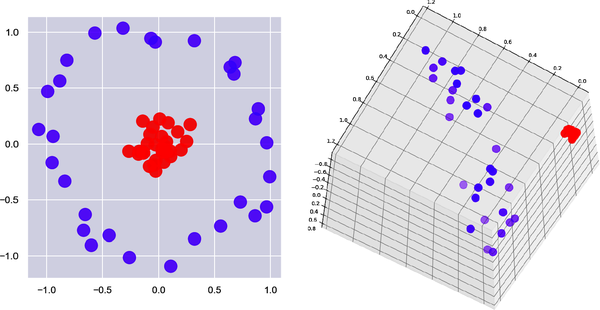
Figure 5-5. Projecting 2D points to 3D to separate two classes

The efficacy of SVMs depends on their ability to compute the dot product of two vectors (or points, which can be treated as vectors) in higher-dimensional space without projecting them into that space—that is, using only the values in the original space. Let’s manufacture a couple of points to work with:

$a=(3,7)$
$b=(2,4)$

We can compute the dot product of these two points this way:

$(3·2)+(7·4)=34$

Of course, the dot product in two dimensions isn’t very helpful. An SVM needs the dot product of these points in 3D space. Let’s use the preceding equations to project a and b to 3D, and then compute the dot product of the result:

$a=(3^2,7^2,3·7·\sqrt{2})=(9,49,29.6984)$
$b=(2^2,4^2,2·4·\sqrt{2})=(4,16,11.3137)$
$(9·4)+(49·16)+(29.6984·11.3137)=1,156$

We now have the dot product of a pair of 2D points in 3D space, but we had to generate coordinates in 3D space to get it. Here’s where it gets interesting. The following function, or kernel trick, produces the same result using only the values in the original 2D space:

$K(a,b)={⟨a,b⟩}^2$

⟨a, b⟩ is simply the dot product of a and b, so ⟨a, b⟩² is the square of the dot product of a and b. We already know how to compute the dot product of a and b. Therefore:

$K((3,7),(2,4))={((3·2)+(7·4))}^2={34}^2=1,156$

This agrees with the result computed by explicitly projecting the points, but with no projection required. That’s the kernel trick in a nutshell. It saves time and memory when going from two dimensions to three. Just imagine the savings when projecting to an infinite number of dimensions—which, you’ll recall, is exactly what the RBF kernel does.

The kernel trick used here wasn’t manufactured from thin air. It happens to be the one used by a degree-2 polynomial kernel. With Scikit, you can fit an SVM classifier with a degree-2 polynomial kernel to a dataset this way:

model = SVC(kernel='poly', degree=2)
model.fit(x, y)

If you apply this to the preceding circular dataset and plot the decision boundary (Figure 5-6, right), the result is almost identical to the one generated by the RBF kernel. Interestingly, a degree-1 polynomial kernel (Figure 5-6, left) produces the same decision boundary as the linear kernel since a line is just a first-degree polynomial.

Kernel tricks are special. Each one is designed to simulate a specific projection into higher dimensions. Scikit gives you a handful of kernels to work with, but there are others that Scikit doesn’t build in. You can extend Scikit with kernels of your own, but the ones that it provides are sufficient for the vast majority of use cases.

Figure 5-6. Degree-1 versus degree-2 polynomial kernel

Hyperparameter Tuning

At the outset, it’s difficult to know which of the built-in kernels will produce the most accurate model. It’s also difficult to know what the right value of C is—that is, the value that provides the best balance between underfitting and overfitting the training data and yields the best results when the model is run with test data. For the RBF and polynomial kernels, there’s a third value called gamma that affects accuracy. And for polynomial kernels, the degree parameter impacts the model’s ability to learn from the training data.

The C parameter controls how aggressively the model fits to the training data. The higher the value, the tighter the fit and the higher the risk of overfitting. Figure 5-7 shows how the RBF kernel fits a model to a set of training data containing three classes with different values of C. The default is C=1 in Scikit, but you can specify a different value to adjust the fit. You can see the danger of overfitting in the lower-right diagram. A point that lies to the extreme right would be classified as a blue, even though it probably belongs to the yellow or brown class. Underfitting is a problem too. In the upper-left example, virtually any data point that isn’t a brown will be classified as a blue.

Figure 5-7. Effect of C on the RBF kernel

An SVM that uses the RBF kernel isn’t properly tuned until you have the right value for gamma too. gamma controls how far the influence of a single data point reaches in computing decision boundaries. Lower values use more points and produce smoother decision boundaries; higher values involve fewer points and fit more tightly to the training data. This is illustrated in Figure 5-8, where increasing gamma while holding C constant closes the decision boundary more tightly around clusters of classes. gamma can be any nonzero positive value, but values between 0 and 1 are the most common. Rather than hardcode a default value for gamma, Scikit picks a default value algorithmically if you don’t specify one.

In practice, data scientists experiment with different kernels and different parameter values to find the combination that produces the most accurate model, a process known as hyperparameter tuning. The usefulness of hyperparameter tuning isn’t unique to SVMs, but you can almost always make an SVM more accurate by finding the optimum combination of kernel type, C, and gamma (and for polynomial kernels, degree).

Figure 5-8. Effect of gamma on the RBF kernel

To aid in the process of hyperparameter tuning, Scikit provides a family of optimizers that includes GridSearchCV, which tries all combinations of a specified set of parameter values with built-in cross-validation to determine which combination produces the most accurate model. These optimizers prevent you from having to write code to do a brute-force search using all the unique combinations of parameter values. To be clear, they do brute-force searches themselves by training the model multiple times, each time with a different combination of values. At the end, you can retrieve the most accurate model from the best_estimator_ attribute, the parameter values that produced the most accurate model from the best_params_ attribute, and the best score from the best_score_ attribute.

Here’s an example that uses Scikit’s SVC class to implement an SVM classifier. For starters, you can create an SVM classifier that uses default parameter values and fit it to a dataset with two lines of code:

model = SVC()
model.fit(x, y)

This uses the RBF kernel with C=1. You can specify the kernel type and values for C and gamma this way:

model = SVC(kernel='poly', C=10, gamma=0.1)
model.fit(x, y)

Suppose you wanted to try two different kernels and five values each for C and gamma to see which combination produces the best results. Rather than write a nested for loop, you could do this:

model = SVC()
 
grid = {
    'C': [0.01, 0.1, 1, 10, 100],
    'gamma': [0.01, 0.25, 0.5, 0.75, 1.0],
    'kernel': ['rbf', 'poly']
}
 
grid_search = GridSearchCV(estimator=model, param_grid=grid, cv=5, verbose=2)
grid_search.fit(x, y) # Train the model with different parameter combinations

The call to fit won’t return for a while. It trains the model 250 times since there are 50 different combinations of kernel, C, and gamma, and cv=5 says to use fivefold cross-validation to assess the results. Once training is complete, you retrieve the best model this way:

best_model = grid_search.best_estimator_

It is not uncommon to run a search regimen such as this one multiple times—the first time with course parameter values, and each time thereafter with narrower ranges of values centered on the values obtained from best_params_. More training time up front is the price you pay for an accurate model. To reiterate, you can almost always make an SVM more accurate by finding the optimum combination of parameters. And for better or worse, brute force is the most effective way to identify the best combination.

model = SVC(probability=True)

Data Normalization

In Chapter 2, I noted that some learning algorithms work better with normalized data. Unnormalized data contains columns of numbers with vastly different ranges—for example, values from 0 to 1 in one column and from 0 to 1,000,000 in another. SVM is a parametric learning algorithm. Training with normalized data is important because SVMs use distances to compute margins. If one dimension spans much larger distances than another, the internal algorithm used to find the maximum margins might have trouble converging on a solution.

The importance of training machine learning models with normalized data isn’t limited to SVMs. Decision trees and learning algorithms such as random forests and gradient-boosted decision trees that rely on decision trees are nonparametric, so they work equally well with normalized and unnormalized data. They are the exception, however. Most other learning algorithms benefit to one degree or another from normalized data. That includes k-nearest neighbors, which although nonparametric uses distance-based calculations internally to discriminate between classes.

Scikit offers several classes for normalizing data. The most commonly used are MinMaxScaler and StandardScaler. The former normalizes data by proportionally reducing the values in each column to values from 0.0 to 1.0. Mathematically, it’s simple. For each column in a dataset, MinMaxScaler subtracts the minimum value in that column from all the column’s values, then it divides each value by the difference between the minimum and maximum values. In the resulting column, the minimum value is 0.0 and the maximum is 1.0.

To demonstrate, I extracted subsets of two columns with vastly different ranges from the breast cancer dataset built into Scikit. Each column contains 100 values. Here are the first 10 rows:

[[1.001e+03 3.001e-01]
 [1.326e+03 8.690e-02]
 [1.203e+03 1.974e-01]
 [3.861e+02 2.414e-01]
 [1.297e+03 1.980e-01]
 [4.771e+02 1.578e-01]
 [1.040e+03 1.127e-01]
 [5.779e+02 9.366e-02]
 [5.198e+02 1.859e-01]
 [4.759e+02 2.273e-01]]

The values in the first column range from 201.9 to 1,878.0; the values in the second column range from 0.000692 to 0.3754. Figure 5-9 shows how the data looks if plotted with the x- and y-axis equally scaled. Because the values in the first column are much larger than the values in the second, the data points appear to form a line. If you adjust the scale of the axes to match the ranges of values in each column, you get a completely different picture (Figure 5-10).

Figure 5-9. Unnormalized data plotted with equally scaled axes

Figure 5-10. Unnormalized data plotted with proportionally scaled axes

Data that is this highly unnormalized can pose a problem for parametric learning algorithms. One way to address that is to apply MinMaxScaler to the data:

from sklearn.preprocessing import MinMaxScaler

scaler = MinMaxScaler()
normalized_data = scaler.fit_transform(data)

Here are the first 10 rows after min-max normalization:

[[0.47676153 0.79904352]
 [0.67066404 0.23006715]
 [0.5972794  0.52496344]
 [0.10989798 0.64238821]
 [0.65336197 0.52656469]
 [0.16419068 0.41928115]
 [0.50002983 0.29892076]
 [0.22433029 0.24810786]
 [0.18966649 0.49427287]
 [0.16347473 0.60475891]]

Figure 5-11 shows a plot of the normalized data with equal axes. The shape of the data didn’t change. What did change is that both columns now contain values ranging from 0.0 to 1.0.

Figure 5-11. Data normalized with MinMaxScaler

SVMs almost always train better with normalized data, but the simple normalization performed by MinMaxScaler sometimes isn’t enough. SVMs tend to respond better to data that is normalized to unit variance using a technique called standardization or Z-score normalization. Unit variance is achieved by doing the following to each column in a dataset:

• Computing the mean and standard deviations of all the values in the column

• Subtracting the mean from each value in the column

• Dividing each value in the column by the standard deviation

This is precisely the transform that Scikit’s StandardScaler class performs on a dataset. Applying unit variance to a dataset is as simple as this:

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
normalized_data = scaler.fit_transform(data)

The values in the original dataset may vary wildly from one column to the next, but the transformed dataset will contain columns of numbers anchored around 0 with ranges that are proportional to each column’s standard deviation. Applying StandardScaler to the dataset produces the following values in the first 10 rows:

[[ 0.93457642  2.36212718]
 [ 1.95483237 -0.35495682]
 [ 1.56870474  1.05328794]
 [-0.99574783  1.61403698]
 [ 1.86379415  1.06093451]
 [-0.71007617  0.5486138 ]
 [ 1.05700714 -0.02615397]
 [-0.39363986 -0.26880538]
 [-0.57603023  0.90672853]
 [-0.71384326  1.4343424 ]]

And it produces the distribution shown in Figure 5-12. Once more, the shape of the data didn’t change, but the values that define that shape changed substantially.

SVMs typically perform best when trained with standardized data, even if all the columns have similar ranges. (The same is true of neural networks, by the way.) The classic case in which columns have similar ranges but benefit from normalization anyway is image data, where each column holds pixel values from 0 to 255. There are exceptions, but it is usually a mistake to throw a bunch of data at an SVM without understanding the distribution of the data—specifically, whether it has unit variance.

Figure 5-12. Data normalized with StandardScaler

Pipelining

If you normalize or standardize the values used to train a machine learning model, you must apply the same transform to values input to the model’s predict method. In other words, if you train a model this way:

model = SVC()
scaler = StandardScaler()
x = scaler.fit_transform(x)
model.fit(x, y)

you make predictions with it this way:

input = [0, 1, 2, 3, 4]
model.predict([scaler.transform([input])

Otherwise, you’ll get nonsensical predictions.

To simplify your code and make it harder to forget to transform training data and prediction data the same way, Scikit offers the make_pipeline function. make_pipeline lets you combine predictive models—what Scikit calls estimators, or instances of classes such as SVC—with transforms applied to data input to those models. Here’s how you use make_pipeline to ensure that any data input to the model is transformed with StandardScaler:

# Train the model
pipe = make_pipeline(StandardScaler(), SVC())
pipe.fit(x, y)
 
# Make a prediction with the model
input = [0, 1, 2, 3, 4]
pipe.predict([input])

Now data used to train the model has StandardScaler applied to it, and data input to make predictions is transformed the same way.

What if you wanted to use GridSearchCV to find the optimum set of parameters for a pipeline that combines a data transform and estimator? It’s not hard, but there’s a trick you need to know about. It involves using class names prefaced with double underscores in the param_grid dictionary passed to GridSearchCV. Here’s an example:

pipe = make_pipeline(StandardScaler(), SVC())
 
grid = {
    'svc__C': [0.01, 0.1, 1, 10, 100],
    'svc__gamma': [0.01, 0.25, 0.5, 0.75, 1.0],
    'svc__kernel': ['rbf', 'poly']
}
 
grid_search = GridSearchCV(estimator=pipe, param_grid=grid, cv=5, verbose=2)
grid_search.fit(x, y) # Train the model with different parameter combinations

This example trains the model 250 times to find the best combination of kernel, C, and gamma for the SVC instance in the pipeline. Note the “svc__” nomenclature, which maps to the SVC instance passed to the make_pipeline function.

Using SVMs for Facial Recognition

Modern facial recognition is often accomplished with neural networks, but support vector machines can do a credible job too. Let’s demonstrate by building a model that recognizes faces. The dataset we’ll use is the Labeled Faces in the Wild (LFW) dataset, which contains more than 13,000 facial images of famous people collected from around the web and is built into Scikit as a sample dataset. Of the more than 5,000 people represented in the dataset, 1,680 have two or more facial images, while only five have 100 or more. We’ll set the minimum number of faces per person to 100, which means that five sets of faces corresponding to five famous people will be imported. Each facial image is labeled with the name of the person the face belongs to.

Start by creating a new Jupyter notebook and using the following statements to load the dataset and crop the facial images:

import numpy as np
import pandas as pd
from sklearn.datasets import fetch_lfw_people
 
faces = fetch_lfw_people(min_faces_per_person=100, slice_=None)
faces.images = faces.images[:, 35:97, 39:86]
faces.data = faces.images.reshape(faces.images.shape[0], faces.images.shape[1] *
                                  faces.images.shape[2])
print(faces.target_names)
print(faces.images.shape)

In total, 1,140 facial images were loaded. Each image measures 47 × 62 pixels for a total of 2,914 pixels per image. That means the dataset contains 2,914 features. Use the following code to show the first 24 images in the dataset and the people to whom the faces belong:

%matplotlib inline
import matplotlib.pyplot as plt
 
fig, ax = plt.subplots(3, 8, figsize=(18, 10))
for i, axi in enumerate(ax.flat):
    axi.imshow(faces.images[i], cmap='gist_gray')
    axi.set(xticks=[], yticks=[], xlabel=faces.target_names[faces.target[i]])

Here is the output:

Check the balance in the dataset by generating a histogram showing how many facial images were imported for each person:

import seaborn as sns
sns.set()

from collections import Counter
counts = Counter(faces.target)
names = {}
 
for key in counts.keys():
    names[faces.target_names[key]] = counts[key]
 
df = pd.DataFrame.from_dict(names, orient='index')
df.plot(kind='bar')

The output reveals that there are far more images of George W. Bush than of anyone else in the dataset:

Classification models are best trained with balanced datasets. Use the following code to reduce the dataset to 100 images of each person:

mask = np.zeros(faces.target.shape, dtype=bool)
 
for target in np.unique(faces.target):
    mask[np.where(faces.target == target)[0][:100]] = 1
     
x = faces.data[mask]
y = faces.target[mask]
x.shape

Note that x contains 500 facial images and y contains the labels that go with them: 0 for Colin Powell, 1 for Donald Rumsfeld, and so on. Now let’s see if an SVM can make sense of the data. We’ll train three different models: one that uses a linear kernel, one that uses a polynomial kernel, and one that uses an RBF kernel. In each case, we’ll use GridSearchCV to optimize hyperparameters. Start with a linear model and four different values of C:

from sklearn.svm import SVC
from sklearn.model_selection import GridSearchCV
 
svc = SVC(kernel='linear')
 
grid = {
    'C': [0.1, 1, 10, 100]
}
 
grid_search = GridSearchCV(estimator=svc, param_grid=grid, cv=5, verbose=2)
grid_search.fit(x, y) # Train the model with different parameters
grid_search.best_score_

This model achieves a cross-validated accuracy of 84.2%. It’s possible that accuracy can be improved by standardizing the image data. Run the same grid search again, but this time use StandardScaler to apply unit variance to all the pixel values:

from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
 
scaler = StandardScaler()
svc = SVC(kernel='linear')
pipe = make_pipeline(scaler, svc)
 
grid = {
    'svc__C': [0.1, 1, 10, 100]
}
 
grid_search = GridSearchCV(estimator=pipe, param_grid=grid, cv=5, verbose=2)
grid_search.fit(x, y)
grid_search.best_score_

Standardizing the data produced an incremental improvement in accuracy. What value of C produced that accuracy?

grid_search.best_params_

Is it possible that a polynomial kernel could outperform a linear kernel? There’s an easy way to find out. Note the introduction of the gamma and degree parameters to the parameter grid. These parameters, along with C, can greatly influence a polynomial kernel’s ability to fit to the training data:

scaler = StandardScaler()
svc = SVC(kernel='poly')
pipe = make_pipeline(scaler, svc)
 
grid = {
    'svc__C': [0.1, 1, 10, 100],
    'svc__gamma': [0.01, 0.25, 0.5, 0.75, 1],
    'svc__degree': [1, 2, 3, 4, 5]
}
 
grid_search = GridSearchCV(estimator=pipe, param_grid=grid, cv=5, verbose=2)
grid_search.fit(x, y) # Train the model with different parameter combinations
grid_search.best_score_

The polynomial kernel achieved the same accuracy as the linear kernel. What parameter values led to this result?

grid_search.best_params_

The best_params_ attribute reveals that the optimum value of degree was 1, which means the polynomial kernel acted like a linear kernel. It’s not surprising, then, that it achieved the same accuracy. Could an RBF kernel do better?

scaler = StandardScaler()
svc = SVC(kernel='rbf')
pipe = make_pipeline(scaler, svc)
 
grid = {
    'svc__C': [0.1, 1, 10, 100],
    'svc__gamma': [0.01, 0.25, 0.5, 0.75, 1.0]
}
 
grid_search = GridSearchCV(estimator=pipe, param_grid=grid, cv=5, verbose=2)
grid_search.fit(x, y)
grid_search.best_score_

The RBF kernel didn’t perform as well as the linear and polynomial kernels. There’s a lesson here. The RBF kernel often fits to nonlinear data better than other kernels, but it doesn’t always fit better. That’s why the best strategy with an SVM is to try different kernels with different parameter values. The best combination will vary from dataset to dataset. For the LFW dataset, it seems that a linear kernel is best. That’s convenient, because the linear kernel is the fastest of all the kernels Scikit provides.

Confusion matrices are a great way to visualize a model’s accuracy. Let’s split the dataset, train an optimized linear model with 80% of the images, test it with the remaining 20%, and show the results in a confusion matrix.

The first step is to split the dataset. Note the stratify=y parameter, which ensures that the training dataset and the test dataset have the same proportion of samples of each class as the original dataset. In this example, the training dataset will contain 20 samples of each of the five people:

from sklearn.model_selection import train_test_split
 
x_train, x_test, y_train, y_test = train_test_split(x, y, train_size=0.8,
                                                    stratify=y, random_state=0)

Now train a linear SVM with the optimum C value revealed by the grid search:

scaler = StandardScaler()
svc = SVC(kernel='linear', C=0.1)
pipe = make_pipeline(scaler, svc)
pipe.fit(x_train, y_train)

Cross-validate the model to confirm its accuracy:

from sklearn.model_selection import cross_val_score
 
cross_val_score(pipe, x, y, cv=5).mean()

Use a confusion matrix to see how the model performs against the test data:

from sklearn.metrics import ConfusionMatrixDisplay as cmd

fig, ax = plt.subplots(figsize=(6, 6))
ax.grid(False)
cmd.from_estimator(pipe, x_test, y_test, display_labels=faces.target_names,
                   cmap='Blues', xticks_rotation='vertical', ax=ax)

Here is the output:

The model correctly identified Colin Powell 16 times out of 20, Donald Rumsfeld 19 times out of 20, and so on. That’s not bad. And it’s a great example of support vector machines at work.

Summary

Support vector machines, or SVMs, frequently fit to datasets better than other learning algorithms. SVMs are maximum-margin classifiers that use kernel tricks to simulate adding dimensions to data. The theory is that data that isn’t linearly separable in m dimensions might be separable in n dimensions if n is higher than m. SVMs are most often used for classification, but they can perform regression too. As an experiment, try replacing GradientBoostingRegressor in the taxi-fare example in Chapter 2 with SVR and using GridSearchCV to optimize the model’s hyperparameters. Which model produces the highest cross-validated coefficient of determination?

SVMs usually train better with data that is normalized to unit variance. That’s true even if the values in all the columns have similar ranges, but it’s especially true if they don’t have similar ranges. Scikit’s StandardScaler class applies unit variance to data. Unit variance is achieved by dividing the values in a column by the mean of all the values in the column and dividing by the standard deviation. Scikit’s make_pipeline function enables you to combine transformers such as StandardScaler and classifiers such as SVC into one logical unit to ensure that data passed to fit, predict, and predict_proba undergoes the same transformations.

SVMs require tuning in order to achieve optimum accuracy. Tuning means finding the right values for parameters such as C, gamma, and kernel, and it entails trying different parameter combinations and assessing the results. Scikit provides classes such as GridSearchCV to help, but they increase training time by training the model once for each unique combination of parameter values.

SVMs can seem magical in their ability to fit mathematical models to complex datasets. But in my view, that magic takes a back seat to the numerical gymnastics performed by principal component analysis (PCA), which solves a variety of problems routinely encountered in machine learning. I often introduce PCA by telling audiences that it’s the best-kept secret in machine learning. After Chapter 6, it will be a secret no longer.