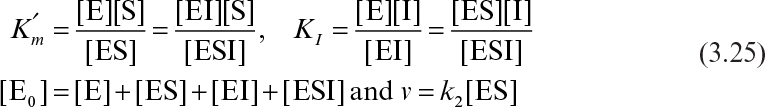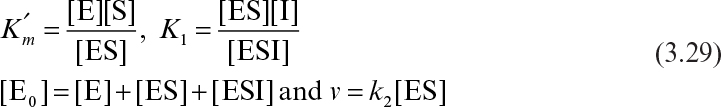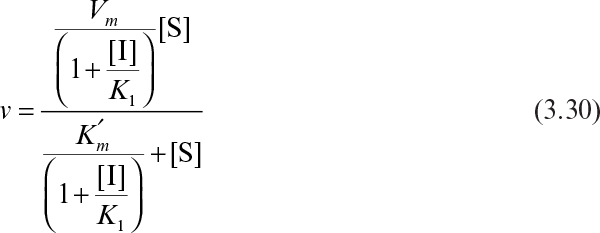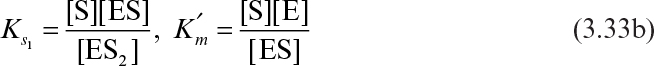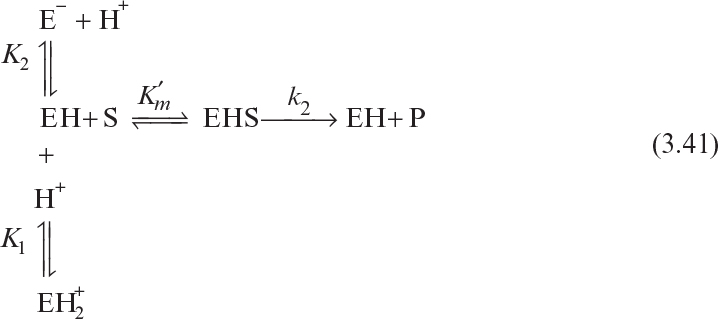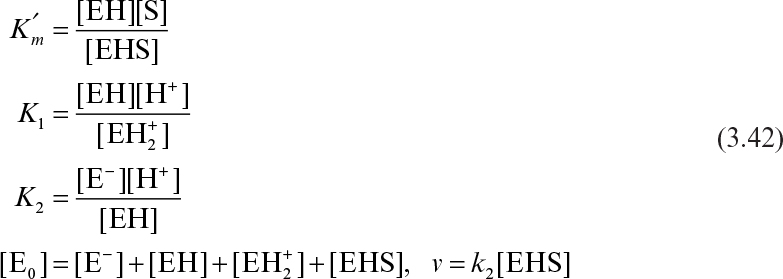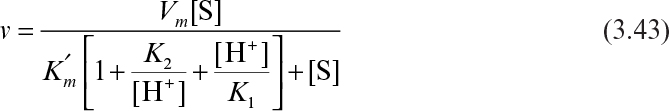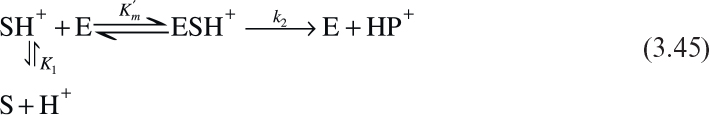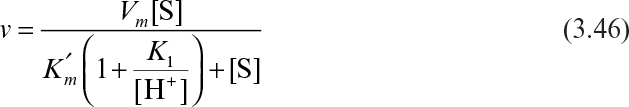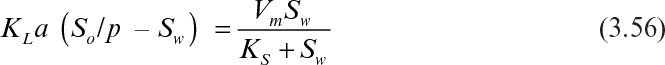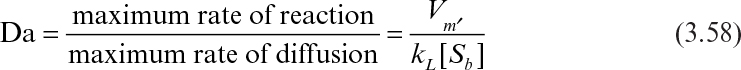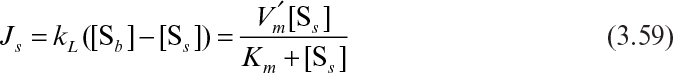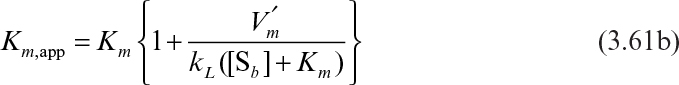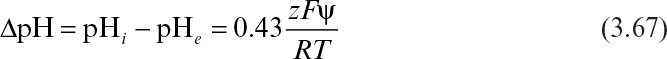3. Enzymes
Enzymes are usually proteins of high molecular weight (15,000 < MW < several million daltons) that act as catalysts. Recently, it has been shown that some RNA molecules are also catalytic, but the vast majority of cellular reactions are mediated by protein catalysts. RNA molecules that have catalytic properties are called ribozymes. Both ribozymes and enzymes are specific, versatile, and very effective biological catalysts, resulting in much higher reaction rates as compared to chemically catalyzed reactions under ambient conditions.
More than 2000 enzymes are known. Enzymes are named by adding the suffix -ase to the end of the substrate, such as urease, or to the end of the reaction catalyzed, such as alcohol dehydrogenase. Some enzymes have a simple structure, such as a folded polypeptide chain (typical of most hydrolytic enzymes). Many enzymes have more than one subunit. Some protein enzymes require a nonprotein group for their activity. This group is either a cofactor, such as metal ions, Mg, Zn, Mn, Fe, or a coenzyme, such as a complex organic molecule, nicotinamide adenine dinucleotide (NAD), flavin adenine dinucleotide (FAD), coenzyme A (CoA), or some vitamins. An enzyme containing a nonprotein group is called a holoenzyme. The protein part of this enzyme is the apoenzyme (holoenzyme = apoenzyme + cofactor). Enzymes that occur in several different molecular forms, but catalyze the same reaction, are called isozymes. Some enzymes are grouped to form enzyme complexes. Enzymes are substrate specific and are classified according to the reaction they catalyze. Major classes of enzymes and their functions are listed in Table 3.1.
3.1. How Enzymes Work
Enzymes lower the activation energy of the reaction catalyzed by binding the substrate and forming an enzyme–substrate complex. Enzymes do not affect the free-energy change or the equilibrium constant. Figure 3.1 illustrates the action of an enzyme from the activation-energy point of view. For example, the activation energy for the decomposition of hydrogen peroxide varies depending on the type of catalysis. The activation energy of the uncatalyzed reaction at 20°C is 18 kilocalories per mole (kcal/mol), whereas the ∆E values for chemically catalyzed (by colloidal platinum) and enzymatically catalyzed (catalase) decomposition are 13 and 7 kcal/mol, respectively. That is, catalase accelerates the rate of reaction by a factor of about 108. This large change in rate for a relatively small change in activation energy is due to the exponential dependence of rate on activation energy.

Figure 3.1. Activation energies of enzymatically catalyzed and uncatalyzed reactions. Note that │ΔG°A2│ < │ΔG°A1│.
The molecular aspects of enzyme–substrate interaction are not yet fully understood. This interaction varies from one enzyme–substrate complex to another. Various studies using x-ray and Raman spectroscopy have revealed the presence of the enzyme–substrate complex. The interaction between the enzyme and its substrate is usually by weak forces. In most cases, van der Waals forces and hydrogen bonding are responsible for the formation of enzyme–substrate complexes. The substrate binds to a specific site on the enzyme known as the active site. The substrate is a relatively small molecule and fits into a certain region on the enzyme molecule, which is a much larger molecule. The simplest model describing this interaction is the lock-and-key model, in which the enzyme represents the lock and the substrate represents the key, as described in Figure 3.2. The induced fit model is a more widely accepted mechanism for enzyme–substrate interaction where the active site of the enzyme goes through some conformational changes to bind the substrate. Enzymatic reaction takes place as a result of those conformational changes.
In multisubstrate enzyme–catalyzed reactions, enzymes can hold substrates such that reactive regions of substrates are close to each other and to the enzyme’s active site, which is known as the proximity effect. Also, enzymes may hold the substrates at certain positions and angles to improve the reaction rate, which is known as the orientation effect. In some enzymes, the formation of an enzyme–substrate complex causes slight changes in the three-dimensional shape of the enzyme. This induced fit of the substrate to the enzyme molecule may contribute to the catalytic activity of the enzyme, too. The enzymes lysozyme and carboxypeptidase A have been observed to change their three-dimensional structure upon complexing with the substrate. Enzyme catalysis is affected not only by the primary structure of enzymes but also by the secondary, tertiary, and quaternary structures. The properties of the active site of enzymes and the folding characteristics have a profound effect on the catalytic activity of enzymes. Certain enzymes require coenzymes and cofactors for proper functioning. Table 3.2 lists some enzymes and their cofactors and coenzymes.
3.2. Enzyme Kinetics
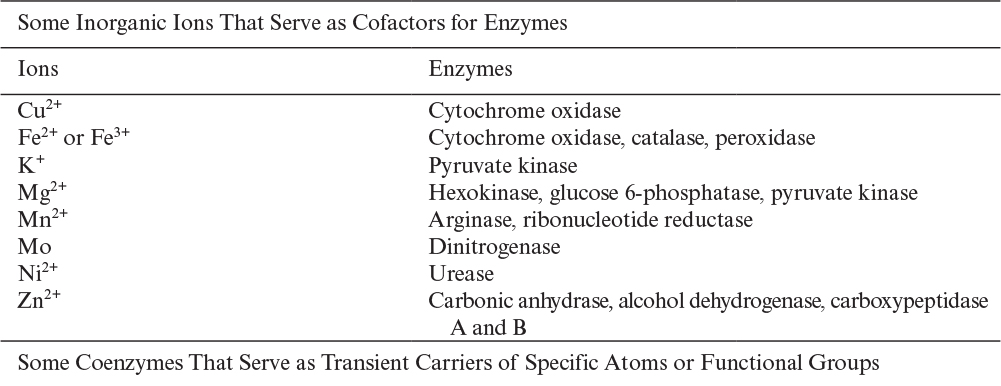
A mathematical model of the kinetics of single-substrate-enzyme-catalyzed reactions was first developed by V. C. R. Henri in 1902 and by L. Michaelis and M. L. Menten in 1913. Kinetics of simple enzyme–catalyzed reactions are often referred to as Michaelis–Menten kinetics or saturation kinetics. The qualitative features of enzyme kinetics are similar to Langmuir–Hinshelwood kinetics (see Figure 3.3). These models are based on data from batch reactors with constant liquid volume in which the initial substrate, [S0], and enzyme, [E0], concentrations are known. More complicated enzyme–substrate interactions such as multisubstrate–multienzyme reactions can take place in biological systems.
An enzyme solution has a fixed number of active sites to which substrates can bind. At high substrate concentrations, all these sites may be occupied by substrates, or the enzyme is saturated. Saturation kinetics can be obtained from a simple reaction scheme that involves a reversible step for enzyme–substrate complex formation and a dissociation step of the enzyme–substrate complex:
It is assumed that the enzyme–substrate complex is established rather rapidly and the rate of the reverse reaction of the second step is negligible. The assumption of an irreversible second reaction often holds only when product accumulation is negligible at the beginning of the reaction. Two major approaches used in developing a rate expression for the enzyme–catalyzed reactions are rapid-equilibrium approach and quasi-steady-state approach.
3.2.1. Mechanistic Models for Simple Enzyme Kinetics
Both the quasi-steady-state approximation and the assumption of rapid equilibrium share the same few initial steps in deriving a rate expression for the mechanism in equation 3.1, where the rate of product formation is
where v is the rate of product formation or substrate consumption in mol/l-s.
The rate constant k2 is often denoted as kcat in the biological literature. The rate of variation of the enzyme–substrate complex is
Since the enzyme is not consumed, the conservation equation on the enzyme yields
At this point, an assumption is required to achieve an analytical solution.
3.2.1.1. The rapid-equilibrium assumption.
Henri, Michaelis, and Menten used essentially this approach. Assuming a rapid equilibrium between the enzyme and substrate to form an [ES] complex, we can use the equilibrium coefficient to express [ES] in terms of [S].
The equilibrium constant is
Since [E] = [E0] – [ES], if enzyme is conserved, then
where ![]() , which is the dissociation constant of the enzyme–substrate complex. Substituting equation 3.7 into equation 3.2 yields
, which is the dissociation constant of the enzyme–substrate complex. Substituting equation 3.7 into equation 3.2 yields
where Vm = k2[E0].
In this case, the maximum forward velocity of the reaction is Vm. Vm changes if more enzyme is added, but the addition of more substrate has no influence on Vm. ![]() is often called the Michaelis–Menten constant, and the prime reminds us that it was derived by assuming rapid equilibrium in the first step. A low value of
is often called the Michaelis–Menten constant, and the prime reminds us that it was derived by assuming rapid equilibrium in the first step. A low value of ![]() suggests that the enzyme has a high affinity for the substrate. Also,
suggests that the enzyme has a high affinity for the substrate. Also, ![]() corresponds to the substrate concentration, giving the half-maximal reaction velocity.
corresponds to the substrate concentration, giving the half-maximal reaction velocity.
An equation of exactly the same form as equation 3.8 can be derived with a different, more general assumption applied to the reaction scheme in equation 3.1.
3.2.1.2. The quasi-steady-state assumption.
In many cases, the assumption of rapid equilibrium following mass-action kinetics is not valid, although the enzyme–substrate reaction still shows saturation-type kinetics.
G. E. Briggs and J. B. S. Haldane first proposed using the quasi-steady-state assumption. In most experimental systems, a closed system (batch reactor) is used in which the initial substrate concentration greatly exceeds the initial enzyme concentration. They suggest that since [E0] was small, d[ES]/dt ≈ 0. (This logic is flawed. Do you see why?) Computer simulations of the actual time course represented by equations 3.2, 3.3, and 3.4 have shown that in a closed system, the quasi-steady-state hypothesis holds after a brief transient if[S0] >> [E0] (e.g., 100×). Figure 3.4 displays one such time course.

Figure 3.4. Time course of the formation of an enzyme–substrate complex and initiation of the steady state, as derived from computer solutions of data obtained in an actual experiment on a typical enzyme. The portion in the dashed box in the top graph is shown in magnified form on the lower graph. (From Lehninger, Principles of Biochemistry, 6th ed., by David L. Nelson et al., Copyright 2013. All rights reserved. Reprinted by permission of W. H. Freeman.)
By applying the quasi-steady-state assumption to equation 3.3, we find
Substituting the enzyme conservation equation 3.4 in equation 3.9 yields
Solving equation 3.10 for [ES],
Substituting equation 3.11 into equation 3.2 yields
where Km is (k–1 + k2)/k1 and Vm is k2[E0]. Under most circumstances (simple experiments), it is impossible to determine whether Km or ![]() is more suitable. Since Km results from the more general derivation, we use it in the rest of our discussions.
is more suitable. Since Km results from the more general derivation, we use it in the rest of our discussions.
3.2.2. Determining Rate Parameters for Michaelis–Menten Kinetics
The determination of values for Km and Vm with high precision may be difficult. Typically, experimental data are obtained from initial-rate experiments. A batch reactor is charged with a known amount of substrate [S0] and enzyme [E0]. The product (or substrate concentration) is plotted against time. The initial slope of this curve is estimated (i.e., v = d[P]/dt|t=0 = d[S]/dt|t=0). This value of v then depends on the values of [E0] and [S0] in the charge to the reactor. Many such experiments at different initial substrate concentrations can be performed to generate many pairs of v0 and [S]0 data. The initial rate data at different [S]0 levels could be plotted as in Figure 3.3; however, the accurate determination of Km from such a plot is very difficult. Consequently, other methods of analyzing such data have been suggested.
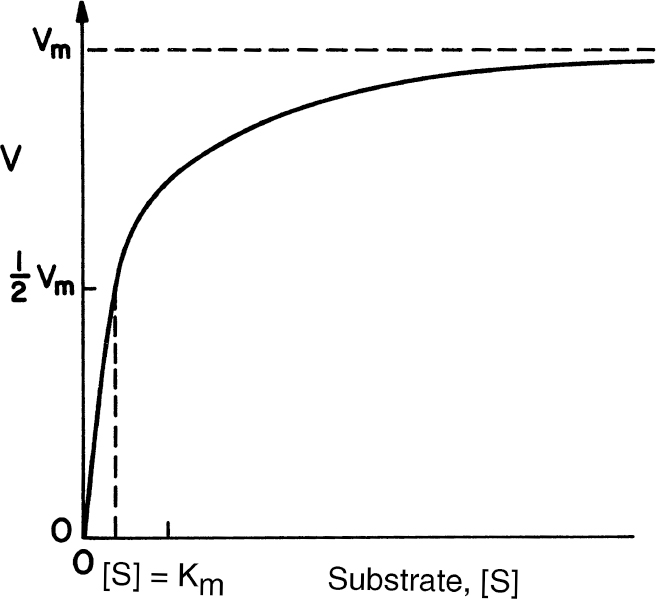
3.2.2.1. Double-reciprocal plot (Lineweaver–Burk plot).
Equation 3.12b can be linearized in double-reciprocal form:
A plot of 1/v versus 1/[S] yields a linear line with a slope of Km/Vm and y-axis intercept of 1/Vm, as depicted in Figure 3.5. A double-reciprocal plot gives good estimates on Vm but not necessarily on Km. Because the error about the reciprocal of a data point is not symmetric, be cautious in applying regression analysis (least squares) to such plots. Data points at low substrate concentrations influence the slope and intercept more than those at high substrate concentrations.
3.2.2.2. Eadie–Hofstee plot.
Equation 3.12b can be rearranged as
A plot of v versus v/[S] results in a line of slope –Km and y-axis intercept of Vm, as depicted in Figure 3.6. Eadie–Hofstee plots can be subject to large errors because both coordinates contain υ, but there is less bias on points at low [S]. This is a good method for estimation of Km but not Vm.
3.2.2.3. Hanes–Woolf plot.
Rearrangement of Equation 3.12b yields
A plot of [S]/v versus [S] results in a line of slope 1/Vm and y-axis intercept of Km/Vm, as depicted in Figure 3.7. This plot is used to determine Vm more accurately.
It is preferable to determine kinetic constants from any of these approaches based on the slope rather than the intercept. The intercept often designates hypothetical cases where S or V approach zero or infinity. Multivariable regression analyses are also commonly used for determination of the kinetic constants using the experimental data.
3.2.2.4. Batch kinetics.
The time course of variation of [S] in a batch enzymatic reaction can be determined from
Equation 3.12b can be integrated to yield
Equation 3.16 can be rearranged to give
A plot of 1/t Ln[S0]/[S] versus {[S0] – [S]}/t results in a line of slope –1Km and intercept of Vm/Km. However, Vm may be better determined from a plot of Ln [S0]/[S] versus time (t), where the slope is Vm/Km and the intercept is {[S0] – [S]}/Km.
3.2.2.5. Interpretation of Km and Vm.
While Km (or ![]() ) is an intrinsic parameter, Vm is not. Km is solely a function of rate parameters and is expected to change with temperature or pH. However, Vm is a function of the rate parameter k2 and the initial enzyme level, [E0]. As [E0] changes, so does Vm. Of course, k2 can be readily calculated if [E0] is known. For highly purified enzyme preparations, it may be possible to express [E0] in terms of mol/l or g/l.
) is an intrinsic parameter, Vm is not. Km is solely a function of rate parameters and is expected to change with temperature or pH. However, Vm is a function of the rate parameter k2 and the initial enzyme level, [E0]. As [E0] changes, so does Vm. Of course, k2 can be readily calculated if [E0] is known. For highly purified enzyme preparations, it may be possible to express [E0] in terms of mol/l or g/l.
When the enzyme is part of a crude preparation, its concentration is in terms of “units.” A unit is the amount of enzyme that gives a predetermined amount of catalytic activity under specific conditions. For example, one unit would be the formation of one μmol product per minute at a specified pH and temperature with a substrate concentration much greater than the value of Km. The specific activity is the number of units of activity per amount of total protein. For example, a crude cell lysate might have a specific activity of 0.2 units/mg protein, which upon purification may increase to 10 units/mg protein. Only enzyme that remains catalytically active will be measured. The enzyme may be denatured if it unfolds or has its three-dimensional shape altered by extreme pH or temperature changes during purification. The denatured enzyme will have no activity.
3.2.3. Models for More Complex Enzyme Kinetics
The kinetics of enzyme reactors can become quite complex. Here we discuss some examples of common kinetic expressions that involve multiple binding sites. These expressions show inhibition or activation by small molecules. These complex kinetic forms are often required within a cell to describe enzymes that regulate cellular function. For example, if too much of a product is formed, the cell may need to slow its production rate. Conversely, it may be necessary to activate an enzyme to a higher rate of conversion to respond to changes in other intracellular chemical concentrations. Some of these examples of cell regulation are given in Chapter 4, “How Cells Work.” Here we focus on the kinetics of individual isolated enzymes, often for industrial use outside of the cell. We must be aware of these kinetics to design properly processes using enzymes as industrial catalysts.
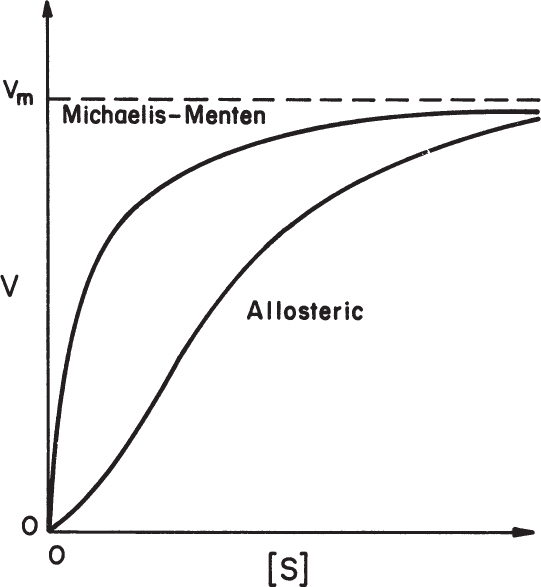
3.2.3.1. Allosteric enzymes.
Some enzymes have more than one substrate-binding site. The binding of one substrate to the enzyme facilitates binding of other substrate molecules. This behavior is known as allostery or cooperative binding, and regulatory enzymes show this behavior. The rate expression in this case is
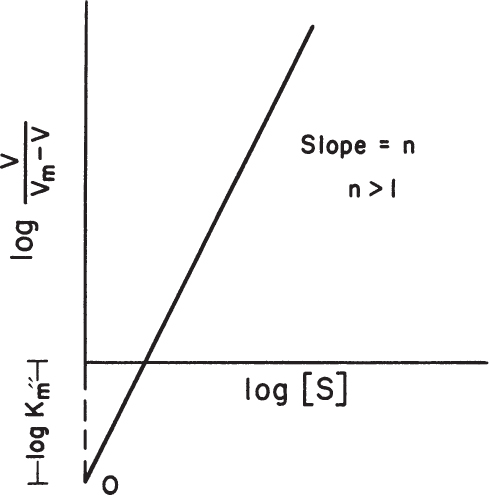
where n = cooperativity coefficient and n > 1 indicates positive cooperativity. Figure 3.8 compares Michaelis–Menten kinetics with allosteric enzyme kinetics, indicating a sigmoidal shape of υ–[S] plot for allosteric enzymes.
The cooperativity coefficient can be determined by rearranging equation 3.18 as follows and by plotting Ln v/(Vm – v) versus Ln[S], as depicted in Figure 3.9:
Depending on the value of n, substrate binding may be cooperative when n > 1, or noncooperative (prohibitive) when n < 1. Substrate binding is independent or not affected from the other bound substrates when n = 1, which is a major assumption for Michaelis–Menten kinetics.
3.2.3.2. Inhibited enzyme kinetics.
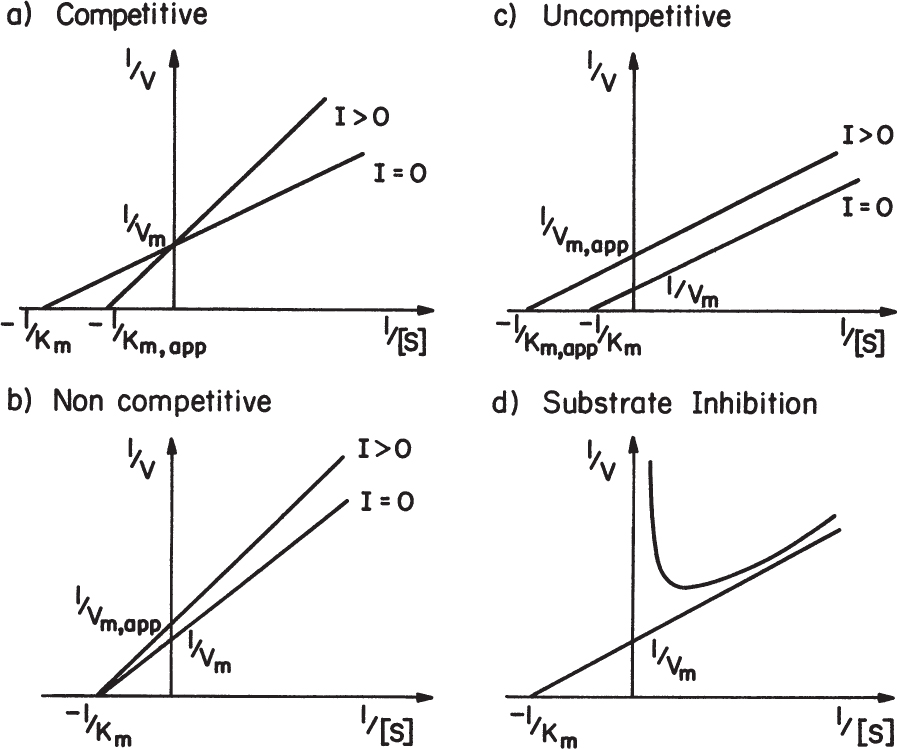
Certain compounds may bind to enzymes and reduce their activity. These compounds are known to be enzyme inhibitors. Enzyme inhibitions may be irreversible or reversible. Irreversible inhibitors such as heavy metals (lead, cadmium, mercury, and others) form a stable complex with enzyme and reduce enzyme activity. Such enzyme inhibition may be reversed only by using chelating agents such as EDTA (ethylenediaminetetraacetic acid) and citrate. Reversible inhibitors may dissociate more easily from the enzyme after binding. The three major classes of reversible enzyme inhibitions are competitive, noncompetitive, and uncompetitive inhibitions. The substrate may act as an inhibitor in some cases.
Competitive inhibitors are usually substrate analogs and compete with substrate for the active site of the enzyme. The competitive enzyme inhibition scheme can be described as
Let us assume rapid equilibrium and a definition of
We can then develop the following equation for the rate of enzymatic conversion:
or
where

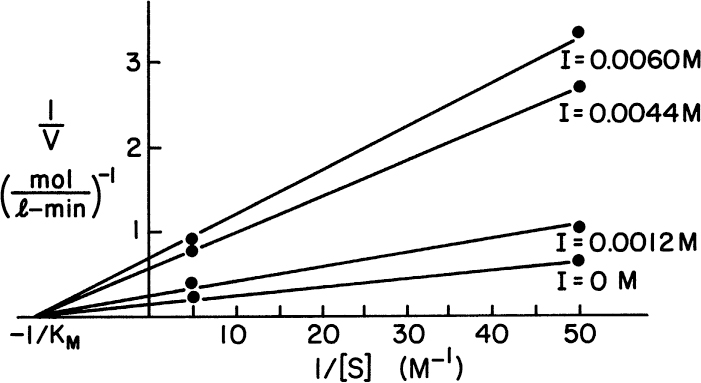
The net effect of competitive inhibition is an increased value of ![]() , and, therefore, reduced reaction rate. Competitive inhibition can be overcome by high concentrations of substrate. Figure 3.10 describes competitive enzyme inhibition in the form of a double-reciprocal plot.
, and, therefore, reduced reaction rate. Competitive inhibition can be overcome by high concentrations of substrate. Figure 3.10 describes competitive enzyme inhibition in the form of a double-reciprocal plot.
Noncompetitive inhibitors are not substrate analogs. Inhibitors bind on sites other than the active site and reduce enzyme affinity to the substrate. Noncompetitive enzyme inhibition can be described as follows:
With the definitions of
we can develop the following rate equation:
or
where
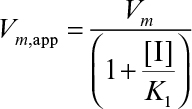
The net effect of noncompetitive inhibition is a reduction in Vm. High substrate concentrations would not overcome noncompetitive inhibition. Other reagents need to be added to block binding of the inhibitor to the enzyme. In some forms of noncompetitive inhibition Vm is reduced and ![]() is increased. This occurs if the complex ESI can form product.
is increased. This occurs if the complex ESI can form product.
Uncompetitive inhibitors bind to the ES complex only and have no affinity for the enzyme itself. The scheme for uncompetitive inhibition follows:
With the definitions of
we can develop the following equation for the rate of reaction:
or
The net effect of uncompetitive inhibition is a reduction in both Vm and ![]() values. Reduction in Vm has a more pronounced effect than reduction in
values. Reduction in Vm has a more pronounced effect than reduction in ![]() and the net result is a reduction in reaction rate. Uncompetitive inhibition is described in Figure 3.10 in the form of a double-reciprocal plot.
and the net result is a reduction in reaction rate. Uncompetitive inhibition is described in Figure 3.10 in the form of a double-reciprocal plot.
Mixed inhibition mechanism is somewhat similar to the noncompetitive enzyme inhibition with the only difference that both the maximum reaction rate (Vm) decreases and the ![]() increases as follows:
increases as follows:
and
In this case, the inhibitors do not bind to the active site allowing the substrate to bind the EI complex to form ESI which has some catalytic activity to produce product.
High substrate concentrations may cause inhibition in some enzymatic reactions, known as substrate inhibition. Substrate inhibition is described in Figure 3.11.
The reaction scheme for uncompetitive substrate inhibition is
Consider the following definitions:
The assumption of rapid equilibrium yields
A double-reciprocal plot describing substrate inhibition is given in Figure 3.10.
At low substrate concentrations, [S]2/Ks1 <<1, and inhibition effect is not observed. The rate is
or
A plot of 1/v versus 1/[S] results in a line of slope ![]() /Vm and intercept of 1/Vm.
/Vm and intercept of 1/Vm.
At high substrate concentrations, ![]() and inhibition is dominant. The rate is
and inhibition is dominant. The rate is
or
A plot of 1/v versus [S] results in a line of slope 1/KS1. Vm and intercept of 1/Vm.
The substrate concentration resulting in the maximum reaction rate can be determined by setting dv/d [S] = 0. The [S]max is given by
3.2.3.3. Enzyme activation.
Just as enzyme inhibitors lower enzymatic activity, some molecules may bind to the enzymes to increase the enzymatic activity. These compounds are known as the enzyme activators, which are usually involved in allosteric enzymes for regulation of the metabolism.
A good example of an enzyme activator is fructose 2,6 biphosphate, which activates phosphofructokinase and increases the rate of metabolism in response to the hormone glucagon.
The activation energy of the enzymatic reaction is reduced upon binding the activator to the enzyme molecule increasing the reaction rate.
An activator molecule can increase the Vm or decrease the ![]() or can do both with a net effect of increasing the rate of enzymatic reaction. In the presence of an activator the enzyme kinetics may take the following form:
or can do both with a net effect of increasing the rate of enzymatic reaction. In the presence of an activator the enzyme kinetics may take the following form:
and
Here (A) is the activator concentration and KA is the dissociation constant for the enzyme–activator complex. The term (1 + (A)/KA) is known as the activation factor.
In the presence of an inhibitor 1, the activator may bind to the inhibitor molecule preventing the inhibitor to bind the enzyme and hence improving the reaction rate. In this case only the ![]() value decreases yielding higher reaction rates.
value decreases yielding higher reaction rates.
3.2.4. Effects of pH and Temperature
Enzyme activity responds directly to changes in the physical environment, such as pH and temperature. It is important to incorporate these effects into kinetic expressions for enzyme activity.
3.2.4.1. pH effects.
Certain enzymes have ionic groups on their active sites, and these ionic groups must be in a suitable form (acid or base) to function. Variations in the pH of the medium result in changes in the ionic form of the active site and changes in the activity of the enzyme and hence the reaction rate. Changes in pH may also alter the three-dimensional shape of the enzyme. For these reasons, enzymes are active only over a certain pH range. The pH of the medium may affect the maximum reaction rate, Km, and the stability of the enzyme. In some cases, the substrate may contain ionic groups, and the pH of the medium affects the affinity of the substrate to the enzyme.
The following scheme may be used to describe pH dependence of the enzymatic reaction rate for ionizing enzymes:
For example, from the definition of
we can derive the following rate expression:
or
where
As a result of this behavior, the pH optimum of the enzyme is between pK1 and pK2.
For ionizing substrate, the following scheme and rate expression can be developed:
Theoretical prediction of the pH optimum of enzymes requires knowledge of the active site characteristics of enzymes, which is very difficult to obtain. The pH optimum for an enzyme is usually determined experimentally. Figure 3.14 depicts variation of enzymatic activity with pH for the enzymes (A) trypsin and (B) cholinesterase.
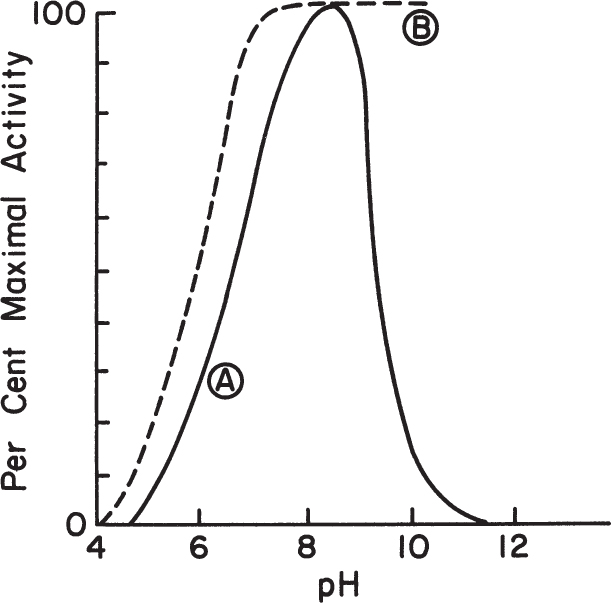
Figure 3.14. The pH-activity profiles of two enzymes. (A) approximate activity for trypsin; (B) approximate activity for cholinesterase.
3.2.4.2. Temperature effects.
The rate of enzyme–catalyzed reactions increases with temperature up to a certain limit. Above a certain temperature, enzyme activity decreases with temperature because of enzyme denaturation. Figure 3.15 depicts the variation of reaction rate with temperature and the presence of an optimal temperature.

Figure 3.15. Effect of temperature on the activity of an enzyme. Here we have assumed a value of Ea = 11 kcal/g-mol and Ed = 70 kcal/g-mol. The descending portion of the curve is due to thermal denaturation and is calculated assuming a 10-min exposure to the temperature. Note that the nature of the plot will depend on the length of time the reaction mixture is exposed to the test temperature.
The ascending part of Figure 3.15 is known as temperature activation. The rate varies according to the Arrhenius equation in this region:
Here Ea is the activation energy (kcal/mol) and [E] is the active enzyme concentration. A plot of Ln υ versus 1/T results in a line of slope –Ea/R.
The descending part of Figure 3.15 is known as temperature inactivation or thermal denaturation. The kinetics of thermal denaturation can be expressed as follows:
or
Here [E0] is the initial enzyme concentration, and kd is the denaturation constant. kd also varies with temperature according to the Arrhenius equation:
Here Ed is the deactivation energy (kcal/mol). Consequently, we get the following:
The activation energies of enzyme–catalyzed reactions are within the 4 to 20 kcal/g-mol range (mostly about 11 kcal/g-mol). Deactivation energies Ed vary between 40 and 130 kcal/g-mol (mostly about 70 kcal/g-mol). That is, enzyme denaturation by temperature is much faster than enzyme activation. A rise in temperature from 30° to 40°C results in a 1.8-fold increase in enzyme activity but a 41-fold increase in enzyme denaturation. Variations in temperature may affect both Vm and Km values of enzymes.
3.2.5. Insoluble Substrates
Enzymes are often used to attack large, insoluble substrates such as wood chips (in biopulping for paper manufacture) or cellulosic residues from agriculture (e.g., cornstalks). In these cases, access to the reaction site on these biopolymers by enzymes is often limited by enzyme diffusion. The number of potential reactive sites exceeds the number of enzyme molecules. This situation is opposite that of the typical situation with soluble substrates, where access to the enzyme’s active site limits reaction. If we consider initial reaction rates and if the reaction is first order with respect to the concentration of enzyme bound to substrate (i.e., [ES]), then we can derive a rate expression:
where
and
The previous equation assumes slow binding of enzyme (i.e., [E] ≈ [E0]), S0 is the number of substrate bonds available initially for breakage, and kdes and kads refer to rates of enzyme desorption and adsorption onto the insoluble matrix, respectively.
3.2.6. Multiphase Enzymatic Reactions
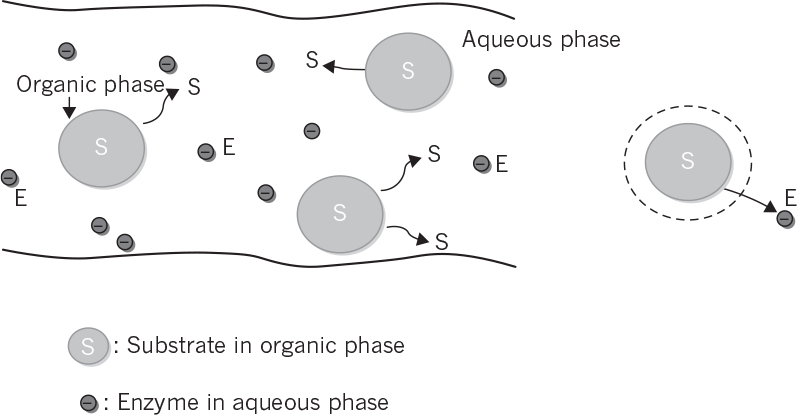
Enzymes function in aqueous media, since most of the cells contain nearly 80% water yielding high water activity in the cytoplasm. When the substrate is effectively not soluble in aqueous media, but primarily soluble in an organic phase, then substrate containing organic phase and enzyme containing aqueous phase would have to come in contact for effective enzymatic catalysis (see Figure 3.16). Organic phase is assumed to be insoluble in water; and the solubility of the substrate between the organic and the aqueous phase differ greatly.
The substrate dissolved in the organic phase diffuses to the aqueous phase, and equilibrium is established between the two phases in the absence of reaction. The ratio of the solubilities of the substrate in organic and aqueous phase is known as the partition coefficient (p).
In this equation, So,e and Sw,e are the substrate concentrations in the organic and aqueous phases at equilibrium, respectively.
The rate of enzymatic reaction in the aqueous phase is limited typically by the rate of substrate transfer from the organic phase because the solubility of the substrate in aqueous phase is very low.
The rate of substrate transfer (RST) from the organic to the aqueous phase is as follows:
Here KL is the mass-transfer coefficient for the substrate transfer from organic to the aqueous phase; a is the interfacial area of the organic and aqueous phases per reaction volume (a = Ai/Vw); and So and Sw are the substrate concentrations in the organic and aqueous phases, respectively. No substrate transfer takes place when Sw = Sw,e.
The rate of enzymatic reaction in the aqueous phase is as follows:
At steady state, the substrate transfer and conversion rates are equal:
When the rate is severely mass-transfer limited, then Sw is negligible. In this case the rate of enzymatic reaction can be approximated as equal to the substrate transfer rate as follows:
In case of considerable substrate concentration in the aqueous phase, Sw is calculated from equation 3.56 in terms of the other parameters, and equation 3.54 or equation 3.55 can be used for calculation of the enzymatic reaction rate.
The substrate concentration in the aqueous phase can also be determined graphically. When the rate of substrate transfer and the enzymatic reaction rates were plotted with respect to Sw, the intersection point would yield the Sw on the x-axis and the rate of substrate transfer on the y-axis.
3.3. Immobilized Enzyme Systems
The restriction of enzyme mobility in a fixed space is known as enzyme immobilization. Immobilization of enzymes provides important advantages, such as enzyme reutilization and elimination of enzyme recovery and purification processes and may provide a better environment for enzyme activity. Because enzymes are expensive, catalyst reuse is critical for many processes. Since some of the intracellular enzymes are membrane bound, immobilized enzymes provide a model system to mimic and understand the action of some membrane-bound intracellular enzymes. Product purity is usually improved, and effluent-handling problems are minimized by immobilization.
3.3.1. Methods of Immobilization
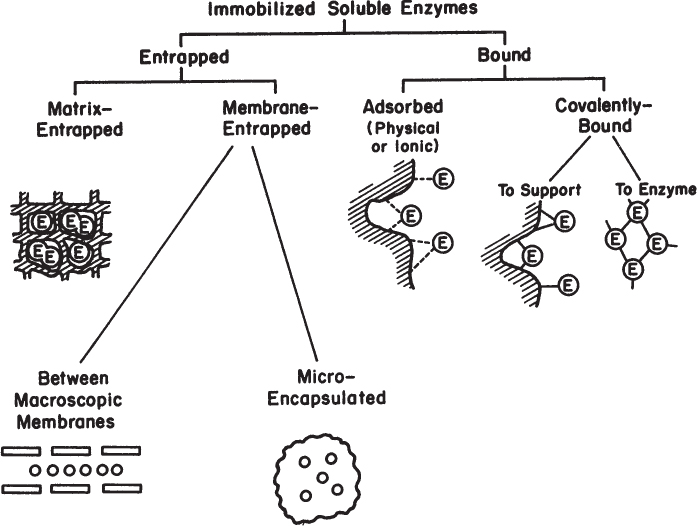
Major methods of immobilization are summarized in Figure 3.17. The two major categories are entrapment and surface immobilization.
3.3.1.1. Entrapment.
Entrapment is the physical enclosure of enzymes in a small space. Matrix entrapment and membrane entrapment, including microencapsulation, are the two major methods of entrapment.
Matrices used for enzyme immobilization are usually polymeric materials such as calcium-alginate, agar, k-carrageenin, polyacrylamide, and collagen. However, some solid matrices, such as activated carbon, porous ceramic, and diatomaceous earth, can also be used for this purpose. The matrix can be a particle, a membrane, or a fiber. When immobilizing in a polymer matrix, enzyme solution is mixed with polymer solution before polymerization takes place. Polymerized gel-containing enzyme can be extruded, or else a template is used to shape the particles from a liquid polymer–enzyme mixture. Entrapment and surface attachment may be used in combination in some cases.
Membrane entrapment of enzymes is possible; for example, hollow fiber units have been used to entrap an enzyme solution between thin, semipermeable membranes. Membranes of nylon, cellulose, polysulfone, and polyacrylate are commonly used. Configurations, other than hollow fibers, are possible, but in all cases a semipermeable membrane is used to retain high-molecular-weight compounds (enzyme) while allowing small-molecular-weight compounds (substrate or products) access to the enzyme.
A special form of membrane entrapment is microencapsulation. In this technique, microscopic hollow spheres are formed. The spheres contain the enzyme solution, and the spheres are enclosed within a porous membrane. The membrane can be polymeric or an enriched interfacial phase formed around a microdrop.
Despite the aforementioned advantages, enzyme entrapment may have its inherent problems, such as enzyme leakage into solution, significant diffusional limitations, reduced enzyme activity and stability, and lack of control of microenvironmental conditions. Enzyme leakage can be overcome by reducing the molecular weight cutoff of membranes or the pore size of solid matrices. Diffusion limitations can be eliminated by reducing the particle size of matrices and/or capsules. Reduced enzyme activity and stability are due to unfavorable microenvironmental conditions, which are difficult to control. However, by using different matrices and chemical ingredients, by changing processing conditions, and by reducing particle or capsule size, more favorable microenvironmental conditions can be obtained. Diffusion barrier is usually less significant in microcapsules as compared to gel beads.
3.3.1.2. Surface immobilization.
The two major types of immobilization of enzymes on the surfaces of support materials are adsorption and covalent binding.
Adsorption is the attachment of enzymes on the surfaces of support particles by weak physical forces, such as van der Waals or dispersion forces. The active site of the adsorbed enzyme is usually unaffected, and nearly full activity is retained upon adsorption. However, desorption of enzymes is a common problem, especially in the presence of strong hydrodynamic forces, because binding forces are weak. Adsorption of enzymes may be stabilized by cross-linking with glutaraldehyde. Glutaraldehyde treatment can denature some proteins. Support materials used for enzyme adsorption can be inorganic materials, such as alumina, silica, porous glass, ceramics, diatomaceous earth, clay, and bentonite, or organic materials, such as cellulose (CMC, DEAE-cellulose), starch, activated carbon, and ion-exchange resins, such as Amberlite, Sephadex, and Dowex. The surfaces of the support materials may need to be pretreated (chemically or physically) for effective immobilization.
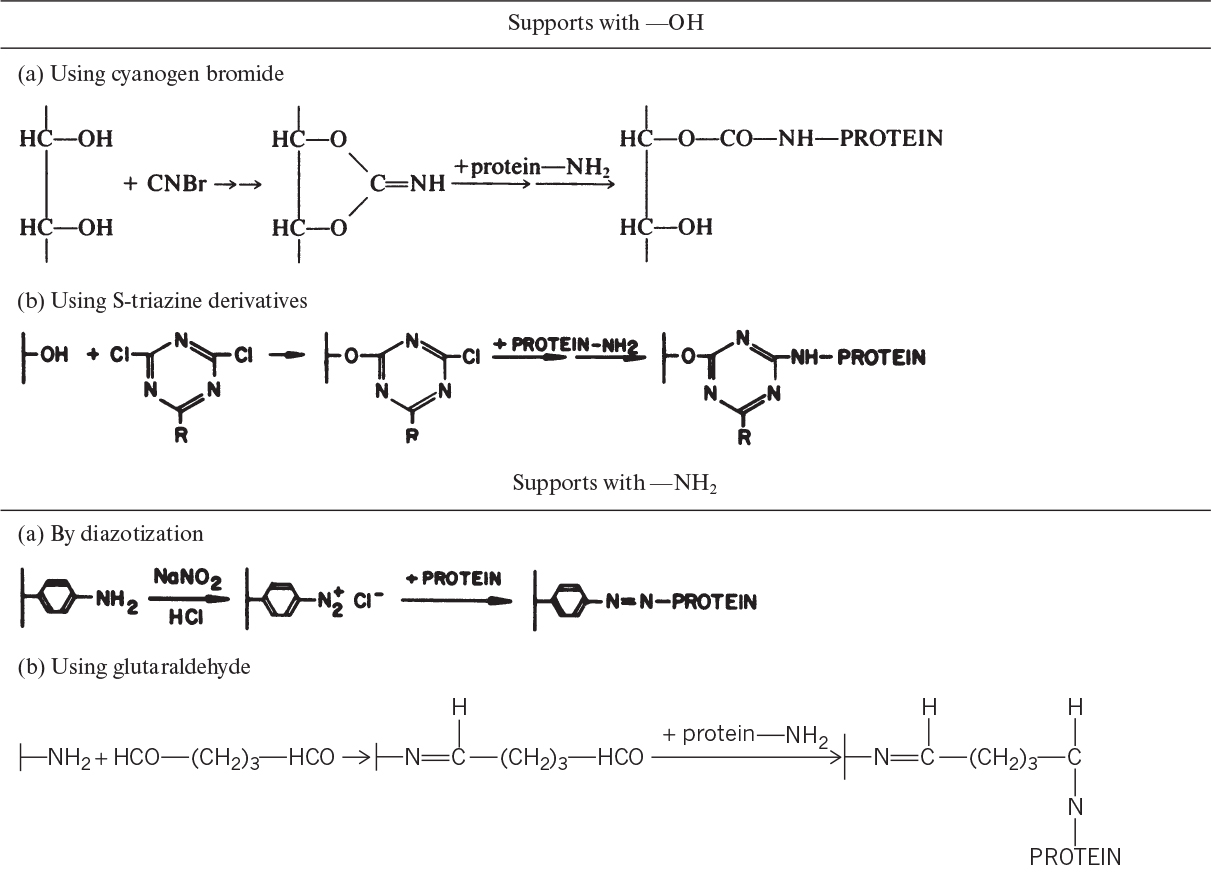
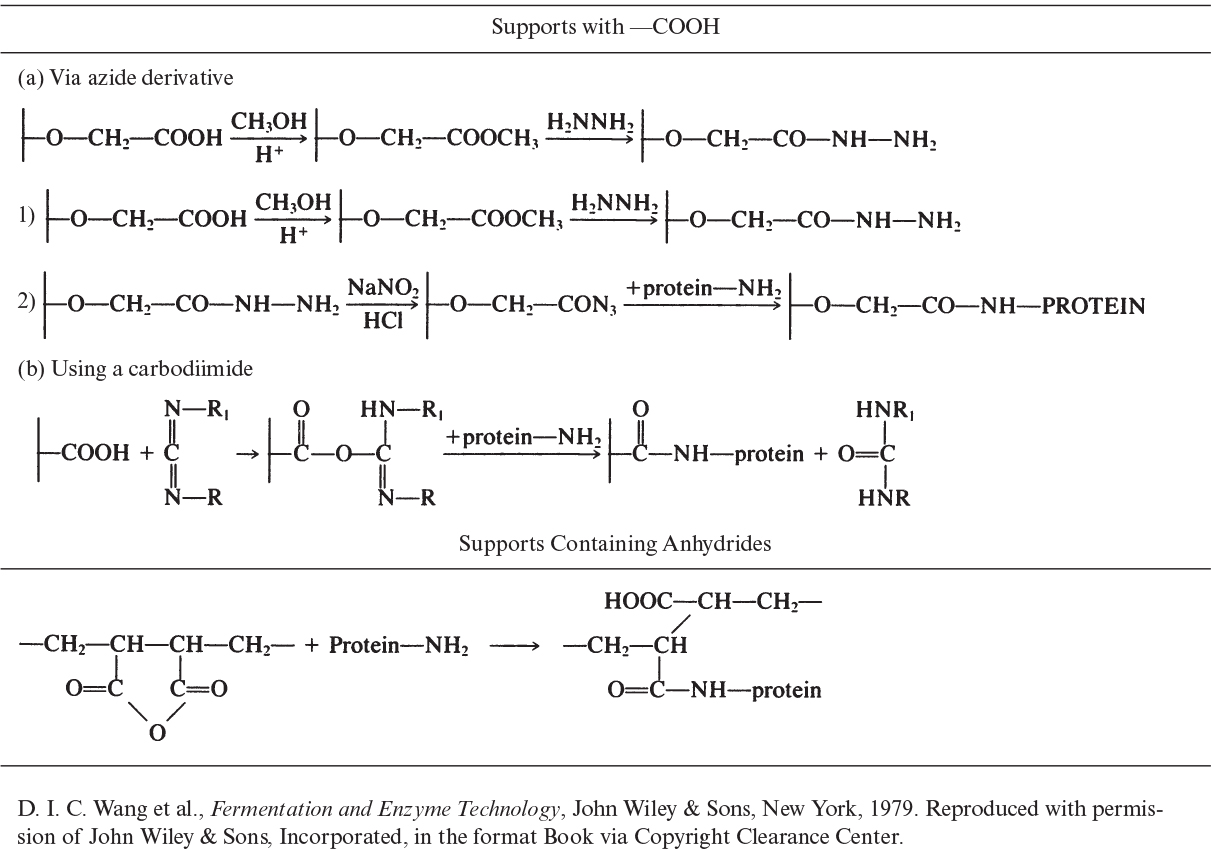
Covalent binding is the retention of enzymes on support surfaces by covalent bond formation. Enzyme molecules bind to support material via certain functional groups, such as amino, carboxyl, hydroxyl, and sulfhydryl groups. These functional groups must not be in the active site. One common trick is to block the active site by flooding the enzyme solution with a competitive inhibitor prior to covalent binding. Functional groups on support material are usually activated by using chemical reagents, such as cyanogen bromide, carbodiimide, and glutaraldehyde. Support materials with various functional groups and the chemical reagents used for the covalent binding of proteins are listed in Table 3.3. Binding groups on the protein molecule are usually side groups (R) or the amino or carboxyl groups of the polypeptide chain.
The cross-linking of enzyme molecules using agents such as glutaraldehyde, bis-diazobenzidine, and 2,2-disulfonic acid is another method of enzyme immobilization. Cross-linking can be achieved in several ways: enzymes can be cross-linked with glutaraldehyde to form an insoluble aggregate, adsorbed enzymes may be cross-linked, or cross-linking may take place following the impregnation of porous support material with enzyme solution. Cross-linking may cause significant changes in the active site of enzymes, and severe diffusion limitations may result.
The most suitable support material and immobilization method vary depending on the enzyme and particular application. Two major criteria used in the selection of support material are the binding capacity of the support material, which is a function of charge density, functional groups, porosity, and hydrophobicity of the support surface; and stability and retention of enzymatic activity, which is a function of functional groups on support material and microenvironmental conditions. If immobilization causes some conformational changes on the enzyme, or if reactive groups on the active site of the enzyme are involved in binding, a loss in enzyme activity can take place upon immobilization. Usually, immobilization results in a loss in enzyme activity and stability. However, in some cases, immobilization may cause an increase in enzyme activity and stability due to more favorable microenvironmental conditions. Because enzymes often have more than one functional site that can bind the surface, an immobilized enzyme preparation may be very heterogeneous. Even when binding does not alter enzyme structure, some enzyme can be bound with the active site oriented away from the substrate solution and toward the support surface, decreasing the access of the substrate to the enzyme. Retention of activity varies with the method used. Table 3.4 summarizes the retention of activity of aminoacylase immobilized by different methods.
3.3.2. Diffusional Limitations in Immobilized Enzyme Systems
Diffusional resistances may be observed at different levels in immobilized enzymes. These resistances vary depending on the nature of the support material (porous, nonporous), hydrodynamical conditions surrounding the support material, and distribution of the enzyme inside or on the surface of the support material. Whether diffusion resistance has a significant effect on the rate of enzymatic reaction rate depends on the relative rate of the reaction rate and diffusion rate, which is characterized by the Damköhler number (Da):
where [Sb] is substrate concentration in bulk liquid, and kL is the mass-transfer coefficient.
The rate of enzymatic conversion may be limited by diffusion of the substrate or reaction, depending on the value of the Damköhler number. If Da >> 1, then the diffusion rate is limiting. For Da << 1, the reaction rate is limiting, and for Da ≈ 1, the diffusion and reaction resistances are comparable. Diffusion and enzymatic reactions may be simultaneous, with enzymes entrapped in a solid matrix, or may be two consecutive phenomena for adsorbed enzymes.
3.3.2.1. Diffusion effects on surface-bound enzymes.
Assume a situation where enzymes are bound and evenly distributed on the surface of a nonporous support material, all enzyme molecules are equally active, and substrate diffuses through a thin liquid film surrounding the support surface to reach the reactive surfaces, as depicted in Figure 3.18. Assume further that the process of immobilization has not altered the protein structure, and the intrinsic kinetic parameters (Vm, Km) are unaltered.
At steady state, the reaction rate is equal to the mass-transfer rate:
where ![]() is the maximum reaction rate per unit of external surface area, and kL is the liquid mass-transfer coefficient. This equation is quadratic in [Ss], the substrate concentration at the surface. It can be solved analytically, but the solution is cumbersome. Furthermore, the value of [Ss] is not amenable to direct experimental observation.
is the maximum reaction rate per unit of external surface area, and kL is the liquid mass-transfer coefficient. This equation is quadratic in [Ss], the substrate concentration at the surface. It can be solved analytically, but the solution is cumbersome. Furthermore, the value of [Ss] is not amenable to direct experimental observation.
Equation 3.59 can be solved graphically, as depicted in Figure 3.19. Such a plot also makes it easy to visualize the effects of parameter changes such as in stirring rate, bulk substrate concentration, or enzyme loading.

Figure 3.19. Graphical solution for amount of reaction per unit surface area for enzyme immobilized on a nonporous catalyst. Curve A results from the intrinsic solution-based kinetic parameters and the surface loading of enzyme. Line B is the mass-transfer equation. The intersection of the two lines is the reaction rate that can be sustained in the system. The responses for two different bulk substrate concentrations are shown.
When the system is strongly mass-transfer limited, [Ss] ≈ 0, since the reaction is rapid compared to mass transfer. As a result, the system behaves as a pseudo-first-order reaction:
When the system is reaction limited (Da << 1), the reaction rate is often expressed as
where, with appropriate assumptions,
Under these circumstances, the apparent Michaelis–Menten constant is a function of stirring speed. Usually, Km,app is estimated experimentally as the value of [Sb], giving one-half of the maximal reaction rate.
3.3.2.2. Diffusion effects in enzymes immobilized in a porous matrix.
When enzymes are immobilized on internal pore surfaces of a porous matrix, substrate diffuses through the tortuous pathway among pores and reacts with enzyme immobilized on pore surfaces. Diffusion and reaction are simultaneous in this case, as depicted in Figure 3.20.
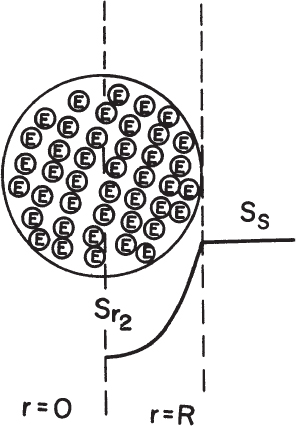
Figure 3.20. Substrate concentration profile in a porous support particle containing immobilized enzymes. Here it is assumed that no external substrate limitation exists so that the bulk and surface concentrations are the same.
Assume that the enzyme is uniformly distributed in a spherical support particle; the reaction kinetics are expressed by Michaelis–Menten kinetics, and there is no partitioning of the substrate between the exterior and interior of the support. Then we write the following equation, stating that diffusion rate is equal to reaction rate at steady state:
Boundary conditions are [S] = [Ss] at r = R and d[S]/dr = 0 at r = 0, where ![]() is the maximum reaction rate per unit volume of support, and De is the effective diffusivity of substrate within the porous matrix.
is the maximum reaction rate per unit volume of support, and De is the effective diffusivity of substrate within the porous matrix.
Equation 3.62 can be written in dimensionless form by defining the following dimensionless variables:
or
where
With boundary conditions of ![]() at
at ![]() and
and ![]() at
at ![]() Equation 3.63b can be numerically solved to determine the substrate profile inside the matrix. The rate of substrate consumption is equal to the rate of substrate transfer through the external surface of the support particle at steady state into the sphere:
Equation 3.63b can be numerically solved to determine the substrate profile inside the matrix. The rate of substrate consumption is equal to the rate of substrate transfer through the external surface of the support particle at steady state into the sphere:
Under diffusion limitations, the rate per unit volume is usually expressed in terms of the effectiveness factor:
The effectiveness factor is defined as the ratio of the reaction rate with diffusion limitation (or diffusion rate) to the reaction rate with no diffusion limitation. The value of the effectiveness factor is a measure of the extent of diffusion limitation. For η < 1, the conversion is diffusion limited, whereas for η ≈ 1 values, conversion is limited by the reaction rate and diffusion limitations are negligible. The factor is a function of φ and β, as depicted in Figure 3.21.
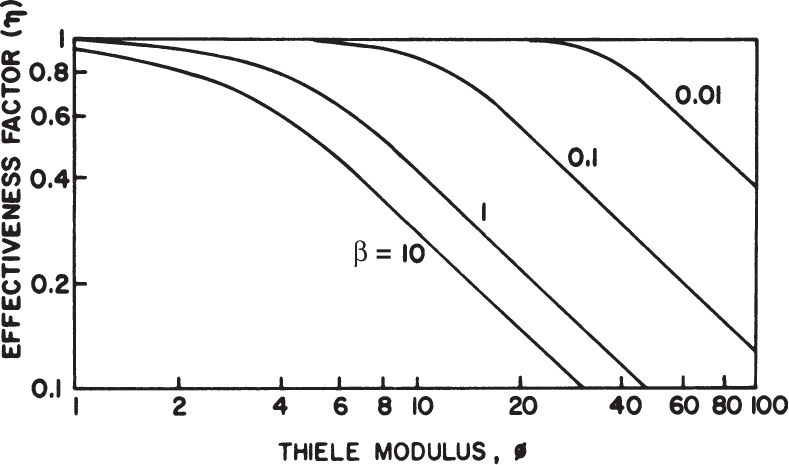
Figure 3.21. Theoretical relationship between the effectiveness factor and first-order Thiele modulus. (D. I. C. Wang et al., Fermentation and Enzyme Technology, John Wiley & Sons, New York, 1979. Reproduced with permission of John Wiley & Sons, Incorporated, in the format Book via Copyright Clearance Center.)
For a zero-order reaction rate (β → 0), and consequently η ≈ 1 for a large range of Thiele modulus values such as 1 < φ < 100. For a first-order reaction rate (β → ∞), η = (φ,β) and h is approximated to the following equation for high values of φ:
When internal diffusion limits the enzymatic reaction rate, the rate-constant Vm,app and Km,app values are not true intrinsic rate constants but apparent values. To obtain true intrinsic rate constants in immobilized enzymes, diffusion resistances should be eliminated by using small particle sizes, a high degree of turbulence around the particles, and high substrate concentrations.
When designing immobilized enzyme systems using a particular support, the main variables are Vm and R, since the substrate concentration, Km, and De are fixed. The particle size (R) should be as small as possible within the constraints of particle integrity, resistance to compression, and the nature of the particle recovery systems. The maximum reaction rate is determined by enzyme activity and concentration in the support. High enzyme content will result in high enzyme activity per unit of reaction volume but low effectiveness factor. Low enzyme content will result in lower enzyme activity per unit volume but a high effectiveness factor. For maximum conversion rates, particle size should be small (Dp ≤ 10 μm) and enzyme loading should be optimized. As depicted in the example in Figure 3.22, Dp ≤ 10 μm and enzyme loadings of less than 10 mg/cm3 are required for high values of the effectiveness factor (η ≥ 0.8).
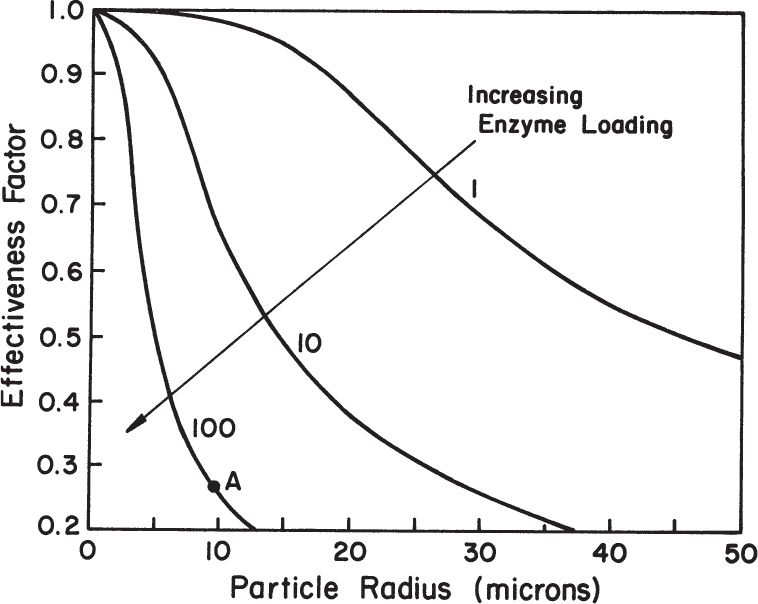
Figure 3.22. The effectiveness factor decreases with increases in enzyme loading or with increases in particle diameter. Point A represents the value of the effectiveness factor for a particle radius of 10 μm with an enzyme loading of 100 mg/cm3, an enzyme activity of 100 μmol/min per mg enzyme, a substrate diffusivity of 5 × 10–6 cm2/s, and a bulk substrate concentration tenfold higher than Km.

Figure 3.23. Double-reciprocal plots for free and immobilized enzymes (Example 3.5).
3.3.3. Electrostatic and Steric Effects in Immobilized Enzyme Systems
When enzymes are immobilized in a charged matrix as a result of a change in the microenvironment of the enzyme, the apparent bulk pH optimum of the immobilized enzyme will shift from that of soluble enzyme. The charged matrix will repel or attract substrates, product, cofactors, and H+ depending on the type and quantity of surface charge. For an enzyme immobilized onto a charged support, the shift in the pH-activity profile is given by
where pHi and pHe are internal and external pH values, respectively; z is the charge (valence) on the substrate; F is the Faraday constant (96,500 coulomb/mol); ψ is the electrostatic potential; and R is the gas constant. Expressions similar to equation 3.67 apply to other nonreactive charged medium components. The intrinsic activity of the enzyme is altered by the local changes in pH and ionic constituents. Further alterations in the apparent kinetics are due to the repulsion or attraction of substrates or inhibitors.
The activity of an enzyme toward a high-molecular-weight substrate is usually reduced upon immobilization to a much greater extent than for a low-molecular-weight substrate, mainly because of steric hindrance by the support. Certain substrates, such as starch, have molecular weights comparable to those of enzymes and may therefore not be able to penetrate to the active sites of immobilized enzymes.
Immobilization also affects the thermal stability of enzymes. Thermal stability often increases upon immobilization due to the presence of thermal diffusion barriers and the constraints on protein unfolding. However, decreases in thermal stability have been noted in a few cases. The pH stability of enzymes may also increase upon immobilization.
3.4. Large-Scale Production of Enzymes
Among various enzymes produced at large scale are proteases (subtilisin, rennet), hydrolases (pectinase, lipase, lactase), isomerases (glucose isomerase), and oxidases (glucose oxidase). These enzymes are produced using overproducing strains of certain organisms. Separation and purification of an enzyme from an organism require disruption of cells, removal of cell debris and nucleic acids, precipitation of proteins, ultrafiltration of the desired enzyme, chromatographic separations (optional), crystallization, and drying. The process scheme varies depending on whether the enzyme is intracellular or extracellular. In some cases, it may be more advantageous to use inactive (dead or resting) cells with the desired enzyme activity in immobilized form. This approach eliminates costly enzyme separation and purification steps and is therefore economically more feasible. Details of protein separations are covered in Chapter 11, “Recovery and Purification of Products.”
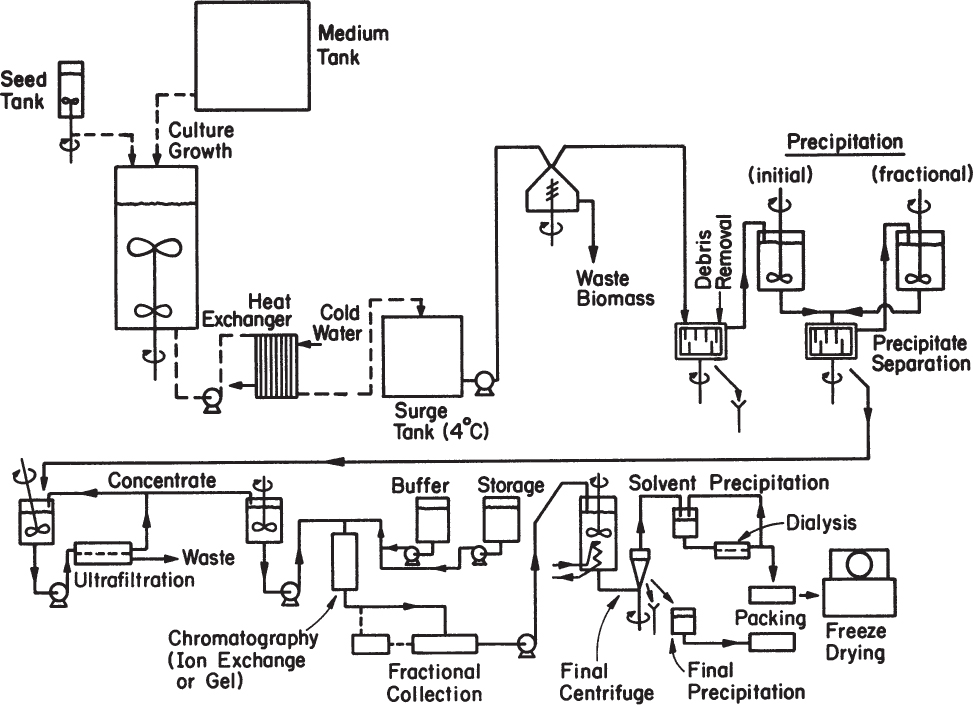
The first step in the large-scale production of enzymes is to cultivate the organisms producing the desired enzyme. Enzyme production can be regulated and fermentation conditions can be optimized for overproduction of the enzyme. Proteases are produced by using overproducing strains of Bacillus, Aspergillus, Rhizopus, and Mucor; pectinases are produced by Aspergillus niger; lactases are produced by yeast and Aspergillus; lipases are produced by certain strains of yeasts and fungi; glucose isomerase is produced by Flavobacterium arborescens or Bacillus coagulans. After the cultivation step, cells are separated from the media usually by filtration or sometimes by centrifugation. Depending on the intracellular or extracellular nature of the enzyme, either the cells or the fermentation broth is further processed to separate and purify the enzyme. The recovery of intracellular enzymes is more complicated and involves the disruption of cells and removal of cell debris and nucleic acids. Figure 3.24 depicts a schematic of an enzyme plant producing intracellular enzymes.
In some cases, an enzyme may be both intracellular and extracellular, which requires processing of both broth and cells. Intracellular enzymes may be released by increasing the permeability of the cell membrane. Certain salts, such as CaCl2, and other chemicals, such as dimethylsulfoxide (DMSO), and pH shift may be used for this purpose. If enzyme release is not complete, then cell disruption may be essential.
The processes used to produce these industrial enzymes have much in common with the processes used to make proteins from recombinant DNA, discussed later.
3.5. Medical and Industrial Utilization of Enzymes
Enzymes have been significant industrial products for more than a hundred years. However, the range of potential applications is increasing rapidly. With the advent of recombinant DNA technology, it has become possible to make formerly rare enzymes in large quantities and hence to reduce cost. Also, in pharmaceutical manufacturing, the desire to make chirally pure compounds is leading to new opportunities. Chirality is important in a product; in a racemic mixture, one enantiomer is often therapeutically useful while the other may cause side effects and add no therapeutic value. The ability of enzymes to recognize chiral isomers and react with only one of them can be a key component in pharmaceutical synthesis. Processes that depend on a mixture of chemical and enzymatic synthesis are being developed for a new generation of pharmaceuticals.
Technological advances have facilitated the use of enzymes over an increasingly broad range of process conditions. Enzymes from organisms that grow in unusual environments (e.g., deep ocean, salt lakes, and hot springs) are increasingly available for study and potential use. New enzymes and better control of reaction conditions allow the use of enzymes in the presence of high concentrations of organics, in high-salt aqueous environments, or at extreme temperatures, pH, or pressures. As we couple new insights into the relationship of enzyme structure to biological function with recombinant DNA technology, we are able to produce enzymes that are human designed or manipulated (see Chapter 14, “Utilizing Genetically Engineered Organisms,” Section 14.9, on protein engineering). We no longer need to depend solely on natural sources for enzymes.
Another emerging technology is the use of cell-free systems. This approach uses cell lysates; such crude mixtures have been used historically for industrial purposes for nonenergy-requiring single-step reactions and are relatively inexpensive. Recent advances allow the use of cell-free production for complex, multistep synthesis of high-value products. Such approaches potentially allow intensification of bioprocesses for complex reaction networks and show potential for industrial applications for products that would normally be intracellular. Such systems have been scaled up to over 100 l.
In 2014, U.S. sales of industrial enzymes were about $4.5 billion, and sales are projected to grow to $6.5 billion by 2020. The products made by enzymatic processes are worth many more billions of dollars. Food and beverage account for about one-third of the market. The detergent market is next in size with animal feed, biofuels, paper and pulp, and textiles being significant. Table 3.5 lists some industrially important enzymes.
Proteases hydrolyze proteins into smaller peptide units and constitute a large and industrially important group of enzymes. Proteases constitute about 60% of the total enzyme market. Industrial proteases are obtained from bacteria (Bacillus), molds (Aspergillus, Rhizopus, and Mucor), animal pancreas, and plants. Most of the industrial proteases are endoproteases. Proteases are used in food processing, such as cheese making (rennet), baking, meat tenderization (papain, trypsin), and brewing (trypsin, pepsin); in detergents for the hydrolysis of protein stains (subtilisin); and in tanning and the medical treatment of wounds.
Pectinases are produced mainly by A. niger. The major components in pectinases are pectin esterase, polygalacturonase, and polymethylgalacturonatelyase. Pectinases are used in fruit juice processing and wine making to increase juice yield, reduce viscosity, and clear the juice.
Lipases hydrolyze lipids into fatty acids and glycerol and are produced from animal pancreas, some molds, and yeasts. Lipases may be used to hydrolyze oils for soap manufacture and to hydrolyze the lipid-fat compounds present in wastewater streams. Interesterification of oils and fats may be catalyzed by lipases. Lipases may also be used in the cheese and butter industry to impart flavor as a result of the hydrolysis of fats. Lipase-containing detergents are an important application of lipases.
Amylases are used for the hydrolysis of starch and are produced by many different organisms, including A. niger and B. subtilis. Three major types of amylases are α-amylase, β-amylase, and glucoamylase. α-amylase breaks α-1,4 glycosidic bonds randomly on the amylose chain and solubilizes amylose. For this reason, α-amylase is known as the starch-liquefying enzyme. β-amylase hydrolyzes α-1,4 glycosidic bonds on the nonreducing ends of amylose and produces maltose residues. β-amylase is known as a saccharifying enzyme. α-1,6 glycosidic linkages in the amylopectin fraction of starch are hydrolyzed by glucoamylase, which is also known as a saccharifying enzyme. In the United States, on the average, nearly 1.3 × 109 lb/yr of glucose is produced by the enzymatic hydrolysis of starch. The enzyme pullulanase also hydrolyzes α-1,6 glycosidic linkages in starch selectively.
Cellulases are used in the hydrolysis of cellulose and are produced by some Trichoderma species, such as Trichoderma viride or T. reesei; by some molds, such as A. niger and Thermomonospora; and by some Clostridium species. Cellulase is an enzyme complex, and its formation is induced by cellulose. Trichoderma cellulase hydrolyzes crystalline cellulose, but Aspergillus cellulase does not. Cellulose is first hydrolyzed to cellobiose by cellulase, and cellobiose is further hydrolyzed to glucose by β-glucosidase. Both of these enzymes are inhibited by their end products, cellobiose and glucose. Cellulases are used in cereal processing, alcohol fermentation from biomass, brewing, and waste treatment.
Hemicellulases hydrolyze hemicellulose to five-carbon sugar units and are produced by some molds, such as white rot fungi and A. niger. Hemicellulases are used in combination with other enzymes in baking doughs, brewing mashes, alcohol fermentation from biomass, and waste treatment.
Lactases are used to hydrolyze lactose in whey to glucose and galactose and are produced by yeast and some Aspergillus species. Lactases are used in the fermentation of cheese whey to ethanol.
Other microbial β-1,4 glucanases produced by B. amyloliquefaciens, A. niger, and Penicillium emersonii, are used in brewing mashes containing barley or malt. These enzymes improve wort filtration and extract yield.
Penicillin acylase is used by the antibiotic industry to convert penicillin G to 6-aminopenicillanic acid (6-APA), which is a precursor for semisynthetic penicillin derivatives.
Among other important industrial application of enzymes is the conversion of fumarate to L-aspartate by aspartase. In industry, this conversion is realized in a packed column of immobilized dead E. coli cells with active aspartase enzyme. Fumarate solution is passed through the column, and aspartate is obtained in the effluent stream. Aspartate is further coupled with L-phenylalanine to produce aspartame, which is a low-calorie sweetener known as NutraSweet.
The conversion of glucose to fructose by immobilized glucose isomerase is an important industrial process. Fructose is nearly 1.7 times sweeter than glucose and is used as a sweetener in soft drinks. Glucose isomerase is an intracellular enzyme and is produced by different organisms, such as Flavobacterium arborescens, B. licheniformis, and some Streptomyces and Arthrobacter species. Immobilized inactive whole cells with glucose isomerase activity are used in a packed column for fructose formation from glucose. Cobalt (Co2+) and magnesium (Mg2+) ions (4 × 10–4 M) enhance enzyme activity. Different immobilization methods are used by different companies. One uses flocculated whole cells of F. arborescens treated with glutaraldehyde in the form of dry spherical particles. Entrapment of whole cells in gelatin treated with glutaraldehyde, the use of glutaraldehyde-treated lysed cells in the form of dry particles, and immobilization of the enzyme on inorganic support particles such as silica and alumina are methods used by other companies.
DL-Acylamino acids are converted to a mixture of L- and D-amino acids by immobilized aminoacylase. L-Amino acids are separated from D-acylamino acid, which is recycled back to the column. L-Amino acids have important applications in food technology and medicine.
Enzymes are commonly used in medicine for diagnosis, therapy, and treatment purposes. Trypsin can be used as an anti-inflammatory agent; lysozyme, which hydrolyzes the cell wall of gram-positive bacteria, is used as an antibacterial agent; streptokinase is used as an anti-inflammatory agent; urokinase is used in dissolving and preventing blood clots. Asparaginase, which catalyzes the conversion of L-asparagine to L-aspartate, is used as an anticancer agent. Cancer cells require L-asparagine and are inhibited by asparaginase. Asparaginase is produced by E. coli. Glucose oxidase catalyzes the oxidation of glucose to gluconic acid and hydrogen peroxide, which can easily be detected. Glucose oxidase is used for the determination of glucose levels in blood and urine. Penicillinases hydrolyze penicillin and are used to treat allergic reactions against penicillin. Tissue plasminogen activator and streptokinase are used in the dissolution of blood clots (particularly following a heart attack or stroke).
The development of biosensors using enzymes as integral components is proceeding rapidly. Two examples of immobilized enzyme electrodes are those used in the determination of glucose and urea by using glucose oxidase and urease immobilized on the electrode membrane. Scarce enzymes (e.g., tissue plasminogen activator) are finding increasing uses, as the techniques of genetic engineering now make it possible to produce usable quantities of such enzymes.
3.6. Summary
Enzymes are protein or glycoprotein molecules that catalyze biologically important reactions. Some RNA molecules may have catalytic activity too. Enzymes are very effective, specific, and versatile biocatalysts. Enzymes bind substrate molecules and reduce the activation energy of the reaction catalyzed, resulting in significant increases in reaction rate. Some protein enzymes require a nonprotein group for their activity as a cofactor.
Simple single-enzyme–catalyzed reaction kinetics can be described by Michaelis–Menten kinetics, which has a hyperbolic form in terms of substrate concentration. The activity of some enzymes can be altered by inhibitory compounds, which bind the enzyme molecule and reduce its activity. Enzyme inhibition may be competitive, noncompetitive, and uncompetitive. High substrate and product concentrations may be inhibitory, too. Enzyme activators increase enzymatic reaction rate upon binding the enzyme molecules.
Enzymes require optimal conditions (pH, temperature, ionic strength) for their maximum activity. Enzymes with an ionizing group on their active site show a distinct optimal pH that corresponds to the natural active form of the enzyme. The activation energy of enzyme–catalyzed reactions is within 4 to 20 kcal/g-mol. Above the optimal temperature, enzymes lose their activity, and the inactivation energy is on the order of 40 to 130 kcal/g-mol.
Enzymes can be used in suspension or in immobilized form. Enzymes can be immobilized by entrapment in a porous matrix, by encapsulation in a semipermeable membrane capsule or between membranes, such as in a hollow-fiber unit, or by adsorption onto a solid support surface. Enzyme immobilization provides enzyme reutilization, eliminates costly enzyme recovery and purification processes, and may result in increased activity by providing a more suitable microenvironment for the enzyme. Enzyme immobilization may result in diffusion limitations within the matrix. Immobilization may also cause enzyme instability, loss of activity, and a shift in optimal conditions (pH, ionic strength). To obtain maximum reaction rates, the particle size of the support material and enzyme loading need to be optimized, and a support material with the correct surface characteristics must be selected.
Enzymes are widely used in industry and have significant medical applications. Among the most widely used enzymes are proteases (papain, trypsin, subtilisin), amylases (starch hydrolysis), rennet (cheese manufacturing), glucose isomerase (glucose-to-fructose conversion), glucose oxidase (glucose-to-gluconic acid conversion), lipases (lipid hydrolysis), and pectinases (pectin hydrolysis). Enzyme production and utilization are a multibillion-dollar business with a great potential for expansion.
Suggestions for Further Reading
BAILEY, J. E., AND D. F. OLLIS, Biochemical Engineering Fundamentals, 2d ed., McGraw-Hill, New York, 1986.
BLANCH, H. W., AND D. S. CLARK, Biochemical Engineering, Marcel Dekker, New York, 1996.
DATTA, S., L. R. CHISTENA, AND Y. R. S. RAJARAM, Enzyme Immobilization: An Overview on Techniques and Support Materials, 3 Biotech 3(1): 1–9, 2013.
FEDOR, M. J., AND J. R. WILLIAMSON, The Catalytic Diversity of RNAs, Nat. Rev. Mol. Cell Biol. 6(5): 399–412, 2005.
LISZKA, M. J., M. E. CLARK, E. SCHNEIDER, AND D. S. CLARK, Nature versus Nurture: Developing Enzymes That Function under Extreme Conditions, Ann. Rev. Chem. Biomol. Eng. 3(1): 77–102, 2012.
SCHMID, A., J. S. DORDICK, B. HAUER, A. KIENER, M. WUBBOLTS, AND B. WITHOLT, Industrial Biocatalysis Today and Tomorrow, Nature 409(6817): 258–268, 2001.
SELLEK, G. A., AND J. B. CHAUDHURI, Biocatalysis in Organic Media Using Enzymes from Extremophiles, Enzyme Microb. Technol. 25(6): 471–482, 1999.
SWARTZ, J. R., Transforming Biochemical Engineering with Cell-Free Biology, AIChE J. 58(1): 5–13, 2012.
Problems
3.1. Consider the following reaction sequence:
Develop a suitable rate expression for production formation [v = k5 (ES)2] by using (a) the equilibrium approach, and (b) the quasi-steady-state approach.
3.2. Consider the reversible product-formation reaction in an enzyme–catalyzed bioreaction:
Develop a rate expression for product-formation using the quasi-steady-state approximation and show that
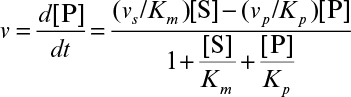

3.3. The enzyme fumarase has the following kinetic constants:
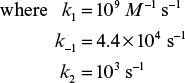
a. What is the value of the Michaelis constant for this enzyme?
b. At an enzyme concentration of 10–6 M, what will be the initial rate of product formation at a substrate concentration of 10–3 M?
[Courtesy of D. J. Kirwan from “Collected Coursework Problems in Biochemical Engineering” compiled by H. W. Blanch for 1977 American Society for Engineering Education Summer School.]
3.4. Data on enzymatic degradation of dichlorophenol at different concentrations are given in the following table:
Assuming the substrate-inhibited kinetics is given by the following equation, determine the constants Vm, Km, and KSI:
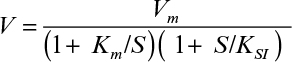
3.5. Biological oxidation of phenylacetic acid is inhibited by propionic acid present in wastewater. The following data were obtained for enzymatic oxidation of phenylacetic acid at different concentrations of propionic acid:

a. What kind of inhibition is this?
b. Determine Vm, Km, and KI.
3.6. Hydrogenase enzyme responsible for hydrogen gas synthesis in photoheterotrophic bacteria is activated by the addition of sodium molybdate into the medium. Hydrogen formation rate varies with the Mo concentration as follows:
a. Assuming that the activator only affects the maximum reaction rate (Vm), determine the activation constant (KA).
b. What would be the reaction rate at Mo = 60 μg/l?
3.7. Enzymes are immobilized on flat surfaces of plates in the form of monolayer (or very thin film) and placed in an agitated reactor for enzymatic reaction. The reactor is operated continuously. The bulk substrate concentration is S0 = 200 mg/l at steady state. When the reactor was operated at different agitation speeds, the following data were obtained:
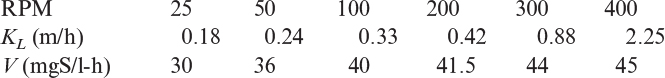
a. Determine surface concentration of the substrate for each RPM.
b. Determine kinetic constants of Vm and Km for the enzymatic reaction.
3.8. The hydration of is catalyzed by carbonic anhydrase as follows:
The following data were obtained for the forward and reverse reaction rates at pH 7.1 and an enzyme concentration of 2.8 × 10–9 M:

v is the initial reaction rate at the given substrate concentration. Calculate the forward and reverse catalytic and Michaelis constants.
(Courtesy of D. J. Kirwan from “Collected Coursework Problems in Biochemical Engineering” compiled by H. W. Blanch for 1977 American Society for Engineering Education Summer School. © American Society for Engineering Education.)
3.9. An inhibitor (I) is added to the enzymatic reaction at a level of 1.0 g/l. The following data were obtained for Km = 9.2 g S/l:
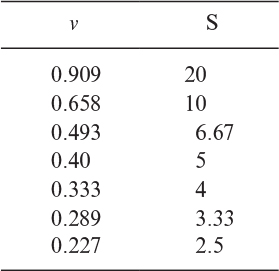
a. Is the inhibitor competitive or noncompetitive?
b. Find KI.
3.10. During a test of kinetics of an enzyme–catalyzed reaction, the following data were recorded:

a. Determine the Michaelis–Menten constant for the reaction with no inhibitor present at 30°C and at 49.6°C.
b. Determine the maximum velocity of the uninhibited reaction at 30°C and an enzyme concentration of 1.6 g/l.
c. Determine the KI for the inhibitor at 30°C and decide what type of inhibitor is being used.
3.11. An enzyme ATPase has a molecular weight of 5 × 104 daltons, a KM value of 10–4 M, and a k2 value of k2 = 104 molecules ATP/min molecule enzyme at 37°C. The reaction catalyzed is the following:
This can also be represented as
Here S is ATP. The enzyme at this temperature is unstable. The enzyme inactivation kinetics are first order:
E = E0e-kdt
Here is the initial enzyme concentration and In an experiment with a partially pure enzyme preparation, of total crude protein (containing enzyme) is added to a 1 ml reaction mixture containing 0.02 M ATP and incubated at 37°C. After 12 hours, the reaction ends (i.e., t → ∞) and the inorganic phosphate (Pi) concentration is found to be 0.002 M, which was initially zero. What fraction of the crude protein preparation was the enzyme? Hint: Since >> Km, the reaction rate can be represented by
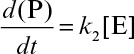
3.12. Assume that for an enzyme immobilized on the surface of a nonporous support material, the external mass-transfer resistance for substrate is not negligible as compared to the reaction rate. The enzyme is subject to substrate inhibition (equation 3.34).
a. Are multiple states possible? Why or why not?
b. Could the effectiveness factor be greater than one?
3.13. The following data were obtained for an enzyme–catalyzed reaction. Determine Vmax and Km by inspection. Plot the data using the Eadie–Hofstee method and determine these constants graphically. Explain the discrepancy in your two determinations. The initial rate data for the enzyme–catalyzed reaction are as follows:
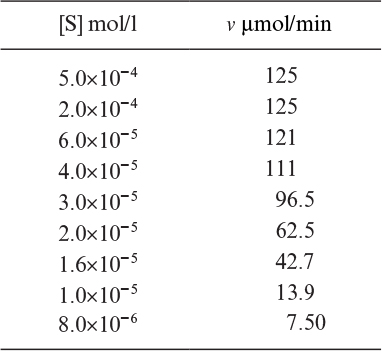
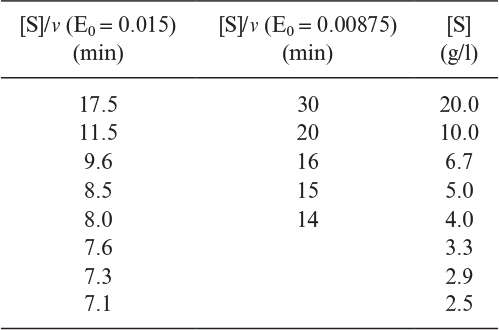
Do these data fit into Michaelis–Menten kinetics? If not, what kind of rate expression would you suggest? Use graphical methods.
3.14. H. H. Weetall and N. B. Havewala report the following data for the production of dextrose from corn starch using both soluble and immobilized (azo-glass beads) glucoamylase in a fully agitated continuous stirred-tank reactor system:
a. Soluble data: T = 60°C,[S0] = 168 mg starch/ml, [E0] = 11,600 units, volume 1000 ml
b. Immobilized data: T = 60°C,[S0] = 336 mg starch/ml, [E0] = 46,400 units initially, immobilized, volume 1000 ml
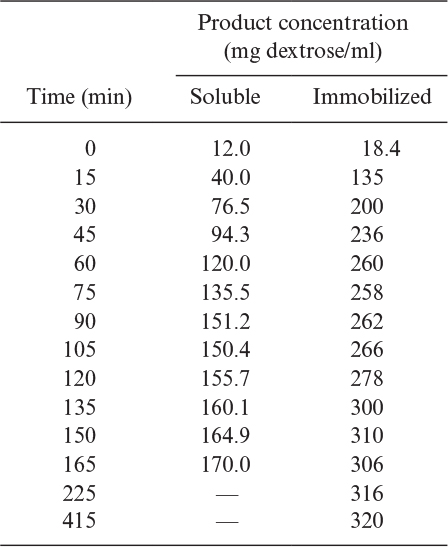
Determine the maximum reaction velocity, (mg/ml-min unit of enzyme) and the saturation constant,
The same authors studied the effect of temperature on the maximum rate of the hydrolysis of corn starch by glucoamylase. The results are tabulated next:

Determine the activation energy (∆E kcal/g-mol) for the soluble and immobilized enzyme reaction.
Using these results, determine if immobilized enzyme is diffusion limited.
(Courtesy of A. E. Humphrey from “Collected Coursework Problems in Biochemical Engineering” compiled by H. W. Blanch for 1977 American Society for Engineering Education Summer School. © American Society for Engineering Education.)
3.15. Michaelis–Menten kinetics are used to describe intracellular reactions. Yet [E0 ≈ [S0]. In in vitro batch reactors, the quasi-steady-state hypothesis does not hold for [E0 ≈ [S0]. The rapid equilibrium assumption also will not hold. Explain why Michaelis–Menten kinetics and the quasi-steady-state approximation are still reasonable descriptions of intracellular enzyme reactions.
3.16. You are working for company A and you join a research group working on immobilized enzymes. Harry, the head of the lab, claims that immobilization improves the stability of the enzyme. His proof is that the enzyme has a half-life of 10 days in free solution, but under identical conditions of temperature, pH, and medium composition, the measured half-life of a packed column is 30 days. The enzyme is immobilized in a porous sphere 5 mm in diameter. Is Harry’s reasoning right? Do you agree with him? Why or why not?
3.17. The following data were obtained from enzymatic oxidation of phenol by phenol oxidase at different phenol concentrations:
a. What type of inhibition is this?
b. Determine the constants Vm, Km, and Ksi.
c. Determine the oxidation rate at [S] = 70 mg/1.
3.18. Uric acid is degraded by uricase enzyme immobilized in porous Ca-alginate beads. Experiments conducted with different bead sizes result in the following rate data:
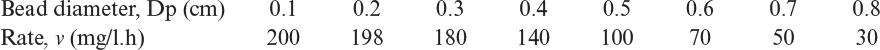
a. Determine the effectiveness factor for particle sizes Dp = 0.5 cm and Dp = 0.7 cm.
b. The following data were obtained for Dp = 0.5 cm at different bulk uric acid concentrations. Assuming negligible liquid film resistance, calculate Vm and Ks for the enzyme. Assume no substrate or product inhibition.
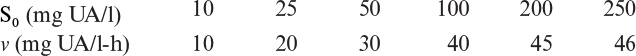
3.19. The enzyme urease is immobilized in Ca-alginate beads 2 mm in diameter. When the urea concentration in the bulk liquid is 0.5 mM, the rate of urea hydrolysis is v = 10 mmol/l-h. Diffusivity of urea in Ca-alginate beads is De = 1.5 × 10–5 cm2/sec, and the Michaelis constant for the enzyme is ![]() = 0.2 mM. By neglecting the liquid film resistance on the beads (i.e., [So] = [Ss]) determine the following:
= 0.2 mM. By neglecting the liquid film resistance on the beads (i.e., [So] = [Ss]) determine the following:
a. Maximum rate of hydrolysis Vm, Thiele modulus (φ), and effectiveness factor (η)
b. The Vm, φ, and η values for a particle size of Dp = 4 mm.
Hint: Assume η = 3/φ for large values of φ(φ>2);
3.20. Decarboxylation of glyoxalate (S) by mitochondria is inhibited by malonate (I). The following data was obtained in batch experiments:
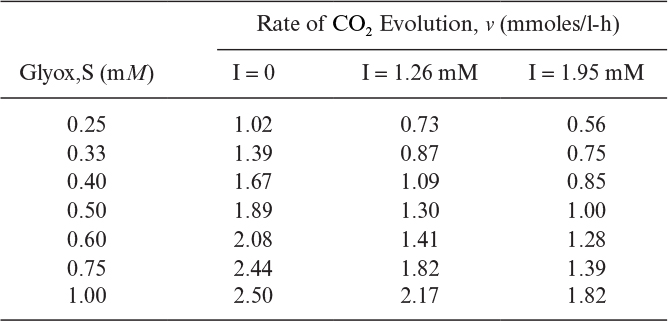
a. What type of inhibition is this?
b. Determine the constants Vm, ![]() , and KI.
, and KI.
3.21. Urea dissolved in aqueous solution is degraded to ammonia and CO2 by the enzyme urease immobilized on surfaces of nonporous polymeric beads. Conversion rate is controlled by transfer of urea to the surface of the beads through liquid film, and the conversion takes place on the surfaces of the beads. The following parameters are given for the system:
kL = 0.2 cm/s; Km = 200 mg/l
![]() = 0.1 mg urea/cm2 support surface -s.
= 0.1 mg urea/cm2 support surface -s.
Sb = 1000 mg urea/l
a. Determine the surface concentration of urea.
b. Determine the rate of urea degradation under mass-transfer-controlled conditions.
3.22. Two enzymes are immobilized on the same flat, nonporous surface. For enzyme A, the substrate is S1. For enzyme B, the substrate is S2. The product of the first reaction is S2:
a. Figure 3.P1 depicts the rate of the first reaction on the surface as a function of local concentrations of S1. If the bulk concentration of S1 is 100 mg/l and the mass-transfer coefficient is 4 × 10–5 cm/s, what is the rate of consumption of for a 1 cm2 surface? What is the surface concentration of S1?
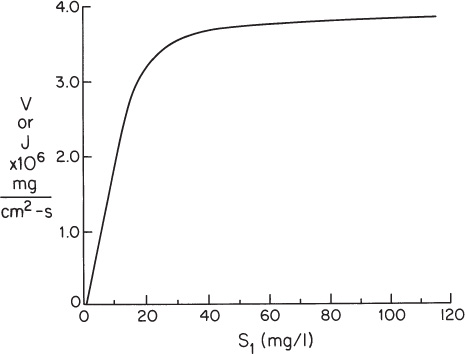
Figure 3P.1. Reaction rate data for problem 3.22. Reaction rate dependence on substrate 1 for reaction catalyzed by EA.
b. The rate of the second reaction follows:
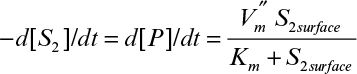
Here Km = 5 mg/1 (or 5 × 10–3 mg/cm3) and ![]() . The bulk concentration of S2 [S2bulk] is maintained as 5 mg/l, and the mass-transfer coefficient is the same for S1 and S2. Calculate [S2surface] and the rate of formation of P (assuming all stoichiometric coefficients are one).
. The bulk concentration of S2 [S2bulk] is maintained as 5 mg/l, and the mass-transfer coefficient is the same for S1 and S2. Calculate [S2surface] and the rate of formation of P (assuming all stoichiometric coefficients are one).
3.23. Consider the case of two enzymes immobilized on the same nonporous, planar surface. S is a substrate used by both enzymes in the following reactions:
The final product P3 is formed by the spontaneous reaction of P1 and P2:
Reactions 1 and 2 occur only at the surface, and reaction 3 is a homogeneous reaction occurring throughout the bulk liquid phase.
Figure 3.P2 gives the predicted reaction-rate dependence of reaction 1 (bottom curve) alone and reaction 2 (top curve) alone based on the measured amount of each enzyme immobilized and assuming the intrinsic reaction kinetics are not altered in the process of immobilization.

Figure 3P.2. Reaction rate data for problem 3.23. The reaction rate data for two different enzymes (E1 and E2) are shown.
a. If kL = 6×10–5 cm/s and the bulk concentration of substrate is 500 mg/l, what is the total rate of substrate disappearance?
b. What is the overall effectiveness factor under the conditions of part a?
c. What will be the ratio of P2 to P1 under the conditions of part a?
d. If you want to produce equimolar amounts of P1 and P2 and if kL = 6 × 10–5 cm/s, what value of bulk substrate concentration must you pick?