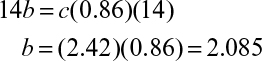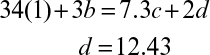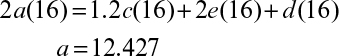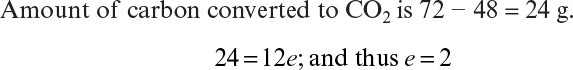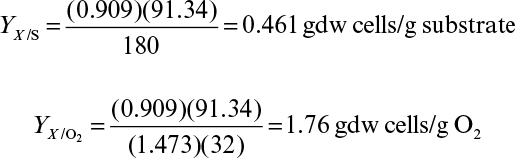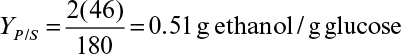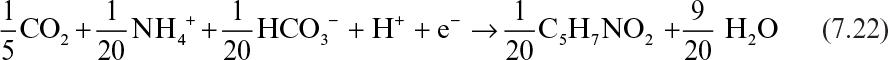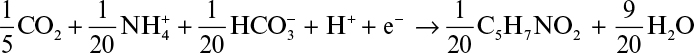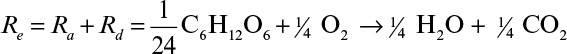7. Stoichiometry of Microbial Growth and Product Formation
Cell growth and product formation are complex processes reflecting the overall kinetics and stoichiometry of the thousands of intracellular reactions that can be observed within a cell. For many process calculations, we wish to compare potential substrates in terms of cell mass yield, or product yield, or evolution of heat. Also, we may need to know how close the system is operating to its thermodynamic limits. (That is, is product yield constrained by kinetic or thermodynamic considerations?) If a system is close to its thermodynamic limit, it would be unwise to try to improve production through mutation or genetic engineering.
Although the cell is complex, the stoichiometry of conversion of substrates into products and cellular materials is often represented by a simple pseudochemical equation. In this chapter, we discuss how these equations can be written and how useful estimates of key yield coefficients can be made.
7.1. Coefficients for ATP Consumption and Oxygen
In Chapter 6, “How Cells Grow,” we discussed the definitions of yield and maintenance coefficients, and we learned how to estimate their values using chemostat culture. In particular, we discussed the overall growth yield coefficient ![]() , which is the maximum yield of cell mass per unit mass of substrate consumed when no maintenance is considered.
, which is the maximum yield of cell mass per unit mass of substrate consumed when no maintenance is considered.
Two other yield and maintenance coefficients of importance are related to adenosine triphosphate (ATP) consumption and oxygen. The ATP yield coefficient, YX/ATP, represents the amount of biomass synthesized per mole of ATP generated. Surprisingly, it has been observed that for many substrates and organisms, ![]() is nearly constant at 10 to 11 g dry weight/mol ATP for heterotrophic growth under anaerobic conditions. The ATP yield for many autotrophic organisms (recall that autotrophic organisms fix CO2) is approximately
is nearly constant at 10 to 11 g dry weight/mol ATP for heterotrophic growth under anaerobic conditions. The ATP yield for many autotrophic organisms (recall that autotrophic organisms fix CO2) is approximately ![]() ≈ 6.5 g/mol ATP. Under aerobic conditions, the values for
≈ 6.5 g/mol ATP. Under aerobic conditions, the values for ![]() are usually greater than 10.5 (see Table 7.1).
are usually greater than 10.5 (see Table 7.1).
Table 7.2 shows calculated ATP yields (maximum theoretical values) for a variety of media. A maintenance coefficient can also be estimated using an equation analogous to the one we developed for substrate yield coefficient in a chemostat:
Here ![]() is the “apparent” yield of biomass and mATP is the rate of ATP consumption for maintenance energy.
is the “apparent” yield of biomass and mATP is the rate of ATP consumption for maintenance energy.
Similarly, yields based on oxygen consumption can be defined and calculated as follows:
As indicated in Chapter 6, Table 6.1, values of YX/O2 can vary from 0.17 to 1.5 g biomass/g O2, depending on substrate and organism.
Information from some measurements can be usefully combined. A particularly important derived parameter is the respiratory quotient (RQ), which is defined as the moles of CO2 produced per mole of oxygen consumed. The RQ value provides an indication of metabolic state (e.g., aerobic growth versus ethanol fermentation in baker’s yeast) and can be used in process control.
We discussed in Chapter 5, “Major Metabolic Pathways,” the P/O ratio, which is the ratio of phosphate bonds formed per unit of oxygen consumed (gmol P/g atom O). The P/O ratio indicates the efficiency of conversion of reducing power into high-energy phosphate bonds in the respiratory chain. For eucaryotes, the P/O ratio approaches 3 when glucose is the substrate, whereas it is significantly less than 3 in procaryotes. A closely related parameter is the proton/oxygen ratio (H/O). This ratio is the number of H+ ions released per mole of oxygen consumed. Electron generation is directly related to proton release. Usually, 4 moles of electrons are generated per mole of oxygen consumed. The generation of electrons results in the expulsion of H+ that can be used directly to drive the transport of some substrates or to generate ATP.
The complexity of mass and energy balances for cellular growth can be decreased greatly through the recognition that some parameters are nearly the same irrespective of the species or substrate involved. These parameters can be referred to as regularities. For example, Table 7.1 shows that ![]() dry wt/mol ATP under aerobic conditions. Three important regularities (identified first by I. G. Minkevich and V. K. Eroshin) are 26.95 kcal/g equivalent of available electrons transferred to oxygen (coefficient of variation of 4%), 4.291 g equivalent of available electrons per quantity of biomass containing 1 g atom carbon, and 0.462 g carbon in biomass per gram of dry biomass. It has also been observed that
dry wt/mol ATP under aerobic conditions. Three important regularities (identified first by I. G. Minkevich and V. K. Eroshin) are 26.95 kcal/g equivalent of available electrons transferred to oxygen (coefficient of variation of 4%), 4.291 g equivalent of available electrons per quantity of biomass containing 1 g atom carbon, and 0.462 g carbon in biomass per gram of dry biomass. It has also been observed that ![]() dry wt/g equivalent of electrons. These observed average values of cell composition and yields facilitate estimation of other growth-related parameters.
dry wt/g equivalent of electrons. These observed average values of cell composition and yields facilitate estimation of other growth-related parameters.
7.2. Stoichiometric Calculations
Conservation laws are absolute and powerful aids in understanding biological reactions and systems. Here we discuss the use of elemental balances and analysis of the energetics of reactions as both constraints on biological systems and as tools to understand what such systems are allowed to do.
7.2.1. Elemental Balances
A material balance on biological reactions can easily be written when the compositions of substrates, products, and cellular material are known. Usually, electron–proton balances are required in addition to elemental balances to determine the stoichiometric coefficients in bioreactions. Accurate determination of the composition of cellular material is a major challenge. Variations in cellular composition with different types of organisms are shown in Table 7.3. A typical cellular composition can be represented as CH1.8O0.5N0.2. One mole of biological material is defined as the amount containing 1 gram atom of carbon, such as CHαOβNδ.
Consider the following simplified biological conversion in which no extracellular products other than H2O and CO2 are produced:
where CHmOn represents 1 mole of carbohydrate, and CHαOβNδ stands for 1 mole of cellular material. Simple elemental balances on C, H, O, and N yield the following equations:
The RQ is
Equations 7.4 and 7.5 constitute five equations for five unknowns: a, b, c, d, and e. With a measured value of RQ, these equations can be solved to determine the stoichiometric coefficients.
7.2.2. Degree of Reduction
In more complex reactions, as in the formation of extracellular products, an additional stoichiometric coefficient is added, requiring more information. Also, elemental balances provide no insight into the energetics of a reaction. Consequently, the concept of degree of reduction has been developed and used for proton–electron balances in bioreactions. The degree of reduction, γ, for organic compounds may be defined as the number of equivalents of available electrons per gram atom C. The available electrons are those that would be transferred to oxygen upon oxidation of a compound to CO2, H2O, and NH3. The degrees of reduction for some key elements are C = 4, H = 1, N = –3, O = –2, P = 5, and S = 6. The degree of reduction of any element in a compound is equal to the valence of this element. For example, 4 is the valence of carbon in CO2, and –3 is the valence of N in NH3. Degrees of reduction for various organic compounds are given in Table 7.4. The following are examples of how to calculate the degree of reduction for substrates:
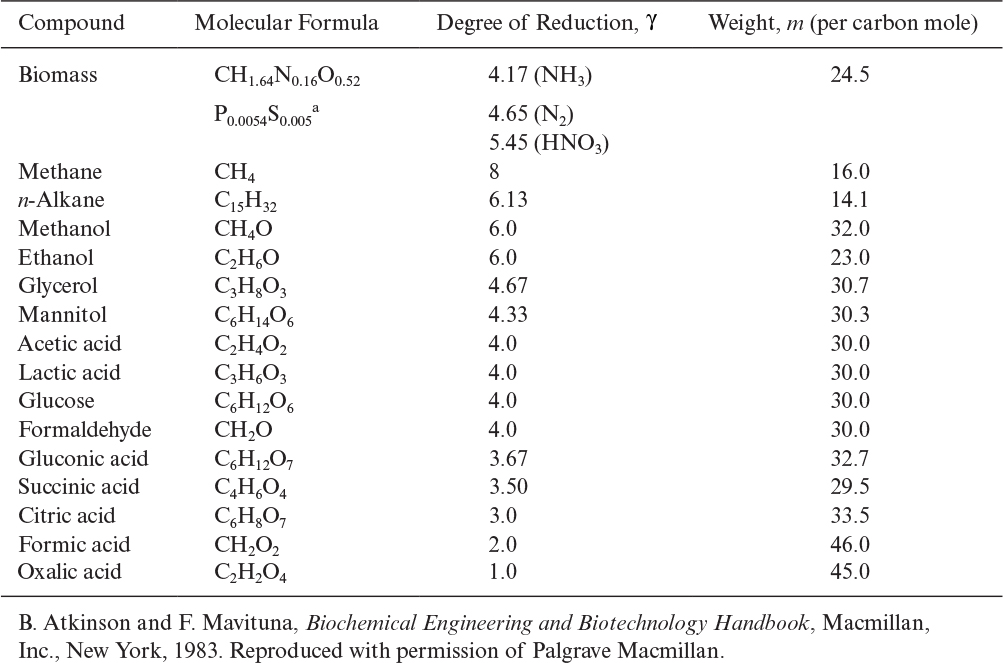
TABLE 7.4. Degree of Reduction and Weight of One Carbon Equivalent of One Mole of Some Substrates and Biomass

A high degree of reduction indicates a low degree of oxidation. That is, γCH4 > γEtOH > γglucose.
Consider the aerobic production of a single extracellular product:
Following are the degrees of reduction of substrate, biomass, and product:
Note that for CO2, H2O, and NH3 the degree of reduction is zero.
Equation 7.6 can lead to elemental balances on C, H, O, and N; an available electron balance; an energy balance; and a total mass balance. Of the equations, only five will be independent. If all the equations are written, then the extra equations can be used to check the consistency of an experimental data set. Because the amount of water formed or used in such reactions is difficult to determine and water is present in great excess, the hydrogen and oxygen balances are difficult to use. For such a data set, we would typically choose a carbon, a nitrogen, and an available-electron balance:
With partial experimental data, it is possible to solve this set of equations. Measurements of RQ and a yield coefficient would, for example, allow the calculation of the remaining coefficients. It should be noted that the coefficient, c, is YX/S (on a molar basis) and d is YP/S (also on a molar basis).
An energy balance for aerobic growth follows:
If ![]() the heat evolved per equivalent of available electrons transferred to oxygen, is constant, equation 7.13 is not independent of equation 7.12. Recall that an observed regularity is 26.95 kcal/g equivalent of available electrons transferred to oxygen, which allows the prediction of heat evolution based on estimates of oxygen consumption.
the heat evolved per equivalent of available electrons transferred to oxygen, is constant, equation 7.13 is not independent of equation 7.12. Recall that an observed regularity is 26.95 kcal/g equivalent of available electrons transferred to oxygen, which allows the prediction of heat evolution based on estimates of oxygen consumption.
Equations 7.12 and 7.13 also allow estimates of the fractional allocation of available electrons or energy for an organic substrate. Equation 7.12 can be rewritten as
where ε is the fraction of available electrons in the organic substrate that is transferred to oxygen, ξb is the fraction of available electrons that is incorporated into biomass, and ξp is the fraction of available electrons that is incorporated into extracellular products.
7.3. Theoretical Predictions of Yield Coefficients
In aerobic fermentations, the growth yield per mole glucose in oxygen molecules is approximately 3.14 ± 0.11 gdw cells/electron, when ammonia is used as the nitrogen source. The number of available electrons per oxygen molecule (O2) is four. When the number of oxygen molecules per mole of substrate consumed is known, the growth yield coefficient, YX/S, can easily be calculated. Consider the aerobic catabolism of glucose:
The total number of available electrons in 1 mole of glucose is 24. The cellular yield per available electron is YX/S = 24(3.14) = 76 gdw cells/mol glucose.
The predicted growth yield coefficient is YX/S = 76/180 = 0.4 gdw cells/g glucose. Most measured values of YX/S for aerobic growth on glucose are 0.38 to 0.51 g/g (see Table 6.1).
The ATP yield (YX/ATP) in anaerobic fermentations is approximately 10.5 ± 2 gdw cells/mol ATP. In aerobic fermentations, this yield varies between 6 and 29. When the energy yield of a metabolic pathway is known (N moles of ATP produced per gram of substrate consumed), the growth yield YX/S can be calculated using the following equation:
YX/S = YX/ATPN
7.4. Estimation of Elemental cell Composition
Cells are made of C, N, O, H, P, S, and minerals (Ca, Mg, Fe, Zn, and others). Elemental composition of the cells varies depending on the type of cells (bacteria, yeasts, molds, animal and plant cells), type of substrate, and growth conditions (T, pH, ORP, DO). A typical bacterial cell contains nearly 45% to 50% C, 10% to 14% N, 20% to 25% O, 6% to 8% H, 2% to 3% P, 0.5% to 1% S, and 5% to 6% ash and is usually symbolized by C5H7NO2 with a molar weight of 113 g/mol bacteria. However, this composition varies depending on the composition of growth medium (C, N, P, O sources) and environmental conditions.
Elemental composition of the cells needs to be determined before balancing biological reactions. This determination is done by filtering and drying the cells at 105°C until constant weight. Elemental analyses are carried out on dry cell mass to determine the percentages of C, N, O, H, P, and S content. Dried cells are further burned in a furnace at 550°C to remove organic fractions (volatile suspended solids) and to determine the ash content. The mass fraction of every element in dry cell mass is then converted to mole fractions to determine the empirical formula for one mole of cell.
The mole number of the ith element is
where Ni is the mole number, mi is the weight, and Mi is the molar weight of the ith elements. The total number of moles is
The mole fraction for the ith element is
Once the mole fractions are determined, the empirical formula is established as follows:
CXc HXH NXN OXO PXP SXS
7.5. Stoichiometry by Oxidation-Reduction Half-Reactions
In biological conversions, a substrate such as glucose is both the source of energy and the material used for biosynthesis of cells and the products. A fraction of the total electrons present in the substrate is transferred to the electron acceptor by metabolic reactions to generate energy in the form of ATPs (ee), and the remaining fraction ends up in the newly synthesized cellular mass (es). The sum of ee and es is 1.0. When electrons are transferred from the substrate to the electron acceptor, the net reaction can be represented by two half-reactions in the form of oxidation and reduction. The electron donor (substrate) is oxidized, and the electron acceptor is reduced. In aerobic oxidation of glucose to CO2 and H2O, glucose-carbon is the electron donor and oxygen is the electron acceptor. The electron donor (C in glucose) is oxidized to CO2 by donating electrons to the electron acceptor (O2), yielding water. This bioconversion can be represented by the following half-reactions based on one mole electron transfer:
By multiplying both sides of the overall reaction by 24, the overall reaction is obtained:
A list of half-reactions for common electron donors is presented in Table 7.5. Electron acceptor is oxygen in aerobic respiration. However, nitrate, sulfate, or Fe (III) may be the electron acceptor in anaerobic respiration. Carbon dioxide is the electron acceptor in anaerobic metabolism of carbonaceous compounds yielding methane as the end product. Table 7.6 summarizes half-reactions for common electron acceptors.
As mentioned before, a fraction of electrons present in the substrate ends up in the newly synthesized biomass. The empirical formula for bacterial cell is usually assumed to be C5H7NO2 which varies depending on the type of cell (yeasts, molds, animal and plant cells) and medium used. As shown in Section 7.4 it is possible to determine a more exact formula for a particular culture. Considering inorganic carbon (CO2 and HCO3–) as carbon and NH4+ as nitrogen source, the half-reaction for cell synthesis can be written as follows for one mole electron transfer:
This is a reduction half-reaction where inorganic carbon is the electron acceptor. When nitrate is used as the N-source, the half-reaction for cell synthesis can be written as follows:
Cell synthesis half-reactions are the electron-acceptor reactions that must accompany an electron-donor reaction such as the reaction shown in equation 7.18.
The fraction of electrons used for energy generation (ee) and for cell synthesis (es) need to be known in balancing microbial reactions. Net energy generation and net biosynthesis reactions are
where Re and Rs are the net energy generation and cell synthesis reactions and Ra, Rd, and Rc are the electron acceptor, electron donor, and cell synthesis (electron acceptor) half-reactions, respectively.
The net reaction based on fractional electron utilization is
Since ee + es = 1, equation 7.25 can be written as
Equation 7.25 or 7.26 can be used in balancing microbial reactions.
7.6. Thermodynamics of Biological Reactions
Like chemical reactions, biological reactions obey thermodynamic laws too. Energy is conserved in all biological reactions. Spontaneous bioreactions result in negative free-energy changes. Therefore, by looking at the free-energy changes in bioreactions, it is possible to determine which reactions would take place spontaneously and which require energy input. Free-energy changes in bioreactions are calculated by using the formation free energies of products and reactants. In general, free-energy change in a reaction is calculated by using the following equation:
where Σ ai Gi is the sum of free energies of the products, Σ bjGj is the sum of free energies of reactants, and ∆G is the free-energy change of the reaction.
Free energy of any compound is defined as
where ![]() is the standard free energy (25°C, 1 atm), R is the gas constant (1.99 cal/mol-K), T is the absolute temperature (K), and Ci is the molar concentration of the ith compound in aqueous solution. Therefore, free-energy change for the following bioreaction is
is the standard free energy (25°C, 1 atm), R is the gas constant (1.99 cal/mol-K), T is the absolute temperature (K), and Ci is the molar concentration of the ith compound in aqueous solution. Therefore, free-energy change for the following bioreaction is
Usually, standard free energies are calculated from the half-reactions of the electron donors and acceptors to determine the energy requirement of a reaction.
For aerobic microbial oxidation of glucose, the electron-donor half-reaction is
1/24 C6H12O6 + ¼ H2O → ¼ CO2 + H+ + e–
The standard free-energy change for this reaction is
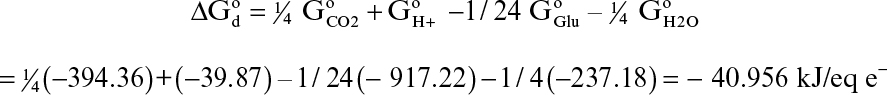
The electron-acceptor half-reaction for the same bioconversion is
The standard free-energy change for this reaction is
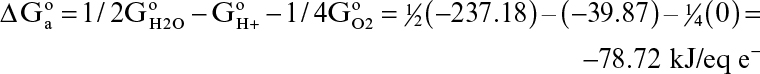
Therefore, the free-energy change for the net reaction is

Therefore, this bioreaction is spontaneous and energetically favorable. Free-energy changes for different electron donor and acceptors have been calculated. Figure 7.1 depicts variation of free-energy changes for different electron donors and acceptors. When glucose is used as the electron donor and oxygen as the electron acceptor in a bioreaction, the free-energy change is around –120 kJ/eq e–, whereas with the nitrate as the electron acceptor the free-energy change becomes nearly –110 kJ/eq e–. The free-energy change is much lower when sulfate is used as the electron acceptor (about –20kJ/eq e–). Under anaerobic conditions, where glucose is the electron donor and CO2 is the acceptor, the free-energy change is –18 kJ/eq e–. The difference between the free-energy changes of the same reaction under aerobic and anaerobic conditions is the reason for differences in growth yield coefficients. Large free-energy changes in aerobic metabolism of glucose result in high aerobic-growth-yield coefficients as compared to that of anaerobic growth.
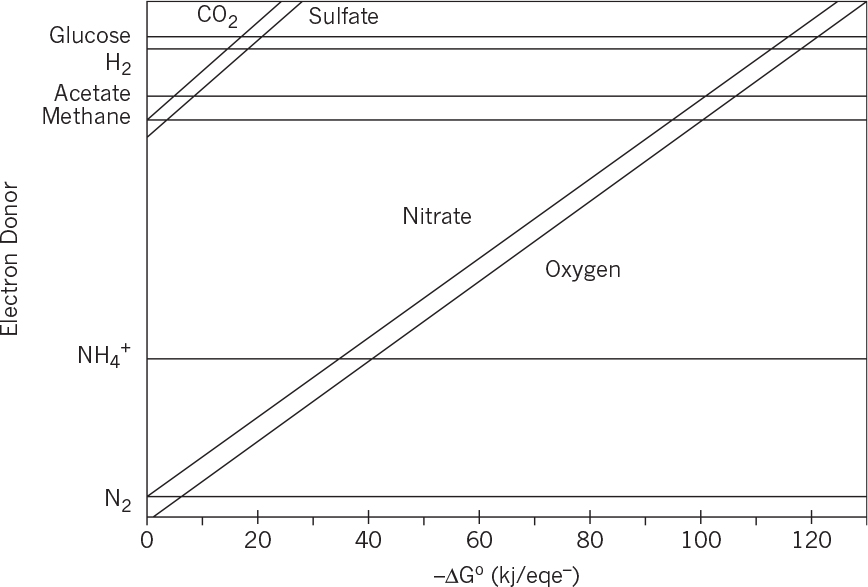
FIGURE 7.1. Variation of reaction free energies for different electron donors and acceptors. The lines represent electron acceptors. (Adapted from Rittmann & McCarty, Environmental Biotechnology, McGraw Hill, 2001.)
7.7. Summary
This chapter reviewed simple methods to determine the reaction stoichiometry for bioreactions. These methods lead to the possibility of predicting yield coefficients for various fermentations using a variety of substrates. By coupling these equations to experimentally measurable parameters, such as the respiratory quotient, we can infer a great deal about the progress of fermentation. Such calculations can also assist in initial process design equations by allowing the prediction of the amount of oxygen required (and consequently heat generated) for a certain conversion of a particular substrate. The prediction of yield coefficients is usually not exact, because unknown or unaccounted metabolic pathways and products may be present. Nonetheless, such calculations provide useful first estimates of such parameters.
Suggestions for Further Reading
BAILEY, J. E., AND D. F. OLLIS, Biochemical Engineering Fundamentals, 2d ed., McGraw-Hill, New York, 1986.
DORAN, P. M., Bioprocess Engineering Principles, 2d ed., Academic Press, Waltham, MA, 2013.
ERICKSON, L. E., I. G. MINKEVICH, AND V. K. EROSHIN, “Application of Mass and Energy Balance Regularities in Fermentation,” Biotechnology and Bioengineering 20: 1595, 1978.
MINKEVICH, I. G., “Mass and Energy Balance for Microbial Product Synthesis: Biochemical and Cultural Aspects,” Biotechnology and Bioengineering 25: 1267, 1983.
RITTMANN, B. E., AND P. L. MCCARTY, Environmental Biotechnology: Principles and Applications, McGraw-Hill, New York, 2001.
ROELS, J. A., Energetics and Kinetics in Biotechnology, Elsevier Science, New York, 1983.
VILLADSEN, J., J. NIELSON, AND G. LIDEN, Bioreaction Engineering Principles, 3d ed., Springer US, New York, 2011.
VAN GULIK, W. M., AND J. J. HEIJNEN, “A Metabolic Network Stoichiometry Analysis of Microbial Growth and Product Formation,” Biotechnology and Bioengineering 48: 181, 1995.
Problems
7.1. Determine the amount of (NH4)2SO4 to be supplied in a fermentation medium where the final cell concentration is 30 g/l in a 1031 culture volume. Assume that the cells are 12% nitrogen by weight and (NH4)2SO4 is the only nitrogen source.
7.2. The growth of baker’s yeast (S. cerevisiae) on glucose may be simply described by the following equation:
In a batch reactor of volume 105 1, the final desired yeast concentration is 50 gdw/l.
a. Determine the concentration and total amount of glucose and (NH4)2SO4 in the nutrient medium.
b. Determine the yield coefficients YX/S (biomass/glucose) and YX/O (biomass/oxygen).
c. Determine the total amount of oxygen required.
d. If the rate of growth at exponential phase is rx = 0.7 gdw/l-h, determine the rate of oxygen consumption (g O2/1-h)
e. Calculate the heat-removal requirements for the reactor (recall equation 6.26).
7.3. The growth of S. cerevisiae on glucose under anaerobic conditions can be described by the following overall reaction:

a. Determine the biomass yield coefficient YX/S.
b. Determine the product yield coefficients YEtOH/S, YCO2/S, YC3H2O/S.
c. Determine the coefficient β.
7.4. Aerobic growth of S. cerevisiae on ethanol is simply described by the following overall reaction:
C2H5OH + a O2 + b NH3 → c CH1.704N0.149O0.408 + d CO2 + e H2O
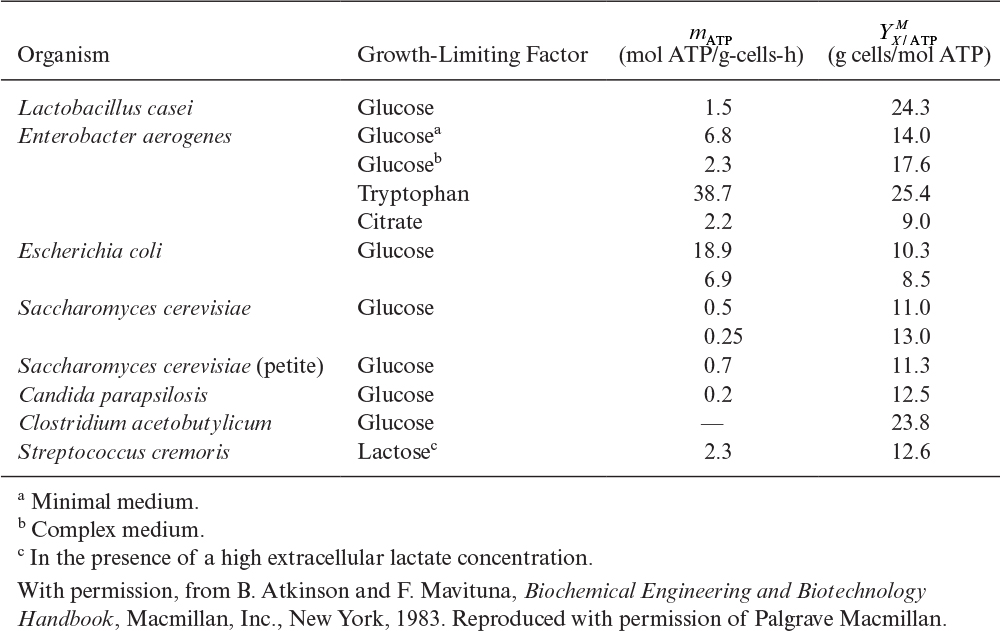
a. Determine the coefficients a, b, c, and d, where RQ = 0.66.
b. Determine the biomass yield coefficient, YX/S, and oxygen yield coefficient, YX/O2 (gdw/g O2).
7.5. Aerobic degradation of benzoic acid by a mixed culture of microorganisms can be represented by the following reaction:
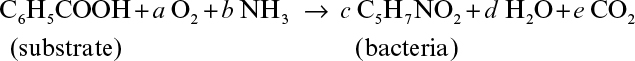
a. Determine a, b, c, d, and e if RQ = 0.9.
b. Determine the yield coefficients, YX/S and YX/O2.
c. Determine degree of reduction for the substrate and bacteria.
7.6. Aerobic degradation of an organic compound by a mixed culture of organisms in waste water can be represented by the following reaction:
C3H6O3 + a O2 + b NH3 → c C5H7NO2 + d H2O + e CO2
a. Determine a, b, c, d, and e if YX/S = 0.4 g X/g S.
b. Determine the yield coefficients YX/O2 and YX/NH3
c. Determine the degree of reductions for the substrate, bacteria, and RQ for the organisms.
7.7. Biological denitrification of nitrate-containing waste waters can be described by the following overall reaction:
a. Determine a, b, c, d, and e if YX/S = 0.5 g X/g N.
b. Determine the degree of reduction of bacteria and methanol.
7.8. The following biological oxidation reaction takes place in biological treatment of an industrial wastewater:
C6H4CH3OH + a O2 + b NH3 → c C5H7NO2 + d CO2 e H2O
a. Determine the coefficients of the equation (a, b, c, d, and e) if RQ = 0.5.
b. Determine Yx/s, and YX/O2.
c. Determine γs and γb.
7.9. Clostridium sp. were used for anaerobic conversion of glucose to acetic acid and H2 as described by the following reaction:
C6H12O6 + a NH3 + b H3PO4 → c C5H7NO2P0.2 + d CH3COOH + e CO2 + f H2
a. Determine the coefficients by writing elemental balances if Yx/s = 0.1 g/g.
b. Determine γs, γb, γAc, and γH2 and write down degree of reduction balance to see if it is satisfied.
c. Determine Yp/s for acetic acid and hydrogen.
7.10. Rhodobacter sp. ferments acetic acid to hydrogen gas and CO2 under photoheterotrophic conditions (anoxygenic photosynthesis) as depicted in the following reaction:
a. Determine the coefficients by using elemental balances.
b. Determine the growth yield coefficient Yx/s and Yp/s.
c. Write down degree of reduction balance for the conversion.
7.11. Elemental analysis of dry cell mass indicates that the cell is composed of 45% C, 25% O, 5% H, 12% N, 2.5% P, 0.5% S, and 10% minerals.
a. By considering 1 g of cell dry weight, determine mole fractions of every element and the cell formula.
b. If the cell formula is C4 H8 O2.2 N1.2 P0.08 S0.02, determine the percent elemental composition (i.e., mass fractions) of dry cell mass.
7.12. In ethanol fermentation from glucose, carbon dioxide is the electron acceptor, and glucose is the electron donor.
a. Write down the electron donor and acceptor half-reactions for ethanol fermentation for one mole electron transfer along with free-energy changes.
b. Determine the overall fermentation reaction for one mole of glucose and the free-energy change without cell-synthesis reaction.
c. Assuming 20% of the electrons in glucose are used for cell synthesis and 80% for energy generation (ee = 0.80 and es = 0.20), write down the reactions for Ra, Rd, and Rc, and determine the overall reaction stoichiometry for one mole of NH4-N.
7.13. In biological nitrification reaction NH4-N is converted to NO3-N under autotrophic conditions by using CO2 as the carbon source in the presence of oxygen. NH4-N is the electron donor, and oxygen is the electron acceptor in this bioconversion, which is realized in the absence of organic carbon source. Ammonium is also used as N-source for cell synthesis. If 85% of electrons are transferred to the product for energy generation and only 15% ends up in cell biomass, determine the following:
a. Write down the electron donor and acceptor half-reactions (Rd and Ra).
b. Write down the half-reaction for cell synthesis (Rc).
c. Write down the overall reaction by considering the electron fractionation.
7.14. Methane formation from acetate is realized under anaerobic conditions where NH4 is the nitrogen source for cell synthesis. Acetate is the electron donor and CO2 is the electron acceptor in this bioconversion. Assuming the cell formula is C5H7NO2 and only 10% of the electrons in the substrate are transferred to the cell biomass, determine the following:
a. Write down the electron donor and the acceptor half-reactions (Rd and Ra).
b. Write down the cell synthesis half-reaction (Rc).
c. Write down the overall reaction by considering that ee = 0.90 and es = 0.10.
7.15. Determine the free-energy changes for methane formation from the electron donors of glucose, acetate, H2 and ethanol where CO2 is the electron acceptor by using Figure 7.1. Comment on the results in terms of cell yield from different substrates.