4.3.2 BICM Pseudo-Capacity
The results from the previous section point out the fact that binary labeling strongly affects the BICM-GMI. Moreover, we have seen that the BICM-GMI curves for a given binary labeling intersect each other for different constellation sizes, which naturally leads to a quite general question: What is the best constellation, binary labeling, and input distribution for the BICM at a given SNR? Once this question is answered, approaching the fundamental limit will depend only on a good design of the binary encoder/decoder.
To formalize the previous question, and in analogy with (4.25), we define the BICM pseudo-capacity for a given constellation size ![]() as
as
where the optimization is over the constellation and its binary labeling, as well as over the vector of bitwise probabilities ![]() that induce a symbol-wise PMF (via (2.72)) satisfying the energy constraint
that induce a symbol-wise PMF (via (2.72)) satisfying the energy constraint ![]() . We use the name BICM pseudo-capacity because, in theory, the quantity in (4.64) might not be the largest achievable rate, which simply comes from the fact that the BICM-GMI is not the largest achievable rate for given
. We use the name BICM pseudo-capacity because, in theory, the quantity in (4.64) might not be the largest achievable rate, which simply comes from the fact that the BICM-GMI is not the largest achievable rate for given ![]() . Nevertheless, the numerical results we present in this section will, in fact, show that the BICM pseudo-capacity can close the gap to the AWGN capacity, and thus, it is indeed a meaningful quantity to study.
. Nevertheless, the numerical results we present in this section will, in fact, show that the BICM pseudo-capacity can close the gap to the AWGN capacity, and thus, it is indeed a meaningful quantity to study.
Similarly to the CM capacity, the BICM pseudo-capacity in (4.64) represents an upper bound on the number of bits per symbol that can be reliably communicated using BICM, i.e., when for each SNR, the constellation, its labeling, and the bits' distribution are optimized.
In general, solutions of the problem in (4.64) are difficult to find, even when both the constellation and the labeling are fixed. This is because, unlike the CM-MI, the BICM-GMI is not a concave function of the input distribution. To clarify this, consider the following example.

Figure 4.13 BICM-GMI 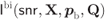 for 8PAM labeled by the BRGC as a function of the bit probabilities for
for 8PAM labeled by the BRGC as a function of the bit probabilities for  and
and  (
( ). The filled black circle shows the optimal value
). The filled black circle shows the optimal value
Although not explicitly mentioned, the results in Fig. 4.13 are obtained by scaling the constellation for each ![]() so that
so that ![]() . To formally define the problem in Example 4.17, we define the BICM constellation and labeling-constrained pseudo-capacity as
. To formally define the problem in Example 4.17, we define the BICM constellation and labeling-constrained pseudo-capacity as
where the optimization is over all the ![]() and
and ![]() is chosen so that
is chosen so that ![]() is satisfied.
is satisfied.
For constellations with a small number of points with a fixed binary labeling, we may use an exhaustive search together with an efficient numerical implementation of the BICM-GMI (which we show in Section 4.5) to solve the problem in (4.65). While this approach has obvious complexity limitations, i.e., the complexity grows exponentially with the number of bits per symbol ![]() , it allows us to obtain an insight into the importance of the bit-level probabilistic shaping in BICM.
, it allows us to obtain an insight into the importance of the bit-level probabilistic shaping in BICM.

Figure 4.14 Functions  and
and  in (4.16) for 8PAM over the AWGN channel and the BRGC, NBC, and FBC. The function
in (4.16) for 8PAM over the AWGN channel and the BRGC, NBC, and FBC. The function  in (4.17) and the SL in (4.18) are also shown
in (4.17) and the SL in (4.18) are also shown
On the basis of the results in Examples 4.15–4.18, some concluding remarks about the BICM pseudo-capacity can be made. First of all, these results show the suboptimality of the BRGC in terms of maximizing the BICM-GMI for a given equally spaced constellation and uniform input distributions. For 8PAM and for low and medium SNR values, the NBC and the FBC give higher BICM capacities than the BRGC. Moreover, for asymptotically low rates, the optimum binary labeling for ![]() PAM constellations is the NBC. The results in these examples also show that a BICM system can be optimum for asymptotically low rates (i.e., it can achieve the SL). This can be obtained by using probabilistic shaping or by properly selecting the binary labeling.
PAM constellations is the NBC. The results in these examples also show that a BICM system can be optimum for asymptotically low rates (i.e., it can achieve the SL). This can be obtained by using probabilistic shaping or by properly selecting the binary labeling.
4.3.3 Useful Relationships
In this section, we provide some useful relationships for the analysis of information-theoretic aspects of BICM transmission.
To show the usefulness of (4.66), consider (for simplicity) the AWGN channel. In this case, the conditional MI ![]() in (4.66) is given by (4.4) and can be expressed as
in (4.66) is given by (4.4) and can be expressed as
where
and where (4.72) follows from (2.75) and from the fact that ![]() ,
, ![]() .
.
In (4.73), we use ![]() to denote a random variable with support
to denote a random variable with support ![]() and PMF
and PMF ![]() given by (2.75), i.e., when the symbols are drawn from the subconstellation
given by (2.75), i.e., when the symbols are drawn from the subconstellation ![]() created by the binary labeling (see, e.g., Fig. 2.16). As the r.h.s. of (4.73) is an MI between
created by the binary labeling (see, e.g., Fig. 2.16). As the r.h.s. of (4.73) is an MI between ![]() and
and ![]() , we use the notation
, we use the notation ![]() . Using (4.72) in (4.66) we obtain
. Using (4.72) in (4.66) we obtain
The expression in (4.74) shows that the BICM-GMI can be expressed as a difference of CM-MIs. This interpretation is useful because it shows that a good characterization of MIs for arbitrary (sub)constellations leads to a good characterization of the BICM-GMI. This is particularly interesting as plenty of results already exist in the literature regarding CM-MIs, which, because of (4.74), can be “reused” to study the BICM-GMI. This approach has been taken, e.g., to study the low- and high-SNR behavior of BICM, where the asymptotic behavior of CM-MIs for arbitrary constellations is used to study the asymptotic behavior of the BICM-GMI.
We note that (4.76) generalizes the L-values defined in Section 3.3 allowing us to deal with arbitrary mismatched metrics ![]() . Theorem 5.1 demonstrates also that the distribution of the generalized L-values (4.76) suffices to calculate the BICM-GMI.
. Theorem 5.1 demonstrates also that the distribution of the generalized L-values (4.76) suffices to calculate the BICM-GMI.
An immediate consequence of Theorem 5.1 is that when ![]() is given by (4.33),
is given by (4.33), ![]() ,
, ![]() , and
, and ![]() . Thus,
. Thus,
In the case of uniformly distributed bits ![]() and for any generalized logarithmic-likelihood ratio (LLR), (4.75) becomes
and for any generalized logarithmic-likelihood ratio (LLR), (4.75) becomes
Furthermore, if we assume the symmetry condition (3.74) is satisfied5 (i.e., ![]() , we obtain from (4.82)
, we obtain from (4.82)
Equivalently, we can express (4.83) as
where
and (4.87), inspired by (3.94), is a numerically stable6 version of (4.86).
Knowing the observations
and the transmitted bits ![]() , (4.85) can be transformed into a simple unbiased estimator of
, (4.85) can be transformed into a simple unbiased estimator of ![]() as
as
In the case of matched bit metrics ![]() with symmetric L-values and uniformly distributed bits, we obtain the estimate of the bit-level GMI via Monte Carlo integration
with symmetric L-values and uniformly distributed bits, we obtain the estimate of the bit-level GMI via Monte Carlo integration
In a simple case of transmission over the scalar channel, i.e., when the model relating the channel outcome ![]() and the input
and the input ![]() is well known, we may calculate the GMI via the formulas provided in Section 4.5 with much better accuracy than the one obtained from (4.89) and (4.90). On the other hand, as it happens very often, the L-values are calculated using nonlinear expressions, and are affected by various random variables. Then, the direct integrals of Section 4.5 are too involved to derive and/or tedious to use. Moreover, because the PDFs
is well known, we may calculate the GMI via the formulas provided in Section 4.5 with much better accuracy than the one obtained from (4.89) and (4.90). On the other hand, as it happens very often, the L-values are calculated using nonlinear expressions, and are affected by various random variables. Then, the direct integrals of Section 4.5 are too involved to derive and/or tedious to use. Moreover, because the PDFs ![]() or
or ![]() are also difficult to estimate (analytically or via histograms), the estimates (4.89) and (4.90) become very convenient.
are also difficult to estimate (analytically or via histograms), the estimates (4.89) and (4.90) become very convenient.
4.4 BICM, CM, and MLC: A Comparison
4.4.1 Achievable Rates
Having analyzed CM and BICM, it is interesting to compare and relate them to multilevel coding (MLC), another popular coded modulation scheme we presented in Section 2.3.2. To this end, we start rewriting the CM-MI using the random variables ![]() , i.e.,
, i.e.,
To obtain (4.97), we used the fact that the mapping ![]() is bijective, and to obtain (4.98), we used the chain rule of mutual information.
is bijective, and to obtain (4.98), we used the chain rule of mutual information.
The quantity ![]() in (4.98) represents an MI between the bit
in (4.98) represents an MI between the bit ![]() and the output, conditioned on the knowledge of the bits
and the output, conditioned on the knowledge of the bits ![]() . This bit-level MI represents the maximum rate that can be used at the
. This bit-level MI represents the maximum rate that can be used at the ![]() th bit position, given a perfect knowledge of the previous
th bit position, given a perfect knowledge of the previous ![]() bits.
bits.
MLC with multistage decoding (MSD) (see Fig. 2.5) is in fact a direct application of (4.98), i.e., ![]() parallel encoders send the encoded oddata using bits' positions
parallel encoders send the encoded oddata using bits' positions ![]() , each of the encoders uses a coding rate
, each of the encoders uses a coding rate ![]() . At the receiver side, the first bit level is decoded and the decisions are passed to the second decoder, which then passes the decisions to the third decoder, and so on, as shown in Fig. 2.6 (a).
. At the receiver side, the first bit level is decoded and the decisions are passed to the second decoder, which then passes the decisions to the third decoder, and so on, as shown in Fig. 2.6 (a).
Although different mapping rules produce different conditional MIs ![]() , the sum (4.98) remains constant. In other words, the sum of achievable rates using MLC encoding/decoding does not depend on the labeling and is equal to CM-MI. On the other hand, when MLC is based on parallel decoding of the individual levels (PDL), i.e., when no information is passed between the
, the sum (4.98) remains constant. In other words, the sum of achievable rates using MLC encoding/decoding does not depend on the labeling and is equal to CM-MI. On the other hand, when MLC is based on parallel decoding of the individual levels (PDL), i.e., when no information is passed between the ![]() decoders (see Fig. 2.6b), BICM and MLC are equivalent in terms of achievable rates, although the main difference still remains: instead of
decoders (see Fig. 2.6b), BICM and MLC are equivalent in terms of achievable rates, although the main difference still remains: instead of ![]() encoder–decoder pairs, BICM uses only one pair.
encoder–decoder pairs, BICM uses only one pair.
Using (4.98) and (4.54), we can express the MI loss caused by BICM as
which clearly shows that the BICM-GMI will be approximately equal to the CM if the differences ![]() are small for all
are small for all ![]() .
.

Figure 4.15 MIs defining the achievable rates for 8PAM labeled by (a) the BRGC and (b) the BSGC over the AWGN channel (see Fig. 2.13). The AWGN capacity  , the CM-MI, and BICM-GMI are also shown. The pairs
, the CM-MI, and BICM-GMI are also shown. The pairs  and
and 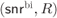 (see (4.109) and (4.113)) for
(see (4.109) and (4.113)) for  are also shown (circles and triangles, respectively)
are also shown (circles and triangles, respectively)
We have already demonstrated in Theorem 4.10 that the GMI is upper bounded by the MI, which indicates that the BICM-GMI is upper bounded by the CM-MI. This property can be also demonstrated analyzing the terms in the r.h.s. of (4.99). We note that, although often evoked in the literature, the data processing theorem cannot be used for the proof because the bits ![]() , the bit
, the bit ![]() , and the observation
, and the observation ![]() do not form a Markov chain.
do not form a Markov chain.
We are now in a position to establish the following inequalities
which hold for any ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , and where
, and where ![]() and
and ![]() are related via (2.72). The second inequality in (4.104) is obvious because of constraining the input distribution to be discrete and unoptimized. The first inequality is due to Theorem 4.24 and is tight only if the bits
are related via (2.72). The second inequality in (4.104) is obvious because of constraining the input distribution to be discrete and unoptimized. The first inequality is due to Theorem 4.24 and is tight only if the bits ![]() conditioned on
conditioned on ![]() are independent, i.e.,
are independent, i.e.,
The expression in (4.105) holds, e.g., when using a 4QAM constellation with Gray labeling. In this case the bits ![]() and
and ![]() modulate the orthogonal dimensions of the constellation:
modulate the orthogonal dimensions of the constellation: ![]() and
and ![]() , respectively.
, respectively.
Similarly to (4.104), for fading channels, we obtain
Furthermore, because ![]() and
and ![]() are concave functions of the SNR, it follows from Jensen's inequality that
are concave functions of the SNR, it follows from Jensen's inequality that
On the other hand, the BICM-GMI is not always a concave function of the SNR,7 and thus, we cannot guarantee an inequality similar to (4.107).
4.4.2 Robustness of the Encoding Scheme
While the rates achievable using MLC are never smaller than those attainable using BICM, it is important to note that the design of MLC, i.e., the choice of the coding rates ![]() for each of the coding levels, requires the knowledge of all the conditional MIs
for each of the coding levels, requires the knowledge of all the conditional MIs ![]() . This brings up an issue related to the robustness of the design with respect to lack of complete knowledge of the channel model.
. This brings up an issue related to the robustness of the design with respect to lack of complete knowledge of the channel model.
To clarify this issue, we now assume that the MLC encoding/decoding scheme is designed for the AWGN channel for a coding rate ![]() . We also assume that the design is done so as to operate at the SNR decoding threshold
. We also assume that the design is done so as to operate at the SNR decoding threshold ![]() , i.e., we design the encoders to ensure successful decoding at the SNR limit defined by the CM-MI, which we denote as
, i.e., we design the encoders to ensure successful decoding at the SNR limit defined by the CM-MI, which we denote as
where ![]() is the inverse of the MI function
is the inverse of the MI function ![]() defined in Section 4.1.
defined in Section 4.1.
The decoding threshold of each of the MLC levels is given by
where ![]() is the inverse of the conditional MI
is the inverse of the conditional MI ![]() .
.
We can thus define the SNR decoding threshold as the value of SNR, for which the message at all MLC levels can be decoded
In order to operate at the CM-MI limit with ![]() we need to satisfy the following:
we need to satisfy the following:
that is, the SNR decoding thresholds for each of the decoders must be the same.
If a BICM scheme is designed for the same coding rate ![]() , the corresponding SNR decoding threshold is given by
, the corresponding SNR decoding threshold is given by
where ![]() is the inverse function of the BICM-GMI.
is the inverse function of the BICM-GMI.
To illustrate the previous definitions, we show in Fig. 4.15 the pairs ![]() and
and ![]() for a rate
for a rate ![]() . The difference
. The difference ![]() can be understood as the SNR penalty caused by using a BICM scheme for a given coding rate
can be understood as the SNR penalty caused by using a BICM scheme for a given coding rate ![]() . For the BRGC, the penalty for
. For the BRGC, the penalty for ![]() is close to zero, however, for the BSGC it increases up to about
is close to zero, however, for the BSGC it increases up to about ![]() .
.
We are now ready to see what happens if MLC and BICM are used when transmitting over a non-AWGN channel. In other words, we are interested in studying how the SNR decoding thresholds change if the design made for the AWGN channel is used in a different channel. This can be the case, e.g., when transmitting over a fading channel which was not foreseen during the design.
If the encoders with the rates ![]() with
with ![]() (designed so as to satisfy (4.112) for the AWGN channel) are used in a fading channel, the corresponding SNR decoding thresholds are given by
(designed so as to satisfy (4.112) for the AWGN channel) are used in a fading channel, the corresponding SNR decoding thresholds are given by
where ![]() is the inverse of the conditional MI
is the inverse of the conditional MI ![]() .
.
Again, successful decoding at all decoding levels of MLC, is possible if ![]() is greater than all the individual SNR decoding thresholds in (4.114), i.e.,
is greater than all the individual SNR decoding thresholds in (4.114), i.e.,
Since the form of ![]() varies with
varies with ![]() , the values of the corresponding inverse functions
, the values of the corresponding inverse functions ![]() will not be the same. Consequently, we cannot guarantee that the condition for the average SNR, similar to (4.112), will be satisfied, and, in general, we will have
will not be the same. Consequently, we cannot guarantee that the condition for the average SNR, similar to (4.112), will be satisfied, and, in general, we will have ![]() .
.
Therefore, the following relationship holds
and the difference ![]() should be interpreted as the SNR penalty because of a “code design mismatch”.
should be interpreted as the SNR penalty because of a “code design mismatch”.
We emphasize that the mismatch happens because the coding rates ![]() were selected using the functions
were selected using the functions ![]() . If, on the other hand, we rather used
. If, on the other hand, we rather used ![]() , then the code designed would be matched to the fading channel. In such a case, the effect of the code design mismatch would appear if MLC were used over the AWGN channel. More generally, the code design mismatch phenomenon will be observed when the model of the channel used for the design is mismatched with respect to the actual channel.
, then the code designed would be matched to the fading channel. In such a case, the effect of the code design mismatch would appear if MLC were used over the AWGN channel. More generally, the code design mismatch phenomenon will be observed when the model of the channel used for the design is mismatched with respect to the actual channel.
Of course, in BICM transmission, the SNR decoding threshold is similar to (4.113), i.e.,
In many cases of practical interest, ![]() but in general, this relationship depends on the mapping as we discussed after (4.108). Of course, the relationship
but in general, this relationship depends on the mapping as we discussed after (4.108). Of course, the relationship ![]() always holds, and we interpret the difference
always holds, and we interpret the difference ![]() as the SNR gap because of the suboptimality of BICM. Unlike in the case of MLC, there is no effect of the code design mismatch: BICM remains “matched” to the channel independently of the underlying channel model.
as the SNR gap because of the suboptimality of BICM. Unlike in the case of MLC, there is no effect of the code design mismatch: BICM remains “matched” to the channel independently of the underlying channel model.

Figure 4.16 Achievable rates for 8PAM using the BRGC. In MLC, the rates  are designed for the AWGN channel and then used in a Rayleigh fading channel. For
are designed for the AWGN channel and then used in a Rayleigh fading channel. For  , the circles correspond to the pairs
, the circles correspond to the pairs  and
and  , the triangle shows
, the triangle shows  , the diamond shows
, the diamond shows  and the squares indicate
and the squares indicate 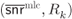 and
and  . The dashed line corresponds to the set of pairs
. The dashed line corresponds to the set of pairs  for
for 
4.5 Numerical Calculation of Mutual Information
In Sections 4.2 and 4.3, we have shown various examples of the CM-MI and the BICM-GMI calculated for the AWGN channel. While we cannot avoid the problem of enumerating the constellation points, we may efficiently calculate the multidimensional integrals (over ![]() ) appearing in the MI expressions using Gauss–Hermite (GH) quadratures. The methods we discussed in Section 4.3.3 may also be used but the numerical quadratures are much more accurate for small values of
) appearing in the MI expressions using Gauss–Hermite (GH) quadratures. The methods we discussed in Section 4.3.3 may also be used but the numerical quadratures are much more accurate for small values of ![]() and, what is more important, they are much more reliable for being used in a numerical optimization.
and, what is more important, they are much more reliable for being used in a numerical optimization.
For any function ![]() with bounded
with bounded ![]() th derivative, the
th derivative, the ![]() -points GH quadrature
-points GH quadrature
is asymptotically (![]() ) exact if we use the quadrature nodes
) exact if we use the quadrature nodes ![]() as the
as the ![]() th root of the Hermite polynomial
th root of the Hermite polynomial
and the weights defined as
The values of ![]() and
and ![]() can be easily found for different values of
can be easily found for different values of ![]() , which determines the trade-off between the computation speed and the accuracy of the quadrature. The expression in (4.118) can be straightforwardly expanded to a quadrature over an
, which determines the trade-off between the computation speed and the accuracy of the quadrature. The expression in (4.118) can be straightforwardly expanded to a quadrature over an ![]() -dimensional space as
-dimensional space as
where ![]() and
and ![]() . It is important to note that the expansion we use in (4.121) is not unique; however, it is a simple way of generalizing (4.118) to
. It is important to note that the expansion we use in (4.121) is not unique; however, it is a simple way of generalizing (4.118) to ![]() dimensions.
dimensions.
The CM-MI in (4.23) and in (4.24) can be expressed, respectively, as
where ![]() and
and ![]() are shown in Table 4.1. To obtain (4.122), we first used the substitution
are shown in Table 4.1. To obtain (4.122), we first used the substitution ![]() , then we used
, then we used ![]() , and then split the logarithm of the quotient as a difference of logarithms. To obtain (4.123), we used
, and then split the logarithm of the quotient as a difference of logarithms. To obtain (4.123), we used ![]() in
in ![]() and split the logarithm of the multiplication as the sum of the logarithms.
and split the logarithm of the multiplication as the sum of the logarithms.
Table 4.1 Six functions used in (4.122)–(4.129) to evaluate the CM-MI and the BICM-GMI
| Function | Expression |
The BICM-GMI in (4.62) and (4.63) can be expressed, respectively, as
where ![]() and
and ![]() are shown in Table 4.1. To obtain (4.124), we first used (4.66), then the substitution
are shown in Table 4.1. To obtain (4.124), we first used (4.66), then the substitution ![]() , and then again split the logarithm of the quotient (in the conditional expectation (4.4)) as a difference of logarithms. The expression (4.125) can be obtained by repeating the procedure and using a uniform input distribution.
, and then again split the logarithm of the quotient (in the conditional expectation (4.4)) as a difference of logarithms. The expression (4.125) can be obtained by repeating the procedure and using a uniform input distribution.
Using (4.121)–(4.123), we obtain the following ready-to-use expressions for the CM-MI
where (4.126) and (4.127) shall be used to evaluate the CM-MI with arbitrary and uniform input distributions, respectively.
Similarly, by using (4.121)–(4.125), we obtain the following ready-to-use expressions for the BICM-GMI
which shall be used to numerically evaluate the BICM-GMI with arbitrary and uniform input distributions, respectively.

Figure 4.17 Average value of absolute error when evaluating  using different number of quadrature points
using different number of quadrature points  for (a) 2PAM and (b) 8PAM. The left axis indicates the values of the error (shown with solid lines) while the right axis indicates the values of the MI (thick dashed lines)
for (a) 2PAM and (b) 8PAM. The left axis indicates the values of the error (shown with solid lines) while the right axis indicates the values of the MI (thick dashed lines)
All the results presented in this chapter were obtained with ![]() , which we found to provide an adequate accuracy in all numerical examples.
, which we found to provide an adequate accuracy in all numerical examples.
4.6 Bibliographical Notes
All the concepts in this chapter can be traced back to Shannon's works [1, 2]. For a detailed treatment of MIs, channel capacity, and so on, we refer the reader to standard textbook such as [3, 4].
The CM-MI has received different names in the literature. It is called joint capacity in [5], (constellation) constrained capacity in [6, 7], and coded modulation capacity in [8–12]. We use the name CM-MI to indicate that no optimization over the input distribution is performed.
The information-theoretical model for BICM was first introduced by Caire et al. using ![]() parallel memoryless BICO channels [8, Fig. 3]. Martinez et al. later refined this model in [10], where it was shown that the model of parallel channels leads to correct conclusions about achievable rates, but may yield incorrect error exponents/cutoff rates. Error exponents for BICM were also studied in [13].
parallel memoryless BICO channels [8, Fig. 3]. Martinez et al. later refined this model in [10], where it was shown that the model of parallel channels leads to correct conclusions about achievable rates, but may yield incorrect error exponents/cutoff rates. Error exponents for BICM were also studied in [13].
The BICM-GMI has received different names in the literature. It is called parallel decoding capacity in [5], receiver constrained capacity in [6], and BICM capacity in [8–12]. Again, we refrain from using the word “capacity” to emphasize the lack of optimization over the input distribution. We adopted the name BICM-GMI, which fits well the finding of Martinez et al. [10] who recognized the BICM decoder as a mismatched decoder and showed that the BICM-GMI in (4.54) corresponds to an achievable rate of such a decoder. Theorem 4.11 is thus adopted from [10] and was also used in [14]. The results on the optimality of matched processing in Theorem 4.10 and Corollary 4.12 were inspired by [15].
As we indicated, the BICM-GMI is an achievable rate but it has not be proven to be the largest achievable rate. For example, a different achievable rate—the so-called LM rate—has been recently studied in [16, Part I]. Finding the largest achievable rate remains as an open research problem. Despite this cautionary statement, the BICM-GMI predicts well the performance of capacity-approaching codes, as shown in Example 4.13 (see also [17, Section 3], [18, Section IV]). The generator polynomials of the TENC used in Example 4.13 were chosen on the basis of the results in [19] and some of the puncturing patterns used were taken from [19, 20].
Changing the distribution of the constellation symbols—known as signal/constellation shaping—has been studied for a number years, see [21–24]. In the context of BICM, geometrical shaping (i.e., design of the constellation under the assumption of uniform distribution of the symbols) was studied in [5, 25, 26], and probabilistic shaping (i.e., varying the probabilities of the symbols and/or bits when using the fixed constellation) was proposed in [27, 28] and developed further in [16, 29–33]. Recently, a numerical algorithm to obtain optimal input distributions in BICM was proposed in [34]. As the BICM-GMI is not the largest achievable rate, probabilistic or geometric shaping in BICM yields what we call in Section 4.3.2 a “pseudo-capacity.”
The expression in (4.66) was first introduced in [9, Proposition 1], [7, eq. (65)] and later generalized in [35, Theorem 2] to multidimensional constellations and arbitrary input distributions. An alternative proof for Theorem 4.22 was presented in [16, Appendix B.1.1]. Achievable rates for 4D constellations for BICM in the context of coherent optical communications have been recently studied in [17].
The solution of (4.64) is in general unknown but results are available in the low-SNR regime. The low-SNR regime of the CM-MI has been studied in [36, 37], where conditions for constellations to achieve the SL are given. The fact that the SL is not always achieved for BICM was first noticed in [9] and later shown to be caused by the selection of the binary labeling [11]. The behavior of BICM in the low-SNR regime was studied in [9, 11, 35, 38, 39] as a function of the constellation and the binary labeling, assuming a uniform input distribution. Results for arbitrary input distributions under the indepence assumption of the bits have been recently presented in [40]. It is shown in [40] that probabilistic shaping offers no extra degrees of freedom in addition to what is provided by geometrical shaping for BICM in the low-SNR regime.
In terms of binary labelings, the NBC was shown to be optimal for ![]() PAM in the low-SNR regime [11, 35] and the FBC was analyzed in [41] for uncoded transmission. The 49 labelings that give different BICM-GMI in Fig. 4.12 correspond to the 49 classes in [42, Tables A.1 and A.2] and the 7 different classes of labelings that appear in Fig. 4.12 for high SNR correspond to those in [42, Table A.1]. The optimality of a Gray code was conjectured in [8, Section III-C] in a rather general setup, i.e., without specifying the Gray code, the constellation, or the SNR regime. This conjecture was later disproved in [43] where it is shown that for low and medium SNR, there exist other labelings that give a higher BICM-GMI (see also [12, Chapter 3]). The numerical results presented in [12, Chapter 3], [44] show that in the high-SNR regime, Gray codes are indeed optimal. A formal proof for the optimality of Gray codes in the high-SNR regime for arbitrary 1D constellations was recently given in [45]. A simple approximation for the BICM-GMI that can be used to optimize the binary labeling of the constellation was recently introduced in [18].
PAM in the low-SNR regime [11, 35] and the FBC was analyzed in [41] for uncoded transmission. The 49 labelings that give different BICM-GMI in Fig. 4.12 correspond to the 49 classes in [42, Tables A.1 and A.2] and the 7 different classes of labelings that appear in Fig. 4.12 for high SNR correspond to those in [42, Table A.1]. The optimality of a Gray code was conjectured in [8, Section III-C] in a rather general setup, i.e., without specifying the Gray code, the constellation, or the SNR regime. This conjecture was later disproved in [43] where it is shown that for low and medium SNR, there exist other labelings that give a higher BICM-GMI (see also [12, Chapter 3]). The numerical results presented in [12, Chapter 3], [44] show that in the high-SNR regime, Gray codes are indeed optimal. A formal proof for the optimality of Gray codes in the high-SNR regime for arbitrary 1D constellations was recently given in [45]. A simple approximation for the BICM-GMI that can be used to optimize the binary labeling of the constellation was recently introduced in [18].
GH quadratures can be found in [46, Section 7.3.4] and tables with the coefficient ![]() and
and ![]() for different values of
for different values of ![]() in [46, Appendix 7.3(b)]. Ready-to-use expressions for computing the CM-MI and BICM-GMI are given in [44].
in [46, Appendix 7.3(b)]. Ready-to-use expressions for computing the CM-MI and BICM-GMI are given in [44].
References
- [1] Shannon, C. E. (1948) A mathematical theory of communications. Bell Syst. Tech. J., 27, 379–423 and 623–656.
- [2] Shannon, C. E. (1949) Communication in the presence of noise. Proc. IRE, 37 (1), 10–21.
- [3] Cover, T. and Thomas, J. (2006) Elements of Information Theory, 2nd edn., John Wiley & Sons, Inc., Hoboken, NJ.
- [4] MacKay, D. J. C. (2005) Information Theory, Inference, and Learning Algorithms, Cambridge University Press.
- [5] Barsoum, M., Jones, C., and Fitz, M. (2007) Constellation design via capacity maximization. IEEE International Symposium on Information Theory (ISIT), June 2007, Nice, France.
- [6] Schreckenbach, F. (2007) Iterative decoding of bit-interleaved coded modulation. PhD dissertation, Technische Universität München, Munich, Germany.
- [7] Brännström, F. and Rasmussen, L. K. (2009) Classification of unique mappings for 8PSK based on bit-wise distance spectra. IEEE Trans. Inf. Theory, 55 (3), 1131–1145.
- [8] Caire, G., Taricco, G., and Biglieri, E. (1998) Bit-interleaved coded modulation. IEEE Trans. Inf. Theory, 44 (3), 927–946.
- [9] Martinez, A., Guillén i Fàbregas, A., and Caire, G. (2008) Bit-interleaved coded modulation in the wideband regime. IEEE Trans. Inf. Theory, 54 (12), 5447–5455.
- [10] Martinez, A., Guillén i Fàbregas, A., Caire, G., and Willems, F. M. J. (2009) Bit-interleaved coded modulation revisited: a mismatched decoding perspective. IEEE Trans. Inf. Theory, 55 (6), 2756–2765.
- [11] Stierstorfer, C. and Fischer, R. F. H. (2009) Asymptotically optimal mappings for BICM with
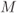 -PAM and
-PAM and  -QAM. IET Electron. Lett., 45 (3), 173–174.
-QAM. IET Electron. Lett., 45 (3), 173–174. - [12] Stierstorfer, C. (2009) A bit-level-based approach to coded multicarrier transmission. PhD dissertation, Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen, Germany.
- [13] Wachsmann, U., Fischer, R. F. H., and Huber, J. B. (1999) Multilevel codes: theoretical concepts and practical design rules. IEEE Trans. Inf. Theory, 45 (5), 1361–1391.
- [14] Nguyen, T. and Lampe, L. (2011) Bit-interleaved coded modulation with mismatched decoding metrics. IEEE Trans. Commun., 59 (2), 437–447.
- [15] Jaldén, J., Fertl, P., and Matz, G. (2010) On the generalized mutual information of BICM systems with approximate demodulation. IEEE Information Theory Workshop (ITW), January 2010, Cairo, Egypt.
- [16] Peng, L. (2012) Fundamentals of bit-interleaved coded modulation and reliable source transmission. PhD dissertation, University of Cambridge, Cambridge.
- [17] Alvarado, A. and Agrell, E. (2014) Achievable rates for four-dimensional coded modulation with a bit-wise receiver. Optical Fiber Conference (OFC), March 2014, San Francisco, CA.
- [18] Alvarado, A., Brännström, F., and Agrell, E. (2014) A simple approximation for the bit-interleaved coded modulation capacity. IEEE Commun. Lett., 18 (3), 495–498.
- [19] Açikel, O. and Ryan, W. (1999) Punctured turbo-codes for BPSK/QPSK channels. IEEE Trans. Commun., 47 (9), 1325–1323.
- [20] Kousa, M. A. and Mugaibel, A. H. (2002) Puncturing effects on turbo codes. Proc. IEE, 149 (3), 132–138.
- [21] Calderbank, A. R. and Ozarow, L. H. (1990) Nonequiprobable signaling on the Gaussian channel. IEEE Trans. Inf. Theory, 36 (4), 726–740.
- [22] Forney, G. D. Jr. and Wei, L.-F. (1989) Multidimensional constellations—Part I: Introduction, figures of merit, and generalized cross constellations. IEEE J. Sel. Areas Commun., 7 (6), 877–892.
- [23] Forney, G. D. Jr. (1989) Multidimensional constellations—Part II: voronoi constellations. IEEE J. Sel. Areas Commun., 7 (6), 941–957.
- [24] Fischer, R. F. H. (2002) Precoding and Signal Shaping for Digital Transmission, John Wiley & Sons, Inc..
- [25] Sommer, D. and Fettweis, G. P. (2000) Signal shaping by non-uniform QAM for AWGN channels and applications using turbo coding. International ITG Conference on Source and Channel Coding (SCC), January 2000, Munich, Germany.
- [26] Goff, S. Y. L. (2003) Signal constellations for bit-interleaved coded modulation. IEEE Trans. Inf. Theory, 49 (1), 307–313.
- [27] Le Goff, S. Y., Sharif, B. S., and Jimaa, S. A. (2004) A new bit-interleaved coded modulation scheme using shaping coding. IEEE Global Telecommunications Conference (GLOBECOM), November–December 2004, Dallas, TX.
- [28] Raphaeli, D. and Gurevitz, A. (2004) Constellation shaping for pragmatic turbo-coded modulation with high spectral efficiency. IEEE Trans. Commun., 52 (3), 341–345.
- [29] Le Goff, S., Sharif, B. S., and Jimaa, S. A. (2005) Bit-interleaved turbo-coded modulation using shaping coding. IEEE Commun. Lett., 9 (3), 246–248.
- [30] Le Goff, S., Khoo, B. K., Tsimenidis, C. C., and Sharif, B. S. (2007) Constellation shaping for bandwidth-efficient turbo-coded modulation with iterative receiver. IEEE Trans. Wirel. Commun., 6 (6), 2223–2233.
- [31] Guillén i Fàbregas, A. and Martinez, A. (2010) Bit-interleaved coded modulation with shaping. IEEE Information Theory Workshop (ITW), August–September 2010, Dublin, Ireland.
- [32] Peng, L., Guillén i Fàbregas, A., and Martinez, A. (2012) Mismatched shaping schemes for bit-interleaved coded modulation. IEEE International Symposium on Information Theory (ISIT), July 2012, Cambridge, MA.
- [33] Valenti, M. and Xiang, X. (2012) Constellation shaping for bit-interleaved LDPC coded APSK. IEEE Trans. Commun., 60 (10), 2960–2970.
- [34] Böcherer, G., Altenbach, F., Alvarado, A., Corroy, S., and Mathar, R. (2012) An efficient algorithm to calculate BICM capacity. IEEE International Symposium on Information Theory (ISIT), July 2012, Cambridge, MA.
- [35] Agrell, E. and Alvarado, A. (2011) Optimal alphabets and binary labelings for BICM at low SNR. IEEE Trans. Inf. Theory, 57 (10), 6650–6672.
- [36] Verdú, S. (2002) Spectral efficiency in the wideband regime. IEEE Trans. Inf. Theory, 48 (6), 1319–1343.
- [37] Prelov, V. V. and Verdú, S. (2004) Second-order asymptotics of mutual information. IEEE Trans. Inf. Theory, 50 (8), 1567–1580.
- [38] Alvarado, A., Agrell, E., Guillén i Fàbregas, A., and Martinez, A. (2010) Corrections to ‘Bit-interleaved coded modulation in the wideband regime’. IEEE Trans. Inf. Theory, 56 (12), 6513.
- [39] Stierstorfer, C. and Fischer, R. F. H. (2008) Mappings for BICM in UWB scenarios. International ITG Conference on Source and Channel Coding (SCC), January 2008, Ulm, Germany.
- [40] Agrell, E. and Alvarado, A. (2013) Signal shaping for BICM at low SNR. IEEE Trans. Inf. Theory, 59 (4), 2396–2410.
- [41] Lassing, J., Ström, E. G., Agrell, E., and Ottosson, T. (2003) Unequal bit-error protection in coherent
 -ary PSK. IEEE Vehicular Technology Conference (VTC-Fall), October 2003, Orlando, FL.
-ary PSK. IEEE Vehicular Technology Conference (VTC-Fall), October 2003, Orlando, FL. - [42] Brännström, F. (2004) Convergence analysis and design of multiple concatenated codes. PhD dissertation, Chalmers University of Technology, Göteborg, Sweden.
- [43] Stierstorfer, C. and Fischer, R. F. H. (2007) (Gray) Mappings for bit-interleaved coded modulation. IEEE Vehicular Technology Conference (VTC-Spring), April 2007, Dublin, Ireland.
- [44] Alvarado, A., Brännström, F., and Agrell, E. (2011) High SNR bounds for the BICM capacity. IEEE Information Theory Workshop (ITW), October 2011, Paraty, Brazil.
- [45] Alvarado, A., Brännström, F., Agrell, E., and Koch, T. (2014) High-SNR asymptotics of mutual information for discrete constellations with applications to BICM. IEEE Trans. Inf. Theory, 60 (2), 1061–1076.
- [46] Hildebrand, F. B. (ed.) (1981) Handbook of Applicable Mathematics: Numerical Methods, Vol. 3, John Wiley & Sons, Inc.

