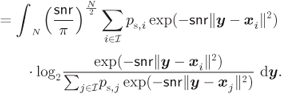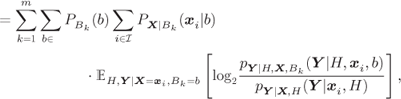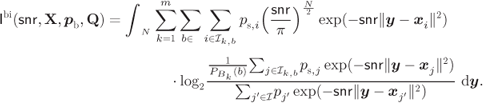Chapter 4
Information-Theoretic Elements
Information theory provides us with fundamental limits on the transmission rates supported by a channel. In this chapter, we analyze these limits for the coded modulation (CM) schemes presented in Chapter 2, paying special attention to bit-interleaved coded modulation (BICM).
This chapter is structured as follows. In Section 4.1, we introduce the concepts of mutual information (MI) and channel capacity; in Section 4.2, we study the maximum transmission rates for general CM systems; and in Section 4.3, for BICM systems. We review their relation and we analyze how they are affected by the choice of the (discrete) constellation. We pay special attention to the selection of the binary labeling and use of probabilistic shaping in BICM. We conclude the chapter by showing in Section 4.5 ready-to-use numerical quadrature formulas to efficiently compute MIs.
4.1 Mutual Information and Channel Capacity
We analyze the transmission model defined by (2.27), i.e., 
, where 
is an 
-dimensional zero-mean Gaussian vector with covariance matrix 
. In this chapter, we are mostly interested in discrete constellations. However, we will initially assume that the input symbols 
are modeled as independent and identically distributed (i.i.d.) continuous random variables characterized by their probability density function (PDF) 
. Considering constellations with continuous support (
) provides us with an upper limit on the performance of discrete constellations. As mentioned before, we also assume that the channel state 
is known at the receiver (through perfect channel estimation) and is not available at the transmitter. The assumption of the transmitter not knowing the channel state is important when analyzing the channel capacity (defined below) for fading channels.
The MI between the random vectors 
and 
conditioned on the channel state 
is denoted by 
and given by1
where 
is given by (2.28).
For future use, we also define the conditional MIs
Although 
is the most common notation for MI found in the literature (which we also used in Chapter 1), throughout this chapter, we also use an alternative notation
which shows that conditioning on 
in (4.1) is equivalent to conditioning on the instantaneous signal-to-noise ratio (SNR); this notation also emphasizes the dependence of the MI on the input PDF 
. This notation allows us to express the MI for a fast fading channel (see Section 2.4) by averaging the MI in (4.5) over the SNR, i.e.,
where 
is given by (4.5). Throughout this chapter, we use the notation 
and 
to denote MIs for the additive white Gaussian noise (AWGN) and fading channels, respectively.
The MIs above have units of 
(or equivalently 
) and they define the maximum transmission rates that can be reliably2 used when the codewords 
are symbols generated randomly according to the continuous distribution PDF 
. More precisely, the converse of Shannon's channel coding theorem states that it is not possible to transmit information reliably above the MI, i.e.,
The channel capacity of a continuous-input continuous-output memoryless channel under average power constraint is defined as the maximum MI, i.e.,
where the optimization is carried out over all input distributions that satisfy the average energy constraint 
. Furthermore, we note that 
is independent of 
because we assumed that the transmitter does not know the channel. Because of this, we do not consider the case when the transmitter, knowing the channel, adjusts the signal's energy to the channel state.
MI curves are typically plotted versus SNR, however, to better appreciate their behavior at low SNR, plotting MI versus the average information bit energy-to-noise ratio 
is preferred. To do this, first note that (4.7) can be expressed using (2.38) as
The notation 
emphasizes that the MI is a function of both 
and 
, which will be useful throughout this chapter. In what follows, however, we discuss 
as a function of 
for a given input distribution, i.e., 
.
The MI is an increasing function of the SNR, and thus, it has an inverse, which we denote by 
. By using this inverse function (for any given 
) in both sides of (4.14), we obtain
Furthermore, by rearranging the terms, we obtain
which shows that 
is bounded from below by 
, which is a function of the rate 
.
In other words, the function 
in (4.16) gives, for a given input distribution 
, a lower bound on the 
needed for reliable transmission at rate 
. For example, for the AWGN channel in Example 4.1, and by using (4.9) in (4.16), we obtain
In this case, the function 
depends solely on 
(and not on 
, as in (4.16)), which follows because 
in (4.9) depends only on 
.
The expressions in (4.17) allow us to find a lower bound on 
when 
, or equivalently, when 
, i.e., in the low-SNR regime. Using (4.17), we obtain
which we refer to as the Shannon limit (SL). The bound in (4.18) corresponds to the minimum average information bit energy-to-noise ratio 
needed to reliably transmit information when 
.
For notation simplicity, in (4.14)–(4.16), we consider nonfading channels. It is important to note, however, that because 
, exactly the same expressions apply to fading channels, i.e., when 
is replaced by 
.
4.2 Coded Modulation
In this section, we focus on the practically relevant case of discrete constellations, and thus, we restrict our analysis to probability mass functions (PMFs) 
with 
nonzero mass points, i.e., 
, 
.
4.2.1 CM Mutual Information
We define the coded modulation mutual information (CM-MI) as the MI between the input and the output of the channel when a discrete constellation is used for transmission. As mentioned in Section 2.5.1, in this case, the transmitted symbols are fully determined by the PMF 
, and thus, we use the matrix 
to denote the support of the PMF (the constellation 
) and the vector 
to denote the probabilities associated with the symbols (the input distribution). The CM-MI can be expressed using (4.2), where the first integral is replaced by a sum and the PDF 
by the PMF 
, i.e.,
where the notation 
emphasizes the dependence of the MI on the input PMF 
(via 
and 
, see (2.41)).
For the AWGN channel with channel transition probability (2.31), the CM-MI in (4.21) can be expressed as
For a uniform input distribution 
in (2.42), the above expression particularizes to
Figure 4.1 
PSK constellations and AWGN channel: (a) CM-MI and (b) 
in (4.16). The AWGN capacity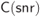 
and the corresponding 
are shown for reference
Figure 4.2 
PAM constellations and AWGN channel: (a) CM-MI and (b) 
in (4.16). The AWGN capacity 
and the corresponding 
are shown for reference
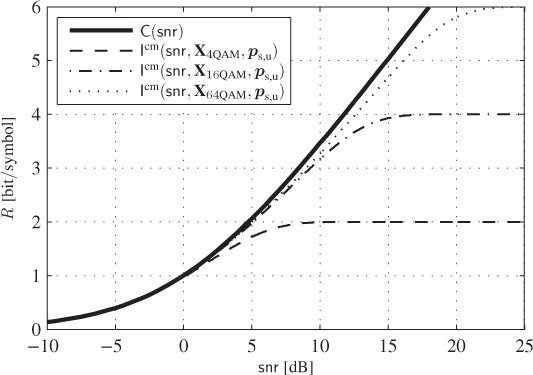
Figure 4.3 CM-MI for 4PSK (4QAM) and for the 
QAM constellations in Fig. 2.11 (
) over the AWGN channel. The AWGN capacity 
in (4.9) is also shown
Figure 4.4 
PAM constellations and Rayleigh fading channel: (a) CM-MI and (b) 
in (4.16). The average capacity 
and the corresponding 
are shown for reference
4.2.2 CM Capacity
The CM-MI 
corresponds to the maximum transmission rate when the codewords' symbols 
are taken from the constellation 
following the PMF 
. In such cases, the role of the receiver is to find the transmitted codewords using 
by applying the maximum likelihood (ML) decoding rule we defined in Chapter 3. In practice, the CM encoder must be designed having the decoding complexity in mind. To ease the implementation of the ML decoder, particular encoding structures are adopted. This is the idea behind trellis-coded modulation (TCM) (see Fig. 2.4), where the convolutional encoder (CENC) generates symbols 
which are mapped directly to constellation symbols 
. In this case, the code can be represented using a trellis structure, which means that the Viterbi algorithm can be used to implement the ML decoding rule, and thus, the decoding complexity is manageable.
The most popular CM schemes are based on uniformly distributed constellation points. However, using a uniform input distribution is not mandatory, and thus, one could think of using an arbitrary PMF (and/or a nonequally spaced constellation) so that the CM-MI is increased. To formalize this, and in analogy with (4.8), we define the CM capacity for a given constellation size 
as
where the optimization over 
and 
is equivalent to the optimization over the PMF 
.
The optimization problem in (4.25) is done under constraint 
, where 
depends on both 
and 
. In principle, a constraint 
could be imposed; however, for the channel in (2.27) we consider here, an increase in 
always results in a higher MI and thus, the constraint is always active.
Again, the optimization result (4.25) should be interpreted as the maximum number of bits per symbol that can be reliably transmitted using a fully optimized 
-point constellation, i.e., when for each SNR value, the constellation and the input distribution are selected in order to maximize the CM-MI. This is usually referred to as signal shaping.
The CM capacity for fading channels is defined as
We note that the optimal constellations 
and 
, i.e., those solving (4.25) or (4.26), are not the same for the AWGN and fading channels. This is different from the case of continuous distributions 
, where the Gaussian distribution is optimal for each value of 
over the AWGN channel and thus, the same distribution yields the capacity of fading channels, cf. Example 4.2.
The joint optimization over both 
and 
is a difficult problem, and thus, one might prefer to solve simpler ones:
The expression (4.28) is typically called geometrical shaping as only the constellation symbols (geometry) are being optimized, while the problem (4.27) is called probabilistic shaping as the probabilities of the constellation symbols are optimized.
Finally, as a pragmatic compromise between the fully optimized signal shaping of (4.25) and the geometric/probabilistic solutions of , we may optimize the distribution 
while maintaining the “structure” of the constellation, i.e., allowing for a scaling of a predefined constellation with a factor 
where 
is the optimal value of 
.
Figure 4.5 Solution of problem (4.27): optimal PMF for an equidistant 8PAM constellation in the AWGN channel
Figure 4.6 Solution of problem (4.28): optimal input distribution for an 
-ary constellation in the AWGN channel
Figure 4.7 Solution of problem (4.29): optimal PMF for an equidistant 8PAM constellation in the AWGN channel
We conclude this section by quantifying the gains obtained by changing the input distribution. We show in Fig. 4.8 (a)3 the CM-MI 
(8PAM with a uniform input distribution), as well as 
in (4.27), 
in (4.28), and 
in (4.29). These results show that the gains offered by probabilistic and geometric shaping are quite small; however, when the mixed optimization in (4.29) is done (i.e., when the probability and the gain 
are jointly optimized), the gap to the AWGN capacity is closed for any 
. To clearly observe this effect, we show in Fig. 4.8 (b) the MI gains offered (with respect to 
) by the two approaches as well as the gain offered by using the optimal (Gaussian) distribution. This figure shows that the optimization in (4.29) gives considerably larger gains, which are close to optimal ones for any 
.
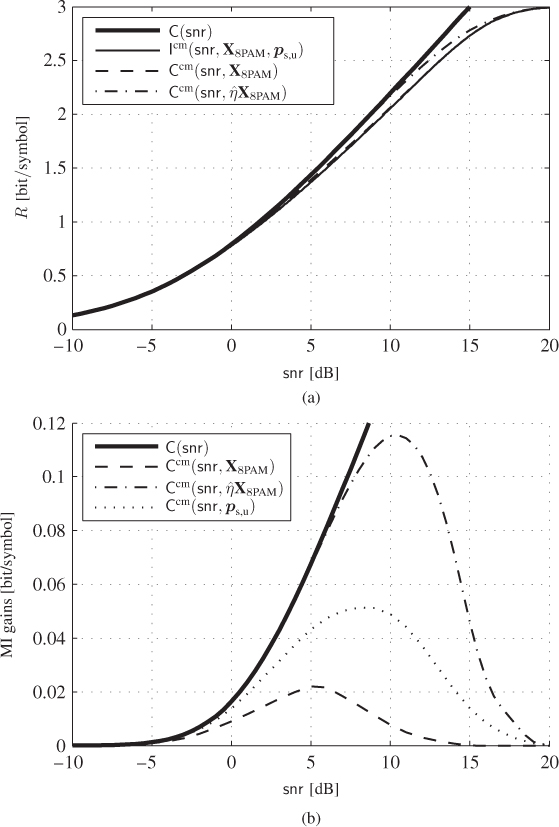
Figure 4.8 (a) The CM-MI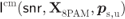 
, the capacities 
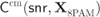in (4.27), 
in (4.28), and 
in (4.29) and (b) their respective MI gains with respect to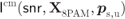 
. The AWGN capacity (a) and the corresponding gain (b) are also shown
4.3 Bit-Interleaved Coded Modulation
In this section, we are interested in finding the rates that can be reliably used by the BICM transceivers shown in Fig. 2.7. We start by defining achievable rates for BICM transceivers with arbitrary input distributions, and we then move to study the problem of optimizing the system's parameters to increase these rates.
4.3.1 BICM Generalized Mutual Information
For the purpose of the discussion below, we rewrite here (3.23) as
where the symbol-decoding metric
is defined via the bit decoding metrics, each given by
The symbol-decoding metric 
is not proportional to 
, i.e., the decoder does not implement the optimal ML decoding. To find achievable rates in this case, we consider the BICM decoder as the so-called mismatched decoder. In this context, for an arbitrary decoding metric 
, reliable communication is possible for rates below the generalized mutual information (GMI) between 
and 
, which is defined as
where
We immediately note that if 
and 
, we obtain
that is, using symbol metrics matched to the conditional PDF of the channel output, we obtain the CM-MI 
in (4.23). This result is generalized in the following theorem.
The following theorem gives an expression for 
in (4.35) when the decoder uses a symbol metric 
given by (4.32) and an arbitrary bit metric 
.
Corollary 4.12 shows that when the symbol metrics are constrained to follow (4.32), the best we can do is to use the bits metrics (4.33). The resulting achievable rates lead to the following definition of the BICM generalized mutual information (BICM-GMI) for fading and nonfading channels as
where the dependence on the constellation symbols 
, their labeling 
, and the bits' PMF 
is made explicit in the argument of 
. The bitwise MIs necessary to calculate the BICM-GMI in (4.54), (4.55) are given by
At this point, some observations are in order:
- The MI in (4.22) is an achievable rate for any CM transmission, provided that the receiver implements the ML decoding rule. The BICM-GMI in (4.54) and (4.55) is an achievable rate for the (suboptimal) BICM decoder.
- The BICM-GMI was originally derived without the notion of mismatched decoding, but based on an equivalent channel model where the interface between the interleaver and deinterleaver in Fig. 2.7 is replaced by
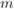parallel memoryless binary-input continuous-output (BICO)channels. Such a model requires the assumption of a quasi-random interleaver. Hence, the value of Theorem 4.11 is that it holds independently of the interleaver's presence. - No converse decoding theorem exists, i.e., while the BICM-GMI defines an achievable rate, it has not been proved to be the largest achievable rate when using a mismatched (BICM) decoder. This makes difficult a rigorous comparison of BICM transceivers because we cannot guarantee that differences in the BICM-GMI will translate into differences between the maximum achievable rates. However, practical coding schemes most often closely follow and do not exceed the BICM-GMI. This justifies its practical use as a design rule for the BICM. We illustrate this in the following example.
Figure 4.9 Throughputs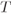 
obtained for the AWGN channel and a PCCENC TENC with 11 different code rates 
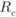for (a) 4PAM and (b) 8PAM labeled by the BRGC. The CM-MI, BICM-GMI, and AWGN capacity 
in (4.9) are also shown
While the quantities (4.54) and (4.55) were originally called the BICM capacity, we avoid using the term “capacity” to point out that no optimization of the input distribution is carried out. Using (4.56), the BICM-GMI in (4.54) can be expressed as
where to pass from (4.58) to (4.59) we used the law of total probability applied to expectations. Moreover, by using (2.75) and by expanding the expectation 
over 
and then over 
, we can express (4.59) as
where to pass from (4.60) to (4.61), we used (2.75) and the fact that the value of 
does not affect the conditional channel transition probability, i.e., 
. The dependence of the BICM-GMI on the labeling 
becomes evident because the sets 
appear in (4.61), and as we showed in Section 2.5.2, these sets define the subconstellations generated by the labeling.
For AWGN channels (
), the BICM-GMI in (4.61) can be expressed as
Furthermore, for uniformly distributed bits, 
for 
, and thus, the BICM-GMI in (4.62) becomes
where we use 
to denote uniformly distributed bits, i.e., 
. In what follows, we show examples of the BICM-GMI for different constellations 
and labelings 
with uniform input distributions.
Figure 4.10 BICM-GMI and CM-MI for 8PSK and 16PSK (see Fig. 2.9) over the AWGN channel (a) and the corresponding functions 
in (4.16) (b). The AWGN capacity 
in (4.9) 
(a) and the function 
in (4.17) together with the SL in (4.18) (b) are also shown
Figure 4.11 BICM-GMI and CM-MI for 8PAM over the AWGN channel (a) and the corresponding functions 
in (4.16) (b). The BICM-GMI is shown for the four binary labelings in Fig. 2.13. The shadowed regions shows the inequalities (4.7) (a) and (4.16) (b) for the BSGC. The AWGN capacity 
in (4.9) 
(a) and the function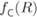 
in (4.17) together with the SL in (4.18) (b) are also shown
Figure 4.12 Functions 
in (4.16) for the BICM-GMI for 4PSK and 8PSK over the AWGN channel and for all binary labelings that produce different BICM-GMI curves. The function 
in (4.17) and the SL in (4.18) are also shown