30.2 ECONOMICS OF COMMODITY FUTURES MARKETS

This section briefly discusses two prominent theories that have been put forward to explain the relationships among futures prices, current spot prices, and expected future spot prices. Understanding these relationships is essential in explaining the potential sources of returns to CTAs and, in particular, trend-following strategies.

30.2.1 Theory of Storage and Convenience Yield

The theory of storage, as initially developed by Kaldor (1939), attempts to explain the relationship between futures prices and current spot prices. The theory emphasizes the importance of holding inventory and the potential benefits derived from the ownership of physical commodities as opposed to having a claim to commodities through forward and futures contracts.1 Ownership of commodities has economic value because it allows owners to absorb demand and supply shocks. Owners can meet an unexpected rise in demand and can avoid production disruptions resulting from supply shocks. The benefit of this ownership is often referred to as convenience yield, which is analogous to the equity dividends received by owners of equity shares and not by owners of futures contracts or other derivatives instruments.

Because commodity markets are volatile, both producers and consumers seek ways to hedge their risks. Derivative markets, such as futures and options, for commodities represent one venue through which producers and consumers of commodities can hedge their risks. Alternatively, they can hedge some of their risks by holding inventories of physical commodities. Indeed, some risks can be reduced only through the physical holding of a commodity. For instance, a manufacturer that uses an industrial commodity such as copper in its production process can hedge against a disruption in the supply of copper only through holding an inventory of copper.

On the other hand, a supplier of copper may also wish to carry an inventory of copper in order to hedge against the risk that there may be an unexpected increase in demand, which in the absence of the inventory can be met only through costly changes in the production process. Academic studies have shown that the convenience yield depends on two primary variables for extractable industrial commodities: (1) the level of inventories and (2) the volatility in commodity prices. The convenience yield increases as the level of inventories declines. Both producers and consumers hold inventories in order to be able to reduce the cost of adjustment to demand or supply shocks. As inventories decline, the risk of not being able to absorb demand or supply shocks increases, leading to an increase in the level of convenience yield. In addition, the convenience yield increases as the volatility of commodity prices increases. The reason is that demand for inventories increases as volatility in demand and supply increases, which in turn leads to an increase in the convenience yield. Of course, higher volatility of demand and supply naturally leads to higher price volatility.

Clearly, the level of convenience yield is also subject to commodity-specific factors. For example, the size of the convenience yield is affected by whether or not there are close substitutes for the commodity and by the amount of time it takes to respond to demand shocks and increase production of the commodity. Therefore, convenience yield is likely to behave differently for industrial and agricultural commodities than for financial products, which tend not to have any convenience yield.2

30.2.2 Cost of Carry Model

In additional to the convenience yield, there are other variables that affect the relationship between futures prices and cash prices of the same commodity. These include the cost of storage and the opportunity cost of capital. The cost of carry model has been developed to present the impact of all of these factors on the relationship between spot and futures prices. To present this model, let F(t,T) denote the futures price observed at time t on a contract that will mature at time T, and let P(t) denote the cash price of the same commodity. If cash and futures markets are free of frictions, such as transaction costs and limits on shorting commodities, then the difference between futures price and spot price of the same commodity (i.e., the basis) can be written as follows:

(30.1)

Here, r is the annual rate of interest and represents the cost of funding the cash position in the commodity; s is the annual rate of storage cost; and c represents, on an annual basis, the benefits of holding the commodity, including any potential income from owning the commodity as well as the convenience yield associated with having an inventory of the commodity. Finally, (T – t) measures the time to maturity of the contract in terms of years.

Example: Suppose the current cash price of one barrel of Brent crude oil is $100, while the three-month futures price is $98 per barrel. If the annual cost of funding is 4% and the annual storage cost is 5%, the implied convenience yield can be calculated with the following equation:

which can be solved as follows:

Thus, the implied convenience yield is 17% per year. The fact that the convenience yield is rather large and positive in this example leads to a negative total cost of carry:

This makes the spot price greater than the futures price. Similarly, if the total cost of carry is positive, then the spot price will be smaller than the futures price. Furthermore, assuming a constant per-period interest rate, storage cost, and convenience yield, these figures imply that longer-maturity futures contracts will have lower prices than will shorter-maturity contracts. Together these figures point to a term structure of futures prices that is downward sloping. In this case, the futures market is said to be in backwardation. On the other hand, if total cost of carry is positive (i.e., the convenience yield is smaller than the cost of funding and storage), then the term structure of futures prices will be upward sloping; in this case, the futures market is said to be in contango.

Since convenience yield is likely to be large and positive when inventory levels are low, one should expect to see a downward-sloping term structure of futures prices when inventory levels are low and commodity prices are displaying higher than normal volatility. Available empirical evidence appears to support the proposition that backwardation in futures markets is generally observed when the levels of inventories are abnormally low and price volatility is high.

It should be clear from the previous analysis that certain adjustments must be made to the cost of carry model depending on whether it is applied to financial futures or to storable commodities.

Convenience yield plays almost no role in describing the relationship between the spot and the futures price when it comes to financial futures. If the underlying financial asset of a futures contract pays a regular income, such as coupon or dividend payments, the potential income will be included in the cost of carry model. However, unlike the convenience yield associated with storable physical commodities, the dividend or coupon income from holding financial assets does not depend on the level of inventory or volatility in the price of the financial assets.

The important implications of the theory of storage (Geman 2005) can be summarized as follows:

• The volatility of commodity prices tends to be inversely related to the level of global inventories. Lower levels of inventory mean that any demand or supply shock has to be absorbed through changes in commodity prices leading to increased volatility.
• Changes in commodity prices and changes in the volatility of commodity prices tend to be positively correlated. The reason is that demand and supply shocks generally lead to spikes in commodity prices when the levels of inventory are low, which is also associated with higher price volatility. This is the opposite of what is observed in equity markets, where higher price volatility is normally associated with lower equity prices.
• Spot prices are more volatile than are futures prices because changes in the levels of production reduce the impact of demand and supply shocks on forward and futures prices. This effect tends to be more pronounced for industrial and energy commodities, where production is not affected by seasonal factors.
• An inventory-dependent convenience yield is an important variable that is increasingly employed by traders and researchers to explain changes in the shape of the term structure of futures prices.

30.2.3 Futures Prices and Expected Future Spot Prices (Theory of Normal Backwardation)

The relationship between the futures price and the expected future spot price of the same commodity has been the subject of many studies. Keynes, credited with the first rigorous examination of this relationship, proposed that futures prices should generally rise through time in order to provide enough incentive for speculators to take long positions in futures contracts. According to Keynes (1930), most hedgers in commodity markets are producers of commodities and therefore have net short positions in futures markets. This requires speculators to take the opposite side of the market and therefore have a net long position in these markets. Speculators will take such a position only if they expect to earn a profit from their long positions, which requires that the futures price rises over time. Since spot and futures prices must be equal at the maturity date of the futures contract, the futures price initially tends to be less than the expected future spot price (assuming that the spot price does not display any trend). The difference between the futures price and the expected future spot price is referred to as the risk premium, which represents the return required by speculators. In this case, one can think of speculators as supplying insurance to hedgers.

This condition is referred to as normal backwardation. Notice that the term backwardation refers to the term structure of futures prices, while the term normal backwardation refers to the relationship between current futures prices and the expected future spot prices. In particular, it refers to the conditions in which the futures price is less than the expected future spot price.

Under normal backwardation, a speculator who has a long position in a futures contract would expect to earn a profit if the actual future spot price is, on average, equal to what the market participants expected to see. On an ex post basis, the speculator would make money as long as the actual spot price is not lower than the expected spot price by more than the risk premium embedded in the futures price. To see this, consider the following expression, which follows normal backwardation theory:

Here, E[P(T)] is the expected future spot price, and π is the risk premium. Notice that at maturity, the futures prices will be equal to the spot price, P(T) = F(T, T). In this expression, π represents the expected profit to a speculator who takes a long position in the futures market. On an ex post basis, the profit earned by the speculator would be P(T) - F(T, T). If the expected future spot price, E[P(T)], is added to and subtracted from this expression, the profit earned by the CTA will depend on the risk premium and the difference between the actual spot price and the expected future spot price.

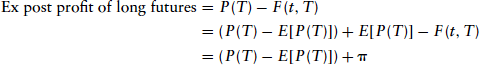
Example: The current spot price for Brent crude oil is $90 per barrel, while the three-month futures price is $95 per barrel. If the three-month expected future spot price is $105 per barrel, the implied risk premium would be π = 105 - 95 = 10. Three months later, the actual spot price for Brent crude is $100. The ex post profit of a long position in a futures contract will be $100 – $95 = $5 per barrel. Suppose the actual spot price turns out to be $89 per barrel, which is $16 less than the expected future spot price, $105. The speculator with a long position would lose $6 per barrel ($89 – $95 = –$6).

It is important to note that one cannot directly test the theory of normal backwardation because the risk premium is not observable. All that can be observed is the ex post gains or losses from futures contracts. Of course, if the theory of normal backwardation is indeed a good representation of futures markets, then one should expect to see positive profits in the long run from taking long positions in the futures market.

The theory of normal backwardation is consistent with both backwardation and contango in the term structure of futures prices. However, empirical observations tend to show that a backwardated term structure is generally associated with the theory of normal backwardation (Gorton, Hayashi, and Rouwenhorst 2008). Note that term structure will be negatively sloped only if the convenience yield is rather large. Furthermore, a large convenience yield is associated with low inventory levels, which generally lead to volatile commodity prices. Because volatile commodity prices tend to increase the demand for hedging, speculators will have to be offered a larger premium in order to take long positions in futures contracts. Therefore, a downward-sloping futures curve is generally more consistent with the presence of a positive risk premium in futures prices.

Keynes's theory of normal backwardation assumes that hedgers are mostly producers of commodities and are, therefore, net short in the futures markets. However, consumers of commodities may have the desire to hedge their risk, which will require them to take a long position in futures contracts. Therefore, to the degree that consumers are eager to hedge their risk, producers of commodities will not need to provide speculators with the incentive to take long positions in futures markets; thus, the risk premium associated with normal backwardation may cease to exist. In fact, if hedging demand by consumers of a commodity is large enough, then speculators will need to be net short in the futures markets. Therefore, hedging pressure could increase the futures price such that it is greater than the expected future spot price. In this case, the risk premium would be negative, and speculators would earn a positive return by being short futures contracts. Given this discussion, one can argue that one way a trend-following strategy could earn a profit would be to identify whether hedgers are net long or net short in futures markets and then establish the opposite position. Furthermore, one could argue that the technical analysis tools employed by trend followers are created to identify changes in hedging pressures and the ensuing trends that may take place.

Academic and practitioner research provides support for this view; that is, in order to generate consistently positive risk-adjusted returns, traders should take long or short positions in commodity futures markets, depending on market conditions. These studies show that strategies that take long positions in futures contracts when markets are in backwardation and short positions when markets are in contango tend to outperform long-only positions on a risk-adjusted basis.3