Chapter 7
Semantic Analysis
A semantic analyzer checks the semantics of a program, that is, whether the language constructs are meaningful or not. A semantic analyzer mainly performs static type checking.
CHAPTER OUTLINE
7.4 Design of Simple Type Checker
7.5 Type Checking of Expressions
7.6 Type Checking of Statements
7.7 Type Checking of Functions
7.8 Equivalence of Type Expressions
A compiler must ensure that the source program follows the syntax and semantic conventions of the source language. Once the syntax is verified, the next task to be performed by a compiler is to check the semantics of the language. A semantic analyzer shown in Figure 7.1 mainly verifies whether the language constructs are meaningful (semantics) or not. This is called even static type checking, which ensures that certain kinds of programming errors will be detected and reported.
7.1 Introduction
Parsing cannot detect some errors. Some errors are captured during compile time called static checking (e.g., type compatibility). Languages like C, C++, C#, Java, and Haskell uses static checking. Static checking is even called early binding. During static checking programming errors are caught early. This causes program execution to be efficient. Static checking not only increases the efficiency and reliability of the compiled program, but also makes execution faster.
Figure 7.1 Role of a Semantic Analyzer in Compilation
Type checking is not only limited to compile time, it is even performed at execution time. This is done with the help of information gathered by a compiler; the information is gathered during compilation of the source program.
Errors that are captured during run time are called dynamic checks (e.g., array bounds check or null pointers dereference check). Languages like Perl, python, and Lisp use dynamic checking. Dynamic checking is also called late binding. Dynamic checking allows some constructs that are rejected during static checking. A sound type system eliminates run-time type checking for type errors. A programming language is strongly-typed, if every program its compiler accepts will execute without type errors. In practice, some of the type checking operations is done at run-time (so, most of the programming languages are not strongly typed).
For example, int x[100]; … x[i] → most of the compilers cannot guarantee that i will be between 0 and 99
A semantic analyzer mainly performs static checking. Static checks can be any one of the following type of checks:
Uniqueness checks: This ensures uniqueness of variables/objects in situations where it is required. For example, in most of the languages no identifier can be used for two different definitions in the same scope.
Flow of control checks: Statements that cause flow of control to leave a construct should have a place to transfer flow of control. If this place is missing, it is confusion. For example, in C language, “break” causes flow of control to exit from the innermost loop. If it is used without a loop, it confuses where to leave the flow of control.
Type checks: A compiler should report an error if an operator is applied to incompatible operands. For example, for binary addition, operands are array and a function is incompatible. In a function, the number of arguments should match with the number of formals and the corresponding types.
Name-related checks: Sometimes, the same name must appear two or more times. For example, in ADA, a loop or a block may have a name that appears at the beginning and end of the construct. The compiler must check whether the same name is used at both places.
What does semantic analysis do? It performs checks of many kinds which may include
- All identifiers are declared before being used.
- Type compatibility.
- Inheritance relationships.
- Classes defined only once.
- Methods in a class defined only once.
- Reserved words are not misused.
In this chapter we focus on type checking. The above examples indicate that most of the other static checks are routine and can be implemented using the techniques of SDT discussed in the previous chapter. Some of them can be combined with other activities. For example, for uniqueness check, while entering the identifier into the symbol table, we can ensure that it is entered only once. Now let us see how to design a type checker.
A type checker verifies that the type of a construct matches with that expected by its context. For example, in C language, the type checker must verify that the operator “%” should have two integer operands dereferencing is applied through a pointer, indexing is done only on an array, a user-defined function is applied with correct number and type of arguments. The goal of a type checker is to ensure that operations are applied to the correct type of operands. Type information collected by a type checker is used later by code generator.
7.2 Type Systems
Consider the assembly language program fragment. Add R1, R2, R3. What are the types of operands R1, R2, R3? Based on the possible type of operands and its values, operations are legal. It doesn’t make sense to add a character and a function pointer in C language. It does make sense to add two float or int values. Irrespective of the type, the assembly language implementation remains the same for add. A language’s type system specifies which operations are valid for which types. A type system is a collection of rules for assigning types to the various parts of a program. A type checker implements a type system. Types are represented by type expressions. Type system has a set of rules defined that take care of extracting the data types of each variables and check for the compatibility during the operation.
7.3 Type Expressions
The type expressions are used to represent the type of a programming language construct. Type expression can be a basic type or formed by recursively applying an operator called a type constructor to other type expressions. The basic types and constructors depend on the source language to be verified. Let us define type expression as follows:
- A basic type is a type expression
- Boolean, char, integer, real, void, type_error
- A type constructor applied to type expressions is a type expression
- Array: array(I, T)
Array(I,T) is a type expression denoting the type of an array with elements of type T and index set I, where T is a type expression. Index set I often represents a range of integers. For example, the Pascal declaration
var C: array[1..20] of integer;
associates the type expression array(1..20, integer) with C.
- Array: array(I, T)
- Product: T1 × T2
- If T1 and T2 are two type expressions, then their Cartesian product T1 × T2 is a type expression. We assume that × associates to the left.
- Record: record((N1 × T1) × (N2 × T2))
A record differs from a product. The fields of a record have names. The record type constructor will be applied to a tuple formed from field types and field names. For example, the Pascal program fragment
type node = record
address : integer ;
data : array [1..15] of char
end;
var node_table : array [1..10] of node ;
declares the type name “node” representing the type expression
record((address×integer) × (data × array(1..15,char)))
and the variable “node_table” to be an array of records of this type.
- Pointer: pointer(T)
Pointer(T) is a type expression denoting the type “pointer to an object of type T where T is a type expression. For example, in Pascal, the declaration
var ptr: *row
declares variable “ptr” to have type pointer(row).
- Function: D → R
Mathematically, a function is a mapping from elements of one set called domain to another set called range. We may treat functions in programming languages as mapping a domain type “Dom” to a range type “Rg.”. The type of such a function will be denoted by the type expression Dom → Rg. For example, the built-in function mod, i.e. modulus of Pascal has type expression int × int → int.
As another example, the Pascal declarationfunction fun(a, b: char) * integer;
says that the domain type of function “fun” is denoted by “char × char” and range type by “pointer(integer).” The type expression of function “fun” is thus denoted as follows:
char × char → pointer(integer)
However, there are some languages like Lisp that allow functions to return objects of arbitrary types. For example, we can define a function “g” of type (integer → integer) → (integer → integer).
That is, function “g” takes as input a function that maps an integer to an integer and “g” produces another function of the same type as output.
Example 1: Write type expression for a pointer to array of real, where the array index ranges from 1 to 100.
Solution: The type expression is pointer(array[1..100, real])
Example 2: Write a type expression for a function whose domains are functions from integers to character and whose ranges are pointer to integer.
Solution:
Type expression is
Domain type expression is integer → character
Range type expression is pointer (integer)
The final type expression is (integer → character) → (pointer(integer))
7.4 Design of Simple Type Checker
Different type systems are designed for different languages. The type checking can be done in two ways. The checking done at compile time is called static checking and the checking done at run time is called dynamic checking. A system is said to be a Sound System if it completely eliminates the dynamic check. In such systems, if the type checker assigns any type other than type error for some fragment of code, then there is no need to check for errors when it is run. Practically this is not always true; for example, if an array X is declared to hold 100 elements. Usually the index would be from 0 to 99 or from 1 to 100 depending on the language support. And there is a statement in the program referred to as X[i]; during compilation this would not guarantee error free at runtime as there is possibility that if the value of i is 120 at run time then there will be an error. Therefore, it is essential that there is a need even for the dynamic check to be done.
Let us consider a simple language that has declaration statements followed by statements, where these statements are simple arithmetic statements, conditional statements, iterative statements, and functional statements. The program block of code can be generated by defining the rules as follows:
Type Declarations
P → D “;” E |
|
|
D → D “;” D |
|
|
| id “:” T |
{add_type(id.entry, T.type) } |
|
T → char |
{T.type := char } |
|
T → integer |
{T.type := int } |
|
:….. |
:….. |
|
T → “*” T1 |
{T.type := pointer(T1.type) } |
|
T → array “[”num “]” of T1 |
{T.type := array(num.value, T1.type) } |
These rules are defined to write the declaration statements followed by expression statements. The semantic rule { add_type(id.entry, T.type) } indicates to associate type in T with the identifier and add this type info into the symbol table during parsing. A semantic rule of the form {T.type := int } associates the type of T to integer. So the above SDT collects type information and stores in symbol table.
7.5 Type Checking of Expressions
Let us see how to type check expressions. The expressions like 3 mod 5, A[10], *p can be generated by the following rules. The semantic rules are defined as follows to extract the type information and to check for compatibility.
E → literal |
{E.type := char} |
|
E → num |
{E.type := int} |
|
E → id |
{E.type := lookup(id.entry)} |
|
E → E1 mod E2 |
{E.type := if E1.type = int and E2.type = int |
|
|
then int |
|
|
else type_error} |
|
E → E1 "[" E2 "]" |
{E.type := if E1.type = array(s, t) and E2.type = int |
|
|
Th en t |
|
|
else type_error} |
|
E → "*" E1 |
{E.type := if E1.type = pointer(t) |
|
|
then t |
|
|
else type_error} |
When we write a statement as i mod 10, then while parsing the element i, it uses the rule as E → id and performs the action of getting the data type for the id from the symbol table using the lookup method. When it parses the lexeme 10, it uses the rule E → num and assigns the type as int. While parsing the complete statement i mod 10, it uses the rule E → E1 mod E2, which checks the data types in both E1 and E2 and if they are the same it returns int otherwise type_error.
7.6 Type Checking of Statements
The statements are simple of the form “a = b + c” or “a = b.” It can be a combination of statements followed by another statement or a conditional statement or iterative. To generate either a simple or a complex group of statements, the rules can be framed as follows: To validate the statement a special data type void is defined, which is assigned to a statement only when it is valid at expression level, otherwise type_error is assigned to indicate that it is invalid. If there is an error at expression level, then it is propagated to the statement, from the statement it is propagated to a set of statements and then to the entire block of program.
|
|
S → id “:=” E |
{S.type := if lookup(id.entry)= E.type |
S → S1 “;” S2 |
then void |
|
else type_error} |
|
{S.type := if S1.type = void and S2.type |
|
= void |
|
then void |
|
else type_error} |
S → if E then S1 |
{S.type := if E.type = boolean |
|
then S1.type |
|
else type_error} |
S → while E do S1 |
{S.type := if E.type = boolean |
|
then S1.type |
|
else type_error} |
7.7 Type Checking of Functions
The rules for writing a function and for associating type expression with non terminal T are written as follows:
T → T1 “→” T2
{T.type := T1.type → T2.type}
E → E1 “(” E2 “)”
{E.type := if E1.type = s → t and E2.type = s
then t else type_error}
These rules specify that an expression formed by applying E1 to E2, the type of E1 must be a function of the form s → t from the type s of E2 to some range type t, makes the type of E1(E2) is t.
7.8 Equivalence of Type Expressions
The two expressions are equal if both are of the same basic type; otherwise, it is type_error. To check for type equivalence of two expressions constructed using basic types, there must be a well-defined procedure to check for the equivalence. Such equivalence between two type expressions is structural equivalence.
7.8.1 Structural Equivalence
A type expression can be a basic type or the one obtained by applying a constructor to the basic type. Two type expressions T1 and T2 are said to be structurally equivalent if they are of the same basic type or obtained by applying same constructor to the same basic type.
An integer is structurally equivalent to another integer
Pointer(char) is structurally equivalent to Pointer(char)
Integer is not structurally equivalent to char
A recursive algorithm for testing the structural equivalence is designed, which considers the basic types and the type constructors for arrays, products, pointers, and functions.
Algorithm: To check structural equivalence of two type expressions.
Input: Expressions s and t
Output: true if equivalent otherwise false.
If s and t are basic types, then return true
else If s = array(s1, s2) and t = array(t1, t2) then
return true if equal(s1, t1) and equal(s2, t2)
else If s = s1 × s2 and t = t1 × t2 then
return true if equal(s1, t1) and equal(s2, t2)
else If s = pointer(s1) and t = pointer(t1) then
return true if equal(s1, t1)
else If s = s1 → s2 and t = t1 → t2 then
return true if equal(s1, t1) and equal(s2, t2)
else return false.
7.8.2 Encoding of Type Expressions
To check equivalence of type expression we can encode type expression using bit representation. For instance, we can use four bits to represent different basic data types as follows:
|
Basic Type |
Encoding | |
|
boolean |
0000 | |
|
char |
0001 | |
|
integer |
0010 | |
|
real |
0011 |
To represent the constructed types expressions, we can use the corresponding number of integers. For instance, let us assume that there are arrays, pointers, and functions where pointer(t) represents as a pointer of type t, freturns(t) represents a function of some argument that returns an object of type t, and array(t) denotes as array of elements of type t. These can be represented by using two bits as follows:
|
Type constructor |
encoding | |
|
pointer |
01 | |
|
array |
10 | |
|
freturns |
11 |
Each of the above constructors is a unary operator. Type expressions formed by applying these constructors to a basic type have a uniform structure. Each constructor can be expressed by a sequence of bits using a simple encoding scheme. For instance, the possible constructed type expressions are integer, freturns(integer), pointer(freturns(integer)), array(pointer(freturns(integer))). If we assume that the maximum number of constructors is three then we require 6 bits to encode the complete type expression. For the above type expressions, the encoding is as follows:
|
Type expression |
encoding | |
|
integer |
000000 0010 | |
|
freturns(integer) |
000011 0010 | |
|
pointer(freturns(integer)) |
000111 0010 | |
|
array(pointer (freturns(integer))) |
100111 0010 |
To check for the equivalence, we can compare the bit sequence because two different type expressions cannot be represented with the same sequence if they are formed with different basic types of type constructors.
Note: Here we considered only three constructed types and four basic types. The bit representation can be modified depending on the number of basic types, number of constructors that may be included, and the maximum number of constructors that can be included.
Merits of structural equivalence
- No type names are needed to check the equivalence.
- Gives exact internal representation of types.
Demerits of structural equivalence
- Very tedious, as substitution has to be done for every type name.
- While checking structural equivalence, infinite looping or cycles may be encountered.
7.8.3 Name Equivalence
In some languages, the type expressions are given names. To handle such situations the type expressions are allowed to be named; hence, even names appear in the type expressions. For example, in Pascal program fragment
| type | link = ↑ node; | |
| var | next : link; | |
| last : link; | ||
| a : ↑ node; | ||
| b,c : ↑ node; |
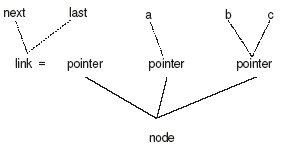
the link is declared as a type node. To check whether next, last, a, b, c are identical, we compare for equivalence in terms of the names in the type expression. Name equivalence views each type name as a distinct type, so two type expressions are name equivalent if and only of they are identical.
Note: link, next, last, a, b, c are structural equivalent
a, b, c – name equivalent
next, last – name equivalent
Merits of Name Equivalence
- Easy to implement
- Types with different names are treated differently
- Faster in checking type equivalence since no substitution is done.
Demerits of Name equivalence
- Not systematic
- Needs a type name for every type expression.
7.8.4 Type Graph
To check for the type equivalence, type graph can be used. To construct a type graph, a node is created for every constructed type or basic type that is encountered. For every type name, a leaf node is created. Two type expressions are said to be equivalent if they are represented by the same node in the type graph. The following graph shows the equivalence for next, last, a, b, and c in the above example.
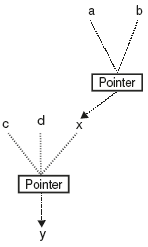
Example 5:
Draw the type graph for the following
type |
x = ↑ y; |
|
var |
a : ↑ x; |
|
b : ↑ x; |
||
c : ↑ y; |
||
d : ↑ y; |
Solution:
A type graph can also have cycles in it. For example, consider the following example in Pascal.
type link = ↑ cell;
type cell = record
x : int,
next : link
end;
Note that type name link is defined in terms of a cell and that cell is defined in terms of a link. So the definitions are recursive. Recursively defined type names can be substituted out by introducing cycles in type graph as shown in Figure 7.2. If pointer(cell) is substituted for link, the type expression shown in Figure 7.3 is obtained for a cell. We cannot use structural equivalence if there are cycles in type expressions.
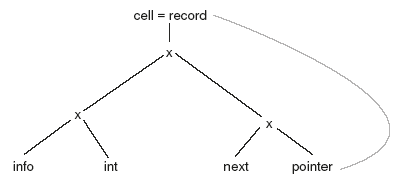
Figure 7.2 Type Graph with Cycles
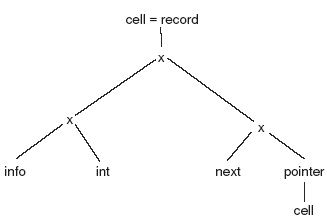
Figure 7.3 Type Graph without Cycles
C uses structural equivalence to avoid cycles like in Figure 7.3. In C the declaration for cell would look like
struct cell {
int info;
struct cell * next;
};
7.9 Type Conversion
In an expression, if there are two operands of different type, then it may be required to convert one type to another in order to perform the operation. For example, the expression “a + b,” if a is of integer and b is real, then to perform the addition a may be converted to real. The type checker can be designed to do this conversion. The conversion done automatically by the compiler is implicit conversion and this process is known as coercion. If the compiler insists the programmer to specify this conversion, then it is said to be explicit. For instance, all conversions in Ada are said to be explicit. The semantic rules for type conversion are listed below.
E → num |
{E.type := int} |
|
E → num.num |
{E.type := real} |
|
E → id |
{E.type := lookup(id.entry)} |
|
E → E1 op E2 |
{E.type := if E1.type = int and E2.type = int |
|
|
then int |
|
|
else if E1.type = int and E2.type = real |
|
|
then real |
|
|
else if E1.type = real and E2.type = int |
|
|
then real |
|
|
else if E1.type = real and E2.type = real |
|
|
then real |
|
|
else type_error} |
7.10 Overloading of Functions and Operators
An operator is overloaded if the same operator performs different operations. For example, in arithmetic expression a + b, the addition operator “+” is overloaded because it performs different operations, when a and b are of different types like integer, real, complex, and so on. Another example of operator overloading is overloaded parenthesis in ada, that i, the expression A(i) has different meanings. It can be the ith element of an array, or a call to function A with argument I, and so on. Operator overloading is resolved when the unique definition for an overloaded operator is determined. The process of resolving overloading is called operator identification because it specifies what operation an operator performs. The overloading of arithmetic operators can be easily resolved by processing only the operands of an operator.
Like operator overloading, the function can also be overloaded. In function overloading, the functions have the same name but different numbers and arguments of different types. In Ada, the operator “*” has the standard meaning that it takes a pair of integers and returns an integer. The function of “*” can be overloaded by adding the following declarations:
Function “*”(a,b: integer) return integer.
Function “*”(a,b: complex) return integer.
Function “*”(a,b: complex) return complex.
By addition of the above declarations, now the operator “*” can take the following possible types:
- It takes a pair of integers and returns an integer
- It takes a pair of integers and returns a complex number
- It takes a pair of complex numbers and returns a complex number
Function overloading can be resolved by the type checker based on the number and types of arguments.
The type checking rule for function by assuming that each expression has a unique type is given as
|
E → E1(E2) |
{ E.type : = t E2.type : = t → u then E.type : = u else E.type : = type_error } |
If the syntax-directed definition for expression has more than one possible type, then type checking can be performed with the following semantic rules:
|
E′ → E |
{E′.type := E.type} | |
|
E → id |
{E.type := lookup(id.entry)} | |
|
E → E1(E2) |
{E.type := { u | there exists an s in E2.type Such that s → u is in E1.type } |
An overloaded identifier may have several types saved in the symbol table. The function lookup() returns this set. The type of expression E1(E2) is u if s is one of the types of E2 and the function maps s to u.
7.11 Polymorphic Functions
A piece of code is said to be polymorphic if the statements in the body can be executed with different types. A function that takes the arguments of different types and executes the same code is a polymorphic function. The type checker designed for a language like Ada that supports polymorphic functions, the type expressions are extended to include the expressions that vary with type variables. The same operation performed on different types is called overloading and are often found in object-oriented programming. For example, let us consider the function that takes two arguments and returns the result.
int add(int, int)
int add(real, real)
real add(real, real)
The type expression for the function add is given as
int × int → int
real × real → int
real × real → real
Solved Problems
- Write type expression for an array of pointer to real, where the array index ranges from 1 to 100.
Solution: The type expression is array[1..100,pointer(real)]
- Write a type expression for a two-dimensional array of integers (that is, an array of arrays) whose rows are indexed from 0 to 9 and whose columns are indexed from –10 to 10.
Solution: Type expression is array[0..9, array[-10..10,integer]]
- Write a type expression for a function whose domains are functions from integers to pointers to integers and whose ranges are records consisting of an integer and a character.
Solution: Type expression is
Domain type expression is integer → pointer(integer)
Let range has two fields a and b of type integer and character respectively.
Range type expression is record((a × integer)(b × character))
The final type expression is (integer → pointer(integer)) → record((a × integer) (b × character))
- Consider the following program in C and the write the type expression for abc.
typedef struct {
int a,b;
} NODE;
NODE abc[100];
Solution: The type expression for NODE is record((a × integer) × (b × integer)) abc is an array of NODE; hence, its type expression is
array[ 0..99, record((a × integer) × (b × integer))] - Consider the following declarations.
type cell=record
info: integer;
next: pointer(cell)
type
link = ↑ cell;
var
next = link;
last = link;
p = ↑ cell;
q,r = ↑ cell;
Among the following, which expressions are structurally equivalent? Which are name equivalent? Justify your answer.
|
Solution: Let |
A = link |
|
B = pointer (cell) |
|
C = pointer (link) |
|
D = Pointer (record ((info × integer) × (next × pointer(cell))). |
To get structural equivalence we need to substitute each type name by its type expression.
We know that, link is a type name. If we substitute pointer (cell) for each appearance of link we get,
A = pointer (cell)
B = pointer (cell)
C = pointer (pointer (cell))
D = Pointer (record ((info × integer) × (next × pointer (cell))).
We know that, cell is also type name given by
type cell=record
info: integer;
next: pointer(cell)
Substituting type expression for cell in A and B, we get
A = pointer (record ((info × integer) × (next × pointer (cell)))
B = pointer (record ((info × integer) × (next × pointer (cell)))
C = pointer( pointer(cell))
D = Pointer (record ((info × integer) × (next × pointer (cell))).
We have not substituted for the type expression of cell in “C” as it is anyway different from A, B, and D. That is, even if we substitute in C, the type expression will not be the same for A, B, C, and D.
We can say that A, B, and D are structurally equivalent.
For name equivalence, we will not do any substitutions. Rather we look at type expressions directly. If they are the same then we say they are name equivalent.
None of A, B, C, D are name equivalent.
Summary
- Static type checking is done at compile time.
- Dynamic checking is done at run time.
- Semantic rules support the type checker for verifying the type of variables.
- A system is said to be a Sound System if it completely eliminates the dynamic check.
- type_error is a special type used for expressing that the type expression is invalid.
- Variables that are name equivalent are said to be structural equivalent.
- Structural equivalent elements need not be name equivalent.
Fill in the Blanks
- __________ is type expression for the char a[10].
- __________ avoids dynamic type checking.
- __________ is the type expression used to express type for statements.
- Two variables that are name equivalent are also __________.
- __________ is a special type used for expressing invalid type.
- The conversion done automatically by the compiler implicitly is known as __________.
- Error checking performed at compile time is __________.
- Error checking performed at run time is__________.
- Static checking is done in languages__________.
- Late binding is also called __________.
Objective Question Bank
- Give type expression for “x” in var x : array[2..20] of tables
- array[0..18, table]
- array[2..20, table]
- array[table, 0..18]
- array[table, 2..20]
- Which of the following is an example of semantic checking?
- E → E1 + E2 {E.val := E1.val + E2.val }
- E → E1 + E2 {E.type := if E1.type = int and E2.type = int
then int
else type_error}
- Both
- None
- Which of the following semantic rule is valid for type checker of E → E + E ?
- {E.type := if E1.type = int && E2.type = int then int else type_error}
- {E.type := if E1.type = int || E2.type = int then int else type_error}
- {E.type := if E1.type = int &! E2.type = int then int else type_error}
- None
- __________ are constructed data types.
- arrays
- structures
- pointer
- all
- While performing type checking __________ special basic types are needed.
- 1
- 2
- 3
- 4
- The semantic way of expressing type of a language construct is called __________.
- semantic expression
- type expression
- type system
- all
- The constructed data types are build using __________ data types.
- Enumerated
- Boolean
- Basic
- Builtin
- Semantic errors can be detected __________.
- only at compile time
- only at run time
- both at compile time and at run time
- none
- Type checking done by the compiler is called __________.
- static checking
- dynamic checking
- semantic checking
- none
- Two type expressions are __________ if two expressions are either the same basic type or are formed by applying the same constructor to structurally equivalent.
- name equivalent
- structural equivalent
- valid
- invalid
Exercises
- Which of the following type expressions are equivalent?
e1 = integer → e1
e2 = integer → (integer → e2)
e3 = integer → (integer → e1)
- Among the following expressions, which expressions are structurally equivalent? Which are name equivalent?
- node.
- pointer(n)
- pointer(node)
- pointer(record(info × integer) × ( next × pointer(n)))
- Express, using type variables, the type of the following functions.
- The function ref that takes as argument an object of any type and returns a pointer to that object.
- A function that takes as arguments an array indexed by integer, with elements of any type, and returns an array whose elements are the objects pointed to by the elements of the given array.
- Compute the type expressions for the following program fragments.
- c: char; i : integer; c mod i mod 3
- p: ↑ integer; a : array[10] of integer; a[p↑]
- f : integer → boolean;
i : integer; j : integer; k : integer;
k : = i
i : = j mod i;
j : = k
Key for Fill in the Blanks
- array[0..9,char]
- sound system
- void
- structural equivalent
- type_error
- coercions
- static checking
- dynamic checking
- C,C++
- dynamic checking
Key for Objective Question Bank
- b
- b
- a
- d
- d
- b
- c
- c
- a
- b

