Chapter 34. Symbolic Logic[1]
This chapter provides background on various types of logic. One can use symbols to represent data and functions to create formulas using the rules of logic. Then the rules of a logic system allow the analyst to reason about formulas made out of the symbols.
Propositional logic, also called the propositional calculus, is based on propositions, or atomic, declarative sentences that can be shown to be either true or false (but not both). Examples of such statements are “The sky is blue today,” “Nine divided by 3 equals 3,” and “All people like chocolate.” Questions, and statements such as “Let's go!” and “Here's hoping for the best,” are not considered declarative because they cannot be argued to be true or false. Propositions are usually represented by lowercase letters—usually those in the middle of the alphabet such as p and q—or by letters with subscripts, such as p1, p2,…, to make more than 26 symbols.
Propositions can be composed into compound sentences using connectives. These compound sentences are more complex propositions, or formulas. Formulas are generally represented by lowercase Greek letters, notably ϕ or ψ. The connectives of propositional logic are as follows.
Negation, written as “¬”, reverses the truth value of a proposition. If proposition p is true, then ¬p is false, and if p is false, ¬p is true.
Disjunction, written as “∨”, joins propositions. If one or both of p and q are true, then p ∨ q is true. If both p and q are false, then p ∨ q is false.
Conjunction, written as “∧”, also joins propositions. If both p and q are true, then p ∧ q is true. If either p or q is false, then p ∧ q is false.
Implication, written as “→”, suggests that one proposition is the logical consequence of another. Formally, p → q if and only if (¬p) ∨ q. In the implication p → q, p is called the premise of the formula and q is the conclusion of the formula. Implication is also referred to as “if…then,” but there are slight differences. “If…then” in natural language assumes a causal role in which the premise enables the conclusion. Implication in logic languages indicates a preservation of truth and not necessarily a causal relationship.
As in arithmetic, logic formulas consisting of symbols and connectives can be ambiguous. Arithmetic expressions and programming language expressions are evaluated according to specific rules, and when the rules are insufficient to distinguish ambiguities, distinctions are generally made using parentheses. For example, in arithmetic, ab + c is not the same as a(b + c). We know that multiplication and division have higher precedence than addition and subtraction, so the expression ab + c is interpreted to mean “multiply a and b and add c” rather than “add b to c and multiply the result by a.” Propositional logic has rules of precedence that behave in a similar fashion.
Negation (¬) has higher precedence than conjunction (∧) and disjunction (∨).
Conjunction (∧) and disjunction (∨) have equal precedence.
Conjunction (∧) and disjunction (∨) have higher precedence than implication (→).
Parentheses group operands and operators, and, as in arithmetic, operations within parentheses have the highest precedence. For example, (¬ p) ∧ q can be written as ¬ p ∧ q to distinguish it from ¬ (p ∧ q), illustrating the first rule of precedence above. Similarly, (p ∧ q) → r can be written as p ∧ q → r, but p ∧ (q → r) requires the parentheses.
Natural deduction is a means of reasoning about propositions, allowing us to draw conclusions. Proof rules let us infer formulas from other formulas. The rules can be applied to a set of premises, formulas that we know or assume to be true, to reach a conclusion, or the formula we wish to establish. A contradiction is a formula that is always false, regardless of p. For example, p ∧ ¬ p is a contradiction. All contradictions are equivalent and are denoted by a special symbol, ⊥, called bottom.
A tautology is a formula that is always true, regardless of p. For example, the expression p ∨ ¬ p is a tautology. All tautologies are equivalent and are denoted by a special symbol, ⊤, called top.
We present 11 rules of natural deduction. For each of the logical connectives, there is an introduction rule and an elimination rule. The introduction rules allow us to deduce information about the conclusion from the premises. The elimination rules allow us to conclude information about the variables used in the premise from the conclusion.
And introduction: If we have concluded (the truth of) p and q, then we can also conclude (the truth of) p ∧ q. In other words, we can say that if p is true and q is true, then p ∧ q is also true.
And elimination: If we have concluded p ∧ q, then we can also conclude p and we can also conclude q. In other words, if p ∧ q is true, then p is true and q is true.
Implication introduction: Assume that p is true temporarily, and, based on this assumption, prove q. Thus, we can conclude p → q. More generally, if we assume the premise and reach the conclusion, we can say that the premise implies the conclusion.
Implication elimination, also called modus ponens: If we have concluded p and p → q, we can also conclude q. More generally, if the premise is true and the implication is true, then the conclusion must be true.
Disjunction introduction: If we can conclude p, then we can conclude p ∨ q. Similarly, if we can conclude q, then we can conclude p ∨ q. If either p or q is true, then p ∨ q.
Disjunction elimination: If we can conclude p ∨ q and want to use it to conclude X, we first assume p and conclude X. Then we assume q and conclude X. Given p ∨ q and these two proofs, we can infer X.
Negation introduction: If we assume p and conclude bottom (⊥), we infer ¬ p.
Negation elimination: If we assume p and ¬ p, we conclude bottom (⊥).
Bottom elimination: If we assume ⊥, a contradiction, then we can prove any proposition p.
Double negation introduction: If we have concluded p, then we can also conclude the double negation of p, ¬¬p. In other words, if p is true, then ¬¬p is also true.
Double negation elimination: If we have concluded ¬¬p, then we can also conclude p. In other words, if ¬¬p is true, then p is also true.
Two commonly used rules that are derived from the rules above are modus tollens and reductio ad absurdum. Modus tollens eliminates an implication. If we have concluded ¬ q and p → q, we can also conclude ¬ p.
Suppose that ¬ q holds. Suppose we assume that a premise p holds and we can prove that p → q holds. By the implication elimination rule above, q holds. But it is impossible for both q and ¬ q to hold, so our assumption about p must be false, which means ¬p. In other words, if the conclusion is false and the implication is true, then the premise must be false. This is an example of a proof technique called reductio ad absurdum or proof by contradiction. A succinct description is: to prove p, assume ¬ p and reach bottom (or a contradiction).
Any set of symbols using symbols for propositions, connectors, and parentheses is a “word” in the alphabet of a logical language. But not all words are meaningful. An important class of meaningful words is the set of well-formed formulas (WFFs). They are defined inductively.
A propositional atom is a WFF.
The negation of a WFF is a WFF.
The conjunction of WFFs is a WFF.
The disjunction of WFFs is a WFF.
An implication between two WFFs is a WFF.
The previous sections show how one may reach a conclusion based on a set of premises and applying the laws of natural deduction. Another way of approaching such a proof is by using truth tables. A truth table is a set of the possible values of a compound proposition based on the possible values (in this case, T for true or F for false) of the atomic propositions. Truth tables for conjunction, disjunction, implication, and negation are shown below.
p | q | p ∧ q | p ∨ q | p → q | ¬ p |
|---|---|---|---|---|---|
T | T | T | T | T | F |
T | F | F | T | F | F |
F | T | F | T | T | T |
F | F | F | F | T | T |
To reach a “proof” by using truth tables, create a truth table for a formula that states that the conjunction of the premises implies the conclusion. Of course, the more atomic propositions there are, the larger the truth table and the more complex this technique becomes. If the truth table of the conjunction of the premises is the same as the truth table of the conclusion, then we say that we have reached a proof.
Definition 34–1. A sequent is a set of formulas (premises) ϕ1, ϕ2, …, ϕn and a conclusion ψ. It is denoted by ϕ1, ϕ2, …, ϕn |– ψ.
Definition 34–2. A sequent is valid if a proof for it can be found.
Definition 34–3. Two formulas ϕ and ψ are provably equivalent if and only if ϕ |–ψ and ψ |– ϕ both are valid.
Definition 34–4. Two formulas that have the same truth table values are called semantically equivalent. If ψ evaluates to true whenever ϕ1, ϕ2, …, ϕn evaluate to true, this is denoted by ϕ1, ϕ2, …, ϕn |= ψ.
These definitions lead to two critical theorems in propositional logic.
The first theorem says that if there is a proof of a conclusion given a set of premises, then the premises and conclusion are semantically equivalent. Formally:
Theorem 34–1. Soundness Theorem of Propositional Logic. Let ϕ1, ϕ2, …, ϕn and ψ be propositional logic formulas. If ϕ1, ϕ2, …, ϕn |– ψ, then ϕ1, ϕ2, …, ϕn |= ψ.
The second theorem says that if a set of premises and a conclusion are semantically equivalent, then there is a natural deduction proof for the sequent. Formally:
Theorem 34–2. Completeness Theorem of Propositional Logic. If ϕ1, ϕ2, …, ϕn |= ψ, then ϕ1, ϕ2, …, ϕn |– ψ.
Mathematical induction is a proof technique that allows us to prove equations true when dealing with arbitrary values. Suppose we want to show that a property M(n) holds for all natural numbers n. To use mathematical induction, we proceed as follows.
Prove that M(1) holds. This is called the base case or basis.
Assert that M(n) holds for n = 1, …, k. This is called the induction hypothesis.
Prove that if M(k) holds, then M(k + 1) holds. This is called the induction step.
Then M(n) is true for all natural numbers n.
EXAMPLE: We wish to prove that the formula for the sum of the first n natural numbers is
We use mathematical induction. Call this formula M(n).
BASIS: M(1) is 1 = 1(1 + 1)/2, which is clearly true.
INDUCTION HYPOTHESIS: M(n) is true for n = 1, …, k.
INDUCTION STEP: Consider 1 + … + k + (k + 1):
| Induction hypothesis |
| Simplifying |
| Factoring |
| Rewriting |
But this is simply M(k + 1). Hence, if M(k) holds, then M(k + 1) holds. This completes the proof.
Predicate logic, also called predicate calculus or first order logic, is based on the concept of predicates and may contain variables, quantifiers, constants, and functions in addition to the components of propositional calculus. Consider the sentence: Every directory contains some files. We would like to express this concept in terms of logic. To do this, we need to introduce the concepts of variables and predicates and a means of capturing the ideas of “every” and “some.”
We define predicates that describe the properties represented by the sentence, using variables x and y to describe any file or directory. Let us assume that
F(x): x is a file
D(y): y is a directory
C(x, y): x is a file in directory y
We next need to define the concepts of “every” and “some.” We define the symbol ∃, the existential quantifier, to denote that something exists. Therefore, a statement containing the notation “∃x” is read “there exists x” or “there is some x.” The concept of “all” is represented by the symbol ∀, called the universal quantifier. The phrase “∀x” is read “for all x.” Both ∃ and ∀ can be combined with the negative connector, ¬, to mean “there does not exist” or “not all.” The sentence Every file belongs to some directory becomes ∀x F(x) → (∃y (D(y) ∧ C(x, y))). More precisely read, our sentence becomes “for every x, if x is a file, then there is some y such that y is a directory and directory y contains file x.”
Variables and constants are the basic terms of predicate logic. More complex terms are constructed using function references on terms. The definition of a function is consistent with the usual definition from mathematics: a function provides a unique output for each input. If one views constants as “functions” without any variable references, then we see that the entire predicate vocabulary consists of function symbols and predicate symbols that range over the set of terms.
A variable is said to be bound if it is quantified with either ∀ or ∃. A variable that is not bound is said to be unbound or free. For example, in ∀x Φ(x, y), x is a bound variable and y is a free variable.
A formula in predicate calculus with predicates P and functions Φ is defined as follows.
If P is a predicate taking n arguments (n ≥ 1) and the arguments are terms defined over the set Φ of functions, then P(t1, t2, …, tn) is a formula.
If φ is a formula, then ¬ φ is also a formula.
If φ and ϕ are formulas, so are φ ∧ ϕ, φ ∨ ϕ, and φ → ϕ.
If φ is a formula and x is a variable, then ∀x φ and ∃ x φ are also formulas.
The natural deduction rules for predicate logic are similar to those in propositional logic. They add new rules for existential and universal quantifiers as well as the distinguished predicate equals, represented by the equality sign (=). The new rules are as follows.
Equality: A term t is equal to itself.
Substitution: Equals may be substituted for equals. If t1 = t2 and x is a free variable in φ(x), then φ(t1) = φ(t2).
Universal quantifier elimination: If you have ∀x φ(x), then you can replace the x in φ(x) by any term t that is free in φ(x).
Universal quantifier introduction: If you can prove some formula φ(x) with x a free variable, you can derive ∀x φ(x).
There are many temporal logic systems. Linear time logic systems view events as sequential. Branching time logic systems view events as concurrent “alternative universes.” Temporal logic systems view time as either a continuous flow of events or a set of discrete events.
Section 20.4.2.2 discussed the use of Control Tree Logic (CTL) in the study and verification of hardware and communications protocols. This section describes the logic itself. CTL views time as branching and discrete.
CTL builds on the concepts of propositional logic. Its building blocks are propositions; the connectors ¬, ∧, ∨, and →; the concepts of ⊥ (bottom, never true) and ⊤ (top, always trivially true); the signs of aggregation ( ), [ ], and { }; and the notion of a well-formed formula.
CTL adds eight temporal connectives to this list. Each connective has two identifying symbols. The first symbol is either “A” or “E”; these symbols are somewhat similar in concept to the symbols ∀ and ∃ of predicate logic. “A” means “along all paths,” whereas “E” means “along at least one path.” The second symbol is “X,” “F,” “G,” or “U.” An “X” refers to “the next state,” an “F” means “some next state,” a “G” means “all future states,” and a “U” means “until some future state.”
The precedence rules for CTL are as follows.
The unary operators ¬, AG, EG, AF, EF, AX, and EX have the highest precedence.
The operators ∧ and ∨ have the next-highest precedence.
The operator → has the next-highest precedence.
The operators AU and EU have the lowest precedence.
We define a well-formed CTL formula as follows.
Top (⊤) is a formula.
Bottom (⊥) is a formula.
All atomic descriptions are formulas.
If φ and ϕ are formulas, so are φ ∧ ϕ, φ ∨ ϕ, ¬φ, φ → ϕ, AXφ, EXφ, A[φUϕ], E[φUϕ], AGφ, EGφ, AF, and EFφ.
It is easiest to define the syntax of CTL in terms of a model of a system. The basic unit of a system model is a set of atoms defined for the system. The model consists of the states of the system, an operator that represents the changes of state, and a function that gives the atoms that hold for a state. More formally:
Definition 34–5. A model is formally defined within CTL as M = (S, ⇒, L), where S is a set of states, ⇒ is the transition operator on the set S such that ∀s ∊ S, ∃s' ∊ S [ s ⇒ s'], L is a labeling function, and L : S → P(atoms).
Here, P(atoms) is the power set (set of all subsets) of the defined atoms.
If M is a model and s is a state, the state satisfies a formula φ if the formula is true in that state. Again, formally:
Definition 34–6. Satisfaction Relation. Let M = (S, ⇒, L) be a model for CTL. Given any s ∊ S, if a CTL formula φ holds in state s, we denote this by M, s |= φ, and say we that state s of model M satisfies formula φ.
For convenience, we write M, s 
φ if state s of model M does not satisfy formula φ.
Let M be a model, let sis be states of M, let p be an atomic proposition of M, and let φ, φ1, and φ2 be CTL formulas. Then:
∀ s ∊ S [ M, s |= ⊤ ].
This says that tautologies hold in all states of the model M.
∀ s ∊ S [ M, s
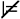⊥ ].This says that contradictions do not hold in any state of the model M.
M, s |= p if and only if p ∊ L(s).
This says that p holds in state s of model M whenever p is in the set of atoms that hold in state s. Conversely, if p is not in that set, then p does not hold in state s.
If M, s
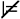φ, then M, s |= ¬ φ.This establishes that if a state does not satisfy a formula, then the state satisfies the negation of that formula.
M, s |= φ1 ∧ φ2 if and only if M, s |= φ1 and M, s |= φ2.
This says that a state satisfies the disjunction of two formulas if and only if it satisfies both formulas.
M, s |= φ1 ∨ φ2 if and only if M, s |= φ1 or M, s |= φ2.
This says that a state satisfies the conjunction of two formulas if and only if it satisfies either formula.
M, s |= φ1 → φ2 if and only if M, s
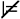φ1 or M, s |= φ2.This says that a state satisfies the implication of two formulas if and only if it satisfies the second, or satisfies neither the first nor the second, formula.
Now consider the temporal connectives.
M, s |= AX φ if and only if ∀s1 such that s → s1 and M, s1 |= φ.
This says that a state satisfies a formula in all possible next states if and only if every state that the original state implies also satisfies the formula.
M, s |= EX φ if and only if ∃s1 such that s → s1 and M, s1 |= φ.
This says that a state satisfies a formula in some next state if and only if at least one state that the original state implies also satisfies the formula.
M, s |= AG φ if and only if ∀ paths s1 → s2 → s3 → …, where s = s1 and ∀si on the path [ M, si |= φ ].
This says that a state satisfies a formula in all future states if and only if every state on every path of transitions beginning at the original state satisfies the formula.
M, s |= EG φ if and only if ∃ a path s1 → s2 → s3 → …, where s = s1 and ∀si on the path [ M, si |= φ ].
This says that there is a path with all states satisfying a formula if and only if every state on a path of transitions beginning at the original state satisfies the formula.
M, s |= AF φ if and only if ∀ paths s1 → s2 → s3 → …, where s = s1, ∃si[M, si |= φ ].
This says that on all paths there will be a state satisfying the formula if and only if every path of transitions beginning at the original state contains at least one state that satisfies the formula.
M, s |= EF φ if and only if ∃ a path s1 → s2 → s3 → …, where s = s1 and ∃si on the path [ M, si |= φ ].
This says that there is a path with one state satisfying the formula if and only if a state on a path of transitions beginning at the original state satisfies the formula.
[1] This chapter was written by Elisabeth C. Sullivan. Ms. Sullivan has granted permission for this material to be used in Computer Security: Art and Science, and any use of this material outside the scope of this text must have the permission of Ms. Sullivan.