GONERIL: Combine together 'gainst the enemy,For those domestic poor particularsAre not to question here. | ||
| --The Tragedy of King Lear, V, i, 29–31. | ||
Organizations usually have multiple policy making units. If two different branches of an organization have conflicting policy needs, or even different policy needs, what policy should the organization as a whole adopt? If one of the policies requires six levels of security, and another three, how can they be composed into a coherent whole—or can they? The answers to these general questions come from information flow models that abstract the essence of security policies. Introduced in 1982, these models focus on each process' view of the system to ensure that no high-level information is visible, or can be deduced, by a low-level process. We begin by reviewing the problem and introducing the notions of noninterference and unwinding. We then expand with variations of noninterference called “nondeducibility” and “restrictiveness.” We conclude by studying the composition of security policies using these models.
Return to the Bell-LaPadula Model for a moment. That model forbids reading of higher-level objects (the simple security condition) and writing to lower-level objects (the *-property). However, writing can take many forms.
This example demonstrates the difficulty of separating policy from mechanism. In the abstract, the CPU is transmitting information from one user to another. This violates the *-property, but it is not writing in any traditional sense of the word, because no operation that alters bits on the disk has occurred. So, either the model is insufficient for preventing Matt and Holly from communicating, or the system is improperly abstracted and a more comprehensive definition of “write” is needed. This is one problem, and in what follows, exploring it will lead to the notions of noninterference and nondeducibility.
The techniques of modular decomposition and bottom-up programming are widely used throughout the disciplines of computer science, including computer security. Many standards, such as the Trusted Network Interpretation of the Trusted Computer Security Evaluation Criteria (see Section 21.2), require secure components to be connected to create a secure distributed or networked system. An obvious question is whether or not the composition of two secure systems is itself secure. For our purposes, we assume that the implementation of those systems is precise with respect to the security policy, and we confine ourselves to the issue of composition of security policies. If their composition is not secure, then the composed system is not secure.
Consider two systems with policies that match the Bell-LaPadula Model. These policies can be represented as lattices. The composed system is therefore the composition of the lattices. The relevant issue is the relationship among the labels (security levels and categories). If they are the same, the composition is simply the lattice itself. If they differ, the new lattice must reflect the relationship among the compartments.
EXAMPLE: Consider two systems with policies modeled by the Bell-LaPadula Model. One, system allie, has two security levels, LOW and HIGH, and two categories, EAST and WEST. The other, system son, has three security levels, LOW, S, and TS, and two categories, EAST and SOUTH. (The two EAST categories have the same meaning, as do the two LOW security levels.) Figure 8-1 shows the lattices of these two systems. The relevant issues are (1) how S and TS compare with HIGH and (2) how SOUTH compares with EAST and WEST.
Figure 8-1. The lattice on the left corresponds to the policy of system allie; the one on the right, to system son.
Assume that HIGH corresponds to a level between S and TS, and that SOUTH is a category disjoint from EAST and WEST. Then the composed lattice has four security levels (LOW, S, HIGH, and TS) and three categories (EAST, WEST, and SOUTH). Drawing the resulting lattice is left as an exercise for the reader.
The security policy of the composite system in the preceding example is a composition of the two security policies of the component systems. If we can change the policies that the components must meet, then composing multiple secure systems to produce a single secure system becomes trivial. However, if we must compose two components that meet a particular policy and show that the resulting composition also meets that same policy, the problem becomes quite difficult. We will explore this surprising fact at length throughout the rest of this chapter.
An interesting question is how to compose systems with different policies to produce a secure policy. Under these conditions, the notion of “security” is not clear: which policy dominates? Gong and Qian [408, 409] suggest the following guiding principles.
Axiom 8–1. Principle of Autonomy: Any access allowed by the security policy of a component must be allowed by the composition of the components.
Axiom 8–2. Principle of Security: Any access forbidden by the security policy of a component must be forbidden by the composition of the components.
The composite system therefore satisfies the security policies of its components because the policies of the components take precedence over the composite. Moreover, a “composition policy” handles the accesses not falling under either principle. If a new access is neither allowed nor forbidden by either principle, it should be disallowed unless it is explicitly permitted by the composition policy.[1]
Gong and Qian [408, 409] show that, given these principles, the problem of determining if an access is secure is of polynomial complexity. Their algorithm is to compute the transitive closure of the allowed accesses under each component's policy and under the composition policy. Then all forbidden accesses in this set are deleted. If the requested access is in the remaining set, it is allowed; otherwise, it is denied.
The dropping of the accesses that violate components' restrictions after the transitive closure has been computed eliminates accesses that are allowed by the composition policy but forbidden by the components. This is dictated by the principle of security. Without it, Bob could read Alice's files in the composition but not within the component.
Determining the minimum set of accesses that the composition policy must forbid in order to enforce both principles is generally in NP.
The example above suggests an alternative view of security phrased in terms of interference. In essence, a system is secure if groups of subjects cannot interfere with one another. In the first example in Section 8.1, the “interference” would be Matt's interfering with Holly's acquiring the CPU for her process. Intuitively, this notion is more inclusive than “writing” and enables us to express policies and models more simply. Gougen and Meseguer [412] used this approach to define security policies.
To begin, we view a system as a state machine consisting of a set S = { s1, ... } of subjects, a set Σ = { σ0, σ1, ... } of states, a set O = { o1, ... } of outputs, and a set Z = { z1, ... } of commands. For notational convenience, we define a set of state transition commands C = S × Z, because in what follows the clearance of the subject executing the command affects the actual command that is performed.
Definition 8–1. A state transition function T: C × Σ → Σ describes the effect of executing command c when in state σ, and an output function P: C × Σ → O describes the output of the machine on executing command c in state σ. Initially, the system is in state σ0.
We do not define any inputs, because either they select the specific commands to be executed or they can be encoded in the set of state transition commands. If the number x is to be input, we simply define a command that corresponds to reading x. We can encode the initial state as a command; the system begins at the empty state (and the first command moves it to σ0). This notation simplifies the abstract system.
In this system, the state transition commands produce outputs. The outputs are therefore functions of the transition commands, and thus are functions of the inputs and the initial state. We have also assumed that the system is deterministic, since the state transition functions are functions, and time is not considered. We will relax this restriction later.
Next, let us relate outputs to state. Two observations will make the formulation straightforward. First, T is inductive in the first argument, because T(c0, σ0) = σ1 and T(ci+1, σi+1) = T(ci+1, T(ci, σi)). This gives us the notion of applying a sequence of commands to an initial state, so let C* be the set of sequences of commands in C—that is, C* is the transitive closure of C under composition. Then T*: C* × Σ → Σ, where
cs = c0, ..., cn ⇒ T*(cs, σi) = T(cn, T(cn–1, ..., T(c0, σi)...))
Second, the output function P is also inductive in the second argument. This allows us to define a similar function P*: C* × Σ → O, which gives the sequence of outputs resulting from a sequence of commands to a system beginning at an initial state.
Given the assumptions above, the outputs provide a record of the system's functioning. The problem is that some subjects are restricted in the outputs (and actions) they can see. In the first example in Section 8.1, Holly should not have seen Matt's outputs, but Matt could see any outputs from Holly. We make this notion rigorous.
Definition 8–2. Let T*(cs, σi) be a sequence of state transitions for a system. Let P*(cs, σi) be the corresponding outputs. Then proj(s, cs, σi) is the set of outputs in P*(cs, σi) that subject s is authorized to see, in the same order as those outputs appear in P*(cs, σi).
In this definition, each command may produce some output, but subjects with insufficient clearance may not be able to see that output, lest they deduce information about the previous state of the system. The function proj(s, cs, σi) is simply the list of outputs resulting from removing the outputs that s is not authorized to see.
This captures the notion that s may not see all outputs because the security policy may restrict s's access to them. However, s may not have knowledge of all commands, either, and so we need a corresponding definition for them.
Definition 8–3. Let G ⊆ S be a group of subjects, and let A ⊆ Z be a set of commands. Define πG(cs) as the subsequence of cs obtained by deleting all elements (s, z) in cs with s ∊ G. Define πA(cs) as the subsequence of cs obtained by deleting all elements (s, z) in cs with z ∊ A. Define πG,A(cs) as the subsequence of cs obtained by deleting all elements (s, z) in cs such that both s ∊ G and z ∊ A.
This purge function π captures the notion that certain command executions must be invisible to some subjects. Applying the purge function to an output string generates the output string corresponding to those commands that the subject is allowed to see. For a specific system, the desired protection domains would dictate the membership of G and A.
Intuitively, if the set of outputs that any user can see corresponds to the set of inputs that that user can see, then the system is secure. The following definition formalizes this as “noninterference.”
Definition 8–4. Let G, G' ⊆ S be distinct groups of subjects and let A ⊆ Z be a set of commands. Users in G executing commands in A are noninterfering with users in G' (written A,G :| G') if and only if, for all sequences cs with elements in C*, and for all s ∊ G', proj(s, cs, σi) = proj(s, πG,A(cs), σi).
If either A or G is not present, we handle it in the obvious way.
We can now formulate an alternative definition of a security policy. By Definition 4–1, a security policy describes states in which forbidden interferences do not occur (authorized states). Viewed in this light [412], we have:
Definition 8–5. A security policy is a set of noninterference assertions.
The set of noninterference relations defined in Definition 8–4 characterize the security policy completely. An alternative, less common but more elegant, approach begins with the notion of a security policy and characterizes noninterference in terms of that definition [858].
Consider a system X as a set of protection domains D = { d1, …, dn }. Associated with X are states, commands, subjects, and transition commands. Whenever a transition command c is executed, the domain in which it is executed is written dom(c).
Definition 8–5A. Let r be a reflexive relation on D × D. Then r defines a security policy for M.
The relation r defines how information can flow. If dirdj, then information can flow from domain di to domain dj. Otherwise, it cannot. Because information can flow within a protection domain, dirdi. Note that this definition says nothing about the content of the security policy; it merely defines what a “policy” is.
We can define a function π' analogous to the π in Definition 8–3, but the commands in A and the subjects in G and G' are now part of the protection domains, so we express π' in terms of protection domains.
Definition 8–3A. Let d ∊ D, c ∊ C, and cs ∊ C*. Then πd'(ν) = ν, where ν is the empty sequence. If dom(c)rd, then πd'(csc) = πd'(cs)c. Otherwise, πd'(csc) = πd'(cs).
This says that if executing c will interfere with protection domain d, then c will be “visible.” Otherwise, the resulting command sequence has the same effect as if c were not executed.
Given this definition, defining noninterference security is immediate.
Definition 8–4A. Let a system consist of a set of domains D. Then it is noninterference-secure with respect to the policy r if P*(c, T*(cs, σ0)) = P*(c, T*(πd'(cs), σ0)).
Rather than defining a projection function (as in Definition 8–2), consider the set of states related by an equivalence relation with respect to a domain of a command.
Definition 8–2A. Let c ∊ C and dom(c) ∊ D, and let ~dom(c) be an equivalence relation on the states of a system X. Then ~dom(c) is output-consistent if σa ~dom(c) σb implies P(c, σa) = P(c, σb).
Two states are output-equivalent if, for the subjects in dom(c), the projections of the outputs for both states after c is applied are the same. This immediately leads to the following lemma.
Lemma 8–1. Let T*(cs, σ0) ~d T*(πd(cs), σ0) for c ∊ C. Then, if ~d is output-consistent, X is noninterference-secure with respect to the policy r.
Proof. Take d = dom(c) for some c ∊ C. Applying Definition 8–2A to the hypothesis of this claim, P*(c, T*(cs, σ0)) = P*(c, T*(πdom(c)(cs), σ0)). But this is the definition of noninterference-secure with respect to r (see Definition 8–4A).
Contrasting this approach with the more common first approach illuminates the importance of the security policy. In the first approach, the security policy was defined in terms of noninterference, but it arose from the conditions that caused the particular set of subjects G and the commands A. So, in some sense, Definition 8–5 is circular. The second approach eliminates this circularity, because noninterference is characterized in terms of a defined security policy. However, the second approach obscures the relationship among subjects, commands, and noninterference requirements because of the abstraction of “protection domains.” The notion of outputs characterizing commands is crucial, because information flow is defined in terms of outputs. So both characterizations have their places.
The unwinding theorem links the security of sequences of state transition commands to the security of the individual state transition commands. The name comes from “unwinding” of the sequence of commands. This theorem is central to the analysis of systems using noninterference, because it reduces the problem of proving that a system design is multilevel-secure to proving that if the system design matches the specifications from which certain lemmata are derived, then the design is mathematically certain to provide multilevel-security correctly.[2]
We follow Rushby's treatment [858]. The next two definitions provide the necessary background.
Definition 8–6. Let r be a policy. Then a system X locally respects r if dom(c) being noninterfering with d ∊ D implies σa ~d T(c, σa).
If the command c does not have any effect on domain d under policy r, then the result of applying c to the current state should appear to have no effect with respect to domain d. When this is true, the system locally respects r.
Definition 8–7. Let r be a policy and d ∊ D. If σa ~d σb implies T(c, σa) ~d T(c, σb), the system X is transition-consistent under policy r.
Transition consistency simply means that states remain equivalent with respect to d for all commands c.
Lemma 8–2. Let c1, c2 ∊ C, d ∊ D, and for some policy r, (dom(c1), d) ∊ r and (dom(c2), d) ∊ r. Then T*(c1c2, σ) = T(c1, T(c2, σ)) = T(c2, T(c1, σ)).
Proof. See Exercise 2.
Theorem 8–1. Unwinding Theorem. Let r be a policy, and let X be a system that is output consistent, transition consistent, and locally respects r. Then X is non-interference secure with respect to the policy r.
Proof. The goal is to establish that σa ~d σb implies T*(cs, σa) ~d T*(πd'(cs), σb). We do this by induction on the length of cs.
Basis. If cs = ν, T*(cs, σa) = σa and πd'(ν) = ν. The claim follows immediately.
Hypothesis. Let cs = c1...cn. Then σa ~d σb implies T*(cs, σa) ~d T*(πd'(cs), σb).
Step. Consider cscn+1. We assume σa ~d σb. We must show the consequent. We consider two distinct cases for T*(πd'(cscn+1), σb).
If (dom(cn+1), d) ∊ r, by definition of T* and definition 8-3A,
T*(πd'(cscn+1), σb) = T*(πd'(cs)cn+1, σb) = T(cn+1, T*(πd'(cs), σb)).
As X is transition consistent, if σa ~d σb, then T(cn+1, σa) ~d T(cn+1, σb). From this and the induction hypothesis,
T(cn+1, T*(cs, σa)) ~d T(cn+1, T*(πd'(cs), σb)).
Substituting for the right side from the previous equality,
T(cn+1, T*(cs, σa)) ~d T*(πd'(cscn+1), σb).
From the definition of T*, this becomes
T*(cscn+1, σa) ~d T*(πd'(cscn+1), σb).
proving the hypothesis.
If (dom(cn+1), d) ∉ r, by definition 8-3A,
T*(πd'(cscn+1), σb) = T*(πd'(cs), σb).
From the induction hypothesis, this means
T*(cs, σa) ~d T*(πd'(cscn+1), σb).
As X locally respects r, σ ~d T(cn+1, σ) for any σ. Then T(cn+1, σa) ~d σa, so
T(cn+1, T*(cs, σa)) ~d T*(cs, σa).
Substituting back, this becomes
T(cn+1, T*(cs, σa)) ~d T*(πd'(cscn+1), σb)
verifying the hypotheses.
In either case, then, the hypothesis holds, completing the induction step.
Having completed the induction, take σa = σb = σ0. Then, by Lemma 8–1, if ~d is output consistent, X is non-interference secure with respect to the policy r.
The significance of Theorem 8–1 is that it provides a basis for analyzing systems that purport to enforce a noninterference policy. Essentially, one establishes the conditions of the theorem for a particular set of commands and states with respect to some policy and a set of protection domains. Then noninterference security with respect to r follows.
Rushby presented a simple example of the use of the unwinding theorem [858]. The goal is to apply the theorem to a system with a static access control matrix. Our question is whether or not the given conditions are sufficient to provide noninterference security.
We begin with a model of the system. As usual, it is composed of subjects and objects. The objects are locations in memory containing some data. The access control matrix controls the reading and writing of the data. The system is in a particular state; the state encapsulates the values in the access control matrix.
Specifically, let L = { 11, …, lm } be the set of objects (locations) in memory or on disk. Let V = { v1, …, vn } be the set of values that the objects may assume. As usual, the set of states is Σ = { σ1, …, σk }. The set D = { d1, …, dj } is the set of protection domains. We also define three functions for convenience.
value: L × Σ → V returns the value stored in the given object when the system is in the given state.
read: D → P(V) returns the set of objects that can be observed under the named domain (here, POW(V) denotes the power set of V).
write: D → P(V) returns the set of objects that can be written under the named domain.
Let s be a subject in the protection domain d, and let o be an object. The functions represent the access control matrix A because the entry corresponding to A[s, o] contains “read” if o ∊ read(d) and contains “write” if o ∊ write(d). This also leads to a natural interpretation of the equivalence relation in Definition 8–2A—namely, that two states are equivalent with respect to a given protection domain if and only if the values of all objects that can be read under that protection domain are the same. Symbolically,
[σa ~dom(c) σb] ⇔ [∀ li ∊ read(d) [value(li, σa) ≠ value(li, T(c, σa))] ]
The system X enforces the relevant access control policy r when the following three conditions are met.
The output of some command c being executed within the protection domain dom(c) depends only on the values for which subjects in dom(c) have read access.
σa ~dom(c) σb ⇒ P(c, σa) = P(c, σb)
If command c changes the value in object li, then c can only use values in objects in the set read(dom(c)) to determine the new value:
[σa ~dom(c) σb and (value(li, T(c, σa)) ≠ value(li, σa) or value(li, T(c, σb)) ≠ value(li, σb)) ] ⇒value(li, T(c, σa)) = value(li, T(c, σb))
The second part of the disjunction ensures that if li ∉ read(dom(c)), the values in li after c is applied to state σa and state σb may differ.
If command c changes the value in object li, then dom(c) provides the subject executing c with write access to li:
value(li, T(c, σa)) ≠ value(li, σa) ⇒ li ∊ write(dom(c))
These requirements are standard for access control mechanisms (in particular, note that they are independent of any particular security policy, although such a policy must exist). We now augment our system with two more requirements for some security policy r.
Let u, v ∊ D. Then urv ⇒ read(u) ⊆ read(v).
This requirement says that if u can interfere with v, then every object that can be read in protection domain u can also be read in protection domain v. This follows from the need of v to read information from something in u. Given this, if an object that could not be read in u could be read in v, but some other object in u could be read in v, information could flow from the first object to the second and hence out of domain u.
li ∊ read(u) and li ∊ write(v) ⇒ vru.
This simply says that if a subject can read an object in domain v, and another subject can read that object in domain u, then domain v can interfere with domain u.
Theorem 8–2. Let X be a system satisfying the five conditions above. Then X is noninterference-secure with respect to the policy r.
Proof. Taking the equivalence relation to be ~d in Definition 8–2A, condition 1 and the definition of “output-consistent” are the same.
We use proof by contradiction to show that X locally respects r. Assume that (dom(c), d) ∊ r but that σa ~d T(c, σa) does not hold. By the interpretation of ~d, this means that there is some object whose value is changed by c:
∃ li ∊ read(d) [value(li, σa) ≠ value(li, T(c, σa))]
By condition 3, li ∊ write(dom(c)). Combining this with the selection of li, both parts of condition 5 hold. By that condition, (dom(c), d) ∊ r. This contradicts the hypothesis, so σa ~d T(c, σa) must hold and X locally respects r.
We next consider transition consistency. Assume that σa ~d σb; we must show that value(li, T(c, σa)) = value(li, T(c, σb)) for li ∊ read(d). We consider three cases, each dealing with the change that c makes in li in states σa and σb.
Let value(li, T(c, σa)) ≠ value(li, σa). By condition 3, li ∊ write(dom(c)). Because li ∊ read(d), condition 5 yields (dom(c), d) ∊ r. By condition 4, read(dom(c)) ⊆ read(d). Because σa ~d σb, σa ~dom(c) σb. Condition 2 then yields the desired result.
If value(li, T(c, σb)) ≠ value(li, σb), an argument similar to case 1 yields the desired result.
Let value(li, T(c, σa)) = value(li, σa) and value(li, T(c, σb)) = value(li, σb). The interpretation of σa ~d σb is that value(li, σa) = value(li, σb) for li ∊ read(d). The result follows immediately.
In all three cases, X is transition-consistent.
Under the stated conditions, X is output-consistent, locally respects r, and is transition-consistent. By the unwinding theorem (Theorem 8–1), then, X is noninterference-secure with respect to the policy r.
All that remains is to verify that the five conditions hold for the system being modeled.
We now extend the preceding noninterference analysis to include policies that are not static. As an example of such a policy, consider an access control matrix for a discretionary access control mechanism. Subjects may revoke permissions, or add permissions, over objects they own. The analysis above assumes that the matrix will be constant; in practice, the matrix rarely is.
We now generalize the notion of noninterference to handle this case. First, we must define a function analogous to πG,A(w).
Definition 8–8. Let G ⊆ S be a group of subjects and let A ⊆ Z be a set of commands. Let p be a predicate defined over elements of C*. Let cs = c1, …, cn ∊ C*. Let ν represent the empty sequence. Then π''(ν) = ν, and π"((c1, ..., cn)) = (c1', ..., cn'), where ci' = ν if p(c1', ..., ci–1') and ci = (s, z) with s ∊ G and z ∊ A; and ci' = ci otherwise.
The essence of the definition lies in the use of the predicate. Informally, π"(cs) is cs; however, when the predicate p is true and an element of cs involves a subject in G and a command in A, the corresponding element of cs is replaced by ν. This deletes that element. From this, the extension to noninterference is straightforward.
Definition 8–9. Let G, G' ⊆ S be groups of subjects and let A ⊆ Z be a set of commands. Let P be a predicate defined over elements of C*. Users in G executing commands in A are noninterfering with users in G' under the condition p (written A,G :| G' if p) if and only if proj(s, cs, σi) = proj(s, π''(cs), σi) for all sequences cs ∊ C* and all s ∊ G.
As noted earlier, Gougen and Meseguer [412] assume that the output is a function of the input. This implies determinism, because a nondeterministic mapping (that is, one with two or more elements of the range corresponding to one element of the domain) is not a function. It also implies uninterruptibility, because differences in timing of interrupts can result in differences in state, and hence in output. For example, suppose a user enters a command to delete a file. This appears to take some time, so the user interrupts the command. If the interrupt occurs before the deletion, the system will be in a different state than if the interrupt occurs after the deletion (but before the command can terminate properly).
McCullough [673] has examined the implications of the determinism for composing systems. Consider composing the following systems. Systems Louie and Dewey compute at the LOW level. System Hughie computes at the HIGH level. The composed system has one output buffer, bL, which anyone can read. It also has one input buffer, bH, which receives input from a HIGH source. Three buffers connect the three systems. Buffer bLH connects Louie to Hughie, and buffer bDH connects Dewey to Hughie. Dewey and Louie write to these buffers, and Hughie reads from them. Both Dewey and Louie can write to the third buffer, bLDH, from which Hughie can read. Figure 8-2 summarizes this composition. Note that all three systems are noninterference-secure. Hughie never outputs anything, so its inputs clearly do not interfere with its (nonexistent) outputs. Similarly, neither Dewey nor Louie input anything, so their (nonexistent) inputs do not interfere with their outputs.
![Composition of systems (from [673], Figure 2).](http://imgdetail.ebookreading.net/software_development/21/0201440997/0201440997__computer-security-art__0201440997__graphics__08fig02.gif)
If all buffers are of finite capacity, and blocking sends and receives are used, the system is not noninterference-secure. Without loss of generality, assume that buffers bDH and bLH have capacity 1. Louie cycles through the following algorithm.
Louie sends a message to bLH. This fills the buffer.
Louie sends a second message to bLH.
Louie sends a 0 to buffer bL.
Louie sends a message to bLDH to signal Hughie that Louie has completed a cycle.
Dewey follows the same algorithm, but uses bDH for bLH and writes a 1 to bL. Hughie reads a bit from bH, receives a message from bLH (if the bit read from bH is 0) or from bDH (if the bit read from bH is 1), and finally does a receive on bLDH (to wait for the buffer to be filled).
Suppose Hughie reads a 0 from bH. It reads a message from bLH. At that point, Louie's second message can go into the buffer and Louie completes step 2. Louie then writes a 0 into bL. Dewey, meanwhile, is blocked at step 1 and so cannot write anything to bL. A similar argument shows that if Hughie reads a 1 from bH, a 1 will appear in the buffer bL. Hence, a HIGH input is copied to a LOW output.
So, even though the systems are noninterference-secure, their composition is not. Exercise 3 examines the influence of the requirement that buffers be finite and of the use of blocking sends and receives.
Gougen and Meseguer [412] characterize security in terms of state transitions. If state transitions caused by high-level commands interfere with a sequence of transitions caused by low-level commands, then the system is not noninterference-secure. But their definition skirts the intent of what a secure system is to provide. The point of security, in the Bell-LaPadula sense, is to restrict the flow of information from a high-level entity to a low-level entity. That is, given a set of low-level outputs, no low-level subject should be able to deduce anything about the high-level outputs. Sutherland [984] reconsidered this issue in these terms.
Consider a system as a “black box” with two sets of inputs, one classified High and the other Low. It also has two outputs, again, one High and the other Low. This is merely a reformulation of the state machine model, because the inputs drive the commands used to create state transitions and generate output. However, the difference in view allows a more intuitive definition of security.
If an observer cleared only for Low can take a sequence of Low inputs and Low outputs, and from them deduce information about the High inputs or outputs, then information has leaked from High to Low. The difference between this notion and that of noninterference is subtle.
We now formalize this notion of “secure.” In what follows, it suffices to consider the Low user deducing information about the High inputs, because the High inputs and Low inputs define the High outputs.[3]
Definition 8–10. An event system is a 4-tuple (E, I, O, T), where E is a set of events, I ⊆ E is a set of input events, O ⊆ E is a set of output events, and T is the set of all possible finite sequences of events that are legal within the system. The set E is also partitioned into H, the set of High events, and L, the set of Low events.
The sets of High inputs and outputs are H ∩ I and H ∩ O, respectively; the sets of Low inputs and outputs are L ∩ I and L ∩ O. Let TLow contain the set of all possible finite sequences of Low events that are legal within the system.
Define a projection function πL: T → TLow that deletes all High inputs from a given trace. Then a Low observer should be unable to deduce anything about the set of High inputs from a trace tLow ∊ TLow. In other words, given any such tLow, the trace t ∊ T that produced tLow is equally likely to be any trace such that π(t) = tLow. More formally:
Definition 8–11. A system is deducibly secure if, for every trace tLow ∊ TLow, the corresponding set of high-level traces contains every possible trace t ∊ T for which πL(t) = tLow.
In general, systems that are deducibly secure are not composable [673]. However, the following modification appears to eliminate the problem that arose during composition of noninterference-secure systems.
Definition 8–12. Strong noninterference is the property of deducible security augmented by the requirement that no High-level output occurs unless a High-level input causes it.
Weber[4] has shown that systems meeting the strong noninterference property are composable. But this property is too restrictive, in the sense that it forbids systems that are obviously secure.
The preceding discussion of noninterference tacitly assumed that the systems involved were deterministic. Specifically, input and output were synchronous. Output depended only on commands triggered by input, and input was processed one datum at a time. This does not model real systems, where asynchronous events (inputs and commands) are the rule rather than the exception.
McCullough [672, 673] generalized noninterference to include nondeterministic systems; such systems that meet the noninterference property are said to meet the generalized noninterference-secure property. McCullough also pointed out that noninterference security is more robust than nondeducible security. Minor changes of assumptions can affect whether or not a system is nondeducibly secure. The following example illustrates this point.
EXAMPLE: Consider a system with two levels (High and Low), two users (Holly, who is cleared for High, and Lucy, who is at the Low level), and one text file at the High level. This file has a fixed size, and the special text symbol 
marks those locations that are empty (unused). Holly can edit the file. Lucy can execute a program that does the following (where char_in_file[n] returns the nth character in the file):
while true do begin n := read_integer_from_user; if n > file_length or char_in_file[n] =
This system is not noninterference-secure, because the high-level inputs (the changes that Holly makes to the text file) affect the low-level outputs. However, the system is deducibly secure if Lucy cannot deduce the contents of the file from the program outputs. If the output of the program is meaningful (for example, “This book is interesting”) or can be made meaningful (for example, “Thqs book ir interexting”), then the system is not nondeducibly secure; otherwise, it is. This sensitivity to assumption requires that deducible security be carefully defined in terms of allowed inferences, and that assumptions be made explicit.
Composing systems that meet the generalized noninterference-secure property does not necessarily produce systems that meet this property. McCullough's demonstration [673] provides insight into both the nature of generalized nonrestrictiveness and the characteristics that make it noncomposable.
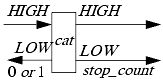
Consider a machine cat, which has two levels, HIGH and LOW, of inputs and outputs. (See Figure 8-3.) Inputs may come from the right or left, and outputs may go to the right or left. The machine accepts HIGH inputs. The HIGH inputs are output on the right, and after some number of inputs, the machine emits two LOW outputs, the first a stop_count output and the second a 0 or a 1, the former if an even number of HIGH inputs and outputs occur, and the latter if an odd number of HIGH inputs and outputs occur.
Cat is noninterference-secure. If there is an even number of HIGH inputs, the output could be 0 (meaning an even number of outputs) or 1 (meaning an odd number of outputs). If there is an odd number of HIGH inputs, the output could be 0 (meaning an odd number of outputs) or 1 (meaning an even number of outputs). So the high-level inputs do not affect the output, as required.
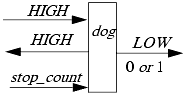
Now define a machine dog to work like cat, with the following changes:
Its HIGH outputs are to the left.
Its LOW outputs of 0 or 1 are to the right.
stop_count is an input from the left, causing dog to emit the 0 or 1.
This machine is summarized in Figure 8-4.
As with cat, dog is noninterference-secure. When stop_count arrives, there may or may not be inputs for which there are not yet corresponding outputs. Hence, the high-level inputs do not affect the low-level output, just as for the machine cat.
Compose these two noninterference-secure machines. (See Figure 8-5.) We require that once an output is transmitted from cat to dog (or vice versa), it arrives. However, the stop_count message may arrive at dog before all input messages have generated corresponding outputs. Suppose cat emits 0 and dog emits 1. Then an even number of HIGH inputs and outputs have occurred on cat, and an odd number on dog. Because every HIGH input on cat is sent to dog, and vice versa, several scenarios arise:
cat has received an odd number of inputs and generated an odd number of outputs, and dog has received an odd number of inputs and generated an even number of outputs. However, because dog has sent an even number of outputs to cat, cat must have had at least one input from the left.
cat has received an odd number of inputs and generated an odd number of outputs, and dog has received an even number of inputs and generated an odd number of outputs. But then an input message from cat has not arrived at dog, which contradicts our assumption.
cat has received an even number of inputs and generated an even number of outputs, and dog has received an even number of inputs and generated an odd number of outputs. However, because dog has sent an odd number of outputs to cat, cat must have had at least one input from the left.
cat has received an even number of inputs and generated an even number of outputs, and dog has received an odd number of inputs and generated an even number of outputs. But then an input message from dog has not arrived at cat, which contradicts our assumption.
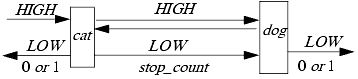
Figure 8-5. The composition machine catdog. Both cat and dog are noninterference-secure, but the composition machine is not.
So, if the composite machine catdog emits a 0 to the left and a 1 to the right, it must have received at least one input from the left. A similar result holds if catdog emits a 1 to the left and a 0 to the right.
It can also be shown (see Exercise 7) that if the outputs from both sides are the same, catdog has received no inputs from the left. Thus, the HIGH inputs affect the LOW outputs, and so the machine catdog is not noninterference-secure.
Zakinthinos and Lee [1069] proved some interesting results related to the composition of noninterference-secure systems. They center their results on the absence of feedback. Intuitively, once information flows from one component to another, no information flows from the second component back to the first.
Definition 8–13. Consider a system with n distinct components. Components ci and cj are connected if any output of ci is an input to cj. If for all ci connected to cj, cj is not connected to any ci, then the system is a feedback-free system.
In other words, for all pairs of components, information can flow in only one direction. Zakinthinos and Lee prove the following theorem.
Theorem 8–3. A feedback-free system composed of noninterference-secure systems is itself noninterference-secure.
Proof. See [1069].
Feedback can be allowed under specific conditions. If at least one low-level input or output occurs before any high-level output is translated into a high-level input, then noninterference is preserved.
Lemma 8–3. A noninterference-secure system can feed a high-level output o to a high-level input i if the arrival of o (at the input of the next component) is delayed until after the next low-level input or output.
Proof. See [1069].
This lemma leads to the following theorem.
Theorem 8–4. A system with feedback as described in Lemma 8–3 and composed of noninterference-secure systems is itself noninterference-secure.
Proof. See [1069].
The problem with the preceding composition is the need for a machine to act the same way whether a low-level input is preceded by a high-level input, a low-level input, or no input. The machine dog does not meet this criterion. If the first message to dog is stop_count, dog emits a 0. If a high-level input precedes stop_count, dog may emit either a 0 or a 1. McCullough used a state model to capture the criteria [673].
Assume a state machine of the type discussed in Section 8.2. Let the machine have two levels, Low and High.
Now consider such a system with the following properties.
For every input ik and state σj there is an element cm ∊ C* such that T*(cm, σj) = σn, where σn ≠ σj.
There exists an equivalence relation ≡ such that:
if the system is in state σi and a high-level sequence of inputs causes a transition from σi to σj, then σi ≡ σj.
if σi ≡ σj and a low-level sequence of inputs i1, …, in causes a system in state σi to transition to state σi', then there is a state σj' such that σi' ≡ σj' and the inputs i1, …, in cause a system in state σj to transition to state σj'.
Let σi ≡ σj. If a high-level sequence of outputs o1, …, on indicates a system in state σi transitioned to state σi', then for some state σj' with σj'≡ σi', a high-level sequence of outputs o1', …, om' indicates a system in state σj transitioned to state σj'.
Let σi ≡ σj, let c and d be high-level output sequences, and let e be a low-level output. If the output sequence ced indicates that a system in state σi transitions to state σi', then there are high-level output sequences c' and d' and a state σj' such that c'ed' indicates that a system in state σj transitions to state σj'.
Property 1 says that T* is a total function and that inputs and commands always move the system to a different state.
Property 2 defines an equivalence relation between two states. The equivalence relation holds if the low-level projections of both states are the same. The first part of this property says that two states are equivalent if either is reachable from the other using only high-level commands. The second part concerns two different states with the same low-level projection. The states resulting from giving the same low-level commands to the two equivalent, original states have the same low-level projections. Taken together, the two parts of property 2 say that if two states are equivalent, high-level commands do not affect the low-level projection of the states (which is, of course, the same). Only low-level commands affect the low-level projections.
Property 3 says that high-level outputs do not indicate changes in the low-level projections of states. Property 4 states that intermingled low-level and high-level outputs cause changes in the low-level state that reflect the low-level outputs only. Assume that two states have the same low-level projection. If there is an output sequence leading from one of these states to a third state, then there is another output sequence leading from the other state to a fourth state, and the third and fourth states have the same low-level projection. Hence, the low-level outputs indicate nothing about the high-level state of the system; only the low-level state is visible, and regardless of the output sequence, the low-level projections of the two results are the same.
Definition 8–14. A system is restrictive if it meets the four properties above.
Intuitively, the problem with composition of generalized noninterference-secure systems is that a high-level output followed by a low-level output may not have the same effect as the low-level input, as we have seen. However, by properties 3 and 4, a restrictive system does not have this problem. Thus, the composition of restrictive systems should be restrictive.
Consider the following composition. Let M1 and M2 be two systems, and let the outputs of M1 be acceptable as inputs to M2. Let μ1i (1 ≤ i ≤ n1) be the states of M1 and let μ2i (1 ≤ i ≤ n2) be the states of M2. The states of the composite machine are pairs of the states of each component. Let e be an event causing a transition. Then e causes the composite machine to change state from (μ1a, μ2a) to (μ1b, μ2b) if any of the following conditions holds.
When M1 is in state μ1a and e occurs, M1 transitions to state μ1b; e is not an event for M2; and μ2a = μ2b.
When M2 is in state μ2a and e occurs, M2 transitions to state μ2b; e is not an event for M1; and μ1a = μ1b.
When M1 is in state μ1a and e occurs, M1 transitions to state μ1b; when M2 is in state μ2a and e occurs, M2 transitions to state μ2b; and e is an input to one machine and an output from the other.
Intuitively, these conditions state that an event causing a transition in the composite system must cause a transition in at least one of the components. Furthermore, if the transition occurs in exactly one of the components, the event must not cause a transition in the other component system when it is not connected to the composite system.
Definition 8–15. (σa, σa) ≡C (σa, σa) if and only if σa ≡ σc and σb ≡ σd.
The equivalence relation ≡C corresponds to the equivalence relation in property 2 for the composite system.
From these, we can show:
Theorem 8–5. The system resulting from the composition of two restrictive systems is itself restrictive.
Proof. See Exercise 8.
Noninterference is an alternative formulation of security policy models. It asserts that a strict separation of subjects requires that all channels, not merely those designed to transmit information, must be closed. The various definitions of noninterference, generalized noninterference, nondeducibility, and restrictiveness are attempts to determine under what conditions different systems with the same security policy can be composed to produce a secure system.
When policies of component systems differ, the issue becomes one of reconciling policies or establishing a systemwide definition of “security” and then demonstrating that the composition meets the definition. The composite system should reflect the principles of security and autonomy. Although establishing whether a particular action is to be allowed is easy, optimizing the checking of accesses is not. Reconciling disparate policies also can be a complex matter, involving technical analysis and politics to determine what the managers of the autonomous components will allow.
Whenever a result is shown to be in NP, approximating the desired result using an approach of polynomial complexity becomes an attractive area of research. How can one approximate the minimum set of accesses that the composite policy must forbid in order to enforce both the principles of autonomy and security?
Models of noninterference, nondeducibility, generalized noninterference, and restrictiveness assume a static protection system, although some basic work on protection systems that change over time has been done for noninterference. How would the composability of these properties, and the results regarding containment of information flow, change if the protection system were dynamic? How does nondeterminism affect these systems? Generalized noninterference deals with nondeterministic systems, but do those results carry into nondeducibility and restrictiveness? What effects would the analogous results have?
Finally, suppose that a system is nondeducibly secure, but there are two possible sets of High actions that correspond to the Low trace. The probability of one set having occurred is 0.99; the probability of the other set having occurred is 0.01. Although the system is nondeducibly secure by the definition (because the Low user cannot determine which of the two possible sets was executed), it is very likely that the first set was executed. This demonstrates that the nondeducible security model does not handle probability; neither do the other models. Incorporating this sense of “probable” is a viable research area.
Security policy composition arises in federated databases [155, 802] and government procurement [741] because of the interconnections among multiple organizations. Rosenthal and Fung [850] discuss the composition of multilevel security policies with differing semantics. Gligor, Gavrila, and Ferraiolo [399] discuss composition policies with a focus on separation of duty.
Studies of information flow include work on all of the models described in this chapter. Graham-Cumming [414] discusses noninterference in the context of CSP to illustrate its use. Allen [16] compares noninterference and nondeducibility using the language CSP. Roscoe, Woodcock, and Wulf [849] develop an approach using process algebra to specify security properties and show how to verify noninterference using it. McLean [684] argues that a trace-based analysis of noninterference offers some advantages over the traditional state-based analysis technique because it allows a more abstract analysis that is valid unless the user interface changes. However, Bevier and Young [92] counter that a state machine model can provide a better link to verification and specification work, and should be pursued.
Johnson and Thayer [524] have developed another definition of security, called “forward correctibility,” that is also composable. It has some advantages over the restrictiveness property. Millen [711] has developed and proved a version of the unwinding theorem for this model.
Gray [420] discusses the application of probability theory to these models. Focardi and Gorrieri [361] agree, pointing out that the issue of nondeterminism is closely related.
The results in this section assert that if components meet certain security requirements, then their composition meets those requirements. The most pessimistic properties of connections are assumed. McDermid and Shi [674] argue that a more realistic approach is to assert that if components meet certain internal security requirements, and their connections meet certain external security requirements, then the entire system is secure.
1: | Draw the lattice described in the first example in Section 8.1.1. |
2: | Prove Lemma 8–2. |
3: | Consider the systems Louie and Dewey in Section 8.2.4.
|
4: | Modify the two-bit system in the first example in Section 8.3 as follows. Whenever a High operation is performed, the High state bit is output. Whenever a Low operation is performed, the Low state bit is output. The initial state is not output (in contrast to the example). Is this version of the two-bit system noninterference-secure with respect to Lucy? Why or why not? |
5: | In the second example in Section 8.3, Lucy sees the output sequence as 011011. Given that she knows the low-level input sequence, list all possible input sequences that match the known low-level input sequence and produce the desired output. |
6: | Prove that a system that meets the definition of generalized noninterference security also meets the definition of deducible security. |
7: | Suppose composite machine catdog (see Section 8.4.1) emits the same value from the left and the right. Show that it has received no inputs from the left. |
8: | Prove Theorem 8–5. |
[1] This differs from Gong and Qian's approach, in which they allow the access unless the composition policy explicitly forbids it, but follows the Principle of Fail-Safe Defaults (see Section 13.2.2).