MARIA: Ay, but you must confine yourselfwithin the modest limits of order. | ||
| --Twelfth Night, I, iii, 8–9. | ||
In 1976, Harrison, Ruzzo, and Ullman [450] proved that in the most general abstract case, the security of computer systems was undecidable and explored some of the limits of this result. In that same year, Jones, Lipton, and Snyder [527] presented a specific system in which security was not only decidable, but decidable in time linear with the size of the system. Minsky [718] suggested a third model to examine what made the general, abstract case undecidable but at least one specific case decidable. Sandhu [870] extended this model to examine the boundary even more closely.
These models explore the most basic question of the art and science of computer security: under what conditions can a generic algorithm determine whether a system is secure? Understanding models and the results derived from them lays the foundations for coping with limits in policy and policy composition as well as applying the theoretical work.
Given a computer system, how can we determine if it is secure? More simply, is there a generic algorithm that allows us to determine whether a computer system is secure? If so, we could simply apply that algorithm to any system; although the algorithm might not tell us where the security problems were, it would tell us whether any existed.
The first question is the definition of “secure.” What policy shall define “secure”? For a general result, the definition should be as broad as possible. We use the access control matrix to express our policy. However, we do not provide any special rights such as copy or own, and the principle of attenuation of privilege does not apply.
Let R be the set of generic (primitive) rights of the system.
Definition 3–1. When a generic right r is added to an element of the access control matrix not already containing r, that right is said to be leaked.
Our policy defines the authorized set of states A to be the set of states in which no command c(x1, ..., xn) can leak r. This means that no generic rights can be added to the matrix.
We do not distinguish between the leaking of rights and an authorized transfer of rights. In our model, there is no authorized transfer of rights. (If we wish to allow such a transfer, we designate the subjects involved as “trusted.” We then eliminate all trusted subjects from the matrix, because the security mechanisms no longer apply to them.)
Let a computer system begin in protection state s0.
Definition 3–2. If a system can never leak the right r, the system (including the initial state s0) is called safe with respect to the right r. If the system can leak the right r (enter an unauthorized state), it is called unsafe with respect to the right r.
We use these terms rather than secure and nonsecure because safety refers to the abstract model and security refers to the actual implementation. Thus, a secure system corresponds to a model safe with respect to all rights, but a model safe with respect to all rights does not ensure a secure system.
Our question (called the safety question) is: Does there exist an algorithm for determining whether a given protection system with initial state s0 is safe with respect to a generic right r?
The simplest case is a system in which the commands are mono-operational (each consisting of a single primitive command). In such a system, the following theorem holds.
Theorem 3–1. [450] There exists an algorithm that will determine whether a given mono-operational protection system with initial state s0 is safe with respect to a generic right r.
Proof. Because all commands are mono-operational, we can identify each command by the type of primitive operation it invokes. Consider the minimal sequence of commands c1, ..., ck needed to leak the right r from the system with initial state s0.
Because no commands can test for the absence of rights in an access control matrix entry, we can omit the delete and destroy commands from the analysis. They do not affect the ability of a right to leak.
Now suppose that multiple create commands occurred during the sequence of commands, causing a leak. Subsequent commands check only for the presence of rights in an access control matrix element. They distinguish between different elements only by the presence (or lack of presence) of a particular right. Suppose that two subjects s1 and s2 are created and the rights in A[s1, o1] and A[s2, o2] are tested. The same test for A[s1, o1] and A[s1, o2] = A[s1, o2] ∪ A[s2, o2] will produce the same result. Hence, all creates are unnecessary except possibly the first (and that only if there are no subjects initially), and any commands entering rights into the new subjects are rewritten to enter the new right into the lone created subject. Similarly, any tests for the presence of rights in the new subjects are rewritten to test for the presence of that right in an existing subject (or, if none initially, the first subject created).
Let |S0| be the number of subjects and |O0| the number of objects in the initial state. Let n be the number of generic rights. Then, in the worst case, one new subject must be created (one command), and the sequence of commands will enter every right into every element of the access control matrix. After the creation, there are |S0| + 1 subjects and |O0| + 1 objects, and (|S0| + 1)(|O0| + 1) elements. Because there are n generic rights, this leads to n(|S0| + 1)(|O0| + 1) commands. Hence, k ≤ n(|S0| + 1)(|O0| + 1) + 1.
By enumerating all possible states we can determine whether the system is safe. Clearly, this may be computationally infeasible, especially if many subjects, objects, and rights are involved, but it is computable. (See Exercise 2.) Unfortunately, this result does not generalize to all protection systems.
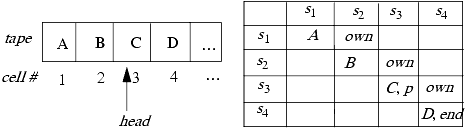
Before proving this, let us review the notation for a Turing machine. A Turing machine T consists of a head and an infinite tape divided into cells numbered 1, 2, ..., from left to right. The machine also has a finite set of states K and a finite set of tape symbols M. The distinguished symbol b ∊ M is a blank and appears on all the cells of the tape at the start of all computations; also, at that time T is in the initial state q0.
The tape head occupies one square of the tape, and can read and write symbols on that cell of the tape, and can move into the cell to the left or right of the cell it currently occupies. The function δ: K × M → K × M × {L, R} describes the action of T. For example, let p, q ∊ K and A, B ∊ M. Then, if δ(p, A) = (q, B, R), when T is in state p and the head rests on a cell with symbol A, the tape head changes the symbol in the cell to B, moves right to the next cell (that is, if the head is in cell i, it moves to cell i + 1), and the Turing machine enters state q. If δ(p, A) = (q, B, L), then the actions would be the same except the head would move to the left unless it were already in the leftmost square (because the head may never move off the tape).
Let the final state be qf; if T enters this state, it halts. The halting problem is to determine whether an arbitrary Turing machine will enter the state qf;, and is known to be undecidable [329].
Given this, we can now present the following theorem.
Theorem 3–2. [450] It is undecidable whether a given state of a given protection system is safe for a given generic right.
Proof. Proof by contradiction. We show that an arbitrary Turing machine can be reduced to the safety problem, with the Turing machine entering a final state corresponding to the leaking of a given generic right. Then, if the safety problem is decidable, we can determine when the Turing machine halts, showing that the halting problem is decidable, which (as we said above) is false.
First, we construct a map from the states and symbols of T to rights in the access control matrix model. Let the set of generic rights be the symbols in M and a set of distinct symbols each representing an element in K; in other words, the set of tape symbols and states are represented by generic rights, one right for each symbol and one for each state.
The cells of the Turing machine tape are sequentially ordered. We consider only the cells that the head has visited, so suppose T has scanned cells 1, 2, ..., n. To simulate this, we represent each cell as a subject and define a distinguished right called own such that si owns si+1 for 1 ≤ i < k. If cell i contains the symbol A, then subject si has A rights over itself. Furthermore, the subject sk, which corresponds to the rightmost cell visited, has end rights over itself; notice that sk+1 has not been created in this case. Finally, if the head is in cell j and T is in state p, then subject sj has p rights over itself also. (To keep the meanings of the rights unambiguous, we require the rights corresponding to the symbols for the tape to be distinct from the rights corresponding to the states.) Figure 3-1 shows an example of this mapping, when the head has visited four cells.
Next, we must translate the Turing machine function δ into access control matrix commands. Suppose that δ(p, A) = (q, B, L) and the head is not in the leftmost cell. Then, in terms of the access control matrix, the rights A and p must be replaced by B in the entry a[si, si] and the right q must be added to a[si–1, si–1]. The following access control matrix command, in which si represents the subject corresponding to the current cell, captures this.
command cp, A(si, si–1) if own in a[si–1, si] and p in a[si, si] and A in a[si, si] then delete p from a[si, si]; delete A from a[si, si]; enter B into a[si, si]; enter q into a[si–1, si–1];end
If the head is in the leftmost cell of the tape, both si and si–1 are s1.
Now consider motion to the right, such as δ(p, A) = (q, B, R). If the head is not in the rightmost cell k, by the same reasoning as for the left motion, we have
command cp, A(si, si+1) if own in a[si, si+1] and p in a[si, si] and A in a[si, si] then delete p from a[si, si]; delete A from a[si, si]; enter B into a[si, si]; enter q into a[si+1, si+1];end
However, if the head is in the rightmost cell k, the command must create a new subject sk+1. Then, to maintain the consistency of the access control matrix, sk is given own rights over the new subject sk+1 and end rights over itself, and sk's end rights over itself must be removed. At that point, the problem is reduced to the problem of regular right motion. So:
command crightmostp, A(sk, sk+1) if end in a[si, si+1] and p in a[si, si] and A in a[si, si] then delete end from a[sk, sk]; create new subject sk+1; enter own into a[sk, sk+1]; enter end from a[sk+1, sk+1]; delete p from a[si, si]; delete A from a[si, si]; enter B into a[si, si]; enter q into a[si+1, si+1];end
Clearly, only one right in any of the access control matrices corresponds to a state, and there will be exactly one end right in the matrix (by the nature of the commands simulating Turing machine actions). Hence, in each configuration of the Turing machine, there is at most one applicable command. Thus, the protection system exactly simulates the Turing machine, given the representation above. Now, if the Turing machine enters state qf, then the protection system has leaked the right qf; otherwise, the protection system is safe for the generic right qf. But whether the Turing machine will enter the (halting) state qf is undecidable, so whether the protection system is safe must be undecidable also.
However, we can generate a list of all unsafe systems.
Theorem 3–3. [269] The set of unsafe systems is recursively enumerable.
Proof. See Exercise 3.
Assume that the create primitive is disallowed. Clearly, the safety question is decidable (simply enumerate all possible sequences of commands from the given state; as no new subjects or objects are created, at some point no new rights can be added to any element of the access control matrix, so if the leak has not yet occurred, it cannot occur). Hence, we have the following theorem.
Theorem 3–4. [450] For protection systems without the create primitives, the question of safety is complete in P-SPACE.
Proof. Consider a Turing machine bounded in polynomial space. A construction similar to that of Theorem 3–2 reduces that Turing machine in polynomial time to an access control matrix whose size is polynomial in the length of the Turing machine input.
If deleting the create primitives makes the safety question decidable, would deleting the delete and destroy primitives but not the create primitive also make the safety question decidable? Such systems are called monotonic because they only increase in size and complexity; they cannot decrease. But:
Theorem 3–5. [451] It is undecidable whether a given configuration of a given monotonic protection system is safe for a given generic right.
Restricting the number of conditions in the commands to two does not help:
Theorem 3–6. [451] The safety question for biconditional monotonic protection systems is undecidable.
But if at most one condition per command is allowed:
Theorem 3–7. [451] The safety question for monoconditional monotonic protection systems is decidable.
This can be made somewhat stronger:
Theorem 3–8. [451] The safety question for monoconditional protection systems with create, enter, and delete primitives (but no destroy primitive) is decidable.
Thus, the safety question is undecidable for generic protection models but is decidable if the protection system is restricted in some way. Two questions arise. First, given a particular system with specific rules for transformation, can we show that the safety question is decidable? Second, what are the weakest restrictions on a protection system that will make the safety question decidable in that system?
Can the safety of a particular system, with specific rules, be established (or disproved)? The answer, not surprisingly, is yes. Such a system is the Take-Grant Protection Model.
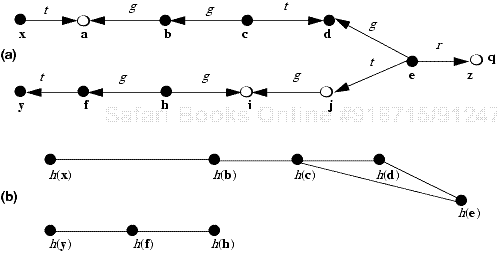
The Take-Grant Protection Model represents a system as a directed graph. Vertices are either subjects (represented by 
) or objects (represented by ○). Vertices that may be either subjects or objects are represented by ⊗. Edges are labeled, and the label indicates the rights that the source vertex has over the destination vertex. Rights are elements of a predefined set R; R contains two distinguished rights: t (for take) and g (for grant).
As the protection state of the system changes, so does the graph. The protection state (and therefore the graph) changes according to four graph rewriting rules:
Take rule: Let x, y, and z be three distinct vertices in a protection graph G0, and let x be a subject. Let there be an edge from x to z labeled γ with t ∊ γ, an edge from z to y labeled β, and α ⊆ β. Then the take rule defines a new graph G1 by adding an edge to the protection graph from x to y labeled α. Graphically,
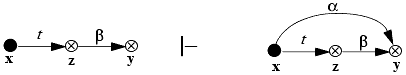
The rule is written “x takes (α to y) from z.”
Grant rule: Let x, y, and z be three distinct vertices in a protection graph G0, and let z be a subject. Let there be an edge from z to x labeled γ with g ∊ γ, an edge from z to y labeled β, and α ⊆ β. Then the grant rule defines a new graph G1 by adding an edge to the protection graph from x to y labeled α. Graphically,
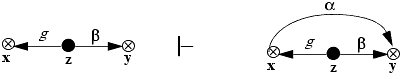
The rule is written “z grants (α to y) to x.”
Create rule: Let x be any subject in a protection graph G0 and let α ⊆ R. Then create defines a new graph G1 by adding a new vertex y to the graph and an edge from x to y labeled α. Graphically,
The rule is written “x creates (α to new vertex) y.”
Remove rule: Let x and y be any distinct vertices in a protection graph G1 such that x is a subject. Let there be an explicit edge from x to y labeled β, and let α ⊆ β. Then remove defines a new graph G1 by deleting the α labels from β. If β becomes empty as a result, the edge itself is deleted. Graphically,
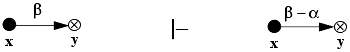
The rule is written “x removes (α to) y.”
Because these rules alter the state of the protection graph, they are called de jure (“by law” or “by right”) rules.
We demonstrate that one configuration of a protection graph can be derived from another by applying the four rules above in succession. The symbol |– means that the graph following it is produced by the action of a graph rewriting rule on the graph preceding it; and the symbol |–* represents a finite number of successive rule applications. Such a sequence of graph rewriting rules is called a witness. A witness is often demonstrated by listing the graph rewriting rules that make up the witness (usually with pictures).
We first wish to determine if a given right α can be shared—that is, given a protection graph G0, can a vertex x obtain α rights over another vertex y? More formally:
Definition 3–3. The predicate can•share(α, x, y, G0) is true for a set of rights α and two vertices x and y if and only if there exists a sequence of protection graphs G1, …, Gn such that G0 |–*Gn using only de jure rules and in Gn there is an edge from x to y labeled α.
To establish the conditions under which this predicate will hold, we must define a few terms.
Definition 3–4. A tg-path is a nonempty sequence v0, …, vn of distinct vertices such that for all i, 0 ≤ i < n, vi is connected to vi+1 by an edge (in either direction) with a label containing t or g.
Definition 3–5. Vertices are tg-connected if there is a tg-path between them.
We can now prove that any two subjects with a tg-path of length 1 can share rights. Four such paths are possible. The take and grant rules in the preceding section account for two of them. Lemmata 3–1 and 3–2 cover the other two cases.
Lemma 3–1.
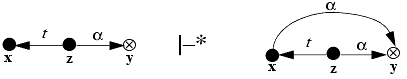
Proof. x creates (tg to new vertex) v.
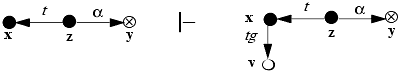
z takes (g to v) from x.
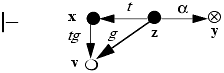
z grants (α to y) to v.
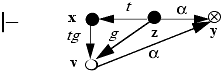
x takes (α to y) from v.
This sequence of rule applications adds an edge labeled α from x to y. A similar proof establishes the following lemma.
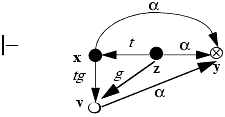
Lemma 3–2.
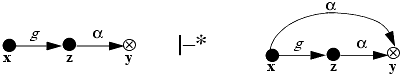
Thus, the take and grant rules are symmetric if the vertices on the tg-path between x and y are subjects. This leads us to the following definition.
Definition 3–6. An island is a maximal tg-connected subject-only subgraph.
Because an island is a maximal tg-only subgraph, a straightforward inductive proof shows that any right possessed by any vertex in the island can be shared with any other vertex in the island.
Transferring rights between islands requires that a subject in one island be able to take the right from a vertex in the other island or that a subject be able to grant the right to an intermediate object from which another subject in the second island may take the right. This observation, coupled with the symmetry of take and grant, leads to a characterization of paths between islands along which rights can be transferred. To express it succinctly, we use the following notation. With each tg-path, associate one or more words over the alphabet in the obvious way. If the {
,
,
,
} path has length 0, then the associated word is the null word ν. notation t* means zero or more occurrences of the character t, so, for example, t*g represents the sequence g, tg, ttg, ....
Definition 3–7. A bridge is a tg-path with endpoints v0 and vn both subjects and the path's associated word in {
,
,
,
}.
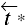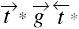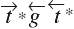The endpoints of a bridge are both subjects, so the right can be transferred from one endpoint of the bridge to the other.
Given this definition, and that every subject vertex is contained in an island (consisting of only that subject vertex, perhaps), we have established conditions under which rights can be shared between subjects in a protection graph.
Theorem 3–9. [641] The predicate subject•can•share(α, x, y, G0) is true if and only if x and y are both subjects and there is an edge from x to y in G0 labeled α, or if the following hold simultaneously:
There is a subject s ∊ G0 with an s-to-y edge labeled α;
There exist islands I1, …, In such that x is in I1, s is in In, and there is a bridge from Ij to Ij+1 (1 ≤ j < n).
Objects complicate this result. Because subjects can act but objects cannot, the transfer may begin with a right possessed by an object and conclude with that right being given to another object. The following two definitions help.
Definition 3–8. A vertex x initially spans to y if x is a subject and there is a tg-path between x and y with an associated word in {
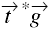} ∪ { ν }.In other words, x initially spans to y if x can grant a right it possesses to y.
Definition 3–9. A vertex x terminally spans to y if x is a subject and there is a tg-path between x and y with an associated word in {
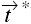} ∪ { ν }.
In other words, x terminally spans to y if x can take any right that y possesses. Note that these two definitions imply that t and g are not symmetric if either the source or destination vertex of the edge labeled t or g is an object.
We can now state and prove necessary and sufficient conditions for rights to be transferred from a vertex y to another vertex x.
Theorem 3–10. [527] The predicate can•share(α, x, y, G0) is true if and only if there is an edge from x to y in G0 labeled α, or if the following hold simultaneously:
There is a vertex s ∊ G0 with an s-to-y edge labeled α.
There exists a subject vertex x' such that x' = x or x' initially spans to x.
There exists a subject vertex s' such that s' = s or s' terminally spans to s.
There exist islands I1, …, In such that x' ∊ I1, s' ∊ In, and there is a bridge from Ij to Ij+1 (1 ≤ j < n).
The idea behind this theorem is simple. Because s' terminally spans to s, s' can acquire α rights to y. Given the definition of island, all subjects in In can acquire those rights. They can be passed along the bridge to a subject in In–1, which means that any subject in In–1 can acquire those same rights. This continues until x' ∊ I1 acquires those rights. Then, as x' initially spans to x, x' can pass the rights to x. Exercise 5 explores a possible alternative representation of this result.
Corollary 3–1. [527] There is an algorithm of complexity O(|V| + |E|) that tests the predicate can•share, where V is the set of vertices and E the set of edges, in G0.
A model abstracts essential details from a situation to aid in its analysis. For example, the question: “Can my competitor access my files?” presumes a knowledge of the rules for sharing files on the computer system (or network). The model must correctly capture these rules to be applicable.
The beauty of the access control matrix model is its malleability; by choosing rights and rules appropriately, an analyst can use it to capture the essence of any situation. The Take-Grant Protection Model presents specific rules and distinguished rights and so can be applied only in specific situations.
The protection state of a system evolves as rules are applied to entities within the system. The question of what states can evolve is thus of interest, because that set of states defines what protection states the (real) system may assume. So, consider the set of states of a particular system that the Take-Grant Protection Model rules can generate. For simplicity, we consider those states arising from a single entity, which (by the Take-Grant rules above) must be a subject.
Theorem 3–11. [942] Let G0 be a protection graph containing exactly one subject vertex and no edges, and let R be a set of rights. Then G0 |–* G if and only if G is a finite directed acyclic graph containing subjects and objects only, with edges labeled from nonempty subsets of R and with at least one subject having no incoming edges.
Proof. (⇒). By construction. Assume that G meets the requirements above. Let x1, …, xn be the set of subjects in G, and without loss of generality let x1 have no incoming edges. Identify v with x1. The graph G' can be constructed from v using the Take-Grant Protection Model rules, as follows:
Perform “v creates (α ∪ { g } to) new xi” for all xi, 2 ≤ i ≤ n, where α is the union of all labels on the edges going into xi in G.
For all pairs of vertices xi and xj in G with xi having α rights over xj, perform “v grants (α to xj) to xi.”
Let β be the set of rights labeling the edge from xi and xj in G (note that β may be empty). Perform “v removes ((α ∪ { g }) – β to) xj.”
The resulting graph G' is the desired graph G.
(⇐). Let v be the initial subject, and let G0 |–* G. By inspection of the rules, G is finite, loop-free, and a directed graph; furthermore, it consists of subjects and objects only, and all edges are labeled with nonempty subsets of R.
Because no rule allows the deletion of vertices, v is in G. Because no rule allows an incoming edge to be added to a vertex without any incoming edges, and v has no incoming edges, it cannot be assigned any.
Corollary 3–2. [944] A k-component, n-edge protection graph can be constructed from t-rule applications, where 2(k – 1) + n ≤ t ≤ 2(k – 1) + 3n.
Using the Take-Grant Protection Model, Snyder [943] showed how some common protection problems could be solved. For example, suppose two processes p and q communicate through a shared buffer b controlled by a trusted entity s (for example, an operating system). The configuration in Figure 3-2a shows the initial protection state of the system. Because s is a trusted entity, the assumption that it has g rights over p and q is reasonable. To create b, and to allow p and q to communicate through it, s does the following:
s creates ({r, w} to new object) b.
s grants ({r, w} to b) to p.
s grants ({r, w} to b) to q.
Figure 3-2. (a) The initial state of the system: s, a trusted entity, can grant rights to untrusted processes p and q. Each process p and q controls its own private information (here represented by files u and v). (b) The trusted entity has created a buffer b shared by the untrusted processes.
This creates the configuration in Figure 3-2(b). The communication channel is two-way; if it is to be one-way, the sender would have write rights and the receiver would have read rights. This configuration also captures the ability of the trusted entity to monitor the communication channel or interfere with it (by altering or creating messages)—a point we will explore in later sections.
The proof of the conditions necessary and sufficient for can•share requires that all subjects involved in the witness cooperate. This is unrealistic. If Professor Olson does not want any students to read her grade file, the notion of “sharing” fails to capture the unwillingness to grant access. This leads to a notion of stealing, in which no owner of any right over an object grants that right to another.
Definition 3–10. Let G0 be a protection graph, let x and y be distinct vertices in G0, and let α be a subset of a set of rights R. The predicate can•steal(α, x, y, G0) is true when there is no edge from x to y labeled α in G0 and there exists a sequence of protection graphs G1, …, Gn for which the following hold simultaneously:
There is an edge from x to y labeled α in Gn.
There is a sequence of rule applications ρ1, ..., ρn such that Gi–1 |– Gi using ρi.
For all vertices v and w in Gi–1, 1 ≤ i < n, if there is an edge from v to y in G0 labeled α, then ρi is not of the form “v grants (α to y) to w.”
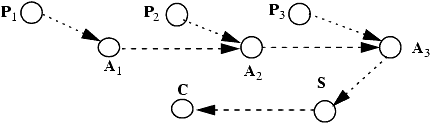
This definition disallows owners of α rights to y from transferring those rights. It does not disallow those owners from transferring other rights. Consider Figure 3-3. The given witness exhibits can•steal(α, s, w, G0). In step (1), the owner of α rights to w grants other rights (specifically, t rights to v) to a different subject, s. Without this step, the theft cannot occur. The definition only forbids grants of the rights to be stolen. Other rights may be granted. One justification for this formulation is the ability of attackers to trick others into surrendering rights. While the owner of the target right would be unlikely to grant that right, the owner might grant other rights. This models the Trojan horse (see Section 22.2), in which the owner of the rights is unaware she is giving them away.
Figure 3-3. A witness to theft in which the owner, u, of the stolen right, α, grants other rights to another subject (t rights to v are granted to s).
Making the target of the theft a subject complicates this situation. According to Definition 3–10, the target may give away any rights as well. In this case, the owner is acting as a moderator between the target and the source and must restrain the transfer of the right through it. This models the case of mandatory access controls.
Theorem 3–12. [944] The predicate can•steal(α, x, y, G0) is true if and only if the following hold simultaneously:
There is no edge from x to y labeled α in G0.
There exists a subject vertex x' such that x' = x or x' initially spans to x.
There exists a vertex s with an edge labeled α to y in G0 and for which can•share(t, x, s, G0) holds.
Proof. (⇒). Assume that the three conditions above hold. If x is a subject, then x need merely obtain t rights to s and then use the take rule to obtain α rights to y. By definition, this satisfies can•steal(α, x, y, G0).
Suppose x is an object. Then Theorem 3–10, can•share(t, x, s, G0), implies that there exists a subject vertex x' that tg-initially spans to x and for which the predicate can•share(t, x', s, G0) is true. Without loss of generality, assume that the tg-initial span is of length 1 and that x' has t rights over s in G0. If x' does not have an edge labeled α to y in G0, then x' takes α rights to y and grants those rights to x, satisfying the definition. If x' has an edge labeled α to y in G0, then x' will create a “surrogate” to which it can give take rights to s:
x' creates (g to new subject) x".
x' grants (t to s) to x".
x' grants (g to x) to x".
Now x" has t rights over s and g rights over x, so the rule applications
x" takes (α to y) from s.
x" grants (α to y) to x.
satisfy the definition. Hence, can•steal(α, x, y, G0) holds if the three conditions in the theorem hold.
(⇐): Assume that can•steal(α, x, y, G0) holds. Then condition (a) of the theorem holds directly from Definition 3–10.
Condition (a) of Definition 3–10 implies can•share(α, x, y, G0). From condition (b) of Theorem 3–10, we immediately obtain condition (b) of this theorem.
Condition (a) of Theorem 3–10 ensures that the vertex s in condition (c) of this theorem exists.
We must show that can•share(t, x, s, G0) holds. Let ρ be a sequence of rule applications. Consider the minimal length sequence of rule applications deriving Gn from G0. Let i be the least index such that Gi–1 |–ρi Gi and such that there is an edge labeled α from some vertex p to y in Gi but not in Gi–1. Then Gi is the first graph in which an edge labeled α to y is added.
Obviously, ρi is not a remove rule. It cannot be a create rule, because y already existed. By condition (c) of Definition 3–10, and the choice of i ensuring that all vertices with α rights to y in Gi are also in G0, ρi cannot be a grant rule. Hence, ρi must be a take rule of the form
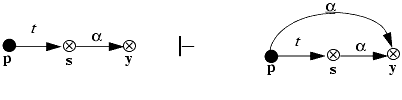
for some vertex s in G0. From this, can•share(t, p, s, G0) holds. By condition (c) of Theorem 3–10, there is a subject s' such that s' = s or s' terminally spans to s, and by condition (d), there exists a sequence of islands I1, …, In such that x' ∊ I1 and s' ∊ In.
If s is an object (and thus s' ≠ s), consider two cases. If s' and p are in the same island, then take p = s'. If they are in different islands, the derivation cannot be of minimal length; choose s' in the same island to exhibit a shorter one. From this, the conditions of Theorem 3–10 have been met, and can•share(t, x, s, G0) holds.
If s is a subject (s' = s), then p ∊ In, and we must show that p ∊ G0 for Theorem 3–10 to hold. If p ∉ G0, then there is a subject q in one of the islands such that can•share(t, q, s, G0) holds. (To see this, note that s ∊ G0 and that none of the de jure rules add new labels to incoming edges on existing vertices.) Because s is an owner of α rights to y in G0, we must derive a witness for this sharing in which s does not grant (α to q). If s and q are distinct, replace each rule application of the form
s grants (α to y) to q
with the sequence
p takes (α to y) from s
p takes (g to q) from s
p grants (α to y) to q
thereby transferring the right (α to y) to q without s granting. If s = q, then the first rule application in this sequence suffices.
Hence, there exists a witness to can•share(t, q, s, G0) in which s does not grant (α to y). This completes the proof.
The notion of theft introduced the issue of cooperation: which subjects are actors in a transfer of rights, and which are not? This raises the issue of the number of actors necessary to transfer a right. More formally, what is the minimum number of actors required to witness a given predicate can•share(α, x, y, G0)?
Consider a subject vertex y. Then y can share rights from any vertex to which it terminally spans and can pass those rights to any vertex to which it initially spans.
Definition 3–11. The access set A(y) with focus y is the set of vertices y, all vertices x to which y initially spans, and all vertices x' to which y terminally spans.
Of course, a focus must be a subject.
Consider two access sets with different foci y and y' that have a vertex z in common. If z ∊ A(y) because y initially spans to z, and z ∊ A(y') because y' initially spans to z, by the definition of initial span, no rights can be transferred between y and y' through z. A similar result holds if both y and y' terminally span to z. However, if one focus initially spans to z and the other terminally spans to z, rights can be transferred through z. Because we care about the transfer of rights, we identify a set of vertices that can be removed from the graph without affecting transfers:
Definition 3–12. The deletion set δ(y, y') contains all vertices z in the set A(y) ∩ A(y') for which (a) y initially spans to z and y' terminally spans to z, (b) y terminally spans to z and y' initially spans to z, (c) z = y, and (d) z = y'.
Given the deletion set, we construct an undirected graph, called the conspiracy graph and represented by H, from G0:
For each subject vertex x in G0, there is a corresponding vertex h(x) in H with the same label.
If δ(y, y') ≠ Ø in G0, there is a line between h(y) and h(y') in H.
The conspiracy graph represents the paths along which subjects can transfer rights. The paths are unidirectional because the rights can be transmitted in either direction. Furthermore, each vertex in H represents an access set focus in G0.
EXAMPLE: In Figure 3-4, the access sets are
A(x) = { x, a } | A(e) = { e, d, i, j } |
A(b) = { b, a } | A(y) = { y } |
A(c) = { c, b, d } | A(f) = { f, y } |
A(d) = { d } | A(h) = { h, f, i } |
The vertex z is not in A(e) because the path from e to z is neither a terminal nor an initial span. For the same reason, the vertex y is not in A(h). Using these sets gives the following nonempty deletion sets:
δ(x, b) = { a } | δ(c, d) = { d } | δ(y, f) = { y } |
δ(b, c) = { b } | δ(c, e) = { d } | δ(h, f) = { f } |
δ(d, e) = { d } |
Although A(e) ∩ A(h) = { i }, the vertex i is in A(e) because e initially spans to i, and i is in A(h) because h initially spans to i. Hence, δ(e, h) = Ø and there is no edge between h(e) and h(h) in G0.
The conspiracy graph exhibits the paths along which rights can be transmitted. Let the set I(p) contain the vertex h(p) and the set of all vertices h(p') such that p' initially spans to p; let the set T(q) contain the vertex h(q) and the set of all vertices h(q') such that q' terminally spans to q. Then:
Theorem 3–13. [944] can•share(α, x, y, G0) is true if and only if there is a path from some h(p) ∊ I(x) to some h(q) ∊ T(y).
Furthermore:
Theorem 3–14. [944] Let L be the number of vertices on a shortest path between h(p) and h(q), with p and q as in Theorem 3–13. Then L conspirators are necessary and sufficient to produce a witness to can•share(α, x, y, G0).
The Take-Grant Protection Model is a counterpoint to the Harrison-Ruzzo-Ullman (HRU) result. It demonstrates that, for a specific system, the safety question is not only decidable but decidable in linear time with respect to the size of the graph. It also explores ancillary issues such as theft and conspiracy.
Given that in specific systems we can answer the safety question, why can't we answer it about generic systems? What is it about the Harrison-Ruzzo-Ullman (HRU) model that makes the safety question undecidable? What characteristics distinguish a model in which the safety question is decidable from a model in which the safety question is not decidable? A series of elegant papers have explored this issue.
The first paper introduced a model called the Schematic Send-Receive (SSR) Protection Model [869]. The Schematic Protection Model (SPM) [870] generalizes these results.
The key notion of the Schematic Protection Model, also called the SPM, is the protection type. This is a label for an entity that determines how control rights affect that entity. For example, if the Take-Grant Protection Model is viewed as an instance of a scheme under the SPM, the protection types are subject and object because the control rights take, grant, create, and remove affect subject entities differently than they do object entities. Moreover, under SPM, the protection type of an entity is set when the entity is created, and cannot change thereafter.
In SPM, a ticket is a description of a single right. An entity has a set of tickets (called a domain) that describe what rights it has over another entity. A ticket consists of an entity name and a right symbol; for example, the ticket X/r allows the possessor of the ticket to apply the right r to the entity X. Although a ticket may contain only one right, if an entity has multiple tickets X/r, X/s, and X/t, we abbreviate them by writing X/rst.
Rights are partitioned into a set of inert rights (RI) or control rights (RC). Applying an inert right does not alter the protection state of the system. For example, reading a file does not modify which entities have access to the document, so read is an inert right. But in the Take-Grant Protection Model, applying the take rule does change the protection state of the system (it gives a subject a new right over an object). Hence, the take right is a control right. SPM ignores the effect of applying inert rights, but not the effect of applying control rights.
The attribute c is a copy flag; every right r has an associated copyable right rc. A ticket with the copy flag can be copied to another domain. The notation r:c means r or rc, with the understanding that all occurrences of r:c are read as r or all are read as rc.
We partition the set of types T into a subject set TS and an object set TO. The type of an entity X is written τ(X). The type of a ticket X/r:c is τ(X/r:c), which is the same as τ(X)/r:c. More formally, let E be the set of entities; then τ:E→T and τ:Ε × R→T × R.
The manipulation of rights is controlled by two relationships: a link predicate and a filter function. Intuitively, the link predicate determines whether the source and target of the transfer are “connected” (in a mathematical sense), and the filter function determines whether the transfer is authorized.
A link predicate is a relation between two subjects. It is local in the sense that its evaluation depends only on the tickets that the two subjects possess. Formally:
Definition 3–13. Let dom(X) be the set of tickets that X possesses. A link predicate linki(X, Y) is a conjunction or disjunction (but not a negation) of the following terms, for any right z ∊ RC.
X/z ∊ dom(X)
X/z ∊ dom(Y)
Y/z ∊ dom(X)
Y/z ∊ dom(Y)
true
A finite set of link predicates { linki | i = 1, …, n } is called a scheme. If only one link predicate is defined, we omit the subscript i.
The filter functions impose conditions on when transfer of tickets can occur. Specifically, a filter function is a function fi: TS × TS→2T×R that has as its range the set of copyable tickets. For a copy to occur, the ticket to be copied must be in the range of the appropriate filter function.
Combining this requirement with the others, a ticket X/r:c can be copied from dom(Y) to dom(Z) if and only if, for some i, the following are true:
X/rc ∊ dom(Y)
linki(Y, Z)
τ(Y)/r:c ∊ fi(τ(Y), τ(Z))
One filter function is defined for each link predicate. As with the link predicates, if there is only one filter function, we omit the subscripts.
Let us take stock of these terms by considering two examples: an owner-based policy and the Take-Grant Protection Model.
In an owner-based policy, a subject U can authorize another subject V to access an object F if and only if U owns F. Here, the set of subjects is the set of users and the set of objects is the set of files. View these as types. Then:
TS = { user }, TO = { file }
In this model, ownership is best viewed as copy attributes—that is, if U owns F, all its tickets for F are copyable. Under this interpretation, the set of control rights is empty because no rights are required to alter the state of the protection graph. All rights are inert. For our example, assume that the r (read), w (write), a (append), and x (execute) rights are defined. Then:
RC = Ø, RI = { r:c, w:c, a:c, x:c }
Because the owner can give the right to any other subject, there is a connection between each pair of subjects and the link predicate is always true:
link(U, V) = true
Finally, tickets can be copied across these connections:
f(user, user) = { file/r, file/w, file/a, file/x }
The Take-Grant Protection Model can be formulated as an instance of SPM. The set of subjects and objects in the Take-Grant model corresponds to the set of subjects and objects in SPM:
TS = { subject }, TO = { object }
The control rights are t (take) and g (grant), because applying them changes the protection state of the graph. All other rights are inert; for our example, we will take them to be r (read) and w (write). All rights can be copied (in fact, the Take-Grant Protection Model implicitly assumes this), so:
RC = { tc, gc }, RI = { rc, wc }
Rights can be transferred along edges labeled t or g, meaning that one vertex on the edge has take or grant rights over the other. Let p and q be subjects. Then the link predicate is
link(p, q) = p/t ∊ dom(q) ∨ q/g ∊ dom(p)
Finally, any right can be transferred, so the filter function is simply
f(subject, subject) = { subject, object } × { tc, gc, rc, wc }
We now explore how the transfer of tickets occurs in SPM.
The demand function d:TS→2T×R authorizes a subject to demand a right from another entity. Let a and b be types. Then a/r:c ∊ d(b) means that every subject of type b can demand a ticket X/r:c for all X such that τ(X) = a. This is a generalization of the take rule in the Take-Grant model. The take rule refers to an individual subject. The demand rule refers to all subjects of a particular type (here, of type b).
Sandhu [871] has demonstrated that a sophisticated construction eliminates the need for the demand operation. Thus, although the demand rule is present in SPM, that rule is omitted from the models that followed SPM.
Creating a new entity requires handling of not only the type of the new entity but also the tickets added by the creation. The type of the new entity is specified by the relation can-create (cc): cc ⊆ TS × T; a subject of type a can create entities of type b if and only if cc(a, b) holds.
In practice, the rule of acyclic creates limits the membership in this relation. Represent the types as vertices, and let a directed edge go from a to b if cc(a, b). The relation cc is acyclic if this graph has no loops except possibly edges from one vertex to itself. Figure 3-5 gives an example of both cyclic and acyclic can-create relations. The rationale for this rule is to eliminate recursion in cc; if a subject of type a can create a subject of type b, none of the descendents of the subject can create a subject of type a. This simplifies the analysis without unduly limiting the applicability of the model.
Figure 3-5. The rule of acyclic creates. (a) The can-create relation cc = { (a, b), (b, c), (b, d), (d, c) }. Because there are no cycles in the graph, cc satisfies the rule of acyclic creates. (b) Same as (a), except that the can-create relation is cc' = cc ∪ { (c, a) }, which induces a cycle; hence, cc' does not follow the rule of acyclic creates.
Let A be a subject of type a = τ(A) and let B be an entity of type b = τ(B). The create-rule cr(a, b) specifies the tickets introduced when a subject of type a creates an entity of type b.
If B is an object, the rule specifies the tickets for B to be placed in dom(A) as a result of the creation. Only inert tickets can be created, so cr(a, b) ⊆ { b/r:c ∊ RI }, and A gets B/r:c if and only if b/r:c ∊ cr(a, b).
If B is a subject, the rule also specifies that the tickets for A be placed in dom(B) as a result of the creation. Assume that types a and b are distinct. Let crp (a, b) be the set of tickets the creation adds to dom(A), and let crc(a, b) be the set of tickets the creation adds to dom(B). Then A gets the ticket A/r:c if a/r:c ∊ crp(a, b) and B gets the ticket A/r:c if a/r:c ∊ crc(a, b). We write cr(a, b) = { a/r:c, b/r:c | r:c ∊ R }. If the types a and b are not distinct, then do the types refer to the creator or the created? To avoid this ambiguity, if a = b, we define self/r:c to be tickets for the creator and a/r:c to be tickets for the created, and we say that cr(a, a) = { a/r:c, self/r:c | r:c ∊ R }. crp(a, b) and crc(a, b) are subsets of cr(a, a), as before.
Recall that the principle of attenuation of privilege (see Section 2.4.3) states that no entity may have more rights than its creator. The attenuating create-rule captures this notion:
Definition 3–14. A create-rule cr(a, a) = crp(a, b)|crc(a, b) is attenuating if:
crc(a, b) ⊆ crp(a, b) and
a/r:c ∊ crp(a, b) ⇒ self/r:c ∊ crp(a, b).
A scheme is attenuating if, for all types a such that cc(a, a), then cr(a, a) is attenuating.
If the graph for cc is constructed as above and has no loops, the scheme is attenuating.
EXAMPLE: The can-create relation for the owner-based policy says that users can create files; hence, cc(user) = { file }. The creator of the file can give itself any inert rights over the file; hence, cr(user, file) = { file/r:c | r ∊ RI }. Figure 3-6 shows the graph that this can-create relation induces; it is clearly acyclic and loop-free, so the scheme is attenuating.
Figure 3-6. The graph at left corresponds to the cc for the owner-based policy. The graph at right corresponds to the Take-Grant Protection Model. Both are acyclic; the left graph is loop-free, but the right graph contains a loop.
In the Take-Grant Protection Model, a subject can create either a subject or an object; hence, cc = { (subject, subject), (subject, object) }. A subject can give itself any rights over the vertices it creates, but it does not give the created subject any rights (although the creator may subsequently apply the grant rule to do so). Hence, crc(a, b) = Ø and crp(a, b) = { subject/tc, subject/gc, subject/rc, subject/wc }, so:
cr(subject, subject) = { subject/tc, subject/gc, subject/rc, subject/wc } | Ø
cr(subject, object) = { object/tc, object/gc, object/rc, object/wc }
Figure 3-6 also shows the graph that this cc induces. It, too, is acyclic, but not loop-free. Because no self tickets are provided (the Take-Grant Protection Model rules are not reflexive), condition 2 of Definition 3–14 fails and the scheme is not attenuating.
Only dom(A) and dom(B) are affected by this operation; no other entity has its domain changed. Thus, the create-rule is local; this means that creation has only a local impact on the state of the system and again mimics real systems.
The goal of this model is to identify types of policies that have tractable safety analyses. Our approach will be to derive a maximal state in which any additional entities or rights do not affect the safety analysis. We then analyze this state.
First, we introduce a flow function that captures the flow of tickets around a particular state of the system being modeled.
Definition 3–15. A legal transition is a change in state caused by an operation that is authorized. A history is a sequence of legal transitions. A derivable state is a state obtainable by beginning at some initial state and applying a history.
In simpler terms, a system begins at an initial state. An authorized operation (such as the copying of a ticket) causes a legal transition. Suppose a sequence of legal transitions moves the system into a (final) state. Then that set of legal transitions forms a history, and the final state is derivable from the history and the initial state.
We represent states by a superscript h. The set of subjects in state h is SUBh, the set of entities is ENTh, and the link and dom relations in the context of state h are 
and domh.
Definition 3–16. If there are two entities X and Y, and either:
for some i,
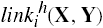orthere is a sequence of subjects X0, …, Xn such that
, 
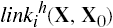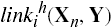, and for k = 1, …, n,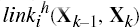 
then there is a pathh from X to Y.
In other words, a pathh from X to Y means that either a single link or a sequence of links connects X and Y. We write this as pathh(X, Y). Multiple pathhs may connect X and Y; in that case, we enumerate them as 
, j = 1, …, m.
The following algorithm defines the set (called the capacity, or cap(pathh(X,Y))) of the tickets that can flow over a pathh from X to Y.
If
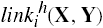, then cap(pathh(X, Y)) = fi(τ(X), τ(Y)).Otherwise, cap(pathh(X, Y)) = { τ(Y)/r:c | τ(Y)/rc ∊ f0(τ(X),τ(X0)) ∧τ(Y)/rc ∊ fk(τ(Xk–1),τ(Xk)) (for k = 1, …, n), ∧ τ(Y)/r:c ∊ fn(τ(Xn),τ(Y)) }.
In this set, the tickets for all but the final link must be copyable. If they are, any tickets in the last link will be in the capacity, whether or not they are copyable.
Now we can define the flow function as the union (sum) of all the capacities between two entities.
Definition 3–17. Let there be m pathhs between subjects X and Y in state h. The flow function flowh:SUBh × SUBh→2T×R is defined as
.
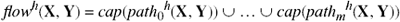Sandhu [870] has shown that the flow function requires O(|T × R| |SUBh|3), and hence the computation's time complexity is polynomial in the number of subjects in the system.
This definition allows us to sharpen our intuition of what a “maximal state” is (and will ultimately enable us to define that state formally). Intuitively, a maximal state maximizes flow between all pairs of subjects. Call the maximal state * and the flow function corresponding to this state flow*; then if a ticket is in flow*(X, Y), there exists a sequence of operations that can copy the ticket from X to Y. This brings up two questions. First, is a maximal state unique? Second, does every system have a maximal state?
We first formally define the notion of maximal state using a relation named ≤0.
Definition 3–18. The relation g ≤0 h is true if and only if, for all pairs of subjects X and Y in SUB0, flowg(X, Y) ⊆ flowh(X, Y). If g ≤0 h and h ≤0 g, g and h are equivalent.
In other words, the relation ≤0 induces a set of equivalence classes on the set of derivable states.
Definition 3–19. For a given system, a state m is maximal if and only if h ≤0 m for every derivable state h.
In a maximal state, the flow function contains all the tickets that can be transferred from one subject to another. Hence, all maximal states are in the same equivalence class and thus are equivalent. This answers our first question.
To show that every system has a maximal state, we first show that for any state in a finite collection of derivable states, there is a maximal state.
Lemma 3–3. Given an arbitrary finite collection H of derivable states, there exists a derivable state m such that, for all h ∊ H, h ≤0 m.
Proof. By induction on |H|.
Basis. Take H = Ø and m to be the initial state. The claim is trivially true.
Induction hypothesis. The claim holds when |H| = n.
Induction step. Let |H'| = n + 1, where H' = G ∪ { h }; thus, |G| = n. Choose g ∊ G such that, for every state x ∊ G, x ≤0 g; such a state's existence is guaranteed by the induction hypothesis.
Consider the states g and h, defined above. Each of these states is established by a history. Let M be an interleaving of these histories that preserves the relative order of transitions with respect to g and h, and with only the first create operation of duplicate create operations in the two histories. Let M attain state m. If either pathg(X, Y) for X, Y ∊ SUBg or pathh(X, Y) for X, Y ∊ SUBh, then pathm(X, Y), as g and h are ancestor states of m and SPM is monotonic. Thus, g ≤0 m and h ≤0 m, so m is a maximal state in H'. This concludes the induction step and the proof.
Take one state from each equivalence class of derivable states. To see that this is finite, consider each pair of subjects in SUB0. The flow function's range is 2T×R, so that function can take on at most 2|T×R| values. Given that there are |SUB0|2 pairs of subjects in the initial state, there can be at most 2|T×R||SUB0|2 distinct equivalence classes.
Theorem 3–15. There exists a maximal state * for every system.
Proof. Take K to be the collection of derivable states that contains exactly one state from each equivalence class of derivable states. From above, this set is finite. The theorem follows from Lemma 3–3.
In this model, the safety question now becomes: Is it possible to have a derivable state with X/r:c in dom(A), or does there exist a subject B with ticket X/rc in the initial state or which can demand X/rc and τ(X)/r:c in flow*(B, A)?
To answer this question, we need to construct a maximal state and test. Generally, this will require the creation of new subjects. In the general case, this is undecidable. But in special cases, this question is decidable. We now consider an important case—that of acyclic attenuating schemes—and determine how to construct the maximal state.
Consider a state h. Intuitively, generating a maximal state m from h will require all three types of operations. Define u to be a state corresponding to h but with a minimal number of new entities created such that m can be derived from u without any create operations. (That is, begin in state h. Use create operations to create as few new entities as possible such that state m can be derived from the new state after the entities are created. The state after the entities are created, but before any other operations occur, is u.) For example, if in the history from h to m, subject X creates two entities of type y, in u there would be only one entity of type y. That entity would act as a surrogate for the two entities that X created. Because m can be derived from u in polynomial time, if u can be created by adding to h a finite number of subjects, the safety question is decidable in polynomial time for such a system.
We now make this formal.
Definition 3–20. ([870], p.425) Given any initial state 0 of an acyclic attenuating scheme, the fully unfolded state u is the state derived by the following algorithm.
(* delete any loops so it's loop-free *) cc' = cc – { (a, a) | a ∊ TS } (* mark all subjects as unfolded *) for X ∊ SUB0 do folded = folded ∪ { X } (* if anything is folded, it has to be unfolded *) while folded ≠ Ø do begin (* subject X is going to be unfolded *) folded = folded – { x } (* for each type X can create, create one entity of *) (* that type and mark it as folded; this will force *) (* the new entity to be unfolded *) for y ∊ TS do begin if cc'(τ(X), y) then X creates Y of type y (* system is in state g here *) if y ∊ SUBg then folded = folded ∪ { X } end end (* now account for the loops; the system is in state h here *) for X ∊ SUBh do if cc(τ(X), τ(X)) then X creates Y of type τ(X) (* currently in desired state u *)
The while loop will terminate because the system is acyclic and attenuating, hence the types of the created entities must all be different—and TS is a finite set.
Definition 3–21. Given any initial state of an acyclic attenuating scheme, for every derivable state h define the surrogate function σ:ENTh→ENTh by
σ(X) = X if X in ENT0
σ(X) = σ(Y) if Y creates X and τ(Y) = τ(X)
σ(X) = τ(Y)-surrogate of σ(Y) if Y creates X and τ(Y) | τ(X)
It is easy to show that τ(σ(A)) = τ(A).
If τ(X) = τ(Y), then σ(X) = σ(Y). If τ(X) ≠ τ(Y), then in the construction of u, σ(X) creates σ(Y) (see the while loop of Definition 3–20). Also, in this construction, σ(X) creates entities X' of type τ(X) = τ(σ(X)) (see the last for loop of Definition 3–20). So, by Definition 3–14, we have the following lemma.
Lemma 3–4. For a system with an acyclic attenuating scheme, if X creates Y, then tickets that would be introduced by pretending that σ(X) creates σ(Y) are in domu(σ(X)) and domu(σ(Y)).
Now, let H be a legal history that derives a state h from the initial state of an acyclic attenuating system. Without loss of generality, we may assume that H's operations are ordered such that all create operations come first, followed by all demand operations, followed by all copy operations. Replace the transitions in H as follows, while preserving their relative order.
Delete all create operations.
Replace “X demands Y/r:c” with “σ(X) demands σ(Y)/r:c.”
Replace “Z copies X/r:c from Y” with “σ(Z) copies σ(X)/r:c from σ(Y).”
Call the new history G. Then:
Lemma 3–5. Every transition in G is legal, and if X/r:c ∊ domh(Y), then σ(X)/r:c ∊ domg(σ(Y)).
Proof. By induction on the number of copy operations in H.
Basis. Assume that H consists only of create and demand operations. Then G consists only of demand operations. By construction, and because σ preserves type, every demand operation in G is legal. Furthermore, X/r:c can appear in domh(Y) in one of three ways. If X/r:c ∊ dom0(Y), then X, Y ∊ ENT0 and σ(X)/r:c ∊ domg(σ(Y)) trivially holds. If a create operation in H put X/r:c ∊ domh(Y), σ(X)/r:c ∊ domg(σ(Y)) by Lemma 3–4. And if a demand operation put X/r:c ∊ domh(Y), then σ(X)/r:c ∊ domg(σ(Y)) follows from the corresponding demand operation in G. This establishes both parts of the claim.
Induction hypothesis. Assume that the claim holds for all histories with k copy operations, and consider a history H with k + 1 copy operations. Let H' be the initial sequence of H composed of k copy operations, and let h' be the state derived from H'.
Induction step. Let G' be the sequence of modified operations corresponding to H'. By the induction hypothesis, G' is a legal history. Let g' be the state derived from G'. Suppose the final operation of H is “Z copies X/r:c from Y.” By construction of G, the final operation of G is “σ(Z) copies σ(X)/r:c from σ(Y).” Now, h differs from h' by at most X/r:c ∊ domh(Z). However, the construction causes the final operation of G to be σ(X)/r:c ∊ domh(σ(Z)), proving the second part of the claim.
Because H' is legal, for H to be legal the following conditions must hold.
X/rc ∊ domh'(Y)
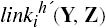
τ(X/r:c) ∊ fi(τ(Y), τ(Z))
The induction hypothesis, the first two conditions above, and X/r:c ∊ domh'(Y) mean that σ(X)/rc ∊ domg'(σ(Y)) and
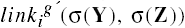. Because σ preserves type, the third condition and the induction hypothesis imply τ(σ(X)/r:c) ∊ fi(τ(σ(Y)), τ(σ(Z))). G' is legal, by the induction hypothesis; so, by these conditions, G is legal. This establishes the lemma.Corollary 3–3. For every i, if
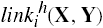, then 
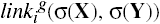.We can now present the following theorem.
Theorem 3–16. For a system with an acyclic attenuating scheme, for every history H that derives h from the initial state, there exists a history G without create operations that derives g from the fully unfolded state u such that
(∀ X, Y ∊ SUBh)[flowh(X, Y) ⊆ flowg(σ(X), σ(Y))]
Proof. It suffices to show that for every pathh from X to Y there is a pathg from σ(X) to σ(Y) for which cap(pathh(X, Y)) = cap(pathg(σ(X), σ(Y)). Induct on the number of links.
Basis. Let the length of the pathh from X to Y be 1. By Definition 3–16, then,
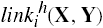, so 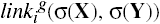by Corollary 3–3. Because σ preserves type, cap(pathh(X, Y)) = cap(pathg(σ(X), σ(Y)), verifying the claim.Induction hypothesis. Assume that the claim holds for every pathh of length k.
Induction step. Consider a pathh from X to Y of length k + 1. Then there exists an entity Z with a pathh from X to Z of length k, and
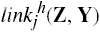. By the induction hypothesis, there is a pathg from σ(X) to σ(Z) with the same capacity as the pathh from X to Z. By Corollary 3–3, we have 
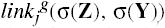. Because σ preserves type, there is a pathg from X to Y with cap(pathh(X, Y)) = cap(pathg(σ(X), σ(Y)), proving the induction step and therefore the theorem.
Thus, any history derived from an initial state u can be simulated by a corresponding history applied to the fully unfolded state v derived from u. The maximal state corresponding to v is #u; the history deriving this state has no creates. From Theorem 3–16, for every history that derives h from the initial state,
(∀ X, Y ∊ SUBh)[flowh(X, Y) ⊆ flow#u(σ(X), σ(Y))]
For X ∊ SUB0, σ(X) = X; therefore, (∀ X, Y ∊ SUB0)[flowh(X, Y) ⊆ flow#u(X, Y)]. This demonstrates the following corollary.
Corollary 3–4. The state #u is a maximal state for a system with an acyclic attenuating scheme.
Not only is #u derivable from u, it is derivable in time polynomial with respect to |SUBu| (and therefore to |SUB0|). Moreover, the straightforward algorithm for computing flow#u will be exponential in |TS| in the worst case. This means that for acyclic attenuating schemes, the safety question is decidable.
The HRU and SPM models present different aspects of the answer to the safety question. The obvious issue is the relationship between these models. For example, if SPM and HRU are equivalent, then SPM provides a more specific answer to the safety question than the HRU analysis does (that is, safety in acyclic attenuating schemes is decidable). If HRU can describe some systems that SPM cannot, then SPM's answer applies only to a limited set of systems. This bears some examination.
Ammann and Sandhu [19] have used SPM to represent multilevel security models, integrity models, and the Take-Grant Protection Model, so SPM subsumes those models. But the HRU model is central to safety analysis problems, and we explore its relationship to SPM in more detail.
How does SPM compare with the HRU model? If the two models are equivalent, then any safety analysis of SPM also applies to HRU and SPM offers some significant advantages over HRU for such analyses.
First, SPM is a higher-level model than HRU. This allows policies to be expressed very succinctly and at a more abstract level than in the access control matrix model. Hence, safety analyses can focus on the limits of the model and not on the details of representation. By way of contrast, safety analyses using the HRU model usually require a detailed mapping of the policy to the model, followed by an analysis.
However, the HRU model allows rights to be revoked and entities to be deleted (the delete, destroy subject, and destroy object rules). The SPM model has no revocation rule. The justification is exactly the same as for the Take-Grant Protection Model analyses that ignore that model's creation rule: what is removed can be replaced. So, in some sense, comparing HRU and SPM directly is unfair. A better comparison is one between SPM and a monotonic HRU scheme, in which there are no revocation rules, and we will use that model for further comparison.
In terms of comprehensiveness, HRU allows multiconditional commands. For example, suppose a system has a parent right, similar to the create right but requiring two subjects to have those rights over one another. Then either subject can execute a multicreate command that creates a new object and gives both subjects r rights over the new object. The multicreate command would be
command multicreate(s0, s1, o) if p in a[s0, s1 ] and r in a[s1, s0 ] then create object o enter r into a[s1, o ]; enter r into a[s2, o ]; end
However, SPM cannot express this command easily because the can-create function allows creators to have at most one type. If s0 and s1 have different types, SPM has no mechanism for creating o. This suggests that SPM is less expressive than HRU.
Ammann and Sandhu [19, 20, 872] revisited the notion of creation in SPM. Implicit in all models discussed so far is the assumption of a single parent. This assumption is not common in nature. (Consider humans, who have two parents.) It is more common in computer science, but (as we shall see) changing paradigms often simplifies solutions.
Consider two users, Anna and Bill, who must cooperate to perform a task but who do not trust each other. This problem of mutual suspicion is one of the oldest problems in security [413] and arises in multiuser computing systems. The usual solution is for Anna to define a proxy and give it only those rights she wishes Bill to have and for Bill to define a proxy similarly. Then Anna gives Bill's proxy the privileges to invoke Anna's proxy, and Bill gives Anna's proxy similar privileges. Working indirectly, the two proxies can work together and perform the task. Multiple indirection is disallowed (or else Anna's proxy could give her rights to Bill's proxy to a third party). Hence, the way the proxies use rights must be restricted, leading to a complex set of rights and manipulations.
Multiple parenting simplifies this model. Anna and Bill jointly create a proxy. Each then gives the proxy only those rights needed to perform the task. Neither parent is allowed to copy rights from the proxy. At this point, the copy operation must embody all restrictions on the manipulation of proxy rights and abilities, which is simpler than restricting the particular application of rights (as must be done in the preceding solution).
The Extended Schematic Protection Model (or ESPM) adds multiple parenting to SPM. The joint creation operation includes the SPM creation operation as a special case. The can-create function becomes
cc ⊆ TS × … × TS × T;
The create rules for the parents in a joint creation operation can allow the parents to get one anothers' rights to the child as well as their own, but this is equivalent to a creation rule in which parent rights are not copied, followed by applications of the copy rule. For simplicity, we require that each parent be given tickets only for its own rights over the new child, and not for rights of other parents.
Let X1, …, Xn be the n subject parents, let Y be the created entity, and let R1,i, R2,i, R4,i ⊆ R for i = 1, …, n. Each creation rule has i components, each of which provides the tickets to the ith parent and the child; for example, the ith rule is
crP(τ(X1), …, τ(Xn), τ(Y)) = Y/R1,i ∪ Xi/R2,i
The child also has a rule of the form
crC(τ(X1), …, τ(Xn), τ(Y)) = Y/R3 ∪ Xi/R4,1 ∪ … ∪ Xn/R4,n
These rules are analogous to the single-parent creation rules, but with one for each parent.
Considering two-parent joint creation operations is sufficient for modeling purposes. To demonstrate this, we show how the two-parent joint creation operation can implement a three-parent joint creation operation.
Let P1, P2, and P3 be three subjects; they will create a (child) entity C. With a three-parent joint creation operation, can-create will be
cc(τ(P1), τ(P2), τ(P3)) = Z ⊆ T
and the type of the child is τ(C) ∊ T. The creation rules are
crP1(τ(P1), τ(P2), τ(P3)) = C/R1,1 ∪ P1/R2,1
crP2(τ(P1), τ(P2), τ(P3)) = C/R1,2 ∪ P1/R2,2
crP3(τ(P1), τ(P2), τ(P3)) = C/R1,3 ∪ P1/R2,3
crC(τ(P1), τ(P2), τ(P3)) = C/R3 ∪ P1/R4,1 ∪ P2/R4,2 ∪ P3/R4,3
Our demonstration requires that we use the two-parent joint creation rule, not the three-parent rule. At the end of the demonstration, the parents and the child should have exactly the same tickets for one another. We will create additional entities and types, but they cannot interact with any other entities (in effect, they do not exist for the rest of the entities). Finally, if the creation fails, the parents get no new tickets.
For convenience, and to simplify the notation, we assume that the parents and child are all of different types.
Define four new entities A1, A2, A3, and S; each Ai, of type ai = τ(Ai), will act as an agent for the corresponding parent Pi, and S, of type s = τ(S), will act as an agent for the child. Let the type t represent parentage—that is, an entity with the ticket X/t has X as a parent. Again, without loss of generality, we assume that a1, a2, a3, s, and t are all new types.
During the construction, each agent will act as a surrogate for its parent; this agent obtains tickets on behalf of the parent, and only after the child is created does the agent give the parent the ticket. That way, if the construction fails, the parent has no new tickets.
Augment the can-create rules as follows:
cc(pi) = a1
cc(p2, a1) = a2
cc(p3, a2) = a3
cc(a3) = s
cc(s) = c
These rules enable the parents to create the agents. The final agent can create the agent for the child, which subsequently creates the child. Note that the second agent has two parents (P2 and A1), as does the third agent (P3 and A2); these rules are the two-parent joint creation operation.
On creation, the creation rules dictate the new tickets given to the parent and the child. The following rules augment the existing rules.
crP(p1, a1) = Ø | crC(p1, a1) = p1/Rtc |
crPfirst(p2, a1, a2) = Ø | |
crPsecond(p3, a2, a3) = Ø | crC(p2, a1, a2) = p2/Rtc ∪ a1/tc |
crPfirst(p3, a3, a3) = Ø | |
crPsecond(p3, a3, a3) = Ø | crC(p3, a2, a3) = p3/Rtc ∪ a2/tc |
crP(a3, s) = Ø | crC(a3, s) = a3/tc |
crP(s, c) = C/Rtc | crC(s, c) = c/R3t |
Here, crPfirst and crPsecond indicate the tickets given to the first and second parents, respectively.
The link predicates indicate over which links rights can flow; essentially, no tickets can flow to the parents until the child is created. The following links restrain flow to the parents by requiring each agent to have its own “parent” right.
link1(A1, A2) = A1/t ∊ dom(A2) ∧ A2/t ∊ dom(A2)
link1(A2, A3) = A2/t ∊ dom(A3) ∧ A3/t ∊ dom(A3)
link2(S, A2) = A3/t ∊ dom(S) ∧ C/t ∊ dom(C)
link3(A1, C) = C/t ∊ dom(A1)
link3(A2, C) = C/t ∊ dom(A2)
link3(A3, C) = C/t ∊ dom(A3)
link4(A1, P1) = P1/t ∊ dom(A1) ∧ A1/t ∊ dom(A1)
link4(A2, P2) = P2/t ∊ dom(A2) ∧ A2/t ∊ dom(A2)
link4(A3, P3) = P3/t ∊ dom(A3) ∧ A3/t ∊ dom(A3)
The filter functions dictate which tickets are copied from one entity to another:
f1(a2, a1) = a1/t ∪ c/Rtc
f1(a3, a2) = a2/t ∪ c/Rtc
f2(s, a3) = a3/t ∪ c/Rtc
f3(a1, c) = p1/R4,1
f3(a2, c) = p2/R4,2
f3(a3, c) = p3/R4,3
f4(a1, p1) = c/R1,1 ∪ p1/R2,1
f4(a2, p2) = c/R1,2 ∪ p2/R2,2
f4(a3, p3) = c/R1,3 ∪ p3/R2,3
Now we begin the construction. The creations proceed in the obvious order; after all are completed, we have
P1 has no relevant tickets.
P2 has no relevant tickets.
P3 has no relevant tickets.
A1 has P1/Rtc.
A2 has P2/Rtc ∪ A1/tc.
A3 has P3/Rtc ∪ A2/tc.
S has A3/tc ∪ C/Rtc.
C has C/R3.
We now apply the links and filter functions to copy rights. The only link predicate that is true is link2(S, A3), so we apply f2; then A3's set of tickets changes, as follows:
A3 has P3/Rtc ∪ A2/tc ∪ A3/t ∪ C/Rtc.
Now link1(A3, A2) is true, so applying f1 yields
A2 has P2/Rtc ∪ A1/tc ∪ A2/t ∪ C/Rtc.
Now link1(A2, A1) is true, so applying f1 again yields
A1 has P1/Rtc ∪ A1/t ∪ C/Rtc.
At this point, all link3s in this construction hold, so
C has C/R3 ∪ P1/R4,1 ∪ P2/R4,2 ∪ P3/R4,3.
Then the filter functions associated with link4, all of which are also true, finish the construction:
P1 has C/R1,1 ∪ P1/R2,1.
P2 has C/R1,2 ∪ P2/R2,2.
P3 has C/R1,3 ∪ P3/R2,3.
This completes the construction. As required, it adds no tickets to P1, P2, P3, and C except those that would be added by the three-parent joint creation operation. The intermediate entities, being of unique types, can have no effect on other entities. Finally, if the creation of C fails, no tickets can be added to P1, P2, and P3 because none of the link predicates in this construction is true; hence, no filter functions apply.
Generalizing this construction to n parents leads to the following theorem.
Theorem 3–17. [19] The two-parent joint creation operation can implement an n-parent joint creation operation with a fixed number of additional types and rights, and augmentations to the link predicates and filter functions.
A logical question is the relationship between ESPM and HRU; Ammann and Sandhu show that the following theorem holds.
Theorem 3–18. [19] Monotonic ESPM and the monotonic HRU model are equivalent.
Furthermore, the safety analysis is similar to that of SPM; the only difference is in the definition of the state function σ. The corresponding function σ' takes the joint creation operation into account; given this, the nature of the unfolding algorithm is roughly analogous to that of SPM. This leads to the equivalent of Theorem 3–16:
Theorem 3–19. [19] For an ESPM system with an acyclic attenuating scheme, for every history H that derives h from the initial state there exists a history G without create operations that derives g from the fully unfolded state u such that
(∀ X, Y ∊ SUBh)[flowh(X, Y) ⊆ flowg(σ'(X), σ'(Y))]
Because the proof is analogous to that of Theorem 3–16, we omit it.
What is the benefit of this alternative representation? If SPM and ESPM model the same systems, the addition of n-parent joint creation operations is not at all interesting. But if ESPM can represent systems that SPM cannot, the addition is very interesting. More generally, how can we compare different models?
Ammann, Sandhu, and Lipton [21] use a graph-based representation to compare different models. An abstract machine represents an access control model; as usual, that machine has a set of states and a set of transformations for moving from one state to another. A directed graph represents a state of this machine. A vertex is an entity; it has an associated type that is static. Each edge corresponds to a right and, like a vertex, has a static type determined on creation. The source of the edge has some right(s) over the target. The allowed operations are as follows.
Initial state operations, which simply create the graph in a particular state
Node creation operations, which add new vertices and edges with those vertices as targets
Edge adding operations, which add new edges between existing vertices
As an example, we simulate the three-parent joint creation operation with two-parent joint creation operations. As before, nodes P1, P2, and P3 are the parents; they create a new node C of type c with edges of type e. First, P1 creates A1, which is of type a, and an edge from P1 to A1 of type e'. Both a and e' are used only in this construction.
Then A1 and P2 create a new node A2, which is of type a, and A2 and P3 create a new node A3, with type a, and edges of type e' as indicated:
Next, A3 creates a new node S, which is of type a, which in turn creates a new node C, of type c:
Finally, an edge adding operation depending on the presence of edges P1→A1, A1→A2, A2→A3, A3→S, and S→C adds an edge of type e from P1 to C. An edge adding operation depending on the presence of edges P2→A2, A2→A3, A3→S, and S→C adds an edge of type e from P2 to C. A last edge adding operation depending on the presence of edges P3→A3, A3→S, and S→C adds an edge of type e from P3 to C:
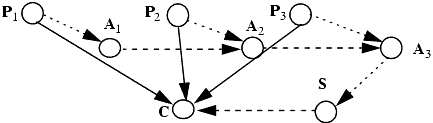
This completes the simulation. Exercise 10 suggests a simpler simulation.
The formal definition of simulation relies on two other notions: a scheme and a correspondence between schemes.
Definition 3–22. A scheme is an abstract finite-state machine that defines finite sets of node types, edge types, initial state operations, node creation operations, and edge adding operations. A model is a set of schemes.
Definition 3–23. Let NT(X) and ET(X) be the sets of node types and edge types, respectively, in scheme X. Then scheme A and scheme B correspond if and only if the graph defining the state in scheme A is identical to the subgraph obtained by taking the state in scheme B and deleting all nodes not in NT(A) and all edges not in ET(A).
Consider the simulation of a scheme C3 with a three-parent joint creation operation by a scheme C2 with a two-parent joint creation operation, as was done earlier. After the three-parent joint creation operation, the C3 state would be as follows:
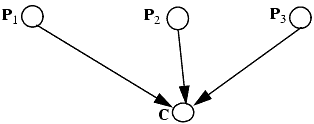
Contrasting this with the result of the C2 construction, and the fact that the types a and e' do not exist in C3, this state in C3 clearly corresponds to the state resulting from the construction in C2.
Intuitively, scheme A simulates scheme B if every state reachable by A corresponds to a state reachable by B. Because A may have more edge types and node types than B, simulation implies that if A can enter a state a, either there is a corresponding state reachable by B or, if not, A can transition to another state a' from a and there is a state reachable by B that corresponds to a'. The last condition means that if scheme A has a halting state, then scheme B must have a corresponding halting state; otherwise, the simulation is incorrect.
Definition 3–24. Scheme A simulates scheme B if and only if both of the following are true.
For every state b reachable by scheme B, there exists some corresponding state a reachable by scheme A; and
For every state a reachable by scheme A, either the corresponding state b is reachable by scheme B or there exists a successor state a' reachable by scheme A that corresponds to a state reachable by scheme B.
Now we can contrast the expressive power of models.
Definition 3–25. If there is a scheme in model MA that no scheme in model MB can simulate, then model MB is less expressive than model MA. If every scheme in model MA can be simulated by a scheme in model MB, then model MB is as expressive as model MA. If MA is as expressive as MB and MB is as expressive as MA, the models are equivalent.
Given these definitions, Ammann, Lipton, and Sandhu prove the following theorem.
Theorem 3–20. [21] Monotonic single-parent models are less expressive than monotonic multiparent models.
Proof. Begin with scheme A in the preceding example. We show by contradiction that this scheme cannot be simulated by any monotonic scheme B with only a single-parent creation operation. (The example does not show this because we are removing the requirement that scheme B begin in the same initial state as scheme A.)
Consider a scheme B that simulates scheme A. Let nodes X1 and X2 in A create node Y1 with edges from X1 and X2 to Y1. Then in scheme B there is a node W that creates Y1 with a single incoming edge from W. The simulation must also use edge adding operations to add edges from X1 to Y1 and from X2 to Y1 (assuming that W ≠ X1 and W ≠ X2).
Let W invoke the single-parent creation operation twice more to create nodes Y2 and Y3 and use the edge adding rules to add edges from X1 to Y1, Y2, and Y3 and from X2 to Y1, Y2, and Y3. The resulting state clearly corresponds to a state in scheme A.
Because scheme A has exactly one node type, Y1, Y2, and Y3 are indistinguishable as far as the application of the node creation and edge adding rules is concerned. So proceed as in the example above: in scheme A, let Y1 and Y2 create Z. In the simulation, without loss of generality, let Y1 create Z using a single-parent creation operation. Then scheme B uses an edge adding operation to add an edge from Y2 to Z—but that same edge adding rule can be used to add one more edge into Z, from Y3. Thus, there are three edges coming into Z, which (as we saw earlier) is a state that scheme A cannot reach, and from which no future state in scheme B that corresponds to a state in scheme A can be reached. Hence, scheme B does not simulate scheme A, which contradicts the hypothesis.
Thus, no such scheme B can exist.
This theorem answers the question posed earlier: because ESPM has a multiparent joint creation operation and SPM has a single-parent creation operation, ESPM is indeed more expressive than SPM.
The strengths of SPM and ESPM appear to derive from the notion of “types.” In particular, ESPM and HRU are equivalent, but the safety properties of ESPM are considerably stronger than those of HRU. Sandhu expanded the access control matrix model by adding a notion of “type” and revisiting the HRU results. This model, called the Typed Access Matrix (TAM) Model [875], has safety properties similar to those of ESPM and supports the notion that types are critical to the safety problem's analysis.
TAM augments the definitions used in the access control matrix model by adding types.
Definition 3–26. There is a finite set of types T, containing a subset of types TS for subjects.
The type of an entity is fixed when the entity is created (or in the initial state) and remains fixed throughout the lifetime of the model. The notion of protection state is similarly augmented.
Definition 3–27. The protection state of a system is (S, O, τ, A), where S is the set of subjects, O is the set of objects, A is the access control matrix, and τ:O→T is a type function that specifies the type of each object. If X ∊ S, then τ(X) ∊ TS, and if X ∊ O, then τ(X) ∊ T – TS.
The TAM primitive operations are the same as for the access control matrix model, except that the create operations are augmented with types.
Precondition: s ∉ S
Primitive command: create subject s of type ts
Postconditions: S' = S ∪{ s }, O' = O ∪{ s },
(∀y ∊ O)[τ'(y) = τ(y)], τ'(s') = ts,
(∀y ∊ O')[a'[s, y] = Ø], (∀x ∊ S')[a'[x, s] = Ø],
(∀x ∊ S)(∀y ∊ O)[a'[x, y] = a[x, y]]
In other words, this primitive command creates a new subject s. Note that s must not exist as a subject or object before this command is executed.
Precondition: o ∉ O
Primitive command: create object o of type to
Postconditions: S' = S, O' = O ∪{ o },
(∀y ∊ O)[τ'(y) = τ(y)], τ'(o') = to,
(∀x ∊ S')[a'[x, o] =,Ø], (∀x ∊ S')(∀y ∊ O)[a'[x, y] = a[x, y]]
In other words, this primitive command creates a new object o. Note that o must not exist before this command is executed.
These primitive operations are combined into commands defined as in the access control matrix model. Commands with conditions are called conditional commands; commands without conditions are called unconditional commands.
Finally, we define the models explicitly.
Definition 3–28. A TAM authorization scheme consists of a finite set of rights R, a finite set of types T, and a finite collection of commands. A TAM system is specified by a TAM scheme and an initial state.
Definition 3–29. The MTAM (Monotonic Typed Access Matrix) Model is the TAM Model without the delete, destroy subject, and destroy object primitive operations.
Definition 3–30. Let α(x1 : t1, …, xk : tk) be a creating command, where x1, …, xk ∊ O and τ(x1) = t1, …, τ(xk) = tk. Then ti is a child type in α(x1 : t1, …, xk : tk) if any of create subject xi of type ti or create object xi of type ti occurs in the body of α(x1 : t1, …, xk : tk). Otherwise, ti is a parent type in α(x1 : t1, …, xk : tk).
From this, we can define the notion of acyclic creations.
Definition 3–31. The creation graph of an MTAM scheme is a directed graph with vertex set V and an edge from u ∊ V to v ∊ V if and only if there is a creating command in which u is a parent type and v is a child type. If the creation graph is acyclic, the MTAM system is said to be acyclic; otherwise, the MTAM system is said to be cyclic.
As an example, consider the following command, where s and p are subjects and f is an object.
command create•havoc(s : u, p : u, f : v, q : w) create subject p of type u; create object f of type v; enter own into a[s,p]; enter r into a[q,p]; enter own into a[p,f]; enter r into a[p,f]; enter w into a[p,f];end
Here, u and v are child types and u and w are parent types. Note that u is both a parent type and a child type. The creation graph corresponding to the MTAM scheme with the single command create•havoc has the edges (u, u), (u, w), (v, u), and (v, w). Thus, this MTAM scheme is cyclic. Were the create subject p of type u deleted from the command, however, u would no longer be a child type, and the resulting MTAM scheme would be acyclic.
Sandhu has shown that the following theorem is true.
Theorem 3–21. [875] Safety is decidable for systems with acyclic MTAM schemes.
The proof is similar in spirit to the proof of Theorem 3–16.
Furthermore, because MTAM subsumes monotonic mono-operational HRU systems, a complexity result follows automatically:
Theorem 3–22. [875] Safety is NP-hard for systems with acyclic MTAM schemes.
However, Sandhu [875] has also developed a surprising result. If all MTAM commands are limited to three parameters, the resulting model (called “ternary MTAM”) is equivalent in expressive power to MTAM. However:
Theorem 3–23. [875] Safety for the acyclic ternary MTAM model is decidable in time polynomial in the size of the initial access control matrix.
The safety problem is a rich problem that has led to the development of several models and analysis techniques. Some of these models are useful in other contexts. We will return, for example, to both the Take-Grant Protection Model and ESPM later. These models provide insights into the boundary line between decidability and undecidability, which speaks to the degree of generality of analysis. Ultimately, however, security (the analogue of safety) is analyzed for a system or for a class of systems, and the models help us understand when such analysis is tractable and when it is not.
The critical research issue is the characterization of the class of models for which the safety question is decidable. The SRM results state sufficiency but not necessity. A set of characteristics that are both necessary and sufficient would show exactly what causes the safety problem to become undecidable, which is an open issue.
Related questions involve the expressive power of the various models. The models allow policies to be expressed more succinctly than in the access control matrix model. Can these more sophisticated models express the same set of policies that the access control matrix model can express? Are there other models that are easy to work with yet allow all protection states of interest to be expressed?
Sandhu and Ganta [877] have explored the effects of allowing testing for the absence of rights in an access control matrix (as opposed to testing for the presence of rights, which all the models described in this chapter do). Biskup [119] presents some variants on the Take-Grant Protection Model, and Budd [154] analyzes safety properties of grammatical protection schemes, which he and Lipton defined earlier [640].
Sandhu has also presented interesting work on the representation of models, and has unified many of them with his transform model [873, 874, 878].
1: | The proof of Theorem 3–1 states the following: Suppose two subjects s1 and s2 are created and the rights in A[s1, o1] and A[s2, o2] are tested. The same test for A[s1, o1] and A[s1, o2] = A[s1, o2] ∪ A[s2, o2] will produce the same result. Justify this statement. Would it be true if one could test for the absence of rights as well as for the presence of rights? |
2: | Devise an algorithm that determines whether or not a system is safe by enumerating all possible states. Is this problem NP-complete? Justify your answer. |
3: | Prove Theorem 3–3. (Hint: Use a diagonalization argument to test each system as the set of protection systems is enumerated. Whenever a protection system leaks a right, add it to the list of unsafe protection systems.) |
4: | Prove or disprove: The claim of Lemma 3–1 holds when x is an object. |
5: | Prove or give a counterexample: The predicate can•share(α, x, y, G0) is true if and only if there is an edge from x to y in G0 labeled α, or if the following hold simultaneously.
|
6: | The Take-Grant Protection Model provides two rights, take and grant, that enable the transfer of other rights. SPM's demand right, in many ways analogous to take, was shown to be unnecessary. Could take similarly be dropped from the Take-Grant Protection Model? |
7: | The discussion of acyclic creates imposes constraints on the types of created subjects but not on the types of created objects. Why not? |
8: | Prove that if a graph for cc is constructed and has no loops, the system is attenuating. |
9: | Consider the construction of the three-parent joint creation operation from the two-parent joint creation operation. In [21], crC(s, c) = c/R3 and link2(S, A3) = A3/t ∊ dom(S). Why is this not sufficient to derive the three-parent joint creation operation from the two-parent joint creation operation? |
10: | The simulation of three-parent creation by two-parent creation using the Ammann, Lipton, and Sandhu scheme mimics the simulation using SPM. Present a simpler, more direct simulation using the Ammann, Lipton, and Sandhu scheme that requires only five operations. |