Chapter 5
Understanding CALCULATE and CALCULATETABLE
In this chapter we continue our journey in discovering the power of the DAX language with a detailed explanation of a single function: CALCULATE. The same considerations apply for CALCULATETABLE, which evaluates and returns a table instead of a scalar value. For simplicity’s sake, we will refer to CALCULATE in the examples, but remember that CALCULATETABLE displays the same behavior.
CALCULATE is the most important, useful, and complex function in DAX, so it deserves a full chapter. The function itself is simple to learn; it only performs a few tasks. Complexity comes from the fact that CALCULATE and CALCULATETABLE are the only functions in DAX that can create new filter contexts. Thus, although they are simple functions, using CALCULATE or CALCULATETABLE in a formula instantly increases its complexity.
This chapter is as tough as the previous chapter was. We suggest you carefully read it once, get a general feeling for CALCULATE, and move on to the remaining part of the book. Then, as soon as you feel lost in a specific formula, come back to this chapter and read it again from the beginning. You will probably discover new information each time you read it.
Introducing CALCULATE and CALCULATETABLE
The previous chapter described the two evaluation contexts: the row context and the filter context. The row context automatically exists for a calculated column, and one can create a row context programmatically by using an iterator. The filter context, on the other hand, is created by the report, and we have not described yet how to programmatically create a filter context. CALCULATE and CALCULATETABLE are the only functions required to operate on the filter context. Indeed, CALCULATE and CALCULATETABLE are the only functions that can create a new filter context by manipulating the existing one. From here onwards, we will show examples based on CALCULATE only, but remember that CALCULATETABLE performs the same operation for DAX expressions returning a table. Later in the book there are more examples using CALCULATETABLE, as in Chapter 12, “Working with tables,” and in Chapter 13, “Authoring queries.”
Creating filter contexts
Here we will introduce the reason why one would want to create new filter contexts with a practical example. As described in the next sections, writing code without being able to create new filter contexts results in verbose and unreadable code. What follows is an example of how creating a new filter context can drastically improve code that, at first, looked rather complex.
Contoso is a company that sells electronic products all around the world. Some products are branded Contoso, whereas others have different brands. One of the reports requires a comparison of the gross margins, both as an amount and as a percentage, of Contoso-branded products against their competitors. The first part of the report requires the following calculations:
Sales Amount := SUMX ( Sales, Sales[Quantity] * Sales[Net Price] ) Gross Margin := SUMX ( Sales, Sales[Quantity] * ( Sales[Net Price] - Sales[Unit Cost] ) ) GM % := DIVIDE ( [Gross Margin], [Sales Amount] )
One beautiful aspect of DAX is that you can build more complex calculations on top of existing measures. In fact, you can appreciate this in the definition of GM %, the measure that computes the percentage of the gross margin against the sales. GM % simply invokes the two original measures as it divides them. If you already have a measure that computes a value, you can call the measure instead of rewriting the full code.
Using the three measures defined above, one can build the first report, as shown in Figure 5-1.
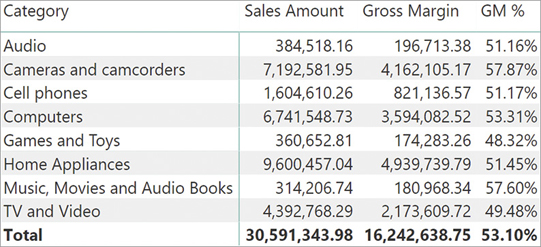
The next step in building the report is more intricate. In fact, the final report we want is the one in Figure 5-2 that shows two additional columns: the gross margin for Contoso-branded products, both as amount and as percentage.

With the knowledge acquired so far, you are already capable of authoring the code for these two measures. Indeed, because the requirement is to restrict the calculation to only one brand, a solution is to use FILTER to restrict the calculation of the gross margin to Contoso products only:
Contoso GM :=
VAR ContosoSales = -- Saves the rows of Sales which are related
FILTER ( -- to Contoso-branded products into a variable
Sales,
RELATED ( 'Product'[Brand] ) = "Contoso"
)
VAR ContosoMargin = -- Iterates over ContosoSales
SUMX ( -- to only compute the margin for Contoso
ContosoSales,
Sales[Quantity] * ( Sales[Net Price] - Sales[Unit Cost] )
)
RETURN
ContosoMarginThe ContosoSales variable contains the rows of Sales related to all the Contoso-branded products. Once the variable is computed, SUMX iterates on ContosoSales to compute the margin. Because the iteration is on the Sales table and the filter is on the Product table, one needs to use RELATED to retrieve the related product for each row in Sales. In a similar way, one can compute the gross margin of Contoso by iterating the ContosoSales variable twice:
Contoso GM % :=
VAR ContosoSales = -- Saves the rows of Sales which are related
FILTER ( -- to Contoso-branded products into a variable
Sales,
RELATED ( 'Product'[Brand] ) = "Contoso"
)
VAR ContosoMargin = -- Iterates over ContosoSales
SUMX ( -- to only compute the margin for Contoso
ContosoSales,
Sales[Quantity] * ( Sales[Net Price] - Sales[Unit Cost] )
)
VAR ContosoSalesAmount = -- Iterates over ContosoSales
SUMX ( -- to only compute the sales amount for Contoso
ContosoSales,
Sales[Quantity] * Sales[Net Price]
)
VAR Ratio =
DIVIDE ( ContosoMargin, ContosoSalesAmount )
RETURN
RatioThe code for Contoso GM % is a bit longer but, from a logical point of view, it follows the same pattern as Contoso GM. Although these measures work, it is easy to note that the initial elegance of DAX is lost. Indeed, the model already contains one measure to compute the gross margin and another measure to compute the gross margin percentage. However, because the new measures needed to be filtered, we had to rewrite the expression to add the condition.
It is worth stressing that the basic measures Gross Margin and GM % can already compute the values for Contoso. In fact, from Figure 5-2 you can note that the gross margin for Contoso is equal to 3,877,070.65 and the percentage is equal to 52.73%. One can obtain the very same numbers by slicing the base measures Gross Margin and GM % by Brand, as shown in Figure 5-3.
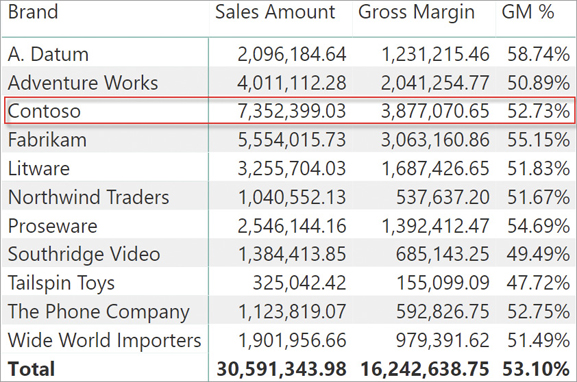
In the highlighted cells, the filter context created by the report is filtering the Contoso brand. The filter context filters the model. Therefore, a filter context placed on the Product[Brand] column filters the Sales table because of the relationship linking Sales to Product. Using the filter context, one can filter a table indirectly because the filter context operates on the whole model.
Thus, if we could make DAX compute the Gross Margin measure by creating a filter context programmatically, which only filters the Contoso-branded products, then our implementation of the last two measures would be much easier. This is possible by using CALCULATE.
The complete description of CALCULATE comes later in this chapter. First, we examine the syntax of CALCULATE:
CALCULATE ( Expression, Condition1, ... ConditionN )
CALCULATE can accept any number of parameters. The only mandatory parameter is the first one, that is, the expression to evaluate. The conditions following the first parameter are called filter arguments. CALCULATE creates a new filter context based on the set of filter arguments. Once the new filter context is computed, CALCULATE applies it to the model, and it proceeds with the evaluation of the expression. Thus, by leveraging CALCULATE, the code for Contoso Margin and Contoso GM % becomes much simpler:
Contoso GM :=
CALCULATE (
[Gross Margin], -- Computes the gross margin
'Product'[Brand] = "Contoso" -- In a filter context where brand = Contoso
)
Contoso GM % :=
CALCULATE (
[GM %], -- Computes the gross margin percentage
'Product'[Brand] = "Contoso" -- In a filter context where brand = Contoso
)Welcome back, simplicity and elegance! By creating a filter context that forces the brand to be Contoso, one can rely on existing measures and change their behavior without having to rewrite the code of the measures.
CALCULATE lets you create new filter contexts by manipulating the filters in the current context. As you have seen, this leads to simple and elegant code. In the next sections we provide a complete and more formal definition of the behavior of CALCULATE, describing in detail what CALCULATE does and how to take advantage of its features. Indeed, so far we have kept the example rather high-level when, in fact, the initial definition of the Contoso measures is not semantically equivalent to the final definition. There are some differences that one needs to understand well.
Introducing CALCULATE
Now that you have had an initial exposure to CALCULATE, it is time to start learning the details of this function. As introduced earlier, CALCULATE is the only DAX function that can modify the filter context; and remember, when we mention CALCULATE, we also include CALCULATETABLE. CALCULATE does not modify a filter context: It creates a new filter context by merging its filter parameters with the existing filter context. Once CALCULATE ends, its filter context is discarded and the previous filter context becomes effective again.
We have introduced the syntax of CALCULATE as
CALCULATE ( Expression, Condition1, ... ConditionN )
The first parameter is the expression that CALCULATE will evaluate. Before evaluating the expression, CALCULATE computes the filter arguments and uses them to manipulate the filter context.
The first important thing to note about CALCULATE is that the filter arguments are not Boolean conditions: The filter arguments are tables. Whenever you use a Boolean condition as a filter argument of CALCULATE, DAX translates it into a table of values.
In the previous section we used this code:
Contoso GM :=
CALCULATE (
[Gross Margin], -- Computes the gross margin
'Product'[Brand] = "Contoso" -- In a filter context where brand = Contoso
)Using a Boolean condition is only a shortcut for the complete CALCULATE syntax. This is known as syntax sugar. It reads this way:
Contoso GM :=
CALCULATE (
[Gross Margin], -- Computes the gross margin
FILTER ( -- Using as valid values for Product[Brand]
ALL ( 'Product'[Brand] ), -- any value for Product[Brand]
'Product'[Brand] = "Contoso" -- which is equal to "Contoso"
)
)The two syntaxes are equivalent, and there are no performance or semantic differences between them. That being said, particularly when you are learning CALCULATE for the first time, it is useful to always read filter arguments as tables. This makes the behavior of CALCULATE more apparent. Once you get used to CALCULATE semantics, the compact version of the syntax is more convenient. It is shorter and easier to read.
A filter argument is a table, that is, a list of values. The table provided as a filter argument defines the list of values that will be visible—for the column—during the evaluation of the expression. In the previous example, FILTER returns a table with one row only, containing a value for Product[Brand] that equals “Contoso”. In other words, “Contoso” is the only value that CALCULATE will make visible for the Product[Brand] column. Therefore, CALCULATE filters the model including only products of the Contoso brand. Consider these two definitions:
Sales Amount :=
SUMX (
Sales,
Sales[Quantity] * Sales[Net Price]
)
Contoso Sales :=
CALCULATE (
[Sales Amount],
FILTER (
ALL ( 'Product'[Brand] ),
'Product'[Brand] = "Contoso"
)
)The filter parameter of FILTER in the CALCULATE of Contoso Sales scans ALL(Product[Brand]); therefore, any previously existing filter on the product brand is overwritten by the new filter. This is more evident when you use the measures in a report that slices by brand. You can see in Figure 5-4 that Contoso Sales reports on all the rows/brands the same value as Sales Amount did for Contoso specifically.
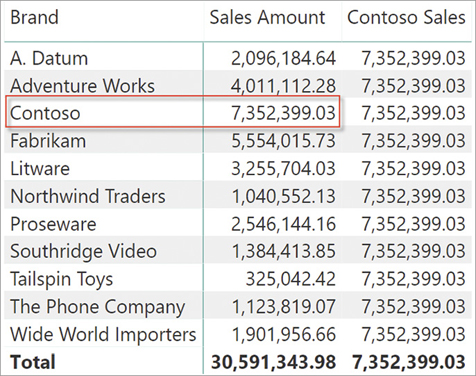
In every row, the report creates a filter context containing the relevant brand. For example, in the row for Litware the original filter context created by the report contains a filter that only shows Litware products. Then, CALCULATE evaluates its filter argument, which returns a table containing only Contoso. The newly created filter overwrites the previously existing filter on the same column. You can see a graphic representation of the process in Figure 5-5.

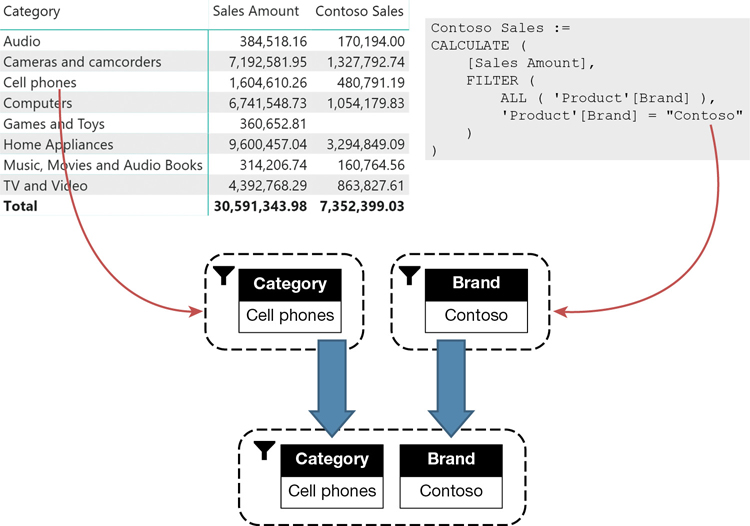
CALCULATE does not overwrite the whole original filter context. It only replaces previously existing filters on the columns contained in the filter argument. In fact, if one changes the report to now slice by Product[Category], the result is different, as shown in Figure 5-6.

Now the report is filtering Product[Category], whereas CALCULATE applies a filter on Product[Brand] to evaluate the Contoso Sales measure. The two filters do not work on the same column of the Product table. Therefore, no overwriting happens, and the two filters work together as a new filter context. As a result, each cell is showing the sales of Contoso for the given category. The scenario is depicted in Figure 5-7.
Now that you have seen the basics of CALCULATE, we can summarize its semantics:
CALCULATE makes a copy of the current filter context.
CALCULATE evaluates each filter argument and produces, for each condition, the list of valid values for the specified columns.
If two or more filter arguments affect the same column, they are merged together using an AND operator (or using the set intersection in mathematical terms).
CALCULATE uses the new condition to replace existing filters on the columns in the model. If a column already has a filter, then the new filter replaces the existing one. On the other hand, if the column does not have a filter, then CALCULATE adds the new filter to the filter context.
Once the new filter context is ready, CALCULATE applies the filter context to the model, and it computes the first argument: the expression. In the end, CALCULATE restores the original filter context, returning the computed result.
![]() Note
Note
CALCULATE does another very important task: It transforms any existing row context into an equivalent filter context. You find a more detailed discussion on this topic later in this chapter, under “Understanding context transition.” Should you do a second reading of this section, do remember: CALCULATE creates a filter context out of the existing row contexts.
CALCULATE accepts filters of two types:
Lists of values, in the form of a table expression. In that case, you provide the exact list of values you want to make visible in the new filter context. The filter can be a table with any number of columns. Only the existing combinations of values in different columns will be considered in the filter.
Boolean conditions, such as Product[Color] = “White”. These filters need to work on a single column because the result needs to be a list of values for a single column. This type of filter argument is also known as predicate.
If you use the syntax with a Boolean condition, DAX transforms it into a list of values. Thus, whenever you write this code:
Sales Amount Red Products :=
CALCULATE (
[Sales Amount],
'Product'[Color] = "Red"
)DAX transforms the expression into this:
Sales Amount Red Products :=
CALCULATE (
[Sales Amount],
FILTER (
ALL ( 'Product'[Color] ),
'Product'[Color] = "Red"
)
)For this reason, you can only reference one column in a filter argument with a Boolean condition. DAX needs to detect the column to iterate in the FILTER function, which is generated in the background automatically. If the Boolean expression references two or more columns, then you must explicitly write the FILTER iteration, as you learn later in this chapter.
Using CALCULATE to compute percentages
Now that we have introduced CALCULATE, we can use it to define several calculations. The goal of this section is to bring your attention to some details about CALCULATE that are not obvious at first sight. Later in this chapter, we will cover more advanced aspects of CALCULATE. For now, we focus on some of the issues you might encounter when you start using CALCULATE.
A pattern that appears often is that of percentages. When working with percentages, it is very important to define exactly the calculation required. In this set of examples, you learn how different uses of CALCULATE and ALL functions provide different results.
We can start with a simple percentage calculation. We want to build the following report showing the sales amount along with the percentage over the grand total. You can see in Figure 5-8 the result we want to obtain.
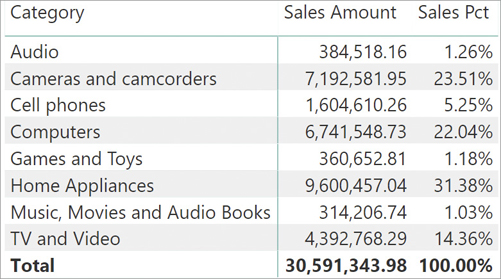
To compute the percentage, one needs to divide the value of Sales Amount in the current filter context by the value of Sales Amount in a filter context that ignores the existing filter on Category. In fact, the value of 1.26% for Audio is computed as 384,518.16 divided by 30,591,343.98.
In each row of the report, the filter context already contains the current category. Thus, for Sales Amount, the result is automatically filtered by the given category. The denominator of the ratio needs to ignore the current filter context, so that it evaluates the grand total. Because the filter arguments of CALCULATE are tables, it is enough to provide a table function that ignores the current filter context on the category and always returns all the categories—regardless of any filter. You previously learned that this function is ALL. Look at the following measure definition:
All Category Sales :=
CALCULATE ( -- Changes the filter context of
[Sales Amount], -- the sales amount
ALL ( 'Product'[Category] ) -- making ALL categories visible
)ALL removes the filter on the Product[Category] column from the filter context. Thus, in any cell of the report, it ignores any filter existing on the categories. The effect is that the filter on the category applied by the row of the report is removed. Look at the result in Figure 5-9. You can see that each row of the report for the All Category Sales measure returns the same value all the way through—the grand total of Sales Amount.

The All Category Sales measure is not useful by itself. It is unlikely a user would want to create a report that shows the same value on all the rows. However, that value is perfect as the denominator of the percentage we are looking to compute. In fact, the formula computing the percentage can be written this way:
Sales Pct :=
VAR CurrentCategorySales = -- CurrentCategorySales contains
[Sales Amount] -- the sales in the current context
VAR AllCategoriesSales = -- AllCategoriesSales contains
CALCULATE ( -- the sales amount in a filter context
[Sales Amount], -- where all the product categories
ALL ( 'Product'[Category] ) -- are visible
)
VAR Ratio =
DIVIDE (
CurrentCategorySales,
AllCategoriesSales
)
RETURN
RatioAs you have seen in this example, mixing table functions and CALCULATE makes it possible to author useful measures easily. We use this technique a lot in the book because it is the primary calculation tool in DAX.
![]() Note
Note
ALL has specific semantics when used as a filter argument of CALCULATE. In fact, it does not replace the filter context with all the values. Instead, CALCULATE uses ALL to remove the filter on the category column from the filter context. The side effects of this behavior are somewhat complex to follow and do not belong in this introductory section. We will cover them in more detail later in this chapter.
As we said in the introduction of this section, it is important to pay attention to small details when authoring percentages like the one we are currently writing. In fact, the percentage works fine if the report is slicing by category. The code removes the filter from the category, but it does not touch any other existing filter. Therefore, if the report adds other filters, the result might not be exactly what one wants to achieve. For example, look at the report in Figure 5-10 where we added the Product[Color] column as a second level of detail in the rows of the report.
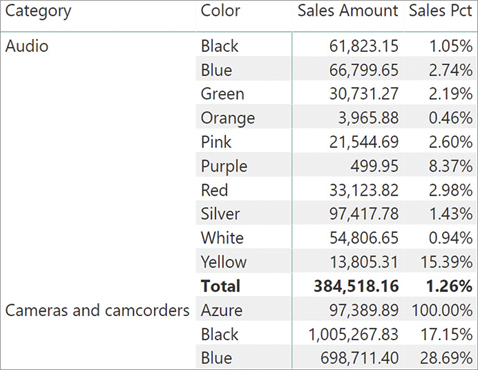
Looking at percentages, the value at the category level is correct, whereas the value at the color level looks wrong. In fact, the color percentages do not add up—neither to the category level nor to 100%. To understand the meaning of these values and how they are evaluated, it is always of great help to focus on one cell and understand exactly what happened to the filter context. Focus on Figure 5-11.
![The figure brings together the code, the report, and symbols to clarify that ALL on Product[Category] removes the filter on Category but leaves the filter on Color intact.](http://images-20200215.ebookreading.net/5/4/4/9780134865867/9780134865867__definitive-guide-to__9780134865867__graphics__05fig11.jpg)
The original filter context created by the report contained both a filter on category and a filter on color. The filter on Product[Color] is not overwritten by CALCULATE, which only removes the filter from Product[Category]. As a result, the final filter context only contains the color. Therefore, the denominator of the ratio contains the sales of all the products of the given color—Black—and of any category.
The calculation being wrong is not an unexpected behavior of CALCULATE. The problem here is that the formula has been designed to specifically work with a filter on a category, leaving any other filter untouched. The same formula makes perfect sense in a different report. Look at what happens if one switches the order of the columns, building a report that slices by color first and category second, as in Figure 5-12.

The report in Figure 5-12 makes a lot more sense. The measure computes the same result, but it is more intuitive thanks to the layout of the report. The percentage shown is the percentage of the category inside the given color. Color by color, the percentage always adds up to 100%.
In other words, when the user is required to compute a percentage, they should pay special attention in determining the denominator of the percentage. CALCULATE and ALL are the primary tools to use, but the specification of the formula depends on the business requirements.
Back to the example: The goal is to fix the calculation so that it computes the percentage against a filter on either the category or the color. There are multiple ways of performing the operation, all leading to slightly different results that are worth examining deeper.
One possible solution is to let CALCULATE remove the filter from both the category and the color. Adding multiple filter arguments to CALCULATE accomplishes this goal:
Sales Pct :=
VAR CurrentCategorySales =
[Sales Amount]
VAR AllCategoriesAndColorSales =
CALCULATE (
[Sales Amount],
ALL ( 'Product'[Category] ), -- The two ALL conditions could also be replaced
ALL ( 'Product'[Color] ) -- by ALL ( 'Product'[Category], 'Product'[Color] )
)
VAR Ratio =
DIVIDE (
CurrentCategorySales,
AllCategoriesAndColorSales
)
RETURN
RatioThis latter version of Sales Pct works fine with the report containing the color and the category, but it still suffers from limitations similar to the previous versions. In fact, it produces the right percentage with color and category—as you can see in Figure 5-13—but it will fail as soon as one adds other columns to the report.

Adding another column to the report would create the same inconsistency noticed so far. If the user wants to create a percentage that removes all the filters on the Product table, they could still use the ALL function passing a whole table as an argument:
Sales Pct All Products :=
VAR CurrentCategorySales =
[Sales Amount]
VAR AllProductSales =
CALCULATE (
[Sales Amount],
ALL ( 'Product' )
)
VAR Ratio =
DIVIDE (
CurrentCategorySales,
AllProductSales
)
RETURN
RatioALL on the Product table removes any filter on any column of the Product table. In Figure 5-14 you can see the result of that calculation.

So far, you have seen that by using CALCULATE and ALL together, you can remove filters—from a column, from multiple columns, or from a whole table. The real power of CALCULATE is that it offers many options to manipulate a filter context, and its capabilities do not end there. In fact, one might want to analyze the percentages by also slicing columns from different tables. For example, if the report is sliced by product category and customer continent, the last measure we created is not perfect yet, as you can see in Figure 5-15.
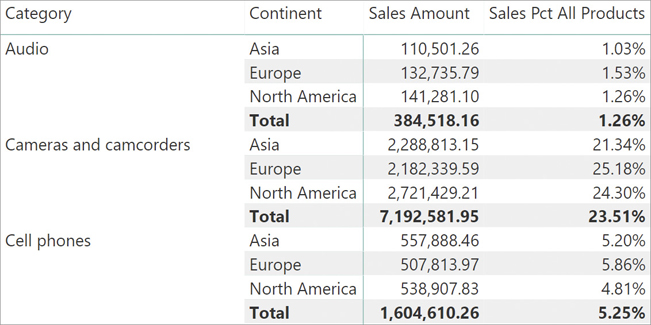
At this point, the problem might be evident to you. The measure at the denominator removes any filter from the Product table, but it leaves the filter on Customer[Continent] intact. Therefore, the denominator computes the total sales of all products in the given continent.
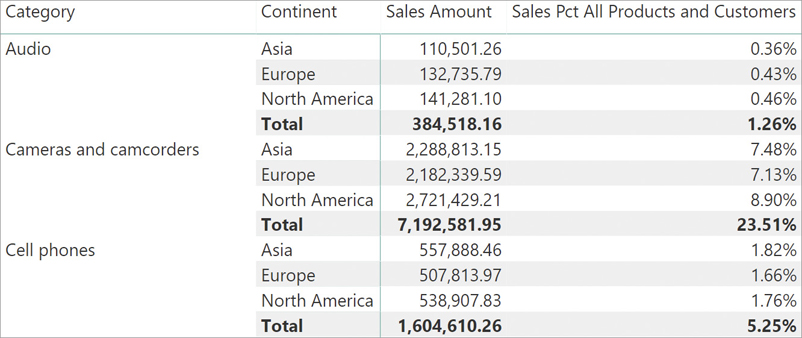
As in the previous scenario, the filter can be removed from multiple tables by putting several filters as arguments of CALCULATE:
Sales Pct All Products and Customers :=
VAR CurrentCategorySales =
[Sales Amount]
VAR AllProductAndCustomersSales =
CALCULATE (
[Sales Amount],
ALL ( 'Product' ),
ALL ( Customer )
)
VAR Ratio =
DIVIDE (
CurrentCategorySales,
AllProductAndCustomersSales
)
RETURN
RatioBy using ALL on two tables, now CALCULATE removes the filters from both tables. The result, as expected, is a percentage that adds up correctly, as you can appreciate in Figure 5-16.
As with two columns, the same challenge comes up with two tables. If a user adds another column from a third table to the context, the measure will not remove the filter from the third table. One possible solution when they want to remove the filter from any table that might affect the calculation is to remove any filter from the fact table itself. In our model the fact table is Sales. Here is a measure that computes an additive percentage no matter what filter is interacting with the Sales table:
Pct All Sales :=
VAR CurrentCategorySales =
[Sales Amount]
VAR AllSales =
CALCULATE (
[Sales Amount],
ALL ( Sales )
)
VAR Ratio =
DIVIDE (
CurrentCategorySales,
AllSales
)
RETURN
RatioThis measure leverages relationships to remove the filter from any table that might filter Sales. At this stage, we cannot explain the details of how it works because it leverages expanded tables, which we introduce in Chapter 14, “Advanced DAX concepts.” You can appreciate its behavior by inspecting Figure 5-17, where we removed the amount from the report and added the calendar year on the columns. Please note that the Calendar Year belongs to the Date table, which is not used in the measure. Nevertheless, the filter on Date is removed as part of the removal of filters from Sales.

Before leaving this long exercise with percentages, we want to show another final example of filter context manipulation. As you can see in Figure 5-17, the percentage is always against the grand total, exactly as expected. What if the goal is to compute a percentage over the grand total of only the current year? In that case, the new filter context created by CALCULATE needs to be prepared carefully. Indeed, the denominator needs to compute the total of sales regardless of any filter apart from the current year. This requires two actions:
Removing all filters from the fact table
Restoring the filter for the year
Beware that the two conditions are applied at the same time, although it might look like the two steps come one after the other. You have already learned how to remove all the filters from the fact table. The last step is learning how to restore an existing filter.
![]() Note
Note
The goal of this section is to explain basic techniques for manipulating the filter context. Later in this chapter you see another easier approach to solve this specific requirement—percentage over the visible grand total—by using ALLSELECTED.
In Chapter 3, “Using basic table functions,” you learned the VALUES function. VALUES returns the list of values of a column in the current filter context. Because the result of VALUES is a table, it can be used as a filter argument for CALCULATE. As a result, CALCULATE applies a filter on the given column, restricting its values to those returned by VALUES. Look at the following code:
Pct All Sales CY :=
VAR CurrentCategorySales =
[Sales Amount]
VAR AllSalesInCurrentYear =
CALCULATE (
[Sales Amount],
ALL ( Sales ),
VALUES ( 'Date'[Calendar Year] )
)
VAR Ratio =
DIVIDE (
CurrentCategorySales,
AllSalesInCurrentYear
)
RETURN
RatioOnce used in the report the measure accounts for 100% for every year, still computing the percentage against any other filter apart from the year. You see this in Figure 5-18.
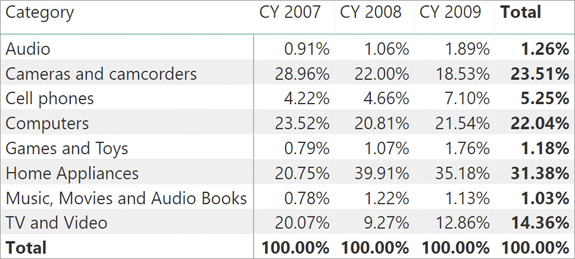
Figure 5-19 depicts the full behavior of this complex formula.

Here is a review of the diagram:
The cell containing 4.22% (sales of Cell Phones for Calendar Year 2007) has a filter context that filters Cell phones for CY 2007.
CALCULATE has two filter arguments: ALL ( Sales ) and VALUES ( Date[Calendar Year] ).
ALL ( Sales ) removes the filter from the Sales table.
VALUES ( Date[Calendar Year] ) evaluates the VALUES function in the original filter context, still affected by the presence of CY 2007 on the columns. As such, it returns the only year visible in the current filter context—that is, CY 2007.
The two filter arguments of CALCULATE are applied to the current filter context, resulting in a filter context that only contains a filter on Calendar Year. The denominator computes the total sales in a filter context with CY 2007 only.
It is of paramount importance to understand clearly that the filter arguments of CALCULATE are evaluated in the original filter context where CALCULATE is called. In fact, CALCULATE changes the filter context, but this only happens after the filter arguments are evaluated.
Using ALL over a table followed by VALUES over a column is a technique used to replace the filter context with a filter over that same column.
![]() Note
Note
The previous example could also have been obtained by using ALLEXCEPT. The semantics of ALL/VALUES is different from ALLEXCEPT. In Chapter 10, “Working with the filter context,” you will see a complete description of the differences between the ALLEXCEPT and the ALL/VALUES techniques.
As you have seen in these examples, CALCULATE, in itself, is not a complex function. Its behavior is simple to describe. At the same time, as soon as you start using CALCULATE, the complexity of the code becomes much higher. Indeed, you need to focus on the filter context and understand exactly how CALCULATE generates the new filter context. A simple percentage hides a lot of complexity, and that complexity is all in the details. Before one really masters the handling of evaluation contexts, DAX is a bit of a mystery. The key to unlocking the full power of the language is all in mastering evaluation contexts. Moreover, in all these examples we only had to manage one CALCULATE. In a complex formula, having four or five different contexts in the same code is not unusual because of the presence of many instances of CALCULATE.
It is a good idea to read this whole section about percentages at least twice. In our experience, a second read is much easier and lets you focus on the important aspects of the code. We wanted to show this example to stress the importance of theory, when it comes to CALCULATE. A small change in the code has an important effect on the numbers computed by the formula. After your second read, proceed with the next sections where we focus more on theory than on practical examples.
Introducing KEEPFILTERS
You learned in the previous sections that the filter arguments of CALCULATE overwrite any previously existing filter on the same column. Thus, the following measure returns the sales of Audio regardless of any previously existing filter on Product[Category]:
Audio Sales :=
CALCULATE (
[Sales Amount],
'Product'[Category] = "Audio"
)As you can see in Figure 5-20, the value of Audio is repeated on all the rows of the report.

CALCULATE overwrites the existing filters on the columns where a new filter is applied. All the remaining columns of the filter context are left intact. In case you do not want to overwrite existing filters, you can wrap the filter argument with KEEPFILTERS. For example, if you want to show the amount of Audio sales when Audio is present in the filter context and a blank value if Audio is not present in the filter context, you can write the following measure:
Audio Sales KeepFilters :=
CALCULATE (
[Sales Amount],
KEEPFILTERS ( 'Product'[Category] = "Audio" )
)KEEPFILTERS is the second CALCULATE modifier that you learn—the first one was ALL. We further cover CALCULATE modifiers later in this chapter. KEEPFILTERS alters the way CALCULATE applies a filter to the new filter context. Instead of overwriting an existing filter over the same column, it adds the new filter to the existing ones. Therefore, only the cells where the filtered category was already included in the filter context will produce a visible result. You see this in Figure 5-21.
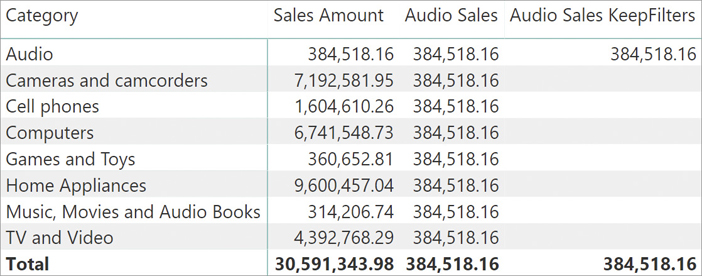
KEEPFILTERS does exactly what its name implies. Instead of overwriting the existing filter, it keeps the existing filter and adds the new filter to the filter context. We can depict the behavior with Figure 5-22.

Because KEEPFILTERS avoids overwriting, the new filter generated by the filter argument of CALCULATE is added to the context. If we look at the cell for the Audio Sales KeepFilters measure in the Cell Phones row, there the resulting filter context contains two filters: one filters Cell Phones; the other filters Audio. The intersection of the two conditions results in an empty set, which produces a blank result.
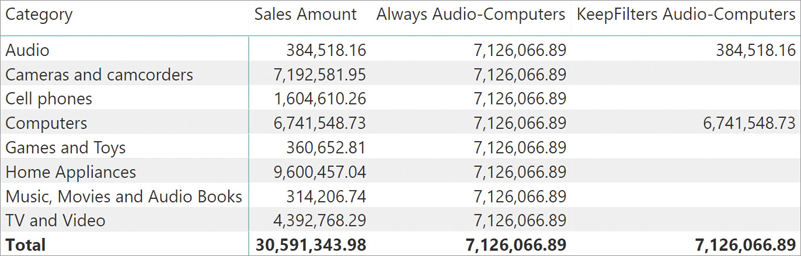
The behavior of KEEPFILTERS is clearer when there are multiple elements selected in a column. For example, consider the following measures; they filter Audio and Computers with and without KEEPFILTERS:
Always Audio-Computers :=
CALCULATE (
[Sales Amount],
'Product'[Category] IN { "Audio", "Computers" }
)
KeepFilters Audio-Computers :=
CALCULATE (
[Sales Amount],
KEEPFILTERS ( 'Product'[Category] IN { "Audio", "Computers" } )
)The report in Figure 5-23 shows that the version with KEEPFILTERS only computes the sales amount values for Audio and for Computers, leaving all other categories blank. The Total row only takes Audio and Computers into account.
KEEPFILTERS can be used either with a predicate or with a table. Indeed, the previous code could also be written in a more verbose way:
KeepFilters Audio-Computers :=
CALCULATE (
[Sales Amount],
KEEPFILTERS (
FILTER (
ALL ( 'Product'[Category] ),
'Product'[Category] IN { "Audio", "Computers" }
)
)
)This is just an example for educational purposes. You should use the simplest predicate syntax available for a filter argument. When filtering a single column, you can avoid writing the FILTER explicitly. Later however, you will see that more complex filter conditions require an explicit FILTER. In those cases, the KEEPFILTERS modifier can be used around the explicit FILTER function, as you see in the next section.
Filtering a single column
In the previous section, we introduced filter arguments referencing a single column in CALCULATE. It is important to note that you can have multiple references to the same column in one expression. For example, the following is a valid syntax because it references the same column (Sales[Net Price]) twice.
Sales 10-100 :=
CALCULATE (
[Sales Amount],
Sales[Net Price] >= 10 && Sales[Net Price] <= 100
)In fact, this is converted into the following syntax:
Sales 10-100 :=
CALCULATE (
[Sales Amount],
FILTER (
ALL ( Sales[Net Price] ),
Sales[Net Price] >= 10 && Sales[Net Price] <= 100
)
)The resulting filter context produced by CALCULATE only adds one filter over the Sales[Net Price] column. One important note about predicates as filter arguments in CALCULATE is that although they look like conditions, they are tables. If you read the first of the last two code snippets, it looks as though CALCULATE evaluates a condition. Instead, CALCULATE evaluates the list of all the values of Sales[Net Price] that satisfy the condition. Then, CALCULATE uses this table of values to apply a filter to the model.
When two conditions are in a logical AND, they can be represented as two separate filters. Indeed, the previous expression is equivalent to the following one:
Sales 10-100 :=
CALCULATE (
[Sales Amount],
Sales[Net Price] >= 10,
Sales[Net Price] <= 100
)However, keep in mind that the multiple filter arguments of CALCULATE are always merged with a logical AND. Thus, you must use a single filter in case of a logical OR statement, such as in the following measure:
Sales Blue+Red :=
CALCULATE (
[Sales Amount],
'Product'[Color] = "Red" || 'Product'[Color] = "Blue"
)By writing multiple filters, you would combine two independent filters in a single filter context. The following measure always produces a blank result because there are no products that are both Blue and Red at the same time:
Sales Blue and Red :=
CALCULATE (
[Sales Amount],
'Product'[Color] = "Red",
'Product'[Color] = "Blue"
)In fact, the previous measure corresponds to the following measure with a single filter:
Sales Blue and Red :=
CALCULATE (
[Sales Amount],
'Product'[Color] = "Red" && 'Product'[Color] = "Blue"
)The filter argument always returns an empty list of colors allowed in the filter context. Therefore, the measure always returns a blank value.
Whenever a filter argument refers to a single column, you can use a predicate. We suggest you do so because the resulting code is much easier to read. You should do so for logical AND conditions too. Nevertheless, never forget that you are relying on syntax-sugaring only. CALCULATE always works with tables, although the compact syntax might suggest otherwise.
On the other hand, whenever there are two or more different column references in a filter argument, it is necessary to write the FILTER condition as a table expression. You learn this in the following section.
Filtering with complex conditions
A filter argument referencing multiple columns requires an explicit table expression. It is important to understand the different techniques available to write such filters. Remember that creating a filter with the minimum number of columns required by the predicate is usually a best practice.
Consider a measure that sums the sales for only the transactions with an amount greater than or equal to 1,000. Getting the amount of each transaction requires the multiplication of the Quantity and Net Price columns. This is because you do not have a column that stores that amount for each row of the Sales table in the sample Contoso database. You might be tempted to write something like the following expression, which unfortunately will not work:
Sales Large Amount :=
CALCULATE (
[Sales Amount],
Sales[Quantity] * Sales[Net Price] >= 1000
)This code is not valid because the filter argument references two different columns in the same expression. As such, it cannot be converted automatically by DAX into a suitable FILTER condition. The best way to write the required filter is by using a table that only has the existing combinations of the columns referenced in the predicate:
Sales Large Amount :=
CALCULATE (
[Sales Amount],
FILTER (
ALL ( Sales[Quantity], Sales[Net Price] ),
Sales[Quantity] * Sales[Net Price] >= 1000
)
)This results in a filter context that has a filter with two columns and a number of rows that correspond to the unique combinations of Quantity and Net Price that satisfy the filter condition. This is shown in Figure 5-24.

This filter produces the result in Figure 5-25.

Be mindful that the slicer in Figure 5-25 is not filtering any value: The two displayed values are the minimum and the maximum values of Net Price. The next step is showing how the measure is interacting with the slicer. In a measure like Sales Large Amount, you need to pay attention when you overwrite existing filters over Quantity or Net Price. Indeed, because the filter argument uses ALL on the two columns, it ignores any previously existing filter on the same columns including, in this example, the filter of the slicer. The report in Figure 5-26 is the same as Figure 5-25 but, this time, the slicer filters for net prices between 500 and 3,000. The result is surprising.

The presence of value of Sales Large Amount for Audio and Music, Movies and Audio Books is unexpected. Indeed, for these two categories there are no sales in the net price range between 500 and 3,000, which is the filter context generated by the slicer. Still, the Sales Large Amount measure is showing a result.
The reason is that the filter context of Net Price created by the slicer is ignored by the Sales Large Amount measure, which overwrites the existing filter over both Quantity and Net Price. If you carefully compare figures 5-25 and 5-26, you will notice that the value of Sales Large Amount is identical, as if the slicer was not added to the report. Indeed, Sales Large Amount is completely ignoring the slicer.
If you focus on a cell, like the value of Sales Large Amount for Audio, the code executed to compute its value is the following:
Sales Large Amount :=
CALCULATE (
CALCULATE (
[Sales Amount],
FILTER (
ALL ( Sales[Quantity], Sales[Net Price] ),
Sales[Quantity] * Sales[Net Price] >= 1000
)
),
'Product'[Category] = "Audio",
Sales[Net Price] >= 500
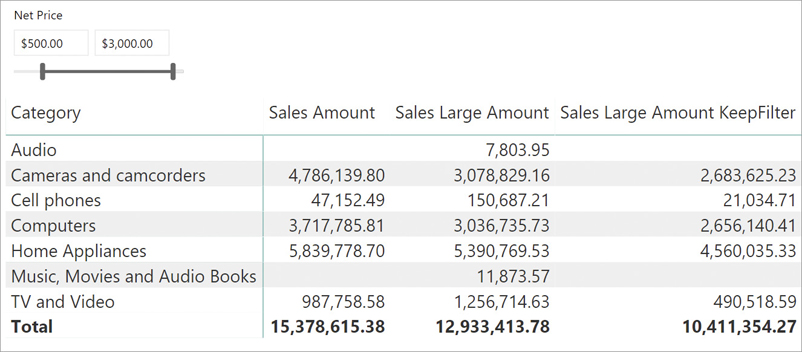
)From the code, you can see that the innermost ALL ignores the filter on Sales[Net Price] set by the outer CALCULATE. In that scenario, you can use KEEPFILTERS to avoid the overwrite of existing filters:
Sales Large Amount KeepFilter :=
CALCULATE (
[Sales Amount],
KEEPFILTERS (
FILTER (
ALL ( Sales[Quantity], Sales[Net Price] ),
Sales[Quantity] * Sales[Net Price] >= 1000
)
)
)The new Sales Large Amount KeepFilter measure produces the result shown in Figure 5-27.
Another way of specifying a complex filter is by using a table filter instead of a column filter. This is one of the preferred techniques of DAX newbies, although it is very dangerous to use. In fact, the previous measure can be written using a table filter:
Sales Large Amount Table :=
CALCULATE (
[Sales Amount],
FILTER (
Sales,
Sales[Quantity] * Sales[Net Price] >= 1000
)
)As you may remember, all the filter arguments of CALCULATE are evaluated in the filter context that exists outside of the CALCULATE itself. Thus, the iteration over Sales only considers the rows filtered in the existing filter context, which contains a filter on Net Price. Therefore, the semantic of the Sales Large Amount Table measure corresponds to the Sales Large Amount KeepFilter measure.
Although this technique looks easy, you should be careful in using it because it could have serious consequences on performance and on result accuracy. We will cover the details of these issues in Chapter 14. For now, just remember that the best practice is to always use a filter with the smallest possible number of columns.
Moreover, you should avoid table filters because they usually are more expensive. The Sales table might be very large, and scanning it row by row to evaluate a predicate can be a time-consuming operation. The filter in Sales Large Amount KeepFilter, on the other hand, only iterates the number of unique combinations of Quantity and Net Price. That number is usually much smaller than the number of rows of the entire Sales table.
Evaluation order in CALCULATE
Whenever you look at DAX code, the natural order of evaluation is innermost first. For example, look at the following expression:
Sales Amount Large :=
SUMX (
FILTER ( Sales, Sales[Quantity] >= 100 ),
Sales[Quantity] * Sales[Net Price]
)DAX needs to evaluate the result of FILTER before starting the evaluation of SUMX. In fact, SUMX iterates a table. Because that table is the result of FILTER, SUMX cannot start executing before FILTER has finished its job. This rule is true for all DAX functions, except for CALCULATE and CALCULATETABLE. Indeed, CALCULATE evaluates its filter arguments first and only at the end does it evaluate the first parameter, which is the expression to evaluate to provide the CALCULATE result.
Moreover, things are a bit more intricate because CALCULATE changes the filter context. All the filter arguments are executed in the filter context outside of CALCULATE, and each filter is evaluated independently. The order of filters within the same CALCULATE does not matter. Consequently, all the following measures are completely equivalent:
Sales Red Contoso :=
CALCULATE (
[Sales Amount],
'Product'[Color] = "Red",
KEEPFILTERS ( 'Product'[Brand] = "Contoso" )
)
Sales Red Contoso :=
CALCULATE (
[Sales Amount],
KEEPFILTERS ( 'Product'[Brand] = "Contoso" ),
'Product'[Color] = "Red"
)
Sales Red Contoso :=
VAR ColorRed =
FILTER (
ALL ( 'Product'[Color] ),
'Product'[Color] = "Red"
)
VAR BrandContoso =
FILTER (
ALL ( 'Product'[Brand] ),
'Product'[Brand] = "Contoso"
)
VAR SalesRedContoso =
CALCULATE (
[Sales Amount],
ColorRed,
KEEPFILTERS ( BrandContoso )
)
RETURN
SalesRedContosoThe version of Sales Red Contoso defined using variables is more verbose than the other versions, but you might want to use it in case the filters are complex expressions with explicit filters. This way, it is easier to understand that the filter is evaluated “before” CALCULATE.
This rule becomes more important in case of nested CALCULATE statements. In fact, the outermost filters are applied first, and the innermost are applied later. Understanding the behavior of nested CALCULATE statements is important, because you encounter this situation every time you nest measures calls. For example, consider the following measures, where Sales Green calls Sales Red:
Sales Red :=
CALCULATE (
[Sales Amount],
'Product'[Color] = "Red"
)
Green calling Red :=
CALCULATE (
[Sales Red],
'Product'[Color] = "Green"
)To make the nested measure call more evident, we can expand Sales Green this way:
Green calling Red Exp :=
CALCULATE (
CALCULATE (
[Sales Amount],
'Product'[Color] = "Red"
),
'Product'[Color] = "Green"
)The order of evaluation is the following:
First, the outer CALCULATE applies the filter, Product[Color] = “Green”.
Second, the inner CALCULATE applies the filter, Product[Color] = “Red”. This filter overwrites the previous filter.
Last, DAX computes [Sales Amount] with a filter for Product[Color] = “Red”.
Therefore, the result of both Red and Green calling Red is still Red, as shown in Figure 5-28.

![]() Note
Note
The description we provided is for educational purposes only. In reality the engine uses lazy evaluation for the filter context. So, in the presence of filter argument overwrites such as the previous code, the outer filter might never be evaluated because it would have been useless. Nevertheless, this behavior is for optimization only. It does not change the semantics of CALCULATE in any way.
We can review the order of the evaluation and how the filter context is evaluated with another example. Consider the following measure:
Sales YB :=
CALCULATE (
CALCULATE (
[Sales Amount],
'Product'[Color] IN { "Yellow", "Black" }
),
'Product'[Color] IN { "Black", "Blue" }
)The evaluation of the filter context produced by Sales YB is visible in Figure 5-29.
As seen before, the innermost filter over Product[Color] overwrites the outermost filters. Therefore, the result of the measure shows the sum of products that are Yellow or Black. By using KEEPFILTERS in the innermost CALCULATE, the filter context is built by keeping the two filters instead of overwriting the existing filter:
Sales YB KeepFilters :=
CALCULATE (
CALCULATE (
[Sales Amount],
KEEPFILTERS ( 'Product'[Color] IN { "Yellow", "Black" } )
),
'Product'[Color] IN { "Black", "Blue" }
)
The evaluation of the filter context produced by Sales YB KeepFilters is visible in Figure 5-30.
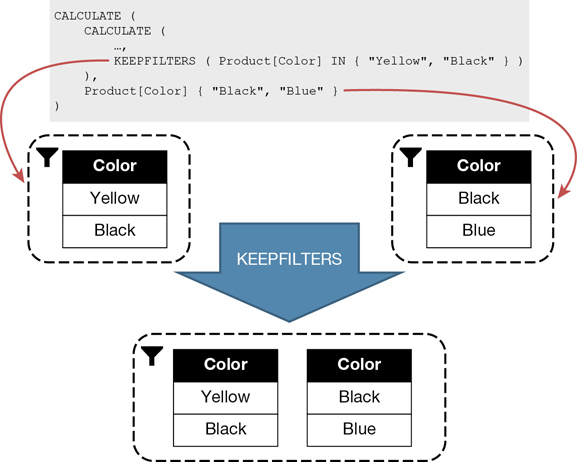
Because the two filters are kept together, they are intersected. Therefore, in the new filter context the only visible color is Black because it is the only value present in both filters.
However, the order of the filter arguments within the same CALCULATE is irrelevant because they are applied to the filter context independently.
Understanding context transition
In Chapter 4, “Understanding evaluation contexts,” we evoked multiple times that the row context and the filter context are different concepts. This still holds true. However, there is one operation performed by CALCULATE that can transform a row context into a filter context. It is the operation of context transition, defined as follows:
CALCULATE invalidates any row context. It automatically adds as filter arguments all the columns that are currently being iterated in any row context—filtering their actual value in the row being iterated.
Context transition is hard to understand at the beginning, and even seasoned DAX coders find it complex to follow all the implications of context transition. We are more than confident that the previous definition does not suffice to fully understand context transition.
Therefore, we are going to describe context transition through several examples of increasing complexity. But before discussing such a delicate concept, let us make sure we thoroughly understand row context and filter context.
Row context and filter context recap
We can recap some important facts about row context and filter context with the aid of Figure 5-31, which shows a report with the Brand on the rows and a diagram describing the evaluation process. Products and Sales in the diagram are not displaying real data. They only contain a few rows to make the points clearer.

The following comments on Figure 5-31 are helpful to monitor your understanding of the whole process for evaluating the Sales Amount measure for the Contoso row:
The report creates a filter context containing a filter for Product[Brand] = “Contoso”.
The filter works on the entire model, filtering both the Product and the Sales tables.
The filter context reduces the number of rows iterated by SUMX while scanning Sales. SUMX only iterates the Sales rows that are related to a Contoso product.
In the figure there are two rows in Sales with product A, which is branded Contoso.
Consequently, SUMX iterates two rows. In the first row it computes 1*11.00 with a partial result of 11.00. In the second row it computes 2*10.99 with a partial result of 21.98.
SUMX returns the sum of the partial results gathered during the iteration.
During the iteration of Sales, SUMX only scans the visible portion of the Sales table, generating a row context for each visible row.
When SUMX iterates the first row, Sales[Quantity] equals 1, whereas Sales[Net Price] equals 11. On the second row, the values are different. Columns have a current value that depends on the iterated row. Potentially, each row iterated has a different value for all the columns.
During the iteration, there is a row context and a filter context. The filter context is still the same that filters Contoso because no CALCULATE has been executed to modify it.
Speaking about context transition, the last statement is the most important. During the iteration the filter context is still active, and it filters Contoso. The row context, on the other hand, is currently iterating the Sales table. Each column of Sales has a given value. The row context is providing the value via the current row. Remember that the row context iterates; the filter context does not.
This is an important detail. We invite you to double-check your understanding in the following scenario. Imagine you create a measure that simply counts the number of rows in the Sales table, with the following code:
NumOfSales := COUNTROWS ( Sales )
Once used in the report, the measure counts the number of Sales rows that are visible in the current filter context. The result shown in Figure 5-32 is as expected: a different number for each brand.

Because there are 37,984 rows in Sales for the Contoso brand, this means that an iteration over Sales for Contoso will iterate exactly 37,984 rows. The Sales Amount measure we used so far would complete its execution after 37,984 multiplications.
With the understanding you have obtained so far, can you guess the result of the following measure on the Contoso row?
Sum Num Of Sales := SUMX ( Sales, COUNTROWS ( Sales ) )
Do not rush in deciding your answer. Take your time, study this simple code carefully, and make an educated guess. In the following paragraph we provide the correct answer.
The filter context is filtering Contoso. From the previous examples, it is understood that SUMX iterates 37,984 times. For each of these 37,984 rows, SUMX computes the number of rows visible in Sales in the current filter context. The filter context is still the same, so for each row the result of COUNTROWS is always 37,984. Consequently, SUMX sums the value of 37,984 for 37,984 times. The result is 37,984 squared. You can confirm this by looking at Figure 5-33, where the measure is displayed in the report.

Now that we have refreshed the main ideas about row context and filter context, we can further discuss the impact of context transition.
Introducing context transition
A row context exists whenever an iteration is happening on a table. Inside an iteration are expressions that depend on the row context itself. The following expression, which you have studied multiple times by now, comes in handy:
Sales Amount :=
SUMX (
Sales,
Sales[Quantity] * Sales[Unit Price]
)The two columns Quantity and Unit Price have a value in the current row context. In the previous section we showed that if the expression used inside an iteration is not strictly bound to the row context, then it is evaluated in the filter context. As such the results are surprising, at least for beginners. Nevertheless, one is completely free to use any function inside a row context. Among the many functions available, one appears to be more special: CALCULATE.
If executed in a row context, CALCULATE invalidates the row context before evaluating its expression. Inside the expression evaluated by CALCULATE, all the previous row contexts will no longer be valid. Thus, the following code produces a syntax error:
Sales Amount :=
SUMX (
Sales,
CALCULATE ( Sales[Quantity] ) -- No row context inside CALCULATE, ERROR !
)The reason is that the value of the Sales[Quantity] column cannot be retrieved inside CALCULATE because CALCULATE invalidates the row context that exists outside of CALCULATE itself. Nevertheless, this is only part of what context transition performs. The second—and most relevant—operation is that CALCULATE adds as filter arguments all the columns of the current row context with their current value. For example, look at the following code:
Sales Amount :=
SUMX (
Sales,
CALCULATE ( SUM ( Sales[Quantity] ) ) -- SUM does not require a row context
)There are no filter arguments in CALCULATE. The only CALCULATE argument is the expression to evaluate. Thus, it looks like CALCULATE will not overwrite the existing filter context. The point is that CALCULATE, because of context transition, is silently creating many filter arguments. It creates a filter for each column in the iterated table. You can use Figure 5-34 to obtain a first look at the behavior of context transition. We used a reduced set of columns for visual purposes.
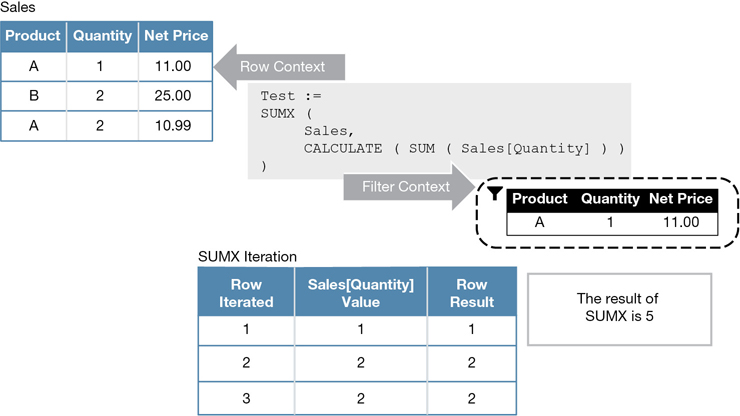
During the iteration CALCULATE starts on the first row, and it computes SUM ( Sales[Quantity] ). Even though there are no filter arguments, CALCULATE adds one filter argument for each of the columns of the iterated table. Namely, there are three columns in the example: Product, Quantity, and Net Price. As a result, the filter context generated by the context transition contains the current value (A, 1, 11.00) for each of the columns (Product, Quantity, Net Price). The process, of course, continues for each one of the three rows during the iteration made by SUMX.
In other words, the execution of the previous SUMX results in these three CALCULATE executions:
CALCULATE (
SUM ( Sales[Quantity] ),
Sales[Product] = "A",
Sales[Quantity] = 1,
Sales[Net Price] = 11
) +
CALCULATE (
SUM ( Sales[Quantity] ),
Sales[Product] = "B",
Sales[Quantity] = 2,
Sales[Net Price] = 25
) +
CALCULATE (
SUM ( Sales[Quantity] ),
Sales[Product] = "A",
Sales[Quantity] = 2,
Sales[Net Price] = 10.99
)These filter arguments are hidden. They are added by the engine automatically, and there is no way to avoid them. In the beginning, context transition seems very strange. Nevertheless, once one gets used to context transition, it is an extremely powerful feature. Hard to master, but extremely powerful.
We summarize the considerations presented earlier, before we further discuss a few of them specifically:
Context transition is expensive. If context transition is used during an iteration on a table with 10 columns and one million rows, then CALCULATE needs to apply 10 filters, one million times. No matter what, it will be a slow operation. This is not to say that relying on context transition should be avoided. However, it does make CALCULATE a feature that needs to be used carefully.
Context transition does not only filter one row. The original row context existing outside of CALCULATE always only points to one row. The row context iterates on a row-by-row basis. When the row context is moved to a filter context through context transition, the newly created filter context filters all the rows with the same set of values. Thus, you should not assume that the context transition creates a filter context with one row only. This is very important, and we will return to this topic in the next sections.
Context transition uses columns that are not present in the formula. Although the columns used in the filter are hidden, they are part of the expression. This makes any formula with CALCULATE much more complex than it first seems. If a context transition is used, then all the columns of the table are part of the expression as hidden filter arguments. This behavior might create unexpected dependencies. This topic is also described later in this section.
Context transition creates a filter context out of a row context. You might remember the evaluation context mantra, “the row context iterates a table, whereas the filter context filters the model.” Once context transition transforms a row context into a filter context, it changes the nature of the filter. Instead of iterating a single row, DAX filters the whole model; relationships become part of the equation. In other words, context transition happening on one table might propagate its filtering effects far from the table the row context originated from.
Context transition is invoked whenever there is a row context. For example, if one uses CALCULATE in a calculated column, context transition occurs. There is an automatic row context inside a calculated column, and this is enough for context transition to occur.
Context transition transforms all the row contexts. When nested iterations are being performed on multiple tables, context transition considers all the row contexts. It invalidates all of them and adds filter arguments for all the columns that are currently being iterated by all the active row contexts.
Context transition invalidates the row contexts. Though we have repeated this concept multiple times, it is worth bringing to your attention again. None of the outer row contexts are valid inside the expression evaluated by CALCULATE. All the outer row contexts are transformed into equivalent filter contexts.
As anticipated earlier in this section, most of these considerations require further explanation. In the remaining part of this section about context transition, we provide a deeper analysis of these main points. Although all these considerations are shown as warnings, in reality they are important features. Being ignorant of certain behaviors can ensure surprising results. Nevertheless, once you master the behavior, you start leveraging it as you see fit. The only difference between a strange behavior and a useful feature—at least in DAX—is your level of knowledge.
Context transition in calculated columns
A calculated column is evaluated in a row context. Therefore, using CALCULATE in a calculated column triggers a context transition. We use this feature to create a calculated column in Product that marks as “High Performance” all the products that—alone—sold more than 1% of the total sales of all the products.
To produce this calculated column, we need two values: the sales of the current product and the total sales of all the products. The former requires filtering the Sales table so that it only computes sales amount for the current product, whereas the latter requires scanning the Sales table with no active filters. Here is the code:
'Product'[Performance] =
VAR TotalSales = -- Sales of all the products
SUMX (
Sales, -- Sales is not filtered
Sales[Quantity] * Sales[Net Price] -- thus here we compute all sales
)
VAR CurrentSales =
CALCULATE ( -- Performs context transition
SUMX (
Sales, -- Sales of the current product only
Sales[Quantity] * Sales[Net Price] -- thus here we compute sales of the
) -- current product only
)
VAR Ratio = 0.01 -- 1% expressed as a real number
VAR Result =
IF (
CurrentSales >= TotalSales * Ratio,
"High Performance product",
"Regular product"
)
RETURN
ResultYou note that there is only one difference between the two variables: TotalSales is executed as a regular iteration, whereas CurrentSales computes the same DAX code within a CALCULATE function. Because this is a calculated column, the row context is transformed into a filter context. The filter context propagates through the model and it reaches Sales, only filtering the sales of the current product.
Thus, even though the two variables look similar, their content is completely different. TotalSales computes the sales of all the products because the filter context in a calculated column is empty and does not filter anything. CurrentSales computes the sales of the current product only thanks to the context transition performed by CALCULATE.
The remaining part of the code is a simple IF statement that checks whether the condition is met and marks the product appropriately. One can use the resulting calculated column in a report like the one visible in Figure 5-35.
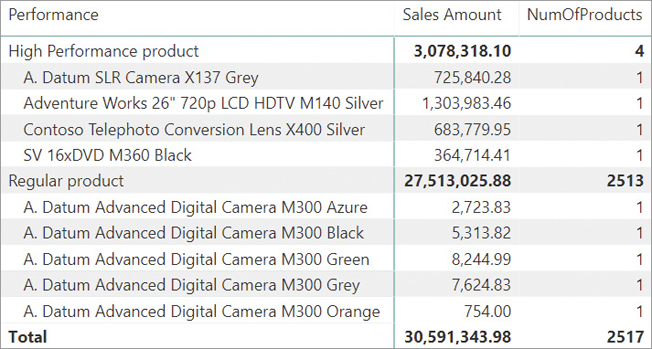
In the code of the Performance calculated column, we used CALCULATE and context transition as a feature. Before moving on, we must check that we considered all the implications. The Product table is small, containing just a few thousand rows. Thus, performance is not an issue. The filter context generated by CALCULATE filters all the columns. Do we have a guarantee that CurrentSales only contains the sales of the current product? In this special case, the answer is yes. The reason is that each row of Product is unique because Product contains a column with a different value for each row—ProductKey. Consequently, the filter context generated by the context transition is guaranteed to only filter one product.
In this case, we could rely on context transition because each row of the iterated table is unique. Beware that this is not always true. We want to demonstrate that with an example that is purposely wrong. We create a calculated column, in Sales, containing this code:
Sales[Wrong Amt] =
CALCULATE (
SUMX (
Sales,
Sales[Quantity] * Sales[Net Price]
)
)Being a calculated column, it runs in a row context. CALCULATE performs the context transition, so SUMX iterates all the rows in Sales with an identical set of values corresponding to the current row in Sales. The problem is that the Sales table does not have any column with unique values. Therefore, there is a chance that multiple identical rows exist and, if they exist, they will be filtered together. In other words, there is no guarantee that SUMX always iterates only one row in the Wrong Amt column.
If you are lucky, there are many duplicated rows, and the value computed by this calculated column is totally wrong. This way, the problem would be clearly visible and immediately recognized. In many real-world scenarios, the number of duplicated rows in tables is tiny, making these inaccurate calculations hard to spot and debug. The sample database we use in this book is no exception. Look at the report in Figure 5-36 showing the correct value for Sales Amount and the wrong value computed by summing the Wrong Amt calculated column.
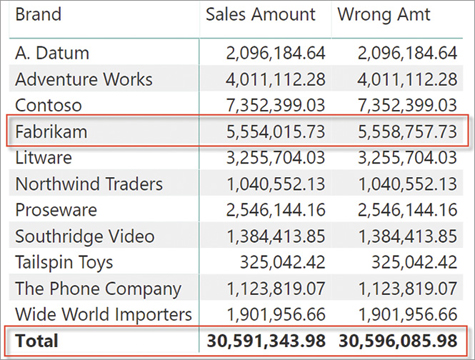
You can see that the difference only exists at the total level and for the Fabrikam brand. There are some duplicates in the Sales table—related to some Fabrikam product—that perform the calculation twice. The presence of these rows might be legitimate: The same customer bought the same product in the same store on the same day in the morning and in the afternoon, but the Sales table only stores the date and not the time of the transaction. Because the number of duplicates is small, most numbers look correct. However, the calculation is wrong because it depends on the content of the table. Inaccurate numbers might appear at any time because of duplicated rows. The more duplicates there are, the worse the result turns out.
In this case, relying on context transition is the wrong choice. Because the table is not guaranteed to only have unique rows, context transition is not safe to use. An expert DAX coder should know this in advance. Besides, the Sales table might contain millions of rows; thus, this calculated column is not only wrong, it is also very slow.
Context transition with measures
Understanding context transition is very important because of another important aspect of DAX.
Every measure reference always has an implicit CALCULATE surrounding it.
Because of CALCULATE, a measure reference generates an implicit context transition if executed in the presence of any row context. This is why in DAX, it is important to use the correct naming convention when writing column references (always including the table name) and measure references (always without the table name). You want to be aware of any implicit context transition writing and reading a DAX expression.
This simple initial definition deserves a longer explanation with several examples. The first one is that translating a measure reference always requires wrapping the expression of the measure within a CALCULATE function. For example, consider the following definition of the Sales Amount measure and of the Product Sales calculated column in the Product table:
Sales Amount :=
SUMX (
Sales,
Sales[Quantity] * Sales[Net Price]
)
'Product'[Product Sales] = [Sales Amount]The Product Sales column correctly computes the sum of Sales Amount only for the current product in the Product table. Indeed, expanding the Sales Amount measure in the definition of Product Sales requires the CALCULATE function that wraps the definition of Sales Amount:
'Product'[Product Sales] =
CALCULATE
SUMX (
Sales,
Sales[Quantity] * Sales[Net Price]
)
)Without CALCULATE, the result of the calculated column would produce the same value for all the products. This would correspond to the sales amount of all the rows in Sales without any filtering by product. The presence of CALCULATE means that context transition occurs, producing in this case the desired result. A measure reference always calls CALCULATE. This is very important and can be used to write short and powerful DAX expressions. However, it could also lead to big mistakes if you forget that the context transition takes place every time the measure is called in a row context.
As a rule of thumb, you can always replace a measure reference with the expression that defines the measure wrapped inside CALCULATE. Consider the following definition of a measure called Max Daily Sales, which computes the maximum value of Sales Amount computed day by day:
Max Daily Sales :=
MAXX (
'Date',
[Sales Amount]
)This formula is intuitive to read. However, Sales Amount must be computed for each date, only filtering the sales of that day. This is exactly what context transition performs. Internally, DAX replaced the Sales Amount measure reference with its definition wrapped by CALCULATE, as in the following example:
Max Daily Sales :=
MAXX (
'Date',
CALCULATE (
SUMX (
Sales,
Sales[Quantity] * Sales[Net Price]
)
)
)We will use this feature extensively in Chapter 7, “Working with iterators and CALCULATE,” when we start writing complex DAX code to solve specific scenarios. This initial description just completes the explanation of context transition, which happens in these cases:
When a CALCULATE or CALCULATETABLE function is called in the presence of any row context.
When there is a measure reference in the presence of any row context because the measure reference internally executes its DAX code within a CALCULATE function.
This powerful behavior might lead to mistakes, mainly due to the incorrect assumption that you can replace a measure reference with the DAX code of its definition. You cannot. This could work when there are no row contexts, like in a measure, but this is not possible when the measure reference appears within a row context. It is easy to forget this rule, so we provide an example of what could happen by making an incorrect assumption.
You may have noticed that in the previous example, we wrote the code for a calculated column repeating the iteration over Sales twice. Here is the code we already presented in the previous example:
'Product'[Performance] =
VAR TotalSales = -- Sales of all the products
SUMX (
Sales, -- Sales is not filtered
Sales[Quantity] * Sales[Net Price] -- thus here we compute all sales
)
VAR CurrentSales =
CALCULATE ( -- Performs the context transition
SUMX (
Sales, -- Sales of the current product only
Sales[Quantity] * Sales[Net Price] -- thus here we compute sales of the
) -- current product only
)
VAR Ratio = 0.01 -- 1% expressed as a real number
VAR Result =
IF (
CurrentSales >= TotalSales * Ratio,
"High Performance product",
"Regular product"
)
RETURN
ResultThe iteration executed by SUMX is the same code for the two variables: One is surrounded by CALCULATE, whereas the other is not. It might seem like a good idea to rewrite the code and use a measure to host the code of the iteration. This could be even more relevant in case the expression is not a simple SUMX but, rather, some more complex code. Unfortunately, this approach will not work because the measure reference will always include a CALCULATE around the expression that the measure replaced.
Imagine creating a measure, Sales Amount, and then a calculated column that calls the measure surrounding it—once with CALCULATE and once without CALCULATE.
Sales Amount :=
SUMX (
Sales,
Sales[Quantity] * Sales[Net Price]
)
'Product'[Performance] =
VAR TotalSales = [Sales Amount]
VAR CurrentSales = CALCULATE ( [Sales Amount] )
VAR Ratio = 0.01
VAR Result =
IF (
CurrentSales >= TotalSales * Ratio,
"High Performance product",
"Regular product"
)
RETURN
ResultThough it looked like a good idea, this calculated column does not compute the expected result. The reason is that both measure references will have their own implicit CALCULATE around them. Thus, TotalSales does not compute the sales of all the products. Instead, it only computes the sales of the current product because the hidden CALCULATE performs a context transition. CurrentSales computes the same value. In CurrentSales, the extra CALCULATE is redundant. Indeed, CALCULATE is already there, only because it is referencing a measure. This is more evident by looking at the code resulting by expanding the Sales Amount measure:
'Product'[Performance] =
VAR TotalSales =
CALCULATE (
SUMX (
Sales,
Sales[Quantity] * Sales[Net Price]
)
)
VAR CurrentSales =
CALCULATE (
CALCULATE (
SUMX (
Sales,
Sales[Quantity] * Sales[Net Price]
)
)
)
VAR Ratio = 0.01
VAR Result =
IF (
CurrentSales >= TotalSales * Ratio,
"High Performance product",
"Regular product"
)
RETURN
ResultWhenever you read a measure call in DAX, you should always read it as if CALCULATE were there. Because it is there. We introduced a rule in Chapter 2, “Introducing DAX,” where we said that it is a best practice to always use the table name in front of columns, and never use the table name in front of measures. The reason is what we are discussing now.
When reading DAX code, it is of paramount importance that the user be immediately able to understand whether the code is referencing a measure or a column. The de facto standard that nearly every DAX coder adopts is to omit the table name in front of measures.
The automatic CALCULATE makes it easy to author formulas that perform complex calculations with iterations. We will use this feature extensively in Chapter 7 when we start writing complex DAX code to solve specific scenarios.
Understanding circular dependencies
When you design a data model, you should pay attention to the complex topic of circular dependencies in formulas. In this section, you learn what circular dependencies are and how to avoid them in your model. Before introducing circular dependencies, it is worth discussing simple, linear dependencies with the aid of an example. Look at the following calculated column:
Sales[Margin] = Sales[Net Price] - Sales[Unit Cost]
The new calculated column depends on two columns: Net Price and Unit Cost. This means that to compute the value of Margin, DAX needs to know in advance the values of the two other columns. Dependencies are an important part of the DAX model because they drive the order in which calculated columns and calculated tables are processed. In the example, Margin can only be computed after Net Price and Unit Cost already have a value. The coder does not need to worry about dependencies. Indeed, DAX handles them gracefully, building a complex graph that drives the order of evaluation of all its internal objects. However, it is possible to write code in such a way that circular dependencies appear in the graph. Circular dependencies happen when DAX cannot determine the order of evaluation of an expression because there is a loop in the chain of dependencies.
For example, consider two calculated columns with the following formulas:
Sales[MarginPct] = DIVIDE ( Sales[Margin], Sales[Unit Cost] ) Sales[Margin] = Sales[MarginPct] * Sales[Unit Cost]
In this code, MarginPct depends on Margin and, at the same time, Margin depends on MarginPct. There is a loop in the chain of dependencies. In that scenario, DAX refuses to accept the last formula and raises the error, “A circular dependency was detected.”
Circular dependencies do not happen frequently because as humans we understand the problem well. B cannot depend on A if, at the same time, A depends on B. Nevertheless, there is a scenario where circular dependency occurs—not because it is one’s intention to do so, but only because one does not consider certain implications by reading DAX code. This scenario includes the use of CALCULATE.
Imagine a calculated column in Sales with the following code:
Sales[AllSalesQty] = CALCULATE ( SUM ( Sales[Quantity] ) )
The interesting question is, which columns does AllSalesQty depend on? Intuitively, one would answer that the new column depends solely on Sales[Quantity] because it is the only column used in the expression. However, it is all too easy to forget the real semantics of CALCULATE and context transition. Because CALCULATE runs in a row context, all current values of all the columns of the table are included in the expression, though hidden. Thus, the real expression evaluated by DAX is the following:
Sales[AllSalesQty] =
CALCULATE (
SUM ( Sales[Quantity] ),
Sales[ProductKey] = <CurrentValueOfProductKey>,
Sales[StoreKey] = <CurrentValueOfStoreKey>,
...,
Sales[Margin] = <CurrentValueOfMargin>
)As you see, the list of columns AllSalesQty depends on is actually the full set of columns of the table. Once CALCULATE is being used in a row context, the calculation suddenly depends on all the columns of the iterated table. This is much more evident in calculated columns, where the row context is present by default.
If one authors a single calculated column using CALCULATE, everything still works fine. The problem appears if one tries to author two separate calculated columns in a table, with both columns using CALCULATE, thus firing context transition in both cases. In fact, the following new calculated column will fail:
Sales[NewAllSalesQty] = CALCULATE ( SUM ( Sales[Quantity] ) )
The reason for this is that CALCULATE adds all the columns of the table as filter arguments. Adding a new column to a table changes the definition of existing columns too. If one were able to create NewAllSalesQty, the code of the two calculated columns would look like this:
Sales[AllSalesQty] =
CALCULATE (
SUM ( Sales[Quantity] ),
Sales[ProductKey] = <CurrentValueOfProductKey>,
...,
Sales[Margin] = <CurrentValueOfMargin>,
Sales[NewAllSalesQty] = <CurrentValueOfNewAllSalesQty>
)
Sales[NewAllSalesQty] =
CALCULATE (
SUM ( Sales[Quantity] ),
Sales[ProductKey] = <CurrentValueOfProductKey>,
...,
Sales[Margin] = <CurrentValueOfMargin>,
Sales[AllSalesQty] = <CurrentValueOfAllSalesQty>
)You can see that the two highlighted rows reference each other. AllSalesQty depends on the value of NewAllSalesQty and, at the same time, NewAllSalesQty depends on the value of AllSalesQty. Although very well hidden, a circular dependency does exist. DAX detects the circular dependency, preventing the code from being accepted.
The problem, although somewhat complex to detect, has a simple solution. If the table on which CALCULATE performs the context transition contains one column with unique values and DAX is aware of that, then the context transition only filters that column from a dependency point of view.
For example, consider a calculated column in the Product table with the following code:
'Product'[ProductSales] = CALCULATE ( SUM ( Sales[Quantity] ) )
In this case, there is no need to add all the columns as filter arguments. In fact, Product contains one column that has a unique value for each row of the Product table—that is ProductKey. This is well-known by the DAX engine because that column is on the one-side of a one-to-many relationship. Consequently, when the context transition occurs, the engine knows that it would be pointless to add a filter to each column. The code would be translated into the following:
'Product'[ProductSales] =
CALCULATE (
SUM ( Sales[Quantity] ),
'Product'[ProductKey] = <CurrentValueOfProductKey>
)As you can see, the ProductSales calculated column in the Product table depends solely on ProductKey. Therefore, one could create many calculated columns using CALCULATE because all of them would only depend on the column with unique values.
![]() Note
Note
The last CALCULATE equivalent statement for the context transition is not totally accurate. We used it for educational purposes only. CALCULATE adds all the columns of the table as filter arguments, even if a row identifier is present. Nevertheless, the internal dependency is only created on the unique column. The presence of the unique column lets DAX evaluate multiple columns with CALCULATE. Still, the semantics of CALCULATE is the same with or without the unique column: All the columns of the iterated table are added as filter arguments.
We already discussed the fact that relying on context transition on a table that contains duplicates is a serious problem. The presence of circular dependencies is another very good reason why one should avoid using CALCULATE and context transition whenever the uniqueness of rows is not guaranteed.
Resorting to a column with unique values for each row is not enough to ensure that CALCULATE only depends on it for the context transition. The data model must be aware of that. How does DAX know that a column contains unique values? There are multiple ways to provide this information to the engine:
When a table is the target (one-side) of a relationship, then the column used to build the relationship is marked as unique. This technique works in any tool.
When a column is selected in the Mark As Date Table setting, then the column is implicitly unique—more on this in Chapter 8, “Time intelligence calculations.”
You can manually set the property of a row identifier for the unique column by using the Table Behavior properties. This technique only works in Power Pivot for Excel and Analysis Services Tabular; it is not available in Power BI at the time of writing.
Any one of these operations informs the DAX engine that the table has a row identifier, stopping the process of a table that does not respect that constraint. When a table has a row identifier, you can use CALCULATE without worrying about circular dependencies. The reason is that the context transition depends on the key column only.
![]() Note
Note
Though described as a feature, this behavior is actually a side effect of an optimization. The semantics of DAX require the dependency from all the columns. A specific optimization introduced very early in the engine only creates the dependency on the primary key of the table. Because many users rely on this behavior today, it has become part of the language. Still, it remains an optimization. In borderline scenarios—for example when using USERELATIONSHIP as part of the formula—the optimization does not kick in, thus recreating the circular dependency error.
CALCULATE modifiers
As you have learned in this chapter, CALCULATE is extremely powerful and produces complex DAX code. So far, we have only covered filter arguments and context transition. There is still one concept required to provide the set of rules to fully understand CALCULATE. It is the concept of CALCULATE modifier.
We introduced two modifiers earlier, when we talked about ALL and KEEPFILTERS. While ALL can be both a modifier and a table function, KEEPFILTERS is always a filter argument modifier—meaning that it changes the way one filter is merged with the original filter context. CALCULATE accepts several different modifiers that change how the new filter context is prepared. However, the most important of all these modifiers is a function that you already know very well: ALL. When ALL is directly used in a CALCULATE filter argument, it acts as a CALCULATE modifier instead of being a table function. Other important modifiers include USERELATIONSHIP, CROSSFILTER, and ALLSELECTED, which have separate descriptions. The ALLEXCEPT, ALLSELECTED, ALLCROSSFILTERED and ALLNOBLANKROW modifiers have the same precedence rules of ALL.
In this section we introduce these modifiers; then we will discuss the order of precedence of the different CALCULATE modifiers and filter arguments. At the end, we will present the final schema of CALCULATE rules.
Understanding USERELATIONSHIP
The first CALCULATE modifier you learn is USERELATIONSHIP. CALCULATE can activate a relationship during the evaluation of its expression by using this modifier. A data model might contain both active and inactive relationships. One might have inactive relationships in the model because there are several relationships between two tables, and only one of them can be active.
As an example, one might have order date and delivery date stored in the Sales table for each order. Typically, the requirement is to perform sales analysis based on the order date, but one might need to consider the delivery date for some specific measures. In that scenario, an option is to create two relationships between Sales and Date: one based on Order Date and another one based on Delivery Date. The model looks like the one in Figure 5-37.
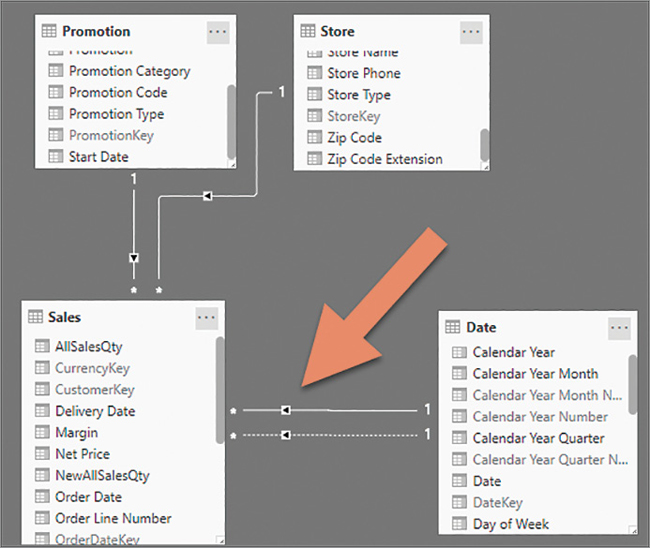
Only one of the two relationships can be active at a time. For example, in this demo model the relationship with Order Date is active, whereas the one linked to Delivery Date is kept inactive. To author a measure that shows the delivered value in a given time period, the relationship with Delivery Date needs to be activated for the duration of the calculation. In this scenario, USERELATIONSHIP is of great help as in the following code:
Delivered Amount:=
CALCULATE (
[Sales Amount],
USERELATIONSHIP ( Sales[Delivery Date], 'Date'[Date] )
)The relationship between Delivery Date and Date is activated during the evaluation of Sales Amount. In the meantime, the relationship with Order Date is deactivated. Keep in mind that at a given point in time, only one relationship can be active between any two tables. Thus, USERELATIONSHIP temporarily activates one relationship, deactivating the one active outside of CALCULATE.
Figure 5-38 shows the difference between Sales Amount based on the Order Date, and the new Delivered Amount measure.

When using USERELATIONSHIP to activate a relationship, you need to be aware of an important aspect: Relationships are defined when a table reference is used, not when RELATED or other relational functions are invoked. We will cover the details of this in Chapter 14 by using expanded tables. For now, an example should suffice. To compute all amounts delivered in 2007, the following formula will not work:
Delivered Amount 2007 v1 :=
CALCULATE (
[Sales Amount],
FILTER (
Sales,
CALCULATE (
RELATED ( 'Date'[Calendar Year] ),
USERELATIONSHIP ( Sales[Delivery Date], 'Date'[Date] )
) = "CY 2007"
)
)In fact, CALCULATE would inactivate the row context generated by the FILTER iteration. Thus, inside the CALCULATE expression, one cannot use the RELATED function at all. One option to author the code would be the following:
Delivered Amount 2007 v2 :=
CALCULATE (
[Sales Amount],
CALCULATETABLE (
FILTER (
Sales,
RELATED ( 'Date'[Calendar Year] ) = "CY 2007"
),
USERELATIONSHIP (
Sales[Delivery Date],
'Date'[Date]
)
)
)In this latter formulation, Sales is referenced after CALCULATE has activated the required relationship. Therefore, the use of RELATED inside FILTER happens with the relationship with Delivery Date active. The Delivered Amount 2007 v2 measure works, but a much better formulation of the same measure relies on default filter context propagation rather than relying on RELATED:
Delivered Amount 2007 v3 :=
CALCULATE (
[Sales Amount],
'Date'[Calendar Year] = "CY 2007",
USERELATIONSHIP (
Sales[Delivery Date],
'Date'[Date]
)
)When you use USERELATIONSHIP in a CALCULATE statement, all the filter arguments are evaluated using the relationship modifiers that appear in the same CALCULATE statement—regardless of their order. For example, in the Delivered Amount 2007 v3 measure, the USERELATIONSHIP modifier affects the predicate filtering Calendar Year, although it is the previous parameter within the same CALCULATE function call.
This behavior makes the use of nondefault relationships a complex operation in calculated column expressions. The invocation of the table is implicit in a calculated column definition. Therefore, you do not have control over it, and you cannot change that behavior by using CALCULATE and USERELATIONSHIP.
One important note is the fact that USERELATIONSHIP does not introduce any filter by itself. Indeed, USERELATIONSHIP is not a filter argument. It is a CALCULATE modifier. It only changes the way other filters are applied to the model. If you carefully look at the definition of Delivered Amount in 2007 v3, you might notice that the filter argument applies a filter on the year 2007, but it does not indicate which relationship to use. Is it using Order Date or Delivery Date? The relationship to use is defined by USERELATIONSHIP.
Thus, CALCULATE first modifies the structure of the model by activating the relationship, and only later does it apply the filter argument. If that were not the case—that is, if the filter argument were always evaluated on the current relationship architecture—then the calculation would not work.
There are precedence rules in the application of filter arguments and of CALCULATE modifiers. The first rule is that CALCULATE modifiers are always applied before any filter argument, so that the effect of filter arguments is applied on the modified version of the model. We discuss precedence of CALCULATE arguments in more detail later.
Understanding CROSSFILTER
The next CALCULATE modifier you learn is CROSSFILTER. CROSSFILTER is somewhat similar to USERELATIONSHIP because it manipulates the architecture of the relationships in the model. Nevertheless, CROSSFILTER can perform two different operations:
It can change the cross-filter direction of a relationship.
It can disable a relationship.
USERELATIONSHIP lets you activate a relationship while disabling the active relationship, but it cannot disable a relationship without activating another one between the same tables. CROSSFILTER works in a different way. CROSSFILTER accepts two parameters, which are the columns involved in the relationship, and a third parameter that can be either NONE, ONEWAY, or BOTH. For example, the following measure computes the distinct count of product colors after activating the relationship between Sales and Product as a bidirectional one:
NumOfColors :=
CALCULATE (
DISTINCTCOUNT ( 'Product'[Color] ),
CROSSFILTER ( Sales[ProductKey], 'Product'[ProductKey], BOTH )
)As is the case with USERELATIONSHIP, CROSSFILTER does not introduce filters by itself. It only changes the structure of the relationships, leaving to other filter arguments the task of applying filters. In the previous example, the effect of the relationship only affects the DISTINCTCOUNT function because CALCULATE has no further filter arguments.
Understanding KEEPFILTERS
We introduced KEEPFILTERS earlier in this chapter as a CALCULATE modifier. Technically, KEEPFILTERS is not a CALCULATE modifier, it is a filter argument modifier. Indeed, it does not change the entire evaluation of CALCULATE. Instead, it changes the way one individual filter argument is applied to the final filter context generated by CALCULATE.
We already discussed in depth the behavior of CALCULATE in the presence of calculations like the following one:
Contoso Sales :=
CALCULATE (
[Sales Amount],
KEEPFILTERS ( 'Product'[Brand] = "Contoso" )
)The presence of KEEPFILTERS means that the filter on Brand does not overwrite a previously existing filter on the same column. Instead, the new filter is added to the filter context, leaving the previous one intact. KEEPFILTERS is applied to the individual filter argument where it is used, and it does not change the semantic of the whole CALCULATE function.
There is another way to use KEEPFILTERS that is less obvious. One can use KEEPFILTERS as a modifier for the table used for an iteration, like in the following code:
ColorBrandSales :=
SUMX (
KEEPFILTERS ( ALL ( 'Product'[Color], 'Product'[Brand] ) ),
[Sales Amount]
)The presence of KEEPFILTERS as the top-level function used in an iteration forces DAX to use KEEPFILTERS on the implicit filter arguments added by CALCULATE during a context transition. In fact, during the iteration over the values of Product[Color] and Product[Brand], SUMX invokes CALCULATE as part of the evaluation of the Sales Amount measure. At that point, the context transition occurs, and the row context becomes a filter context by adding a filter argument for Color and Brand.
Because the iteration started with KEEPFILTERS, context transition will not overwrite existing filters. It will intersect the existing filters instead. It is uncommon to use KEEPFILTERS as the top-level function in an iteration. We will cover some examples of this advanced use later in Chapter 10.
Understanding ALL in CALCULATE
ALL is a table function, as you learned in Chapter 3. Nevertheless, ALL acts as a CALCULATE modifier when used as a filter argument in CALCULATE. The function name is the same, but the semantics of ALL as a CALCULATE modifier is slightly different than what one would expect.
Looking at the following code, one might think that ALL returns all the years, and that it changes the filter context making all years visible:
All Years Sales :=
CALCULATE (
[Sales Amount],
ALL ( 'Date'[Year] )
)However, this is not true. When used as a top-level function in a filter argument of CALCULATE, ALL removes an existing filter instead of creating a new one. A proper name for ALL would have been REMOVEFILTER. For historical reasons, the name remained ALL and it is a good idea to know exactly how the function behaves.
If one considers ALL as a table function, they would interpret the CALCULATE behavior like in Figure 5-39.

The innermost ALL over Date[Year] is a top-level ALL function call in CALCULATE. As such, it does not behave as a table function. It should really be read as REMOVEFILTER. In fact, instead of returning all the years, in that case ALL acts as a CALCULATE modifier that removes any filter from its argument. What really happens inside CALCULATE is the diagram of Figure 5-40.
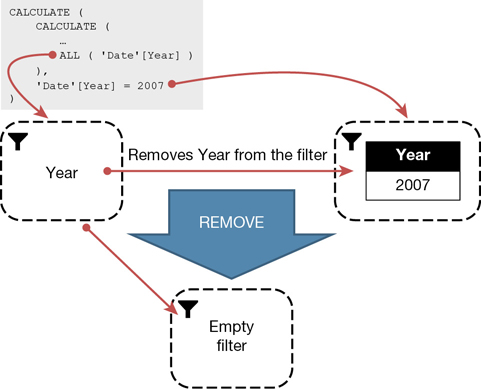
The difference between the two behaviors is subtle. In most calculations, the slight difference in semantics will go unnoticed. Nevertheless, when we start authoring more advanced code, this small difference will make a big impact. For now, the important detail is that when ALL is used as REMOVEFILTER, it acts as a CALCULATE modifier instead of acting as a table function.
This is important because of the order of precedence of filters in CALCULATE. The CALCULATE modifiers are applied to the final filter context before explicit filter arguments. Thus, consider the presence of ALL on a column where KEEPFILTERS is being used on another explicit filter over that column; it produces the same result as a filter applied to that same column without KEEPFILTERS. In other words, the following definitions of the Sales Red measure produce the same result:
Sales Red :=
CALCULATE (
[Sales Amount],
'Product'[Color] = "Red"
)
Sales Red :=
CALCULATE (
[Sales Amount],
KEEPFILTERS ( 'Product'[Color] = "Red" ),
ALL ( 'Product'[Color] )
)The reason is that ALL is a CALCULATE modifier. Therefore, ALL is applied before KEEPFILTERS. Moreover, the same precedence rule of ALL is shared by other functions with the same ALL prefix: These are ALL, ALLSELECTED, ALLNOBLANKROW, ALLCROSSFILTERED, and ALLEXCEPT. We generally refer to these functions as the ALL* functions. As a rule, ALL* functions are CALCULATE modifiers when used as top-level functions in CALCULATE filter arguments.
Introducing ALL and ALLSELECTED with no parameters
We introduced ALLSELECTED in Chapter 3. We introduced it early on, mainly because of how useful it is. Like all the ALL* functions, ALLSELECTED acts as a CALCULATE modifier when used as a top-level function in CALCULATE. Moreover, when introducing ALLSELECTED, we described it as a table function that can return the values of either a column or a table.
The following code computes a percentage over the total number of colors selected outside of the current visual. The reason is that ALLSELECTED restores the filter context outside of the current visual on the Product[Color] column.
SalesPct :=
DIVIDE (
[Sales],
CALCULATE (
[Sales],
ALLSELECTED ( 'Product'[Color] )
)
)One achieves a similar result using ALLSELECTED ( Product ), which executes ALLSELECTED on top of a whole table. Nevertheless, when used as a CALCULATE modifier, both ALL and ALLSELECTED can also work without any parameter.
Thus, the following is a valid syntax:
SalesPct :=
DIVIDE (
[Sales],
CALCULATE (
[Sales],
ALLSELECTED ( )
)
)As you can easily notice, in this case ALLSELECTED cannot be a table function. It is a CALCULATE modifier that instructs CALCULATE to restore the filter context that was active outside of the current visual. The way this whole calculation works is rather complex. We will take the behavior of ALL-SELECTED to the next level in Chapter 14. Similarly, ALL with no parameters clears the filter context from all the tables in the model, restoring a filter context with no filters active.
Now that we have completed the overall structure of CALCULATE, we can finally discuss in detail the order of evaluation of all the elements involving CALCULATE.
CALCULATE rules
In this final section of a long and difficult chapter, we are now able to provide the definitive guide to CALCULATE. You might want to reference this section multiple times, while reading the remaining part of the book. Whenever you need to recall the complex behavior of CALCULATE, you will find the answer in this section.
Do not fear coming back here multiple times. We started working with DAX many years ago, and we must still remind ourselves of these rules for complex formulas. DAX is a clean and powerful language, but it is easy to forget small details here and there that are actually crucial in determining the calculation outcome of particular scenarios.
To recap, this is the overall picture of CALCULATE:
CALCULATE is executed in an evaluation context, which contains a filter context and might contain one or more row contexts. This is the original context.
CALCULATE creates a new filter context, in which it evaluates its first argument. This is the new filter context. The new filter context only contains a filter context. All the row contexts disappear in the new filter context because of the context transition.
CALCULATE accepts three kinds of parameters:
One expression that will be evaluated in the new filter context. This is always the first argument.
A set of explicit filter arguments that manipulate the original filter context. Each filter argument might have a modifier, such as KEEPFILTERS.
A set of CALCULATE modifiers that can change the model and/or the structure of the original filter context, by removing some filters or by altering the relationships architecture.
When the original context includes one or more row contexts, CALCULATE performs a context transition adding implicit and hidden filter arguments. The implicit filter arguments obtained by row contexts iterating table expressions marked as KEEPFILTERS are also modified by KEEPFILTERS.
When using all these parameters, CALCULATE follows a very precise algorithm. It needs to be well understood if the developer hopes to be able to make sense of certain complex calculations.
CALCULATE evaluates all the explicit filter arguments in the original evaluation context. This includes both the original row contexts (if any) and the original filter context. All explicit filter arguments are evaluated independently in the original evaluation context. Once this evaluation is finished, CALCULATE starts building the new filter context.
CALCULATE makes a copy of the original filter context to prepare the new filter context. It discards the original row contexts because the new evaluation context will not contain any row context.
CALCULATE performs the context transition. It uses the current value of columns in the original row contexts to provide a filter with a unique value for all the columns currently being iterated in the original row contexts. This filter may or may not contain one individual row. There is no guarantee that the new filter context contains a single row at this point. If there are no row contexts active, this step is skipped. Once all implicit filters created by the context transition are applied to the new filter context, CALCULATE moves on to the next step.
CALCULATE evaluates the CALCULATE modifiers USERELATIONSHIP, CROSSFILTER, and ALL*. This step happens after step 3. This is very important because it means that one can remove the effects of the context transition by using ALL, as described in Chapter 10. The CALCULATE modifiers are applied after the context transition, so they can alter the effects of the context transition.
CALCULATE evaluates all the explicit filter arguments in the original filter context. It applies their result to the new filter context generated after step 4. These filter arguments are applied to the new filter context once the context transition has happened so they can overwrite it, after filter removal—their filter is not removed by any ALL* modifier—and after the relationship architecture has been updated. However, the evaluation of filter arguments happens in the original filter context, and it is not affected by any other modifier or filter within the same CALCULATE function.
The filter context generated after point (5) is the new filter context used by CALCULATE in the evaluation of its expression.
