6.1 Change and Noise
One of the most effective and robust methods for time series forecasting is exponential smoothing. This result has been established in the so-called M-competitions, in which more than 20 forecasting methods were compared for their performance across over 3,000 time series from different industries and contexts (Makridakis and Hibon 2000). The good news is that exponential smoothing is not only an effective, versatile, and robust method but is also, at its core, intuitive and easy to understand and interpret. Another important aspect of the method is that the data storage and computational requirements for exponential smoothing are minimal, and the method can thus be applied with ease to a large number of time series in real time. The theoretical work on exponential smoothing is by now extensive; it can be shown that this method is the optimal one (i.e., one minimizing squared forecast errors) for random walks with noise and a variety of other models of time series (Chatfield et al. 2001; Gardner 2006).
To illustrate how exponential smoothing works, we begin with a simple time series without trend and seasonality. In such a series, variance in demand from period to period is driven either by random changes to the level (i.e., long-term shocks to the time series) or by random noise (i.e., short-term shocks to the time series). The essential forecasting task then becomes estimating the level of the series in each time period and using that level as a forecast for the next period. The key to effectively estimate the level in each period is to differentiate level changes from random noise (i.e., long-term shocks from short-term shocks). As discussed in Chapter 5, if we believe that there are no random-level changes in the time series (i.e., the series is stable), then our best estimate of the level involves using all of our available data by calculating a long-run average over the whole time series. If we believe that there is no random noise in the series (i.e., we can observe the level), our estimate of the level is simply the most recent observation, discounting everything that happens further in the past. Not surprisingly then, the “right” thing to do in a time series that contains both random-level changes and random noise is something in-between these two extremes—that is, calculate a weighted average over all available data, with weights decreasing the further we go back in time. This approach to forecasting, in essence, is exponential smoothing.
Formally, let the index t describe the time period of a time series. The level estimate (=Level) in each period t according to exponential smoothing is then given by the following equation:

In this equation, the coefficient alpha (α) is a smoothing parameter and lies somewhere between 0 and 1 (we will pick up the topic on what value to choose for α later in this chapter). The Forecast Error in period t is simply the difference between the actual demand (=Demand) in period t and the forecast made for time period t.

In other words, exponential smoothing follows the simple logic of feedback and response. The forecaster derives an estimate of the current level of the time series, which he/she uses as the forecast. This forecast is then compared to the actual demand in the series in the next period, and the level estimate is revised according to the discrepancy between the forecast and actual demand. The forecast for the next time period is then simply equivalent to the current level estimate, since we assumed a time series without trend and seasonality, that is:

Substituting equations (2) and (3) into equation (1), we obtain

Exponential smoothing can therefore also be interpreted as a weighted average between our previous forecasts and the currently observed demand.
Curious readers have probably noticed that the method suffers from a “chicken-or-egg” problem: Creating an exponential smoothing forecast requires a previous forecast, which naturally creates the question of how to generate the first forecast. The method needs to be initialized with an appropriate value for the very first forecast. Different initializations are possible, ranging from the very first demand data point over an average of the first few demands to the overall average demand.
With a bit more replacement, equation (4) can in turn be converted into a weighted average over all past demand observations, where the weight of a demand observation that is i time periods away from the present is given as follows:

Equation (5) implies an exponential decay in the weight attached to a particular demand observation the further this observation lies in the past. This is the reason why the technique is referred to as “exponential” smoothing. Figure 6.1 shows the weights assigned to past demand observations for typical values of α. We see that higher values of α yield weight curves that drop faster as we go into the past. That is, the more recent past is weighted higher compared to the more distant past if α is higher. Thus, forecasts will be more adaptive to changes in the market for higher values of α. We further discuss how to set the value of α below.
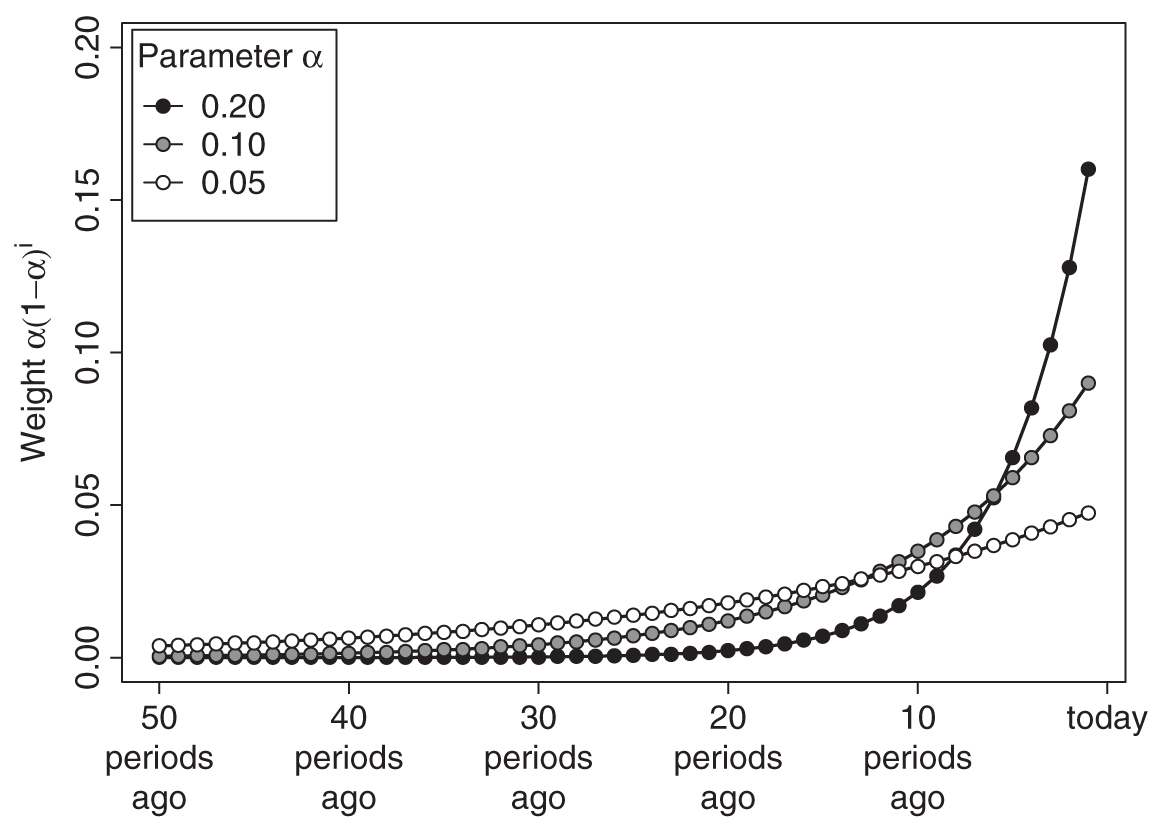
Figure 6.1 Weights for past demand under exponential smoothing
Forecasts created through exponential smoothing can thus be thought of as a weighted average of all past demand data, where the weight associated with each demand decays exponentially the more distant a demand observation is from the present. It is important, though, that one does not actually have to calculate a weighted average over all past demand in order to apply exponential smoothing; as long as a forecaster consistently follows equation (1), all that is needed is a memory of the most recent forecast and an observation of actual demand to update the level estimate. For that reason, the data storage and retrieval requirements for exponential smoothing are comparatively low. Consistently applying the method simply generates forecasts as if in each period one would calculate a weighted average over all past demand with exponentially decaying weights, as shown in Figure 6.1.
A technique that is sometimes used as an alternative to single exponential smoothing is moving averages. In a moving average of size n, the most recent n demand observations are averaged with equal weights to create a forecast for the future. This method is in essence similar to calculating a weighted average over all past demand observations, with the most recent n observations receiving equal weights and all other observations receiving zero weight. While this method is easy to understand, it naturally leads to the question why there should be such a step change in weighing past demands; that is, while under exponential smoothing all past demand observations receive some weight1 (just decaying the more you move into the past), moving averages assign equal weights for a while and then no weight at all to the history of demand.
6.2. Optimal Smoothing Parameters
The choice of the “right” smoothing parameter α in exponential smoothing is certainly important. Conceptually, a high α corresponds to a belief that variation in the time series is mostly due to random-level changes; a low α corresponds to a belief that this variation in the series is mostly due to random noise. Consider equation (4) for α = 1. In this special case, which is the highest α possible, the level estimate in each period is equivalent to the currently observed demand, which means that one believes that the time series follows a pure random walk, such as series 2 in Figure 5.2. Conversely, consider equation (5) for α close to 0. In this case, the weight attached to each demand observation in the past is essentially the same, and exponential smoothing corresponds to calculating a long-run unweighted average. This would be the right thing to do for a stable time series such as series 1 in Figure 5.2. Choosing the right α thus corresponds to choosing the type of time series that a focal time series resembles more; series that look more like series 1 should receive a higher α; series that look more like series 2 should receive a lower α. In practice, forecasters do not need to make this choice, but can rely on optimization procedures that will fit exponential smoothing models to past data, minimizing the discrepancy between hypothetical past forecasts and actual past demand observations by changing the α. The output of this optimization is a good smoothing parameter to use for forecasting and can be interpreted as a measure of how much the demand environment in the past has changed over time. High values of α mean that the market was very volatile and constantly changing, whereas low values of α imply a relatively stable market with little persistent change.
6.3 Extensions
One can extend the logic of exponential smoothing to more complex time series. Take, for example, a time series with an (additive) trend and no seasonality. In this case, one proceeds with updating the level estimate in accordance with equation (1), but then additionally estimates the trend in time period t as follows:

This method is also referred to as “Holt’s method.” Notice the similarity between equations (4) and (6). In equation (6), beta (β) is another smoothing parameter that captures the degree to which a forecaster believes that the trend of a time series is changing. A high β would indicate a trend that can rapidly change over time, and a low β would correspond to a more or less stable trend. We again need to initialize the trend component to start the forecasting method, for example, by taking the difference between the first two demands or the average trend over the entire demand history. Given that we assumed an additive trend, the resulting one-period-ahead forecast is then given by

Usually, forecasters do not only need to predict one period ahead into the future, but longer forecasting horizons are a necessity for successful planning. In production planning, for example, the required forecast horizon is given by the maximum lead time among all suppliers for a product—often as far out as 6 to 8 months. Exponential smoothing easily extends to forecasts further into the future as well; for example, in this case of a model with additive trend and no seasonality, the h-step-ahead forecast into the future is calculated as follows:

This discussion requires emphasizing an important insight and common mistake for those not versed in applying forecasting methods: Estimates are only updated if new information is available. Thus, the same level and trend estimates are used to project the one-step-ahead and two-step-ahead forecasts at time period t. One cannot, in a meaningful way, update level or trend estimates after making the one-step-ahead forecast and before making the two-step-ahead forecast. In the extreme, in smoothing models without a trend or seasonality, this means that all forecasts for future periods are the same; that is, if we expect the time series to be a “level only” time series without a trend or seasonality, we estimate the level once, and that estimate becomes our best guess for what demand looks like in all future periods. Of course, we understand that this forecast will become worse and worse the more we project into the future owing to the potential instability of the time series (which is a topic we have explored already in Chapter 3), but this expectation does not change the fact that we cannot derive a better estimate for what happens further out in the future at the current time. After observing the next time period, new data becomes available, and we can again update our estimates of the level and thus our forecasts for the future. Thus, the two-step-ahead forecast made in period t (for period t+2) is usually different from the one-step-ahead forecast made in period t+1 (for period t+2).
We note that our trended exponential smoothing forecast extrapolates trends indefinitely. This aspect of the method could be unrealistic for long-range forecasts. For instance, if we detect a negative (downward) trend, extrapolating this trend out will yield negative demand forecasts at some point in the future. Or assume that we are forecasting market penetration and find an upward trend—in this case, if we forecast out far enough, we will get forecasts of market penetration above 100 percent. Thus, trended forecasts should always be truncated appropriately. In addition, few processes grow without bounds, and it is often better to dampen the trend component as we project it out into the future. Such trend dampening will not make a big difference for short-range forecasting, but will have a strong impact on long-range forecasting (Gardner and McKenzie 1985).
Similar extensions allow exponential smoothing to apply to time series with seasonality as well. Seasonality parameters are estimated separately from the trend and level components, and an additional smoothing parameter γ (gamma) is used to reflect the degree of confidence a forecaster has that the seasonality in the time series remains stable over time. Such an exponential smoothing approach, with additive trend and seasonality, is often referred to as Holt-Winters exponential smoothing.
The parameter estimation of exponential smoothing models can be unduly influenced if the sample used for fitting the smoothing model includes outlier data. Fortunately, these data problems are by now well understood, and good solutions exist that allow forecasters to automatically prefilter and replace unusual observations in the dataset before estimating smoothing model parameters (Gelper, Fried, and Croux 2010).
In summary, exponential smoothing can be generalized to many different forms of time series. A priori, it is sometimes not clear which exponential smoothing model to use; however, one can essentially run a forecasting competition to figure out which model works best on past data (see Chapter 12). In this context, the innovation state space framework for exponential smoothing is sometimes applied (Hyndman et al. 2008). One can think of five different variants of trends in time series (none, additive, additive dampened, multiplicative, multiplicative dampened) and three different variants of seasonality (none, additive, multiplicative). Further, one can conceptualize random errors in two different variants (additive, multiplicative). As a result, there are 5 × 3 × 2 = 30 different versions of exponential smoothing possible; this is sometimes referred to as Pegels’ classification, and the formulas for applying the exponential smoothing logic in each of these versions are well known (www.otexts.org/fpp/7/7; Gardner 2006). To make this framework work, one can define a hold-out sample (subportion) of the data available, fit each of these 30 models to the data not in the hold-out sample, and finally forecast using each separate model into the hold-out period. One then selects the model from this competition that provides the best fit to the data in the hold-out sample, together with the exponential smoothing parameters that generates this best fit, and applies this estimated model to generate forecasts. This application of exponential smoothing seems to be a current gold standard for pure time series forecasting methods and performs very well in general forecasting competitions (Hyndman 2002). A publicly available program that allows using this approach in Excel is available through the add-on PEERForecaster (http://peerforecaster.com/). Similarly, forecasters using the statistical software R can install a free package called “forecast” implementing this forecasting framework as well.
6.4. Key Takeaways
• Exponential smoothing is a simple and surprisingly effective forecasting technique. It can model trend and seasonality components.
• Exponential smoothing can be interpreted as feedback-response learning, as a weighted average between most recent forecast and demand, or as a weighted average of all past demand observations with exponentially declining weights. All three interpretations are equivalent.
• Your software will usually determine the optimal exponential smoothing model as well as the smoothing parameters automatically. High parameters imply that components are changing quickly over time; low parameters imply relatively stable components.
• Trends will be extrapolated indefinitely. Consider dampening trends for long-range forecasts. Do not include trends in your model unless you have solid evidence that a trend exists.
• There are up to 30 different forms of exponential smoothing models; modern software will usually select which of these works the best in a time series using a hold-out sample.
______________
1Note that the weight assigned under exponential smoothing to a period in the distant past can become very small (particularly with a high α) but remains positive nonetheless.
