14.1 Multivariate Time Series
So far, this book has focused on forecasting individual demand time series, one at a time. Limiting our discussion in this way was useful to create focus; however, in most practical situations, forecasters may have to deal with thousands of time series at once. Further, these time series are related to each other, either because products are substitutes or complements or because hierarchical levels overlap. Further, forecasters have an interest in many different hierarchical levels. Consider, for example, that several time series may represent a portfolio of products; products are grouped into categories, but also in turn are divided into multiple stock-keeping units (SKUs) as variants of the product, differing in color, size, flavor, and so forth. The more a market has been horizontally and vertically differentiated into different target groups, the more does forecasting a product really mean forecasting a multitude of SKUs. Aggregate production planning may simply require a volume forecast at the product level, but a detailed production and procurement planning will also require more precise forecasts related to the mix of products demanded. Promotion planning will require forecasts at the product or product category level. Similarly, the overlap in the bills of material in our product portfolio may create a hierarchical divide: Suppose we bake both blueberry and chocolate chip muffins. We need forecasts of demand for both muffin types separately to plan production, but when sourcing flour, we only need a forecast of our total flour demand and do not care which type of muffin a particular pound of flour ends up in.
Another reason for recognizing forecast hierarchies lies in the spatial separation of markets; continents or sales regions are often divided into countries, which in turn are divided into states or markets. A retail company may need, for example, store-specific forecasts for particular SKUs to determine the store replenishment policy, but will also need forecasts for the same SKUs at their distribution center to in turn plan the replenishment of the distribution center. Similarly, in business-to-business settings, salespeople may need customer-specific forecasts, whereas production planners need a forecast of the total demand across all customers. Finally, time can be seen as another form of hierarchy in forecasts. An online fashion retailer may need forecasts of daily goods movements to schedule the warehouse workforce. The same retailer will also need forecasts for the entire fashion season, which can range from a few weeks to a few months, to procure products from the countries of origin.
To add to the complexity of forecasting hierarchies, the different hierarchies are often crossed with each other. For instance, a consumer goods manufacturer may be interested in sales to retailer A in region X, but also in sales to retailer B in region Y, crossing geographical and customer hierarchies. This example also illustrates that these two hierarchies are often closely aligned, but not identical. The challenge in forecasting hierarchies lies in creating a consistent set of forecasts at different levels.
If we ignore the hierarchical and interdependent nature of our forecasting portfolio, we could take the time series at different aggregation levels—say, sales of SKU A, sales of SKU B, and total sales in the category containing A and B—as different time series and forecast them separately. The problem with this approach is that forecasts will not be hierarchically consistent. Whereas historical demands of different SKUs add up to total historical category demand, the forecasts of different SKUs will almost certainly not add up to the forecast on the category level. “The sum of the forecasts is not equal to the forecast of the sum.” There are various ways of addressing this problem, all with their advantages and disadvantages, which we will describe next. Figure 14.1 shows a simple example hierarchy consisting of three SKUs, each with 3 years of history and 1 hold-out year.

Figure 14.1 An example hierarchy with three SKUs’ time series
14.2 Bottom-Up Forecasting
The simplest form of hierarchical forecasting is the bottom-up approach. This method works just the way it sounds: We take the time series at the most granular level, forecast each of these disaggregate series, and then aggregate the forecasts up to the desired level of aggregation (without separately forecasting at higher levels). This method is indeed often used without being identified as such, especially for bills of materials. For instance, every bakery that forecasts its sales of blueberry and chocolate chip muffins separately multiplies each forecast number with a specific number of cups of flour and finally aggregates the separate forecasts for flour to get a final aggregate flour demand forecast. This corresponds to bottom-up forecasting with conversion factors (the number of cups of flour per dozen muffins).
One advantage of this approach lies in its simplicity. It is very easy to implement this method, and the process of bottom-up forecasting offers only little opportunity for mistakes. In addition, it is also very easy to explain this approach to a nontechnical audience. The method is also very robust: even if we badly misforecast one series, the effect will be largely confined to this series and the level of aggregation just above it—the grand total will not be perturbed a lot. In addition, bottom-up forecasting works very well with causal forecasts, since you know the value of your causal effect, like the price, on the most fine-grained level. Finally, bottom-up forecasting can lead to less errors in judgment for nonsubstitutable products, increasing the accuracy of forecasts if human judgment plays an essential role in the forecasting process (Kremer, Siemsen, and Thomas 2016).
However, bottom-up forecasting also offers challenges. First, the more granular and disaggregated the historical time series are, the more intermittent they will be, especially if different hierarchies are crossed. On a single SKU × store × day level, many demand histories may consist of little else but zeros. On a higher aggregation level, for example, SKU × week across all stores, the time series may be more regular. Forecasts for intermittent demands are notoriously hard, unreliable, and noisy (see Chapter 9). Second, while specific causal factors will be well defined on a fine-grained level, general dynamics will be very hard to detect. For instance, a set of time series may be seasonal, but the seasonal signal may be very weak and difficult to detect and exploit on the level of single series. Seasonality may be visible on an aggregate level but not at the granular level. In such a case, fitting seasonality on the lower level may even decrease accuracy (Kolassa 2016b).
Figure 14.2 shows bottom-up forecasting applied to the example hierarchy from Figure 14.1. The trend in SKU A and seasonality in SKU B are captured well, and the forecast on the total level consequently shows both weak trend and weak seasonality.
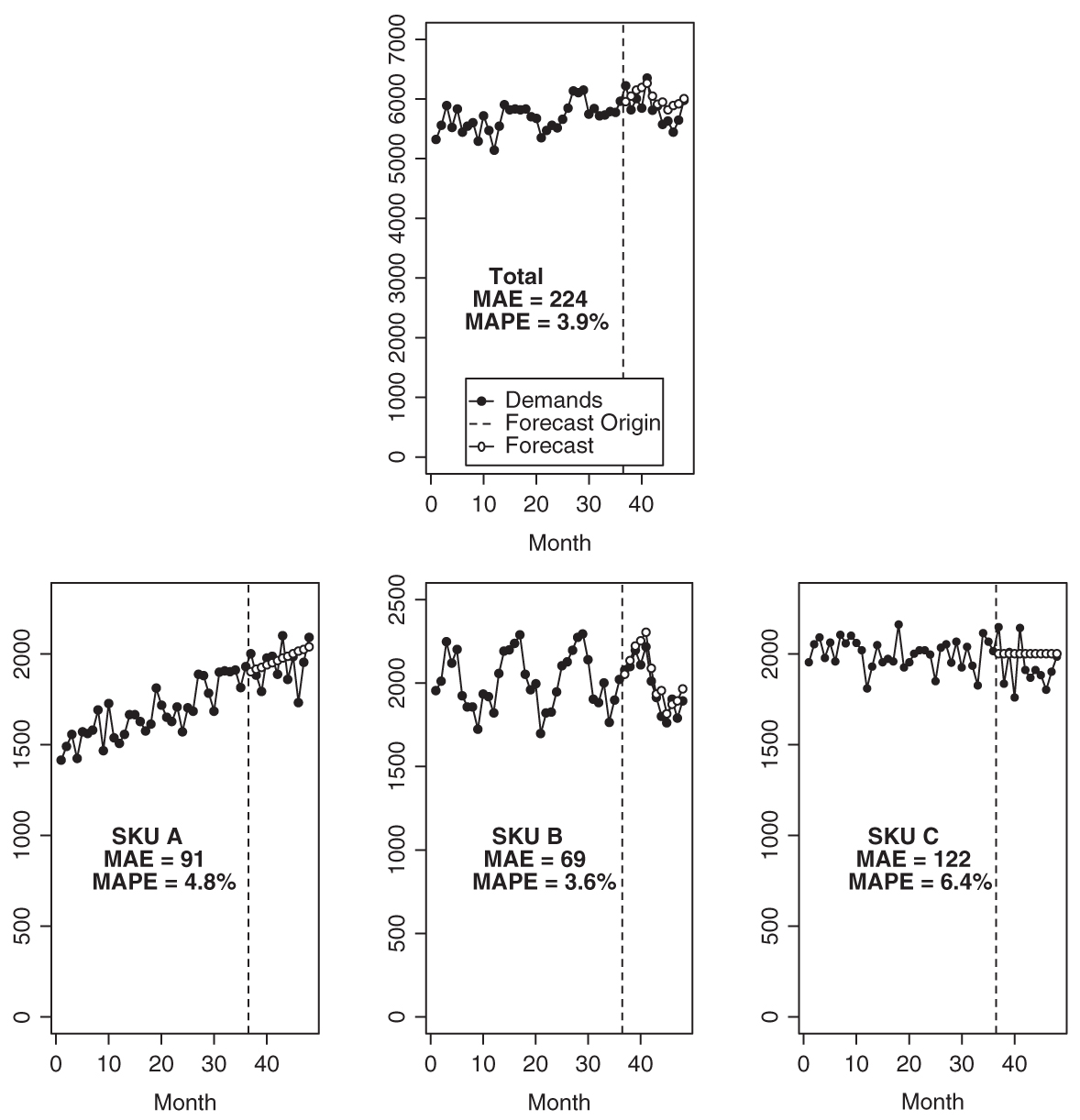
Figure 14.2 Bottom-up forecasts
14.3 Top-Down Forecasting
Top-down forecasting is a somewhat more complex method than bottom-up forecasting. As the name implies, this process means that we first forecast at the highest level of hierarchy (or hierarchies) and then disaggregate forecasts down to lower levels as required. What is more complex about top-down forecasting? The added complexity comes from the fact that we need to decide on how exactly to disaggregate the higher level forecasts. And this in turn is nothing else than forecasting the proportions in which, say, different SKUs will make up total category sales in a given future month. Of course, these proportions could change over time.
One way of forecasting proportions is to disregard the changes in proportions over time. Following this approach, we could disaggregate by calculating proportions of all historical sales, then use these to disaggregate future total forecasts (“disaggregation by historical proportions”). This method implies betting that historical proportions will continue to be valid in the future. Similarly, we could use only the most recent proportions to disaggregate our predictions (“disaggregation by recent proportions”). This would imply betting on proportions that constantly change, and the debate from Section 5.3 on stability vs. change is as valid in this context as it was before. Alternatively, we could forecast the totals as above, but also forecast lower level demand series and break down total forecasts proportionally to lower level forecasts (“disaggregation by forecast proportions”). Any number of forecast algorithms—seasonal or not, trended or not—could be used for this purpose. The forecasts for the top level (used to forecast total demands) do not need to be calculated using the same method as the forecasts for lower levels (only used to derive breakdown proportions).
On the plus side, top-down forecasting is still very simple to use and explain, almost as simple as bottom-up forecasting. And in explaining a concrete implementation of the process, the question of how to forecast the disaggregation proportions (which is a more complex issue) can often be relegated to a technical footnote. Further, top-down forecasting can have the advantage of better incorporating inter-relationships between time series, particularly in the context of substitutable products (Kremer, Siemsen, and Thomas 2016). On the down side, the other advantages and disadvantages of top-down forecasting mirror those of the bottom-up approach. Whereas bottom-up forecasting is very robust to single misforecasts, top-down forecasting faithfully pushes every error on the top level down to every other level. Furthermore, top-down forecasting often gets the total forecast right, but the way how this total is composed of separate lower level demands crucially depends on how we forecast the future proportions—if demand gradually shifts from SKU A to B because of slow changes in customer taste, we need to include this explicitly in our proportion forecasts, or we will not see this market shift in the disaggregated forecasts.
While causal factors like prices are well defined for bottom-up forecasting (although their effect may be hard to detect; see Kolassa 2016b), they are not as well defined for top-down forecasting. Prices are defined on single SKUs, not on “all products” level. We could of course use averages of causal factors, for example, average prices in product hierarchies. However, if we use unweighted averages, we relatively overweight slow-selling products—and if we use weighted averages of prices, weighting each SKU’s price with its sales to account for its importance in the product hierarchy, then we have to solve the problem of how to calculate these weights for the forecast period. We might be tempted to calculate a weighted average price, where we weight each SKU’s price with its forecast sales, but this would be putting the cart before the horse, since forecasting the bottom levels is exactly what we are trying to do.
Figure 14.3 shows top-down forecasting, using disaggregation by historical proportions, applied to the example hierarchy from Figure 14.1. As trend and seasonal signal are only weak on the total level, the automatic model selection picks single exponential smoothing. Consequently, the disaggregated forecasts on SKU level do not exhibit trend or seasonality, either. Top-down forecasting is obviously not appropriate in this example, because the bottom-level time series exhibit obvious but different signals (trend in SKU A, seasonality in SKU B, nothing in SKU C). If the bottom-level series exhibit similar but weak signals, top-down forecasting may perform better than bottom-up (Kolassa 2016b).

Figure 14.3 Top-down forecasts
14.4 Middle-Out Forecasting
Middle-out forecasting is a middle road between bottom-up and top-down forecasting. Pick a “middle” level in your hierarchy. Aggregate historical data up to this level. Forecast. Disaggregate the forecasts back down and aggregate them up as required. This approach combines the advantages and disadvantages of bottom-up and top-down forecasting. Demands aggregated to a middle level in the hierarchy will be less sparse than on the bottom level, so we will get much better defined seasonal and similar signals. Similarly, it may be easier to derive aggregate causal factors when going to a middle level than when going all the way to the top level. For instance, if all products of a given brand have a “20 percent off” promotion, we can aggregate historical demands to total brand sales and apply a common “20 percent off promotion” predictor to the aggregate. (However we would need to explicitly model differential sensitivity to price reductions for different SKUs in the brand—a simple approach would yield the same forecast uplift for all products.)
Once we have the forecasts on a middle level, aggregating them up is just as simple as aggregating up bottom-level forecasts in a bottom-up approach. And conversely, disaggregating middle-level forecasts down to a more fine-grained level is similar to disaggregating top-level forecasts in a top-down approach: we again need to decide on how to forecast disaggregation proportions, for instance (the simplest way), doing disaggregation by historical proportions.
14.5 Optimal Reconciliation Forecasting
One recently developed approach, and a completely new way of looking at hierarchical forecasting, is the so-called optimal reconciliation approach (Hyndman et al. 2011; Hyndman and Athanasopoulos 2014). The key insight underlying this approach is to go back to the original problem of hierarchical forecasting: if we separately forecast all of our time series on all aggregation levels, then the point forecasts will not be sum consistent. They will not “fit” together. If things do not “fit” the way they are, we can calculate a “best (possible) fit” between forecasts made directly for a particular hierarchical level and forecasts made indirectly by either summing up or disaggregating from different levels, using methods similar to regression. We will not go into the statistical details of this method—readers can refer to Hyndman et al. (2011) for these or look at the “hts” package for R.
Calculating optimally reconciled hierarchical forecasts provides a number of advantages. One benefit is that the final forecasts use all component forecasts on all aggregation levels. We can use different forecasting methods on different levels or even mix statistical and judgmental forecasts. Thus, we can model dynamics on the levels where they are best fit, for example, price influences on a brand level and seasonality on a category level. We therefore do not need to worry about making hard decisions about how to aggregate causal factors—if it is unclear how to aggregate a factor, we can simply leave it out in forecasting on this particular aggregation level. And it turns out that the optimal reconciliation approach frequently yields better forecasts on all aggregation levels, beating bottom-up, top-down, and middle-out in accuracy, because it combines so many different sources of information.
Optimal reconciliation of course also has drawbacks. One is that the specifics are somewhat harder to understand and to communicate than for the three “classical” approaches. Another disadvantage is that while it works very well with “small” hierarchies, it quickly poses computational and numerical challenges for realistic hierarchies in demand forecasting, which could contain thousands of nodes arranged in multiple levels in multiple crossed hierarchies. For single (noncrossed) hierarchies, or for crossed hierarchies that are all of height 2 (“grouped” hierarchies), one can do smart algorithmic tricks (Hyndman, Lee, and Wang 2016), but the general case of crossed hierarchies is still intractable.
Figure 14.4 shows optimal combination forecasting applied to the example hierarchy from Figure 14.1. As in bottom-up forecasting (Figure 14.2), the trend in SKU A and seasonality in SKU B are captured well, and the forecast on the total level consequently shows both weak trend and weak seasonality. However, note that errors for optimal combination forecasts are even lower than for bottom-up forecasts. This is a frequent finding.

Figure 14.4 Optimal combination forecasts
14.6 Other Approaches
Hierarchical structures allow forecast improvements even if we are not really interested in hierarchical forecasts per se. For example, we may only need SKU-level forecasts but still be interested in whether product groups allow us to improve these SKU-level forecasts. For instance, seasonality is often more easily estimated on aggregate levels. We could therefore aggregate data to higher levels, then extract seasonal patterns or indices, deseasonalize lower-level time series, forecast the deseasonalized series, and finally apply the group-level seasonal indices again to properly incorporate seasonality at the lower level. Mohammadipour et al. (2015) explain this approach in more depth. The same method could be applied in calculating the effects of trend, promotions, or any other dynamic on an aggregate level, even if we are not interested in forecasts on this aggregate level as such.
One point should be kept in mind when we forecast hierarchical data: the hierarchies we are given are often not set up with forecasting in mind. For instance, products grouped by supplier may sort different varieties of apples into different hierarchies, although they appear the same to customers and would profit from hierarchical forecasting. It may be worthwhile to create separate “forecasting hierarchies” and to check whether these improve forecasts (Mohammadipour et al. 2015).
14.7 Key Takeaways
• If you have a small hierarchy and can use dedicated software like R’s hts package or have people sufficiently versed in linear algebra who can code the reconciliation themselves, go for the optimal reconciliation approach. If the optimal reconciliation approach is not possible, use one of the other (i.e., bottom-up, top-down, or middle-out) methods.
• If you are most interested in top-level forecasts, with the other levels “nice to have,” or if you are worried about extensive substitutability among your products, use top-down forecasting.
• If you are most interested in bottom-level forecasts, with the other levels “nice to have,” or many of your products are not substitutes, use bottom-up forecasting.
• If you cannot decide, use middle-out forecasting. Either pick a middle level that makes sense from a business point of view, for example, the level in the product hierarchy at which you plan marketing activities, or try different levels and look which one yields the best forecast overall.
• Never be afraid of including hierarchical information, even if you are not interested in forecasts at higher levels of aggregation. It may improve your lower-level forecasts.
• Consider creating additional “forecasting hierarchies” if that helps getting the job done.
