Causal Models and Leading Indicators
8.1 Leading Indicators
The time series forecasting methods discussed in the previous two chapters have one key advantage: the only data they require are the time series data themselves; no additional data are needed to estimate a smoothing parameter, or the parameters of an ARIMA model, and use it for forecasting. However, firms often have a range of additional information available that could be used to create demand forecasts as well, such as consumer confidence indices, advertising projections, reservations made or orders already placed, and so forth. Using such information falls into the domain of causal modeling and leading indicators.
A useful leading indicator is given by additional data that is available (or predictable) in advance, not prohibitively costly to obtain, and that improves forecasting performance when used in a forecasting model. Of course, the cost of obtaining such data has to be judged in comparison to the improvement in forecasting performance that will result from using it. An important point here is that the leading indicator needs to provide more information than what is contained in the time series already; leading indicators are often subject to the same seasonal effects than a focal time series, and simple correlations between leading indicators and the focal series can be a result of their joint seasonality. A key to a successful evaluation of the performance of leading indicators is not simply to demonstrate a correlation between the leading indicator and your demand time series but also to show that using the leading indicator in forecasting improves upon forecasts when used in addition to the time series itself.
In order to use leading indicators for forecasting, we need to know or be able to forecast their values for the future. We may be able to forecast advertising budgets rather well. Conversely, assume that we wish to forecast the sales of a weather-sensitive product like garden furniture or ice cream. If the weather is nice and sunny, we will sell more than if it is rainy and wet. However, if we want to use weather information to improve forecasts, we will need to feed the forecasted weather into our causal forecast algorithm, and of course the question is then whether we can forecast the weather sufficiently well far enough into the future to improve on sales forecasts that do not use the weather. Of course, we are assuming that the obvious seasonality is already included in our “weatherless” forecasts.
To illustrate the use of leading indicators, consider a dataset on sales and advertising. The dataset contains 3 years of monthly data on sales as well as advertising expenses during the month for a dietary weight control product (Abraham and Ledolter 1983). A time series plot of the dataset is given in Figure 8.1. One could apply some form of exponential smoothing to the sales data to create a forecast—or one could attempt to use advertising expenses to predict sales. An easy way to examine whether advertising expenses explain higher sales is to calculate the correlation coefficient between these variables. In Microsoft Excel, this can be easily done using the = CORREL function. In this case, the correlation between the two measures is r = 0.63, which is statistically significant; this would indicate that, from a statistical perspective, advertising expenses relate to sales.

Figure 8.1 Time series on sales and advertising
So is advertising a useful leading indicator? The first question would be whether the advertising expenses for a month are actually known in advance. Usually, the advertising budgets are set according to some plan, so many firms will know their advertising expenses for a future month in advance. However, the time lag with which this information is available then effectively determines the forecast horizon that can be achieved. If advertising expenses are known only 1 month in advance, they can only be used for 1-month-ahead predictions.
A related discussion would be whether there is a time lag between spending money on advertising and these expenses having any influence on sales; in this case, one can check for a possible time lag involved by comparing the correlation between sales and current advertising expenses (r = 0.63) to the correlation between sales and last month’s advertising expenses (r = 0.30), or even the expenses from 1 month earlier (r = 0.34). Clearly the correlation is strongest with the current advertising expenses, indicating that a time lag is probably not a major worry for forecasting. Some drivers of demand can also influence multiple time periods. Promotions, for example, clearly influence demand for the period in which they happen, but some of that extra demand due to the promotion in a period may simply be shifted demand from the time period succeeding the promotion.
Another discussion one can have is whether the underlying relationship is actually causal. One could, for example, argue for reverse-causality (i.e., it is not advertising that is driving sales, but sales that is driving advertising) or alternative explanations (i.e., if companies advertise, they also stock more product, leading to higher service levels and sales). These questions are empirically hard to resolve, although much progress has been made in recent years in econometrics to better address questions of causality, and interested readers are referred to Angrist and Pischke (2009) for a good overview of these methods.
It is essential to emphasize that forecasting does not require a causal relationship; forecasting is, in that sense, a very pragmatic profession. As long as data enable us to predict the future better, we do not need to be certain that the underlying relationship is truly causal. While we can have more confidence that the relationship we use for forecasting remains stable over time if we understand the underlying causality, being unable to demonstrate causality does not necessarily prevent us from exploiting an empirical relationship to make predictions. In other words, if we know that a statistical relationship exists between the number of storks in a country and the birthrate of a country (r = 0.62; see Matthews 2000), can we use this relationship to predict the birth rate of a country for which we have counted only the number of storks but know nothing else about? The answer is yes (assuming we can forecast the number of storks well enough). In the absence of other data, exploiting this relationship may be the best we can do. However, questioning causality may lead us to better predictors. In this case, the number of storks in a country relates to country size, which in turn relates to birth rates. Using country size will probably lead to better predictions of births than using the number of storks.
In this context, “big data” is providing forecasters with new opportunities to find leading indicators that help in the prediction of their time series. Google, for example, provides two tools available for free: Google Trends and Google Correlate (Choi and Varian 2012). Google Trends allows forecasters to examine the frequency of certain search terms relative to all searches over time. Google Correlate provides the functionality to upload your own time series and then examine which search terms correlate the most with your uploaded time series. A recent example focusing on end-consumer personal consumption expenses in different categories shows how incorporating this information into standard forecasting methods can lead to large increases in forecasting accuracy (Schmidt and Vosen 2013). Note, however, that while Google Trends offers current data, Google Correlate only comes with a time lag of up to 6 months. In that sense, Google Correlate offers a tool to identify possible search terms that may become viable leading indicators, and Google Trends allows downloading and using this data for forecasting in real time.
8.2 Combination With Time Series
Going back to our advertising and sales data from the previous section, the key question to answer is how much we actually gain by using the advertising data, that is, how much better we can predict sales if we exploit the relationship between advertising and sales, as opposed to simply using the time series history of sales to predict the future. To answer this question, we devise a forecasting competition (see Chapter 12) by splitting the dataset at hand into an estimation sample (years 1–2) and a hold-out sample (year 3). The estimation sample is used to estimate the relationship between advertising and sales; the hold-out sample is used to test the predictions of that model. Specifically, we will calculate a rolling origin forecast. That is, we take the history from January 2013 to December 2014, fit a model, and forecast for January 2015. Next, we move the forecast origin by 1 month, taking the history from January 2013 to January 2015, fitting a model and forecasting for February 2015, and so forth. In each step, we estimate the following regression equation using data from the first months:

Estimating a regression equation here essentially means finding values of a0 and a1 that minimize the squared values of Errort across the estimation sample. Interested readers who require more background on the topic of regression are referred to a different book by the same publisher (Richardson 2011). A regression equation can be estimated in Excel if the data analysis tool pack is installed. A free add-in for Excel that allows for more detailed analysis is available at http://regressit.com/. In our case, in the first step, we estimate the equation to obtain the following estimates for a0 and a1:

These estimates indicate that for prediction purposes, every dollar spent in advertising is associated with $1.97 in extra sales on average. It becomes important to emphasize that this is not necessarily a causal effect, and these numbers should not be used to plan advertising spending; however, if we know what the advertising budget is, we can multiply that number with 1.97 (and subtract 15.92) to create a prediction of sales in that period. In the second step, we have one additional historical data point, so our estimated model changes slightly:

This rolling regression approach is easy to do for all 12 months in the hold-out sample (i.e., year 33) and leads to a mean absolute error (MAE; see Chapter 11 on forecast error measures) of 15.07 across the hold-out sample. How good is this forecast? A reasonable comparison is a pure time series forecast that would not have required any information on advertising. To that purpose, we estimated exponential smoothing forecasts (as described in Chapter 4), again using rolling forecasts. The winning models across our 12 forecast origins generally were models with additive or multiplicative errors, without trends or seasonality. The resulting MAE from these model forecasts is 22.03, higher than the MAE from our simple regression model.
We can see from Figure 8.2 that the two sets of forecasts are very different. Which forecast should one trust? The MAE from exponential smoothing models is higher. But does that mean that one should rely solely on the advertising data? Or can these two methods somehow be combined to provide better forecasts? One way to combine time series models with leading indicators is to allow for the regression equation to estimate seasonal factors (and/or trends). Since trends played little role in our data, we will ignore them for now. To incorporate seasonality into the regression equation, we code 11 “dummy” variables in our dataset, one for each month except for December. A code of “1” indicates that a particular observation in the dataset takes place in that particular month; the variables are 0 otherwise. If all variables are coded as “0” for an observation, that observation took place in December.1 We then estimate the following multivariate regression equation:

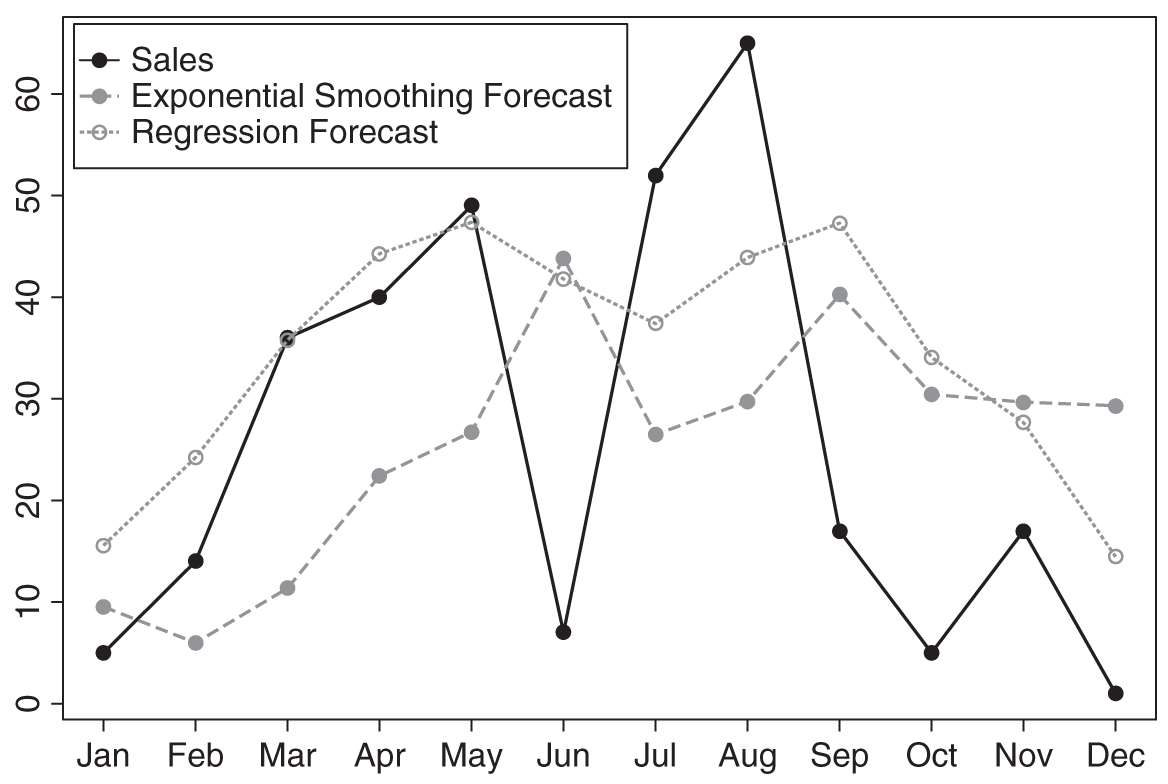
Figure 8.2 Rolling regression and exponential smoothing forecasts in the hold-out sample
This equation now accounts for seasonality according to different months. However, the way seasonality is included limits the effects of seasonality to be additive in nature and does not allow the seasonality effects to change over time. We calculated forecasts for the hold-out samples using this revised specification. The resulting MAE (=15.84) is worse than in the original model, indicating that incorporating seasonality in this fashion was not beneficial. Is there possibly a better way of combining time series information with advertising information to create a better forecast? The correlation between forecast errors from the exponential smoothing model and advertising expenses for that month in the hold-out sample is 0.41; while this could simply be due to randomness, since statistical significance is hard to show in such small samples, it gives us some indication that advertising may contain relevant information that is not captured by the sales time series alone.
This question of forecasting with multiple methods has been studied extensively in the literature on forecast combination, and there is much evidence that combining forecasts from different methods provides superior forecasts (Armstrong 2001). In our case, we could simply take the average of the exponential smoothing and the regression forecast. While such a strategy often works to improve performance, in our case, the resulting MAE is not improved (=17.53). In general, if a time series is very unstable, using the simple average instead of some optimal weight seems appropriate (Armstrong and Collopy 1998) and should be considered as an option to combine forecasts from multiple methods.
8.3 Key Takeaways
• Known drivers of demand can dramatically improve your forecast. Consider including them in a causal model.
• It is not sufficient to demonstrate that a driver correlates with demand; rather, for the driver to be useful in forecasting, the forecasting performance improvement that can be obtained by using the demand driver, compared to simple time series models without the driver, needs to outweigh the cost of obtaining the necessary data.
• A driver’s influence on demand may lag behind its occurrence and may influence more than a single time period.
• For forecasting demands with a causal driver, we need to measure and forecast the driver. An unforecastable driver, like the specific weather on a day 3 months ahead, is useless.
• Regression models with leading indicators can be combined with time series models to create better forecasts.
______________
1In general, a categorical variable with N categories requires N—1 dummy variables to represent in a regression equation, since the absence of all other categories indicates the presence of the omitted category. If N dummy variables are used instead (in addition to a regression intercept), these variables become perfectly correlated as a set, and estimating the regression equation will not be possible.
