High-Entropy Alloys
Basic Concepts
High-entropy alloys (HEAs) have emerged as an important class of materials in the last one decade with immense potential both at the level of fundamental understanding and also in terms of applications. This chapter deals with the basic concepts that underpin this new class of alloys. It starts with the definition of HEAs and how they differ from other multicomponent alloys such as Ni-base superalloys. Then it gives a classification of alloys in terms of the number of components. A notation that is commonly used to represent composition in these alloys, particularly the nonequiatomic alloys with alloying additions, is brought out. Finally, four core effects of HEAs are elucidated, namely, high-entropy, severe lattice distortion, sluggish diffusion, and cocktail effects.
Keywords
Classification; definition; notation; core effects; severe lattice distortion; sluggish diffusion; cocktail effect
2.1 Introduction
As the combinations of composition and processes for producing HEAs are numerous and as each HEA has its own microstructure and properties to be identified and understood, the research work is truly limitless (Zhang et al., 2014). It becomes very important to consider the basic concepts relating to HEAs at the very beginning, including the origin of high entropy, classification, definition, composition notation, and the four core effects of HEAs.
2.2 Classification of Phase Diagrams and Alloy Systems
Phase diagrams and the systems they describe are often classified and named after the number, in Latin, of components in the system. They can be christened based on their number of components as unary, binary, ternary, quaternary, quinary, sexinary, septenary, octonary, nonary, and denary from single- to 10-component alloys, respectively. It is suggested that this nomenclature recommended by ASM Handbook Volume 3 (1992) may be followed. This volume acquires renewed interest as phase diagrams are the beginning of wisdom, as observed by Hume-Rothery.
There are very few binary engineering alloys that are commercially in use and most alloys are actually multicomponent alloys. However, most of these multicomponent alloys are still based on one principal element and are named after the principal elements, such as Fe-, Al-, Cu-, Ni-, and Ti-based alloys. These alloys may consist of solid solutions and/or intermetallic compounds (crystalline or quasicrystalline). These often include interstitial compounds, known as Hagg phases. Under nonequilibrium conditions some of the alloys form metallic glasses.
Cantor (2007), has recently shown that the total number of possible alloys (N) that can be formed with C number of components, when each alloy differs in composition by x%, can be written as N=(100/x)C−1. If we consider 60 different elements (excluding those that are too radioactive, toxic, rare, and/or otherwise difficult to use) in the periodic table to combine with each other to form alloys, the total number of possible alloys turns out to be about 10177, if each alloy differs in composition by 0.1%. Even if we reduce the number of elements to 40 that can be used to make the alloys and considering that each alloy differs in composition by 1%, the total number of possible alloys turns out to be 1078, which is an astronomical number, considering that there are only 1066 atoms in the galaxy (Cantor, 2007).
The mutual solubility between solvent and solute components in a binary alloy system could be judged by Hume-Rothery rules, namely, crystal structure, atomic size difference, valence, and electronegativity. In fact, all these factors also influence the interaction between different elements and make the enthalpy of mixing either negative (attractive interaction leading to ordering and the formation of intermetallic compounds), positive (repulsive interaction leading to clustering and segregation), or near zero (leading to the formation of disordered solid solutions). The competition between enthalpy of mixing and entropy of mixing further affects the solubility between two components. When solubility is limited, terminal solid solutions based on each component can be obtained in the phase diagram. When a solid solution forms at all compositions, it is called an isomorphous system. But continuous solid solutions in binary alloy system are not common because the conditions for its formation are very strict to fulfill. Available binary alloy phase diagrams (Massalski, 2001) indicate that the total number of isomorphous binary and ternary systems is only 153 and 248, respectively.
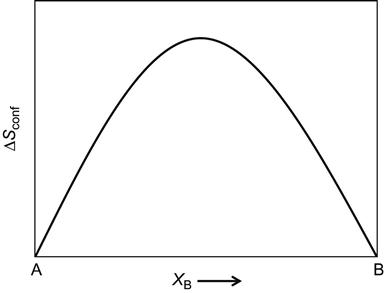
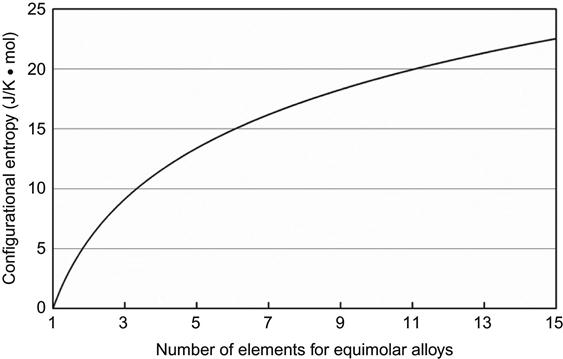
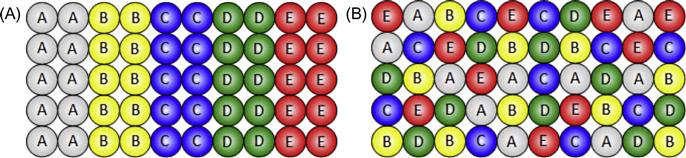
While such terminal solutions are well known in binary, ternary and quaternary alloy systems, it is curious to know whether we can obtain solid solution phases in the center of higher order phase diagrams or not. In fact, formation of such solid solutions in the center of the phase diagram has not been explored much (Figure 2.1). In a significant deviation from traditional ways of making alloys, Cantor et al. (2004) and Yeh et al. (2004b) independently came up with the idea of preparing equiatomic or near-equiatomic multicomponent alloys. Yeh et al. (2004b) popularized these alloys as “HEAs” by pointing out the known thermodynamic fact that configurational entropy of a binary alloy (ΔSconf =−R(XA ln XA+XB ln XB)) is a maximum when the elements are in equiatomic proportions (Figure 2.2) and that the maximum configurational entropy (ΔSconf,max=RlnN) in any system increases with increasing number of elements (N) in the system (Figure 2.3). He emphasized that the high mixing entropy (in this book “configurational entropy” is referred to as “mixing entropy/entropy of mixing” in some places to be in tune with literature. However, both these terms should be treated as same) in HEAs would have a profound effect on the constituent phases, kinetics of phase formation, lattice strain, and thus properties. In particular, it enhances the mutual solubility between constituent components and leads to simpler phases and microstructure not expected before. This simplification originating from high-entropy effect is thus very important in such multicomponent alloys. Therefore, many possible new materials, new phenomena, new theories, and new applications are foreseen in the twenty-first century (Yeh et al., 2004b).
This concept has opened up flood gates of research activity and over the past decade about 400 papers have been published on HEAs, out of which about 100 are from Yeh’s group itself. Though Yeh et al. (2004b) originally proposed that due to the large mixing entropy, HEAs tend to form solid solutions including disordered and partially ordered solid solutions intense research in recent years has been done on the rules or criteria using parameters including configurational entropy, enthalpy of mixing and the atomic size difference between different elements to predict the nature of phase formed in the alloy. Furthermore, computational thermodynamics methods such as CALPHAD have been used for predicting phase diagrams for HEAs in a more direct manner.
In addition to studying the basic phases and microstructure of different equiatomic multicomponent alloys ranging from five to twenty components (Cantor et al., 2004), Cantor et al. (2002) introduced a second strategy of equiatomic substitution of elements in binary alloys, wherein various similar elements are substituted in equal proportions in a binary system. This research was motivated by a desire to determine favorable compositions for the formation of metallic glasses (Figure 2.4). For example, in Zr50Cu50 alloy, he substituted 75% of Zr with Ti, Hf and Nb such that all four elements are in equiatomic proportions. Likewise, Cu was substituted partially with Ag and Ni so that all the three elements are in equiatomic proportions to arrive at a final septenary alloy composition of (Ti0.25Zr0.25Hf0.25Nb0.25)50(Cu0.33Ag0.33Ni0.33)50. Even though this alloy has seven components, it can still be treated as a pseudobinary system and Cantor and his group have demonstrated good glass forming ability in a number of such pseudobinary alloys. They have also added Al to the alloy to form pseudoternary alloys. Of course such substitution of like elements in place of the two components need not be in equal proportions and several metallic glasses are known with such nature, for example, an Fe80B20 glassy alloy, in which Fe can be substituted by a number of transition elements such as Cr, Co, and Ni and B can be substituted by other metalloids such as Si and C. One can demonstrate similar substitution even in case of intermetallic compounds (NiAl, wherein Ni can be substituted by Fe, Co) and even in oxides such BaTiO3, wherein Ba can be substituted by Sr and Ti can be substituted by Zr. Under such a substitution strategy with chemically similar elements, it is indeed very probable to generate similar or improved behavior and properties by using higher number of components.
Gibbs phase rule, which gives the degrees of freedom (F) a system has while maintaining equilibrium between a number of phases (P) containing a certain number of components (C), at constant pressure, can be expressed as
Gibbs phase rule thus gives the maximum number of phases possible in a system of C components under equilibrium. The phase rule indicates that condensed systems (the system that does not have the gaseous phase) cannot have more than C+1 number of phases in equilibrium. Thus, binary, ternary, quaternary, and quinary systems cannot have more than 3, 4, 5, and 6 phases in equilibrium, respectively. However, such a condition of finding the maximum number of phases is observed in any system under a specific condition wherein the degrees of freedom are zero (invariant condition). This does not mean that the system cannot have less number of phases and for example, a quinary condensed system can have any number of phases in equilibrium ranging from 1 to 6 at various compositions and temperatures.
However, it is important to note that the number of phases observed in these HEAs is significantly less than the maximum number of phases expected from the phase rule, suggesting that large configurational entropy in these alloys enhances the mutual solubility for forming solid solution phases (disordered or partially ordered) and thus restricts the formation of a large number of phases. Furthermore, HEAs being multiprincipal-element alloys, the diffusivities of atoms are expected to be low and hence the formation of a number of phases is kinetically constrained in such alloys. Thus, the observation of less number of phases in HEAs is not only due to high configurational entropy of these alloys but also due to low diffusivities in these multicomponent alloys. These merits are often useful in controlling microstructure and properties of a material for practical applications.
2.3 Definition of HEAs
Each high-entropy alloy contains multiple elements, often five or more in equiatomic or near-equiatomic ratios, and minor elements (Yeh et al., 2004b). The basic principle behind HEAs is that significantly high mixing entropies of solid solution phases enhance their stability as compared with intermetallic compounds, especially at high temperatures. This enhancement allows them to be easily synthesized, processed, analyzed, manipulated, and utilized by us. In a broad sense, HEAs are preferentially defined as those alloys containing at least five principal elements, each having the atomic percentage between 5% and 35%. The atomic percentage of each minor element, if any, is hence less than 5% (Yeh et al., 2004b).
Why are such multiprincipal-element alloys called HEAs? From statistical thermodynamics, Boltzmann’s equation (Gaskell, 1995; Swalin, 1972) can be used for calculating configurational entropy of a system:
where k is Boltzmann’s constant and w is the number of ways in which the available energy can be mixed or shared among the particles of the system. Thus the configurational entropy change per mole for the formation of a solid solution from n elements with xi mole fraction is:
Let us consider an equiatomic alloy at its liquid state or regular solid solution state. Its configurational entropy per mole can be calculated as follows (Yeh et al., 2004b; Yeh, 2006):
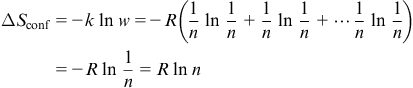
where R is the gas constant, 8.314 J/K mol.
Figure 2.5 shows an example illustrating the formation of quinary equiatomic alloy from five elements. From the above equation, ΔSconf can be calculated as R ln 5=1.61R. For a nonequiatomic HEA, the mixing entropy would be lower than that for an equiatomic alloy. Consider a nonequiatomic alloy Al1.5CoCr0.5FeNi0.5 (or Al33.3Co22.2Cr11.1Fe22.2Ni11.1 in at.%). Its configurational entropy can be calculated as 1.523R which is slightly smaller than 1.61R of the equiatomic alloy AlCoCrFeNi.
Although total mixing entropy has four contributions such as configurational, vibrational, magnetic dipole, and electronic randomness, configurational entropy is dominant over other three contributions (Fultz, 2010; Swalin, 1972). Among the other three, the excess vibrational entropy due to mixing at high temperatures could be calculated from Debye temperatures (Swalin, 1972). Negative contribution of excess vibrational entropy to overall mixing entropy might occur and could be enhanced by attractive interactions between unlike atomic pairs. Table 2.1 lists the configurational entropies of equiatomic alloys with increasing number of components in terms of gas constant R. The entropy increases as the number of element increases. From Richards’ rule, ΔHf/Tm=ΔSf ~R, the entropy change per mole, ΔSf, from solid to liquid during melting is about one gas constant R, and the enthalpy change or latent heat per mole, ΔHf, can be estimated as RTm, where Tm is the melting point. Because ΔHf can be regarded as the energy required to destroy about one twelfth of all bonds in the solid, the mixing entropy of R per mole in random solid solution is quite large to lower its mixing free energy, ΔGmix, since ΔGmix=ΔHmix−TΔSmix by the amount of RT. For example, the amount at 1000 K is RT=8.314 kJ/mol. It is also well known that an ideal monoatomic gas (including metals) per mole has a kinetic energy or internal energy of 1.5RT. Therefore, such a free energy lowering causes the solid solution phases to have a greater ability to compete with intermetallic compounds, which usually have much lower ΔSconf due to their ordered nature. That means the tendency to form the mixing state of constituent elements would be increased by increased mixing entropy, especially at high temperatures.
Table 2.1
Configurational Entropies of Equiatomic Alloys with Constituent Elements up to 13
| N | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| ΔSconf | 0 | 0.69R | 1.1R | 1.39R | 1.61R | 1.79R | 1.95R | 2.08R | 2.2R | 2.3R | 2.4R | 2.49R | 2.57R |

It can be seen from Table 2.1 and Figure 2.3 that the configurational entropy of ternary equiatomic alloy is already slightly higher than 1R and that of quinary alloy is higher than 1R by 61%. Furthermore, the formation enthalpies of two typical strong intermetallic compounds, NiAl and TiAl, divided by their respective melting points, lead to 1.38R and 2.06R, respectively (Yeh et al., 2004b). Thus, it is reasonable to think that a ΔSconf of 1.5R (even not including other three mixing entropy contributions mentioned above) is large enough against the strong ordering of such atomic pairs with strong bonding energies at high temperatures. The ΔSconf of 1.5R is recommended as a borderline between high- and medium-entropy alloys. In addition, 1R is recommended as the borderline for medium- and low-entropy alloys because a mixing entropy smaller than 1R is expected to have less power to compete with those strong bonding energies (Yeh, 2013a). Based on this, the alloys world is schematically shown in Figure 2.6. Similar mixing entropy effect may be expected in ceramics and polymers. Larger number of components in ceramics and polymers is expected to yield higher mixing entropy effect. Therefore, as shown in Figure 2.6B, ceramics can be grouped into three categories as low-, medium-, and high-entropy ceramics (HECs). Similarly, polymers also have three similar categories. Previously, borderlines for alloys world were set as 0.69 and 1.61R, respectively, and thus have some difference from Figure 2.6A (Yeh, 2006, 2013a; Yeh et al., 2007b). This is because the previous ones are based on the number of principal elements, i.e. 2 and 5, respectively.
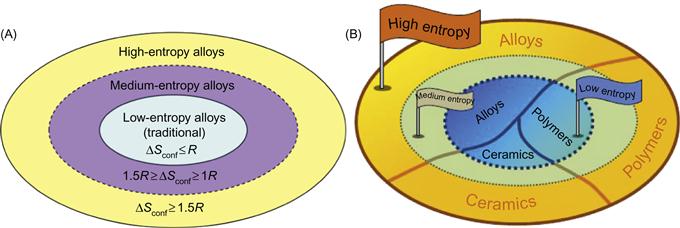
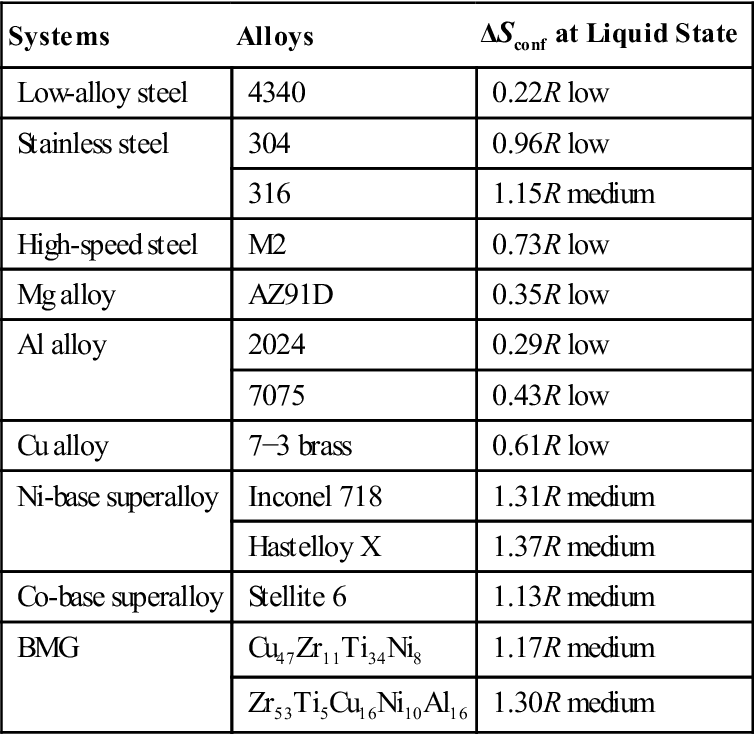
Table 2.2 gives the configurational entropies calculated for typical traditional alloys in their liquid state or random state. From this table, most alloys have low entropy (smaller than 1R) whereas some concentrated alloys of Ni-base, Co-base superalloys, and BMGs (bulk metallic glasses) have medium entropy between 1 and 1.5R. That means none of the traditional alloys have high mixing entropy ≥1.5R.
Table 2.2
Configurational Entropies Calculated for Typical Traditional Alloys at Their Liquid State or Random State (Yeh, 2013a)
| Systems | Alloys | ΔSconf at Liquid State |
| Low-alloy steel | 4340 | 0.22R low |
| Stainless steel | 304 | 0.96R low |
| 316 | 1.15R medium | |
| High-speed steel | M2 | 0.73R low |
| Mg alloy | AZ91D | 0.35R low |
| Al alloy | 2024 | 0.29R low |
| 7075 | 0.43R low | |
| Cu alloy | 7−3 brass | 0.61R low |
| Ni-base superalloy | Inconel 718 | 1.31R medium |
| Hastelloy X | 1.37R medium | |
| Co-base superalloy | Stellite 6 | 1.13R medium |
| BMG | Cu47Zr11Ti34Ni8 | 1.17R medium |
| Zr53Ti5Cu16Ni10Al16 | 1.30R medium |
Based on the above, the composition definition of HEAs in a broad sense can be explained to some extent from configurational entropy calculation. From the configurational entropy equation, we can observe that an element having a concentration of 5 at.% would contribute a mixing entropy of 0.05R ln 0.05=0.15R, which is just 10% of minimum requirement of 1.5R for HEAs. So, we could regard an element in an amount ≥5 at.% as a principal element. For elements with concentrations of 4, 3, 2, and 1 at.%, the contributions are 0.129R, 0.105R, 0.078R and 0.046R, respectively. So, we regard an element with <5% as minor element (Yeh, 2013a).
There arises a question from the definition: what is the upper bound of the number of metallic principal elements? For 5-, 10-, 12-, 13-, 14-, 15-, 20-, and 40-component equiatomic alloys, the total configurational entropies are 1.61R, 2.3R, 2.49R, 2.57R, 2.64R, 2.71R, 3.0R, and 3.69R, respectively. Beyond the 13 component alloy system, the increase is only 0.07R for each additional element, which is relatively small. Hence a practical number of principal element between 5 & 13 was suggested (Yeh et al., 2004b; Yeh, 2013a). That means more principal elements will not get significant benefit from the high-entropy effect but might increase the complexity in handling raw materials or recycling the alloys.
Indeed, it is not easy to give a clear-cut composition definition for HEAs. The composition definition is just a guideline. An alloy with some deviation from this composition definition might still be regarded as a HEA. For example, an alloy with 21-component equiatomic alloy is surely a HEA, even though each element has a concentration smaller than 5 at.%. Miracle et al. (2014) suggest that the definition, Sconf ≥1.5R, based on configurational entropy change is an operational definition of HEAs since the entropy change can be calculated for any alloy with an ideal or regular configurational entropy at the random solid solution state. In addition, this definition has more information and is more consistent than definitions based on alloy composition or on the value of Sconf at low temperatures. This operational definition also includes HEAs with two or more phases at low temperatures.
If we use the above composition definition and the practical upper bound of 13 principal elements, at an arbitrary choice of a group of 13 metallic elements, we can obtain a total of 7099 possibilities for designing equiatomic HEAs from 5 to 13 elements (Yeh et al., 2004b):
For any system, we may design equiatomic HEAs like AlCoCrCuFeNi. We may also design nonequiatomic HEAs with minor alloying elements like AlCo0.5CrCuFe1.5Ni1.2B0.1C0.15 for further modification of microstructure and properties. Since the number of common metals is much larger than 13, HEA systems are numerous and HEAs are even more in number.
2.4 Composition Notation
As the composition of each HEA does not contain a single principal element, the sequence of the composing elements in the chemical formula could be shown in many different ways. For the sake of easy identification and to make comparisons between alloys of the same system or alloys belonging to different systems, one common method is to put the element name of principal elements in alphabetical sequence, and finally put minor elements behind but in similar alphabetical sequence. This is convenient but does not carry additional meaning. Ordering the elements by atomic number or Mendeleev number may have more significance but lacks the convenience of alphabetical order. The concentration could be expressed as atomic ratio, or atomic percentage in the subscript position. For example, the expressions for two equiatomic alloys, AlCoCrFeNiTi and CoCrCuFeMnMoNiZr, conform to this rule.
The expressions for two nonequiatomic alloys, Al0.5Co1.5CrFeNi1.5Ti0.5 and CoCr0.5Cu0.5Fe1.5Mn0.5Mo0.3NiZr0.4, in atomic ratio also follow this rule. These two compositions could also be expressed as Al8.3Co25Cr16.7Fe16.7Ni25Ti8.3 and Co17.5Cr8.8Cu8.8Fe26.3Mn8.8Mo5.3Ni17.5Zr7.0 in at.%. In addition, the two nonequiatomic alloys with minor additions can be expressed as Al0.5Co1.5CrFeNi1.5Ti0.5B0.1C0.2 and CoCr0.5Cu0.5Fe1.5Mn0.5Mo0.2NiZr0.2C0.1Si0.15 in atomic ratio. Molar ratio has also been used in HEA literature simply because molar ratio is equal to atomic ratio (the number of atoms in one mole of HEAs is an Avogadro’s number). However, this rule need not be strictly followed if some composition feature is to be emphasized. A suitable expression can be used to reveal the specialty. For example, the notation Al0.5CoxCrFeNi1.5Ti0.5B0.1C0.2 (x=0.5, 0.75, 1.0, 1.25, 1.5) represents five compositions in which Co is varied from 0.5 to 1.5.
HECs have also been developed and investigated based on the similar alloy concept of HEAs. Their components corresponding to elements in HEAs are binary nitrides (e.g., AlN, CrN, Si3N4, TiN), binary carbides (e.g., Cr3C2, SiC, TiC, VC), binary borides (e.g., CrB, NbB2, TaB, TiB2). The compositions of HECs are also preferentially defined as those ceramics containing at least five principal components, each having a mole percentage between 5% and 35%. The free energy of mixing of a HEC is the change between the free energy of the HEC and the overall free energy of components in their standard state before mixing. The enthalpy of mixing and entropy of mixing are also similar changes. The binary compound has no mixing entropy and enthalpy. The mixing entropy can be calculated by the mixing of elements since N atoms occupy one set of sublattice whereas metal atoms randomly occupy another set of sublattice. The mixing enthalpy is mainly from lattice distortion energy or lattice strain energy since the chemical bonding between metals and nitrogen after mixing similarly can be found in the unmixed state. Their composition formula in stoichiometric ratio could be (Al,Cr,Ta,Ti,Zr)N in atomic ratio, or (Al,Cr,Ta,Ti,Zr)50N50 in atomic percentage. If the metal elements are known to be in equiatomic ratio, then (AlCrTaTiZr)N in atomic ratio, or (AlCrTaTiZr)50N50 in atomic percentage could be used. On the other hand, the formula in nonstoichiometric ratio could be (Al,Cr,Ta,Ti,Zr)1−xNx in atomic ratio, or (Al,Cr,Ta,Ti,Zr)100−yNy in atomic percentage. If carbon is involved, it could have the form (Al,Cr,Ta,Ti,Zr)1−u−vNuCv or (Al,Cr,Ta,Ti,Zr)100−s−tNsCt.
2.5 Four Core Effects of HEAs
There are many factors affecting microstructure and properties of HEAs. Among these, four core effects are most basic (Yeh, 2013a). Because HEAs contain at least five major elements, and conventional alloys are based on one or two metal elements, different basic effects exist between these two categories. The four core effects are high-entropy, severe lattice distortion, sluggish diffusion, and cocktail effects (Yeh, 2006, 2013a). For thermodynamics, high-entropy effect could interfere with complex phase formation. For kinetics, sluggish diffusion effect could slow down phase transformation. For structure, severe lattice distortion effect could alter properties to an extent. For properties, a cocktail effect brings excess to the quantities predicted by the mixture rule due to mutual interactions of unlike atoms and severe lattice distortion.
2.5.1 High-Entropy Effect
High-entropy effect is the most important effect because it can enhance the formation of solid solutions and makes the microstructure much simpler than expected. Based on physical metallurgy concepts, we easily expect such alloys to have many different interactions among elements and thus form many different kinds of binary, ternary, quaternary compounds, and/or segregated phases. Thus, such alloys would possess complicated structure not only difficult to analyze but also brittle by nature. This expectation in fact neglects the effect of high mixing entropy.
As for the mixing enthalpy, ΔHmix, it can be calculated as (de Boer et al., 1988; Takeuchi and Inoue, 2000, 2005):
where xk is the mole fraction of nonmetallic element k in the system and ![]() is the mixing enthalpy per mole of an equiatomic i−j alloy in the solid state. The transformation enthalpies of k-element from its standard state to metallic state are 30, 180, 310, 37, 25, and 17 kJ/mol for B, C, N, Si, Ge, and P, respectively.
is the mixing enthalpy per mole of an equiatomic i−j alloy in the solid state. The transformation enthalpies of k-element from its standard state to metallic state are 30, 180, 310, 37, 25, and 17 kJ/mol for B, C, N, Si, Ge, and P, respectively.
As the Gibbs free energy of mixing, ΔGmix, is
where ΔHmix and ΔSmix are the enthalpy of mixing and entropy of mixing, respectively, higher number of element would potentially lower the mixing free energy, especially at high temperatures by contributing larger ΔSmix.
In the solid state of an alloy, although there are numerous possible states, the equilibrium state is the one having the lowest free energy of mixing according the second law of thermodynamics. There are three possible categories of competing states, that is, elemental phases, intermetallic compounds and solid solution phases below the lowest melting point of the alloy (Yeh, 2013a). Elemental phase is the terminal solid solution based on one metal element. Intermetallic compound is a stoichiometric compound having specific superlattices, such as NiAl having B2 structure and Ni3Ti having D024 structure. Solid solution is the phase with the complete mixing or significant mixing of all elements in the structure of BCC (body-centered cubic), FCC, or HCP (hexagonal close-packed). Intermetallic phases or intermediate phases based on intermetallic compounds are also regarded as solid solutions, but they are partially ordered solid solutions (Cullity and Stock, 2001; Reed-Hill and Abbaschian, 1994). In such phases, different constituent elements tend to occupy different set of lattice sites.
In order to reveal the high-entropy effect which enhances the formation of solid solution phases and inhibits the formation of intermetallic compounds, consider a high-entropy alloy composed of those constituent elements with stronger bonding between each other. If strain energy contribution (due to atomic size difference) to mixing enthalpy is neglected for simplicity, the free energies of mixing for various kinds of state are shown in Table 2.3 (Yeh, 2013a). Elemental phases have small negative ΔHmix and ΔSmix because they are based on one major element. Compound phases have large negative ΔHmix but small ΔSmix because ordered structures have small configurational entropy. But random solid solution phases containing multicomponents have medium negative ΔHmix and highest ΔSmix. Why multicomponent solid solutions have medium ΔHmix? This is because there exists a proportion of unlike atomic pairs in solution phases. For example, a mole of atoms, N0, of NiAl intermetallic compound (B2) in complete ordering has (1/2)×8N0 Ni![]() Al bonds (coordination number in ordered BCC is 8), whereas a mole of NiAl random solid solution would have (1/2)×(1/2)×8N0 Ni
Al bonds (coordination number in ordered BCC is 8), whereas a mole of NiAl random solid solution would have (1/2)×(1/2)×8N0 Ni![]() Al bonds.
Al bonds.
Table 2.3
Comparisons of ΔHmix, ΔSmix, and ΔGmix Among Elemental Phases, Compounds, Ordered Solid Solutions, and Random Solid Solutions for n-element HEAs with Stronger Bonding Between Composing Elements
| Comparative States | Elemental Phases | Compounds | Intermediate Phases | Random Solid Solutions |
| ~0 | Large negative | Less large negative | Medium negative | |
| ~0 | ~0 | Medium | ||
| ~0 | Large negative | Larger negative | Larger negative |
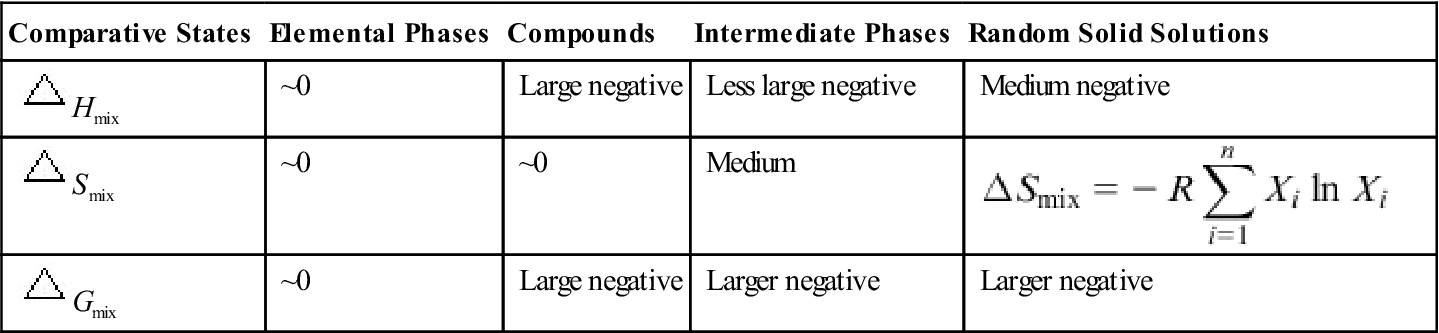
Strain energy from atomic size difference is not included in ΔHmix (Yeh, 2013a).
That means the mixing enthalpy in the random solution state is half that of the completely ordered state. Assuming that all heats of mixing for unlike atom pairs are the same, ΔHmix of the random solution state for quinary equiatomic alloy is 4/5 of that of its completely ordered state. Similarly, for septenary equiatomic alloy, the ratio is 6/7 (~0.86). Therefore, a higher number of elements would allow the random solution state to have the mixing enthalpy much closer to that of the completely ordered state. With the aid of its high mixing entropy in lowering the overall mixing free energy, random solution state would be more favorable in thermal stability than the ordered state. Although not all heats of mixing for unlike atom pairs are the same in reality, the tendency to increase the degree of disorder at equilibrium is unchanged. That is, at least, partially ordered solid solution phases having multicomponent composition and a certain degree of disorder instead of stoichiometric compounds are favorable at equilibrium. This is the reason why the state of intermediate phases as shown in Table 2.3 could be often favorable. Obviously this tendency toward disordered state is stronger at higher temperature due to −TΔSmix effect. Miracle et al. (2014) have made a rough, order-of-magnitude thermodynamic analysis to demonstrate this effect. The analysis suggests that ΔSconf of HEAs may be sufficient to destabilize 5–10% of intermetallic compounds (those with the lowest enthalpies of formation) at room temperature. An additional 30–55% of ordered compounds may be suppressed in HEAs at 1500 K. Roughly 50% of the intermetallic compounds may be stable at 300 K but unstable at 1500 K. They also pointed out that this effect also offers a new approach for controlling microstructure (via particle dissolution and subsequent controlled precipitation) and properties in particulate-strengthened HEAs.
Consider another case where one HEA contains an element which has strong repulsion force to other elements, that is, it has large positive mixing enthalpy with other elements. It is expected that the element will segregate to form an elemental phase with little solubility with other elements. Mixing entropy effect is still not sufficient to overcome the large enthalpy effect. Suppose the element has weak repulsion force, that is, has small positive mixing enthalpy, with some other elements, its segregation phase will contain higher concentration of these elements due to mixing entropy effect and becomes a concentrated solid solution with a major element.
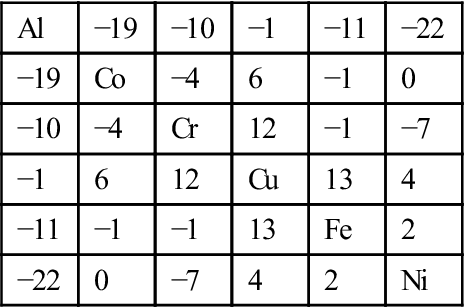
In general, if the heats of mixing for unlike atomic pairs have smaller difference, simple solid solution phases would be dominant in the equilibrium state. For example, CoCrFeMnNi alloy has small difference in such heats of mixing as shown in Table 2.4 (de Boer et al., 1988) and thus form a simple FCC solution even full annealed at all temperatures (Otto et al., 2013a; Tsai et al., 2013b). Refractory HfNbTaTiZr alloy has small difference as shown in Table 2.5 (de Boer et al., 1988) and can form a simple BCC phase in the as-cast state (Senkov et al., 2011a). Conversely, large difference among the heats of mixing for unlike atomic pairs might generate more than two phases. For example, Al has stronger bonding with Ni, Co, Fe, and Cr but Cu has repulsive bond with Fe, Cr, and Co as shown in Table 2.6 (de Boer et al., 1988). As a result, equiatomic AlFeCoCrCuNi alloy forms Cu-rich FCC+multicomponent FCC+multicomponent BCC (A2) at high temperatures above 600°C, and has B2 precipitates in the Cu-rich FCC and spinodally decomposed structure of A2+B2 phases from A2 phase during cooling. B2 solid solution containing multicomponents is in fact the intermediate phase derived from NiAl-type compound (Zhang et al., 2008b).
Table 2.4
Binary Mixing Enthalpies, ΔHmixij (kJ/mol), for Unlike Atom Pairs in Co![]() Cr
Cr![]() Fe
Fe![]() Mn
Mn![]() Ni Alloys (de Boer et al., 1988)
Ni Alloys (de Boer et al., 1988)
| Cr | −3.8 | 5.9 | 6.8 | 6.4 |
| −3.8 | Mn | −4.7 | 2.2 | −14 |
| 5.9 | −4.7 | Fe | −1.3 | −4.6 |
| 6.8 | 2.2 | −1.3 | Co | 0.0 |
| 6.4 | −14 | −4.6 | 0.0 | Ni |
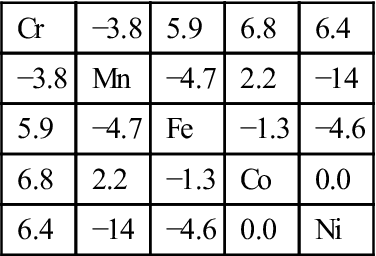
Table 2.5
Binary Mixing Enthalpies, ΔHmixij (kJ/mol), for Unlike Atom Pairs in Hf![]() Nb
Nb![]() Ta
Ta![]() Ti
Ti![]() Zr Alloys (de Boer et al., 1988)
Zr Alloys (de Boer et al., 1988)
| Hf | 4 | 3 | 0 | 0 |
| 4 | Nb | 0 | 2 | 4 |
| 3 | 0 | Ta | 1 | 3 |
| 0 | 2 | 1 | Ti | 0 |
| 0 | 4 | 3 | 0 | Zr |
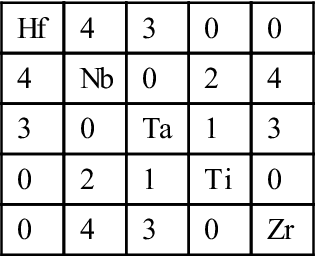
Table 2.6
Binary Mixing Enthalpies, ΔHmixij (kJ/mol), for Unlike Atom Pairs in Al![]() Co
Co![]() Cr
Cr![]() Cu
Cu![]() Fe
Fe![]() Ni Alloys (de Boer et al., 1988)
Ni Alloys (de Boer et al., 1988)
| Al | −19 | −10 | −1 | −11 | −22 |
| −19 | Co | −4 | 6 | −1 | 0 |
| −10 | −4 | Cr | 12 | −1 | −7 |
| −1 | 6 | 12 | Cu | 13 | 4 |
| −11 | −1 | −1 | 13 | Fe | 2 |
| −22 | 0 | −7 | 4 | 2 | Ni |
The atomic size difference among elements in a HEA also affects the stability of disordered solid solution phases. This is because large atomic size difference would cause the lattice to be heavily distorted and contribute strain energy to mixing enthalpy and thus mixing free energy. On the other hand, there are a variety of structures which preferentially form under large atomic size difference. It has been known that atomic size is one of the main factors which determine the structure of intermetallic compounds or intermediate phases (Porter and Easterling, 1992; Massalski, 1989, Pettifor, 1996; de Graef and McHenry, 2012). For example, when the component atoms differ in size by a factor of about 1.1–1.6, it is possible for these atoms to fill space most efficiently by the arrangement into ordered structures based on MgCu2, MgZn2, and MgNi2, that is, the so-called Laves phases. Another case is that when very small atoms such as H, B, C, and N are incorporated, interstitial compounds might form in the formulas MX, M2X, MX2, and M6X, where M can be Zr, Ti, V, Cr, etc. and X represents the small atoms. Therefore, it can be said that large atomic size difference might enhance the formation of different compounds or intermediate phases.
2.5.2 Severe Lattice Distortion Effect
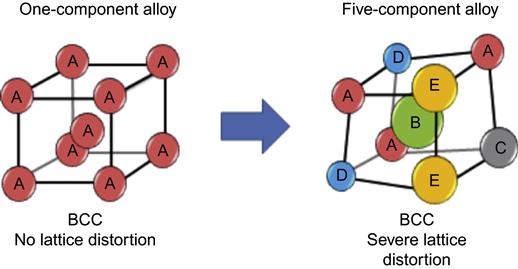
Because the multicomponent matrix of each solid solution phase in HEAs is a whole-solute matrix, every atom is surrounded by different kinds of atom and thus suffers lattice strain and stress mainly due to the atomic size difference as shown in Figure 2.7, an example with 10 kinds of atoms. The average lattice exists because it can be determined by x-ray diffraction. Besides atomic size difference, different bonding energy and crystal structure among constituent elements are also expected to cause even higher lattice distortion in consideration of the nonsymmetrical neighboring atoms, that is, nonsymmetrical bindings and electronic structure, around an atom, and the variation of such nonsymmetry from site to site (Yeh et al., 2007a; Tsai et al., 2013b). Thus, most lattice sites and overall lattice distortion would be more severe than that in conventional alloys in which most matrix atoms (or solvent atoms) have the same kind of atoms as their neighbors. Figure 2.8 shows the severe lattice distortion of a five-component BCC lattice. The three-dimensional unit cell is highly distorted.

Lattice distortion not only affects various properties but also reduces the thermal effect on properties. Hardness and strength effectively increase because of large solution hardening in the heavily distorted lattice. For example, Vickers hardness of FCC equiatomic alloy CoCrFeMnNi is 1192 MPa in the homogenized state which is higher than that 864 MPa obtained by the mixture rule. Hardness value of refractory BCC equiatomic alloy MoNbTaVW is 5250 MPa which is three times that obtained by the mixture rule (Senkov et al., 2010). It appears that FCC alloys display much smaller solution hardening than BCC alloys. This might be due to that FCC lattice has 12 nearest neighbors whereas BCC one has 8 nearest neighbors. For the same set of elements, FCC lattice has smaller fraction of unlike atomic pairs in the first nearest neighbors and thus a smaller distortion strain and solution hardening than BCC lattice. Besides, CoCrFeMnNi alloy has smaller atomic size difference than MoNbTaVW and thus smaller total distortion.
For the x-ray diffraction peak intensity, the distorted atomic planes increase x-ray diffuse scattering effect and give smaller peak intensity (Yeh et al., 2007a). Lattice distortion also causes electron scattering and significant decrease in electrical conductivity. This in turn reduces the electron contribution to thermal conductivity by electron conduction. Phonon scattering also becomes larger in the distorted lattice and decrease the thermal conductivity (Kao et al., 2011). All these properties in HEAs are found to be quite insensitive to temperature. For example, the temperature coefficients of resistivity are quite small in HEAs. This is because of the fact that the lattice distortion caused by thermal vibration of atoms is relatively small as compared with the severe lattice distortion (Yeh et al., 2007a).
2.5.3 Sluggish Diffusion Effect
In diffusion-controlled phase transformation, the formation of new phases requires cooperative diffusion of many different kinds of atoms to accomplish the partitioning of composition in HEAs. As explained in the last section, a HEA mainly contains random solid solution, and/or ordered solid solution. Their matrices could be regarded as whole-solute matrices. As a result, the diffusion of an atom in a whole-solute matrix would be very different from that in the matrix of conventional alloys. A vacancy in the whole-solute matrix is in fact surrounded and competed by different-element atoms during diffusion. It has been proposed that slower diffusion and higher activation energy would occur in HEAs due to larger fluctuation of lattice potential energy (LPE) between lattice sites (Tsai et al., 2013b). The abundant low-LPE sites can serve as traps and hinder the diffusion of atoms. This leads to the sluggish diffusion effect.
Tsai et al. (2013b) made diffusion couples from a near-ideal solution system of Co![]() Cr
Cr![]() Fe
Fe![]() Mn
Mn![]() Ni to analyze the diffusion data of each element in the matrix. The results concluded that the sequence in the order of decreasing diffusion rate was Mn, Cr, Fe, Co, and Ni. Diffusion coefficients of each elements at T/Tm in the Co
Ni to analyze the diffusion data of each element in the matrix. The results concluded that the sequence in the order of decreasing diffusion rate was Mn, Cr, Fe, Co, and Ni. Diffusion coefficients of each elements at T/Tm in the Co![]() Cr
Cr![]() Fe
Fe![]() Mn
Mn![]() Ni alloy system were the smallest in comparison to similar FCC matrices including Fe
Ni alloy system were the smallest in comparison to similar FCC matrices including Fe![]() Cr
Cr![]() Ni(
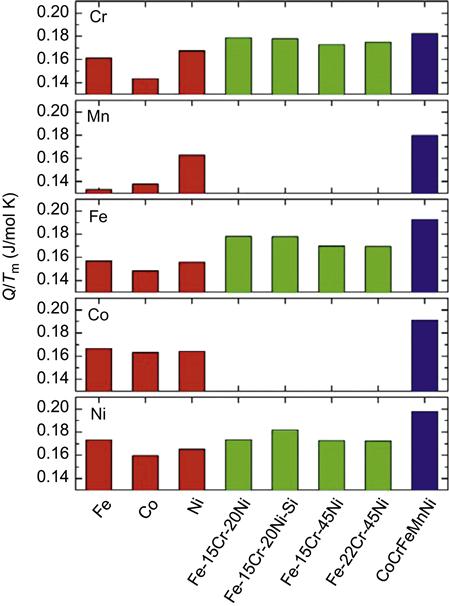
Ni(![]() Si) alloys and pure Fe, Co, and Ni metal. In addition, the melting point normalized activation energies, Q/Tm, in the HEA were the largest as shown in Figure 2.9. Also note that for the same element, the degree of sluggish diffusion is related to the number of elements in that matrix. For example, the Q/Tm values in the present HEAs are the highest; those in Fe
Si) alloys and pure Fe, Co, and Ni metal. In addition, the melting point normalized activation energies, Q/Tm, in the HEA were the largest as shown in Figure 2.9. Also note that for the same element, the degree of sluggish diffusion is related to the number of elements in that matrix. For example, the Q/Tm values in the present HEAs are the highest; those in Fe![]() Cr
Cr![]() Ni(
Ni(![]() Si) alloys are the second; and those in pure metals are the lowest. This suggests that greater the number of elements, slower is the diffusion rate (Tsai et al., 2013b).
Si) alloys are the second; and those in pure metals are the lowest. This suggests that greater the number of elements, slower is the diffusion rate (Tsai et al., 2013b).
It is expected that sluggish diffusion might affect phase nucleation, growth and distribution, and morphology of new phase through diffusion-controlled phase transformation. It also provides various advantages in controlling microstructure and properties: easiness to get supersaturated state and fine precipitates, increased recrystallization temperature, slower grain growth, reduced particle coarsening rate, and increased creep resistance. As an example, Liu et al. (2013) found a significantly high value of activation energy (~321 kJ/mol) and slow coarsening kinetics on the grain growth behavior of CoCrFeMnNi HEA following cold rolling and annealing, which is in agreement with the sluggish diffusion effect. As a result, sluggish diffusion is in general positive for improving properties of HEAs. For example, fine precipitation and grain structure could improve the combination of strength and toughness. Improved creep resistance could prolong the life of parts used at high temperatures.
2.5.4 Cocktail Effect
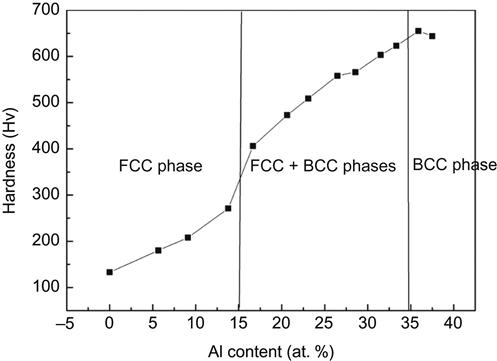
The article on “Alloyed pleasures: multimetallic cocktails” by Ranganathan (2003) caught the imagination of scientists in this area and the paper attracted about 100 citations in the past decade. In HEAs, cocktail effect is used to emphasize the enhancement of the properties by at least five major elements. Because HEAs might have single phase, two phases, three phases, or more depending on the composition and processing, the whole properties are from the overall contribution of the constituent phases. This relates with the phase size, shape, distribution, phase boundaries, and properties of each phase. Moreover, each phase is a multicomponent solid solution and can be regarded as an atomic-scale composite. Its composite properties not only come from the basic properties of elements by the mixture rule but also from the mutual interactions among all the elements and from the severe lattice distortion. Mutual interaction and lattice distortion would bring excess quantities in addition to those predicted by the mixture rule. As a whole, “cocktail effect” ranges from atomic-scale multicomponent composite effect to microscale multiphase composite effect. Figure 2.10 (Yeh, 2006) shows the cocktail effect introduced by the interaction of constituent elements in the AlxCoCrCuFeAl alloy, which leads to a phase transformation from an FCC structure to a BCC when the Al content is increased beyond critical value.
To illustrate the cocktail effect, two examples are introduced. In the first example, refractory HEAs developed by Air Force Research Laboratory have melting points very much higher than that of Ni-base and Co-base superalloys (Senkov et al., 2010, 2011b). They mainly consist of refractory elements having melting temperatures above 1650°C. By the mixture rule, quaternary equiatomic alloy MoNbTaW and quinary equiatomic alloy MoNbTaVW have melting points above 2600°C. They actually found that both alloys display much higher softening resistance than superalloys and have yield strength above 400 MPa at 1600°C (Senkov et al., 2011a). Such refractory HEAs are thus expected to have promising potential in those applications at very high temperatures. In the second example, Zhang et al. (2013b) studied CoNiFe(AlSi)0–0.8 alloys for obtaining the optimum combination of magnetic, electrical, and mechanical properties. The best alloy is CoNiFe(AlSi)0.2 with saturation magnetization (1.15 T), coercivity (1400 A/m), electrical resistivity (69.5 µΩ-cm), yield strength (342 MPa), and strain without fracture (50%). This demonstrates that the alloy is an excellent soft magnetic material for many potential applications (Zhang et al., 2013b). This finding was based on suitable alloy design which used equiatomic ferromagnetic elements (Fe, Co, and Ni) for forming ductile FCC phase (atomic packing density higher than BCC), and suitable addition of nonmagnetic elements (Al and Si having slightly antiparallel magnetic coupling with Fe, Co, and Ni) to increase lattice distortion. As a result, it brought up a positive cocktail effect in achieving high magnetization, low coercivity, good plasticity, high strength, and high electrical resistance. Therefore, it is important for an alloy designer to understand related factors involved before selecting suitable composition and processes.
