Two key terms, isochore and isopach, are often used synonymously in the petroleum industry as measures of thickness, but they are different. An isochore map (Fig. 14-1a) delineates the true vertical thickness of a stratigraphic interval, whereas an isopach map (Fig. 14-1b) illustrates the true stratigraphic thickness of a stratigraphic interval. These two terms are often confused with respect to their geologic meaning. It is vital for both exploration and development work that the correct meaning and, more importantly, the correct application of these two thicknesses be understood.
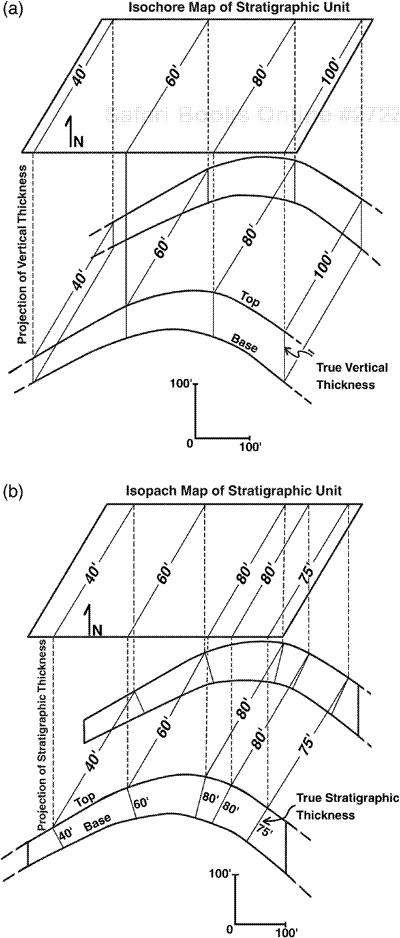
Figure 14-1. (a) An isochore map delineates the true vertical thickness of a stratigraphic interval, such as a rock unit containing a reservoir. (b) An isopach map delineates the true stratigraphic thickness of a stratigraphic interval. The same dipping stratigraphic unit is used in both (a) and (b), with the same edge-of-map boundaries. Note different thickness values assigned to the isochore map versus the isopach map of the same unit.
An isochored or isopached unit may be as small as an individual sand only a few feet thick, or as large as several thousand feet thick and encompassing a number of stratigraphic units. An isopach map is extremely useful in determining the stratigraphic framework or the structural relationship responsible for a given type of sedimentation, and for recognizing paleohigh areas. The shape of a basin, the position of the shoreline, areas of uplift, and under some circumstances the amount of vertical uplift and erosion, can be recognized by mapping the variations in thickness of a given stratigraphic interval (Bishop 1960).
Isochore and isopach maps are used for a number of purposes by the petroleum geologist, including (1) depositional environment studies, (2) genetic sand studies, (3) growth history analyses, (4) depositional fairway studies, (5) derivative mapping, (6) the history of fault movement, and (7) calculation of hydrocarbon volumes.
In this chapter, we discuss several different types of isochore and isopach maps important to the evaluation of petroleum potential. These include interval isopach maps and net sand and net pay isochore maps. An interval isopach map delineates the true stratigraphic thickness of a specific unit or units.
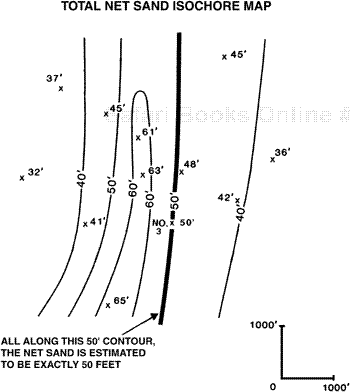
An isochore map may be based on the total vertical thickness of a specific unit or based on an aggregate vertical thickness of a particular rock type within a stratigraphic unit. For example, a given unit may consist of interbedded permeable and impermeable strata. An isochore map can be made for the total unit consisting of both permeable and impermeable strata, or an isochore map can represent the aggregate vertical thickness of only the reservoir-quality rock within that stratigraphic unit. For simplicity and brevity in this chapter, we use the term net sand isochore map to refer to a map of only the reservoir-quality rock. Therefore, a net sand isochore map representsthe aggregate vertical thickness of reservoir-quality rock present in a particular stratigraphic interval, which is illustrated in Fig. 14-2. The techniques and calculations to derive vertical thickness are explained in detail in this chapter. The fluid contained in a stratigraphic unit may be hydrocarbons or water, or any combination of the two. Figure 14-3 shows a net sand isochore map of the 10,500-ft Sand in Golden Meadow Field, Lafourche Parish, Louisiana, USA. A net pay isochore map delineates the aggregate vertical thickness of reservoir-quality rock that contains hydrocarbons (gas, oil, or both). An example is shown in Fig. 14-5.
(From Tearpock and Harris 1987. Published by permission of Tenneco Oil Company.)
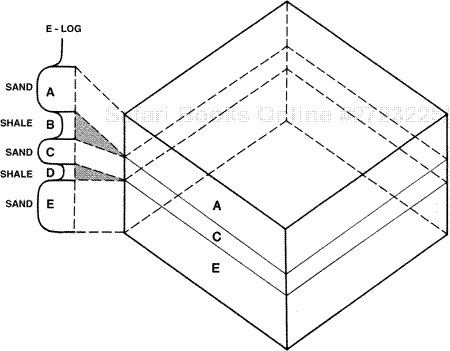
Figure 14-2. Net sand consists of porous reservoir-quality rock. All nonreservoir-quality rock is ignored.
Net sand and net pay isochore maps of subsurface units are usually prepared from well log data, whereas interval isopach maps may be constructed from well log data and seismic data, where coverage is adequate. As with structure maps, the completeness and accuracy of an isochore or isopach map depends upon the amount and accuracy of data available. Even in isochore and isopach mapping, we cannot get away from the importance of log correlation work. Well log data, particularly correlations, should be studied very carefully in order to prepare an accurate and precise isochore map.
For volumetric reserve calculations, we are interested in obtaining the volume of a reservoir (solid material plus fluid-filled pore space). In this book, we use the volume unit acre-foot, which is standard practice within the United States. One acre-foot is equivalent to 1233.48 cubic meters, and to 0.123348 hectare-meters. To many people, an acre-foot is an abstract measurement, but the concept is relatively simple. One acre-foot can be defined as that volume of rock plus fluid contained in an area one acre in size, with a thickness of one foot. How big is an acre? There is a very easy way for some people to visualize the size of an acre. One acre contains just about the same area as an American football field from goal line to goal line. A football field 300 ft long and 160 ft wide is equal to 48,000 sq ft, whereas one acre is equal to 43,560 sq ft. If we fill, with oil, a box that is one foot deep and the size of an American football field, the total volume of oil is just about equal to one acre-foot. In terms of barrels of oil, there are 7758 barrels (1233 cubic meters) of oil in one acre-foot. However, a reservoir volume of one acre-foot is actually comprised of solid material plus fluids that occupy the pore space. So a calculation of oil in place in a reservoir must take into account pore space and water saturation, as well as other factors. In creating a net pay map, we assume that within a net sand interval that contains hydrocarbons, all pore spaces are filled with hydrocarbons. The later calculation of hydrocarbons-in-place takes account of water saturation. In most cases, the structurally lower limit of a reservoir is a hydrocarbon/water contact, typically defined on the basis of parameters related to economic productivity, such as porosity and water saturation.
Most individual rock bodies do not consist exclusively of permeable rock; shale and other impermeable rock material are commonly distributed throughout the rock body as interbedded shale or impervious (tight) zones. The percentage and distribution of shale members or impervious zones varies widely within rock units. Net sand and net pay isochore maps are drawn on net effective sand (porous and permeable sand) only; therefore, shale and other nonreservoir-quality rock must be subtracted from the total interval to determine the net effective sand for isochore mapping.
In a given oil or gas well, the net effective sand to be used for isochore mapping is normally determined by detailed analysis of 5-in. well logs, supplemented by available core analysis. In Chapter 4, in the section Annotation and Documentation, we outline a method for annotating the percentage and distribution of net sand and impermeable layers that are present within a particular productive unit (Fig. 4-47). Once the net sand is determined for each well, a net sand map can be prepared for that sand. The aggregate of net sand for any particular well may contain water or hydrocarbons; net pay is that portion of the net sand that contains hydrocarbons.
For a net sand or net pay map, the gross, or overall, interval to be mapped extends from the top of porosity to the base of porosity within the productive unit. Within that interval, the amounts of net sand and net pay vary with location. The net/gross ratio is the amount of net sand divided by the thickness of the gross interval, as determined from well logs and core analyses. The net/gross ratio within a productive unit can be mapped, based on log and core data, and used to estimate net sand and net pay at selected locations within the unit, as described in a later section in this chapter.
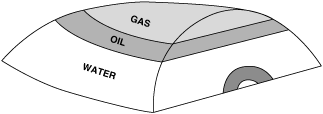
The procedure used in constructing an isochore map depends on whether the reservoir being mapped is a bottom water or an edge water reservoir. A bottom water reservoir is a reservoir that is completely underlain by water (Fig. 14-4). An edge water reservoir is one not completely underlain by water; some portion(s) of the productive unit is completely filled with hydrocarbons, and water underlies the remainder of the reservoir (Fig. 14-6).
(From Tearpock and Harris 1987. Published by permission of Tenneco Oil Company.)
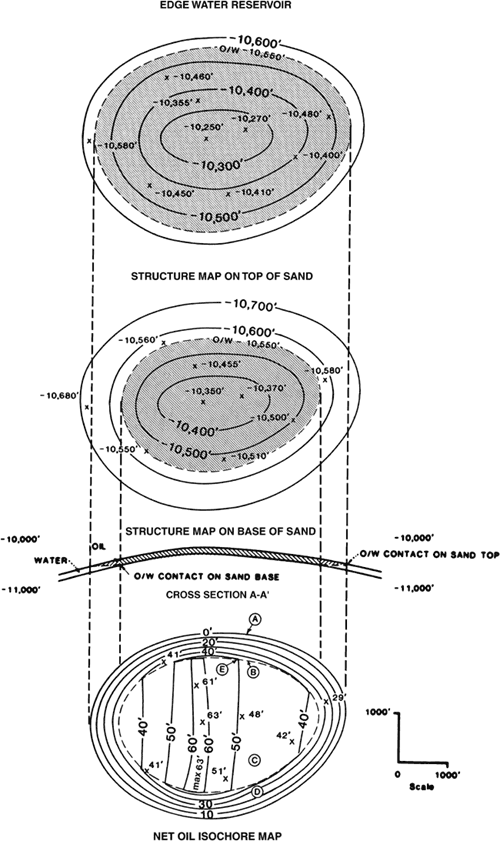
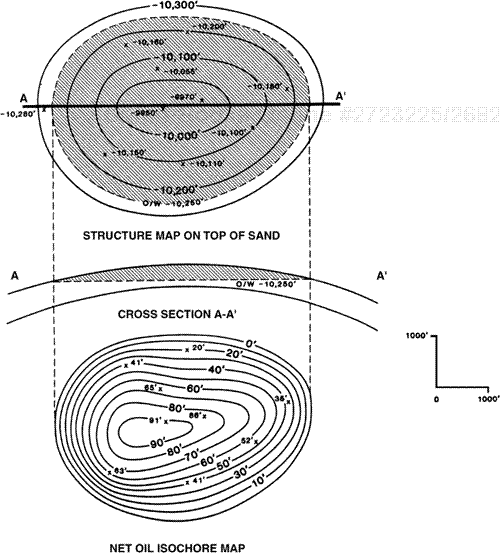
Figure 14-5. Structure map of the top of porosity, cross section, and net oil isochore map for a bottom water reservoir. A net oil isochore map is a map showing the vertical aggregate thickness of reservoir-quality rock containing hydrocarbons.
It is important to be able to visualize a hydrocarbon reservoir in 3D. Your ability to understand the configuration of a reservoir can affect the location of development wells, completion practices, and planned production.
Figure 14-4 is a 3D model of a bottom water reservoir. This hydrocarbon accumulation, consisting of oil and gas, is trapped within an anticlinal structure. Notice how the oil and gas are segmented within the reservoir and completely underlain by water.
Figure 14-5 illustrates, in both map and cross-sectional views, a bottom water oil reservoir. Looking at the cross section in the center of the figure, we can see the oil/water contact. The hydrocarbons are completely underlain by water; therefore, nowhere in the productive unit is there a full thickness of oil. At any location within the reservoir, the amount of net pay equals the amount of net sand above the oil/water contact.
The construction of a net pay isochore map for a bottom water reservoir requires a structure map on the top of porosity for a given productive unit, net pay values for each well in the reservoir, and the depth of the hydrocarbon/water contact. The following procedure is used to construct the net pay isochore map for a bottom water reservoir (Fig. 14-5).
Post the net pay values for each well on a base map. If deviated wells are included, the net pay values must be corrected to true vertical thickness.
Overlay the isochore base map on the top-of-porosity structure map for the reservoir, and draw the outer limit of the hydrocarbon-bearing reservoir. The outer limit may be any boundary, or combination of boundaries, such as an oil/water contact, fault, pinchout, or permeability barrier. Where this outer limit of the productive reservoir area is a hydrocarbon/water contact, it becomes the zero contour line on the net pay isochore map, as shown in Fig. 14-5. In this case, the outer limit of the reservoir is an oil/water contact at a depth of –10,250 ft. However, if a boundary of part of a reservoir is a more or less vertical surface, such as a vertical fault or a vertical salt face, then the amount of net pay adjacent to this surface will exceed zero.
Contour the net pay isochore map, which is contained within the area outlined by the zero line on the base map. Be sure to honor all posted net pay values. The net pay contours may generally conform to the structure contours. Net pay contours are commonly drawn as being equally spaced. However, due to variations in net sand thickness within the reservoir, the isochore contours need not be equally spaced. Figure 14-5 is a net pay map of a reservoir in which the net oil contours reflect the structure in a general way, yet the contours are proportionally spaced due to variation in net sand within the productive unit. If the well control is limited, additional points of contour control may be obtained by using a method called walking wells or by using a net/gross ratio map, each of which allows us to estimate net pay at chosen points in a reservoir. These methods are explained in detail later in this chapter.
Always indicate the maximum or minimum thicknesses of pay within the area bounded by a maximum or closed minimum net pay contour (Fig. 14-5), as this information is necessary for volumetric calculation after planimetering of the net pay map.
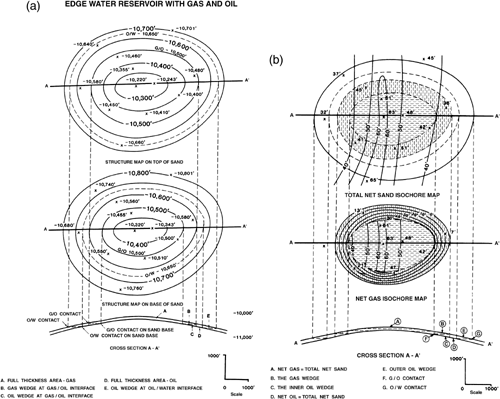
Figure 14-6 is a 3D model of an edge water reservoir containing oil and gas. The hydrocarbons are trapped within an anticlinal structure. Compare the configuration of this reservoir with the bottom water reservoir model in Fig. 14-4. In this example of an edge water reservoir, part of the productive unit is filled with gas, part is filled with oil, and wedge-shaped volumes of gas and oil are also present. It is obvious that this type of reservoir is more complex and more difficult to visualize in three dimensions.
Figure 14-7 illustrates in map and cross-sectional views an edge water reservoir containing oil. The cross section shows an oil-filled part of the productive unit and a wedge of oil that is underlain by a wedge of water. Between the oil/water contact on the top of the unit (top of porosity) and the oil/water contact on the base of the unit (base of porosity), an oil wedge overlies a water wedge. Up-dip of the oil/water contact on the base of porosity, the reservoir is full of oil from the top to base of porosity. That area is the full thickness area of the reservoir. In the full thickness area, net pay equals net sand. In the wedge, net pay equals the amount of net sand above the water level.
Edge water reservoirs are obviously more complex than bottom water reservoirs. An edge water reservoir can be extremely complex if it contains both oil and gas and is cut by one or more faults. When mapping a reservoir cut by faults, consideration may be given to mapping one or more fault wedges in addition to mapping the hydrocarbon wedges above water. The result may be a complex isochore map. Fault wedges are discussed in detail later in this chapter.
An understanding of the reservoir type and configuration is very important in such decisions as the location of development wells, completion practices, and production plans. Take a few minutes and review Fig. 14-6, especially the areas of multiple wedge zones.
The generally accepted method for construction of a net hydrocarbon isochore map for an edge water reservoir is called the Wharton Method, after J. B. Wharton (1948). The data needed to construct a net hydrocarbon isochore map for this type reservoir are
a structure map on the top of porosity of the productive unit;
a structure map on the base of porosity of the productive unit;
a net sand isochore map (with a contour interval equal to that to be used in the net pay map);
net pay values for all available wells; and
depth or elevation of all fluid contacts (oil/water, gas/water, oil/gas).
We first outline the procedure for construction of a net hydrocarbon isochore map for an edge water reservoir containing a single type of hydrocarbon. For this example, we consider the rock type to be sandstone and the hydrocarbon to be oil. The procedure is illustrated in Fig. 14-8.
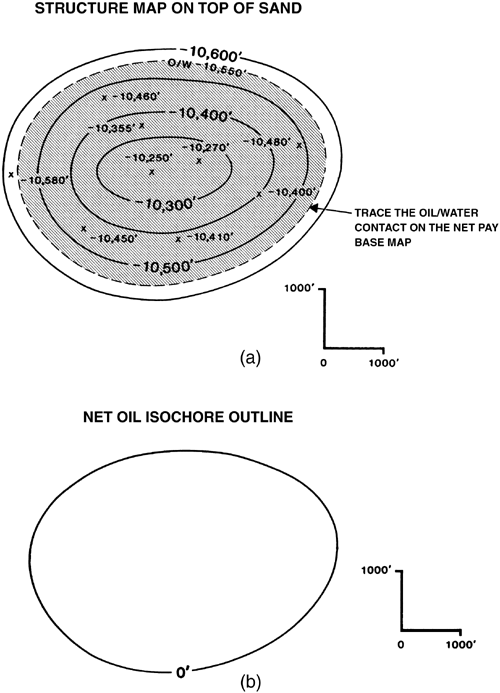
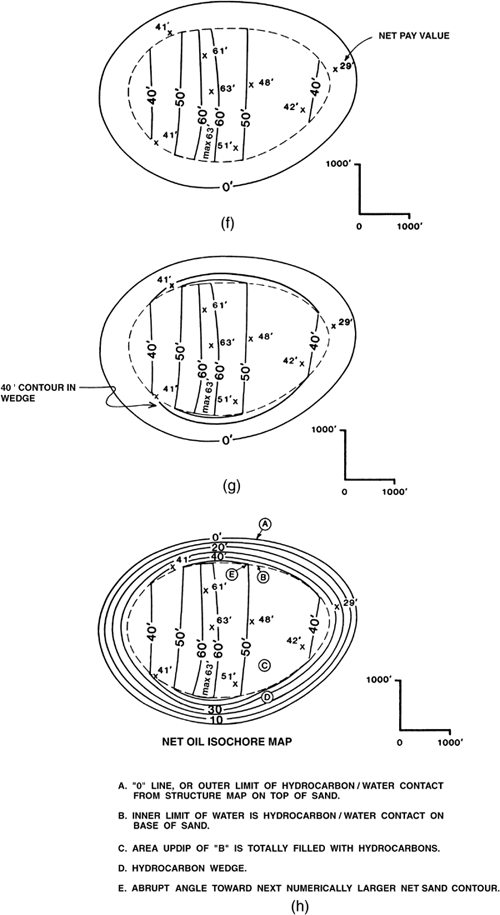
Figure 14-8. (a) Overlay a net oil base map on the structure map of the top of sand (top of porosity). The oil/water contact is traced on the overlay. (b) The oil/water contact becomes the zero contour line on the net oil isochore map. (c) Overlay the net oil isochore map on the structure map of the base of sand (base of porosity), and trace the oil/water contact as a dashed line. (d) Isochore base map delineating the two major areas comprising the net oil isochore map: (1) oil wedge from the zero line to the inner limit of water (oil/water contact on the base of the sand), and (2) the area of full hydrocarbon thickness. (e) To contour the full thickness area, superimpose the net oil isochore map on a net sand isochore map and trace the net sand contours inside the inner limit of water (dashed line). (f) Net oil isochore map with contours drawn for the oil-filled area. (g) All full thickness area contours that intersect the inner limit of water must connect through the wedge with contours of equal value (see text for procedure). (h) Completed net oil isochore map with important points of isochore construction listed.
Start with a base map with all the well control spotted.
Place the base map over the structure map on the top of the unit (top of porosity) (Fig. 14-8a), and trace the outer limit of the productive reservoir. In this example, the limit is the oil/water contact on the top of the unit, and it becomes the zero line on the net oil isochore map, as in the previous example. The zero line is shown in Fig. 14-8b. From this point forward, we refer to the base map as the net oil isochore map.
Place the net oil isochore map over the structure map on the base of the unit (base of porosity) (Fig. 14-8c), and trace the oil/water contact on the isochore map using a dashed line. This dashed line represents the inner limit of water for the reservoir. Within the area inside this dashed line, oil fills the productive unit (Fig. 14-8d), and this area is referred to as the full thickness area. The intersection of the oil/water contact with the top and base of the unit outline the wedge zone.
Post net pay values for all wells within the reservoir, corrected to true vertical thickness, on the net oil isochore map.
In the full thickness area, the entire net sand is filled with oil, so the net oil in this area equals the amount of net sand, as interpreted on the net sand isochore map. Notice that the net sand contours are based on all wells, within and outside the reservoir. Therefore, to contour the full thickness area, place the net oil isochore map over the net sand isochore map as shown in Fig. 14-8e, and trace the contours within the dashed-line area onto the net oil isochore map. Label the maximum thickness of oil (63 ft) within the area enclosed by the maximum net pay contour (60 ft). The full thickness area of the net oil isochore map is now finished, as illustrated in Fig. 14-8f.
The next step is to contour the oil wedge. The wedge zone is the area between the oil/water contact on the top of the unit and the oil/water contact on the base of the unit, as shown in Fig. 14-8d and f. The oil wedge overlies a water wedge (see cross section in Fig. 14-10). All well data in the wedge must be honored. In the full thickness area, net sand distribution controls the net pay contours. However, in the oil wedge, the structural attitude of the productive unit and the distribution of impermeable rock within the unit, influence the position of net pay contours. The contours conform in general to the structure contours, but they are not necessarily equally spaced (variations in contour spacing are discussed below). As the first step in contouring the wedge, draw the net pay contours from the full thickness area into the wedge. Notice in Fig. 14-8g that the full thickness contour lines turn abruptly at the inner limit of water, in the direction of increasing sand thickness (in the direction of the next net sand contour of higher value). They connect through the wedge with contours of the same value elsewhere in the full thickness area. Lastly, draw the net pay contours in the oil wedge that do not correspond to contours within the full thickness area. Honor the well data within the wedge, and more or less equally space contours where data is lacking (Fig. 14-8h). If the dip of the productive unit is more irregular than in this example, then that variation in structure may be considered in contouring the wedge.
The completed net oil isochore map is shown in Fig. 14-8h. This figure highlights five important points of the net pay isochore map construction. We recommend that you leave the dashed inner limit of water on the net pay isochore map. It allows others to review and verify that you have used the water contact on the base of porosity correctly in creating the net pay map.
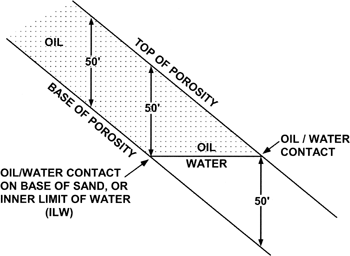
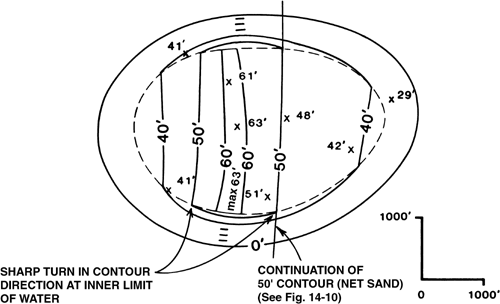
The method of connecting the full thickness contours to those in the wedge zone is extremely important and deserves special attention. Why can we not extend the net pay contours in the full thickness area on trend, past the inner limit of water and into the wedge? Look at Fig. 14-9, which is similar to Fig. 14-8g. Let’s discuss the construction of the easternmost 50-ft contour in the figure. Why must this contour line sharply change direction at the inner limit of water on the net oil isochore map, rather than continue straight into the wedge zone? Figure 14-10 is a diagrammatic cross section along the 50-ft net sand contour. Everywhere along the cross section are exactly 50 ft of net sand. In the portion of the reservoir that is up-dip to the oil/water contact on the base of porosity (inner limit of water), oil fills the entire 50 ft of net sand. However, a point one foot down-dip of the inner limit of water is within the wedge zone, where the sand contains both oil and water. Therefore, anywhere outside the inner limit of water, both oil and water are present and, since the total net sand is still 50 ft thick, there must be less than 50 ft of oil. The 50-ft net pay contour, therefore, cannot continue along the 50-ft net sand contour down-dip of the inner limit of water.
(Modified from Tearpock and Harris 1987. Published by permission of Tenneco Oil Company.)
Figure 14-9. Full thickness net pay contours make an abrupt turn at the inner limit of water, toward the next net sand contour of higher value.
Where must the 50-ft contour from the full thickness area be drawn in the wedge zone? It must be drawn through an area of 50 ft of net oil in the wedge zone. This area exists only where the net sand is greater than 50 ft. In Fig. 14-8e, notice that the net sand increases in thickness west of the 50-ft contour to a maximum of 63 ft. Therefore, the 50-ft contour, at its intersection with the inner limit of water, must turn sharply toward the area of thicker sand. Since contour lines must close, the contour connects to the west to connect with the other 50-ft contour in the full thickness area (Fig. 14-8g).
This procedure must be undertaken for all contour lines contained within the full thickness area of the net pay isochore map. The correct application of this technique is most important. If the full thickness area net pay contours are carried incorrectly into the wedge zone, the volume of hydrocarbons determined for the reservoir will be overestimated.
Figure 14-11a and b present a summary of the foregoing method for preparing a net pay isochore map for an edge water reservoir containing one type of hydrocarbon.

(Modified from Tearpock and Harris 1987. Published by permission of Tenneco Oil Company.)
Figure 14-11. (a) - (b) Summary of method for constructing a net hydrocarbon isochore map for an edge water reservoir containing one hydrocarbon (oil or gas).
Comprehension of, and commitment to, the foregoing procedure will help you avoid the most common pitfall in net pay mapping, which is the mapping of more net pay than net sand that is filled with hydrocarbons. In the full thickness area, a net pay contour corresponds exactly to a net sand contour. In the hydrocarbon wedge, a net pay contour corresponds to that same amount of net sand above the water level. Therefore, in the wedge, a net pay contour of a given value must be within an area where the total net sand is of greater value. Always overlay and compare the net pay contour map to the net sand contour map in order to check that the positions of the net pay contours are reasonable.
Two methods may be used to estimate the volumes of oil and gas in a reservoir containing both types of hydrocarbons. The simplest and quickest method is to construct a total net hydrocarbon isochore map and a net gas isochore map, calculate the volumes of each, and subtract the gas volume from the total hydrocarbon volume to determine the oil volume. This method is appropriate when only one lease owner is involved or when only the total estimated volumes of oil and gas are required (there being no interest in the actual distribution of oil and gas within the reservoir). Where a reservoir underlies two or more separate ownerships, it is very important to know the estimated volumes of gas and oil under each lease. In this case, net gas and net oil isochore maps must be constructed, preferably using the procedure outlined in this section.
Construct the net gas isochore map first. Draw the basic maps used in the Wharton method, which are the structure map on top of porosity, structure map on base of porosity, and net sand isochore map. Using these maps, construct the net gas isochore map as shown in Fig. 14-12a and b. The net gas isochore map is constructed using the same procedure explained in the previous section on edge water reservoirs containing one type of hydrocarbon. The only difference in this case is that the gas/oil contact defines the down-dip, outer limit of the gas reservoir, whereas in the previous cases the limit was determined by a hydrocarbon/water contact.
(Modified from Tearpock and Harris 1987. Published by permission of Tenneco Oil Company.)
Figure 14-12. (a) - (b) Summary of procedure to construct a net gas isochore map for a reservoir containing both oil and gas.
The last map to be constructed is the net oil isochore map. This map differs from the previous maps in that it has two wedge zones, an inner wedge zone (gas/oil) and an outer wedge zone (oil/water), as shown on the cross section in Fig. 14-12a. The outer oil wedge and any full thickness areas are constructed using the Wharton method, as previously discussed; the inner oil wedge requires additional steps.
Figure 14-13a shows a partitioned map (without wells) for the oil reservoir, with an inner wedge and an outer wedge of oil, and an area of full thickness in between. The fluid contacts on the structure maps are used to determine the zero net pay limits and dashed wedge limits by tracing them onto the net oil map.
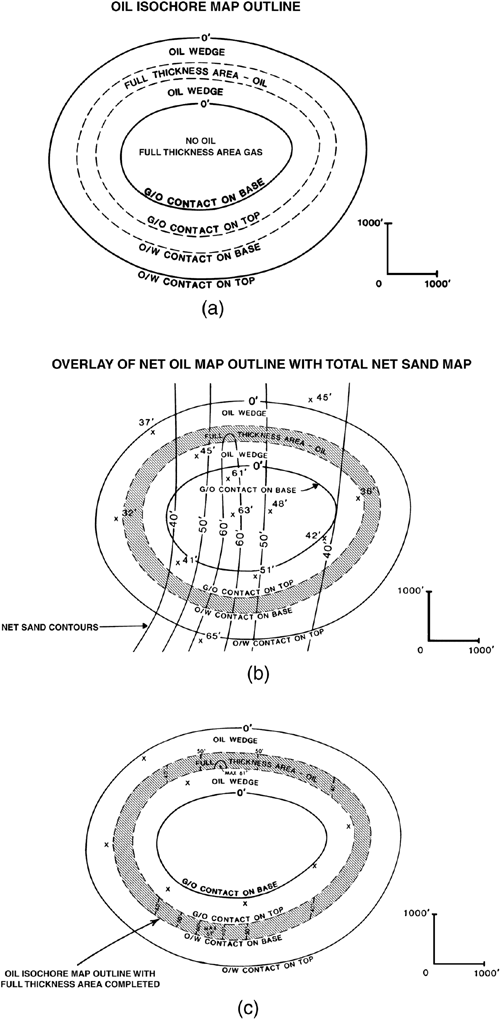
(From Tearpock and Harris 1987. Published by permission of Tenneco Oil Company.)
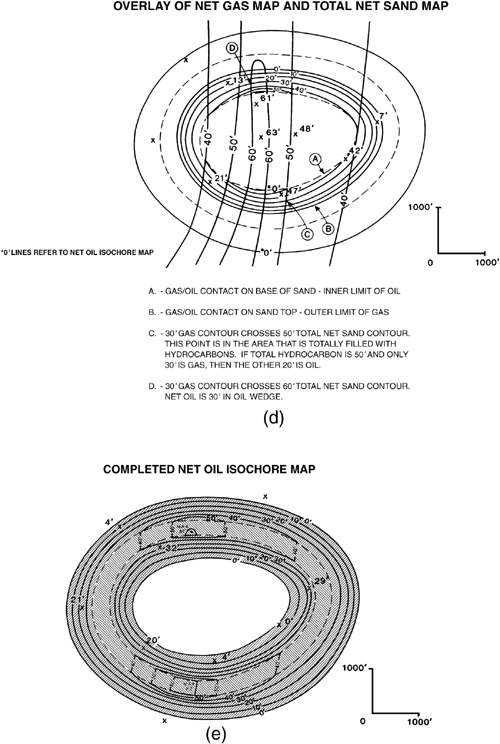
Figure 14-13. (a) Outline of oil isochore map showing the inner and outer wedge zones and the full thickness area. (b) Overlay of net oil isochore map on the net sand isochore map. The contours in the area of full oil thickness are equal to the net sand contours. (c) Full thickness area is contoured. (d) Overlay of net gas and net sand isochore maps used to aid in the construction of the inner oil wedge contours. (e) Completed net oil isochore map.
First, contour the area containing a full thickness of oil. Post the net oil values next to each well and overlay the isochore base map onto the net sand isochore map, as shown in Fig. 14-13b. Trace the net sand contours on the net oil map only within the full thickness area of oil, as shown in Fig. 14-13c. Indicate the maximum thickness of oil in each of the areas enclosed by the 60-ft net pay contours. This portion of the isochore map is now complete.
We now contour the inner oil wedge on the map, to be followed by contouring of the outer oil wedge. By referring to the cross section in Fig. 14-12b, we see that within the inner oil wedge, the sum of net oil-filled and net gas-filled sand equals the total net sand. Therefore, in order to determine the amount of net oil in the inner wedge zone, the following procedure is used. Overlay the net gas isochore map on the net sand isochore map, and note each location where the contours on the two separate maps cross. The net oil sand value at each contour intersection is equal to the difference in values of the two contours. For example, at point C in Fig. 14-13d, the 30-ft contour line on the net gas isochore map crosses the 50-ft contour line on the net sand isochore map. By subtracting the 30 ft of net gas from the 50 ft of net sand, a value of 20 ft of net oil is obtained for this point. Take a minute and review the data at point D. As indicated, a known value is established wherever a contour line on the net gas isochore crosses a contour line on the net sand isochore. The net oil sand value at each intersection is the difference in values of the two contours. Figure 14-13d shows 48 points of control, plus data from four wells, to aid in contouring the inner wedge zone of the oil isochore map. Overlay the net oil map on the net gas and net sand maps, mark selected points with the corresponding value of oil, and then contour the inner oil wedge. The net pay contours at the edge of the full thickness area turn abruptly towards the thicker net sand values (Fig. 14-13e), just as described in the contouring of a single-phase reservoir.
When contouring the inner oil wedge, the net oil isochore map should be overlain on both the net gas and net sand isochore maps. This allows mapping the inner oil wedge with the constraint, and thus the assurance, that the sum of the net gas and net oil does not exceed the total net sand. This is one of the most complex, and therefore most difficult, areas to construct within an isochore map.
Finally, contour the outer wedge precisely as described in the previous section on contouring the wedge in a single-phase reservoir (Fig. 14-8h). We now have constructed the inner and outer wedges and the full thickness area for the oil isochore. The completed net oil isochore map is shown in Fig. 14-13e.
With limited well control in the wedge zone of a reservoir and a fairly even distribution of impermeable rock within the productive unit, the most common method for contouring the wedge is to combine proportional and equal spacing of the net pay contours, while honoring the available well control. This is how the outer oil wedge and gas wedge in the last example were constructed. Typically, you may equally space contours between the outermost wells and the zero net pay contour. Within the area of well control, proportionally space the contours according to the net pay values and the well locations. Contouring in this manner assumes that the vertical distribution of net sand is uniform in the reservoir. On the other hand, the horizontal distribution of net sand may not be uniform and, if so, the net pay contours will reflect that stratigraphy only to the extent of the density of control points. The configuration of the contours within a wedge is primarily controlled by the structural attitude of the productive unit and the distribution of net sand and impermeable rock within the overall unit. So if the distribution of nonreservoir-quality rock (e.g., shale) is fairly uniform both vertically and horizontally, the primary influence on the contours in the wedge is the structural attitude of the unit. In such a case, the contours should more or less conform to the structure contours and be more or less proportionally and equally spaced.
If the well control in the wedge is limited and sand distribution varies significantly horizontally, we can use the ratio of net sand to gross interval (net/gross ratio) within the productive unit to approximate net pay within the wedge. This allows us to more accurately contour in the wedge than if we simply equally and proportionally space the contours. Using the wells within and outside the reservoir, first calculate the net/gross ratio in each of the wells. Then map the net/gross ratio in the area of the reservoir, using contours with a typical contour interval of 5 percent or 10 percent (0.05 or 0.10). When we map the net/gross ratio, we make the assumption that the distribution of net sand is uniform vertically. This means that, at any point in the reservoir, the net/gross ratio is the same above the water level as it is for the entire thickness. Once the map is complete, estimate the net pay at selected points in the wedge. At a given point, calculate the gross interval thickness above the water level as the difference in depth between the top of porosity and the water level. Multiply this calculated gross interval by the net/gross ratio to estimate the net sand above the water level, which is equal to net pay at the selected point.
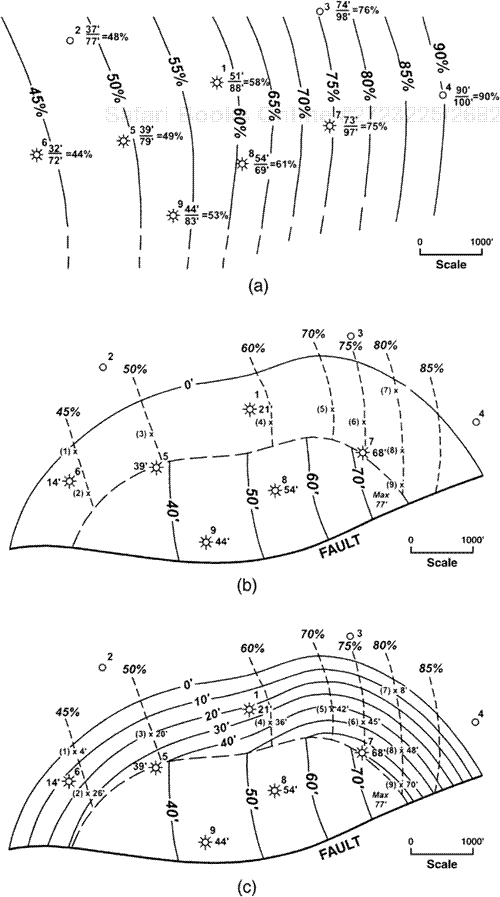
We use the maps in Fig. 14-14 as an example of the technique, applied to an edge water gas reservoir with a gas/water contact at –8350 ft. The net/gross mapping technique begins after construction of the outline of the net pay map and contouring of net pay within the full thickness area (Fig. 14-14b). As the first step in constructing a net/gross ratio map, calculate the net/gross ratio for wells within and outside the reservoir. Figure 14-14a shows the net/gross ratio calculation beside each well in the area of study. Contour the values using a contour interval of 5 percent, or 0.05. Then estimate net pay at selected points within the wedge. Figure 14-14b is a partially completed net pay isochore map of the reservoir, shown as an overlay on some contours in the net/gross map. For efficiency, select estimated net pay points to lie directly on the net/gross contours, such as points (1) through (9). As an example, use point (3) on the 50 percent contour. Calculate the gross interval thickness above the water level at point (3) by taking the difference in depth between the gas/water contact at –8350 ft and the top of porosity at point (3), which is –8310 ft on the structure map (not shown). The gross interval thus equals 40 ft. Then estimate the net pay by using the following calculation.
gross interval above the water level | = | 40 ft |
net/gross | = | 0.50 |
net | = | (0.50)(40 ft) |
= | 20 ft net sand above the water level | |
net pay | = | 20 ft |
Using the same procedure, create as many points of estimated pay as necessary for adequate control. Figure 14-14c shows the completed net pay map for the reservoir.
The net/gross mapping method provides added control for contouring net pay in the hydrocarbon wedge. The method is reasonably accurate if net sand is more or less uniform in vertical distribution. However, the method is significantly less accurate if the reservoir includes intervals of impermeable rock that vary considerably in thickness. For a reservoir with this erratic vertical distribution of net sand and impervious rock, we recommend estimating net pay by using the walking wells method, described in the next section.
A technique called walking wells can be used to improve the accuracy of the contouring in the hydrocarbon wedge. At times, we may wish to better define the distribution of net pay sand within the wedge instead of just using the proportionally spaced method. For example, a dispute exists as to the equity of various leases overlying a reservoir, and the reservoir is being mapped for equity determination between various companies. Furthermore, the distribution of net sand versus impermeable rock varies within the reservoir, such as both thick and thin shale intervals occurring within the productive unit. In such cases, a more detailed estimate of the reserves in the wedge zone may be required.
Our purpose in walking a well is to estimate the net pay at selected points within the wedge. To accomplish this, we assume that the stratigraphy seen in a given well log is representative of the stratigraphy along a designated net sand contour line extending through the wedge. In our imagination, we will move, or walk, the well along this line and estimate net pay at selected points, as described below.
Let’s say we wish to construct a net gas isochore map, with a 10-ft contour interval, for a sandstone reservoir with limited well control. We want additional control in the gas wedge, so we decide to walk a well through the wedge and estimate the amount of net gas at selected points. Any well to be walked can be located in the reservoir itself, or even down-dip of the hydrocarbon/water contact and thus outside the reservoir. The key point in walking a well is to choose a well that can be walked parallel to the nearest contour line on the net sand isochore map. This is a critical point because when walking a well through the wedge, the assumption is made that the amount and distribution of net sand, as seen in the well log, are the same within the reservoir in a direction parallel to the net sand contours. For example, if a well has 50 ft of net sand, it will fall on the 50-ft total net sand contour line. Construction of this 50-ft contour line assumes that exactly 50 ft of net sand exists all along this contour line, not just at the well location (Fig. 14-15). If a series of wells were drilled along this contour line, each well should encounter exactly 50 ft of net sand. We further make the assumption that along the net sand contour line (at least for any limited distance), the distribution of net sand and impermeable rock, as seen in the well, remains constant within the unit being mapped. This assumption regarding the rock distribution may not be true along the 50-ft contour over long distances, or on opposite limbs of a fold, because of changes in depositional environments, variable structural growth histories, and other factors. However, it is a reasonable assumption to make for a limited distance from the well, parallel to the nearest net sand contour line.
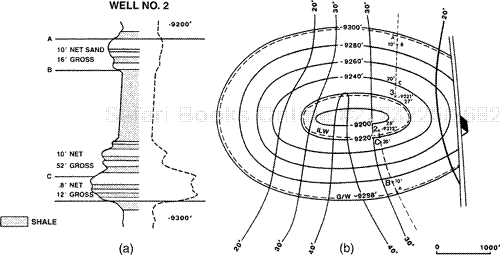
Use three maps in walking a well through the wedge zone. First, lay the structure map of the top of porosity over the net sand isochore map. Then overlay the net gas base map on the two maps, as shown in Fig. 14-16a. We wish to walk Well No. 2, which is located near the crest of the structure, through the wedge zone in order to estimate net pay in part of the reservoir. We walk the well along the dashed line, parallel to the 50-ft net sand contour.
(From Tearpock and Harris 1987. Published by permission of Tenneco Oil Company.)
Figure 14-16. (a) Net gas base map overlain on top-of-porosity structure map and net sand isochore map. Walk Well No. 2 through the wedge zone along the dashed line, parallel to the nearest net sand contour line (50 ft). (b) Five-inch detailed log for the 9200-ft Reservoir, showing increments of 10 ft of net sand per gross feet of interval. (c) Completed gas isochore map for the 9200-ft Reservoir. The contour spacing in the southeastern portion of the wedge zone was improved by walking Well No. 2.
Notice that the inner limit of water (ILW) is shown on the structure map of the top of porosity as a means to delimit the full thickness area on this map. From its position on the base-of-porosity structure map, the ILW was simply traced on the top-of-porosity structure map. Now we have the data necessary to make a net pay isochore map after walking the well, as described in the following procedure.
Preparatory to walking a well, use a detailed 5-in. electric log to determine the net sand in the well and the distribution of sand and impermeable rock. The 5-in detailed electric log for Well No. 2 is shown in Fig. 14-16b. The well contains 48 ft of net sand, and the log shows increments of 10 ft of net sand per gross feet of interval, so chosen because we use a 10-ft contour interval in the net pay map. The productive unit is full of gas in Well No. 2, at its position in the full thickness area.
Overlay the top-of-porosity structure map on the net sand map, then overlay the net gas base map. Trace the gas/water contact as a zero net gas contour on the base map, and trace the limit of the full thickness area as a dashed line.
On the net gas map, lightly mark a dashed line for the well path, parallel to the nearest net sand contour. The net sand contour map may be removed for now; use it later in net pay mapping of the full thickness area and for checking positions of net pay contours in the wedge.
To begin walking Well No. 2, move the well, from its actual structural position, along the well path and place it such that the top of porosity in the productive unit is at the gas/water contact at –9298 ft, which corresponds to the zero contour line on the net gas isochore map (Point A in Fig. 14-16a). A well drilled at this location would (1) encounter the top of porosity of the productive unit at the gas/water contact, (2) contain 48 ft of net sand, and (3) have no pay.
Starting at the top of the sand on the electric log, determine the number of vertical gross feet of section containing 10 ft of net sand. In Fig. 14-16b, a total of 16 ft of gross section includes the 10 ft of net sand. From Point A, move the well up-structure 16 ft, along the dashed line to locate Point B at –9282 ft. This Point B becomes a 10-ft net gas data point for contouring the gas wedge, because a well drilled at Point B would encounter the top of the sand 16 ft above the gas/water contact, and it would contain 10 ft of net gas sand.
To determine the location of the 20-ft net gas point, start at the base of the previous 10-ft net sand section in the log and repeat the procedure. In this example (Fig. 14-16b), it requires 21 vertical gross ft to obtain the next 10 ft of reservoir-quality sand. Move the well up-structure 21 ft from Point B, along the dashed line, to locate Point C at –9261 ft. Point C is the 20-ft net gas data point at 37 ft (16 ft + 21 ft) above the water level.
Continue the same procedure until the well is back at its original structural position. Erase the dashed well path on the net gas map.
Using this method, the well may be walked completely across the wedge, resulting in a more accurate contour spacing than using the method incorporating equal spaced and proportionally spaced contours. We make no assumption about the vertical distribution of net sand being uniform. We use the real distribution of net sand in an actual well to estimate net sand distribution in a part of the reservoir. Figure 14-16c shows the completed net gas isochore map constructed for this reservoir, incorporating the data obtained from walking Well No. 2.
We can walk as many wells as we deem necessary. However, we emphasize strongly that a well must be walked parallel to the nearest contour line on the net sand isochore map. Significant net pay contouring errors can occur if this procedure is not followed. Consider Well No. 5 in the western portion of the reservoir (Fig. 14-17). If we wish to develop a more accurate contour spacing in this area of the reservoir, can Well No. 5 be walked from the water level up-dip to the inner limit of water, along the dashed line? The answer is no. Well No. 5 has 28 ft of net sand. If the well is walked from the gas/water contact up-dip, it will be walked into an area of greater net sand than is actually present in the well, as seen on the net sand map. Therefore, Well No. 5 cannot be walked to improve the contour spacing in this area of the wedge. Caution must be taken when walking wells to be sure that the assumptions made in choosing a well to walk are geologically reasonable and can be supported by a net sand isochore map or, if necessary, additional study of sand distribution.
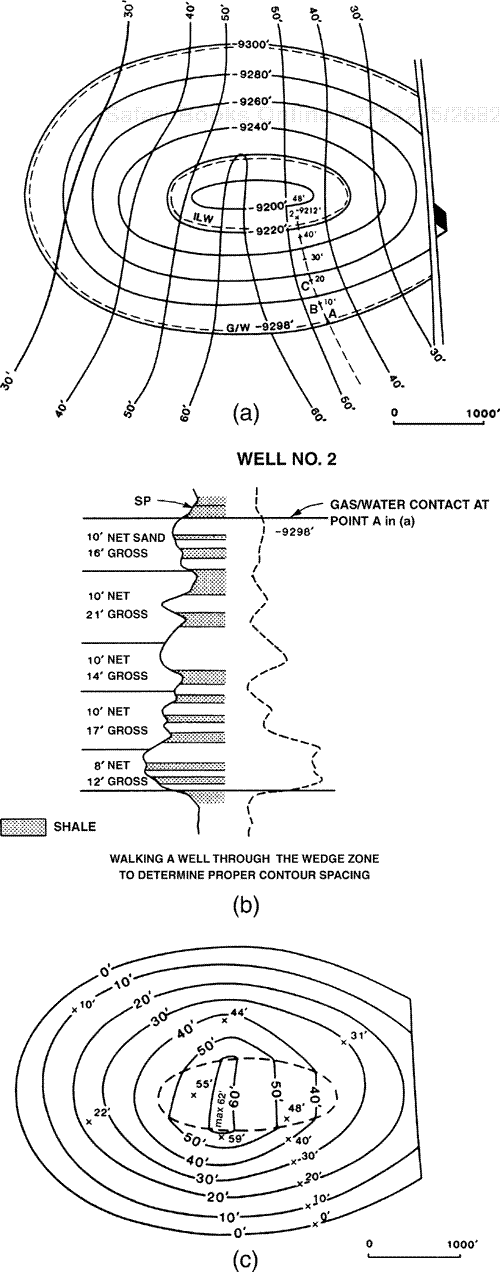
(Modified from Tearpock and Harris 1987. Published by permission of Tenneco Oil Company.)
Figure 14-17. Structure map superimposed onto the net sand isochore map. Well No. 5 in the western portion of the reservoir cannot be walked through the wedge zone to improve the spacing of net pay contours.
If a reservoir is encountered with one or more significant shale intervals between net sand, such as that shown in Well No. 2 in Fig. 14-18a, the accurate construction of the net hydrocarbon isochore map within the wedge may depend upon the walking of wells through the wedge. It is obvious from a review of the 5-in. detail log for Well No. 2 that the net sand and impervious rock are not evenly distributed throughout the gross interval. Therefore, the use of the equally spaced contour method for contouring the wedge would result in significant error.
(From Tearpock and Harris 1987. Published by permission of Tenneco Oil Company.)
Figure 14-18. (a) Five-inch detailed electric log for Well No. 2. The sand and impermeable rock are not evenly distributed throughout this productive unit. (b) Top-of-porosity structure map superimposed on the net sand isochore map. The dashed lines indicate paths along which Wells No. 2 and 3 were walked through the wedge zone to improve the net gas contour spacing.
The map in Fig. 14-18b shows the location of Well No. 2, in its position on structure, and the placement of the 10-ft and 20-ft net gas values used for contouring the net gas isochore map based on walking Well No. 2 through the wedge. Notice that the first 10 ft of net sand are obtained in 16 ft of gross interval; however, it takes another 52 ft of gross interval to obtain another 10 ft of net pay sand. Therefore, the estimated 10-ft net gas point is at –9282 ft (16 ft above the water level of –9298 ft), and the estimated 20-ft net gas point is at –9230 ft (68 ft above the water level). Well No. 3 was also walked to generate the 10-ft and 20-ft net gas points shown in Fig. 14-18b.
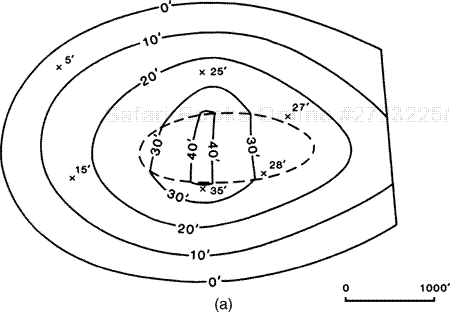
Figure 14-19a shows a net gas isochore map prepared for this reservoir using a combination of equally spaced and proportionally spaced contours within the wedge, which honor the net pay values assigned to each well. Figure 14-19b is a net gas isochore map prepared by walking Wells No. 2 and 3 through the wedge. Observe the significant difference between the two net gas isochore maps. If there were several leases involved in this gas reservoir, the net gas isochore map prepared by walking the wells would provide a more accurate map for assigning equities to each lease.
(From Tearpock and Harris 1987. Published by permission of Tenneco Oil Company.)
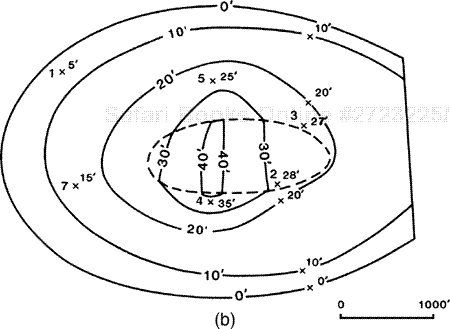
Figure 14-19. (a) Net gas isochore map based on equally and proportionally spaced contours. (b) Net gas isochore map with the contour spacing based on walking Wells No. 2 and 3 through the wedge. Compare this map to that shown in Fig. 14-19a.
Several other methods exist for constructing accurate net pay isochore maps. For example, there is a more accurate method of estimating pay when we walk wells. Also, using the method that employs the construction of a net-to-gross ratio map for the entire productive unit provides estimates of net pay at points within the wedge. In this section of the chapter, we review the more detailed method of walking wells.
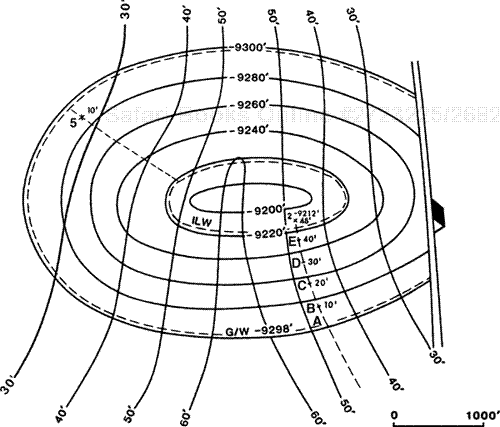
Using the same reservoir as in Fig. 14-18, we illustrate the more detailed technique of walking wells. Figure 14-20 shows a north-south diagrammatic cross section along the path used to walk Well No. 2. On the right side of the figure, we position Well No. 2 so that the top of the sand is at the gas/water contact (–9298 ft). On the left side of the figure, we position the well at the inner limit of water (–9218 ft) where the base of porosity is at the gas/water contact. From the right, Well No. 2 must be walked 16 ft up-structure from the gas/water contact to –9282 ft, to obtain 10 ft of net pay sand. From this point up-dip to –9248 ft, the well gains no additional pay because the section being raised above the water level contains nothing but shale. So at –9248 ft, the net pay remains 10 ft. At this point, the gas/water contact intersects the top of the lower sand member; therefore, moving up-structure from this position, the well gains additional pay. Continuing to walk the well up-dip, it must reach –9230 ft before an additional 10 ft of net sand, in the lower member, lies above the water contact. So we estimate 20 ft of net pay at –9230 ft. At the edge of the full thickness area, with the gas/water contact on the base of sand, all the net sand (28 ft) lies above the water contact. From this point to the actual well location, shown on the far left in the figure, the reservoir contains 28 ft of estimated pay.
On the cross section, two locations have 10 ft of net gas sand (–9282 ft and–9248 ft), and the area between these points has a constant 10 ft of net gas sand. The accuracy of the net gas isochore map can be improved by constructing a map honoring the two 10-ft net pay values. Well No. 3 was also walked through the wedge zone, as indicated in Fig. 14-18b, to aid in the construction of the net pay isochore map.
Figure 14-21 shows the resulting net gas isochore map. At first glance, it may appear as if an important contouring rule was broken in the construction of the isochore map: contours cannot merge or split. However, no rules are broken. The two 10-ft contour lines that appear to merge represent the limits of a very wide 10-ft contour line. Everywhere within the area of the wide contour, the net gas has a constant value of 10 ft.
One may ask, since the sands are so far apart and separated by such a thick shale break, why we would not map each sand separately and construct two isochore maps. In the western part of the reservoir, some of the sands within the two sand members shale-out, and sands develop within the thick shale interval. The result is a reservoir consisting of interfingering shales and sands in which there is productive communication throughout the reservoir, with the sands acting as a single reservoir. Therefore, the thick shale wedge is localized in the eastern section of the reservoir. The rapid decrease in width of the 10-ft contour line reflects the fact that the shale interval decreases to the west. If such a shale interval were known to be continuous over the entire reservoir, it would be necessary to prepare a structure map for each sand member and construct a separate net pay isochore map for each sand member.
The procedure outlined in this section is more involved than the two previous methods shown, but the technique provides further accuracy in the construction of a net hydrocarbon isochore map. The method chosen to prepare a net hydrocarbon isochore map depends upon a number of factors, including the available time, detail, and accuracy required.
True vertical thickness (TVT) is the thickness of an interval measured in a vertical direction. As mentioned in several sections of the text (see Chapter 4), vertical thickness is a very important measurement. It is this vertical thickness that is required to measure the vertical separation (equal to missing or repeated section in a well) of a fault. It is also the thickness required to accurately count net sand and net pay from 5-in. detailed logs, and it is the thickness used to construct net sand and net pay isochore maps. As described in the introduction to this chapter, the vertical thicknesses of net sand and net pay typically represent aggregate vertical thicknesses.
In a vertical well, the actual thickness measured on the electric log is the TVT. In the case of a directionally drilled well, however, a correction factor must be applied to correct the exaggerated or diminished measured log thickness (MLT) to TVT.
For a horizontal reservoir (zero bed dip), the thickness that is used for net sand or net pay isochore mapping equals the true stratigraphic thickness (TST) (Fig. 14-22). However, if the same reservoir is rotated to some angle, such as 20 deg, the thickness of the reservoir required for net sand and net pay isochore mapping does not equal the stratigraphic thickness. Figure 14-22 illustrates the cross-sectional area of a reservoir with a fixed width in the third dimension, and we use the cross section to represent the volume of the reservoir. The horizontal reservoir (zero bed dip) in the lower portion of the figure has a cross-sectional area of 50,000 sq ft. The reservoir has a length of 500 ft, as seen in map view, and a thickness of 100 ft. Since the dip of the reservoir is zero, the TVT equals the TST (100 ft). If the same reservoir rotates to an angle of 45 deg, as shown in the upper portion of the figure, the length of the reservoir shortens to 354 ft in map view. The cross-sectional area of the reservoir does not change, as the TST remains 100 ft. In order to map the reservoir and maintain a cross-sectional area of 50,000 sq ft, the thickness to be used must exceed 100 ft. The TVT of the dipping reservoir measures to be 141.25 ft, and 141.25 ft × 354 ft = 50,002.5 sq ft. We conclude from this example that as a reservoir of fixed length rotates from the horizontal, the areal extent of the reservoir decreases in map view; therefore, in order to maintain the same cross-sectional area or volume of the reservoir, the shortened length must be multiplied by the TVT.
For directionally drilled wells, the log thickness of a given stratigraphic interval can either be thicker, equal to, or thinner than that seen in a vertical well drilled through the same stratigraphic section. A correction factor must be applied to the MLT in most deviated wells to convert the borehole thickness to TVT. The correction factor consists of two parts: (1) the correction for wellbore deviation angle within the interval of interest, and (2) the correction for bed dip. Any one of equations (4-3), (4-4), (4-5), or (4-6) in Chapter 4 may be used to calculate this correction factor. In Chapter 4, we used the equations to estimate the TVT of missing or repeated section in a well as the result of a fault. Remember, the vertical separation of a fault at a well equals the TVT of the stratigraphic section missing or repeated in the wellbore. In this chapter, we look at the same correction factor equations in order to convert deviated wellbore thickness to TVT, for use in net sand and net pay isochore mapping.
For convenience, we repeat the correction factor equation (4-6). Equation(4-6), which is a 3D equation, is the preferred equation to use for correction factors because this one equation can be used to calculate the thickness correction factor regardless of the direction of wellbore deviation, and the true dip of the beds is used instead of the apparent dip required in the two-dimensional equations. Recall from Chapter 4 that we refer to this equation as Setchell’s equation.
TVT | = | True Vertical Thickness |
MLT | = | Measured Log Thickness |
ψ | = | wellbore deviation angle |
φ | = | true bed dip |
α | = | Δ Azimuth (acute angle between the wellbore azimuth and the azimuth of true bed dip) |
If the beds are horizontal, then Setchell’s equation reduces to the simple correction factor equation
which is equivalent to correcting for wellbore deviation only.
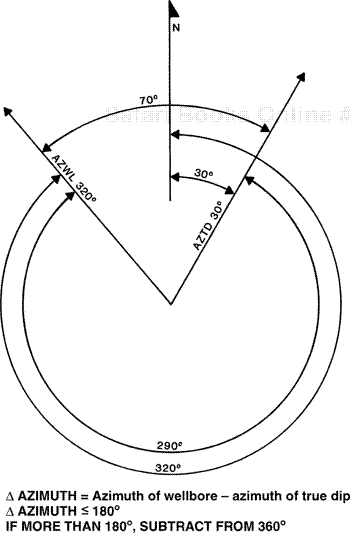
Figure 14-23 illustrates the measurement of azimuth and Δ azimuth for use in Eq. (4-6). For convenience, the Δ azimuth used in the equation is typically the acute angle between the azimuth of the wellbore and the azimuth of the true bed dip.
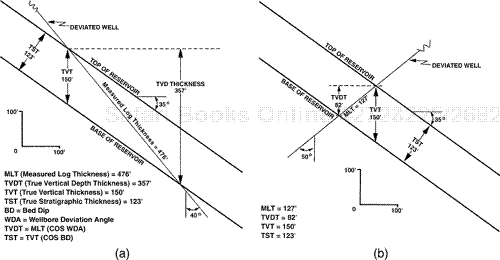
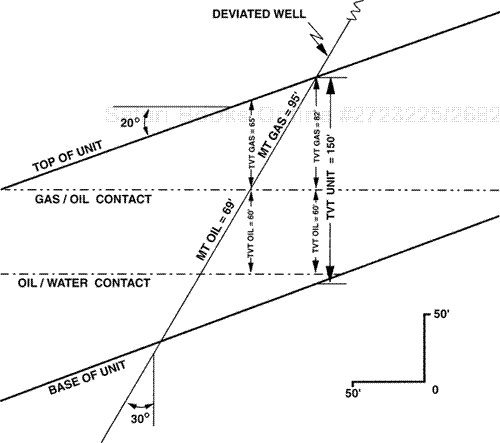
In order to more closely examine the two directionally drilled wells shown in Fig. 14-24, look first at the well drilled to the east in a down-dip direction (Fig. 14-24a). Consider the interval to be a reservoir filled with gas or oil. The reservoir has a MLT of 476 ft. We apply the correction factor for wellbore deviation only, using Eq. (4-3). The MLT reduces to 357 ft, shown in the figure as the TVD thickness, or the true vertical depth thickness (TVDT). This thickness also exceeds the TVT of the interval, because the correction for only wellbore deviation does not take into account the dip of the beds. The TVDT is that thickness of an interval obtained from a true vertical depth (TVD) log and, for dipping beds, TVDT does not equal TVT (see Chapter 4). With the final correction for bed dip, the MLT converts to the TVT of 150 ft, shown in Fig. 14-24a at the penetration point of the wellbore in the top of the reservoir. Note that the TST is 123 ft.
The TST is calculated by multiplying the TVT by the cosine of the angle of bed dip (35 deg in this example).
The well in Fig. 14-24b deviates up-dip, to the west. The MLT of 127 ft measures less than the TVT. Applying a correction factor for the well deviation angle alone, which is equivalent to the correction to TVDT, provides an even smaller thickness of 82 ft. When Eq. (4-6), the correction factor equation for both bed dip and wellbore deviation, is applied, the MLT converts to the TVT of 150 ft, the value needed for net sand and net pay mapping. As an exercise, use Eq. (4-6) to calculate the TVT for the two wells in Fig. 14-24 and to confirm the results shown.
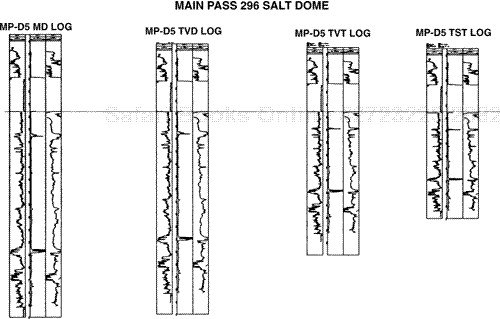
Various computer programs can be used to create TVD, TVT, and TST logs from measured depth (MD) logs for use in mapping. The deviated well log data, the directional survey for the well, and bed dip information are necessary as input data. The log data are obtained from the logging company tapes or digitized from the actual log. The directional survey data are furnished by the directional company that worked the well. The bed dip information can be obtained either from completed structure maps or from a dipmeter. The output logs can be in standard presentation or at any scale desired. The logs in Fig. 14-25 were created by using IEPS (Integrated Exploration and Production System). The log sections for Well No. MP-D5, shown from left to right in the figure, represent the (1) measured depth log, (2) true vertical depth log, (3) true vertical thickness log, and (4) true stratigraphic thickness log. This well is in an area of significant bed dip. Notice the similarity of the MD log and the TVD log. This is so because the TVD log thickness is equivalent to a correction for wellbore deviation only, and not bed dip. However, the TVT log shows a considerable reduction in thickness from the MD log because the TVT log reflects corrections for both wellbore deviation and bed dip.
(From Tearpock and Harris 1987. Published by permission of Tenneco Oil Company.)
Figure 14-25. Computer-generated electric logs illustrating the difference in thickness between measured depth, true vertical depth, true vertical thickness, and true stratigraphic thickness logs, generated for the same well.
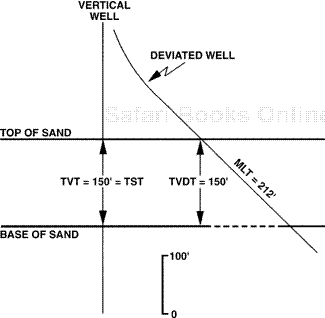
We caution here that TVD logs, which are a standard part of the log suite for a deviated well, are used too often for purposes that are not applicable with this log. A widespread misunderstanding exists that a TVD log prepared from a MD log can be used to (1) correlate with other well logs, (2) determine the vertical separation for a fault, and (3) count net sand and net pay for isochore mapping. Remember, a TVD log is corrected only for wellbore deviation, and not bed dip. In areas of flat-lying beds, a TVD log is equivalent to a TVT log because the only correction factor required is for wellbore deviation (Fig. 14-26). However, if the beds are dipping (particularly over 10 deg), a TVD log typically does not represent the log thickness required to aid in correlation work, to determine the vertical separation for a fault, or for use in net sand and net pay counting. For these purposes, we must correct a deviated well log so that the log thickness represents the TVT. Look again at Fig. 14-25 and observe the significant difference in thickness between the TVD and the TVT logs. To determine the vertical separation of a fault by correlation of a faulted well with a deviated well, and to count all net sand and net pay from a deviated well log, we must use a TVT log or its equivalent. By the equivalent of a TVT log, we mean calculating and using correction factors if a TVT log is unavailable, which is commonly the case. Therefore, for each interval on the deviated well log requiring the conversion of MLT to TVT, determine correction factors and apply them to the MLTs of the intervals of interest.
Figure 14-27 presents an example of two separate net pay isochore maps prepared for a reservoir on the flank of a salt dome in the offshore Gulf of Mexico. Notice that there are two platforms from which wells were drilled. Platform D is located in the up-structure position, with the D Platform wells directionally drilled down-dip. The A platform is located on the flank of the structure, with most of the A Platform wells directionally drilled up-dip.
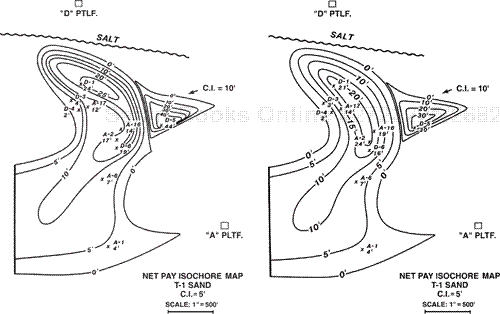
(From Tearpock and Harris 1987. Published by permission of Tenneco Oil Company.)
Figure 14-27. (a) Net pay isochore map for the T-1 Sand, Reservoir A. The net pay values for the deviated wells from Platforms A and D were corrected only for wellbore deviation. (b) Net pay isochore map for the T-1 Sand, Reservoir A. The net pay values for the deviated wells from Platform A and D were corrected for wellbore deviation and bed dip. Compare the net pay value for each well with those shown in Fig. 14-27a.
Figure 14-27a shows a net pay isochore map prepared for the T-1 Sand, Reservoir A. The net pay values posted on the net pay isochore map were corrected for borehole deviation, but not for bed dip of about 35 deg at this location on the flank of the structure. In addition to the error of failing to correct the net pay values for bed dip, several other serious isochoring problems exist but are not discussed here.
Figure 14-27b presents a net pay isochore map for the same reservoir with new net pay values, which were generated after correction for borehole deviation and bed dip. This new isochore map was prepared solely to compare the effect of the correction factor for bed dip on the ultimate calculation of the total volume of the reservoir. Therefore, the isochore errors made in Fig. 14-27a (not discussed here) are incorporated in the net pay isochore map in Fig. 14-27b. The planimetered volume for the isochore map in Fig. 14-27a, with MLTs corrected for bed dip, is 524 acre-feet, whereas the map in Fig. 14-27b with uncorrected MLTs provides a volume of 617 acre-feet. Therefore, the estimated hydrocarbon volume for the map prepared without correcting the net pay thickness values for bed dip is 18 percent greater than the isochore map prepared by taking into account the correction factor for bed dip. So, based on the incorrect map, the volumetric calculation overstates the reserves by 18 percent.
In a situation like this, we would expect the error factor to be larger than 18 percent, and it would be in most cases. However, look at Wells No. A-2 and D-5. Well No. A-2 was corrected upward from 17 ft net pay to 24 ft net pay, whereas Well No. D-5 was corrected downward from 44 ft net pay to 30 ft net pay. It so happens that the D Platform wells, drilled down-dip, result in a reduction in net pay values when the correction factor for bed dip is considered, whereas the A Platform wells, drilled up-dip, result in an increase in net pay. Therefore, a significant part of the error is negated because of the directions in which the wells were drilled.
This reservoir is only one of a number of oil and gas reservoirs that are productive within this field. A complete remapping of the field was undertaken when several major mapping errors, such as the one shown here, were identified. The remapping of the field resulted in a significant write-down of hydrocarbon reserves that were overestimated because of mapping errors, such as the failure to incorporate the proper correction factors in determining net pay values. Several development wells planned for the field based on the overestimated reserves were not required, saving the company millions of dollars in unnecessary wells. This example illustrates the impact that correction factors can have on estimated hydrocarbon volumes determined from volumetric calculations using net pay isochore maps.
We have seen error factors of several hundred percent. In one example, the net pay used for the reserve estimate from a deviated well was 750 ft, when in fact the actual TVT value was about 150 ft. This is a major error, resulting in a significant overestimation of reserves.
The mathematical equations that are used for converting log thicknesses to true vertical thicknesses were reviewed in Chapter 4 and in the previous section in this chapter, but some additional discussion is required regarding these correction factors when dealing with deviated wells that penetrate fluid contacts. The mathematical treatment in these situations is not as straightforward as for deviated wellbores within the full thickness area of a reservoir.
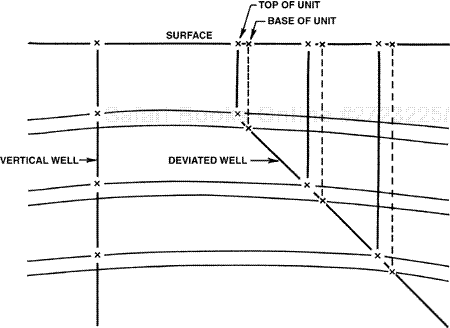
Normally, we determine net sand and net pay values for isochore mapping at the position where a well penetrates the top of the reservoir. For a vertical well, the penetration points of all horizons are at the same location in map view, directly under the surface location of the well (Fig. 14-28). However, for a directionally drilled well, the intersections of the well with the top and base of a stratigraphic unit occur in different locations with respect to the surface location of the well, as seen in map view along the path of the well (Fig. 14-28).
In many cases, due to the low angle of wellbore deviation or the minimal thickness of a sand, the calculation and positioning of the net sand or net pay values at the point where the well penetrates the top of porosity of the productive unit provides sufficient accuracy. There are situations involving highly deviated wells, fluid contacts, dipping beds, or thick sands, however, where a single data point for net sand or net pay at the penetration point of the well at the top of the reservoir may be insufficient, as well as being incorrectly calculated or posted for isochore mapping. These special conditions are discussed here.
Equation (4-6) can be used to calculate the correction factor for reservoir TVT within the full thickness area, where no fluid contacts exist in the well (Fig. 14-29, well on the right). In this figure, the deviated well penetrates a reservoir with a TVT of 150 ft. The log thickness measures 219 ft from the depth where the well penetrates the top of the reservoir to its penetration at the reservoir base. Using Eq. (4-6) and the data given in Fig. 14-29, the 219 ft of MLT convert to 150 ft TVT. Observe an oil/water contact just down-dip from the well’s penetration of the base of the reservoir. The entire wellbore penetration is therefore confined to the full thickness area of the reservoir, with no fluid contacts present in the well.
The well on the left in Fig. 14-29 penetrates an oil/water contact. The MLT of the entire stratigraphic interval is 282 ft. What correction factor equation would you use for this MLT to calculate TVT of the oil column, at the penetration point of the top of the reservoir? In this particular situation where the penetration point is within the full thickness area, Setchell’s equation, applied to the MLT of 282 ft, will provide the TVT of the oil at the penetration point in the top of the reservoir.
Application of Setchell’s equation to the MLT of the net oil (less than 282 ft) would result in an incorrect TVT at the penetration point in the top of the reservoir. However, if you wish to obtain the value of the vertical feet of oil directly above the penetration point of the wellbore at the oil/water contact, the use of the Setchell equation provides this value of net pay in the wedge. We will discuss this situation next.
Now consider the following situation. A well penetrates the top of an oil reservoir within the oil wedge; i.e., directly above the oil/water contact. The following data apply to the well and well log.
Wellbore deviation is 30 deg due west;
Bed dip is 20 deg due west;
MLT of net sand within the productive unit, from top to base, is 219 ft; and
MLT of net sand from the top of the unit to the oil/water contact is 115 ft.
What is the vertical thickness of the oil column under the penetration point of the well at the top of the reservoir? Draw a cross section showing the relationship of the well to the productive unit and, using Eq. (4-6), calculate the TVT of the oil under the penetration point at the top of the reservoir. Is the correct answer 150 ft, 100 ft, or 79 ft? If you calculated 150 ft, this thickness is equal to the total true vertical thickness of net sand directly under the penetration point of the well at the top of the sand (Fig. 14-30). If you calculated 79 ft, this is the vertical thickness of net oil pay directly above the point where the well penetrates the oil/water contact. A review of Fig. 14-30 shows that the oil/water contact is a horizontal surface. Therefore, we do not have to consider any bed dip correction factor to calculate the net pay directly under the penetration point. No bed dip affects the TVT of the net oil sand, since the oil/water contact is a horizontal surface, and the penetration point at the top of the sand is a point directly over the oil/water contact. Therefore, the Eq. (4-6), as applied to calculation of net oil sand directly beneath the penetration point of the well at the top of the sand, reduces to the correction factor for wellbore deviation multiplied by the MLT from the top of the sand to the oil/water contact, which is 115 ft. The net oil pay calculates as

Figure 14-30. Deviated well penetrates the reservoir within the oil wedge (directly above the oil/water contact). TVT of oil column, directly below the penetration point of the well at the top of the reservoir, is calculated by simply multiplying the MLT of oil by the cosine of the wellbore deviation angle.
Notice the result if we consider bed dip, as well as wellbore deviation, to determine the correction factor for this case; i.e., if we incorporate bed dip equal to 20 deg in Setchell’s equation, Eq. (4-6). Then we are calculating the correction factor used to determine the TVT of total net sand at the penetration point at the top of the reservoir, as well as the correction factor for the TVT of net oil sand directly above the penetration point of the well at the oil/water contact (Fig. 14-30). Calculating the correction factor (CF) in Setchell’s equation,
CF | = | [cos ψ – (sin ψ cos α tan φ)] |
TVT | = | MLT × CF |
Using the data provided in Fig. 14-30, the correction factor is based on
Wellbore deviation (ψ) | = | 30 deg |
True bed dip (φ) | = | 20 deg |
Delta azimuth (α) | = | 0 deg |
Therefore
CF | = | [cos 30° – (sin 30° cos 0° tan 20°)] |
CF | = | 0.866 – (0.5)(1)(0.364) |
CF | = | 0.684 |
The true vertical thickness of the net sand at the penetration point of the well at the top of the sand is
TVT
=
MLT × CF
TVT
=
(219 ft)(0.684)
TVT
=
150 ft
The true vertical thickness of the net oil pay sand above the penetration point of the well at the oil/water contact is
TVT | = | (MLT from top of sand to the oil/water contact)(CF) |
TVT | = | (115 ft)(0.684) |
TVT | = | 79 ft |
The preceding discussion shows that a fluid contact in a deviated well is a special condition for which only the correction factor for wellbore deviation may be required to convert a MLT to TVT, even though the beds are dipping at a significant angle. We make an important conclusion here: Wherever the penetration point of a well at the top of a reservoir is above a fluid contact (in the wedge), as in Fig. 14-30, the dip of the beds can be considered zero in the equation for determining the net pay TVT at the penetration point at the top of the reservoir. In other words, use the simple equation TVT = MLT cos ψ. Furthermore, as shown in Fig. 14-30, if the actual reservoir bed dip and the MLT of the net pay sand are used in Eq. (4-6), Setchell’s equation, then the TVT of the net pay is calculated directly above the point of penetration of the oil/water contact. Spot this point on the net oil map and use its TVT net pay value in the contouring of net oil, in addition to using the net pay value at the penetration point at the top of the reservoir.
Figure 14-31 illustrates a situation in which a reservoir containing oil and gas is penetrated by a deviated well. In this case, the vertical thicknesses of the oil and gas columns must be determined for isochore mapping. Using the data provided in the figure, verify the TVT for the oil and for the gas at two separate locations: (1) directly beneath the penetration point of the well at the top of the reservoir, and (2) the penetration point of the gas/oil contact. Finally, calculate the TVT of water, oil, and gas at the point where the well penetrates the oil/water contact (dashed line).
Figure 14-32 illustrates a well deviated in an up-dip direction, penetrating an oil reservoir in the oil wedge. The same procedures as previously discussed are used to calculate the TVT of oil at the locations where the well penetrates the top of the reservoir and the oil/water contact. If desired, the TVT of oil can also be calculated at the position where the well penetrates the base of the productive unit. First, calculate the TVT of the water column at this location, and then subtract this value from the TVT of the total net sand to arrive at the vertical thickness for oil.
By having a good understanding of the geometric relationship of the productive unit, well-bore, and fluid contacts, we can use this knowledge to our advantage. The calculation of the net gas or net oil at various points in a well, such as the well’s penetration point at the top of the productive unit, base of the unit, or at fluid contacts, can provide additional net pay values. These values can be used in the preparation of the net gas or net oil isochore maps, providing additional control in the wedge zones.
The detailed calculations shown in this section are not always required or justified. However, the use of these techniques may prove to be very important where detailed, accurate mapping is needed for some specific reserve estimate, development plan, enhanced recovery program, unitization, equity determination, or litigation.
We discuss the effect of mapping on a structure top versus a porosity top with regard to structure mapping in Chapter 8, and here we review this special condition as it relates to net pay isochore maps. We mention in Chapter 8 that the upper portion of a reservoir unit may be composed of nonreservoir-quality rock. The terms tight zone and tight streak refer to an interval of impermeable rock. Although the top of the unit may represent the actual stratigraphically equivalent top, it does not constitute the top of reservoir-quality rock. Therefore, the structure map prepared to interpret the structure may not be useful to map and evaluate the reservoir itself.
Once the structure mapping is complete, the question arises as to whether a separate map on the top of porosity is required for accurate delineation of the reservoir and for use in the construction of net hydrocarbon isochore maps, from which estimates of reserves are made. Two parameters are considered in evaluating the importance of the nonreservoir-quality rock: (1) the thickness of the tight zone, and (2) the relief of the structure. A thick tight zone has a greater effect on ultimate reserve estimates than one that is thin. Low-relief structures introduce greater error in delineating the limits of a reservoir than steeply dipping structures, particularly if the low-relief structure contains a reservoir with bottom water. This is true because a steeply dipping reservoir is associated with a relatively small wedge zone when compared to the total area of the reservoir.
On a low-relief structure, the wedge zone of a reservoir can represent a significant portion of the total reservoir area (Fig. 14-33). Figure 14-33a shows in map and cross-sectional views a low-relief bottom water reservoir mapped on the top of a productive unit, which consists of nonreservoir-quality rock in the upper 75 ft. The same reservoir is mapped on the top of porosity in Fig. 14-33b. The net oil isochore map prepared from each structure map is shown in Fig. 14-33c. The same net pay values are assigned to each well in both isochore maps. In this case, because the reservoir is on a low-relief structure, the difference in reservoir volume between the isochore map based on the top of structure and the isochore map based on top of porosity is 637 acre-feet, or a significant overestimate of 32 percent (Fig. 14-33d). Consequently, the volume of recoverable hydrocarbons is overestimated by 32 percent.
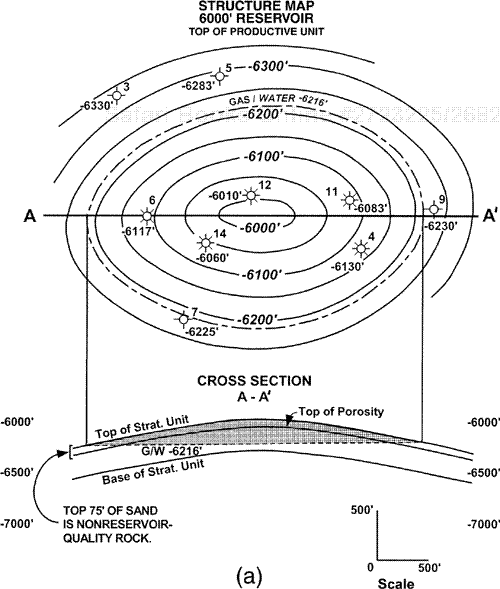
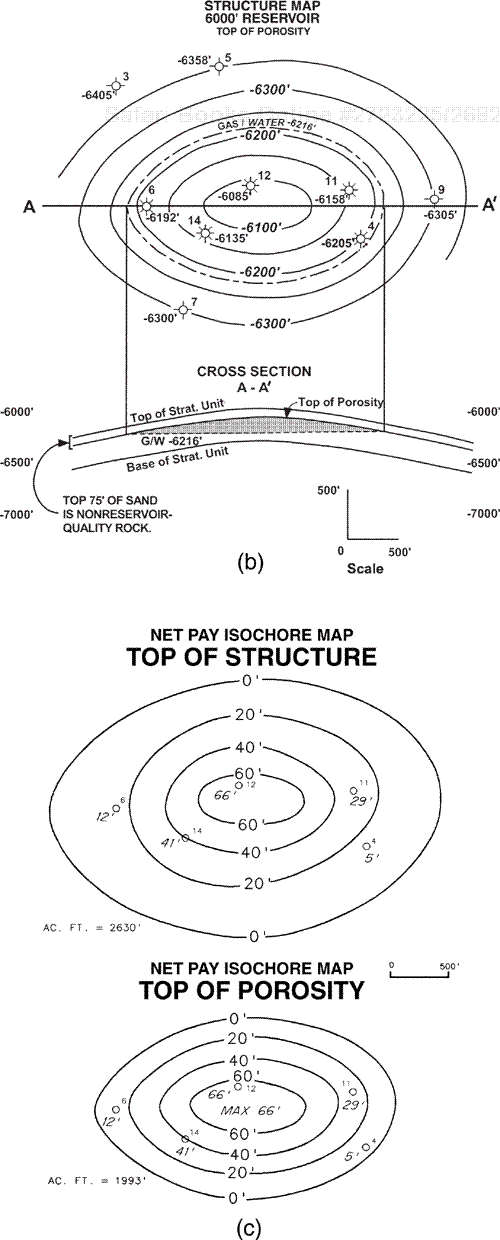

Figure 14-33. (a) The structure map on the top of the stratigraphic unit containing the 6000-ft Reservoir, and the cross section A-A′. Upper 75 ft of the unit contains nonreservoir-quality rock. (b) The structure map on top of porosity (6000-ft Reservoir) and the cross section A-A′. (c) Two separate net pay isochore maps: (1) the upper isochore map is based on the structure map on the top of the stratigraphic unit, and (2) the lower isochore map is based on the top-of-porosity structure map. Net pay values for all the wells are the same for each map. (d) There is a 32 percent reduction in reservoir volume for the net pay isochore map constructed from the top of porosity map versus the net pay isochore map constructed from the top of the stratigraphic unit. This is a significant reduction in volume.
The decision to prepare a separate map on the top of porosity, where the upper portion of a productive unit is tight, needs to be made on a reservoir-by-reservoir basis. Depending upon the geometry of the reservoir and thickness of the tight zone, the difference in volume between a map on the top of the unit and one on the top of porosity may be too insignificant to warrant additional mapping.
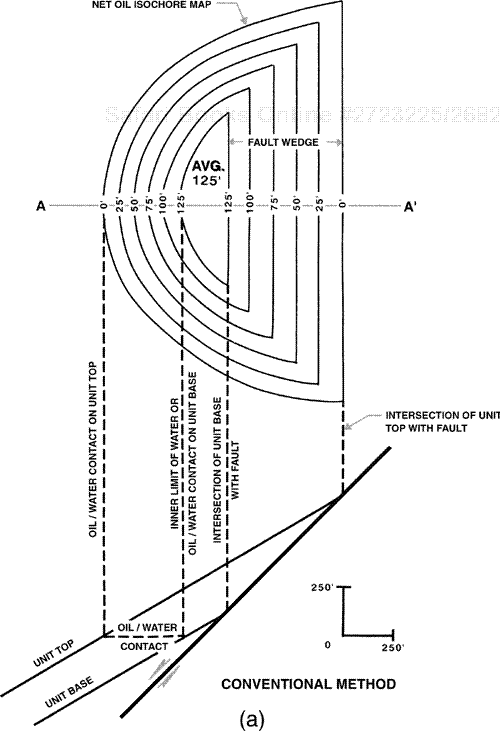
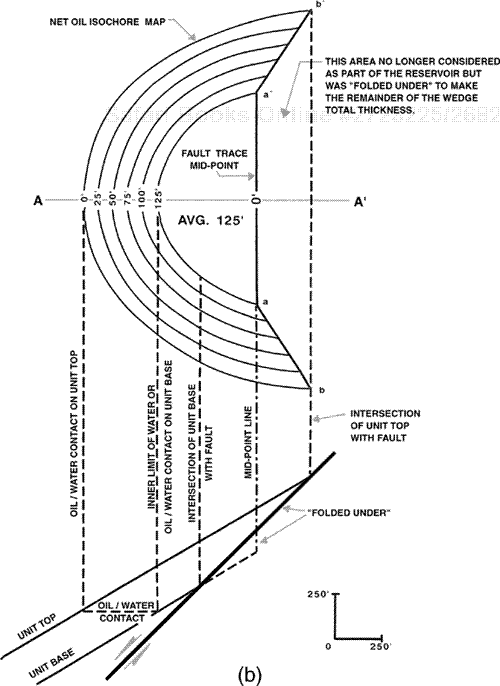
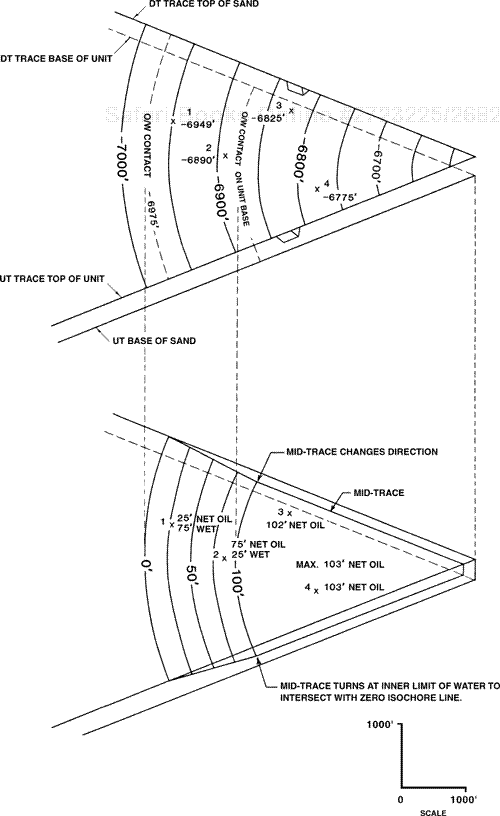
A fault wedge within a reservoir is defined as a wedge-shaped section of strata bounded by a fault. It is commonly just as important to map net pay within the fault wedge of a productive reservoir as it is to map net pay within the hydrocarbon wedge above water. If a productive unit is thin or the dip of the bounding fault is a high angle, the reservoir volume affected by the fault wedge may be insignificant and can be ignored for all practical purposes. In cases where the reservoir is thick or the fault dips at a low angle, the reservoir volume within the fault wedge may be significant and must therefore be included when constructing the net pay isochore map. There are several ways to handle the mapping of a fault wedge. It may be contoured in the conventional way, or a mid-trace (mid-point) method can be used.
The conventional method of contouring the fault wedge is the most accurate and should be employed whenever possible. With this method, the wedge is actually contoured using all control points in the same manner as contouring a water wedge. As with a water wedge, where the impermeable zones (shale, tight rock, etc.) are fairly evenly distributed throughout the reservoir section, the fault wedge net pay contours may be evenly spaced in the wedge zone. All the control points must be honored, however, even though it may cause an uneven spacing of the contours. Figure 14-34 shows an example of a structure map on the top of a productive unit. We use a simple, idealized map in order to provide a clear concept of mapping the fault wedge. The reservoir is bounded on the east by a west-dipping fault, with the remainder of the reservoir bounded by an oil/water contact at –8000 ft. The structure map shows the intersection of the top of the productive unit with the fault, as well as the intersection of the fault with the base of the unit (shown as a dashed line). The area between these two intersections is the area of fault wedge. In this case, the fault dips to the west at 45 deg and the productive unit dips at 30 deg. It is readily apparent from the fault intersections with the top and base of the unit that the fault wedge comprises a large portion of this reservoir. For simplicity, we assume the reservoir to have 50 percent net sand and 50 percent shale, evenly distributed throughout the gross interval. Because of this even shale distribution, we can evenly space the contours in both the hydrocarbon and fault wedges. The reservoir is in the downthrown fault block, so the control required to map the fault wedge in this example includes the intersections of the top and base of the productive unit with the fault. The upthrown trace of the fault, and therefore the fault gap as seen on a structure map, plays no part in mapping the fault wedge.
Figure 14-35a illustrates the net oil isochore map for this reservoir with both the water and fault wedges conventionally contoured. The cross section A-A′, drawn below the net oil isochore map, depicts certain key control points in the reservoir, including the oil/water contact on the top of the productive unit, the inner limit of water (the oil/water contact on the base of the unit), the intersection of the base of the reservoir with the fault, and the intersection of the top of the reservoir with the fault. These key control points play an important part in the construction of the wedges for this net oil isochore map.
The use of the conventional method of contouring the fault wedge can be tedious and at times unjustified. In such cases, we can use a shortcut method for contouring the fault wedge, referred to as the Mid-Trace Method, or Mid-Point Method (Fig. 14-35b). To construct an isochore map using this method, first draw a line that is one-half way between the intersections of the top and base of the reservoir with the fault. This line is the mid-trace. Draw the line to stop at the inner limit of water, shown as points a and a′ in Fig. 14-35b. Next, extend this line from the inner limit of water straight to the intersection of the fault with the oil/water contact on the top of the reservoir, as indicated by a-b and a′-b′ on the figure. This line b-a-a′-b′ becomes a boundary of the reservoir. Any part of the reservoir in the fault wedge, but outside this boundary line, is considered as being folded under to convert the wedge zone inside this line to an area of full thickness. This is illustrated in the cross section below the net oil isochore map in Fig. 14-35b. Notice that this procedure extends the full thickness area to the mid-trace. Next, extend all contours in the hydrocarbon wedge to intersect with line segments a-b and a′-b′, as illustrated in the figure. The finished map includes an enlarged full thickness area (125 ft of net pay) plus a wedge.
Figure 14-36 illustrates the use of the mid-trace method of contouring a fault wedge with a reservoir bounded by two intersecting faults. Note that the mid-trace extension, from the inner limit of water to the intersection of the fault with the oil/water contact on the top of the unit, is in opposite directions on the individual fault wedges. Remember, always draw a line from the mid-trace to the intersection of the zero net pay contour with the fault.
Although faults play a very important role in the trapping of hydrocarbons, studies have shown that some faults are nonsealing, thereby permitting the migration of hydrocarbons from one fault block to the next. One of the most common situations resulting in a nonsealing fault is the juxta-position of permeable stratigraphic units across a fault, with capillary properties of the fault zone being insufficient to create a seal. This can occur where a fault does not have sufficient displacement to separate an entire permeable unit from one fault block to the next, or where juxtaposition of different permeable units exists.
Hydrocarbon accumulations can occur on both sides of a nonsealing fault if a trap exists in the up-structure fault block. The accumulations would have a common water level. With non-sealing faults, it is important to map fault wedges because they can contain significant amounts of hydrocarbons. We contour the fault wedge basically the same as presented in the previous section, with one exception. Since there is hydrocarbon pay upthrown and downthrown to the fault, two reservoirs and two fault wedges must be mapped to account for all the hydrocarbon volume. The isochore maps for the two reservoirs can be constructed individually or contoured as one map.
Figures 14-37 and 14-38 illustrate an example of reservoirs juxtaposed across a nonsealing fault. A productive sandstone unit contains two fault-separated reservoirs on the southern flank of a salt structure. Figure 14-37a shows the structure map on the top of porosity in Reservoirs A and B. The reservoirs are limited to the north by a vertical salt face, to the east and west by faults, and in the down-dip direction by a common gas/water contact at –10,550 ft. The interval from top to base is in excess of 200 ft thick and it is all reservoir-quality sand. Fault B, with a vertical separation of 200 ft, has insufficient displacement to completely separate the sand, so part of the sand is juxtaposed across the fault. The same gas/water contact in both Reservoirs A and B indicates that the fault is nonsealing and that the two reservoirs are in communication. Figure 14-37b through d are the structure map on the base of the 9500-ft Sand, the fault surface map, and the net sand map respectively. These maps are required for isochore construction.

Figure 14-38. (a) Net gas isochore map for Reservoir A. The map includes two fault wedges and a water wedge. (b) Net gas isochore map for Reservoir B. Fault wedge and water wedge are significant portions of the reservoir volume. (c) Composite net gas isochore map for Reservoirs A and B. Notice the complexity in the mapping of the two fault wedges created by Fault B when both reservoirs are mapped together.
The net gas isochore maps for the Reservoirs A and B can be constructed separately or as one single net gas isochore map. Figure 14-38a and b show the individually constructed net gas isochore maps for Reservoirs A and B respectively. Notice that the fault wedges for Faults A and B comprise a significant portion of each of the reservoirs. Figure 14-38c illustrates how the two reservoirs can be mapped together by combining the wedges for Fault B. Cross section A-A′ shows about 75 ft of sand juxtaposed across the fault at this position in the reservoir.
Isochore maps in which the fault wedges are combined, such as the one shown in Fig. 14-38c, are difficult to construct and can easily result in errors. We recommend for simplicity of construction and planimetering that, even with nonsealing faults, each reservoir and fault wedge be mapped separately, as shown in Fig. 14-38a and b.
We use a net pay map to determine the volume of a reservoir, so we want to consider how this volume, as depicted by the map, corresponds to the actual structural configuration of the reservoir. Figure 14-39 relates the net pay map depiction of volume of a gas-on-oil accumulation to the structural configuration of the productive unit. The cross section in the center of the figure shows the actual structural configurations of the oil reservoir and the gas reservoir. The cross sections in the lower portion of the figure show the varying thickness of each reservoir, with each represented as a polygon with a flat base. If we consider possible changes in thickness in the third dimension, then each polygon represents an irregular solid that has a volume equal to that of the reservoir. It is important to notice that the depicted volume is not a true representation of the structural configuration of the reservoir. The reservoir has been artificially flattened, or piled up (referred to as isochore piling), to represent the same volume that exists within the structure. The net pay map will be planimetered, and then the depicted volumetric solid is used in the calculation of the reservoir volume.
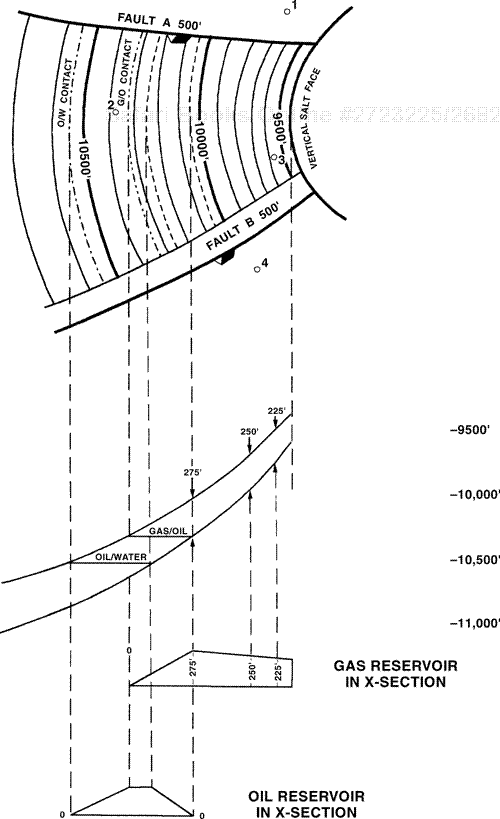
Figure 14-39. In the preparation of a net hydrocarbon isochore map, the configuration of the reservoir is completely rearranged and the base is artificially flattened. Compare the configuration of the net gas and net oil cross sections in the lower portion of the figure to that of the structure cross section in the center.
Two methods are commonly used to determine reservoir volume from net pay isochore maps, the Horizontal Slice Method and the Vertical Slice Method.
One way to determine volume of a reservoir is to horizontally slice the depicted reservoir solid, and sum the volumes of the layers to calculate total volume of the reservoir. For the horizontal slice method, two equations are generally used to determine the volume from a net pay isochore map that has been planimetered (Craft and Hawkins 1959). The first determines the volume of the frustum of a pyramid.
where
h | = | Interval thickness between isochore lines |
An | = | Area enclosed by lower value isochore line |
An + 1 | = | Area enclosed by higher value isochore line |
This equation is used to determine the volume of a layer between successive slices, which are based on vertical thickness and represented on the map by net pay contour lines (Fig. 14-40). The total volume of the reservoir is the sum of these separate volumes.
The second equation used in the horizontal slice method determines the volume of a trapezoid.
or, for a series of successive trapezoids,
where
A0 | = | Area enclosed by the zero isochore line |
A1, A2... An | = | Areas enclosed by successive contour lines |
tavg | = | Average thickness within the maximum thickness contour line |
The pyramidal equation usually provides the most accurate results; however, because of its simplicity, the trapezoidal equation is commonly used. Since the trapezoidal equation introduces an error of about 2 percent where the ratio of successive areas is 0.5, a common convention is used to employ both equations. Wherever the ratio of the areas within any two successive isochore lines is smaller than 0.5, the pyramidal equation is applied. Wherever the ratio of the areas within any two successive isochore lines is larger than 0.5, the trapezoidal equation is used. Computer programs, for calculating reservoir volumes from net pay maps, are capable of combining the pyramidal and trapezoidal equations in the manner described. However, the programs may vary in the cutoff ratio that is used, so that ratio for a given program should be determined by the user.
Figure 14-40 and Table 14-1 outline the volume determination using the horizontal slice method. Take a few minutes and review this example to obtain a good understanding of the procedure.
Table 14-1.
Area | Planimeter Area Sq. In. | Area Acres | Ratio of Areas | Interval H Feet | Equation | ΔV Ac. Ft. |
|---|---|---|---|---|---|---|
A0 | 19.64 | 450 | – | – | – | – |
A1 | 16.34 | 375 | 0.83 | 5 | Trapezoid | 2063 |
A2 | 13.19 | 303 | 0.80 | 5 | Trapezoid | 1695 |
A3 | 10.05 | 231 | 0.76 | 5 | Trapezoid | 1335 |
A4 | 6.69 | 154 | 0.67 | 5 | Trapezoid | 963 |
A5 | 3.22 | 74 | 0.48 | 5 | Pyramid | 558 |
A6 | 0.00 | 0 | 0.00 | 4 | Pyramid | 99 |
------- | ||||||
Total ac. ft. | 6713[*] | |||||
[*] The percentage difference in acre-feet between the horizontal and vertical slice methods is less than 1%. | ||||||
The vertical slice method sums the volumes of vertical slices through the depicted reservoir volume (Fig. 14-41). The method is sometimes referred to as the donut method because the individual areas used to determine the reservoir volume fall between successive contour lines and commonly appear to be donut-shaped. Many people consider this method to be less confusing than the horizontal slice method, particularly if isochore maps have a number of thick and thin areas. The equation for the vertical slice method is
where
h | = | Average thickness between successive contour lines |
A0 | = | Zero contour line |
A1 | = | Next higher value, or next successive, contour line |
An | = | Highest value contour line |
havg | = | Average thickness within An |
Figure 14-41 and Table 14-2 illustrate the procedure for volume determinations using the vertical slice method. The reservoir used for this example is the same one used for the horizontal slice method (Fig. 14-40), so the results can be compared. The difference in calculated volume between the horizontal and vertical slice methods, for the example in Figs. 14-40 and 14-41, is less than 1 percent.
Table 14-2.
Area | Planimeter Area Sq. In. | Area Acres | Difference in Areas An-1 – An | Average Thickness Feet | V Ac. Ft. |
|---|---|---|---|---|---|
A0 | 19.64 | 450 | – | – | – |
A1 | 16.34 | 375 | 75 | 2.5 | 187 |
A2 | 13.19 | 303 | 72 | 7.5 | 540 |
A3 | 10.05 | 231 | 72 | 12.5 | 900 |
A4 | 6.69 | 154 | 77 | 17.5 | 1347 |
A5 | 3.22 | 74 | 80 | 22.5 | 1800 |
A6 | 0.00 | 0 | 74 | 27.0 | 1998 |
-------- | |||||
Total ac. ft. | 6772[*] | ||||
[*] The percentage difference in acre-feet between the horizontal and vertical slice methods is less than 1%. | |||||
The choice of using the horizontal or vertical slice methods is usually based on individual preference, since both methods are reasonably accurate. The choice is less important than the assurance that the method is used correctly, avoiding planimetering pitfalls. It is therefore of utmost importance that anyone doing actual planimetering be thoroughly familiar with the pitfalls that can be encountered when planimetering and with the mathematical programs for volume calculations.
A geoscientist may spend months working on a prospect with the end result being a net pay isochore map prepared to estimate the hydrocarbon volume for the prospect. If the isochore map is planimetered incorrectly, as a result of carelessness or a lack of understanding of the planimetering procedures, a viable project can be mistakenly rejected. We highly recommend that all planimetered work be spot-checked by the geologist or reservoir engineer who prepared the net pay isochore map.
Reservoir engineering must be involved in all phases of oil and gas prospect evaluation from the initial phases of exploration through field development. Prior to any wells being drilled on a prospect, the most likely reservoir engineering parameters must be assumed in a preliminary evaluation to estimate the potential hydrocarbons. Initial drilling provides basic reservoir parameters, but offset information from analogous fields are used to predict the performance of the new discovery. Finally, during the field’s productive life, performance data needs to be constantly evaluated to allow revisions to the original assumptions and to develop and modify the field’s depletion plan. The last phase is especially critical to optimize drainage of recoverable reserves yielding maximum productivity and revenue.
An excellent review of the history of reservoir engineering is found in Craft and Hawkins (1959). One of the major benefits to the geologist of becoming familiar with basic reservoir engineering is to understand what a reservoir engineer requires for the evaluation of hydrocarbon reserves. A list of the symbols, nomenclature, and other pertinent information adopted by the Society of Petroleum Engineers for use in reservoir engineering can be found at the Society’s website (www.spe.org). It is essential for a geologist to become familiar with the basics of petroleum engineering and to work closely with the petroleum engineer to obtain the necessary data to evaluate hydrocarbon reserves.
After the identification of hydrocarbons in a permeable stratigraphic unit, a plan must be established to estimate the in-place volumes of these hydrocarbons and what might be expected to be recovered. Recoverable hydrocarbons are referred to as hydrocarbon reserves. Because the productive characteristics of a reservoir or field may not be fully known until it is maturely developed, offset analogous reservoirs need to be considered as models to the development of any new discovery. With a model to follow, various reservoir-engineering parameters such as reservoir porosity, permeability, and water saturation can be estimated to allow volumetric analyses of the reservoir or field to estimate potentially recoverable reserves.
Reservoir bulk volume is calculated from net hydrocarbon isochore maps, as discussed in Chapter 10. From detailed log analysis, rock properties can be identified. As an example, interstitial water saturation must be estimated for reserve determinations. Detailed reservoir petrophysics for use in calculating reserves is beyond the scope of this book; however, a presentation of general reservoir engineering may be helpful, and it is outlined here.
Using the letter symbols G and N, initial in-place volumes of oil and gas can be determined by the following equations.
and
where
G | = | original gas-in-place, in cu ft |
N | = | original oil-in-place, in barrels |
φ | = | effective porosity, fraction |
Swi | = | interstitial water saturation, fraction |
B | = | formation volume factor, dimensionless |
43,560 | = | cu ft per acre-foot |
7758 | = | barrels per acre-foot |
subscript o | = | oil-bearing zone |
subscript g | = | gas-bearing zone |
Bgi | = | standard cu ft/reservoir cu ft |
Boi | = | reservoir barrels/stock tank barrels |
Equation (14-4) is used to estimate original gas-in-place. There are several unknown factors in the equation that must be determined. The formation volume factor (FVF) is defined as the relationship of gas volumes from surface conditions to reservoir conditions. For gas reservoirs, Bgi is expressed in standard cubic feet per cubic foot, SCF/cu ft. The porosity is expressed as a fraction of the bulk volume, and the interstitial water (Sw) is a fraction of the pore volume.
To determine the unit recovery for a gas reservoir, the final reserve volume per acre-foot is determined based on the reservoir drive mechanism. This fractional recovery, or recovery factor, represents the difference between the initial unit-in-place gas and the final, or abandonment, unit-in-place gas.
or
where
Bgi | = | formation volume factor at initial conditions |
Bga | = | formation volume factor at abandonment conditions |
This recovery factor is indicative of depletion drive reservoirs, where interstitial water saturation remains unchanged and, conversely, gas saturation remains constant. The other end of the spectrum with regard to drive mechanisms is a strong water drive, where produced gas is being replaced by encroaching water (there is no appreciable pressure loss and Bgi= Bga). The recovery factor for a water-drive gas reservoir, which is representative of the change in gas and water saturations in the reservoir due to production, is shown in the following equation.
where
Swi | = | interstitial water saturation, fraction |
Sgr | = | residual gas saturation, fraction |
Oil reservoirs are often more difficult to analyze for a number of reasons, including the presence in some reservoirs of both oil and gas. If an oil reservoir is found without free gas, the oil is said to be undersaturated. An oil reservoir with a free gas cap is indicative of a saturated oil reservoir.
Equation (14-5) is used to volumetrically determine original oil-in-place. The variables in Eq. (14-5) are very similar to those discussed for Eq. (14-4). If we consider an undersaturated oil reservoir under a strong water drive, the recovery factor is based on the following equation.
where
Sor = residual oil saturation, decimal
Where there is an initial gas cap, the oil is saturated. In such cases, the reservoir can be produced under drive mechanisms other than water drive. These include dissolved gas, gas cap, or a combination drive. The opposite end of the recovery factor spectrum from a water drive reservoir is that of a dissolved gas drive reservoir.
where
Swi | = | interstitial water saturation, fraction |
Sga | = | gas saturation at abandonment, fraction |
Boi | = | initial formation volume factor |
Boa | = | formation volume factor at abandonment |
RF | = | recovery factory, percent |
Once reservoir or field production has been established and sufficient quantities of hydrocarbons produced, performance data can be used to estimate original and remaining reserves, and to forecast future performance. It is good practice to monitor both production and reservoir pressure data. These points of reference are invaluable in evaluating reservoir heterogeneities and are applicable to material balance equations.
Various performance curves can be used to evaluate reserves and forecast future production trends. The most common performance curves are those which plot the production of oil, gas, and water versus time. In many instances, performance evaluation is by far the most accurate method for estimating the original in-place volume of hydrocarbons, estimating recoverable reserves, and forecasting future performance. The following is a partial list of the types of performance curves that can be plotted.
Monthly production (oil or gas) versus time
Flowing tubing pressure versus time
Bottom-hole pressure data versus cumulative production
Percent oil cut versus cumulative production
Water yield versus cumulative gas production
A detailed discussion of these performance curves is beyond the scope of this book. We again refer you to Craft and Hawkins (1959).
As discussed in the beginning of this chapter, an isopach map is one in which the true stratigraphic thickness of a single stratigraphic interval is contoured, such as a stratigraphic unit or an interval between two stratigraphic markers. Such a map is referred to as an interval isopach map. Interval isopach maps are particularly useful in determining the history of movement along faults and of development of growth structures, such as salt dome structures and folds, as well as being useful in the interpretation of depositional environments and paleostructures.
The full application of interval isopach maps is beyond the scope of this text. More specifically, we address the determination and use of the proper interval thicknesses obtained from well logs or seismic data to be used for construction of interval isopach maps. Interval isopach maps reveal the true stratigraphic thicknesses of units rather than vertical thicknesses. The TST is the thickness measured perpendicular to the top and base of the stratigraphic interval. Where strata have no dip or have only gentle dips, TST equals or approximates TVT. But with increasing dip, the differences become substantial and a correction factor is applied to TVT to obtain TST. The relationship is given as
where
TST | = | true stratigraphic thickness |
TVT | = | true vertical thickness |
φ | = | true bed dip |
For example, with a 10-deg bed dip, an interval with a TST of 100 ft has a vertical thickness of 101.5 ft; at a 20-deg dip, the vertical thickness is 106.5 ft. At a 45-deg dip, however, the vertical thickness becomes 141 ft, which is significantly different than the stratigraphic thickness. If the true vertical thickness is the value contoured, the map is more correctly referred to as an isochore map. Therefore, net sand and net pay maps are isochore maps.
The determination of stratigraphic thickness from well logs presents a few complications. In areas of nearly flat-lying beds, the TVT approximates TST. The determination of stratigraphic thickness does, however, become more complicated around steeply dipping structures. Figure 14-42 shows the effect of changing bed dip on vertical well log thickness of a stratigraphic unit whose TST is constant. With zero bed dip, TVT equals TST. At a 20-deg bed dip, the TVT is only 1.06 times TST. At a 40-deg bed dip, the TVT is equal to 1.30 times TST, and at 60 deg, the TVT is twice as thick as the TST. Assuming vertical wells, if the upper and lower markers chosen for interval isopaching are parallel or nearly so (that is, they are at or near the same dip), Eq. (14-10) can be used to convert vertical thickness to stratigraphic thickness.
If the thickness of the interval changes, and thus the dips of the upper and lower surfaces of the interval are different, then the correction factor based on the cosine of a single bed dip, either at the upper surface or lower surface, will not be accurate. For such cases, another equation is required (Tearpock and Harris 1987).
where
TST | = | true stratigraphic thickness |
TVT | = | true vertical thickness |
α | = | dip of upper horizon |
φ | = | dip of lower horizon |
Figure 14-43 shows the equation and an example problem. This equation takes into account the dip of the upper and lower surfaces and the vertical thickness of the interval.
Finally, in the case of deviated wells, the measured log thickness must be first corrected to TVT, and then corrected to TST. The procedure for vertical thickness conversions is discussed in this chapter and in Chapter 4.
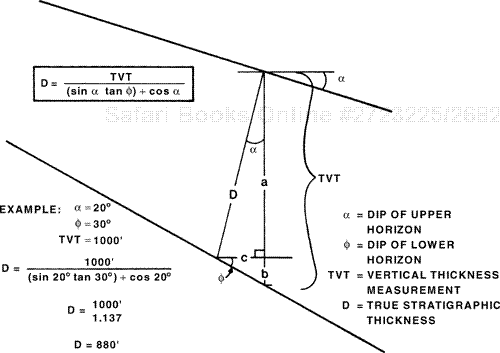
(Prepared by C. Harmon. Modifiedfrom Tearpock and Harris 1987. Published by permission of Tenneco OilCompany.)
Figure 14-43. Cross section showing the geometric relationship between two horizons that have different angles of dip. Equation (14-11) is used in this typeof situation to convert TVT to TST.
To avoid making laborious stratigraphic thickness calculations, the graph in Fig. 14-44 can be used to calculate TST if the vertical thickness and the dips of the upper and lower surfaces are known. The horizontal axis represents the dip of the upper surface, and the vertical axis represents the correction factor. The curves within the graph represent the values obtained by subtracting the dip of the upper surface from the dip of the lower surface (note positive and negative values). Consider the following example.
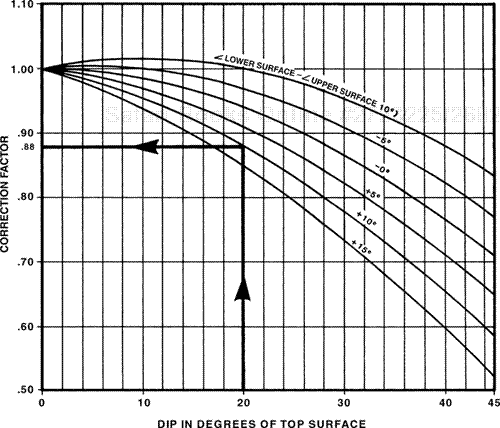
(Prepared by C. Harmon. From Tearpock and Harris 1987. Published by permission of Tenneco Oil Company.)
Figure 14-44. Graph derived from Eq. (14-11) and used to determine the correction factor for converting TVT of a stratigraphic interval to TST, where the upper and lower surfaces dip at different angles.
Data:
Dip of upper surface | = | 20 deg |
Dip of lowersurface | = | 30 deg |
TVT | = | 1000 ft |
To use the graph, first subtract the dip of the upper surface from the lower surface. This value determines which of the curved lines to use for the correction factor.
Enter the graph on the horizontal axis at 20 deg and project vertically until the line intersects the curve with value equal to the dip of the lower surface minus the dip of the upper surface. In this case, it is the +10-deg curve.
From the intersection with the curve, project horizontally to the left to intersect the vertical axis and determine the correction factor. In this case, it is 0.88.
Therefore,
TST | = | (1000 ft)(0.88) |
TST | = | 880 ft |
Using seismic data for interval isopach construction can give you many additional data points between well control. In areas of relatively low dip (10 deg or less) and parallel horizons, the TVT calculated from seismic is a close approximation of the TST. The procedure in this type of area is straightforward: The time-converted depth of the upper horizon is subtracted from the time-converted depth of the lower horizon to arrive at an interval thickness. The basic requirement is an accurate time–depth function.
In areas of steeper dip and nonparallel horizons, you should be aware of some visual pitfalls inherent in seismic sections. The basic point to remember is that a time section is not a cross section. It is distorted due to the two very different dimensions displayed on a section: time along the vertical axis and distance along the horizontal axis. These dimensional differences often introduce some very pronounced vertical exaggeration.
To illustrate this, observe the two horizons indicated in Fig. 14-45a. They obviously diverge from one another as the interval thickens into a fault. How do we determine the TST of the interval? The first inclination is to draw a perpendicular line, shown as A on the figure, from the top horizon to intersect the bottom horizon, and calculate trigonometrically the stratigraphic thickness using the time-converted depths at both points, along with the lateral distance between the two points. THIS IS WRONG.

(Prepared by C. Harmon. From Tearpock and Harris 1987. Published by permission of Tenneco Oil Company.)
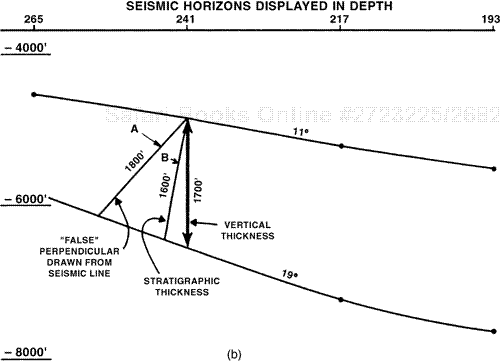
Figure 14-45. (a) Which line, A or B, represents the true stratigraphic thickness of the designated interval? (b) True (1:1 scale) cross section of the seismic interval shown in (a).
To see graphically what is actually present, look at Fig. 14-45b, which shows the horizons converted to depth and displayed at a true 1:1 scale. Line A, drawn earlier as perpendicular to the top horizon on the seismic line, is in fact a longer segment than the true perpendicular, which is line B on the seismic line and cross section. The reason for this pitfall is that the seismic line, at this depth, has about a 2:1 vertical exaggeration. In this case, you would post a larger thickness for the interval than is actually present. To obtain corrected data points, you need to apply Eq. (14-11), which uses the dip of the top and bottom horizons, and the vertical thickness of the interval. The graph in Fig. 14-44 can also be used to determine the stratigraphic thickness.
In summary, seismic information can be a valuable source of interval thickness data, as long as you are aware of the visual distortion inherent in seismic data and properly account for it in the calculation of stratigraphic thicknesses.